1

10. Ruch płaski ciała sztywnego

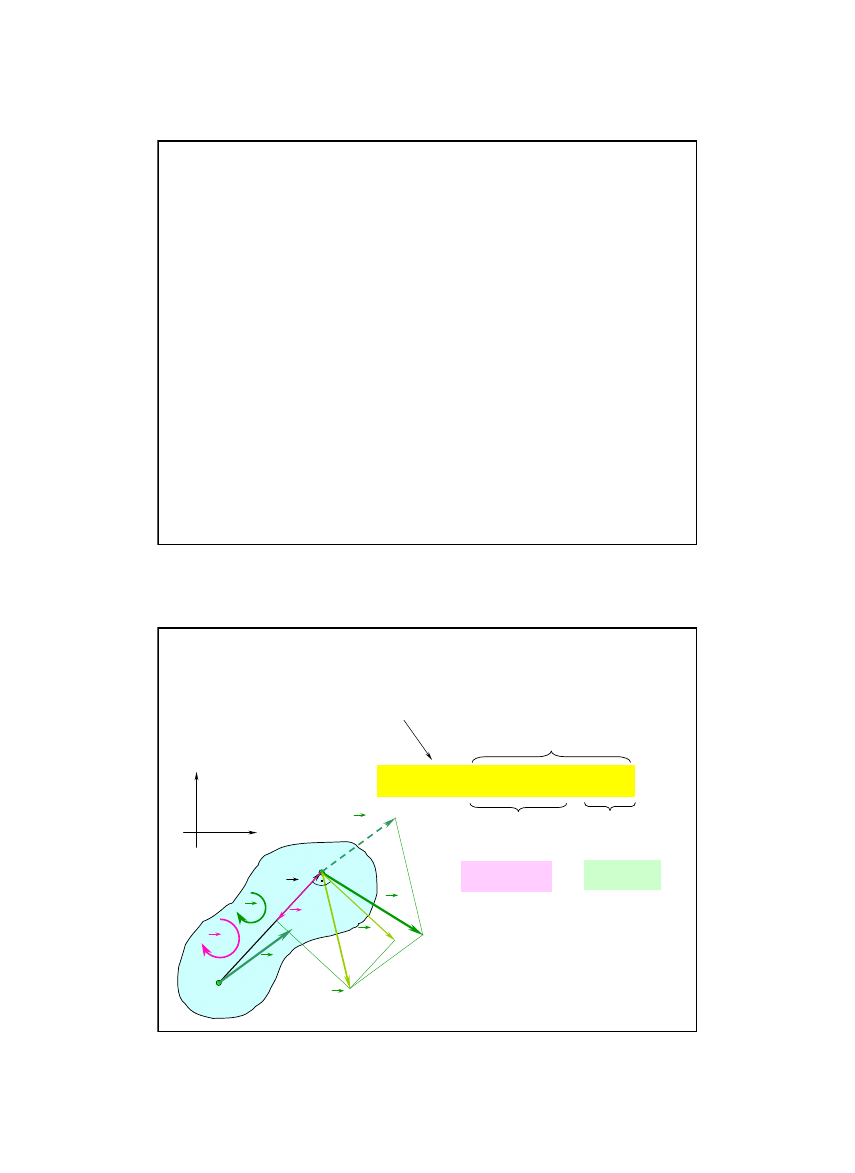
2. Przyspieszenie w ruchu płaskim

A

a

A

ω

x

y

O

ρ

B

a

B

a

B/A

Metody wyznaczania przyspieszenia w ruchu płaskim

1. Analityczna

Dane: a

A

,

ω

ω

ω

ω, εεεε

Szukane: a

B

(

)

ρ

ε

ρ

ω

ω

r

r

r

r

r

r

r

×

+

×

×

+

=

A

B

a

a

ε

a

A

przyspieszenie punktu B

względem bieguna A

n

A

B

a

/

r

t

A

B

a

/

r

normalne

(dośrodkowe)

styczne

ρ

ω

2

/

=

n

A

B

a

ερ

=

t

A

B

a

/

a

B/A

n

a

B/A

t

A

B

a

/

r

przyspieszenie

bieguna A

2

A

a

A

x

y

O

B

ω

s

a

a

B

ϕ

ϕ

ρ

A

ρ

B

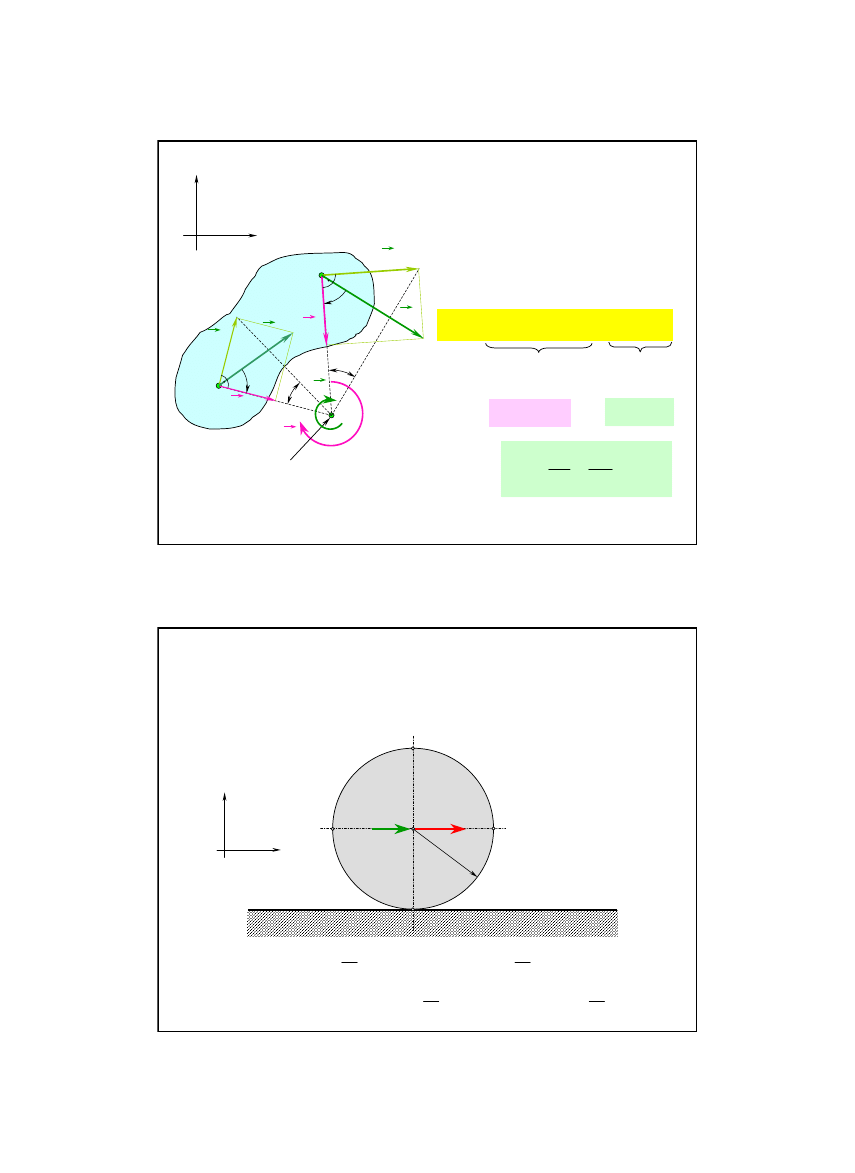
Metody wyznaczania przyspieszenia w ruchu płaskim

2. Na podstawie położenia

chwilowego środka przyspieszeń

Dane: położenie s

a

Szukane: a

A

chwilowy środek przyspieszeń

punkt związany (również myślowo) z ciałem,

którego

przyspieszenie

w danej chwili

równe jest zeru

ε

a

A

n

a

A

t

a

B

n

a

B

t

α

α

(

)

A

A

A

a

ρ

ε

ρ

ω

ω

r

r

r

r

r

r

×

+

×

×

=

n

A

a

r

t
A

a

r

normalne

(dośrodkowe)

styczne

A

n
A

a

ρ

ω

2

=

A

t
A

a

ερ

=

const

a

a

tg

n
A

t
A

=

=

=

2

ω

ε

α

Zadanie 1/10-2
Wyznaczyć przyspieszenie punktów

A

,

B

,

C

i

D

toczącego się bez

poślizgu krążka o promieniu

r

. Dana jest prędkość środka krążka

υ

O

oraz przyspieszenie

a

O

.

υ

O

A

B

C

D

r

O

a

O

r

a

a

a

r

a

a

a

a

r

a

a

a

a

r

a

a

Dy

Cy

By

Ay

Dx

Cx

Bx

Ax

2

0

0

2

0

0

2

0

0

0

2

0

0

0

2

υ

υ

υ

υ

=

−

=

−

=

=

=

−

=

=

+

=

x

y

Odp.:

3

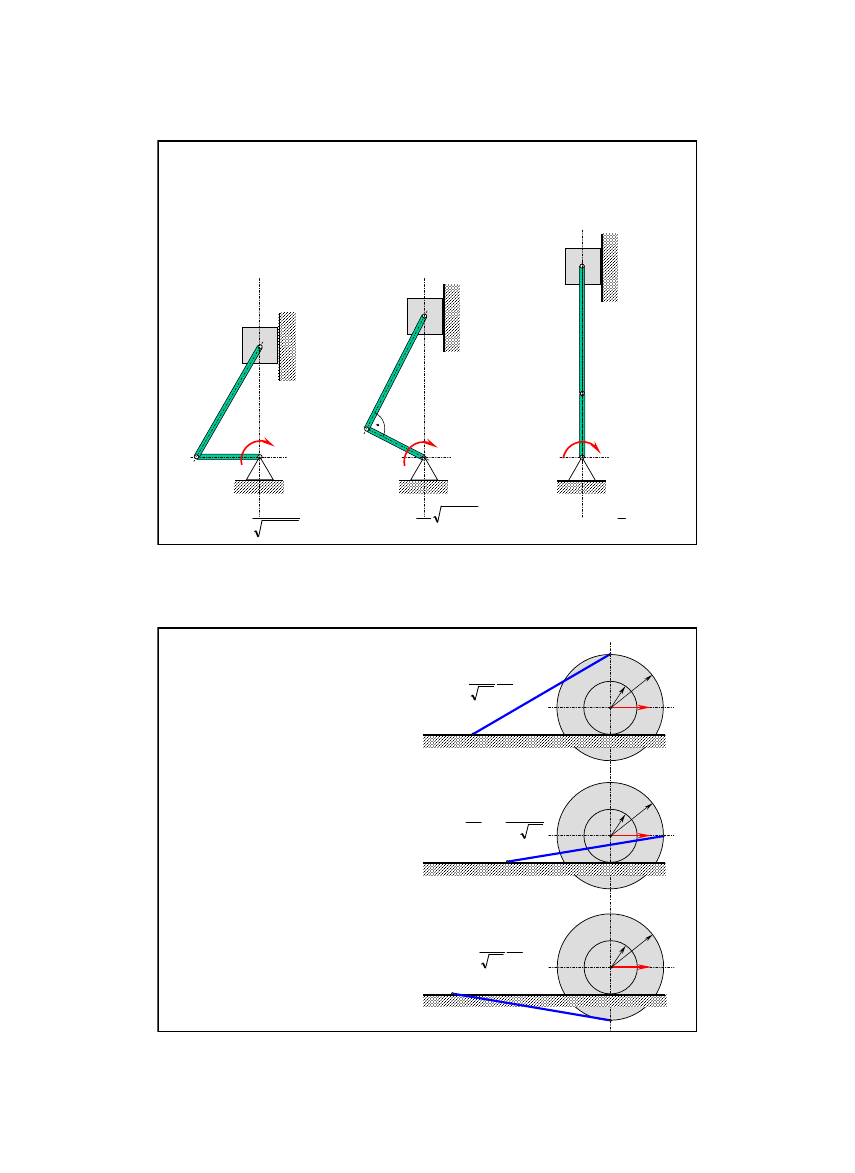
Zadanie 2/10-2
W mechanizmie korbowym korba

OA

o długości

r

obraca się ze stałą

prędkością kątową

ω

0

wokół nieruchomej osi. Wyznaczyć przyspie-

szenie suwaka

B

w położeniach mechanizmu pokazanych na rysunku.

Długość korbowodu

AB

równa jest

l

.

O

A

r

ω

0

l

B

B

A

r

l

O

ω

0

B

A

r

l

O

ω

0

a

)

c

)

b

)

2

2

2

2

0

r

l

r

a

B

−

=

ω

2

2

4

4

2

0

r

l

l

r

a

B

+

−

=

ω

Odp.:













+

−

=

l

r

r

a

B

1

2

0

ω

dodatnie

w górę

Zadanie 3/10-2
Szpula o promieniach

r

i 2

r

toczy się bez poślizgu po
prostej.

Prędkość

ś

rodka

szpuli jest stała i wynosi

υ

0

.

Ze szpulą

związany jest

przegubowo

pręt

AB

o

długości

6r

, którego koniec

B

ś

lizga się po wspomnianej

prostej.

Wyznaczyć

przyspieszenie

końca

B

pręta w położeniach

pokazanych na rysunku.

r

2

r

υ

0

a

)

c

)

b

)

r

2

r

υ

0

r

2

r

υ

0

A

B

A

6

r

B

A

B

r

a

B

2

0

27

6

υ

−

=

r

a

B

2

0

35

2

υ

−

=













−

−

=

35

35

72

1

2

2

0

r

a

B

υ

Odp.: - dodatnie w prawo

4

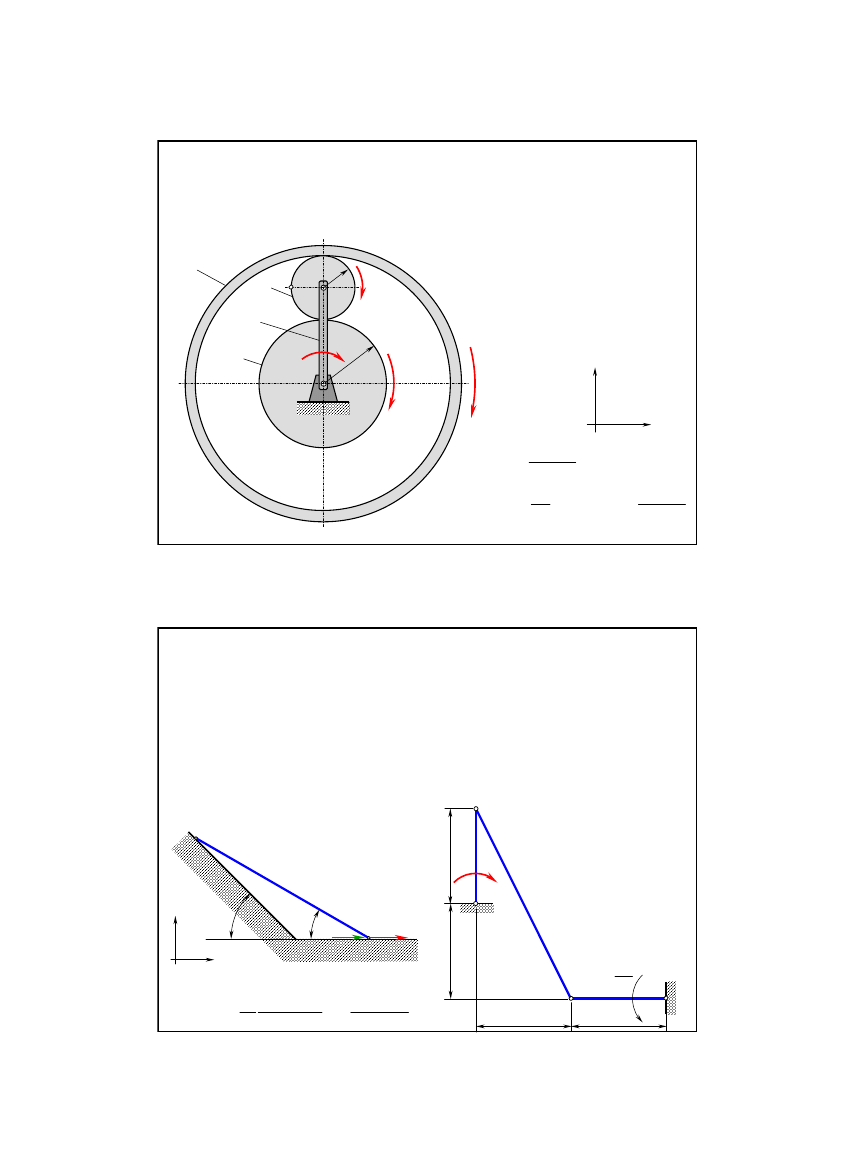
Zadanie 4/10-2
Mechanizm planetarny składa się z koła centralnego

1

o promieniu

r

1

, satelity

2

o promieniu

r

2

, jarzma

3

oraz koła zewnętrznego

4

.

Podane prędkości kątowe są
stałe. Obliczyć przyspieszenie
punktu A w przypadkach:

a)

ω

1

=0

ω

3

=

ω

0

b)

ω

1

=

ω

0

ω

4

=0

r

1

r

2

O

1

O

2

1

2

3

4

ω

1

ω

2

ω

4

ω

3

A

Odp.:

x

y

(

)

(

)

2

1

2

0

2

2

2

1

2

0

r

r

a

r

r

r

a

Ay

Ax

+

−

=

+

=

ω

ω

(

)

2

1

2

1

2

0

2

2

1

2

0

4

4

r

r

r

a

r

r

a

Ay

Ax

+

−

=

=

ω

ω

a)

b)

Zadanie 5/10-2
Pręt

AB

o długości

l

ś

lizga się

po dwóch prostych nachylo-
nych pod kątem

α

=45°.

Wyznaczyć przyspieszenie

końca

B

jeśli pręt tworzy z

prostą poziomą kąt

β

=30° zaś

prędkość końca

A

wynosi

υ

A

a jego przyspieszenie

a

A

.

α

β

B

A

υ

A

l

a

A

Zadanie 6/10-2
Mechanizm składa się z 3 prę-
tów połączonych przegubowo.
Pręty

O

1

A

oraz

O

2

B

mogą obra-

cać się wokół nieruchomych osi

O

1

i

O

2

. Pręt

O

1

A

obraca się ze

stałą prędkością kątową

ω

0

.

O

1

O

2

A

B

a

a

a

a

ω

0

Wyznaczyć przyspieszenie

kątowe pręta

O

2

B

.

(

)

(

)

β

α

β

β

α

α

υ

α

α

−

+

−

=

−

=

=

cos

cos

cos

sin

sin

cos

3

2

2

A

A

B

B

By

B

Bx

a

l

a

a

a

a

a

Odp.:

x

y

4

2

0

2

ω

ε

=

B

O