
FUNKCJE ANALITYCZNE
JEDNOSEMESTRALNY WYKÃLAD DLA SEKCJI NIETEORETYCZNYCH
INSTYTUT MATEMATYKI UJ, 2008
Zbigniew BÃlocki
Spis tre´sci
1. Podstawowe wÃlasno´sci liczb zespolonych
2
2. R´o˙zniczkowanie funkcji zespolonych
5
3. CaÃlkowanie funkcji zespolonych
9
4. Twierdzenie caÃlkowe Cauchy’ego
11
5. Wz´or caÃlkowy Cauchy’ego
14
6. Podstawowe wÃlasno´sci funkcji holomorficznych
15
7. Szeregi pot
,
egowe
17
8. Podstawowe wÃlasno´sci funkcji holomorficznych, cd.
19
9. Funkcje analityczne
21
10. Globalne twierdzenie caÃlkowe Cauchy’ego
22
11. Szeregi Laurenta
25
12. Osobliwo´sci funkcji holomorficznych
27
13. Twierdzenie o residuach
29
13a. Obliczanie pewnych caÃlek rzeczywistych
30
14. Lokalizowanie zer funkcji holomorficznych
34
15. Odwzorowania konforemne
36
16. Sfera Riemanna
39
17. Funkcje harmoniczne
40
18. Iloczyny niesko´
nczone
43
19. Funkcja ζ Riemanna
46
20. Rodziny normalne, iteracja funkcji wymiernych
48
Literatura
51
Zagadnienia na egzamin ustny
52
Typeset by AMS-TEX

2
ZBIGNIEW BÃLOCKI
1. Podstawowe wÃlasno´sci liczb zespolonych
Liczb
,
a zespolon
,
a nazywamy par
,
e liczb rzeczywistych, zbi´or liczb zespolonych C
to zatem dokÃladnie zbi´or R
2
. Element z = (x, y) ∈ C zapisujemy w postaci x + iy.
Na zbiorze C wprowadzamy mno˙zenie (zgodnie z reguÃl
,
a i
2
= −1):
(x
1
+ iy
1
)(x
2
+ iy
2
) = x
1
x
2
− y
1
y
2
+ i(x
2
y
1
+ x
1
y
2
).
Mo˙zna Ãlatwo pokaza´c
´
Cwiczenie
, ˙ze C z dodawaniem wektorowym w R
2
oraz
tak wprowadzonym mno˙zeniem jest ciaÃlem. Je˙zeli z = x + iy, to x nazywamy
cz
,
e´sci
,
a rzeczywist
,
a, natomiast y cz
,
e´sci
,
a urojon
,
a liczby z; ozn. x = Re z, y = Im z.
Ka˙zd
,
a liczb
,
e zespolon
,
a z mo˙zemy r´owie˙z zapisa´c przy pomocy wsp´oÃlrz
,
ednych bie-
gunowych:
z = r(cos ϕ + i sin ϕ),
gdzie r = |z| =
p
x
2
+ y
2
, za´s ϕ jest k
,
atem pomi
,
edzy odcinkami [0, 1] i [0, z]
(gdy z 6= 0) - nazywamy go argumentem liczby z. Zachodzi oczywi´scie nier´owno´s´c
tr´ojk
,
ata
|z + w| ≤ |z| + |w|,
z, w ∈ C,
mo˙zna r´ownie˙z Ãlatwo pokaza´c
´
Cwiczenie
, ˙ze
|zw| = |z| |w|,
z, w ∈ C.
Chcemy teraz zdefiniowa´c zespolon
,
a funkcj
,
e wykÃladnicz
,
a exp : C → C. Dla
z = x + iy ∈ C oczekujemy, ˙ze e
z
= e
x
e
iy
, czyli wystarczy okre´sli´c e
it
dla t ∈ R.
Chcemy by funkcja ta speÃlniaÃla
d
dt
e
it
= ie
it
,
e
0
= 1,
a wi
,
ec (oznaczaj
,
ac e
it
= A + iB) A
0
= −B, B
0
= A, A(0) = 1, B(0) = 0. Jedynym
rozwi
,
azaniem tego ukÃladu s
,
a funkcje A = cos t, B = sin t. Funkcj
,
e wykÃladnicz
,
a
definiujemy zatem nast
,
epuj
,
aco:
e
z
:= e
x
(cos y + i sin y),
z = x + iy ∈ C.
Mo˙zna Ãlatwo pokaza´c
´
Cwiczenie
jej nast
,
epuj
,
ace wÃlasno´sci
e
z+w
= e
z
e
w
,
z, w ∈ C,
d
dt
e
tz
= ze
tz
,
t ∈ R, z ∈ C.
Z faktu, ˙ze |e
z
| = e
x
oraz dzi
,
eki temu, ˙ze y jest argumentem liczby e
z
wynika, ˙ze
funkcja wykÃladnicza proste pionowe x = x
0
odwzorowuje na okr
,
egi o promieniu e
x
0
,
natomiast proste poziome y = y
0
na p´oÃlproste otwarte o pocz
,
atku w 0 o argumencie
y
0
.
Wracaj
,
ac do wsp´oÃlrz
,
ednych biegunowych, mo˙zemy je teraz zapisa´c w postaci
z = re
iϕ
. Dla z 6= 0 przez arg z oznaczamy zbi´or argument´ow liczby z, tzn.
arg z := {ϕ ∈ R : z = |z|e
iϕ
}.

FUNKCJE ANALITYCZNE
3
Poniewa˙z e
i(ϕ+2π)
= e
iϕ
, dla dowolnego ϕ
0
∈ arg z mamy
arg z = {ϕ
0
+ 2kπ : k ∈ Z}.
Dla ka˙zdego z ∈ C
∗
(:= C \ {0}) znajdziemy dokÃladnie jeden element arg z nale˙z
,
acy
do przedziaÃlu [−π, π). Nazywamy go argumentem gÃl´ownym liczby z i oznaczamy
Arg z. Funkcja Arg , okre´slona na C
∗
, jest nieci
,
agÃla na p´oÃlprostej (−∞, 0).
Mo˙zemy teraz poda´c geometryczn
,
a interpretacj
,
e mno˙zenia w C: je˙zeli z = re
iϕ
,
w = ρe
iψ
, to zw = rρe
i(ϕ+ψ)
; czyli mno˙zymy dÃlugo´sci, a dodajemy argumenty.
Mo˙zemy st
,
ad r´ownie˙z wywnioskowa´c wz´or de Moivre’a: z tego, ˙ze (e
iϕ
)
n
= e
inϕ
otrzymamy
(cos ϕ + i sin ϕ)
n
= cos(nϕ) + i sin(nϕ),
ϕ ∈ R, n ∈ N.
Dla danego z ∈ C oraz n ∈ N przez pierwiastek z stopnia n rozumiemy zbi´or
n
√
z := {w ∈ C : w
n
= z}.
Zapisuj
,
ac z i w we wsp´oÃlrz
,
ednych biegunowych:
z = re
iϕ
,
w = ρe
iψ
,
otrzymamy warunki
ρ = r
1/n
,
ψ =
ϕ + 2kπ
n
, k ∈ Z.
Poniewa˙z e
iψ
= e
i(ψ+2π)
, dla k = 0, 1, . . . , n − 1 otrzymamy wszystkie rozwi
,
azania.
Zatem
n
√
z = {|z|
1/n
e
i(ϕ+2kπ)/n
: k = 0, 1, . . . , n − 1}.
W szczeg´olno´sci, pierwiastek stopnia n z liczby niezerowej jest zawsze zbiorem n
elementowym.
´
Cwiczenie
Udowodni´c, ˙ze rozwi
,
azaniem r´ownania kwadratowego w C:
az
2
+ bz + c = 0,
gdzie a ∈ C
∗
, b, c ∈ C, jest
z =
−b +
√
∆
2a
,
gdzie ∆ = b
2
− 4ac, przy czym
√
∆ jest zbiorem dwuelementowym je˙zeli ∆ 6= 0 - w
tym przypadku zawsze otrzymamy dwa rozwi
,
azania (jedno je˙zeli ∆ = 0).
W przypadku wielomian´ow dowolnego stopnia mamy rezultat niekonstruktywny,
tzw. zasadnicze twierdzenie algebry.
Twierdzenie 1.1. Ka˙zdy niestaÃly wielomian zespolony ma pierwiastek.
Powy˙zszy rezultat mo˙zna udowodni´c w spos´ob elementarny przy pomocy lematu
d’Alemberta (oryginalny dow´od z 1746 r. zawieraÃl luk
,
e):
Lemat 1.2. ZaÃl´o˙zmy, ˙ze P jest niestaÃlym wielomianem zespolonym oraz, ˙ze dla
pewnego z
0
∈ C mamy P (z
0
) 6= 0. Wtedy dla ka˙zdego otoczenia U punktu z
0
znajdziemy z ∈ U takie, ˙ze |P (z)| < |P (z
0
)|.

4
ZBIGNIEW BÃLOCKI
Dow´od. (Argand, 1806) Niech
P (z) = a
0
+ a
1
z + · · · + a
n
z
n
.
Wtedy
P (z
0
+ h) = a
0
+ a
1
(z
0
+ h) + · · · + a
n
(z
0
+ h)
n
= P (z
0
) + A
1
h + · · · + A
n
h
n
,
gdzie wsp´oÃlczynniki A
j
zale˙z
,
a tylko od P i z
0
. Kt´ory´s z nich na pewno nie znika,
gdy˙z w przeciwnym wypadku wielomian P byÃlby staÃly. Niech j b
,
edzie najmniej-
szym indeksem, dla kt´orego A
j
6= 0. Mamy zatem
P (z
0
+ h) = P (z
0
) + A
j
h
j
+ R(h),
gdzie
|R(h)| < |A
j
h
j
|,
gdy |h| jest odp. maÃle, h 6= 0. Mo˙zemy znale´z´c h o dowolnie maÃlym |h|, dla kt´orego
A
j
h
j
ma argument przeciwny do argumentu P (z
0
). Wtedy
|P (z
0
+ h)| ≤ |P (z
0
) + A
j
h
j
| + |R(h)| = |P (z
0
)| − |A
j
h
j
| + |R(h)| < |P (z
0
)|.
¤
Dow´od Twierdzenia 1.1. Oznaczaj
,
ac P jak w dowodzie Lematu 1.2 i zakÃladaj
,
ac,
˙ze a
n
6= 0, mamy
|P (z)| ≥ |a
n
| |z|
n
− |a
0
+ a
1
z + · · · + a
n−1
z
n−1
|
≥ |a
n
| |z|
n
− |a
0
| − |a
1
| |z| − · · · − |a
n−1
| |z|
n−1
.
Mo˙zemy w szczeg´olno´sci znale´z´c R > 0 takie, ˙ze |P (z)| > |P (0)|, gdy |z| = R.
Funkcja |P | jest ci
,
agÃla na C (bo oczywiste jest, ˙ze mno˙zenie jest odwzorowaniem
ci
,
agÃlym), znajdziemy zatem z
0
∈ K(0, R) takie, ˙ze
|P (z
0
)| = min
K(0,R)
|P |.
Je˙zeli P (z
0
) 6= 0, to dzi
,
eki Lematowi 1.2 znajdziemy z ∈ K(0, R) takie, ˙ze |P (z)| <
|P (z
0
)| - sprzeczno´s´c. ¤
Dla z ∈ C
∗
definiujemy
log z := {w ∈ C : e
w
= z}
(dla z = 0 ten zbi´or jest oczywi´scie pusty). Je˙zeli zapiszemy w = η + iξ, z = re
iϕ
,
to otrzymamy r´ownanie e
η
e
iξ
= re
iϕ
. Zatem η = log r = log |z|, natomiast ξ =
ϕ + 2kπ, k ∈ Z. Ostatecznie
log z = log |z| + iarg z.
Liczb
,
e
Log z := log |z| + iArg z
FUNKCJE ANALITYCZNE
5
nazywamy logarytmem gÃl´ownym z.
Przy pomocy logarytmu mo˙zemy zdefiniowa´c pot
,
egi zespolone: dla z ∈ C
∗
,
w ∈ C kÃladziemy
z
w
= e
w log z
.
Zauwa˙zmy, ˙ze
z
1/n
= e
1
n
(log |z|+iarg z)
= |z|
1/n
e
i
arg z
n
,
czyli otrzymamy to samo, co przy definicji pierwiastka.
´
Cwiczenie
Obliczy´c i
i
.
Przypomnijmy, ˙ze
e
iϕ
= cos ϕ + i sin ϕ,
ϕ ∈ R.
Zespolone funkcje trygonometryczne mo˙zna Ãlatwo wyprowadzi´c ze wzor´ow Eulera:
e
iz
= cos z + i sin z,
e
−iz
= cos z − i sin z.
St
,
ad
cos z :=
e
iz
+ e
−iz
2
,
sin z :=
e
iz
− e
−iz
2i
.
Mamy r´ownie˙z
cosh z := cos(iz) =
e
z
+ e
−z
2
,
sinh z := −i sin(iz) =
e
z
− e
−z
2
.
´
Cwiczenie
Pokaza´c, ˙ze arccos z = −i log(z +
√
z
2
− 1).
Dla liczby zespolonej z = x + iy definiujemy jej sprz
,
e˙zenie: z := x − iy. Natych-
miast otrzymujemy, ˙ze
|z|
2
= zz.
´
Cwiczenie
Pokaza´c, ˙ze (zw) = z w oraz e
z
= e
z
.
2. R´
o˙zniczkowanie funkcji zespolonych
Oczywi´scie ka˙zde odwzorowanie liniowe C → C jest postaci
(2.1)
C 3 z 7−→ az ∈ C
dla pewnego a ∈ C. Poniewa˙z C = R
2
, mo˙zemy r´ownie˙z rozpatrywa´c r´ownania
liniowe w sensie rzeczywistym - b
,
ed
,
a one postaci
C = R
2
3 z 7−→ Az 3 R
2
= C,
6
ZBIGNIEW BÃLOCKI
gdzie
(2.2)
A =
µ
p q
s
t
¶
,
p, q, s, t ∈ R.
Takie odwzorowania C → C b
,
edziemy nazywa´c R-liniowymi, natomiast odwzorowa-
nia postaci (2.1) C-liniowymi. Mo˙zna Ãlatwo sprawdzi´c, ˙ze ka˙zde odwzorowanie
C-liniowe jest R-liniowe, przy czym A jest postaci
A =
µ
α −β
β
α
¶
,
gdzie a = α + iβ. Z drugiej strony, dane odwzorowanie R-liniowe jest C-liniowe
wtedy i tylko wtedy, gdy p = t i q = −s w (2.2) (
´
Cwiczenie
).
Niech f b
,
edzie funkcj
,
a o warto´sciach zespolonych okre´slon
,
a w pewnym otoczeniu
punktu z
0
∈ C. Analogicznie jak w przypadku rzeczywistym powiemy, ˙ze f jest
C-r´o˙zniczkowalna w punkcie z
0
, je˙zeli istnieje granica
lim
z→z
0
f (z) − f (z
0
)
z − z
0
∈ C.
Granic
,
e t
,
e nazywamy pochodn
,
a zespolon
,
a funkcji f w z
0
i oznaczamy przez f
0
(z
0
).
Jest oczywiste, ˙ze ka˙zda funkcja C-r´o˙zniczkowalna w z
0
jest w ci
,
agÃla w z
0
. W
podobny spos´ob jak w przypadku rzeczywistym dowodzimy podstawowych wÃlas-
no´sci funkcji C-r´o˙zniczkowalnych.
Propozycja 2.1. Je˙zeli funkcje f, g s
,
a C-r´o˙zniczkowalne w z
0
, to funkcje f ± g,
f g oraz f /g (ta ostatnia pod warunkiem, ˙ze g(z
0
) 6= 0) s
,
a C-r´o˙zniczkowalne w z
0
oraz w z
0
mamy
(f ± g)
0
= f
0
± g
0
,
(f g)
0
= f
0
g + f g
0
,
µ
f
g
¶
0
=
f
0
g − f g
0
g
2
.
¤
Propozycja 2.2. Je˙zeli f jest C-r´o˙zniczkowalna w z
0
, za´s g jest C-r´o˙zniczkowalna
w f (z
0
), to g ◦ f jest C-r´o˙zniczkowalna w z
0
oraz
(g ◦ f )
0
(z
0
) = g
0
(f (z
0
)) f
0
(z
0
).
¤
Przypomnijmy, ˙ze funkcja zespolona f jest r´o˙zniczkowalna w z
0
w klasycznym
sensie (b
,
edziemy wtedy m´owi´c, ˙ze jest ona R-r´o˙zniczkowalna), je˙zeli istnieje odwzo-
rowanie R-liniowe A takie, ˙ze
lim
z→z
0
|f (z) − f (z
0
) − A(z − z
0
)|
|z − z
0
|
= 0.
Je˙zeli f = u + iv, gdzie u, v s
,
a funkcjami rzeczywistymi, to
A =
µ
u
x
(z
0
) u
y
(z
0
)
v
x
(z
0
)
v
y
(z
0
)
¶

FUNKCJE ANALITYCZNE
7
(ozn. u
x
= ∂u/∂x, u
y
= ∂u/∂y). Zauwa˙zmy, ˙ze ka˙zda funkcja C-r´o˙zniczkowalna
jest R-r´o˙zniczkowalna, przy czym
A =
µ
Re f
0
(z
0
) −Im f
0
(z
0
)
Im f
0
(z
0
)
Re f
0
(z
0
)
¶
.
PrzykÃlad. Funkcja f (z) = z, z ∈ C, jest R-r´o˙zniczkowalna w ka˙zdym punkcie (jest
nawet R-liniowa), ale nigdzie nie jest C-r´o˙zniczkowalna: zauwa˙zmy, ˙ze dla t ∈ R
mamy
z − z
0
z − z
0
=
½
1,
je˙zeli z = z
0
+ t,
−1,
je˙zeli z = z
0
+ it,
czyli odpowiednia granica nie istnieje.
ZaÃl´o˙zmy, ˙ze f = u + iv jest R-r´o˙zniczkowalna w z
0
. Oznaczaj
,
ac f
x
= u
x
+ iv
x
,
f
y
= u
y
+ iv
y
mamy
f (z) = f (z
0
) + f
x
(z
0
)(x − x
0
) + f
y
(z
0
)(y − y
0
) + o(|z − z
0
|).
Poniewa˙z
(2.3)
x =
z + z
2
,
y =
z − z
2i
,
otrzymamy
f (z) = f (z
0
) +
f
x
(z
0
) − if
y
(z
0
)
2
(z − z
0
) +
f
x
(z
0
) + if
y
(z
0
)
2
(z − z
0
) + o(|z − z
0
|).
Dla funkcji R-r´o˙zniczkowalnej definiujemy pochodne formalne
(2.4)
∂f
∂z
(= f
z
) :=
1
2
µ
∂f
∂x
− i
∂f
∂y
¶
,
∂f
∂z
(= f
z
) :=
1
2
µ
∂f
∂x
+ i
∂f
∂y
¶
.
Pochodne cz
,
astkowe ∂/∂z i ∂/∂z prowadzi´c mo˙zemy r´ownie˙z przy pomocy formy
df : mamy
f
x
dx + f
y
dy = df = f
z
dz + f
z
dz = f
z
(dx + idy) + f
z
(dx − idy),
a st
,
ad
(2.5)
½
f
x
= f
z
+ f
z
,
f
y
= i(f
z
− f
z
),
sk
,
ad Ãlatwo dostaniemy (2.4).
´
Cwiczenie
Pokaza´c, ˙ze dla dowolnej funkcji R-r´o˙zniczkowalnej f mamy
µ
∂f
∂z
¶
=
∂f
∂z
,
µ
∂f
∂z
¶
=
∂f
∂z
.

8
ZBIGNIEW BÃLOCKI
´
Cwiczenie
Obliczy´c f
z
oraz f
z
, gdzie f (z) = |z|
2
Re (z
8
).
Dla funkcji R-r´o˙zniczkowalnej w z
0
mamy wi
,
ec
f (z) = f (z
0
) + f
z
(z
0
)(z − z
0
) + f
z
(z
0
)(z − z
0
) + o(|z − z
0
|)
oraz, dla z 6= z
0
,
f (z) − f (z
0
)
z − z
0
= f
z
(z
0
) + f
z
(z
0
)
z − z
0
z − z
0
+
o(|z − z
0
|)
z − z
0
.
Wsp´olnie z ostatnim przykÃladem daje to nast
,
epuj
,
ac
,
a charakteryzacj
,
e funkcji C-
r´o˙zniczkowalnych:
Propozycja 2.3. Funkcja zespolona f = u + iv jest C-r´o˙zniczkowalna w punkcie
z
o
wtedy i tylko wtedy, gdy f jest R-r´o˙zniczkowalna w z
0
oraz f
z
(z
0
) = 0, tzn. w z
0
speÃlnione s
,
a r´ownania Cauchy’ego-Riemanna:
½
u
x
= v
y
,
u
y
= −v
x
.
W takiej sytuacji f
0
(z
0
) = f
z
(z
0
). ¤
Powiemy, ˙ze funkcja f : Ω → C (Ω b
,
edzie zawsze oznaczaÃlo obszar w C) jest
holomorficzna, je˙zeli jest ona C-r´o˙zniczkowalna w ka˙zdym punkcie. Zbi´or wszyst-
kich funkcji holomorficznych w Ω oznaczamy przez O(Ω), natomiast przez O
∗
(Ω)
zbi´or nigdzie nieznikaj
,
acych funkcji holomorficznych. Z Propozycji 2.1 i 2.2 wynika,
˙ze suma, iloczyn, iloraz i zÃlo˙zenie funkcji holomorficznych s
,
a funkcjami holomor-
ficznymi. Je˙zeli f = u + iv jest R-r´o˙zniczkowalna, to f jest holomorficzna wtedy i
tylko wtedy, gdy speÃlnione s
,
a r´ownania Cauchy’ego-Riemanna.
´
Cwiczenie
Pokaza´c, ˙ze e
z
jest jedyn
,
a funkcj
,
a z O(C) tak
,
a, ˙ze f
0
= f oraz f (0) = 1.
´
Cwiczenie
Pokaza´c, ˙ze cos, sin, cosh, sinh ∈ O(C) oraz obliczy´c pochodne zespolo-
ne tych funkcji.
Propozycja 2.4. ZaÃl´o˙zmy, ˙ze f jest holomorficzna i klasy C
1
w pewnym otoczeniu
z
0
∈ C oraz f
0
(z
0
) 6= 0. Wtedy istnieje U - otwarte otoczenie z
0
oraz V - otwarte
otoczenie f (z
0
), t.˙ze f : U → V jest bijekcj
,
a, f
−1
jest holomorficzna oraz
(2.6)
(f
−1
)
0
(f (z)) =
1
f
0
(z)
,
z ∈ U.
Dow´od. Je˙zeli zapiszemy f = u + iv, to rzeczywista r´o˙zniczka f ma posta´c
A :=
µ
u
x
u
y
v
x
v
y
¶
=
µ
u
x
u
y
−u
y
u
x
¶
dzi
,
eki r´ownaniom Cauchy’ego-Riemanna. Z drugiej strony, wprost z definicji C-
r´o˙zniczkowalno´sci
f
0
= f
x
= u
x
− iu
y
.
Mamy wi
,
ec
det A = u
2
x
+ u
2
y
= |f
0
|
2
.
FUNKCJE ANALITYCZNE
9
Dzi
,
eki temu, ˙ze f
0
(z
0
) 6= 0, z rzeczywistego twierdzenia o lokalnym dyfeomorfizmie
wynika, ˙ze istniej
,
a odp. otoczenia U i V , t.˙ze f : U → V jest bijekcj
,
a klasy C
1
oraz
f
−1
jest r´ownie˙z klasy C
1
. Zapiszmy f
−1
= α + iβ. R´o˙zniczka f
−1
jest r´owna
µ
α
x
α
y
β
x
β
y
¶
= A
−1
=
1
u
2
x
+ u
2
y
µ
u
x
−u
y
u
y
u
x
¶
.
W szczeg´olno´sci α
x
= β
y
, α
y
= −β
x
, czyli f
−1
jest holomorficzna. FormuÃl
,
e (2.6)
dostaniemy r´o˙zniczkuj
,
ac wz´or
f
−1
(f (z)) = z,
z ∈ U.
¤
´
Cwiczenie
Pokaza´c, ˙ze Log z ∈ O(C \ (−∞, 0]) oraz (Log z)
0
= 1/z.
Podamy teraz formuÃl
,
e na r´o˙zniczkowanie zÃlo˙zenia funkcji zespolonej z krzyw
,
a.
ZaÃl´o˙zmy, ˙ze funkcje f : Ω → C oraz γ = (γ
1
, γ
2
) : (a, b) → Ω s
,
a r´o˙zniczkowalne
(w klasycznym sensie). Wtedy, korzystaj
,
ac z (rzeczywistej) formuÃly na pochodn
,
a
zÃlo˙zenia oraz z (2.3), (2.5), otrzymamy
(2.7)
d
dt
f (γ(t)) = f
x
(γ(t)) γ
0
1
(t) + f
y
(γ(t)) γ
0
2
(t)
= f
z
(γ(t)) γ
0
(t) + f
z
(γ(t))γ
0
(t).
3. CaÃlkowanie funkcji zespolonych
Niech a, b ∈ R, a < b. Funkcj
,
e γ : [a, b] → C nazywamy drog
,
a, je˙zeli γ jest
ci
,
agÃla oraz γ jest kawaÃlkami klasy C
1
, tzn. istniej
,
a a = t
0
< t
1
< · · · < t
n
= b
takie, ˙ze γ ∈ C
1
([t
j
, t
j+1
]), j = 0, 1, . . . , n − 1. Punkt γ(a) nazywamy pocz
,
atkiem
za´s γ(b) ko´
ncem drogi γ. Obraz γ b
,
edziemy oznacza´c γ
∗
. Je˙zeli γ(a) = γ(b), to γ
nazywamy drog
,
a zamkni
,
et
,
a.
ZaÃl´o˙zmy, ˙ze f : γ([a, b]) → C jest funkcj
,
a ci
,
agÃl
,
a. Definiujemy
Z
γ
f (z)dz :=
Z
b
a
f (γ(t))γ
0
(t)dt.
(Powy˙zsz
,
a definicj
,
e otrzymamy tak˙ze rozpatruj
,
ac cz
,
e´s´c rzeczywist
,
a i urojon
,
a formy
r´o˙zniczkowej f dz = (u + iv)(dx + idy).) Zauwa˙zmy, ˙ze funkcja pod caÃlk
,
a jest
caÃlkowalna w sensie Riemanna niezale˙znie od tego jakie warto´sci przyjmuje w punk-
tach t
j
. Ponadto, je˙zeli ϕ : [c, d] → [a, b] jest dyfeomorfizmem, to e
γ := γ ◦ ϕ jest
drog
,
a tak
,
a, ˙ze e
γ
∗
= γ
∗
oraz
Z
e
γ
f (z)dz =
Z
d
c
f (γ(ϕ(s)))γ
0
(ϕ(s))ϕ
0
(s)ds =
( R
γ
f (z)dz,
je˙zeli ϕ
0
> 0;
−
R
γ
f (z)dz,
je˙zeli ϕ
0
< 0.
Zatem, je˙zeli γ|
(a,b)
jest iniekcj
,
a, to
R
γ
f (z)dz zale˙zy tylko od obrazu γ oraz od
kierunku, w kt´orym caÃlkujemy, tzn. od orientacji. W takiej sytuacji b
,
edziemy
cz
,
esto uto˙zsamia´c drogi z ich obrazem oraz odpowiedni
,
a orientacj
,
a.

10
ZBIGNIEW BÃLOCKI
W szczeg´olno´sci, je˙zeli D jest obszarem, kt´orego brzeg mo˙zna iniektywnie spara-
metryzowa´c drog
,
a zamkni
,
et
,
a, to mo˙zemy m´owi´c o dodatniej orientacji ∂D - b
,
edzie
ni
,
a dowolna parametryzacja o kierunku odwrotnym do ruchu wskaz´owek zegara.
CaÃlka
R
∂D
f (z)dz ma w´owczas sens, gdy˙z nie zale˙zy od wyboru takiej parametryza-
cji (i jest ona zgodna z caÃlk
,
a z formy po krzywej gÃladkiej). B
,
edziemy u˙zywa´c tego
oznaczenia przede wszystkim, gdy D jest koÃlem lub wn
,
etrzem tr´ojk
,
ata.
Je˙zeli f jest okre´slone w pewnym otoczeniu γ
∗
i ma tam funkcj
,
e pierwotn
,
a, tzn.
istnieje funkcja holomorficzna F taka, ˙ze F
0
= f , to z (2.7) otrzymamy
(3.1)
Z
γ
f (z)dz =
Z
b
a
d
dt
F (γ(t)) dt = F (γ(b)) − F (γ(a)).
W szczeg´olno´sci, je˙zeli γ jest drog
,
a zamkni
,
et
,
a, to
R
γ
f (z)dz = 0.
´
Cwiczenie
Pokaza´c, ˙ze je˙zeli funkcja f = u + iv ma pierwotn
,
a, to pole wektorowe
(v, u) jest potencjalne, tzn. (v, u) = ∇χ dla pewnej funkcji χ.
PrzykÃlad. Dla n ∈ Z, z
0
∈ C oraz r > 0 obliczymy
Z
∂K(z
0
,r)
(z − z
0
)
n
dz.
Dla n 6= −1 pierwotn
,
a funkcji podcaÃlkowej jest funkcja (z−z
0
)
n+1
/(n+1), okre´slona
na C \ {z
0
}. W tym przypadku wi
,
ec, dzi
,
eki (3.1), nasza caÃlka znika. Dla n = −1
poÃl´o˙zmy γ
j
(t) = z
0
+ re
it
, a
j
≤ t ≤ b
j
, gdzie a
j
jest pewnym ci
,
agiem malej
,
acym
do zera, za´s b
j
rosn
,
acym do 2π. Wtedy, tak˙ze z (3.1), mamy
Z
∂K(z
0
,r)
dz
z − z
0
= lim
j→∞
Z
γ
j
dz
z − z
0
= lim
j→∞
¡
Log (re
ib
j
) − Log (re
ia
j
)
¢
= 2πi.
Otrzymali´smy wi
,
ec
(3.2)
Z
∂K(z
0
,r)
(z − z
0
)
n
dz =
½
0,
je˙zeli n 6= −1;
2πi,
je˙zeli n = −1.
Pokazuje to w szczeg´olno´sci, ˙ze funkcja 1/(z − z
0
) nie ma pierwotnej w ˙zadnym
pier´scieniu o ´srodku w z
0
.
Je˙zeli z, w ∈ C, to przez [z, w] oznaczamy drog
,
e dan
,
a przez parametryzacj
,
e
γ(t) = (1 − t)z + tw, t ∈ [0, 1].
´
Cwiczenie
Obliczy´c
Z
[1,i]
Log z dz.
´
Cwiczenie
Podobnie jak powy˙zej pokaza´c, ˙ze
Z
∂K(z
0
,r)
dζ
ζ − z
= 2πi,
z ∈ K(z
0
, r).
Zauwa˙zmy, ˙ze
(3.3)
¯
¯
¯
¯
Z
γ
f (z)dz
¯
¯
¯
¯ ≤
Z
b
a
|f (γ(t))| |γ
0
(t)|dt ≤ l(γ) max
γ
|f |,

FUNKCJE ANALITYCZNE
11
gdzie
l(γ) :=
Z
b
a
|γ
0
(t)|dt
jest dÃlugo´sci
,
a γ.
4. Twierdzenie caÃlkowe Cauchy’ego
Podstawow
,
a wÃlasno´sci
,
a geometryczn
,
a funkcji holomorficznych jest twierdzenie
caÃlkowe Cauchy’ego. ÃLatwo wynika ono ze wzoru Greena w nast
,
epuj
,
acym przy-
padku (Cauchy, 1825): zaÃl´o˙zmy, ˙ze f jest funkcj
,
a holomorficzn
,
a klasy C
1
w ob-
szarze Ω, natomiast γ jest drog
,
a zamkni
,
et
,
a w Ω, kt´ora parametryzuje brzeg klasy
C
1
obszaru D b Ω. Wtedy
Z
γ
f (z)dz =
Z
D
d(f dz) =
Z
D
f
z
dz ∧ dz = 0.
GÃl´ownym problemem w uog´olnieniu tego faktu jest pozbycie si
,
e zaÃlo˙zenia, ˙ze f jest
klasy C
1
. ZostaÃlo to dokonane przez Goursata w 1900 r. Podstawowym krokiem
w dowodzie og´olnej wersji twierdzenia caÃlkowego Cauchy’ego byÃlo wykazanie jego
wzmocnionej wersji dla brzegu tr´ojk
,
ata (sam Goursat rozpatrywaÃl czworok
,
aty, jak
jednak wkr´otce zauwa˙zyÃl Pringsheim, naturalnym obiektami metody Goursata byÃly
tr´ojk
,
aty):
Twierdzenie 4.1. ZaÃl´o˙zmy, ˙ze f ∈ O(Ω \ {z
0
}) ∩ C(Ω), gdzie z
0
∈ Ω. Wtedy dla
dowolnego tr´ojk
,
ata T ⊂ Ω (czyli otoczki wypukÃlej trzech niewsp´oÃlliniowych punkt´ow)
mamy
Z
∂T
f (z)dz = 0.
Dow´od. ZaÃl´o˙zmy najpierw, ˙ze z
0
/
∈ T . Przez z
1
, z
2
, z
3
oznaczmy wierzchoÃlki T .
Rozpatruj
,
ac punkty (z
j
+ z
k
)/2, j, k = 1, 2, 3, dzielimy tr´ojk
,
at T na cztery tr´ojk
,
aty
T
1
, . . . , T
4
. Mamy wtedy
Z
∂T
f (z)dz =
4
X
j=1
Z
∂T
j
f (z)dz.
Wybieraj
,
ac jako T
1
odpowiedni z tr´ojk
,
at´ow T
1
, . . . , T
4
otrzymamy
¯
¯
¯
¯
Z
∂T
f (z)dz
¯
¯
¯
¯ ≤ 4
¯
¯
¯
¯
Z
∂T
1
f (z)dz
¯
¯
¯
¯ .
Zauwa˙zmy tak˙ze, ˙ze l(∂T
1
) = l(∂T )/2. W ten sam spos´ob wybieramy indukcyjnie
tr´ojk
,
aty T
n
, n = 1, 2, . . . , tak, ˙ze
¯
¯
¯
¯
¯
Z
∂T
n−1
f (z)dz
¯
¯
¯
¯
¯
≤ 4
¯
¯
¯
¯
Z
∂T
n
f (z)dz
¯
¯
¯
¯

12
ZBIGNIEW BÃLOCKI
oraz l(∂T
n
) = l(∂T
n−1
)/2. Otrzymali´smy zatem zst
,
epuj
,
acy ci
,
ag tr´ojk
,
at´ow T
n
taki,
˙ze
(4.1)
¯
¯
¯
¯
Z
∂T
f (z)dz
¯
¯
¯
¯ ≤ 4
n
¯
¯
¯
¯
Z
∂T
n
f (z)dz
¯
¯
¯
¯
oraz
(4.2)
diam(T
n
) ≤
l(∂T
n
)
2
=
l(∂T )
2
n+1
.
Z twierdzenia Cantora wynika, ˙ze
∞
\
n=1
T
n
= {e
z}
dla pewnego e
z ∈ T . Z C-r´o˙zniczkowalno´sci f w e
z mamy
f (z) = f (e
z) +
¡
f
0
(e
z) + ε(z)
¢
(z − e
z),
gdzie
lim
z→e
z
ε(z) = 0.
Poniewa˙z funkcja f (e
z) + f
0
(e
z)(z − e
z) ma pierwotn
,
a, z (3.1) i (3.3) wynika, ˙ze
¯
¯
¯
¯
Z
∂T
n
f (z)dz
¯
¯
¯
¯ =
¯
¯
¯
¯
Z
∂T
n
ε(z)(z − e
z)dz
¯
¯
¯
¯ ≤ l(∂T
n
)diam(T
n
) max
T
n
|ε|.
Korzystaj
,
ac z (4.1) i (4.2) otrzymamy dla ka˙zdego n
¯
¯
¯
¯
Z
∂T
f (z)dz
¯
¯
¯
¯ ≤
(l(∂T ))
2
2
max
T
n
|ε|,
czyli twierdzenie zachodzi przy zaÃlo˙zeniu, ˙ze z
0
/
∈ T .
Je˙zeli z
0
∈ T , to dziel
,
ac T na trzy (lub dwa) mniejsze tr´ojk
,
aty, kt´orych wierz-
choÃlkiem jest z
0
widzimy, ˙ze bez straty og´olno´sci mo˙zemy zaÃlo˙zy´c, ˙ze z
0
jest jednym
z wierzchoÃlk´ow T . Je˙zeli teraz podzielimy T na tr´ojk
,
at T
0
n
o wierzchoÃlku w z
0
oraz
czworok
,
at Q
n
tak, ˙ze l(T
0
n
) d
,
a˙zy do 0, to z poprzedniej cz
,
e´sci wnioskujemy, ˙ze
Z
Q
n
f (z)dz = 0,
zatem
¯
¯
¯
¯
Z
∂T
f (z)dz
¯
¯
¯
¯ =
¯
¯
¯
¯
¯
Z
∂T
0
n
f (z)dz
¯
¯
¯
¯
¯
≤ l(T
0
n
) max
T
|f |.
¤
PrzykÃlady. i) Niech f (z) = e
−z
2
i dla R > 0 niech T
R
b
,
edzie tr´ojk
,
atem o wierz-
choÃlkach 0, R, R + iR. Z Twierdzenia 4.1 mamy
Z
∂T
R
f (z)dz = 0.

FUNKCJE ANALITYCZNE
13
Mamy tak˙ze, gdy R → ∞,
i)
Z
[0,R]
e
−z
2
dz −→
Z
∞
0
e
−x
2
dx =
√
π
2
,
ii)
¯
¯
¯
¯
¯
Z
[R,R+Ri]
e
−z
2
dz
¯
¯
¯
¯
¯
=
¯
¯
¯
¯
¯
i
Z
R
0
e
t
2
−R
2
−2iRt
dt
¯
¯
¯
¯
¯
≤
Z
R
0
e
t
2
−R
2
dt ≤
Z
R
0
e
Rt−R
2
dt → 0,
iii)
Z
[R+Ri,0]
e
−z
2
dz = −(1 + i)
Z
R
0
e
−2it
2
dt,
sk
,
ad Ãlatwo wnioskujemy, ˙ze
Z
∞
0
cos t
2
dt =
Z
∞
0
sin t
2
dt =
r
π
8
.
Nast
,
epnym krokiem jest pokazanie zwi
,
azku twierdzenia caÃlkowego Cauchy’ego z
istnieniem funkcji pierwotnej:
Twierdzenie 4.2. Niech f b
,
edzie funkcj
,
a ci
,
agÃl
,
a w Ω. Wtedy nast
,
epuj
,
ace warunki
s
,
a r´ownowa˙zne
i) Istnieje F ∈ O(Ω) takie, ˙ze F
0
= f ;
ii)
Z
γ
f (z)dz = 0 dla ka˙zdej drogi zamkni
,
etej γ w Ω.
Je˙zeli Ω jest obszarem gwia´zdzistym, to powy˙zsze warunki s
,
a r´ownowa˙zne nast
,
epu-
j
,
acej wÃlasno´sci
iii)
Z
∂T
f (z)dz = 0 dla ka˙zdego tr´ojk
,
ata T ⊂ Ω.
Dow´od. Implikacja i)⇒ii) wynika natychmiast z (3.1). W celu pokazania implikacji
przeciwnej ustalmy z
0
∈ Ω. Dla z ∈ Ω niech γ b
,
edzie dowoln
,
a drog
,
a Ãl
,
acz
,
ac
,
a z
0
oraz z. KÃladziemy
F (z) :=
Z
γ
f (ζ)dζ.
Dzi
,
eki i) wida´c, ˙ze definicja F nie zale˙zy od wyboru γ. Dla odp. maÃlych h mamy
(4.3)
F (z + h) − F (z) =
Z
[z,z+h]
f (ζ)dζ,
a st
,
ad, dzi
,
eki (3.3),
¯
¯
¯
¯
F (z + h) − F (z)
h
− f (z)
¯
¯
¯
¯ =
¯
¯
¯
¯
¯
1
h
Z
[z,z+h]
(f (ζ) − f (z))dζ
¯
¯
¯
¯
¯
≤
sup
ζ∈[z,z+h]
|f (ζ) − f (z)|.
Z ci
,
agÃlo´sci f w z wynika, ˙ze ostatnie wyra˙zenie d
,
a˙zy do 0. Otrzymali´smy zatem,
˙ze F ∈ O(Ω) oraz F
0
= f .
Je˙zeli Ω jest gwia´zdzisty, to implikacja ii)⇒iii) jest trywialna, natomiast, zakÃla-
daj
,
ac, ˙ze zachodzi iii) i ˙ze Ω jest gwia´zdzisty wzgl
,
edem z
0
, kÃladziemy
F (z) :=
Z
[z
0
,z]
f (z)dz,
z ∈ Ω.
14
ZBIGNIEW BÃLOCKI
Z iii) wynika, ˙ze zachodzi (4.3) i identycznie jak poprzednio dowodzimy, ˙ze F
0
=
f . ¤
Z Twierdze´
n 4.1 i 4.2 wynika wersja twierdzenia Cauchy’ego dla zbior´ow gwia´z-
dzistych:
Wniosek 4.3. Je˙zeli obszar Ω jest gwia´zdzisty i f ∈ O(Ω\{z
0
})∩C(Ω) dla pewnego
z
0
∈ Ω, to
Z
γ
f (z)dz = 0
dla ka˙zdej drogi zamkni
,
etej γ w Ω. ¤
5. Wz´
or caÃlkowy Cauchy’ego
Podstawow
,
a wÃlasno´sci
,
a funkcji holomorficznych jest wz´or caÃlkowy Cauchy’ego
(1831), kt´ory odtwarza dan
,
a funkcj
,
e wewn
,
atrz koÃla z jej warto´sci na brzegu.
Twierdzenie 5.1. Je˙zeli f jest funkcj
,
a holomorficzn
,
a w otoczeniu koÃla K(z
0
, r),
to
(5.1)
f (z) =
1
2πi
Z
∂K(z
0
,r)
f (ζ)
ζ − z
dζ,
z ∈ K(z
0
, r).
Co wi
,
ecej, f jest C-r´o˙zniczkowalna dowoln
,
a ilo´s´c razy oraz
f
(n)
(z) =
n!
2πi
Z
∂K(z
0
,r)
f (ζ)
(ζ − z)
n+1
dζ,
z ∈ K(z
0
, r), n = 1, 2, . . .
Dow´od. Niech Ω b
,
edzie gwia´zdzistym otoczeniem K(z
0
, r), w kt´orym funkcja f jest
okre´slona. Dla ζ ∈ Ω zdefiniujmy
g(ζ) :=
f (ζ) − f (z)
ζ − z
,
ζ 6= z,
f
0
(z),
ζ = z.
Wtedy g ∈ O(Ω \ {z}) ∩ C(Ω), zatem Wniosek 3.3 implikuje, ˙ze
0 =
Z
∂K(z
0
,r)
g(ζ)dζ =
Z
∂K(z
0
,r)
f (ζ)
ζ − z
dζ − 2πif (z).
Otrzymali´smy zatem (5.1). Druga cz
,
e´s´c tezy wynika z faktu, ˙ze mo˙zemy teraz
r´o˙zniczkowa´c pod znakiem caÃlki, zauwa˙zmy, ˙ze
µ
∂
∂z
¶
n
µ
1
ζ − z
¶
=0,
µ
∂
∂z
¶
n
µ
1
ζ − z
¶
=
1
(ζ − z)
n+1
.
¤

FUNKCJE ANALITYCZNE
15
Druga cz
,
e´s´c Twierdzenia 5.1 jest specjalnym przypadkiem og´olnego rezulatu o
holomorficzno´sci funkcji danej wzorem caÃlkowym dla dowolnej drogi (nazywanego
lematem o produkcji funkcji holomorficznych):
Lemat 5.2. ZaÃl´o˙zmy, ˙ze γ jest dowoln
,
a drog
,
a w C, natomiast g funkcj
,
a ci
,
agÃl
,
a na
γ
∗
. PoÃl´o˙zmy
f (z) :=
Z
γ
g(ζ)
ζ − z
dζ,
z ∈ C \ γ
∗
.
Wtedy f ∈ O(C \ γ
∗
), f jest C-r´o˙zniczkowalna dowoln
,
a ilo´s´c razy oraz dla n =
1, 2, . . . mamy
f
(n)
(z) = n!
Z
γ
g(ζ)
(ζ − z)
n+1
dζ,
z ∈ C \ γ
∗
.
¤
´
Cwiczenie
Obliczy´c
Z
∂K(0,2)
e
−z
(z + 1)
2
dz.
Je˙zeli rozpatrzymy wz´or Cauchy’ego dla z = z
0
oraz parametryzacj
,
e ζ = z
0
+re
it
,
0 ≤ t ≤ 2π, otrzymamy twierdzenie o warto´sci ´sredniej:
Wniosek 5.3. (Poisson, 1823) Je˙zeli f jest funkcj
,
a holomorficzn
,
a w otoczeniu koÃla
K(z
0
, r), to
f (z
0
) =
1
2π
Z
2π
0
f (z
0
+ re
it
)dt.
¤
Bezpo´sredni
,
a konsekwecj
,
a wzoru Cauchy’ego jest tak˙ze nier´owno´s´c Cauchy’ego
(1835):
Twierdzenie 5.4. Niech f ∈ O(K(z
0
, r)) b
,
edzie taka, ˙ze |f | ≤ M dla pewnej
staÃlej M . Wtedy
|f
(n)
(z
0
)| ≤
n! M
r
n
,
n = 1, 2, . . .
Dow´od. Wystarczy zastosowa´c wz´or Cauchy’ego w kole K(z
0
, ρ) dla ρ < r oraz
(3.3), a nast
,
epnie skorzysta´c z dowolno´sci ρ. ¤
6. Podstawowe wÃlasno´sci funkcji holomorficznych
Udowodnimy teraz szereg wÃlasno´sci funkcji holomorficznych wynikaj
,
acych ze
wzoru Cauchy’ego. Pokazali´smy, ˙ze ka˙zda funkcja holomorficzna jest C-r´o˙znicz-
kowalna dowoln
,
a ilo´s´c razy. W szczeg´olno´sci, ka˙zda funkcja, kt´ora lokalnie ma
pierwotn
,
a jest holomorficzna. Z Twierdzenia 4.2 wynika zatem rezultat odwrotny
do twierdzenia caÃlkowego Cauchy’ego:
Twierdzenie 6.1. (Morera, 1886) ZaÃl´o˙zmy, ˙ze funkcja f ∈ C(Ω) speÃlnia
Z
∂T
f (z) dz = 0
dla ka˙zdego tr´ojk
,
ata T ⊂ Ω. Wtedy f ∈ O(Ω). ¤
16
ZBIGNIEW BÃLOCKI
Funkcj
,
e holomorficzn
,
a okre´slon
,
a na C nazywamy caÃlkowit
,
a.
Twierdzenie 6.2. (Liouville, 1847, Cauchy, 1844) Ka˙zda ograniczona funkcja
caÃlkowita jest staÃla.
Dow´od. Je˙zeli |f | ≤ M na C, to z nier´owno´sci Cauchy’ego wynika, ˙ze |f
0
(z)| ≤ M/r
dla ka˙zdego z ∈ C i r > 0. Je˙zeli wi
,
ec r → ∞, to dostaniemy, ˙ze f
0
= 0 na C. Ale
to oznacza, ˙ze r´ownie˙z pochodna rzeczywista f wsz
,
edzie znika. ¤
´
Cwiczenie
Pokaza´c, ˙ze je˙zeli funkcja f ∈ O(C) jest taka, ˙ze Re f ≤ M dla pewnej
staÃlej M , to f jest staÃla.
´
Cwiczenie
Pokaza´c, ˙ze je˙zeli funkcja caÃlkowita f speÃlnia
|f (z)| ≤ C|z|
n
, gdy |z| ≥ R,
dla pewnych C, R > 0, to f musi by´c wielomianem stopnia ≤ n.
Z twierdzenia Liouville’a w Ãlatwy spos´ob wynika zasadnicze twierdzenie algebry.
Bo je˙zeli niestaÃly wielomian P nie miaÃlby pierwiastka, to f := 1/P byÃloby funkcj
,
a
caÃlkowit
,
a. Co wi
,
ecej
lim
|z|→∞
|f (z)| = 0.
W szczeg´olno´sci, f byÃlaby funkcj
,
a ograniczon
,
a, a wi
,
ec na mocy twierdzenia Liou-
ville’a otrzymaliby´smy, ˙ze P jest staÃly.
Nast
,
epnym rezulatem jest zasada maksimum dla funkcji holomorficznych:
Twierdzenie 6.3. Je˙zeli f jest funkcj
,
a holomorficzn
,
a w obszarze Ω tak
,
a, ˙ze |f |
osi
,
aga maksimum w Ω, to f jest staÃla.
Dow´od. Dla K(z
0
, r) ⊂ Ω z twierdzenia o warto´sci ´sredniej wynika, ˙ze
|f (z
0
)| ≤
1
2π
Z
2π
0
|f (z
0
+ re
it
)|dt.
Je´sli zatem |f | ≤ |f (z
0
)| na ∂K(z
0
, r), to z ci
,
agÃlo´sci |f | wynika, ˙ze |f | = |f (z
0
)|
na ∂K(z
0
, r), a wobec dowolno´sci r, tak˙ze w K(z
0
, r). Twierdzimy, ˙ze je˙zeli |f | =
|f (z
0
)| w K(z
0
, r), to wtedy f = f (z
0
) w K(z
0
, r). Je˙zeli f (z
0
) = 0, to jest to
oczywiste, mo˙zemy wi
,
ec zaÃlo˙zy´c, ˙ze f 6= 0 w K(z
0
, r). Mamy
0 = (|f |
2
)
z
= f
z
f + (f
z
)f = f
0
f ,
a zatem f
0
= 0, wi
,
ec f = f (z
0
) w K(z
0
, r). Pokazali´smy wi
,
ec, ˙ze je˙zeli max
K(z
0
,r)
|f | =
|f (z
0
)|, to f = f (z
0
) w K(z
0
, r).
Je˙zeli teraz |f | osi
,
aga maksimum w z
0
∈ Ω, to kÃladziemy
Ω
0
:= {z ∈ Ω : f (z) = f (z
0
)}.
Zbi´or ten jest oczywi´scie domkni
,
ety, natomiast z pierwszej cz
,
e´sci dowodu wynika,
˙ze jest on r´ownie˙z otwarty, co oznacza, ˙ze Ω
0
= Ω. ¤
Twierdzenie 6.3 to sÃlaba zasada maksimum (zakÃladamy, ˙ze maksimum jest glo-
balne), niedÃlugo poka˙zemy wzmocnienie Twierdzenia 6.3 (przy zaÃlo˙zeniu, ˙ze mak-
simum jest lokalne).
FUNKCJE ANALITYCZNE
17
´
Cwiczenie
Niech wielomian P (z) = a
0
+a
1
z +· · ·+a
n
z
n
b
,
edzie taki, ˙ze |P (z)| ≤ 1,
gdy |z| = 1. Pokaza´c, ˙ze |a
j
| ≤ 1, j = 1, . . . , n.
´
Cwiczenie
Niech f b
,
edzie funkcj
,
a holomorficzn
,
a w otoczeniu pier´scienia {1 ≤
|z| ≤ 3} tak
,
a, ˙ze |f | ≤ 1, gdy |z| = 1 oraz |f | ≤ 9, gdy |z| = 3. Pokaza´c, ˙ze
|f (z)| ≤ 4, gdy |z| = 2.
Przy pomocy wzoru Cauchy’ego mo˙zemy te˙z Ãlatwo udowodni´c podstawowy rezul-
tat dotycz
,
acy ci
,
ag´ow funkcji holomorficznych:
Twierdzenie 6.4. (Weierstrass, 1841) Je˙zeli f
n
jest ci
,
agiem funkcji holomor-
ficznych w Ω zbie˙znym lokalnie jednostajnie do funkcji f , to f jest funkcj
,
a holomor-
ficzn
,
a oraz dla ka˙zdego k = 1, 2, . . . mamy lokalnie jednostajn
,
a zbie˙zno´s´c f
(k)
n
→
f
(k)
.
Dow´od. Niech K(z
0
, r) ⊂ Ω. Funkcje f
n
speÃlniaj
,
a wz´or Cauchy’ego (3.6), zatem
speÃlnia go r´ownie˙z f . Z Lematu 4.2 wynika, ˙ze f jest holomorficzna w K(z
0
, r).
Co wi
,
ecej, z nier´owno´sci Cauchy’ego (stosowanej w kole K(z, r/2) ⊂ K(z
0
, r), z ∈
K(z
0
, r/2)) dostaniemy
max
K(z
0
,r/2)
|f
(k)
n
− f
(k)
| ≤
k!
(r/2)
k
max
K(z
0
,r)
|f
n
− f |.
¤
7. Szeregi pot
,
egowe
Wyra˙zenie
(7.1)
∞
X
n=0
a
n
(z − z
0
)
n
,
z ∈ C
nazywamy szeregiem pot
,
egowym o ´srodku w z
0
∈ C i wsp´oÃlczynnikach a
n
∈ C,
n = 0, 1, . . . .
PrzykÃlad. Szereg geometryczny
∞
X
n=0
z
n
. Jest on zbie˙zny wtedy i tylko wtedy, gdy
|z| < 1. Wynika to ze wzoru
1 + z + · · · + z
n
=
1 − z
n+1
1 − z
,
z 6= 1.
Mo˙zemy zatem zapisa´c
(7.2)
∞
X
n=0
z
n
=
1
1 − z
,
|z| < 1.
Twierdzenie 7.1. (Cauchy, 1821, Hadamard, 1892) PoÃl´o˙zmy
(7.3)
R :=
1
lim sup
n→∞
n
p
|a
n
|
.

18
ZBIGNIEW BÃLOCKI
Wtedy szereg (7.1) jest bezwzgl
,
ednie i lokalnie jednostajnie zbie˙zny w kole K(z
0
, R)
oraz rozbie˙zny dla ka˙zdego z ∈ C \ K(z
0
, R).
Dow´od. Dla z ∈ K(z
0
, R) niech r i λ b
,
ed
,
a takie, ˙ze |z − z
0
| ≤ r < R oraz r/R <
λ < 1. Wtedy dla n odp. du˙zego mamy
n
p
|a
n
| ≤ λ/r, zatem
¯
¯
¯
¯
¯
N
2
X
n=N
1
a
n
(z − z
0
)
n
¯
¯
¯
¯
¯
≤
N
2
X
n=N
1
|a
n
(z − z
0
)
n
| ≤
∞
X
n=N
1
λ
n
=
λ
N
1
1 − λ
→ 0,
gdy N
1
→ ∞. Z warunku Cauchy’ego zbie˙zno´sci otrzymali´smy zatem bezwzgl
,
edn
,
a
i jednostajn
,
a zbie˙zno´s´c szeregu na K(z
0
, r).
Z drugiej strony, je˙zeli |z − z
0
| > R, to istnieje podci
,
ag a
n
k
taki, ˙ze
nk
p
|a
n
k
| ≥
1/|z − z
0
|, co oznacza, ˙ze |a
n
k
(z − z
0
)
n
k
| ≥ 1, nie jest zatem speÃlniony warunek
konieczny zbie˙zno´sci szeregu. ¤
KoÃlo K(z
0
, R) z Twierdzenia 7.1 nazywamy koÃlem zbie˙zno´sci, za´s R promieniem
zbie˙zno´sci szeregu (7.1). FormuÃla (7.3) na promie´
n zbie˙zno´sci szeregu pot
,
egowego
nosi nazw
,
e wzoru Cauchy’ego-Hadamarda. Zauwa˙zmy, ˙ze promie´
n zbie˙zno´sci sze-
regu (7.1) jest dodatni wtedy i tylko wtedy, gdy istnieje M > 0 takie, ˙ze dla n odp.
du˙zego mamy |a
n
| ≤ M
n
- wtedy R ≥ 1/M .
Twierdzenie 7.1 nie rozstrzyga zbie˙zno´sci szeregu pot
,
egowego na brzegu koÃla
zbie˙zno´sci:
PrzykÃlady. KoÃlem zbie˙zno´sci ka˙zdego z szereg´ow
∞
X
n=0
z
n
,
∞
X
n=1
z
n
n
,
∞
X
n=1
z
n
n
2
jest K(0, 1).
i) Szereg
P
z
n
jest rozbie˙zny we wszystkich punktach z brzegu koÃla zbie˙zno´sci.
ii) Szereg
P
z
n
/n
2
jest zbie˙zny bezwzgl
,
ednie na brzegu.
iii) Szereg
P
z
n
/n jest rozbie˙zny w 1 i zbie˙zny warunkowo na ∂K(0, 1) \ {1}
(
´
Cwiczenie
).
Istotn
,
a wÃlasno´sci
,
a szereg´ow pot
,
egowych jest jednoznaczno´s´c ich wsp´oÃlczynni-
k´ow:
Propozycja 7.2. ZaÃl´o˙zmy, ˙ze szeregi pot
,
egowe
P
a
n
(z − z
0
)
n
oraz
P
b
n
(z − z
0
)
n
s
,
a zbie˙zne do tych samych warto´sci na zbiorze A takim, ˙ze z
0
jest punktem skupienia
A. Wtedy a
n
= b
n
dla wszystkich n.
Dow´od. Bez straty og´olno´sci mo˙zemy zaÃlo˙zy´c, ˙ze b
n
= 0 dla wszystkich n. Przy-
pu´s´cmy, ˙ze a
m
6= 0 dla pewnego m i wybierzmy najmniejsze takie m. Wtedy
∞
X
n=0
a
n
(z − z
0
)
n
= (z − z
0
)
m
∞
X
n=0
a
n+m
(z − z
0
)
n
,
z 6= z
0
.
Szereg
P
∞
n=0
a
n+m
(z−z
0
)
n
, zbie˙zny do pewnej funkcji ci
,
agÃlej w otoczeniu z
0
(dzi
,
eki
Twierdzeniu 7.1), znika dla z ∈ A, zatem znika r´ownie˙z w z
0
, czyli a
m
= 0 -
sprzeczno´s´c. ¤
PrzykÃlad. Rozpatrzmy ci
,
ag Fibonacciego (1202):
a
0
= 0, a
1
= 1, a
n
= a
n−2
+ a
n−1
,
n = 2, 3, . . .
FUNKCJE ANALITYCZNE
19
´
Cwiczenie
Pokaza´c, ˙ze w pewnym (rzeczywistym) otoczeniu 0 mamy
∞
X
n=0
a
n
x
n
=
x
1 − x − x
2
oraz, rozwijaj
,
ac praw
,
a stron
,
e w szereg pot
,
egowy, ˙ze
a
n
=
1
√
5
"Ã
1 +
√
5
2
!
n
−
Ã
1 −
√
5
2
!
n
#
(de Moivre, 1730).
Nast
,
epuj
,
acy rezultat jest bezpo´sredni
,
a konsekwencj
,
a Twierdzenia 6.4 (mo˙zna go
zreszt
,
a udowodni´c w bardziej elementarny spos´ob):
Twierdzenie 7.3. Suma szeregu pot
,
egowego jest funkcj
,
a holomorficzn
,
a w kole
zbie˙zno´sci. Szereg pot
,
egowy mo˙zna r´o˙zniczkowa´c wyraz po wyrazie. ¤
8. Podstawowe wÃlasno´sci funkcji holomorficznych, cd.
Udowodnimy najpierw, ˙ze ka˙zda funkcja holomorficzna w kole jest granic
,
a sze-
regu pot
,
egowego, czyli wynik odwrotny do Twierdzenia 7.3:
Twierdzenie 8.1. ZaÃl´o˙zmy, ˙ze f ∈ O(Ω). Wtedy dla ka˙zdego z
0
∈ Ω funkcja f
rozwija si
,
e w szereg Taylora w kole K(z
0
, dist(z
0
, ∂Ω)), tzn.
f (z) =
∞
X
n=0
f
(n)
(z
0
)
n!
(z − z
0
)
n
,
|z − z
0
| < dist(z
0
, ∂Ω).
Dow´od. Niech r b
,
edzie takie, ˙ze |z − z
0
| < r < dist(z
0
, ∂Ω). Skorzystamy ze wzoru
Cauchy’ego (5.1). Dla ζ ∈ ∂K(z
0
, r) dzi
,
eki (7.2) mamy
1
ζ − z
=
1
ζ − z
0
1
1 −
z−z
0
ζ−z
0
=
∞
X
n=0
(z − z
0
)
n
(ζ − z
0
)
n+1
,
przy czym zbie˙zno´s´c jest jednostajna dla ζ ∈ ∂K(z
0
, r). Zatem
f (z) =
1
2πi
Z
∂K(z
0
,r)
f (ζ)
ζ − z
dζ
=
1
2πi
∞
X
n=0
(z − z
0
)
n
Z
∂K(z
0
,r)
f (ζ)
(ζ − z
0
)
n+1
dζ
=
∞
X
n=0
f
(n)
(z
0
)
n!
(z − z
0
)
n
.
¤
Pokazali´smy zatem, ˙ze funkcje holomorficzne to dokÃladnie te funkcje, kt´ore
mo˙zna lokalnie rozwin
,
a´c w szereg pot
,
egowy (b
,
ed
,
acy r´ownocze´snie szeregiem Tay-
lora tej funkcji). Co wi
,
ecej, szereg Taylora funkcji holomorficznej w danym punkcie

20
ZBIGNIEW BÃLOCKI
jest zbie˙zny w ka˙zdym kole o ´srodku w tym punkcie, w kt´orym funkcja ta jest
okre´slona.
Zasad
,
e identyczno´sci dla funkcji holomorficznych Ãlatwo teraz wynika z zasady
identyczno´sci dla szereg´ow pot
,
egowych (Propozycja 7.2):
Twierdzenie 8.2. Niech f, g b
,
ed
,
a funkcjami holomorficznymi w obszarze Ω. Za-
Ãl´o˙zmy, ˙ze f = g na zbiorze A ⊂ Ω posiadaj
,
acym punkt skupienia w Ω. Wtedy f = g
w Ω.
Dow´od. Je˙zeli z
0
jest punktem skupienia zbioru A, to z Twierdzenia 7.6 i Propozycji
7.2 wynika, ˙ze f = g w dowolnym kole K(z
0
, r) ⊂ Ω. Zatem zbi´or Ω
0
= {z ∈ Ω :
f = g w pewnym otoczeniu z} jest domkni
,
ety w Ω. Poniewa˙z jest on r´ownie˙z
oczywi´scie otwarty, otrzymujemy Ω
0
= Ω. ¤
´
Cwiczenie
i) Czy istnieje f ∈ O(∆) takie, ˙ze f (1/n) = n/(n + 1), n = 2, 3, . . . ?
ii) Czy istnieje f ∈ O(∆) takie, ˙ze f (1/n) = n/(n + 2), n = 2, 3, . . . ?
iii) Czy istnieje f ∈ O(∆) takie, ˙ze f (1/n) = e
−n
, n = 2, 3, . . . ?
(Ozn. ∆ := K(0, 1).)
Z Twierdze´
n 6.3 i 8.2 wynika natychmiast mocna zasada maksimum dla funkcji
holomorficznych.
Twierdzenie 8.3. Je˙zeli f jest funkcj
,
a holomorficzn
,
a w obszarze Ω tak
,
a, ˙ze |f |
osi
,
aga maksimum lokalne w Ω, to f jest staÃla. ¤
Korzystaj
,
ac z zasady identyczno´sci oraz zasady maksimum mo˙zna udowodni´c
twierdzenie o odwzorowaniu otwartym:
Twierdzenie 8.4. NiestaÃle funkcje holomorficzne okre´slone na obszarze w C s
,
a
odwzorowaniami otwartymi.
Dow´od. Trzeba pokaza´c, ˙ze je˙zeli f jest funkcj
,
a holomorficzn
,
a w otoczeniu koÃla
K(z
0
, r), to istnieje δ > 0 takie, ˙ze f (K(z
0
, r)) ⊃ K(w
0
, δ), gdzie w
0
= f (z
0
).
Wybieramy ε ∈ (0, r) tak, ˙ze w
0
/
∈ f (∂K(z
0
, ε)). Gdyby takie ε nie istniaÃlo, to
dla ka˙zdego odp. maÃlego ε > 0 znale´zliby´smy punkty z
ε
takie, ˙ze |z
0
− z
ε
| = ε
oraz f (z
ε
) = w
0
. Dzi
,
eki zasadzie identyczno´sci staÃloby to w sprzeczno´sci z tym, ˙ze
funkcja f nie jest staÃla. KÃladziemy teraz
δ :=
1
2
min
ζ∈∂K(z
0
,ε)
|f (ζ) − w
0
|.
Z definicji ε wynika, ˙ze δ > 0. Dla w ∈ K(w
0
, δ) musimy teraz znale´z´c z ∈ K(z
0
, r)
takie, ˙ze f (z) = w. Przypu´s´cmy, ˙ze takie z nie istnieje. Z definicji δ mamy
|f (ζ) − w| ≥ |f (ζ) − w
0
| − |w
0
− w| > δ,
ζ ∈ ∂K(z
0
, ε).
Funkcja z 7→ 1/(f (z) − w) jest wi
,
ec holomorficzna w otoczeniu K(z
0
, ε), zatem z
zasady maksimum wynika, ˙ze
1
|f (z) − w|
≤
max
ζ∈∂K(z
0
,ε)
1
|f (ζ) − w|
<
1
δ
,
z ∈ K(z
0
, ε).
Dla z = z
0
otrzymamy |w
0
− w| > δ - sprzeczno´s´c. ¤
FUNKCJE ANALITYCZNE
21
Zauwa˙zmy, ˙ze w przypadku rzeczywistym nawet wielomiany nie musz
,
a by´c od-
wzorowaniami otwartymi, np. f (x) = x
2
.
´
Cwiczenie
Pokaza´c, ˙ze z twierdzenia o odwzorowaniu otwartym Ãlatwo wynika sÃlaba
zasada maksimum (Twierdzenie 6.3) oraz lemat d’Alemberta (Lemat 1.2).
9. Funkcje analityczne
Funkcj
,
e f : (a, b) → R nazywamy analityczn
,
a, je˙zeli dla ka˙zdego x
0
∈ (a, b)
istnieje r > 0 takie, ˙ze f jest rozwijalna w szereg Taylora w przedziale (x
0
−r, x
0
+r).
Korzystaj
,
ac z wÃlasno´sci szereg´ow pot
,
egowych mo˙zna elementarnie pokaza´c nast
,
e-
puj
,
acy fakt:
Propozycja 9.1. Je˙zeli funkcje f, g s
,
a funkcjami analitycznymi, to r´ownie˙z funk-
cje f ± g, f g oraz f /g (ta ostatnia pod warunkiem, ˙ze g 6= 0) s
,
a analityczne.
PrzykÃlad. Funkcja 1/(1 + x
2
) jest analityczna na R dzi
,
eki Propozycji 9.1. Szereg
Taylora w 0 ma posta´c (korzystamy z (7.2))
1
1 + x
2
=
∞
X
n=0
(−1)
n
x
2n
.
Szereg ten jest zbie˙zny tylko w przedziale (−1, 1), a wi
,
ec, w przeciwie´
nstwie do
przypadku zespolonego, funkcji analitycznej nie mo˙zna zawsze rozwin
,
a´c w szereg
Taylora w maksymalnym przedziale, w kt´orym funkcja jest okre´slona.
Funkcje analityczne s
,
a ´sci´sle zwi
,
azane z funkcjami holomorficznymi dzi
,
eki nast
,
e-
puj
,
acej charakteryzacji:
Propozycja 9.2. Ka˙zda funkcja analityczna na (a, b) jest zacie´snieniem pewnej
funkcji holomorficznej okre´slonej w pewnym otoczeniu (a, b) w C.
Dow´od. Je˙zeli dla α ∈ (a, b) mamy
f (x) =
∞
X
n=0
a
n
(x − α)
n
,
x ∈ (α − r
α
, α + r
α
),
to jest oczywiste (dzi
,
eki Twierdzeniu 7.1), ˙ze zespolony szereg
P
∞
n=0
a
n
(z − α)
n
jest zbie˙zny do funkcji holomorficznej f
α
w kole K(α, r
α
). Co wi
,
ecej, z zasady
identyczno´sci wynika, ˙ze f
α
= f
β
w K(α, r
α
) ∩ K(β, r
β
). Na obszarze
[
α∈(a,b)
K(α, r
α
) ⊂ C
mo˙zemy wi
,
ec dobrze zdefiniowa´c funkcj
,
e holomorficzn
,
a e
f := f
α
na K(α, r
α
). ¤
Zauwa˙zmy, ˙ze Propozycja 9.1 wynika z Propozycji 9.2 i wÃlasno´sci funkcji holo-
morficznych. To, ˙ze promie´
n zbie˙zno´sci szeregu Taylora funkcji 1/(1 + x
2
) w 0
wynosi 1 wynika z tego, ˙ze jej jednoznacznie okre´slone zespolone przedÃlu˙zenie, czyli
funkcja 1/(1 + z
2
), ma osobliwo´sci w ±i.

22
ZBIGNIEW BÃLOCKI
Podobnie mo˙zemy znale´z´c promie´
n zbie˙zno´sci szeregu Taylora w 0 funkcji
x
e
x
− 1
=
Ã
∞
X
n=0
x
n
(n + 1)!
!
−1
.
Jest ona zacie´snieniem do R funkcji z/(e
z
− 1), kt´ora jest holomorficzna w (maksy-
malnym) obszarze C \ {2kπi : k ∈ Z
∗
}. Szukany promie´
n jest wi
,
ec r´owny 2π.
Znalezienie go bez korzystania z analizy zespolonej byÃloby niepor´ownanie trud-
niejsze.
10. Globalne twierdzenie caÃlkowe Cauchy’ego
B
,
edziemy chcieli uog´olni´c twierdzenie caÃlkowe Cauchy’ego (zob. Wniosek 4.3)
na szersz
,
a klas
,
e obszar´ow i dr´og zamkni
,
etych. W tym celu wprowadzimy poj
,
ecie
indeksu drogi zamkni
,
etej w C.
Propozycja 10.1. Dla drogi zamkni
,
etej γ : [a, b] → C poÃl´o˙zmy
Ind
γ
(z) =
1
2πi
Z
γ
dζ
ζ − z
,
z ∈ C \ γ
∗
.
Wtedy
i) Ind
γ
jest funkcj
,
a o warto´sciach caÃlkowitych;
ii) Ind
γ
jest staÃla na ka˙zdej skÃladowej sp´ojnej zbioru C \ γ
∗
;
iii) Ind
γ
≡ 0 na skÃladowej nieograniczonej C \ γ
∗
;
iv) Liczba Ind
γ
(z) jest r´owna liczbie obrot´ow (w kierunku odwrotnym do ruchu
wskaz´owek zegara) wektora o pocz
,
atku w z i ko´
ncu w γ(t), a ≤ t ≤ b, dookoÃla z.
Dow´od. i) PoÃl´o˙zmy
ϕ(t) = exp
µZ
t
a
γ
0
(s)
γ(s) − z
ds
¶
,
t ∈ [a, b],
wtedy ϕ
0
= ϕγ
0
/(γ − z), a st
,
ad (ϕ/(γ − z))
0
= 0 (tam, gdzie γ jest klasy C
1
).
St
,
ad wynika, ˙ze funkcja ϕ/(γ − z) jest staÃla. Korzystaj
,
ac z faktu, ˙ze ϕ(a) = 1,
otrzymujemy
exp
µZ
t
a
γ
0
(s)
γ(s) − z
ds
¶
=
γ(t) − z
γ(a) − z
,
t ∈ [a, b].
Dla t = b oznacza to, ˙ze exp(2πi Ind
γ
(z)) = 1, co jest r´ownowa˙zne temu, ˙ze
Ind
γ
(z) ∈ Z.
ii) Wynika natychmiast z i) i z tego, ˙ze Ind
γ
jest funkcj
,
a ci
,
agÃl
,
a (a dzi
,
eki lematowi
o produkcji funkcji holomorficznych nawet holomorficzn
,
a) na C \ γ
∗
.
iii) Z definicji Ind
γ
Ãlatwo otrzymujemy
lim
|z|→∞
Ind
γ
(z) = 0
i wystarczy skorzysta´c z ii).

FUNKCJE ANALITYCZNE
23
iv) Przez A(t), t ∈ [a, b], oznaczymy caÃlkowity przyrost argumentu wektora
γ(s)−z, gdy s ro´snie od a do t. Znajdziemy podziaÃl a = t
0
< t
1
< · · · < t
n
= b taki,
˙ze γ([t
j−1
, t
j
]) jest zawarte w kole niezawieraj
,
acym z, j = 1, . . . , n. Dla danego j
mo˙zemy wtedy wybra´c logarytm tak, by byÃl ci
,
agÃly na γ([t
j−1
, t
j
]). Otrzymamy
2πi Ind
γ
(z) =
n
X
j=1
Z
t
j
t
j−1
γ
0
(t)
γ(t) − z
dt
=
n
X
j=1
(log(γ(t
j
) − z) − log(γ(t
j−1
) − z))
=
n
X
j=1
µ
log
¯
¯
¯
¯
γ(t
j
) − z
γ(t
j−1
) − z
¯
¯
¯
¯ + i(A(t
j
) − A(t
j−1
))
¶
= i(A(b) − A(a)).
¤
W dalszym ci
,
agu wygodnie b
,
edzie caÃlkowa´c funkcje zespolone po sko´
nczonej
sumie dr´og (np. po brzegu gÃladkiego obszaru wielosp´ojnego). Niech γ
1
, . . . , γ
k
b
,
ed
,
a
drogami w C. Tworz
,
a one Ãla´
ncuch, kt´ory zapisujemy Γ = γ
1
+ · · · + γ
k
. Obrazem
Ãla´
ncucha Γ jest Γ
∗
= γ
∗
1
∪ · · · ∪ γ
∗
k
. Mamy wtedy
(10.1)
Z
Γ
f (z)dz :=
k
X
j=1
Z
γ
j
f (z)dz,
f ∈ C(Γ
∗
),
przy czym praw
,
a stron
,
e mo˙zemy traktowa´c jako formaln
,
a definicj
,
e Ãla´
ncucha Γ,
tzn. jako funkcjonaÃl liniowy okre´slony na C(Γ
∗
). Zauwa˙zmy, ˙ze tak naprawd
,
e do
tej pory dla danej drogi γ interesowaÃl nas wÃla´sciwie tylko funkcjonaÃl
C(γ
∗
) 3 f 7→
Z
γ
f (z)dz ∈ C.
Dlatego te˙z sum
,
e γ
1
+· · ·+γ
k
nale˙zy rozumie´c jako sum
,
e odpowiednich funkcjonaÃl´ow
(a oczywi´scie nie jako sum
,
e algebraiczn
,
a funkcji γ
1
, . . . , γ
k
, kt´ora zreszt
,
a nie mia-
Ãlaby w og´olnym przypadku sensu). W oczywisty spos´ob definiujemy sum
,
e i r´o˙znic
,
e
dw´och Ãla´
ncuch´ow. DÃlugo´sci
,
a Ãla´
ncucha Γ = γ
1
+· · ·+γ
k
jest l(Γ) = l(γ
1
)+· · ·+l(γ
k
).
Jest oczywiste (dzi
,
eki (3.3)), ˙ze norma funkcjonaÃlu (10.1) nie przekracza l(Γ).
Je˙zeli wszystkie drogi γ
1
, . . . , γ
k
s
,
a zamkni
,
ete, to Ãla´
ncuch Γ = γ
1
+ · · · + γ
k
nazywamy cyklem. Na cykle mo˙zemy rozszerzy´c poj
,
ecie indeksu:
Ind
Γ
(z) :=
k
X
j=1
Ind
γ
j
(z) =
1
2πi
Z
Γ
dζ
ζ − z
,
z ∈ C \ Γ
∗
.
Poni˙zsze twierdzenie precyzyjnie charakteryzuje cykle, dla kt´orych zachodzi
twierdzenie caÃlkowe oraz wz´or caÃlkowy Cauchy’ego (jest ono czasami nazywane
twierdzeniem Cauchy’ego-Dixona):
Twierdzenie 10.2. Dla cyklu Γ w obszarze Ω NWSR
i) Ind
Γ
(z) f (z) =
1
2πi
Z
Γ
f (ζ)
ζ − z
dζ,
z ∈ Ω \ Γ,
f ∈ O(Ω) (wz´or caÃlkowy
Cauchy’ego);
ii)
Z
Γ
f (z)dz = 0,
f ∈ O(Ω) (twierdzenie caÃlkowe Cauchy’ego);
iii) Ind
Γ
(z) = 0,
z ∈ C \ Ω.

24
ZBIGNIEW BÃLOCKI
Dow´od. (Dixon, 1971) i)⇒ii) Dla f ∈ O(Ω) i z ∈ Ω \ Γ niech h(ζ) := (ζ − z)f (ζ).
Wtedy korzystaj
,
ac z i) mamy
0 = Ind
Γ
(z) h(z) =
1
2πi
Z
Γ
f (ζ)dζ.
ii)⇒iii) Dla z ∈ C \ Ω funkcja f (ζ) := 1/(ζ − z) jest holomorficzna w Ω.
iii)⇒i) Niech f ∈ O(Ω). Dla z, w ∈ Ω poÃl´o˙zmy
g(z, w) :=
(
f (z)−f (w)
z−w
,
z 6= w,
f
0
(z),
z = w.
Twierdzimy, ˙ze g ∈ C(Ω × Ω). Jest oczywiste, ˙ze funkcja g jest ci
,
agÃla na ∆ =
{(z, w) ∈ Ω × Ω : z = w} oraz na Ω × Ω \ ∆. Dla z, w ∈ K(a, r), z 6= w, gdzie r > 0
jest takie ˙ze K(a, r) ⊂ Ω, ze wzoru Cauchy’ego dla koÃla otrzymamy
g(z, w) − g(a, a) =
1
2πi
Z
∂K(a,r)
·
1
z − w
µ
f (ζ)
ζ − z
−
f (ζ)
ζ − w
¶
−
f (ζ)
(ζ − a)
2
¸
dζ
=
1
2πi
Z
∂K(a,r)
f (ζ)
µ
1
(ζ − z)(ζ − w)
−
1
(ζ − a)
2
¶
dζ.
Wyra˙zenie w nawiasie d
,
a˙zy do 0 jednostajnie na ∂K(a, r), gdy (z, w) → (a, a), a
wi
,
ec g ∈ C(Ω × Ω).
Zdefiniujmy
h(z) :=
1
2πi
Z
Γ
g(ζ, z) dζ,
z ∈ Ω,
1
2πi
Z
Γ
f (ζ)
ζ − z
dζ,
z ∈ C \ Ω.
Zauwa˙zmy, ˙ze
(10.2)
h(z) =
1
2πi
Z
Γ
g(ζ, z) dζ =
1
2πi
Z
Γ
f (ζ)
ζ − z
dζ − Ind
Γ
(z) f (z),
z ∈ Ω \ Γ
∗
.
Z ci
,
agÃlo´sci g wynika, ˙ze h jest ci
,
agÃla w Ω. Dla tr´ojk
,
ata T ⊂ Ω z twierdzenia
Fubiniego mamy
Z
∂T
h(z)dz =
1
2πi
Z
Γ
Z
∂T
g(ζ, z)dz dζ = 0
(dzi
,
eki Wnioskowi 4.3), z twierdzenia Morery otrzymamy zatem holomorficzno´s´c h
w Ω.
Je˙zeli U jest skÃladow
,
a sp´ojn
,
a C \ Γ
∗
tak
,
a, ˙ze U 6⊂ Ω, to dzi
,
eki iii) i Propozycji
10.1.ii mamy Ind
Γ
(z) = 0, z ∈ U , a wi
,
ec z (10.2)
h(z) =
1
2πi
Z
Γ
g(ζ, z) dζ =
1
2πi
Z
Γ
f (ζ)
ζ − z
dζ,
z ∈ U.
Z lematu o produkcji funkcji holomorficznych otrzymamy h ∈ O(U ). ÃL
,
acz
,
ac to z
tym, ˙ze h ∈ O(Ω) wnioskujemy, ˙ze h jest funkcj
,
a caÃlkowit
,
a. Co wi
,
ecej
lim
|z|→∞
h(z) = 0,

FUNKCJE ANALITYCZNE
25
z twierdzenia Liouville’a mamy zatem h ≡ 0. Z (10.2) otrzymujemy i). ¤
M´owimy, ˙ze cykl Γ jest homologiczny zeru w Ω, je˙zeli speÃlniony jest warunek iii)
w Twierdzeniu 10.2.
11. Szeregi Laurenta
Pokazali´smy, ˙ze ka˙zd
,
a funkcj
,
e holomorficzn
,
a w kole mo˙zna przedstawi´c jako sum
,
e
szeregu pot
,
egowego. Poka˙zemy teraz, ˙ze funkcje okre´slone w pier´scieniu
P (z
0
, r, R) := {z ∈ C : r < |z − z
0
| < R} = K(z
0
, R) \ K(z
0
, r)
rozwijaj
,
a si
,
e w uog´olniony szereg pot
,
egowy zawieraj
,
acy r´ownie˙z pot
,
egi ujemne:
Twierdzenie 11.1. (Laurent, 1843, Weierstrass, 1841) Je˙zeli f ∈ O(P (z
0
, r, R)),
gdzie 0 ≤ r < R ≤ ∞, to dla z ∈ P (z
0
, r, R) mamy
f (z) =
∞
X
n=−∞
a
n
(z − z
0
)
n
=
∞
X
n=0
a
n
(z − z
0
)
n
+
∞
X
k=1
a
−k
(z − z
0
)
−k
,
(tzn. oba szeregi s
,
a zbie˙zne), gdzie dla dowolnego ρ ∈ (r, R)
(11.1)
a
n
=
1
2πi
Z
∂B(z
0
,ρ)
f (ζ)
(ζ − z
0
)
n+1
dζ,
n ∈ Z.
Dow´od. Niech r
0
, R
0
b
,
ed
,
a takie, ˙ze r < r
0
< R
0
< R. Wtedy ∂P (z
0
, r
0
, R
0
) jest
cyklem (orientacja dodatnia wzgl
,
edem wn
,
etrza, czyli zgodnie z kierunkiem ruchu
wskaz´owek zegara na ∂K(z
0
, r
0
) i z kierunkiem odwrotnym na ∂K(z
0
, R
0
)) takim,
˙ze
Ind
∂P (z
0
,r
0
,R
0
)
(z) =
½
0,
z ∈ C \ P (z
0
, r
0
, R
0
),
1,
z ∈ P (z
0
, r
0
, R
0
).
SpeÃlniony jest wi
,
ec warunek iii) w Twierdzeniu 10.2 (z Ω = P (z
0
, r, R)). Dzi
,
eki
r´ownowa˙znemu warunkowi ii) dostaniemy teraz niezale˙zno´s´c prawej strony (11.1)
od ρ (bo funkcja podcaÃlkowa jest holomorficzna w P (z
0
, r, R)). Z i) otrzymamy
natomiast dla z ∈ P (z
0
, r
0
, R
0
)
f (z) =
1
2πi
Z
∂P (z
0
,r,R)
f (ζ)
ζ − z
dζ =
1
2πi
ÃZ
∂K(z
0
,R)
−
Z
∂K(z
0
,r)
!
.
Rozumujemy teraz jak w dowodzie Twierdzenia 8.1. Z (7.2) otrzymamy
1
ζ − z
=
∞
X
n=0
(z − z
0
)
n
(ζ − z
0
)
n+1
,
ζ ∈ ∂K(z
0
, R),
−
∞
X
k=1
(ζ − z
0
)
k−1
(z − z
0
)
k
,
ζ ∈ ∂K(z
0
, r),
przy czym zbie˙zno´s´c jest jednostajna wzgl
,
edem ζ na, odpowiednio, ∂K(z
0
, R) i
∂K(z
0
, r). ¤

26
ZBIGNIEW BÃLOCKI
Szereg postaci
(11.2)
∞
X
n=−∞
a
n
(z − z
0
)
n
nazywamy szeregiem Laurenta. Jest on sum
,
a dw´och szereg´ow: cz
,
e´sci regularnej
X
n≥0
a
n
(z − z
0
)
n
= a
0
+ a
1
(z − z
0
) + . . . ,
oraz cz
,
e´sci osobliwej
X
n≤−1
a
n
(z − z
0
)
n
=
a
−1
z − z
0
+
a
−2
(z − z
0
)
2
+ . . .
M´owimy, ˙ze szereg Laurenta (11.2) jest zbie˙zny w z, je˙zeli w z zbie˙zna jest jego
cz
,
e´s´c regularna oraz cz
,
e´s´c osobliwa.
Twierdzenie 11.2. Cz
,
e´s´c regularna szeregu Laurenta (11.2) jest zbie˙zna bezwzgl
,
ed-
nie i lokalnie jednostajnie w kole K(z
0
, R), rozbie˙zna dla ka˙zdego z ∈ C \ K(z
0
, R),
gdzie
R =
1
lim sup
n→∞
|a
n
|
1/n
.
Cz
,
e´s´c osobliwa szeregu Laurenta (11.2) jest zbie˙zna bezwzgl
,
ednie i lokalnie jedno-
stajnie w C \ K(z
0
, r), rozbie˙zna dla ka˙zdego z ∈ K(z
0
, r), gdzie
r = lim sup
k→∞
|a
−k
|
1/k
=
1
lim sup
n→−∞
|a
n
|
1/n
.
Je˙zeli r < R, to szereg Laurenta (11.2) jest zbie˙zny bezwzgl
,
ednie i lokalnie jedno-
stajnie w pier´scieniu P (z
0
, r, R), rozbie˙zny dla ka˙zdego z ∈ C \ P (z
0
, r, R).
Dow´od. Pierwsza cz
,
e´s´c to dokÃladnie Twierdzenie 7.1. Po podstawieniu
w =
1
z − z
0
,
cz
,
e´s´c osobliwa b
,
edzie miaÃla posta´c
X
n≤−1
a
n
(z − z
0
)
n
=
∞
X
k=1
a
−k
w
k
,
a promie´
n zbie˙zno´sci tego szeregu jest r´owny 1/r. St
,
ad wynika druga cz
,
e´s´c twier-
dzenia, za´s trzecia jest natychmiastow
,
a konsekwencj
,
a pierwszych dw´och. ¤
Z Twierdzenia 11.2 wynika w szczeg´olno´sci, ˙ze zbie˙zno´s´c w Twierdzeniu 11.1 jest
bezwzgl
,
edna i lokalnie jednostajna na P (z
0
, r, R).
FUNKCJE ANALITYCZNE
27
Mamy nast
,
epuj
,
aca zasad
,
e identyczno´sci dla szereg´ow Laurenta:
Twierdzenie 11.3. Je˙zeli szeregi Laurenta
∞
X
n=−∞
a
n
(z − z
0
)
n
,
∞
X
n=−∞
b
n
(z − z
0
)
n
s
,
a jednostajnie zbie˙zne do tej samej granicy na okr
,
egu ∂K(z
0
, ρ) dla pewnego ρ > 0,
to a
n
= b
n
dla ka˙zdego n ∈ Z.
Dow´od. Bez straty og´olno´sci mo˙zemy zaÃlo˙zy´c, ˙ze b
n
= 0, n ∈ Z. ZaÃlo˙zenie oznacza,
˙ze mamy jednostajn
,
a zbie˙zno´s´c
(11.3)
∞
X
n=−∞
a
n
ρ
n
e
int
= 0,
t ∈ [0, 2π].
Zbie˙zno´s´c jednostajna implikuje zbie˙zno´s´c w L
2
([0, 2π]). Dla n, m ∈ Z mamy
he
int
, e
imt
i =
Z
2π
0
e
i(n−m)t
dt =
½
0,
n 6= m,
2π,
n = m.
Mno˙z
,
ac skalarnie obie strony (11.3) przez e
imt
otrzymamy a
m
= 0, m ∈ Z. ¤
´
Cwiczenie
Rozwin
,
a´c funkcj
,
e 1/(z
2
− z) w szeregi Laurenta w pier´scieniach {0 <
|z| < 1} oraz {1 < |z| < ∞}.
12. Osobliwo´sci funkcji holomorficznych
M´owimy, ˙ze funkcja holomorficzna f ma osobliwo´s´c izolowan
,
a w punkcie z
0
, je˙zeli
f ∈ O(U \ {z
0
}), gdzie U jest otwartym otoczeniem punktu z
0
w C. Z Twierdzenia
11.1 (dla r = 0 oraz R takiego, ˙ze K(z
0
, R) ⊂ U ) wynika, ˙ze w otoczeniu z
0
funkcj
,
e
f mo˙zemy rozwin
,
a´c w szereg Laurenta
(12.1)
f (z) =
∞
X
n=−∞
a
n
(z − z
0
)
n
,
gdzie wsp´oÃlczynniki a
n
s
,
a wyznaczone jednoznacznie (dzi
,
eki Twierdzeniu 11.3; s
,
a
one dane przez (11.1)). Je˙zeli a
n
= 0 dla n = −1, −2, . . . , to m´owimy, ˙ze f ma
osobliwo´s´c pozorn
,
a w z
0
. Je˙zeli istnieje m ≥ 1 takie, ˙ze a
−m
6= 0 oraz a
n
= 0
dla n < −m, to m´owimy, ˙ze f ma biegun rz
,
edu m w z
0
(je˙zeli m = 1, to biegun
nazywamy prostym). W pozostaÃlych przypadkach (tzn., gdy istnieje niesko´
nczenie
wiele n < 0 takich, ˙ze a
n
6= 0) m´owimy, ˙ze f ma istotn
,
a osobliwo´s´c w z
0
.
Jest jasne, ˙ze funkcja holomorficzna ma pozorn
,
a osobliwo´s´c w z
0
wtedy i tylko
wtedy, gdy przedÃlu˙za si
,
e do funkcji holomorficznej w otoczeniu z
0
(z tego powodu
osobliwo´sci pozorne s
,
a r´ownie˙z nazywane usuwalnymi). Je˙zeli f ma biegun rz
,
edu
m w z
0
, to
(12.2)
f (z) =
a
−m
(z − z
0
)
m
+
a
−m+1
(z − z
0
)
m−1
+ . . . =
h(z)
(z − z
0
)
m
,
gdzie h jest funkcj
,
a holomorficzn
,
a w otoczeniu z
0
tak
,
a, ˙ze h(z
0
) = a
−m
6= 0.

28
ZBIGNIEW BÃLOCKI
Z drugiej strony, je˙zeli g jest holomorficzna w otoczeniu z
0
, g 6≡ 0 i g(z
0
) = 0, to
g(z) = b
m
(z − z
0
)
m
+ b
m+1
(z − z
0
)
m+1
+ · · · = (z − z
0
)
m
e
h(z),
gdzie m ≥ 1, za´s e
h jest funkcj
,
a holomorficzn
,
a w otoczeniu z
0
tak
,
a, ˙ze e
h(z
0
) = a
m
6=
0. Takie m nazywamy krotno´sci
,
a zera funkcji g w z
0
. Jest to r´ownowa˙zne temu, ˙ze
g(z
0
) = g
0
(z
0
) = · · · = g
(m−1)
(z
0
) = 0, g
(m)
(z
0
) 6= 0
(dzi
,
eki wzorowi Taylora).
Z powy˙zszych rozwa˙za´
n wida´c, ˙ze dla funkcji holomorficznej f w otoczeniu z
0
mamy
f ma w z
0
zero krotno´sci m ⇔ 1/f ma w z
0
biegun rz
,
edu m.
Og´olniej, je˙zeli f, g s
,
a holomorficzne w otoczeniu z
0
i maj
,
a w z
0
zera krotno´sci,
odpowiednio, m i k, to f /g ma w z
0
zero krotno´sci m − k, je˙zeli m > k, oraz
biegun rz
,
edu k − m, je˙zeli m < k. (Je˙zeli m = k, to f /g jest funkcj
,
a holomorficzn
,
a
w otoczeniu z
0
nieznikaj
,
ac
,
a w z
0
). W szczeg´olno´sci, funkcja f /g nie mo˙ze mie´c
istotnej osobliwo´sci.
PrzykÃlad. Funkcja
e
1/z
=
∞
X
k=0
1
k!z
k
ma istotn
,
a osobliwo´s´c w 0.
Jak wynika z poprzednich rezultat´ow (z Twierdze´
n 4.1 i 6.1), ka˙zda funkcja
holomorficzna posiadaj
,
aca osobliwo´s´c izolowan
,
a w z
0
, kt´or
,
a mo˙zna przedÃlu˙zy´c do
funkcji ci
,
aglej w z
0
, ma w z
0
osobliwo´s´c pozorn
,
a. Ten fakt udowodniÃl Riemann
w 1851 r. Poni˙zszy, og´olniejszy rezultat jest nazywany twierdzeniem Riemanna o
usuwaniu osobliwo´sci:
Twierdzenie 12.1. Przypu´s´cmy, ˙ze funkcja holomorficzna f ma w z
0
osobliwo´s´c
izolowan
,
a oraz jest ograniczona w otoczeniu z
0
. Wtedy f ma osobliwo´s´c pozorn
,
a w
z
0
.
Dow´od. Niech h(z) := (z − z
0
)f (z). Wtedy dla pewnego otoczeniu U punktu z
0
mamy h ∈ O(U \ {z
0
}) ∩ C(U ), a st
,
ad h ∈ O(U ). Poniewa˙z h ma w z
0
zero
krotno´sci ≥ 1, a z − z
0
zero krotno´sci 1, to f (z) = h(z)/(z − z
0
) ma w z
0
osobliwo´s´c
pozorn
,
a. ¤
Twierdzenie 12.2. (Casorati, 1868, Weierstrass, 1876, Sochocki, 1873) Je˙zeli
funkcja holomorficzna f ma w z
0
istotn
,
a osobliwo´s´c, to dla ka˙zdego odp. maÃlego
otwartego otoczenia V punktu z
0
, zbi´or f (V \ {z
0
}) jest g
,
esty w C.
Dow´od. Przypu´s´cmy, ˙ze twierdzenie nie jest prawdziwe, tzn. istnieje w
0
∈ C oraz
ε > 0 takie, ˙ze K(w
0
, ε) ∩ f (V \ {z
0
}) = ∅. Oznacza to, ˙ze |f − w
0
| ≥ ε w V \ {z
0
}.
Funkcja g := 1/(f −w
0
) jest wi
,
ec ograniczona w V \{z
0
}, z Twierdzenia 12.1 wynika
zatem, ˙ze ma w z
0
pozorn
,
a osobliwo´s´c. Czyli funkcja f = w
0
+ 1/g nie mo˙ze mie´c
w z
0
istotnej osobliwo´sci - sprzeczno´s´c. ¤

FUNKCJE ANALITYCZNE
29
Uwaga. Znacznie mocniejsze (ale i trudniejsze do udowodnienia) ni˙z Twierdzenie
12.2 jest tzw. wielkie twierdzenie Picarda (1879): przy zaÃlo˙zeniach Twierdzenia
12.2 zbi´or f (V \ {z
0
}) omija co najwy˙zej jedn
,
a warto´s´c w C.
´
Cwiczenie
Zweryfikowa´c wielkie twierdzenie Picarda w nast
,
epuj
,
acych przypad-
kach: e
1/z
(omija jedn
,
a warto´s´c), cos(1/z) (nie omija ˙zadnej warto´sci).
Mo˙zemy teraz skojarzy´c rodzaje osobliwo´sci izolowanych z istnieniem odpowied-
nich granic:
Twierdzenie 12.3. ZaÃl´o˙zmy, ˙ze funkcja holomorficzna f ma osobliwo´s´c izolowan
,
a
w z
0
. Wtedy
i) f ma pozorn
,
a osobliwo´s´c w z
0
⇔ istnieje lim
z→z
0
f (z) ∈ C;
ii) f ma biegun w z
0
⇔ lim
z→z
0
f (z) = ∞ (tzn. lim
z→z
0
|f (z)| = ∞);
iii) f ma istotn
,
a osobliwo´s´c w z
0
⇔ nie istnieje lim
z→z
0
f (z) (ani z C ani ∞).
Dow´od. i) Natychmiastowa konsekwencja Twierdzenia 12.1 (a nawet Twierdze´
n 4.1
i 6.1).
ii) Z (12.2) wynika ⇒, natomiast ⇐ wnioskujemy z i) (f nie ma pozornej oso-
bliwo´sci) i Twierdzenia 12.2 (f nie ma istotnej osobliwo´sci).
iii) Natychmiastowa konsekwencja i) oraz ii). ¤
13. Twierdzenie o residuach
Niech f b
,
edzie funkcj
,
a holomorficzn
,
a posiadaj
,
ac
,
a osobliwo´s´c izolowan
,
a w z
0
.
W pewnym otoczeniu z
0
mamy rozwini
,
ecie f w szereg Laurenta (12.1), kt´ory jest
jednostajnie zbie˙zny na ∂K(z
0
, r) dla r > 0 odp. maÃlego. Mamy wtedy
(13.1)
Z
∂K(z
0
,r)
f (z)dz =
∞
X
n=−∞
a
n
Z
∂K(z
0
,r)
(z − z
0
)
n
dz = 2πia
−1
.
Liczb
,
e a
−1
z rozwini
,
ecia (12.1) nazywamy residuum funkcji f w punkcie z
0
i oz-
naczamy res
z
0
f .
´
Cwiczenie
Skonstruowa´c funkcj
,
e f ∈ O(C \ {0, 1}) maj
,
ac
,
a istotn
,
a osobliwo´s´c w
0, biegun rz
,
edu 2 w 1 oraz tak
,
a, ˙ze res
1
f = 3.
Przypu´s´cmy, ˙ze f ma w z
0
biegun rz
,
edu m. Wtedy
f (z) =
a
−m
(z − z
0
)
m
+
a
−m+1
(z − z
0
)
m−1
+ . . . =
h(z)
(z − z
0
)
m
,
gdzie funkcja
h(z) = a
−m
+ a
−m+1
(z − z
0
) + . . .
jest holomorficzna w otoczeniu z
0
. Ze wzoru Taylora otrzymamy
a
−m+k
=
h
(k)
(z
0
)
k!
,
k = 0, 1, . . .

30
ZBIGNIEW BÃLOCKI
Dla k = m − 1 dostaniemy nast
,
epuj
,
acy rezultat, kt´ory jest podstawowym narz
,
e-
dziem przy obliczaniu residu´ow w przypadku biegun´ow:
Propozycja 13.1. Je˙zeli funkcja holomorficzna f ma biegun rz
,
edu m w z
0
, to
res
z
0
f =
1
(m − 1)!
µ
d
dz
¶
m−1
¡
(z − z
0
)
m
f (z)
¢
¯
¯
¯
¯
¯
z=z
0
.
¤
SformuÃlujemy teraz i udowodnimy twierdzenie o residuach:
Twierdzenie 13.2. Niech Γ b
,
edzie cyklem homologicznym zeru w obszarze Ω.
ZaÃl´o˙zmy, ˙ze z
1
, . . . , z
k
∈ Ω \ Γ (z
j
6= z
l
dla j 6= l) i ˙ze f ∈ O(Ω \ {z
1
, . . . , z
k
}).
Wtedy
Z
Γ
f (z)dz = 2πi
k
X
j=1
Ind
Γ
(z
j
) res
z
j
f.
Dow´od. Znajdziemy r > 0 takie, ˙ze K(z
j
, r) ∩ K(z
l
, r) = ∅ dla j 6= l oraz K(z
j
, r) ∩
Γ = ∅, j, l = 1, . . . , k. Zastosujemy Twierdzenie 10.2 dla cyklu
e
Γ := Γ −
k
X
j=1
Ind
Γ
(z
j
) ∂K(z
j
, r)
i obszaru Ω \ {z
1
, . . . , z
k
}. SpeÃlniony jest warunek iii), zatem z ii)
0 =
Z
e
Γ
f (z)dz =
Z
Γ
f (z)dz −
k
X
j=1
Ind
Γ
(z
j
)
Z
∂K(z
j
,r)
f (z)dz
i wystarczy skorzysta´c z (13.1). ¤
13a. Obliczanie pewnych caÃlek rzeczywistych
Twierdzenie o residuach pozwala obliczy´c wiele rzeczywistych caÃlek okre´slonych.
Poni˙zej przedstawimy kilka rodzaj´ow takich caÃlek. B
,
edzie to sÃlu˙zyÃlo przede wszyst-
kim zaprezentowaniu mo˙zliwych metod zastosowania twierdzenia o residuach, z caÃl
,
a
pewno´scia poni˙zsza lista nie wyczerpuje przypadk´ow, gdzie mo˙zna je u˙zy´c.
I) CaÃlki postaci
Z
2π
0
R(cos t, sin t)dt,
gdzie R jest funkcj
,
a wymiern
,
a (czyli R = P/Q, gdzie P i Q s
,
a wielomianami dw´och
zmiennych; wielomian Q w tym przypadku nie mo˙ze mie´c zer na rzeczywistym
okr
,
egu jednostkowym). Podstawiaj
,
ac z = e
it
otrzymamy
cos t = Re z =
z + z
2
=
z + 1/z
2
,
sin t = Im z =
z − z
2i
=
z − 1/z
2i
FUNKCJE ANALITYCZNE
31
oraz dz = ie
it
dt = izdt. Mamy wi
,
ec
Z
2π
0
R(cos t, sin t)dt =
Z
∂K(0,1)
R
µ
z + 1/z
2
,
z − 1/z
2i
¶
dz
iz
=
Z
∂K(0,1)
e
R(z)dz,
gdzie e
R jest funkcj
,
a wymiern
,
a, nie maj
,
ac
,
a osobliwo´sci na ∂K(0, 1).
´
Cwiczenie
Pokaza´c, ˙ze
Z
2π
0
sin
2
t
5 + 4 cos t
dt =
π
4
.
II) CaÃlki postaci
Z
∞
−∞
P (x)
Q(x)
dx,
gdzie P, Q s
,
a wielomianami rzeczywistymi takimi, ˙ze Q 6= 0 na R oraz deg Q ≥
deg P + 2 (mamy wtedy pewno´s´c, ˙ze funkcja P/Q jest sumowalna na R). Dla
R > 0 przez C
+
R
:= {z ∈ ∂K(0, R) : Im z ≥ 0} oznaczmy g´orn
,
a poÃlow
,
e okr
,
egu
∂K(0, R) (o pocz
,
atku w R i ko´
ncu w −R). Dla R odp. du˙zego wielomian Q(z) nie
ma zer na ∂K(0, R) oraz
¯
¯
¯
¯
¯
Z
C
+
R
P (z)
Q(z)
dz
¯
¯
¯
¯
¯
≤ CR
deg P −deg Q
πR → 0,
gdy R → ∞. Mamy wi
,
ec
Z
∞
−∞
P (x)
Q(x)
dx = lim
R→∞
Z
[−R,R]+C
+
R
P (z)
Q(z)
dz
co Ãlatwo policzymy przy pomocy twierdzenia o residuach.
´
Cwiczenie
Pokaza´c, ˙ze
Z
∞
−∞
dx
x
4
+ 1
=
π
√
2
.
III) CaÃlki postaci
(13.2)
Z
∞
−∞
P (x) cos x
Q(x)
dx,
Z
∞
−∞
P (x) sin x
Q(x)
dx,
gdzie P, Q s
,
a wielomianami rzeczywistymi. Je˙zeli Q 6= 0 na R oraz deg Q ≥ deg P +
2, to funkcje podcaÃlkowe w (13.2) s
,
a sumowalne. Zauwa˙zmy, ˙ze caÃlki (13.2) s
,
a,
odpowiednio, cz
,
e´sci
,
a rzeczywist
,
a i urojon
,
a caÃlki
Z
∞
−∞
P (x)e
ix
Q(x)
dx.
W dodatku, dzi
,
eki temu, ˙ze |e
iz
| ≤ 1, gdy Im z ≥ 0, mamy
(13.3)
¯
¯
¯
¯
¯
Z
C
+
R
P (z)e
iz
Q(z)
dz
¯
¯
¯
¯
¯
≤ CR
deg P −deg Q
πR → 0
32
ZBIGNIEW BÃLOCKI
(zauwa˙zmy, ˙ze nie mogliby´smy powt´orzy´c tego rozumowania, gdyby´smy zamiast
e
iz
wzi
,
eli funkcje, odpowiednio, cos z i sin z). Podobnie jak poprzednio wystarczy
teraz skorzysta´c z twierdzenia o residuach caÃlkuj
,
ac funkcj
,
e P (z)e
iz
/Q(z) po brzegu
odp. p´oÃlkoÃla bior
,
ac cz
,
e´sci rzeczywiste i urojone.
´
Cwiczenie
Pokaza´c, ˙ze
Z
∞
0
cos(3x)
x
2
+ 4
dx =
π
4e
6
.
Je˙zeli wielomiany P, Q s
,
a takie, ˙ze Q 6= 0 na R i deg Q = deg P + 1, to mo˙zna
pokaza´c, ˙ze funkcje podcaÃlkowe w (13.2) nie s
,
a sumowalne na R. Poka˙zemy jednak,
˙ze w tym wypadku istniej
,
a warto´sci gÃl´owne caÃlek (13.2) (je˙zeli istnieje granica
lim
a
0
→a
−
b
0
→b
+
Z
b
0
a
0
f (x)dx,
to nazywamy j
,
a warto´sci
,
a gÃl´own
,
a caÃlki
R
b
a
f (x)dx i oznaczamy tak˙ze
R
b
a
f (x)dx).
Powtarzamy poprzednie rozumowanie korzystaj
,
ac z nast
,
epuj
,
acego lematu Jordana;
dostaniemy ponownie formuÃl
,
e (13.4).
Lemat 13.3. Je˙zeli wielomiany P, Q s
,
a takie ˙ze deg Q ≥ deg P + 1, to
lim
R→∞
Z
C
+
R
P (z)e
iz
Q(z)
dz = 0.
Dow´od. B
,
edziemy szacowa´c troch
,
e dokÃladniej ni˙z w (13.3). Dla z = x + iy ∈ C
+
R
i R odp. du˙zego mamy |P (z)/Q(z)| ≤ C/R oraz |e
iz
| = e
−y
. Parametryzuj
,
ac C
+
R
przez Re
it
, t ∈ [0, π], otrzymamy
(13.5)
¯
¯
¯
¯
¯
Z
C
+
R
P (z)e
iz
Q(z)
dz
¯
¯
¯
¯
¯
≤ C
Z
π
0
e
−R sin t
dt.
Teza lematu wynika teraz np. z twierdzenia Lebesgue’a o zbie˙zno´sci ograniczo-
nej. ¤
´
Cwiczenie
Udowodni´c zbie˙zno´s´c prawej strony (13.5) do 0 bez stosowania twier-
dzenia Lebesgue’a o zbie˙zno´sci ograniczonej: korzystaj
,
ac z tego, ˙ze − sin t ≤ −2t/π
dla t ∈ [0, π/2], pokaza´c, ˙ze
Z
π
0
e
−R sin t
dt ≤ π
1 − e
−R
R
.
Mo˙zemy obliczy´c warto´sci gÃl´owne caÃlek (13.2) dla wielomian´ow rzeczywistych
P, Q takich, ˙ze deg Q ≥ deg P + 1 dopuszczaj
,
ac dodatkowo mo˙zliwo´s´c zerowania
si
,
e wielomianu Q na R (przez warto´s´c gÃl´own
,
a takiej caÃlki rozumiemy granic
,
e caÃlek
po sko´
nczonej sumie odpowiednich przedziaÃl´ow zwartych). Mo˙zemy to zrobi´c w
przypadku, gdy funkcja Q(z) ma pojedyncze zera na R. Wynika to z nast
,
epuj
,
acego
lematu:
Lemat 13.4. ZaÃl´o˙zmy, ˙ze funkcja holomorficzna f ma prosty biegun w z
0
i ˙ze
0 ≤ α < β ≤ 2π. Dla r > 0 niech γ
r
(t) := z
0
+ re
it
, α ≤ t ≤ β. Wtedy
lim
r→0
+
Z
γ
r
f (z)dz = i(β − α)res
z
0
f.

FUNKCJE ANALITYCZNE
33
Dow´od. Znajdziemy funkcj
,
e holomorficzn
,
a g w otoczeniu z
0
tak
,
a, ˙ze
f (z) =
a
1
z − z
0
+ g
0
(z).
Wtedy dla r > 0 odp. maÃlego mamy
Z
γ
r
f (z)dz = i(β − α)a
−1
+ g(z
0
+ re
iβ
) − g(z
0
+ re
iα
)
i przy r → 0 dostaniemy to co trzeba. ¤
´
Cwiczenie
Pokaza´c, ˙ze (warto´s´c gÃl´owna)
Z
∞
−∞
x sin(2x)
x
2
− 1
dx = π cos 2.
IV) CaÃlki postaci
(13.6)
Z
∞
0
P (x)
x
a
Q(x)
dx,
gdzie 0 < a < 1, za´s P, Q s
,
a wielomianami rzeczywistymi takimi, ˙ze deg Q ≥
deg P + 1 oraz Q 6= 0 na [0, ∞). Przy takich zaÃlo˙zeniach funkcja podcaÃlkowa jest
sumowalna na (0, ∞). Rozpatrzmy funkcj
,
e
g(z) := z
a
= e
a log z
= e
a(log |z|+iarg z)
= |z|
a
e
iaarg z
.
Wybieramy argument z z przedziaÃlu (0, 2π), tak, ˙ze g ∈ O(C \ [0, ∞)). Dla x ∈
(0, ∞) mamy
g
+
(x) : = lim
y→0
+
g(x + iy) = x
a
,
g
−
(x) : = lim
y→0
−
g(x + iy) = e
2πai
x
a
.
Mo˙zna pokaza´c
´
Cwiczenie
, ˙ze przy powy˙zszych zaÃlo˙zeniach mamy
lim
R→∞
Z
∂K(z
0
,R)
P (z)
z
a
Q(z)
dz = lim
r→0
+
Z
∂K(z
0
,r)
P (z)
z
a
Q(z)
dz = 0.
CaÃlkuj
,
ac funkcj
,
e P (z)/(z
a
Q(z)) po cyklu ∂K(0, R) + [R, r] − ∂K(0, r) + [r, R], przy
czym rozpatrujemy warto´sci g
−
na [R, r] oraz g
+
na [r, R], obliczymy (13.6).
´
Cwiczenie
Pokaza´c, ˙ze
Z
∞
0
√
x
x
2
+ 1
dx =
π
√
2
.
Podobnie jak poprzednio, korzystaj
,
ac z Lematu 13.4, mo˙zemy tak˙ze policzy´c
warto´s´c gÃl´own
,
a caÃlki (13.6), je˙zeli Q ma pojedyncze zera na (0, ∞).
´
Cwiczenie
Pokaza´c, ˙ze
Z
∞
0
√
x
x
2
− 1
dx =
π
2
.
Przy pomocy twierdzenia o residuach mo˙zna policzy´c wiele innych rodzaj´ow
caÃlek okre´slonych.
34
ZBIGNIEW BÃLOCKI
´
Cwiczenie
CaÃlkuj
,
ac po odpowiednio zmodyfikowanym brzegu p´oÃlkola K(0, R) ∩
{Re z > 0} pokaza´c, ˙ze
Z
∞
0
log x
x
2
− 1
dx = −
π
2
4
.
´
Cwiczenie
CaÃlkuj
,
ac funkcj
,
e e
az
/(1 + e
z
) po brzegu prostok
,
ata o wierzchoÃlkach w
±R, ±R + 2πi pokaza´c, ˙ze
Z
∞
−∞
e
ax
1 + e
x
dx =
π
sin(aπ)
,
0 < a < 1.
´
Cwiczenie
Pokaza´c, ˙ze
Z
∞
−∞
e
ax
1 − e
x
dx = π cot(aπ),
0 < a < 1.
´
Cwiczenie
CaÃlkuj
,
ac funkcj
,
e 1/(1 + z
3
) po brzegu zbioru {ρe
it
: 0 ≤ t ≤ 2π/3, 0 ≤
ρ ≤ R} pokaza´c, ˙ze
Z
∞
0
dx
1 + x
3
=
2π
√
3
9
.
14. Lokalizowanie zer funkcji holomorficznych
Przedstawimy teraz pewne og´olne wÃlasno´sci funkcji holomorficznych, kt´ore mo˙z-
na udowodni´c przy pomocy twierdzenia o residuach. Pierwsz
,
a z nich b
,
edzie zasada
argumentu, kt´ora pozwala lokalizowa´c zera oraz bieguny funkcji holomorficznych.
Przed jej sformuÃlowaniem jedna uwaga techniczna: je˙zeli Γ = γ
1
+ · · · + γ
k
jest
Ãla´
ncuchem, a f funkcj
,
a holomorficzn
,
a w otoczeniu Γ
∗
, to przez f ◦ Γ rozumiemy
Ãla´
ncuch f ◦ γ
1
+ · · · + f ◦ γ
k
. Jest oczywiste, ˙ze je˙zeli Γ jest cyklem, to jest nim
tak˙ze f ◦ Γ.
Wprowadzamy jeszcze jedn
,
a definicj
,
e: funkcj
,
e f nazywamy meromorficzn
,
a w
obszarze Ω, je˙zeli istnieje zbi´or dyskretny A ⊂ Ω taki, ˙ze f jest holomorficzna w
Ω \ A oraz w ka˙zdym punkcie A funkcja f ma albo biegun albo pozorn
,
a osobliwo´s´c.
Twierdzenie 14.1. ZaÃl´o˙zmy, ˙ze D jest ograniczonym obszarem w C takim, ˙ze
∂D = Γ
∗
dla pewnego cyklu takiego, ˙ze Ind
Γ
(z) = 1 dla z ∈ D. Niech f b
,
edzie
funkcj
,
a meromorficzn
,
a w otoczeniu D nie maj
,
ac
,
a zer ani biegun´ow na ∂D. Wtedy
Ind
f ◦Γ
(0) = Z − B,
gdzie Z oznacza liczb
,
e zer funkcji f w D liczonych razem z krotno´sciami, natomiast
B sum
,
e rz
,
ed´ow wszystkich biegun´ow funkcji f w D.
Dow´od. Zauwa˙zmy, ˙ze (podobnie jak w dowodzie Twierdzenia 10.8)
Ind
f ◦Γ
(0) =
1
2πi
Z
Γ
f
0
(ζ)
f (ζ)
dζ.

FUNKCJE ANALITYCZNE
35
Do obliczenia tej caÃlki wykorzystamy twierdzenie o residuach. Zauwa˙zmy, ˙ze funk-
cja podcaÃlkowa f
0
/f ma osobliwo´sci dokÃladnie tam, gdzie f ma zera lub bieguny.
Je˙zeli f ma w z
0
zero krotno´sci m, to, zapisuj
,
ac f (z) = (z − z
0
)
m
h(z), gdzie
h(z
0
) 6= 0, mamy
f
0
(z)
f (z)
=
m
z − z
0
+
h
0
(z)
h(z)
,
a zatem res
z
0
(f
0
/f ) = m. Powy˙zsze rozumowanie dziaÃla tak˙ze, gdy m jest ujemn
,
a
liczb
,
a caÃlkowit
,
a. Oznacza to, ˙ze je˙zeli f ma w z
0
biegun rz
,
edu k, to res
z
0
(f
0
/f ) =
−k. Wystarczy teraz skorzysta´c z twierdzenia o residuach. ¤
PrzykÃlad. Szukamy ile pierwiastk´ow w p´oÃlpÃlaszczy´znie {Re z ≥ 0} ma wielomian
P (z) := z
4
+ 2z
3
+ 3z
2
+ z + 2. Dla R odp. du˙zego badamy ile razy obraz przez P
brzegu p´oÃlkola {|z| ≤ R, Re z ≥ 0}. Dla t ∈ R mamy
P (it) = t
4
− 3t
2
+ 2 + it(1 − 2t
2
).
Sprawdzamy najpierw kiedy P (it), gdy t przechodzi od R do −R, przecina p´oÃlosie,
dostaniemy nast
,
epuj
,
ac
,
a tabel
,
e:
t
Re P (it)
Im P (it)
R
++
+
√
2
0
+
1
0
+
√
2/2
+
0
0
+
0
−
√
2/2
+
0
−1
0
−
−
√
2
0
−
−R
++
−
Pierwsza i ostatnia linia oznaczaj
,
a, ˙ze cz
,
e´s´c rzeczywista jest znacznie wi
,
eksza ni˙z
cz
,
e´s´c urojona, tzn. argument P (iR) d
,
a˙zy do 0, gdy R → ±∞. Z powy˙zszego za-
chowania si
,
e krzywej P (it) wnioskujemy, ˙ze ,,przychodzi z kierunku wschodniego i
tam wraca” nie obracaj
,
ac si
,
e przy tym wok´oÃl zera. Poniewa˙z dla du˙zych z wielo-
mian P (z) zachowuje si
,
e jak cz
,
e´s´c wiod
,
aca z
4
, kt´ora dla z = Re
it
, 0 ≤ t ≤ π,
obraca si
,
e dwa razy wok´oÃl zera, wnioskujemy, ˙ze w rozpatrywanym obszarze P
ma dwa pierwiastki (liczone z krotno´sciami). Pozostaje jeszcze pytanie czy istnieje
pierwiastek podw´ojny? Je˙zeli tak, to speÃlnia on ukÃlad r´owna´
n
½
z
4
+ 2z
3
+ 3z
2
+ z + 2 = 0
4z
3
+ 6z
2
+ 6z + 1 = 0,
kt´ory, jak mo˙zna pokaza´c
´
Cwiczenie
, nie ma rozwi
,
aza´
n.
´
Cwiczenie
Znale´z´c liczb
,
e pierwiastk´ow wielomianu 2z
4
+ z
3
− 5z
2
+ z + 2 w p´oÃl-
pÃlaszczy´znie {Re z < 0}.

36
ZBIGNIEW BÃLOCKI
Twierdzenie 14.2. (Rouch´e, 1862) Niech D b
,
edzie ograniczonym obszarem w C.
ZaÃl´o˙zmy, ˙ze f, g s
,
a funkcjami holomorficznymi w D, ci
,
agÃlymi na D i takimi, ˙ze
|g| < |f | na ∂D. Wtedy f i f + g maj
,
a tyle samo zer w D liczonych z krotno´sciami.
Dow´od. Dzi
,
eki Lematowi 10.3 mo˙zemy zaÃlo˙zy´c, ˙ze D jest jak w Twierdzeniu 14.1,
natomiast f i g s
,
a holomorficzne w otoczeniu D. Dla t ∈ [0, 1] na Γ
∗
= ∂D mamy
|f + tg| ≥ |f | − t|g| > 0. Funkcja
[0, 1] 3 t 7−→ Ind
(f +tg)◦Γ
(0) =
1
2πi
Z
Γ
f
0
(ζ) + tg
0
(ζ)
f (ζ) + tg(ζ)
dζ ∈ Z,
jest wi
,
ec ci
,
agÃla, musi by´c zatem staÃla. Dla t = 0 i t = 1 z zasady argumentu
dostaniemy tez
,
e. ¤
´
Cwiczenie
Znale´z´c liczb
,
e pierwiastk´ow wielomianu z
6
+ 4z
2
− 1 w kole K(0, 1).
Korzystaj
,
ac z twierdzenia Rouch´ego mo˙zna poda´c kolejny dow´od zasadniczego
twierdzenia algebry: je˙zeli P (z) = a
0
+a
1
z+· · ·+a
n
z
n
, a
n
6= 0, n ≥ 1, jest wielomia-
nem zespolonym, to znajdziemy R > 0 takie, ˙ze |a
0
+a
1
z +· · ·+a
n−1
z
n−1
| < |a
n
|R
n
dla z ∈ ∂K(0, R). Wnioskujemy, ˙ze P ma w K(0, R) tyle samo zer liczonych z
krotno´sciami co a
n
z
n
, czyli n.
Mo˙zemy teraz opisa´c topologiczne zachowanie si
,
e funkcji holomorficznych w
pobli˙zu zera krotno´sci m:
Twierdzenie 14.3. Je˙zeli funkcja holomorficzna f ma w z
0
zero krotno´sci m, to
istnieje otoczeniu U punktu z
0
takie, ˙ze odwzorowanie f jest m-krotne na U \ {z
0
}
(tzn. dla ka˙zdego w ∈ f (U ) \ {0}) zbi´or f
−1
(w) ∩ (U \ {z
0
}) jest m-elementowy).
Dow´od. Zapiszmy f (z) = a
m
(z − z
0
)
m
+ g(z), gdzie a
m
6= 0, za´s g jest funkcj
,
a
holomorficzn
,
a w otoczeniu z
0
tak
,
a, ˙ze |g(z)| ≤ C|z − z
0
|
m+1
. Dla r > 0 odp.
maÃlego mamy ρ := |a
m
|r
m
− Cr
m+1
> 0. Dla w ∈ K(0, ρ) mamy
|g(z) − w| < Cr
m+1
+ ρ = |a
m
(z − z
0
)
m
|,
z ∈ ∂K(z
0
, r),
a wi
,
ec z twierdzenia Rouch´ego wynika, ˙ze funkcja f − w ma w K(z
0
, r) m zer
liczonych z krotno´sciami. Je˙zeli kt´ore´s z tych zer nie jest pojedyncze, to mamy
w nim f
0
= 0. Dla r > 0 odp. maÃlego mamy jednak f
0
6= 0 na K(z
0
, r) \ {z
0
}
(bo inaczej z zasady identyczno´sci funkcja f byÃlaby staÃla, co jest niemo˙zliwe w
naszym przypadku), czyli tam wszystkie zera musz
,
a by´c pojedyncze. Bierzemy
wtedy U := f
−1
(K(0, ρ)) ∩ K(z
0
, r). ¤
15. Odwzorowania konforemne
Niech D b
,
edzie obszarem w C. Odwzorowanie f : D → C nazywamy lokalnie
konforemnym, je˙zeli f jest lokalnym dyfeomorfizmem klasy C
1
oraz f zachowuje
k
,
aty oraz orientacj
,
e, tzn. je˙zeli γ
1
, γ
2
: (−ε, ε) → D s
,
a krzywymi klasy C
1
takimi,
˙ze γ
1
(0) = γ
2
(0), γ
0
1
6= 0, γ
0
2
6= 0, to k
,
at zorientowany pomi
,
edzy wektorami γ
0
1
(0)
a γ
0
2
(0) jest r´owny k
,
atowi zorientowanemu pomi
,
edzy wektorami (f ◦ γ
1
)
0
(0) a (f ◦
γ
2
)
0
(0).
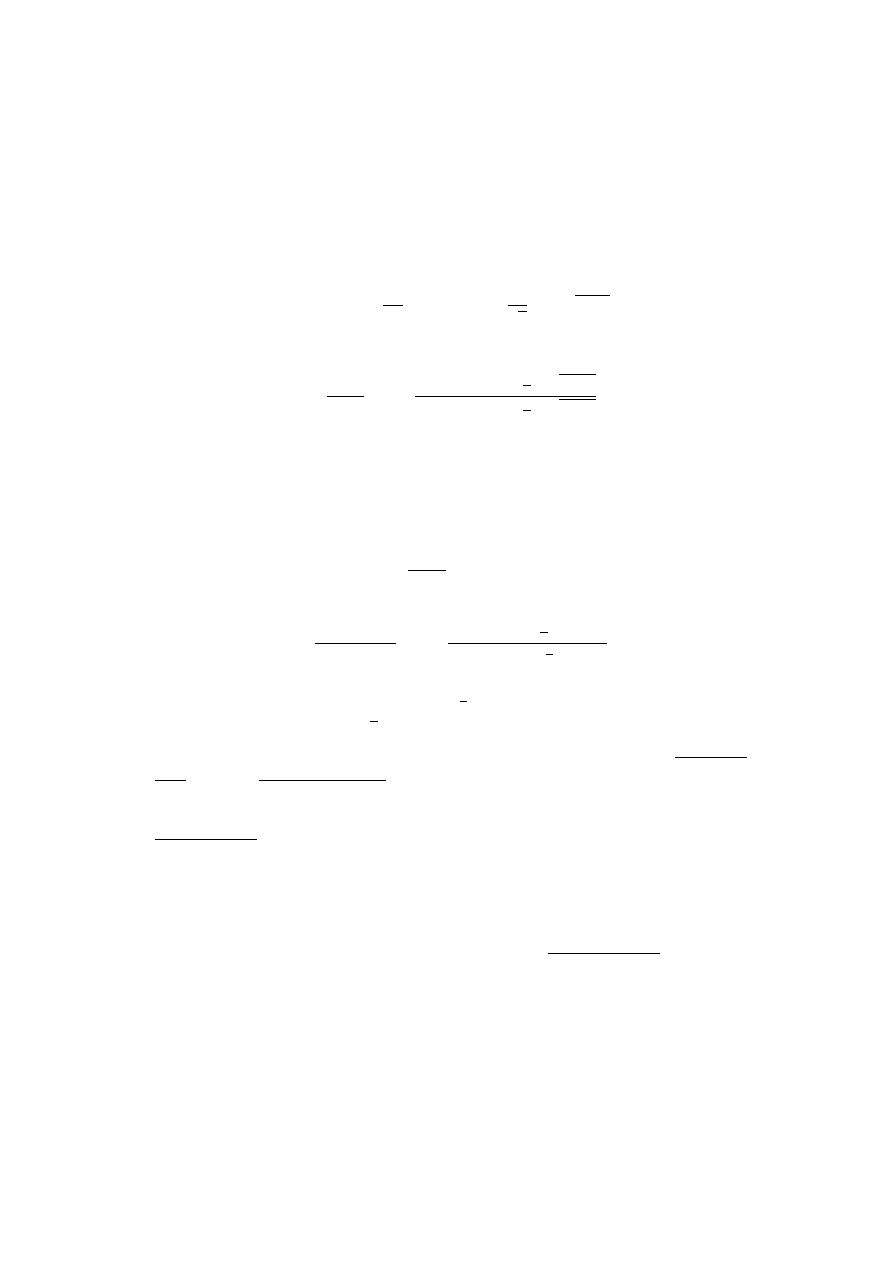
FUNKCJE ANALITYCZNE
37
Propozycja 15.1. Dla odwzorowania f : D → C NWSR
i) f jest lokalnie konforemne;
ii) f ∈ O(D), f
0
6= 0;
iii) f ∈ O(D), f jest lokalnie jednokrotne.
Dow´od. ii)⇔iii) wynika natychmiast z Propozycji 2.4 i Twierdzenia 14.3.
i)⇔ii) Przypomnijmy (zob. (2.7)), ˙ze dla dowolnej krzywej γ mamy
(f ◦ γ)
0
(0) =
∂f
∂z
(γ(0)) γ
0
(0) +
∂f
∂z
(γ(0)) γ
0
(0).
Zachowywanie k
,
at´ow zorientowanych jest wi
,
ec r´ownowa˙zne temu, ˙ze
arg
γ
0
1
(0)
γ
0
2
(0)
= arg
f
z
(z
0
)γ
0
1
(0) + f
z
(z
0
)γ
0
1
(0)
f
z
(z
0
)γ
0
2
(0) + f
z
(z
0
)γ
0
2
(0)
,
gdzie γ
1
(0) = γ
2
(0) = z
0
. Je˙zeli wi
,
ec f jest funkcj
,
a holomorficzn
,
a tak
,
a, ˙ze f
0
=
∂f /∂z 6= 0, to f jest lokalnym dyfeomorfizmem (bo Jac f = |f
0
|
2
) oraz zachowuje
k
,
aty i orientacj
,
e.
Z drugiej strony, je˙zeli rozpatrzymy krzywe postaci γ
ϑ
(t) = z
0
+ e
iϑ
t dla ustalo-
nego z
0
∈ D i dowolnego ϑ ∈ R, to
arg
γ
0
ϑ
(0)
γ
0
0
(0)
= arg e
iϑ
,
natomiast
arg
(f ◦ γ
ϑ
)
0
(0)
(f ◦ γ
0
)
0
(0)
= arg
f
z
(z
0
)e
iϑ
+ f
z
(z
0
)e
−iϑ
f
z
(z
0
) + f
z
(z
0
)
.
Je˙zeli wi
,
ec f jest odwzorowaniem lokalnie konforemnym, to w szczeg´olno´sci dla
ka˙zdego ϑ ∈ R argument liczby f
z
(z
0
) + f
z
(z
0
)e
−2iϑ
byÃlby niezale˙zny od ϑ, a jest
to mo˙zliwe tylko wtedy, gdy f
z
(z
0
) = 0. ¤
Odwzorowanie f : D → G, gdzie D, G s
,
a obszarami w C, nazywamy konforem-
nym (lub te˙z biholomorficznym), je˙zeli f jest holomorficzn
,
a bijekcj
,
a. Z Propo-
zycji 15.1 wynika, ˙ze wtedy f jest w szczeg´olno´sci lokalnie konforemne, za´s dzi
,
eki
Propozycji 2.4 odwzorowanie f
−1
jest tak˙ze konforemne. Dwa obszary nazywamy
konforemnymi, je˙zeli istnieje odwzorowanie konforemne pomi
,
edzy nimi. Zauwa˙zmy,
˙ze ka˙zde odwzorowanie holomorficzne jednokrotne f jest odwzorowaniem konforem-
nym na obraz.
PrzykÃlad. PÃlaszczyzna zespolona C nie jest obszarem konforemnym z ∆ - jest to
natychmiastowy wniosek z twierdzenia Liouville’a.
Odwzorowanie konforemne f : D → D nazywamy automorfizmem obszaru D,
przez Aut (D) oznaczamy zbi´or wszystkich automorfizm´ow obszaru D. Ma on
struktur
,
e grupy (wzgl
,
edem skÃladania odwzorowa´
n). Zauwa˙zmy, ˙ze je˙zeli obszary
D i G s
,
a konforemne, to grupy Aut (D) i Aut (G) s
,
a izomorficzne: je˙zeli f : D → G
jest odwzorowaniem konforemnym, to odwzorowanie
Aut (D) 3 g 7−→ f ◦ g ◦ f
−1
∈ Aut (G)
jest izomorfizmem.

38
ZBIGNIEW BÃLOCKI
Opiszemy teraz dokÃladnie automorfizmy ∆ oraz C:
Twierdzenie 15.2. Aut (∆) =
½
λ
z − a
1 − az
: λ, a ∈ C, |λ| = 1, |a| < 1
¾
.
Dow´od. W celu wykazania ⊃ mo˙zemy zaÃlo˙zy´c, ˙ze λ = 1. Dla a ∈ ∆ oznaczmy
T
a
(z) =
z − a
1 − az
.
Zauwa˙zmy, ˙ze
|1 − az|
2
− |z − a|
2
= (1 − |a|
2
)(1 − |z|
2
),
sk
,
ad wynika, ˙ze T
a
(∆) ⊂ ∆. ÃLatwo sprawdzi´c, ˙ze T
−a
jest odwzorowaniem odwrot-
nym do T
a
, sk
,
ad wynika, ˙ze T
a
∈ Aut (∆).
W celu wykazania ⊂ skorzystamy z lematu Schwarza (1884):
Lemat 15.3. Je˙zeli f ∈ O(∆, ∆) jest takie, ˙ze f (0) = 0, to
|f (z)| ≤ |z|,
z ∈ ∆,
oraz |f
0
(0)| ≤ 1.
Co wi
,
ecej, je˙zeli |f (z
0
)| = |z
0
| dla pewnego z
0
∈ ∆
∗
lub |f
0
(0)| = 1, to f jest postaci
f (z) = λz, gdzie |λ| = 1, tzn. f jest obrotem.
Dow´od. Funkcja
g(z) :=
½
f (z)/z,
z ∈ ∆
∗
,
f
0
(0),
z = 0,
jest holomorficzna w ∆. Dla r ∈ (0, 1) mamy |g(z)| ≤ 1/r, je˙zeli |z| = r. Z zasady
maksimum wynika zatem, ˙ze |g(z)| ≤ 1/r, gdy |z| ≤ r, otrzymamy wi
,
ec, ˙ze |g| ≤ 1
w ∆. To pokazuje pierwsz
,
a cz
,
e´s´c lematu. Druga cz
,
e´s´c wynika z tego, ˙ze je˙zeli
|g(z
0
)| = 1 dla pewnego z
0
∈ ∆, to funkcja g jest staÃla. ¤
Koniec dowodu Twierdzenia 15.2. Niech f ∈ Aut (∆). Odwzorowanie e
f := f ◦ T
a
∈
Aut (∆) speÃlnia e
f (0) = 0, je˙zeli a = −f
−1
(0). Z lematu Schwarza (lub z nier´owno´sci
Cauchy’ego) wynika, ˙ze | e
f
0
(0)| ≤ 1. Z drugiej strony, 1 ≥ |( e
f
−1
)
0
(0)| = 1/| e
f
0
(0)|,
a wi
,
ec | e
f
0
(0)| = 1. Korzystaj
,
ac z ostatniej cz
,
e´sci lematu Schwarza znajdziemy λ,
|λ| = 1, takie, ˙ze e
f (ζ) = λζ, ζ ∈ ∆. St
,
ad f = λT
−a
. ¤
Propozycja 15.4. Aut (C) = {az + b : a ∈ C
∗
, b ∈ C}.
Dow´od. ⊃ jest oczywiste. Je˙zeli f ∈ Aut (C), to f ma osobliwo´s´c izolowan
,
a w ∞,
z Twierdzenia 12.2 wynika, ˙ze nie jest to osobliwo´s´c istotna (bo f jest bijekcj
,
a).
Funkcja f musi wi
,
ec by´c wielomianem, je˙zeli stopie´
n tego wielomianu byÃlby r´o˙zny
od 1, to f nie byÃloby bijekcj
,
a. ¤
´
Cwiczenie
Pokaza´c, ˙ze dla ka˙zdych par r´o˙znych punkt´ow z
1
, z
2
oraz w
1
, w
2
w C
(z
1
6= z
2
, w
1
6= w
2
) istnieje dokÃladnie jedno f ∈ Aut (C) takie, ˙ze f (z
j
) = w
j
,
j = 1, 2.
Podstawowym rezultatem w teorii odwzorowa´
n konforemnych jest nast
,
epuj
,
ace
twierdzenie Riemanna (1851 - pierwsze precyzyjne dowody podali Koebe i Poincar´e
na pocz
,
atku XX w.). Podamy je bez dowodu:
Twierdzenie 15.5. Ka˙zdy obszar jednosp´ojny w C, z wyj
,
atkiem caÃlej pÃlaszczyzny,
jest konforemny z dyskiem jednostkowym ∆.

FUNKCJE ANALITYCZNE
39
16. Sfera Riemanna
Sfera Riemanna P := C ∪ {∞} to przestrze´
n topologiczna b
,
ed
,
aca uzwarceniem
C. Je˙zeli Ω jest obszarem w P, to mo˙zemy m´owi´c o funkcjach holomorficznych
na Ω: funkcja f jest holomorficzna w otoczeniu ∞, je˙zeli funkcja ζ 7→ f (1/ζ) jest
holomorficzna w otoczeniu 0. Mo˙zemy tak˙ze m´owi´c o funkcjach holomorficznych
Ω → P: w przypadku, gdy f (z
0
) = ∞, to ˙z
,
adamy by funkcja 1/f byÃla holomorficzna
w otoczeniu z
0
. Dla obszar´ow D, G ⊂ P odwzorowania konforemne i automorfizmy
definiujemy oczywi´scie tak jak poprzednio.
Propozycja 16.1. i) O(Ω, P) = {funkcje meromorficzne na Ω};
ii) O(C) ∩ O(P, P) = {wielomiany};
iii) O(P, P) \ {∞} = {funkcje wymierne}.
Dow´od. i) SpeÃlnianie przez funkcj
,
e f jakiegokolwiek z tych dw´och warunk´ow oz-
nacza, ˙ze w otoczeniu ka˙zdego punktu f lub 1/f jest holomorficzna.
ii) Je´sli funkcja caÃlkowita ma nie jest wielomianem, to w ∞ ma istotn
,
a osobli-
wo´s´c.
iii) Niech f = P/Q b
,
edzie funkcj
,
a wymiern
,
a, gdzie P, Q s
,
a wielomianami bez
wsp´olnego dzielnika (czyli ich zbiory zer s
,
a rozÃl
,
aczne). Jest oczywiste, ˙ze f |
C\Q
−1
(0)
jest funkcj
,
a holomorficzn
,
a, przedÃlu˙zaj
,
ac
,
a si
,
e do odwzorowania ci
,
agÃlego P → P. Z
twierdzenia Riemanna o usuwaniu osobliwo´sci wynika wi
,
ec, ˙ze f ∈ O(P, P).
ZaÃl´o˙zmy z kolei, ˙ze f ∈ O(P, P), f 6= const. Wtedy zbi´or f
−1
(∞) jest sko´
nczony
(bo gdyby nie byÃl, to ze zwarto´sci P miaÃlby punkt skupienia, wi
,
ec z zasady iden-
tyczno´sci wynikaÃloby, ˙ze f = const). Stosuj
,
ac zmian
,
e zmiennych w P postaci
z
0
= 1/(z − z
0
), gdzie z
0
/
∈ f
−1
(∞), bez straty og´olno´sci mo˙zemy zaÃlo˙zy´c, ˙ze
zbi´or f
−1
(∞) = {z
1
, . . . , z
n
} nie zawiera ∞. Wtedy funkcja f |
C\{z
1
,...,z
n
}
jest
holomorficzna oraz z ci
,
agÃlo´sci f na P oczywi´scie mamy lim
z→z
j
f (z) = ∞, czyli f ma
bieguny w z
1
, . . . , z
n
. Istniej
,
a zatem liczby naturalne m
1
, . . . , m
n
takie, ˙ze
P (z) := (z − z
1
)
m
1
. . . (z − z
n
)
m
n
f (z) ∈ O(C).
Co wi
,
ecej, lim
z→∞
P (z) = ∞ (bo f (∞) 6= ∞), czyli P jest wielomianem. ¤
Propozycja 16.2. Aut (P) =
½
az + b
cz + d
: a, b, c, d ∈ C, ad − bc 6= 0
¾
.
Dow´od. Niech a, b, c, d ∈ C b
,
ed
,
a takie, ˙ze ad − bc 6= 0. Je˙zeli c 6= 0, to
(16.1)
az + b
cz + d
=
a
c
−
ad − bc
c(cz + d)
,
sk
,
ad Ãlatwo wynika ⊃ (je˙zeli c = 0, to mamy odwzorowanie liniowe). Dla f ∈ Aut (P)
korzystamy z Propozycji 15.4: je˙zeli f (∞) = ∞, to f |
C
∈ Aut (C), je˙zeli za´s
f (∞) ∈ C to odwzorowanie
C 3 z 7−→
1
f (z) − f (∞)
∈ C
jest liniowe dzi
,
eki Propozycji 16.1.ii, sk
,
ad otrzymujemy ⊂. ¤
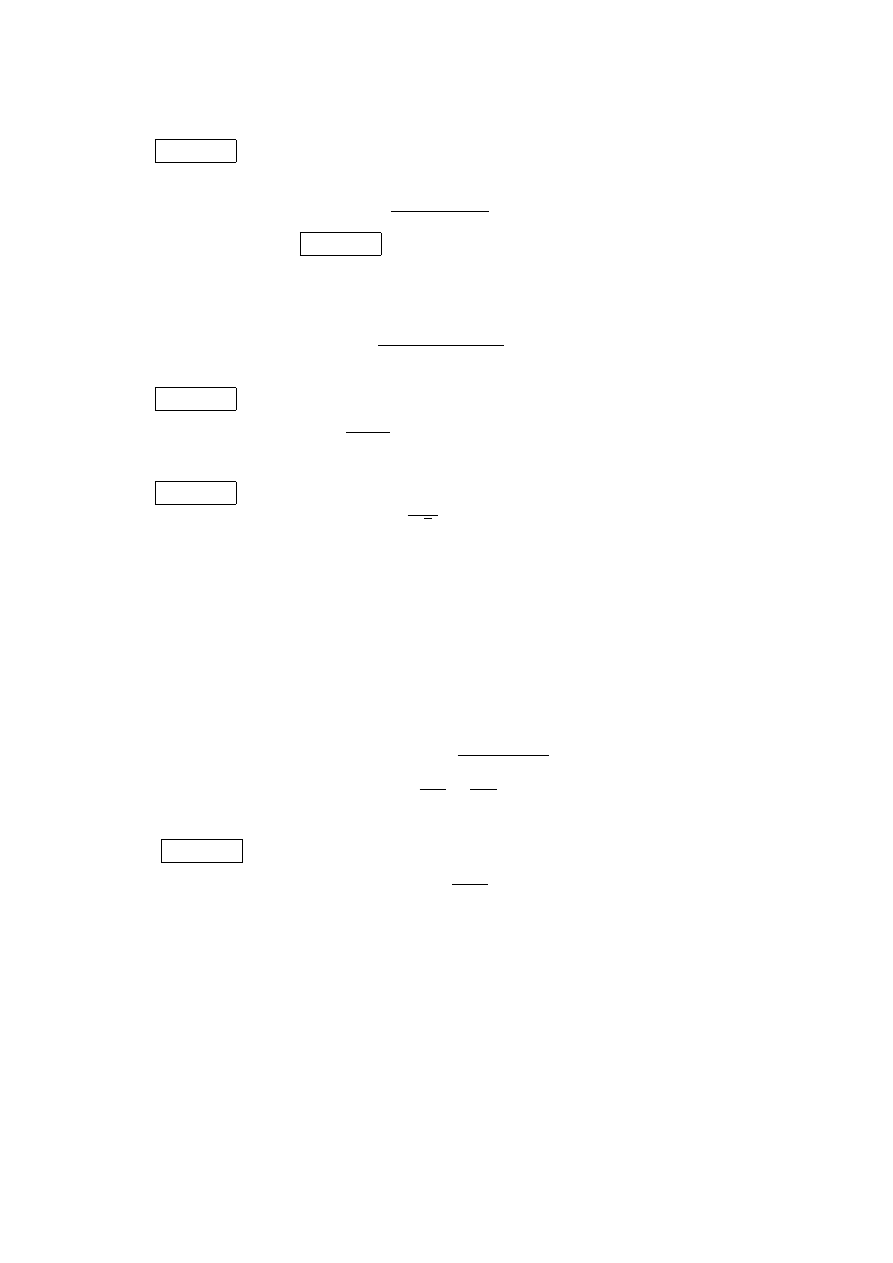
40
ZBIGNIEW BÃLOCKI
´
Cwiczenie
Pokaza´c, ˙ze dla ka˙zdej pary tr´ojek r´o˙znych punkt´ow z
1
, z
2
, z
3
oraz
w
1
, w
2
, w
3
z P istnieje dokÃladnie jedno f ∈ Aut (P) takie, ˙ze f (z
j
) = w
j
, j = 1, 2, 3.
Elementy Aut (P) nazywamy homografiami. Z (16.1) wynika, ˙ze ka˙zda homo-
grafia jest zÃlo˙zeniem odwzorowa´
n liniowych i odwzorowania z 7→ 1/z. Dzi
,
eki temu
mo˙zna pokaza´c, ˙ze (
´
Cwiczenie
)
i) ka˙zda homografia przeksztaÃlca okr
,
ag w P (tj. okr
,
ag lub prost
,
a w C) w okr
,
ag
w P;
ii) ka˙zda homografia zachowuje dwustosunek ka˙zdej czw´orki punkt´ow:
(z
1
, z
2
, z
3
, z
4
) :=
(z
1
− z
2
)(z
3
− z
4
)
(z
1
− z
4
)(z
3
− z
2
)
,
z
1
, z
2
, z
3
, z
4
∈ P.
´
Cwiczenie
Znale´z´c odwzorowanie konforemne ∆ → H, gdzie H := {Im z > 0}.
Pokaza´c, ˙ze Aut (H) =
½
az + b
cz + d
: a, b, c, d ∈ R, ad − bc > 0
¾
. Wywnioskowa´c, ˙ze
grupa Aut (∆) jest izomorficzna z grup
,
a P SL(R, 2).
´
Cwiczenie
i) Pokaza´c, ˙ze wszystkie inwolucje (tj. elementy f 6= id takie, ˙ze
f
2
= id) grupy Aut (∆) s
,
a postaci
a−z
1−az
, a ∈ ∆.
ii) Wykaza´c, ˙ze inwolucje w Aut (∆) nigdy nie s
,
a przemienne ze sob
,
a.
iii) Pokaza´c, ˙ze wszystkie inwolucje grupy Aut (C) s
,
a postaci −z + b, b ∈ C i ˙ze
nigdy nie s
,
a one przemienne ze sob
,
a.
iv) Udowodni´c, ˙ze iloczyny dw´och inwolucji w Aut (C) s
,
a zawsze przemienne,
natomiast w Aut (∆) zwykle nie s
,
a.
v) W grupie Aut (P) znale´z´c przemienne inwolucje. Wywnioskowa´c, ˙ze ˙zadna
para z grup Aut (∆), Aut (C) i Aut (P) nie jest izomorficzna (w sensie teorii grup).
17. Funkcje harmoniczne
Funkcj
,
e h : Ω → R (Ω ⊂ C) nazywamy harmoniczn
,
a, je˙zeli h jest klasy C
2
oraz
∆h :=
∂
2
h
∂x
2
+
∂
2
h
∂y
2
= 0.
Zbi´or funkcji harmonicznych w Ω oznaczamy H(Ω). Mo˙zna Ãlatwo sprawdzi´c, ˙ze
(
´
Cwiczenie
)
∆ = 4
∂
2
∂z∂ ¯
z
.
Korzystaj
,
ac z tego (i odpowiednika (2.7)) dostaniemy nast
,
epuj
,
ace zwi
,
azki funkcji
harmonicznych z holomorficznymi:
Propozycja 17.1. i) f ∈ O(Ω, e
Ω), h ∈ H(e
Ω) ⇒ h ◦ f ∈ H(Ω);
ii) f ∈ O(Ω) ⇒ Re f, Im f ∈ H(Ω).
iii) f ∈ O(Ω), f 6= 0 ⇒ log |f | ∈ H(Ω). ¤
Lokalnie zachodzi r´ownie˙z rezultat odwrotny do ii):
Twierdzenie 17.2. Je˙zeli u jest funkcj
,
a harmoniczn
,
a w kole otwartym, to znaj-
dziemy w nim funkcj
,
e holomorficzn
,
a f tak
,
a, ˙ze u = Re f . Jest ona jednoznacznie
wyznaczona z dokÃladno´sci
,
a do staÃlej.

FUNKCJE ANALITYCZNE
41
Dow´od. Zauwa˙zmy, ˙ze je˙zeli funkcja f = u + iv byÃlaby holomorficzna, to z r´owna´
n
Cauchy’ego-Riemanna mieliby´smy f
0
= u
x
+ iv
x
= u
x
− iu
y
.
Je˙zeli teraz u
jest harmoniczna, to funkcja g := u
x
− iu
y
jest holomorficzna (bo speÃlnione s
,
a
r´ownania Cauchy’ego-Riemanna), wi
,
ec w kole (kt´ory jest obszarem gwia´zdzistym)
ma pierwotn
,
a f = e
u + iv. Mamy g = f
0
= e
u
x
+ iv
x
= e
u
x
− ie
u
y
, czyli u
x
= e
u
x
,
u
y
= e
u
y
. St
,
ad e
u = u + const i mo˙zemy zaÃlo˙zy´c, ˙ze e
u = u. Podobne rozumowanie
pokazuje tak˙ze, ˙ze f jest wyznaczona jednoznacznie z dokÃladno´sci
,
a do staÃlej. ¤
Z twierdzenia Riemanna wynika, ˙ze w Twierdzeniu 17.2 mogliby´smy wzi
,
a´c do-
wolny obszar jednosp´ojny.
Wniosek 17.3. Funkcje harmoniczne s
,
a klasy C
∞
. ¤
Funkcje harmoniczne u, v nazywamy sprz
,
e˙zonymi, je˙zeli u + iv jest funkcj
,
a holo-
morficzn
,
a.
PrzykÃlad. Funkcja log |z| jest harmoniczna w C
∗
. W C \ (−∞, 0] funkcj
,
a do niej
sprz
,
e˙zon
,
a jest Arg z, kt´orej jednak nie mo˙zna ci
,
agle przedÃlu˙zy´c na C
∗
. Pokazuje
to, ˙ze funkcja log |z| nie ma funkcji sprz
,
e˙zonej w C
∗
.
´
Cwiczenie
Znale´z´c funkcj
,
e sprz
,
e˙zon
,
a do funkcji x
3
− 3xy
2
− x
2
+ y
2
+ x.
Je˙zeli u, v s
,
a sprz
,
e˙zonymi funkcjami harmonicznymi, to z r´owna´
n Cauchy’ego-
Riemanna natychmiast wynika, ˙ze u
x
v
x
+ u
y
v
y
= 0. Oznacza to, ˙ze gradienty
obu funkcji w danym punkcie s
,
a do siebie prostopadÃle, sk
,
ad wnioskujemy, ˙ze w
przypadku generycznym (gdy te gradienty nie znikaj
,
a) krzywe poziomicowe funkcji
sprz
,
e˙zonych przecinaj
,
a si
,
e pod k
,
atem prostym.
Przypu´s´cmy teraz, ˙ze h jest funkcj
,
a harmoniczn
,
a w otoczeniu koÃla K(z
0
, r).
Dzi
,
eki Twierdzeniu 17.2 znajdziemy funkcj
,
e holomorficzn
,
a f w otoczeniu K(z
0
, r)
tak
,
a, ˙ze h = Re f . Z twierdzenia o warto´sci ´sredniej dla funkcji holomorficznych
mamy
f (z
0
) =
1
2π
Z
2π
0
f (z
0
+ re
it
)dt.
Bior
,
ac cz
,
e´sci rzeczywiste dostaniemy twierdzenie o warto´sci ´sredniej dla funkcji
harmonicznych:
Twierdzenie 17.4. Je˙zeli h jest funkcj
,
a harmoniczn
,
a w otoczeniu K(z
0
, r), to
h(z
0
) =
1
2π
Z
2π
0
h(z
0
+ re
it
)dt.
¤
Udowodnimy teraz zasad
,
e maksimum dla funkcji harmonicznych:
Twierdzenie 17.5. Je˙zeli h ∈ H(Ω) osi
,
aga maksimum lokalne w obszarze Ω, to h
jest staÃla.
Dow´od. ZaÃl´o˙zmy, ˙ze h ma maksimum lokalne w z
0
. Podobnie jak w dowodzie
Twierdzenia 6.3, korzystaj
,
ac z Twierdzenia 17.4, Ãlatwo pokazujemy, ˙ze funkcja h
jest staÃla na K(z
0
, r) dla pewnego r > 0. PoÃl´o˙zmy Ω
0
:= int{h = h(z
0
)}. Zbi´or
Ω
0
jest wi
,
ec niepusty, otwarty, trzeba jeszcze pokaza´c, ˙ze jest domkni
,
ety. Je˙zeli
e
z ∈ Ω
0
, to w kole K(e
z, e
r) ⊂ Ω mamy h = Re f dla pewnego f ∈ O(K(e
z, e
r)).
Poniewa˙z Re f jest staÃla w niepustym zbiorze otwartym Ω
0
∩ K(e
z, r), to f jest

42
ZBIGNIEW BÃLOCKI
r´ownie˙z staÃla w pewnej (niepustej) skÃladowej tego zbioru, a z zasady identyczno´sci
dla funkcji holomorficznych, tak˙ze na caÃlym K(e
z, e
r). Wnioskujemy, ˙ze e
z ∈ Ω
0
. ¤
Korzystaj
,
ac z zasady maksimum dla funkcji harmonicznych mo˙zna pokaza´c, ˙ze
pier´scienie w C s
,
a konforemne wtedy i tylko wtedy, gdy s
,
a liniowo izomorficzne (fakt
ten podamy bez dowodu). Pokazuje to, ˙ze odpowiednik twierdzenia Riemanna nie
zachodzi dla obszar´ow wielosp´ojnych, tzn. konforemno´s´c nie jest w tym wypadku
r´ownowa˙zna homeomorficzno´sci.
Twierdzenie 17.6. Niech z
j
∈ C, 0 < r
j
< R
j
< ∞, j = 1, 2. Pier´scienie
P (z
1
, r
1
, R
1
), P (z
2
, r
2
, R
2
) s
,
a konforemne wtedy i tylko, gdy R
1
/r
1
= R
2
/r
2
.
Chcemy teraz znale´z´c odpowiednik wzoru Cauchy’ego dla funkcji harmonicznych,
tj. wyrazi´c jej warto´sci wewn
,
atrz koÃla przy pomocy warto´sci na brzegu. Przyjmijmy
dla uproszczenia, ˙ze K(z
0
, r) = ∆ i ˙ze funkcja h jest harmoniczna w otoczeniu ∆.
Dla a ∈ ∆ funkcja h ◦ T
−a
jest harmoniczna w otoczeniu ∆. Dzi
,
eki Twierdzeniu
17.4 mamy wi
,
ec
h(a) = h(T
−a
(0)) =
1
2π
Z
2π
0
h(T
−a
(e
it
)) dt.
Stosuj
,
ac podstawienie e
is
= T
−a
(e
it
), tzn. e
it
= T
a
(e
is
), otrzymamy
h(a) =
1
2π
Z
2π
0
T
0
a
(e
is
)
T
a
(e
is
)
e
is
h(e
is
) ds =
1
2π
Z
2π
0
1 − |a|
2
|e
is
− a|
2
h(e
is
) ds.
Po podstawieniu z = z
0
+ ra otrzymamy nast
,
epuj
,
acy wz´or Poissona:
Twierdzenie 17.7. Je˙zeli h jest funkcj
,
a harmoniczn
,
a w otoczeniu K(z
0
, r), to
h(z) =
1
2π
Z
2π
0
r
2
− |z − z
0
|
2
|z − z
0
− re
it
|
2
h(z
0
+ re
it
) dt,
z ∈ K(z
0
, r).
¤
Przy pomocy wzoru Poissona mo˙zemy teraz rozwi
,
aza´c problem Dirichleta dla
koÃla:
Twierdzenie 17.8. Dla ustalonego koÃla K(z
0
, r) oraz ϕ ∈ C(∂K(z
0
, r)) poÃl´o˙zmy
h(z) :=
1
2π
Z
2π
0
r
2
− |z − z
0
|
2
|z − z
0
− re
it
|
2
ϕ(z
0
+ re
it
) dt,
z ∈ K(z
0
, r).
Wtedy h jest jedyn
,
a funkcj
,
a speÃlniaj
,
ac
,
a nast
,
epuj
,
ace wÃlasno´sci:
h ∈ H(K(z
0
, r)) ∩ C(K(z
0
, r)),
h = ϕ na ∂K(z
0
, r).
Dow´od. Jednoznaczno´s´c wynika Ãlatwo z zasady maksimum zastosowanej dla r´o˙znicy
dw´och rozwi
,
aza´
n. Zauwa˙zmy, ˙ze
Re
ζ + z
ζ − z
=
|ζ|
2
− |z|
2
|ζ − z|
2
,
ζ, z ∈ C, ζ 6= z,

FUNKCJE ANALITYCZNE
43
sk
,
ad wynika, ˙ze j
,
adro Poissona
r
2
− |z − z
0
|
2
|z − z
0
− re
it
|
2
jest funkcj
,
a harmoniczn
,
a wzgl
,
edem z. St
,
ad Ãlatwo wnioskujemy, ˙ze h jest funkcj
,
a
harmoniczn
,
a w K(z
0
, r). Musimy jeszcze pokaza´c, ˙ze
(17.1)
lim
z→w
z∈K(z
0
,r)
h(z) = ϕ(w),
w ∈ ∂K(z
0
, r).
Dla z ∈ K(z
0
, r) i ustalonego w ∈ ∂K(z
0
, r) mamy (korzystamy z Twierdzenia
17.7 dla h ≡ 1)
h(z) − ϕ(w) =
1
2π
Z
2π
0
r
2
− |z − z
0
|
2
|z − z
0
− re
it
|
2
¡
ϕ(z
0
+ re
it
) − ϕ(w)
¢
dt.
Ustalmy teraz ε > 0. Znajdziemy δ > 0 takie, ˙ze |ϕ(z
0
+ re
it
) − ϕ(w)| ≤ ε,
gdy |z
0
+ re
it
− w| ≤ δ. Mo˙zemy teraz podzieli´c przedziaÃl [0, 2π] na dwa rozÃl
,
aczne
podzbiory A i B takie, ˙ze |ϕ(z
0
+re
it
)−ϕ(w)| ≤ ε, gdy t ∈ A, oraz |z
0
+re
it
−w| ≥ δ,
gdy t ∈ B. Dla z ∈ ∂K(z
0
, r) odp. bliskiego w mamy wtedy
|h(z) − ϕ(w)| ≤
1
2π
Z
2π
0
r
2
− |z − z
0
|
2
|z − z
0
− re
it
|
2
¯
¯
¡
ϕ(z
0
+ re
it
) − ϕ(w)
¢¯
¯ dt
=
1
2π
µZ
A
+
Z
B
¶
≤ ε + 2M
r
2
− |z − z
0
|
2
(δ − |z − w|)
2
,
gdzie M := max
∂K(z
0
,r)
|ϕ|. St
,
ad otrzymamy (17.1). ¤
18. Iloczyny niesko´
nczone
Dla ci
,
agu b
n
∈ C m´owimy, ˙ze iloczyn
Q
∞
n=1
b
n
jest zbie˙zny, je˙zeli istnieje granica
lim
N →∞
N
Y
n=1
b
n
∈ C.
Granic
,
e t
,
e oznaczamy
Q
∞
n=1
b
n
. Zbie˙zno´s´c iloczynu
Q
(1 + a
n
) ma zwi
,
azek ze
zbie˙zno´sci
,
a szeregu
P
a
n
. Np. je˙zeli a
n
≥ 0 dla wszystkich n, to
1 + a
1
+ · · · + a
N
≤ (1 + a
1
) . . . (1 + a
N
) ≤ e
a
1
+···+a
N
,
(korzystaj
,
ac z tego, ˙ze 1 + x ≤ e
x
dla x ∈ R), czyli w tym przypadku zbie˙zno´sci te
s
,
a r´ownowa˙zne.

44
ZBIGNIEW BÃLOCKI
W og´olnym przypadku mamy nast
,
epuj
,
acy rezultat dotycz
,
acy zbie˙zno´sci iloczy-
n´ow niesko´
nczonych:
Twierdzenie 18.1. ZaÃl´o˙zmy, ˙ze szereg
P
a
n
jest bezwzgl
,
ednie zbie˙zny. Wtedy
i) iloczyn
Q
(1 + a
n
) jest zbie˙zny;
ii)
Q
(1 + a
n
) = 0 ⇔ 1 + a
n
0
= 0 dla pewnego n
0
.
Dow´od. i) Oznaczmy p
N
:=
Q
N
n=1
(1 + a
n
). Zbie˙zno´s´c ci
,
agu p
N
jest r´ownowa˙zna
zbie˙zno´sci szeregu
P
(p
N
− p
N −1
) (bo sumy cz
,
e´sciowe tego szeregu to dokÃladnie
ci
,
ag p
N
). Mamy
(18.1)
|p
N
− p
N −1
| = |a
N
| |p
N −1
| ≤ |a
N
|(1 + |a
1
|) . . . (1 + |a
N −1
|)
≤ |a
N
|e
|a
1
|+···+|a
N −1
|
≤ |a
N
| exp
¡
∞
X
n=1
|a
n
|
¢
.
Dostaniemy bezwzgl
,
edn
,
a zbie˙zno´s´c szeregu
P
(p
N
− p
N −1
).
ii) Implikacja ⇐ jest oczywista, natomiast w celu udowodnienia ⇒ poka˙zemy, ˙ze
je˙zeli m jest takie, ˙ze |a
n
| < 1 dla n > m, to
H :=
m
Y
n=1
(1 + a
n
) = 0,
sk
,
ad wynika, ˙ze a
n
0
+ 1 = 0 dla pewnego n
0
≤ m. Takie m istnieje, gdy˙z w
szczeg´olno´sci a
n
→ 0. Mamy wtedy nawet |a
n
| ≤ λ < 1 dla n > m. Dla N > m
|p
N
| = |H|
N
Y
n=m+1
|1 + a
n
|.
Z kolei dla n > m
|1 + a
n
| ≥ 1 − |a
n
| ≥ e
−b|a
n
|
,
gdzie b := −λ
−1
log(1 − λ) > 0 (z wypukÃlo´sci funkcji e
−bx
dostajemy 1 − x ≥ e
−bx
dla x ∈ [0, λ]). Otrzymamy
|p
N
| ≥ |H| exp
¡
− b
∞
X
n=m+1
|a
n
|
¢
.
Z zaÃlo˙zenia mamy p
N
→ 0, sk
,
ad wnioskujemy, ˙ze H = 0. ¤
Twierdzenie 18.2. Niech f
n
b
,
edzie ci
,
agiem funkcji holomorficznych w obszarze Ω
takim, ˙ze szereg
P
|f
n
| jest lokalnie ograniczony w Ω (tzn. szereg
P
f
n
jest lokalnie
bezwzgl
,
ednie jednostajnie zbie˙zny). Wtedy
i) I :=
Q
(1 + f
n
) ∈ O(Ω) (zbie˙zno´s´c lokalnie jednostajna);
ii) I(z
0
) = 0 ⇔ f
n
0
(z
0
) + 1 = 0 dla pewnego n
0
.
Dow´od. i) Oznaczmy I
N
:=
Q
N
n=1
(1 + f
n
). Z (18.1) wynika, ˙ze szereg
P
|I
N
−
I
N −1
| jest lokalnie jednostajnie zbie˙zny w Ω, a zatem ci
,
ag I
N
jest zbie˙zny lokalnie

FUNKCJE ANALITYCZNE
45
jednostajnie w Ω. Z Twierdzenia 6.4 wnioskujemy, ˙ze jego granica jest funkcj
,
a
holomorficzn
,
a.
ii) Wynika natychmiast z Twierdzenia 18.1. ¤
Iloczyny niesko´
nczone mo˙zna wykorzysta´c do konstrukcji funkcji holomorficz-
nych o z g´ory zadanych zerach. Z zasady identyczno´sci wynika, ˙ze zera te nie mog
,
a
mie´c punktu skupienia. Okazuje si
,
e, ˙ze jest to jedyne ograniczenie:
Twierdzenie 18.3. (Weierstrass, 1876) Niech z
n
b
,
edzie ci
,
agiem r´o˙znych punkt´ow
w obszarze Ω bez punkt´ow skupienia w Ω. Niech m
n
b
,
edzie dowolnym ci
,
agiem liczb
naturalnych. Wtedy istnieje funkcja f ∈ O(Ω) taka, ˙ze z
1
, z
2
, . . . s
,
a wszystkimi
zerami funkcji f o krotno´sciach, odpowiednio, m
1
, m
2
, . . .
Je˙zeli np. Ω = C, z
n
6= 0, z
n
→ ∞ (tzn. ci
,
ag z
n
nie ma punkt´ow skupienia), to
dzi
,
eki Twierdzeniu 18.2 iloczyn niesko´
nczony
∞
Y
n=1
µ
1 −
z
z
n
¶
definiuje funkcj
,
e caÃlkowit
,
a pod warunkiem, ˙ze
∞
X
n=1
1
|z
n
|
< ∞,
czyli je˙zeli ci
,
ag z
n
d
,
a˙zy odp. szybko do ∞. W celu pozbycia si
,
e tego dodatkowego
zaÃlo˙zenia trzeba zamieni´c wyra˙zenie 1−z/z
n
na wyra˙zenie, kt´ore tak˙ze znika dla z =
z
n
, ale kt´ore jest bli˙zej 1 dla z w pobli˙zu z
n
. PosÃlu˙z
,
a do tego czynniki Weierstrassa
E
n
(z) := (1 − z) exp
µ
z +
z
2
2
+ · · · +
z
n
n
¶
.
Lemat 18.4. Je˙zeli |z| ≤ 1 oraz n = 1, 2, . . . , to
|E
n
(z) − 1| ≤ |z|
n+1
.
Dow´od. Mamy
E
0
n
(z) = −z
n
exp
µ
z +
z
2
2
+ · · · +
z
n
n
¶
= −z
n
∞
X
j=0
c
j
z
j
,
gdzie c
j
≥ 0. St
,
ad wynika, ˙ze funkcja 1 − E
n
ma w 0 zero rz
,
edu n + 1 oraz
f (z) :=
1 − E
n
(z)
z
n+1
=
∞
X
j=0
a
j
z
j
,
gdzie a
j
= c
j
/(j + n + 1) ≥ 0 dla wszystkich j. Wnioskujemy, ˙ze |f (z)| ≤ f (1) = 1,
gdy |z| ≤ 1. ¤

46
ZBIGNIEW BÃLOCKI
Wracaj
,
ac teraz do problemu konstrukcji funkcji caÃlkowitej o zadanych zerach
z
n
→ ∞, z
n
6= 0, mo˙zemy zdefiniowa´c
f (z) :=
∞
Y
n=1
E
n
µ
z
z
n
¶
.
Wtedy z Lematu 18.4 mamy |E
n
(z/z
n
)−1| ≤ |z/z
n
|
n+1
, z Twierdzenia 18.2 wynika
wi
,
ec, ˙ze powy˙zszy iloczyn niesko´
nczony jest lokalnie jednostajnie zbie˙zny na C oraz,
˙ze zeruje si
,
e dokÃladnie w punktach z
n
, przy czym krotno´s´c zera jest taka ile razy
dany punkt pojawia si
,
e w ci
,
agu z
n
.
Podobne rozumowanie mo˙zemy przeprowadzi´c tak˙ze w og´olnym przypadku:
Dow´od Twierdzenia 18.3. Stosuj
,
ac zmian
,
e zmiennych w P postaci z
0
= 1/(z − z
0
),
gdzie z
0
∈ Ω \ {z
1
, z
2
, . . . } jest ustalone, bez straty og´olno´sci mo˙zemy zaÃlo˙zy´c, ˙ze Ω
jest obszarem w P zawieraj
,
acym ∞, przy czym z
n
6= ∞, n = 1, 2, . . . Niech e
z
n
b
,
edzie
ci
,
agiem postaci z
1
, . . . , z
1
, z
2
, . . . , z
2
, . . . , gdzie ka˙zdy z punkt´ow z
n
powtarza si
,
e m
n
razy. Niech a
n
∈ ∂Ω b
,
ed
,
a takie, ˙ze dist (e
z
n
, ∂Ω) = |e
z
n
− a
n
|. Ci
,
ag e
z
n
ma punkty
skupienia tylko na ∂Ω, kt´ory jest zbiorem zwartym w C, a zatem |e
z
n
− a
n
| → 0.
KÃladziemy
f (z) :=
∞
Y
n=1
E
n
µ
e
z
n
− a
n
z − a
n
¶
.
Z Lematu 18.4 mamy
¯
¯
¯
¯E
n
µ
e
z
n
− a
n
z − a
n
¶
− 1
¯
¯
¯
¯ ≤
¯
¯
¯
¯
e
z
n
− a
n
z − a
n
¯
¯
¯
¯
n+1
.
Z Twierdzenia 18.2 otrzymamy wi
,
ec lokalnie jednostajn
,
a zbie˙zno´s´c powy˙zszego
iloczynu niesko´
nczonego w Ω \ {∞}. Co wi
,
ecej, f jest ograniczone w pobli˙zu ∞,
a wi
,
ec przedÃlu˙za si
,
e do funkcji holomorficznej w Ω. Z Twierdzenia 18.2 wynika
ponadto, ˙ze f nie ma zer poza ci
,
agiem z
n
, jest tak˙ze jasne, ˙ze ich krotno´s´c jest
r´owna m
n
. ¤
Definiuj
,
ac zbi´or funkcji meromorficznych na danym obszarze pokazali´smy, ˙ze
jest on lokalnie ciaÃlem uÃlamk´ow pier´scienia funkcji holomorficznych. Korzystaj
,
ac z
twierdzenia Weierstrassa mo˙zna Ãlatwo pokaza´c, ˙ze jest on w istocie ciaÃlem uÃlamk´ow:
Twierdzenie 18.5. Ka˙zd
,
a funkcj
,
e meromorficzn
,
a w obszarze Ω mo˙zna zapisa´c w
postaci f /g, gdzie f, g ∈ O(Ω).
Dow´od. Niech h b
,
edzie funkcj
,
a meromorficzn
,
a w Ω. Z Twierdzenia 18.3 wynika,
˙ze istnieje funkcja g ∈ O(Ω) taka, ˙ze zbi´or zer funkcji g jest taki sam jak zbi´or
biegun´ow funkcji h, przy czym krotno´sci zer s
,
a takie same jak rz
,
edy biegun´ow.
Jest jasne, ˙ze wtedy funkcja f := gh ma tylko pozorne osobliwo´sci. ¤
19. Funkcja
ζ
Riemanna
KÃladziemy
(19.1)
ζ(s) :=
∞
X
n=1
1
n
s
,
s > 1.

FUNKCJE ANALITYCZNE
47
Zauwa˙zmy, ˙ze
ζ(s) =
X
n6=2k
1
n
s
+
1
2
s
ζ(s),
czyli
µ
1 −
1
2
s
¶
ζ(s) =
X
n6=2k
1
n
s
.
Post
,
epuj
,
ac podobnie z lew
,
a stron
,
a zamiast ζ(s) otrzymamy
µ
1 −
1
2
s
¶ µ
1 −
1
3
s
¶
ζ(s) =
X
n6=2k
n6=3k
1
n
s
.
Kontynuuj
,
ac ten proces dla wszystkich liczb pierwszych widzimy, ˙ze prawa strona
d
,
a˙zy do 1, ze zbie˙zno´sci szeregu
P
p
p
−s
(p b
,
edzie zawsze oznaczaÃlo liczby pierwsze)
dla s > 1 otrzymamy wi
,
ec nast
,
epuj
,
acy rezultat, mi
,
edzy innymi dzi
,
eki kt´oremu
funkcja ζ jest jednym z gÃl´ownych obiekt´ow badanych w teorii liczb.
Propozycja 19.1. (Euler, 1748) Dla s > 1 mamy
(19.2)
1
ζ(s)
=
Y
p
µ
1 −
1
p
s
¶
.
¤
Wnioskujemy st
,
ad w szczeg´olno´sci, ˙ze szereg
P
p
1/p jest rozbie˙zny.
Chcemy przedÃlu˙zy´c funkcj
,
e ζ dla zespolonych s. Dla s = σ + it mamy |n
−s
| =
n
−σ
, sk
,
ad wynika, ˙ze szereg
P
n
−s
jest bezwzgl
,
ednie i lokalnie jednostajnie zbie˙zny
w p´oÃlpÃlaszczy´znie {Re s > 1}. FormuÃla (19.1) dobrze zatem definiuje funkcj
,
e ζ dla
takich s. Mamy tak˙ze
ζ(s) −
1
s − 1
=
∞
X
n=1
Z
n+1
n
(n
−s
− x
−s
)dx,
Re s > 1,
oraz
¯
¯
¯
¯
Z
n+1
n
(n
−s
− x
−s
)dx
¯
¯
¯
¯ =
¯
¯
¯
¯s
Z
n+1
n
Z
x
n
y
−1−s
dy dx
¯
¯
¯
¯ ≤ |s|n
−1−σ
,
a wi
,
ec funkcja ζ(s) − 1/(s − 1) przedÃlu˙za si
,
e do funkcji holomorficznej w p´oÃlpÃlasz-
czy´znie {Re s > 0} (dzi
,
eki zasadzie identyczno´sci takie przedÃlu˙zenie jest oczywi´scie
jednoznaczne). Udowodnili´smy wi
,
ec nast
,
epuj
,
acy fakt:
Propozycja 19.2. Funkcj
,
e ζ mo˙zna jednoznacznie przedÃlu˙zy´c do funkcji holomor-
ficznej w obszarze {Re s > 0} \ {1}. W 1 ma ona biegun prosty z residuum r´ownym
1. ¤
W rzeczywisto´sci mo˙zna pokaza´c, ˙ze ζ przedÃlu˙za si
,
e do funkcji holomorficznej w
C \ {1} z zerami w −2, −4, . . . (s
,
a to tzw. trywialne zera funkcji ζ). Okazuje si
,
e
wtedy np., ˙ze ζ(−1) = −1/12, co mo˙zemy zapisa´c
1 + 2 + 3 + · · · = −
1
12
.
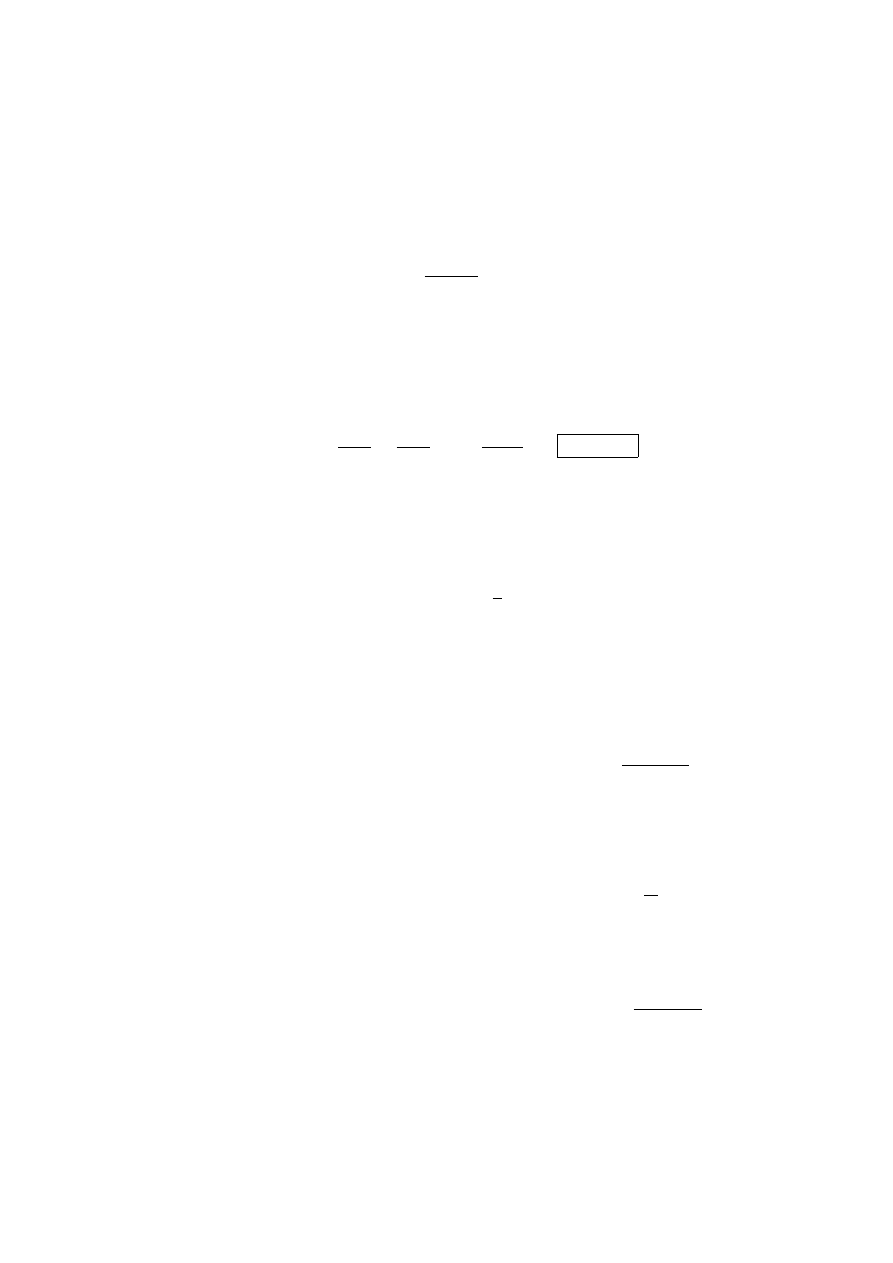
48
ZBIGNIEW BÃLOCKI
Z (19.2) wynika, ˙ze ζ nie ma zer w zbiorze {Re ζ > 1}. Hipoteza Riemanna
m´owi, ˙ze wszystkie nietrywialne zera funkcji ζ le˙z
,
a na prostej {Re s = 1/2} (mo˙zna
pokaza´c, ˙ze s
,
a one symetryczne wzgl
,
edem punktu 1/2). Okazuje si
,
e, ˙ze nietrywialne
zera funkcji ζ maj
,
a bardzo bliski zwi
,
azek z rozkÃladem liczb pierwszych. Niech π(x)
oznacza liczb
,
e liczb pierwszych ≤ x. Twierdzenie o liczbach pierwszych m´owi, ˙ze
lim
x→∞
π(x)
x/ log x
= 1.
Jego dow´od zostaÃl naszkicowany przez Riemanna w 1859 r. i precyzyjnie udowod-
niony niezale˙znie przez Hadamarda i de la Vall´ee-Poussina w 1896 r. Jednym z
gÃl´ownych krok´ow w jego dowodzie jest wykazanie, ˙ze funkcja ζ nie ma zer na prostej
Re ζ = 1.
PoÃl´o˙zmy
li(x) :=
Z
x
2
dy
log y
=
x
log x
+ O
µ
x
log
2
x
¶
(
´
Cwiczenie
).
Mo˙zna pokaza´c, ˙ze je˙zeli ζ nie miaÃloby zer w {Re s ≥ θ}, gdzie 1/2 < θ < 1, to
π(x) = li(x) + O(x
θ
log x).
Sama za´s hipoteza Riemanna okazuje si
,
e by´c r´ownowa˙zna to˙zsamo´sci
π(x) = li(x) + O(
√
x log x).
OpisywaÃloby to wi
,
ec rozkÃlad liczb pierwszych w znacznie dokÃladniejszy spos´ob ni˙z
twierdzenie o liczbach pierwszych.
20. Rodziny normalne, iteracja funkcji wymiernych
Dla ustalonego obszaru Ω ⊂ P rodzin
,
e G ⊂ O(Ω, P) nazywamy normaln
,
a, je˙zeli z
ka˙zdego ci
,
agu w G mo˙zna wybra´c podci
,
ag zbie˙zny lokalnie jednostajnie (w metryce
sferycznej na P) w Ω. Mo˙zna pokaza´c, ˙ze wÃlasno´s´c normalno´sci ma charakter czysto
lokalny wzgl
,
edem Ω (je˙zeli rodzina G ⊂ O(Ω, P) jest lokalnie normalna w Ω, to dla
ci
,
agu f
n
∈ G i ci
,
agu zbior´ow zwartych K
j
⊂ Ω rosn
,
acego do Ω znajdziemy podci
,
agi
f
j
n
k
zbie˙zne jednostajnie w K
j
; stosuj
,
ac rozumowanie przek
,
atniowe znajdziemy odp.
podci
,
ag zbie˙zny jednostajnie na dowolnym K
j
).
PrzykÃlad. Rodzina {z
n
}
n≥1
⊂ O(C) jest normalna w ∆ oraz w C \ ∆, ale nie jest
normalna w ˙zadnym obszarze maj
,
acym niepuste przeci
,
ecie z ∂∆.
Podstawowym rezulatem dotycz
,
acym rodzin normalnych jest nast
,
epuj
,
acy fakt
(podamy go bez dowodu):
Twierdzenie 20.1. (Montel, 1912) Rodzina O(Ω, C \ {0, 1}) jest normalna.
Twierdzenie Montela jest gÃl
,
ebokim rezultatem, wynika z niego Ãlatwo np. wielkie
twierdzenie Picarda:
Twierdzenie 20.2. (Picard, 1879) Funkcja holomorficzna posiadaj
,
aca istotn
,
a oso-
bliwo´s´c omija co najwy˙zej jedn
,
a warto´s´c.

FUNKCJE ANALITYCZNE
49
Dow´od. Przypu´s´cmy, ˙ze funkcja holomorficzna f w {0 < |z − z
0
| < ε}, posiadaj
,
aca
istotn
,
a osobliwos´s´c w z
0
, omija dwie warto´sci w
0
6= w
1
. SkÃladaj
,
ac f z odp. funkcj
,
a
liniow
,
a mo˙zemy zaÃlo˙zy´c, ˙ze w
0
= 0, w
1
= 1. Z twierdzenia Montela wynika,
˙ze ci
,
ag f
n
(z) := f (z/n) jest rodzin
,
a normaln
,
a. Znajdziemy zatem podci
,
ag f
n
k
albo jednostajnie zbie˙zny na okr
,
egu ∂K(z
0
, ε/2) albo jednostajnie rozbie˙zny do
∞ na tym okr
,
egu. W pierwszym przypadku f byÃloby jednostajnie ograniczone
na okr
,
egach ∂K(z
0
, ε/(2n
k
)), sk
,
ad (i z zasady maksimum) wynikaÃloby, ˙ze funkcja
f jest ograniczona w pobli˙zu z
0
. W drugim przypadku podobnie dostaliby´smy
lim
z→z
0
f (z) = ∞. Otrzymaliby´smy wi
,
ec, ˙ze z
0
jest albo osobliwo´sci
,
a usuwaln
,
a
albo biegunem - sprzeczno´s´c. ¤
Twierdzenie Montela okazuje si
,
e by´c szczeg´olnie przydatne do badania iteracji
funkcji wymiernych. B
,
edziemy teraz stale zakÃlada´c, ˙ze R = P/Q jest funkcj
,
a
wymiern
,
a (kt´or
,
a traktujemy jako odwzorowanie holomorficzne P → P), gdzie P, Q
s
,
a wielomianami zespolonymi bez wsp´olnych zer. ZakÃladamy tak˙ze, ˙ze d = deg R :=
max{deg P, deg Q} ≥ 2. Oznacza to, ˙ze dla w spoza sko´
nczonego podzbioru P zbi´or
R
−1
(w) jest dokÃladnie d-elementowy. Przez R
n
= R◦· · ·◦R oznaczamy n-t
,
a iteracj
,
e
odwzorowania R.
Zbi´or Fatou F funkcji R definiujemy jako zbi´or wszystkich z ∈ P takich, ˙ze
ci
,
ag R
n
jest rodzin
,
a normaln
,
a w pewnym otoczeniu z. DopeÃlnienie zbioru Fatou
J := P \ F to zbi´or Julii funkcji R. Oczyw´scie F jest otwarty, za´s J jest zwarty.
Zbiory te zostaÃly zdefiniowane niezale˙znie przez tych dw´och matematyk´ow w 1918
r.
Przedstawimy teraz bez dowod´ow podstawowe wÃlasno´sci zbioru Julii (udowod-
nione niezale˙znie przez Fatou i Julia w 1918 r. w ramach konkursu ogÃloszonego
przez francusk
,
a Akademi
,
e Nauk).
Twierdzenie 20.3. i) J 6= ∅;
ii) R
−1
(J ) = J ;
iii) Zbi´or Julii odwzorowania R
N
, N ≥ 1, jest taki sam jak zbi´or Julii R;
iv) Je˙zeli J ma niepuste wn
,
etrze, to J = P;
v) Dla ka˙zdego z
0
∈ J zbi´or
S
n≥1
R
−n
(z
0
) jest g
,
esty w J ;
vi) J jest zbiorem doskonaÃlym, tzn. nie zawiera punkt´ow izolowanych.
Przyjrzymy si
,
e teraz dokÃladniej przypadkowi, gdy R = P jest wielomianem
(stopnia d ≥ 2):
Twierdzenie 20.4. Dla wielomianu P poÃl´o˙zmy
K := {z ∈ C : ci
,
ag P
n
(z) jest ograniczony}.
Wtedy K jest zbiorem zwartym w C, ∂K = J oraz K jest wypeÃlnionym zbiorem
Julii, tzn. K = J ∪ U, gdzie U jest sum
,
a skÃladowych ograniczonych C \ J .
Dow´od. Znajdziemy r > 0 i λ > 1 takie, ˙ze |P (z)| ≥ λ|z|, gdy |z| ≥ r, a zatem
|P
n
(z)| ≥ λ
n
|z|, gdy |z| ≥ r i n ≥ 1. Wynika st
,
ad, ˙ze K ⊂ K(0, r) oraz
(20.1)
C \ K =
[
n≥1
P
−n
({|z| > r}).
W szczeg´olno´sci, K jest zwarty. Zauwa˙zmy, ˙ze z ∈ P (K) ⇔ z ∈ K, tzn. P
−1
(K) =
K. Z kolei P (z) ∈ ∂K oznacza, ˙ze P (z) ∈ K oraz istnieje ci
,
ag w
k
∈ C \ K zbie˙zny do

50
ZBIGNIEW BÃLOCKI
z. Np. dzi
,
eki otwarto´sci P jest to r´ownowa˙zne istnieniu ci
,
agu z
k
l
∈ C \ K zbie˙znego
do z i takiego, ˙ze P (z
k
l
) = w
k
l
. Mamy wi
,
ec P
−1
(∂K) = ∂K.
Je˙zeli z ∈ ∂K, to ci
,
ag P
n
(z) jest ograniczony, ale z (20.1) mamy P
n
→ ∞
lokalnie jednostajnie na C \ K, a wi
,
ec na ˙zadnym otoczeniu punktu z ci
,
ag P
n
nie
jest rodzin
,
a normaln
,
a, czyli ∂K ⊂ J . Poniewa˙z C \ K ⊂ F, to J ⊂ K i, dzi
,
eki i),
K 6= ∅. Niech z
0
∈ ∂K. Z v) wynika, ˙ze zbi´or
S
n≥1
P
−n
(z
0
) jest g
,
esty w J . Zbi´or
ten jest jednak zawarty w ∂K (bo P
−1
(∂K) = ∂K), a wi
,
ec ∂K jest g
,
esty w J . St
,
ad
∂K = J.
Mamy ∂U ⊂ K, wi
,
ec z zasady maksimum i dzi
,
eki temu, ˙ze P (K) ⊂ K dostaniemy
U ⊂ K. Pokazali´smy, ˙ze ∂K ∪ U ⊂ K i ˙ze U jest sum
,
a skÃladowych ograniczonych
C \ ∂K. Poniewa˙z skÃladowa nieograniczona C \ ∂K nie ma punkt´ow wsp´olnych z K,
mamy ∂K ∪ U = K. ¤
PrzykÃlady. i) Dla P (z) = z
2
mamy J = ∂∆.
ii) Niech P (z) = z
2
− 2. Mo˙zna pokaza´c
´
Cwiczenie
, ˙ze funkcja f (ζ) = ζ + 1/ζ
odwzorowuje konforemnie obszar {|ζ| > 1} na C \ [−2, 2]. Mamy tak˙ze (f
−1
◦ P ◦
f )(ζ) = ζ
2
. Wynika st
,
ad, ˙ze P
n
→ ∞ na C \ [−2, 2]. Z drugiej strony P ([−2, 2]) ⊂
[−2, 2], a wi
,
ec z Twierdzenia 20.4 J = K = [−2, 2].
W og´olnym przypadku jednak dynamika wielomianu kwadratowego P
c
(z) :=
z
2
+ c, c ∈ C, jest bardzo skomplikowana i zbiory Julii J
c
wielomianu P
c
maj
,
a
zwykle struktur
,
e fraktali. Zbi´or Mandelbrota (Brook, Matelski, 1978, Mandelbrot,
1980) M to zbi´or tych c ∈ C, dla kt´orych ci
,
ag P
n
c
(0) jest ograniczony.
Mo˙zna udowodni´c (zob. np. [2]), ˙ze M jest sp´ojny i jednosp´ojny, ale otwartym
problemem pozostaje lokalna sp´ojno´s´c M. Mo˙zna tak˙ze pokaza´c, ˙ze je˙zeli c ∈ M,
to J
c
jest sp´ojny, natomiast dla c /
∈ M zbi´or J
c
jest caÃlkowicie niesp´ojny (tzn.
wszystkie skÃladowe sp´ojne J
c
s
,
a jednopunktowe).

FUNKCJE ANALITYCZNE
51
Literatura
[1]
E. Bombieri, Problems of the Millenium: Riemann Hypothesis,
zob.
http://www.claymath.org/millennium/Riemann Hypothesis.
[2]
L. Carleson, T.W. Gamelin, Complex Dynamics, Springer-Verlag, New
York, 1993.
[3]
J.B. Conway, Functions of One Complex Variable, Springer-Verlag, New
York, 1986.
[4]
J.B. Conway, Functions of One Complex Variable II, Springer-Verlag, New
York, 1995.
[5]
N.D. Elkies, Introduction to Analytic Number Theory, lecture notes, 1998,
zob. http://www.math.harvard.edu/eelkies/M259.98/index.html.
[6]
R.E. Greene, S.G. Krantz, Function theory of one complex variable, Amer-
ican Mathematical Society, Providence, RI, 2006.
[7]
R. Remmert, Theory of Complex Functions, Springer-Verlag, New York,1991.
[8]
W. Rudin, Analiza rzeczywista i zespolona, PWN, Warszawa, 1986.
[9]
E.B. Saff, A.D. Snider, Fundamentals of Complex Analysis for Mathemtics,
Science, and Engineering, wyd. 2, Prentice Hall, Englewood Cliffs, NJ, 1993.
[10] S. Saks, A. Zygmund, Analytic functions, Monografie Matematyczne 28,
PTM, Warszawa-WrocÃlaw, 1952.
[11] J. Stillwell, Mathematics and its History, wyd. 2, Springer-Verlag, New
York, 2001.

52
ZBIGNIEW BÃLOCKI
Zagadnienia na egzamin ustny
Uwaga. Powy˙zszy tekst oraz poni˙zsze zagadnienia maj
,
a charakter pomocniczy (nie-
wykluczone s
,
a pytania dodatkowe wykraczaj
,
ace poza poni˙zsze zagadnienia). Na
egzaminie ustnym obowi
,
azuje caÃly materiaÃl przedstawiony na wykÃladzie poza na-
st
,
epuj
,
acymi cz
,
e´sciami: dowodami Twierdze´
n 8.4 (twierdzenie o odwzorowaniu ot-
wartym), 10.2 (twierdzenie Cauchy’ego-Dixona) i 17.8 (problem Dirichleta w kole)
oraz sekcjami 13a (Obliczanie pewnych caÃlek rzeczywistych) i wi
,
ekszo´sci
,
a 20 (Ro-
dziny normalne, iteracja funkcji wymiernych) - z wyj
,
atkiem dowodu wielkiego
twierdzenia Picarda.
- SformuÃlowa´c i udowodni´c lemat d’Alemberta.
- SformuÃlowa´c zasadnicze twierdzenie algebry i udowodni´c je trzema r´o˙znymi spo-
sobami (korzystaj
,
ac odp. z lematu d’Alemberta, twierdzenia Liouville’a i twier-
dzenia Rouch´e).
- SformuÃlowa´c i udowodni´c wz´or na pochodn
,
a zÃlo˙zenia funkcji.
- Wyprowadzi´c wz´or na pochodne formalne ∂f /∂z, ∂f /∂z przy pomocy ∂f /∂x,
∂f /∂y. Pokaza´c, ˙ze funkcja zespolona jest C-r´o˙zniczkowalna wtedy i tylko wtedy,
gdy speÃlnia r´ownania Cauchy’ego-Riemanna.
- SformuÃlowa´c i udowodni´c wz´or na pochodn
,
a funkcji odwrotnej.
- SformuÃlowa´c i udowodni´c twierdzenie caÃlkowe Cauchy’ego dla tr´ojk
,
ata.
- Pokaza´c, ˙ze istnienie funkcji pierwotnej jest r´ownowa˙zne znikaniu caÃlek po dro-
gach zamkni
,
etych.
- SformuÃlowa´c i udowodni´c wz´or caÃlkowy Cauchy’ego dla koÃla.
- SformuÃlowa´c i udowodni´c lemat o produkcji funkcji holomorficznych.
- SformuÃlowa´c i udowodni´c twierdzenie o warto´sci ´sredniej dla funkcji holomor-
ficznych.
- SformuÃlowa´c i udowodni´c nier´owno´s´c Cauchy’ego.
- SformuÃlowa´c i udowodni´c twierdzenie Morery.
- SformuÃlowa´c i udowodni´c twierdzenie Liouville’a.
- SformuÃlowa´c i udowodni´c sÃlab
,
a i mocn
,
a zasad
,
e maksimum dla funkcji holomor-
ficznych.
- SformuÃlowa´c i udowodni´c twierdzenie Weierstrassa o ci
,
agach funkcji holomor-
ficznych.
- SformuÃlowa´c i udowodni´c wz´or Cauchy’ego-Hadamarda na promie´
n zbie˙zno´sci
szeregu pot
,
egowego.
- SformuÃlowa´c i udowodni´c zasad
,
e identyczno´sci dla szereg´ow pot
,
egowych i funkcji
holomorficznych.
- Pokaza´c, ˙ze ka˙zda funkcja holomorficzna w kole rozwija si
,
e w nim w szereg
pot
,
egowy.
- Poda´c definicj
,
e funkcji analitycznej. Poda´c przykÃlad funkcji klasy C
∞
, kt´ora
nie jest analityczna. Poda´c zwi
,
azek funkcji analitycznych z funkcjami holomor-
ficznymi. W jaki spos´ob znale´z´c promie´
n zbie˙zno´sci szeregu Taylora funkcji
analitycznej w danym punkcie?
- Poda´c definicj
,
e indeksu drogi zamkni
,
etej wzgl
,
edem punktu. Poda´c i udowodni´c
podstawowe wÃlasno´sci oraz interpretacj
,
e geometryczn
,
a.
- Pokaza´c, ˙ze funkcje holomorficzne w pier´scieniu mo˙zna rozwin
,
a´c w szereg Lau-
renta.
- SformuÃlowa´c i udowodni´c twierdzenie o obszarze zbie˙zno´sci szeregu Laurenta.

FUNKCJE ANALITYCZNE
53
- SformuÃlowa´c i udowodni´c zasad
,
e identyczno´sci dla szereg´ow Laurenta.
- Poda´c definicj
,
e osobliwo´sci pozornej, bieguna i osobliwo´sci istotnej (ka˙zdy przy-
padek zilustrowa´c przykÃladem). Om´owi´c rodzaj zera lub osobliwo´sci w punkcie
z
0
funkcji postaci f /g, gdzie f, g s
,
a funkcjami holomorficznymi w otoczeniu z
0
.
- SformuÃlowa´c i udowodni´c twierdzenie Riemanna o usuwaniu osobliwo´sci.
- SformuÃlowa´c i udowodni´c twierdzenie Casoratiego-Weierstrassa-Sochockiego.
- SformuÃlowa´c i udowodni´c twierdzenie charakteryzuj
,
ace rodzaj osobliwo´sci izolo-
wanej funkcji holomorficznej przy pomocy granic.
- Wyprowadzi´c formuÃl
,
e na residuum w punkcie, w kt´orym funkcja holomorficzna
ma biegun rz
,
edu m.
- SformuÃlowa´c i udowodni´c twierdzenie o residuach.
- SformuÃlowa´c i udowodni´c zasad
,
e argumentu.
- SformuÃlowa´c i udowodni´c twierdzenie Rouch´ego.
- Udowodni´c, ˙ze funkcja holomorficzna w pobli˙zu zera krotno´sci m jest odwzoro-
waniem m-krotnym.
- Poda´c definicj
,
e odwzorowania lokalnie konforemnego. Pokaza´c, ˙ze poj
,
ecie to
jest r´ownowa˙zne funkcji holomorficznej o nieznikaj
,
acej pochodnej (lub lokalnie
iniektywnej).
- Poda´c i udowodni´c charakteryzacj
,
e automorfizm´ow holomorficznych koÃla oraz
pÃlaszczyzny.
- SformuÃlowa´c i udowodni´c lemat Schwarza.
- Pokaza´c, ˙ze odwzorowania holomorficzne P → P to dokÃladnie funkcje wymierne.
- Poda´c i udowodni´c charakteryzacj
,
e automorfizm´ow sfery Riemanna.
- Pokaza´c, ˙ze ka˙zda funkcja harmoniczna jest lokalnie cz
,
e´sci
,
a rzeczywist
,
a funkcji
holomorficznej.
- Udowodni´c zasad
,
e maksimum dla funkcji harmonicznych.
- Udowodni´c wz´or Poissona.
- Pokaza´c, ˙ze iloczyn niesko´
nczony
Q
(1 + f
n
), gdzie f
n
s
,
a funkcjami holomor-
ficznymi, jest zbie˙zny lokalnie jednostajnie, je˙zeli szereg
P
|f
n
| jest lokalnie
ograniczony.
- Pokaza´c, ˙ze je˙zeli szereg
P
a
n
jest bezwzgl
,
ednie zbie˙zny, to iloczyn niesko´
nczony
Q
(1 + a
n
) znika wtedy i tylko wtedy, gdy znika jeden ze skÃladnik´ow.
- Poda´c definicj
,
e czynnik´ow Weierstrassa E
n
. Pokaza´c, ˙ze |E
n
(z) − 1| ≤ |z|
n+1
,
gdy |z| ≤ 1.
- SformuÃlowa´c i udowodni´c twierdzenie Weierstrassa o istnieniu funkcji holomor-
ficznej o zadanych zerach. Pokaza´c, ˙ze funkcje meromorficzne tworz
,
a (globalnie)
ciaÃlo uÃlamk´ow pier´scienia funkcji holomorficznych.
- Poda´c definicj
,
e funkcji ζ Riemanna w p´oÃlpÃlaszczy´znie Re s > 1. Wyprowadzi´c
przedstawienie funkcji ζ przy pomocy liczb pierwszych (iloczyn Eulera).
- Pokaza´c, ˙ze funkcja ζ Riemanna przedÃlu˙za si
,
e do funkcji holomorficznej w ob-
szarze {Re s > 0} \ {1}. Jaka jest jej osobliwo´s´c w 1? SformuÃlowa´c hipotez
,
e
Riemanna.
- SformuÃlowa´c i udowodni´c wielkie twierdzenie Picarda.
Wyszukiwarka
Podobne podstrony:
ćwiczenia usprawniające funkcje słuchowe, Dla dzieciaczków, Ćwiczenia
Funkcje Analityczne Notatki do Nieznany
Część III Własności ogólne funkcji analitycznych
Część IV Pewne klasy funkcji analitycznych
Funkcje Analityczne Zadania
egz, e (5), EGZAMIN Z CHEMII ANALITYCZNEJ DLA II ROKU CHEMII 2003/2004
H Toruńczyk Wykład z funkcji analitycznych
egz, e (7), EGZAMIN Z CHEMII ANALITYCZNEJ DLA II ROKU CHEMII 2003/2004
Elementy algebry liniowej z geometrią analityczną dla informatyków
funkcje analityczne, MATERIALY, Bazy danych
Funkcje analityczne
Stanisław Saks i Antoni Zygmund Funkcje analityczne
Część III Własności ogólne funkcji analitycznych
Elementy algebry liniowej z geometrią analityczną dla informatyków
Funkcje zadania dla studentów
Zadania funkcje analityczne (liczby zespolone)
więcej podobnych podstron