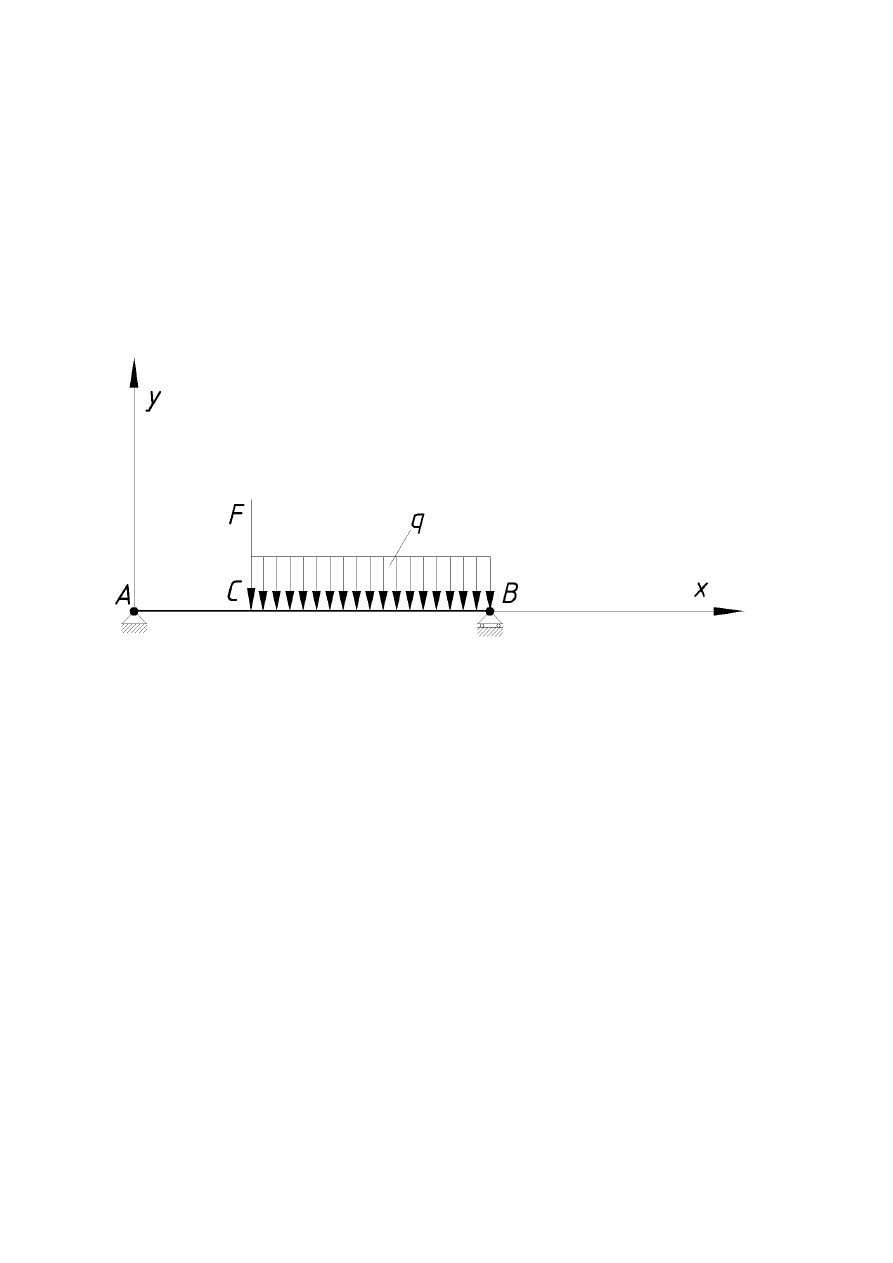
-1-

Wytrzymałość materiałów II GiG NIESTACJONARNE

19.05.2013 r.

Obliczenia momentów zginających i sił poprzecznych w belkach

Zadanie 1

Belka AB o długości 5 m została podparta na swoich końcach (rys.1). Na odcinku CB o

długości b = 3m działa na belkę obciążenie ciągłe q = 3kN/m. Ponadto w punkcie C działa na

belkę siła skupiona F = 2 kN. Obliczyć rozkład momentów zginających oraz sił tnących na

całej długości belki.

Rys. 1 [1]

W pierwszej kolejności przyjmujemy zwroty działania sił. W naszym przypadku

przyjmujemy, że wartości sił są zgodne z przyjętym systemem w układzie kartezjańskim, a

więc umieszczając punkt A w środku naszego układu (x,y) przyjmujemy, że wszystkie siły

mające zwrot zgodny ze zwrotem osi y będą miały wartości dodatnie, a siły skierowane

przeciwnie do kierunku osi y wartości ujemne.

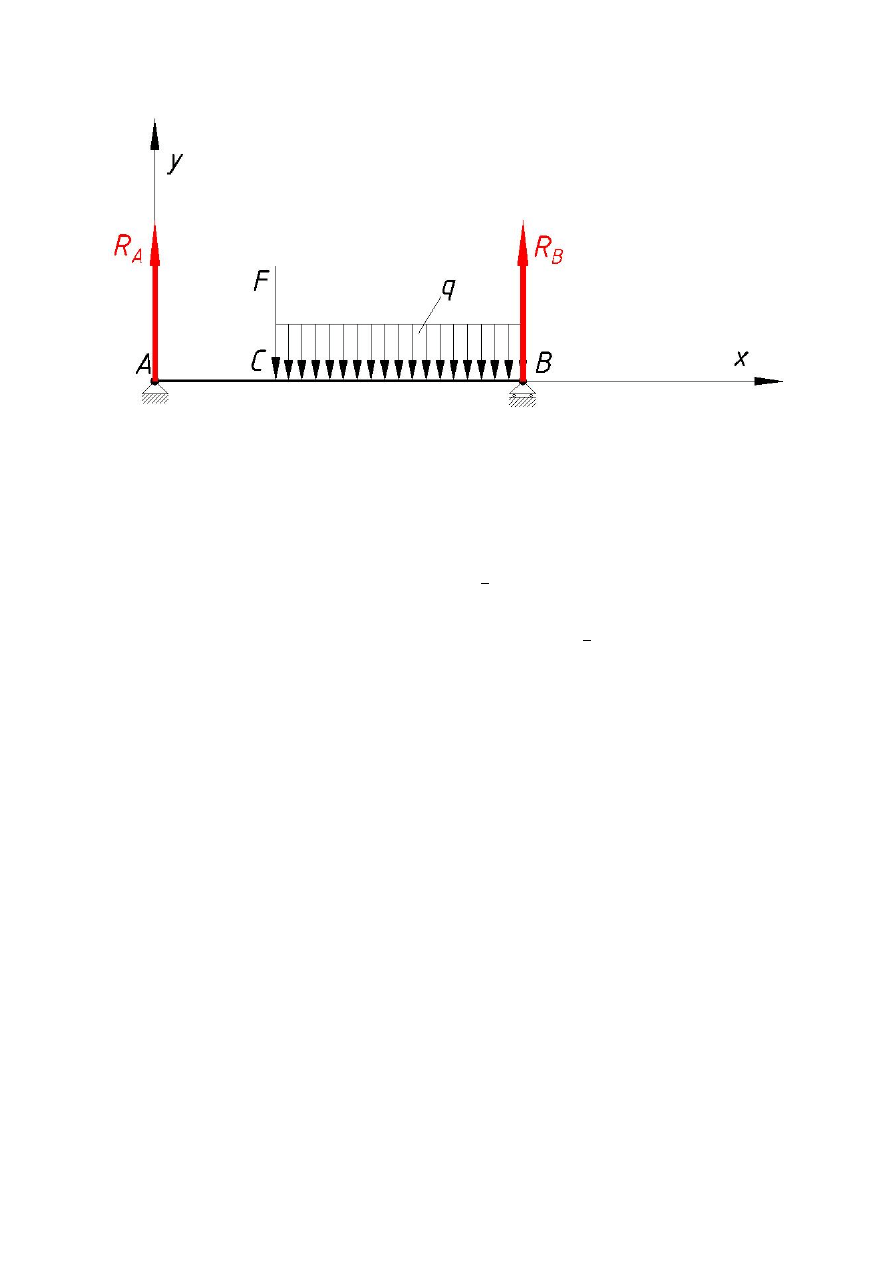
Kolejnym krokiem jest zaznaczenie reakcji działających w podporach.

Proponuję używać do tego celu koloru czerwonego (rys.2).

-2-

Rys. 2 (Opracowanie własne)

Ze względu na to, że w podporze A, która jest podporą stałą, składowa reakcji, leżąca w osi x

naszego układu jest równa „0”, można ją pominąć.

Układamy warunki równowagi statycznej dla belki:

I.

II.

SPRAWDZENIE

III.

Po podstawieniu danych do dwóch pierwszych równań obliczamy reakcje R

A

= 3,9 kN,

R

B

= 7,1 kN, których poprawność stwierdzamy podstawiając dane do równania trzeciego:

3,9+7,1-2-3·3=0

Zatem strona lewa równa się stronie prawej:

L = P

Znaki dodatnie oznaczają poprawność przyjętych zwrotów reakcji.

Możemy przejść do wyznaczania momentów gnących i sił poprzecznych (tnących) w belce.

-3-

Proponuję skonstruować do tego celu niniejszą tabelę:

Nr.

Prze-

działu

Przedział

T (x)

(siła tnąca)

Mg (x)

(Moment gnący)

Obliczenia

x

T

[kN]

Mg

[kN·m]

W pierwszej kolejności wyznaczamy wzory na momenty gnące w każdym z przedziałów.

Wyodrębniamy więc dwa przedziały zmienności obciążenia, a więc zmienności momentów

zginających i sił poprzecznych (tnących) (rys.3 i rys.4).

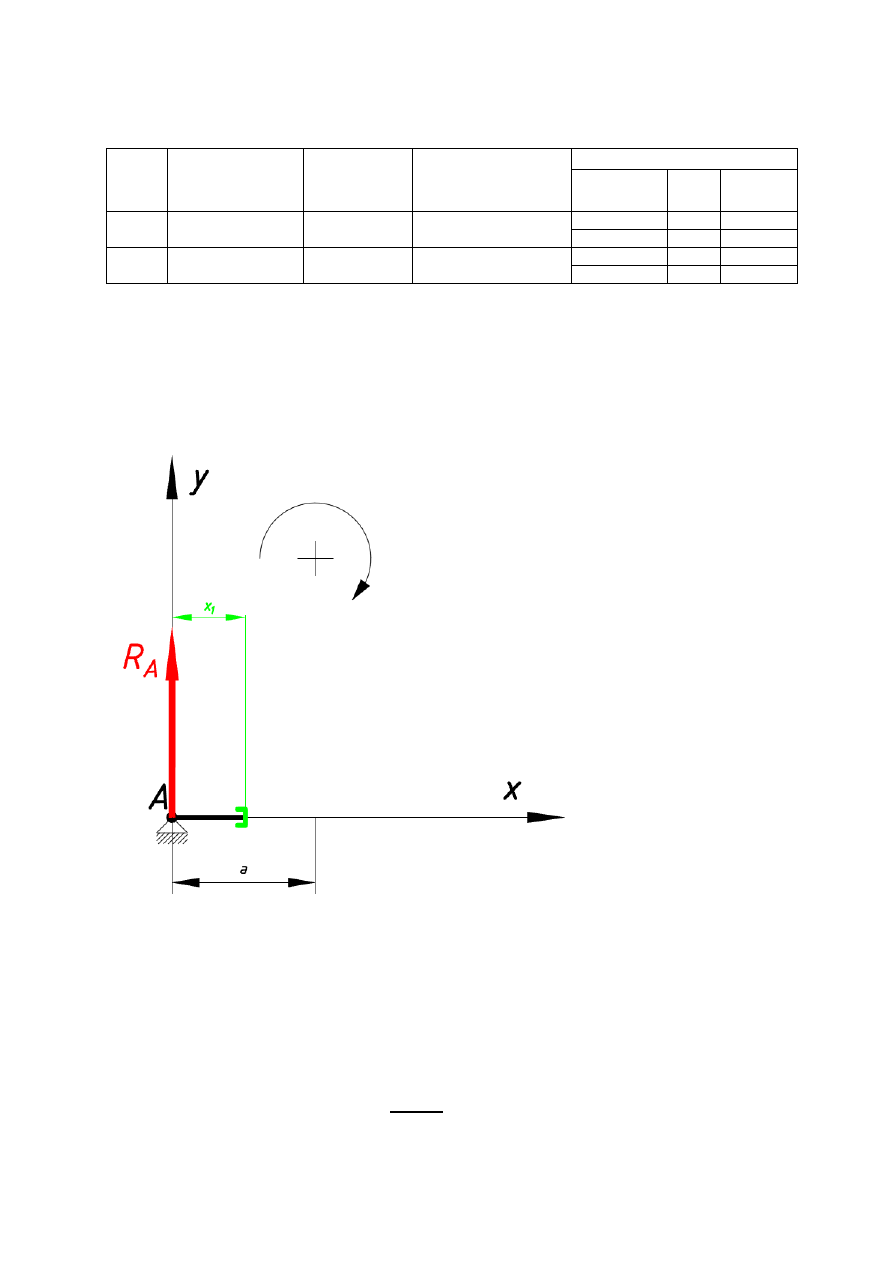
Przedział 1: 0 ≤ x

1

≤ a

Rys. 3 (Opracowanie własne)

Ogólne równania momentów i sił tnących w przedziale pierwszym mają postać:

M(x

1

) = R

A

·x

1

T(x

1

) = R

A

= const

Równania powyższe muszą spełniać zależność:

Siła poprzeczna (tnąca) to pochodna z momentu gnącego.

dM(x

1

)

dx

1

= x

1

,

-4-

a więc

d

dx

1

R

A

x

1

=

,

L = P.

Wartości momentów i sił na granicach przedziału są następujące:

M x

1

=0 =

0 k m,

M x

=2 m =

k m,

x

1

=

0 = x

1

=

2 m = k

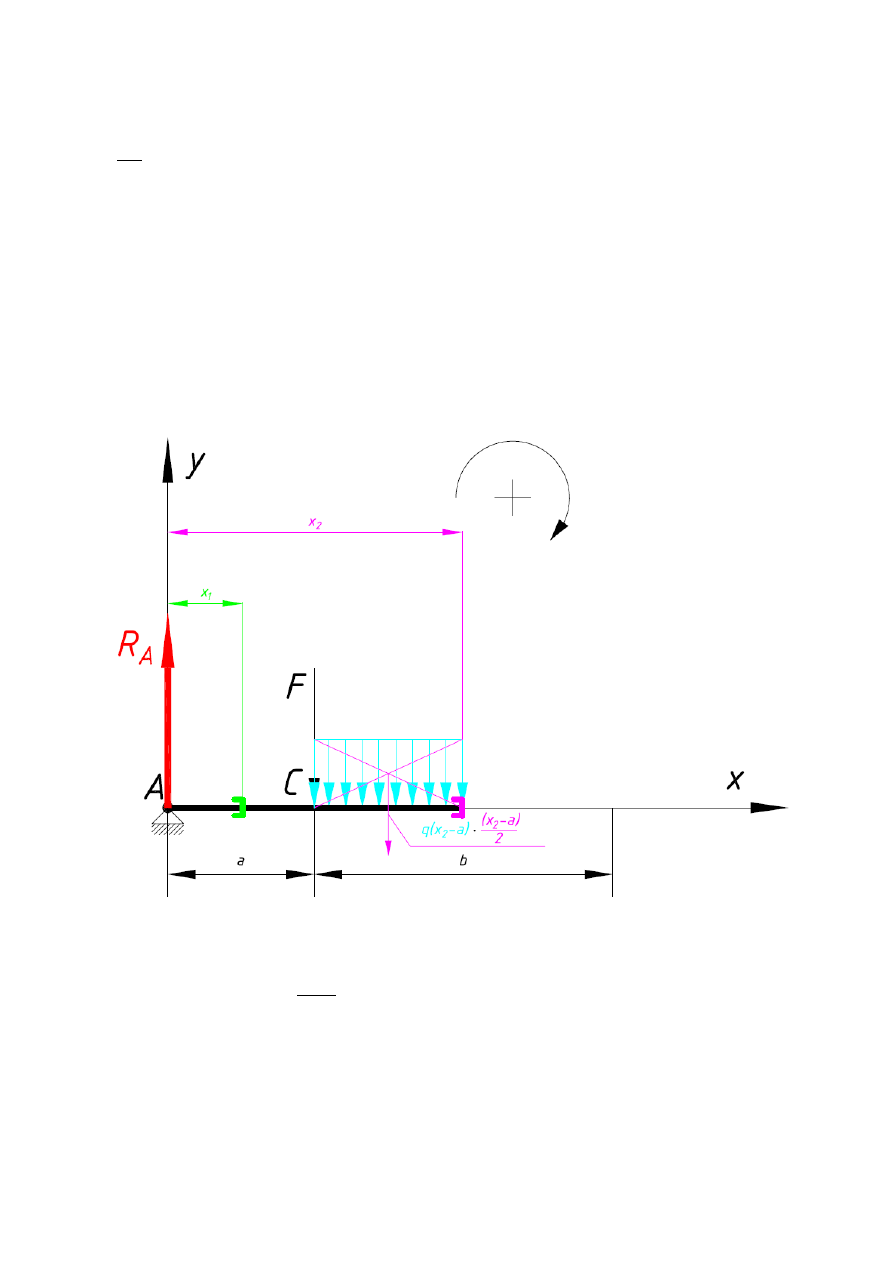
Przedział 2: 2m ≤ x

2

≤ 5 m

Rys. 4 (Opracowanie własne)

W przedziale drugim równania ogólne są następujące:

M x

2

=R

A

x

2

-F

x

2

-a

-q

x

2

-a

2

2

,

x

2

=R

A

-F-q

x

2

-a

.

Równania momentów zginających oraz sił tnących muszą spełniać zależność:

Siła poprzeczna (tnąca) to pochodna z momentu gnącego.

-5-

dM(x

2

)

dx

2

= x

2

,

a więc

d

dx

2

R

A

x

2

F(x

2

a) q

x

2

a

2

2

=R

A

F q x

2

a ,

L = P

Wartości momentów i sił na granicach przedziału drugiego są następujące:

M x

2

=2 m =

k m, M x

2

=5 m =

0 k m

x

2

=2 m =1 k , x

2

=5 m =

- 1 k

A zatem tabelka końcowa po uzupełnieniu wyników prezentuje się następująco:

Nr.

Prze-

działu

Przedział

T

(Siła tnąca)

Mg

(Moment gnący)

Obliczenia

x

T

[kN]

Mg

[kN·m]

1

0 ≤ x

1

≤ a

R

A

R

A

·x

1

0

3,9

0

a = 2 m

3,9

7,8

2

a ≤ x

2

≤ (a+b)

R

A

- F- q(x

2

-a)

R

A·

x

2

- F·(x

2

-a)

- q·(x

2

-a)·

a = 2m

1,9

7,8

(a+b) = 5 m

-7,1

0

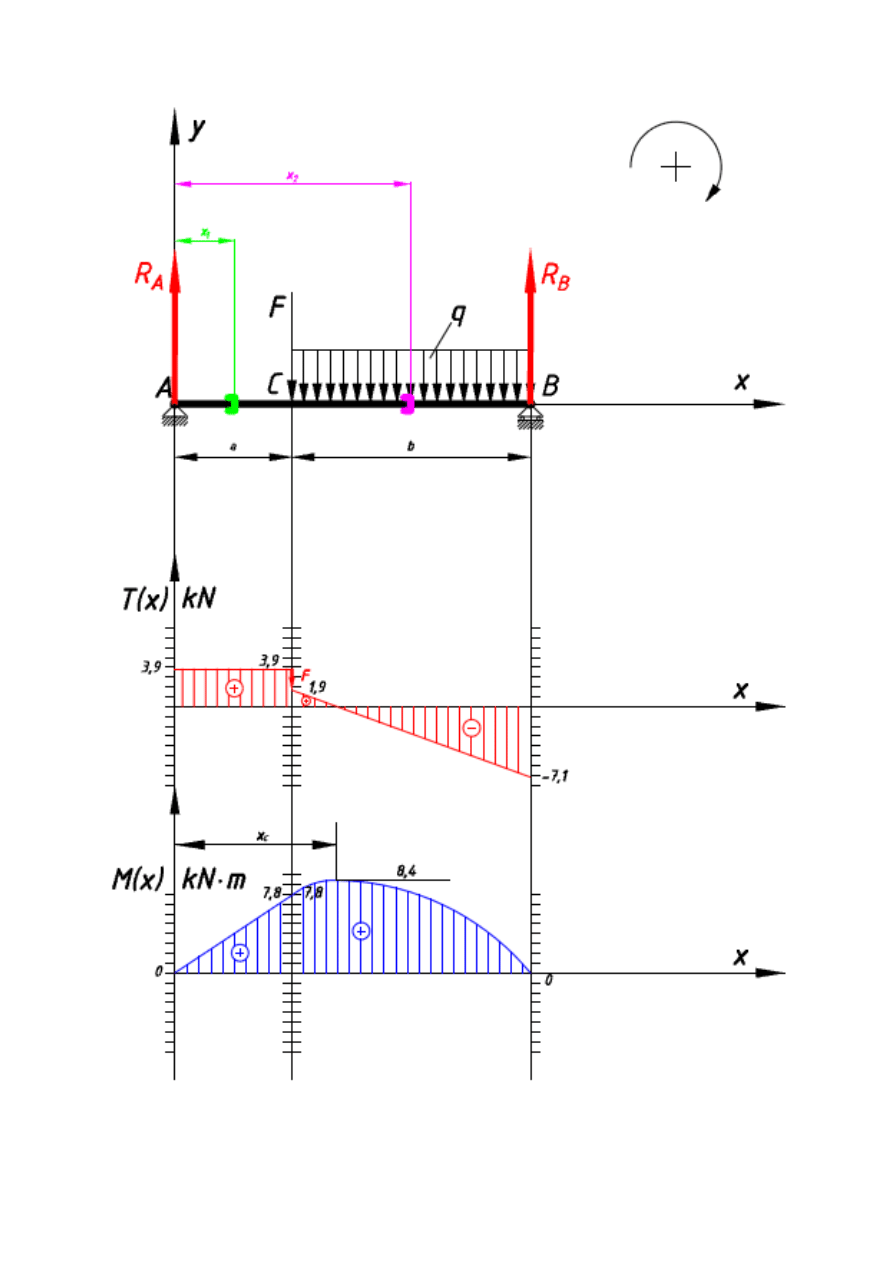
Wykresy sił tnących i momentów gnących w belce przedstawiono na rysunku nr.5:

-6-

Rys. 5 (Opracowanie własne)

-7-

Wykres sił tnących

W przedziale pierwszym wartość sił tnących jest stała i wynosi T(x

1

) = const = - 3,9 kN, co

odpowiada wartości reakcji podporowej R

A.

Na granicy przedziałów następuje przeskok o wartość 2 kN równą sile skupionej F

przyłożonej w tym miejscu. Następnie siły zmieniają się od wartości 1,9 kN do -7,1 kN.

Równanie opisujące charakter tych zmian T(x

2

) jest równaniem linii prostej i dlatego w ten

sposób połączymy obie wartości sił tnących obliczone na krańcach przedziału drugiego.

Wartość siły tnącej na końcu belki przyjmuje taką wartość, aby reakcja podporowa R

B

= 7,1

kN

mogła ją zrównoważyć [1].

Wykres momentów zginających

W przedziale pierwszym wartości momentu zginającego zmieniają się od 0 do 7,8 kNm

według zależności podanej równaniem M (x

1

) , które w sensie matematycznym jest

równaniem prostej przechodzącej przez początek układu współrzędnych.

W przedziale drugim, wykres przechodzi w sposób ciągły w równanie kwadratowe dane

równaniem M(x

2

). Jest to fragment paraboli skierowanej wypukłością ku górze, która posiada

lokalne ekstremum w punkcie x

0

, który znajdziemy obliczając miejsce zerowania się

pochodnej momentu, czyli siły tnącej [1]:

T(x

2

= x

0

) = 0

R

A

- F – q(x

0

-a)= 0.

Po podstawieniu danych otrzymujemy x

0

= 2.633 m.

Następnie obliczymy wartość momentu maksymalnego:

M

MAX

= M(x

2

-x

0

)

M

MAX

=

R

A

x

0

-F(x

0

-a)-q

x

0

-a

2

2

stąd moment M

m a x

= 8,4 kNm.

Zadania przykładowe

Zadanie 2

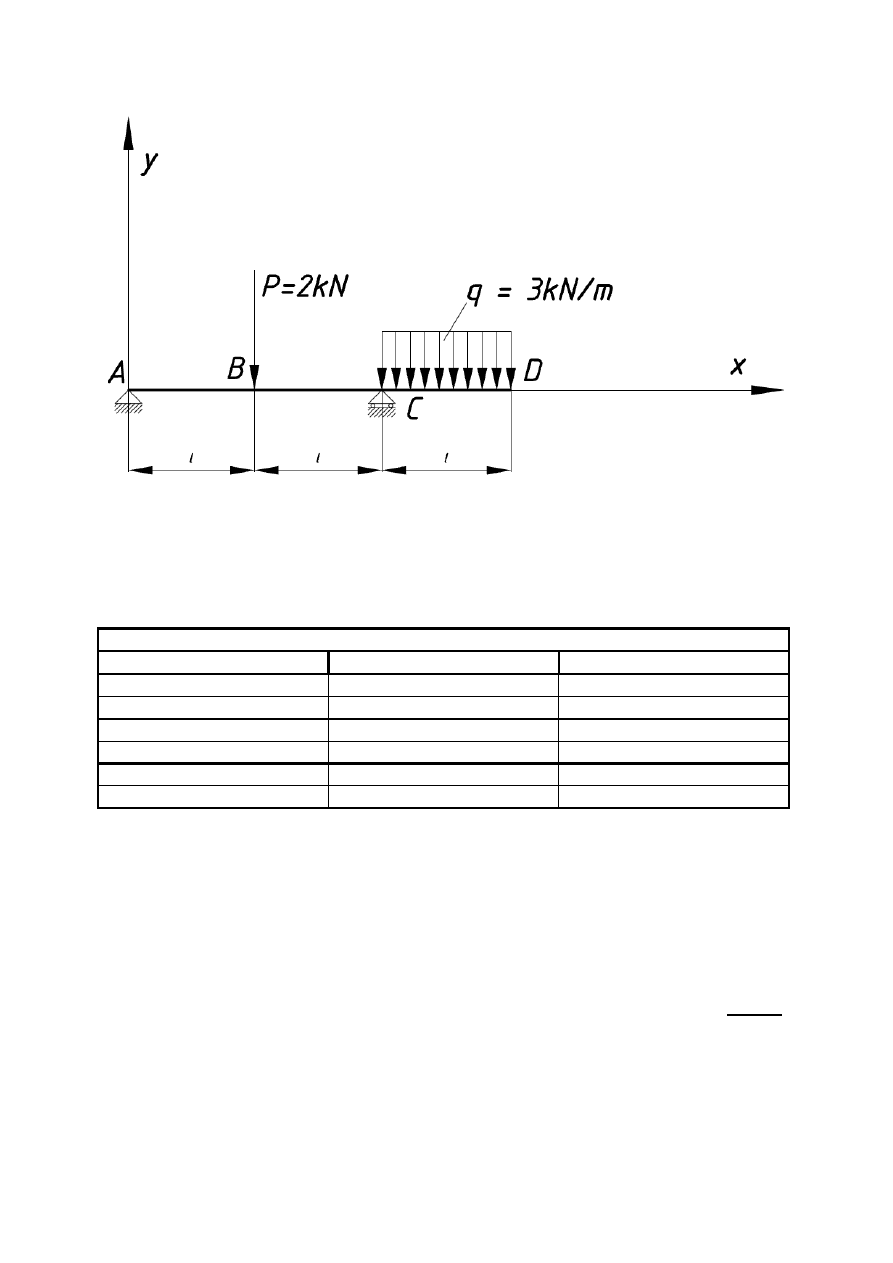
Belka AB o długości 5 m została podparta w punktach A i C (rys.6). W punkcie B działa na

belkę siła skupiona P = 2 kN. Ponadto na odcinku CD działa na belkę obciążenie ciągłe q = 3

kN/m. Długość l = 1 m. Obliczyć rozkład momentów zginających oraz sił tnących na całej

długości belki.

-8-

Rys. 6 (Opracowanie własne)

Odpowiedź:

R

A

= 0,25 kN, R

C

= 4,75 kN

Obliczenia

x

T [kN]

M [kNm]

0

0,25

0

l

0,25

0,25

l

-1,75

0,25

2l

-1,75

-1,5

2l

3,00

-1,5

3l

0

0

Uwaga !

Wszędzie tam gdzie mamy do czynienia z obciążeniem ciągłym, wykresem momentów

gnących będzie funkcja drugiego stopnia (kwadratowa). O tym czy wykres funkcji będzie

wklęsły (ramiona w górę), czy wypukły (ramiona w dół) decyduje znak „+” lub „-” przed

współczynnikiem kwadratowym równania.

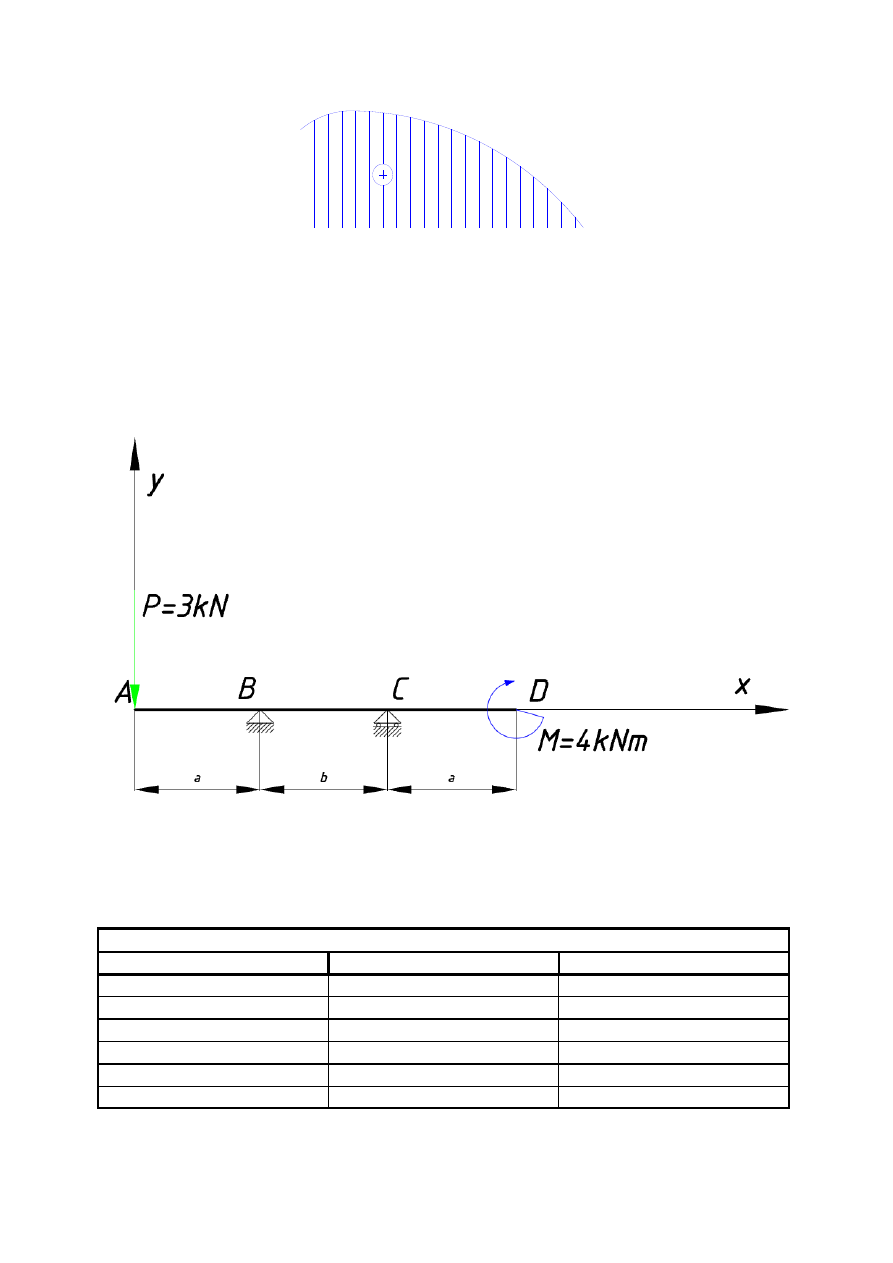
Z przykładu 1: W przedziale 2 występuje składnik równania kwadratowego

.

Wykres momentów w tym przedziale z uwagi na ujemny znak jest parabolą wypukłą,

skierowaną

ramionami

do

dołu

(rys.7).

-9-

Rys. 7 (Opracowanie własne)

Zad 3

Belka AD o długości 4 m została podparta w punktach B i C (rys.8). W punkcie A działa na

belkę siła skupiona P = 3 kN. Ponadto w punkcie D działa na belkę para sił o momencie

zginającym M = 4 kNm. Odcinek a = 1 m, natomiast b = 2 m . Obliczyć rozkład momentów

zginających oraz sił tnących na całej długości belki.

Rys. 8 (Opracowanie własne)

Odpowiedź:

R

B

= 2,5 kN, R

C

= 0,5 kN

Obliczenia

x

T [kN]

M [kNm]

0

-3,00

0

a

-3,00

-3,00

a

-0,50

-3,00

(a+b)

-0,50

-4,00

(a+b)

0

-4,00

(2a+b)

0

-4,00

-10-

Zad 4

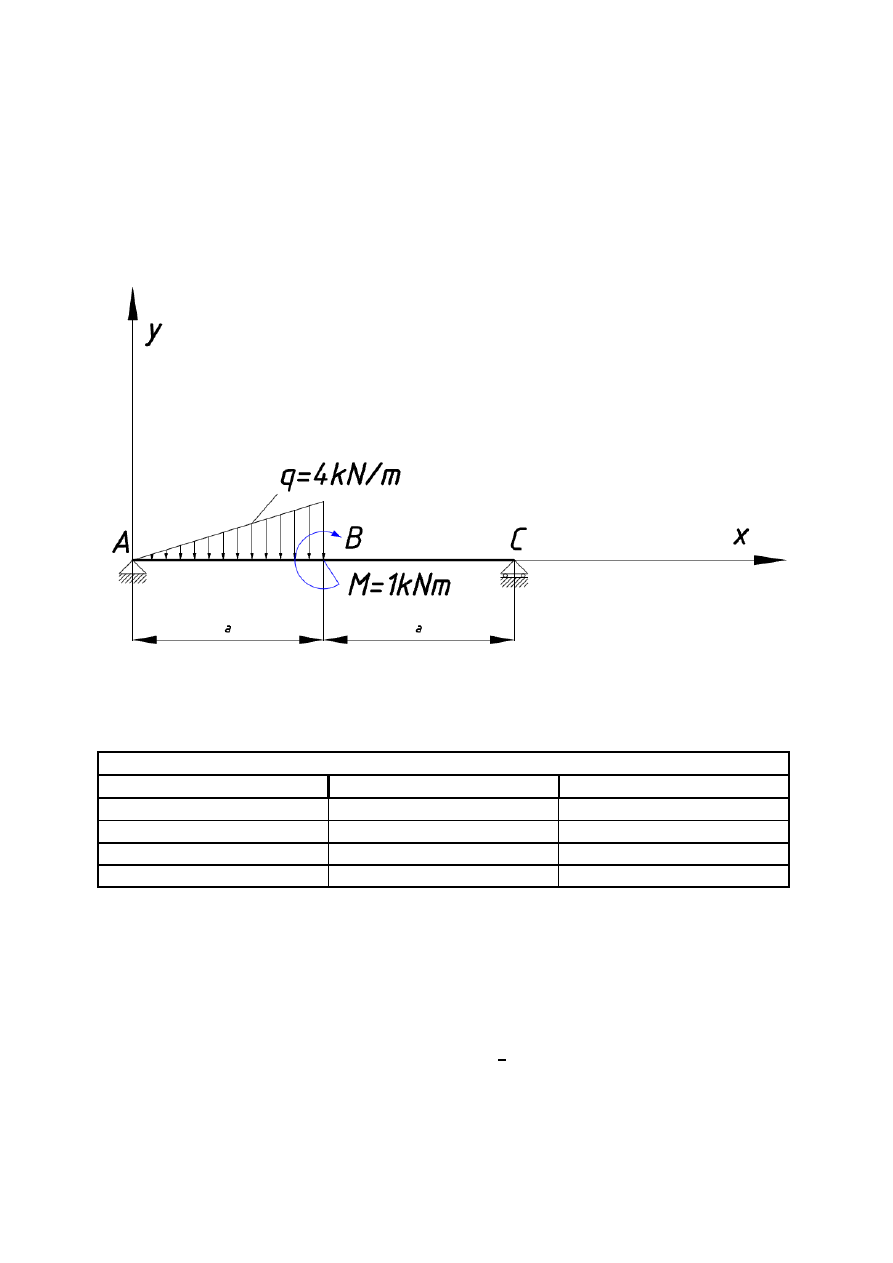
Wykonaj wykresy sił tnących i momentów gnących w belce AC podpartej swobodnie w obu

końcach i obciążonej na lewej połowie obciążeniem ciągłym zmieniającym się liniowo od

zera do natężenia q = 4 kN/m w środku długości belki i obciążonej dodatkowo momentem

M=1kNm (rys.9). Odcinek a = 1 m.

Rys. 9 (Opracowanie własne)

Odpowiedź:

R

A

= 0,830 kN, R

C

= 1,170 kN

Obliczenia

x [m]

T [kN]

M [kNm]

0

0,830

0

1

-0,503

0,163

1

-1,170

-1,163

2

-1,170

0

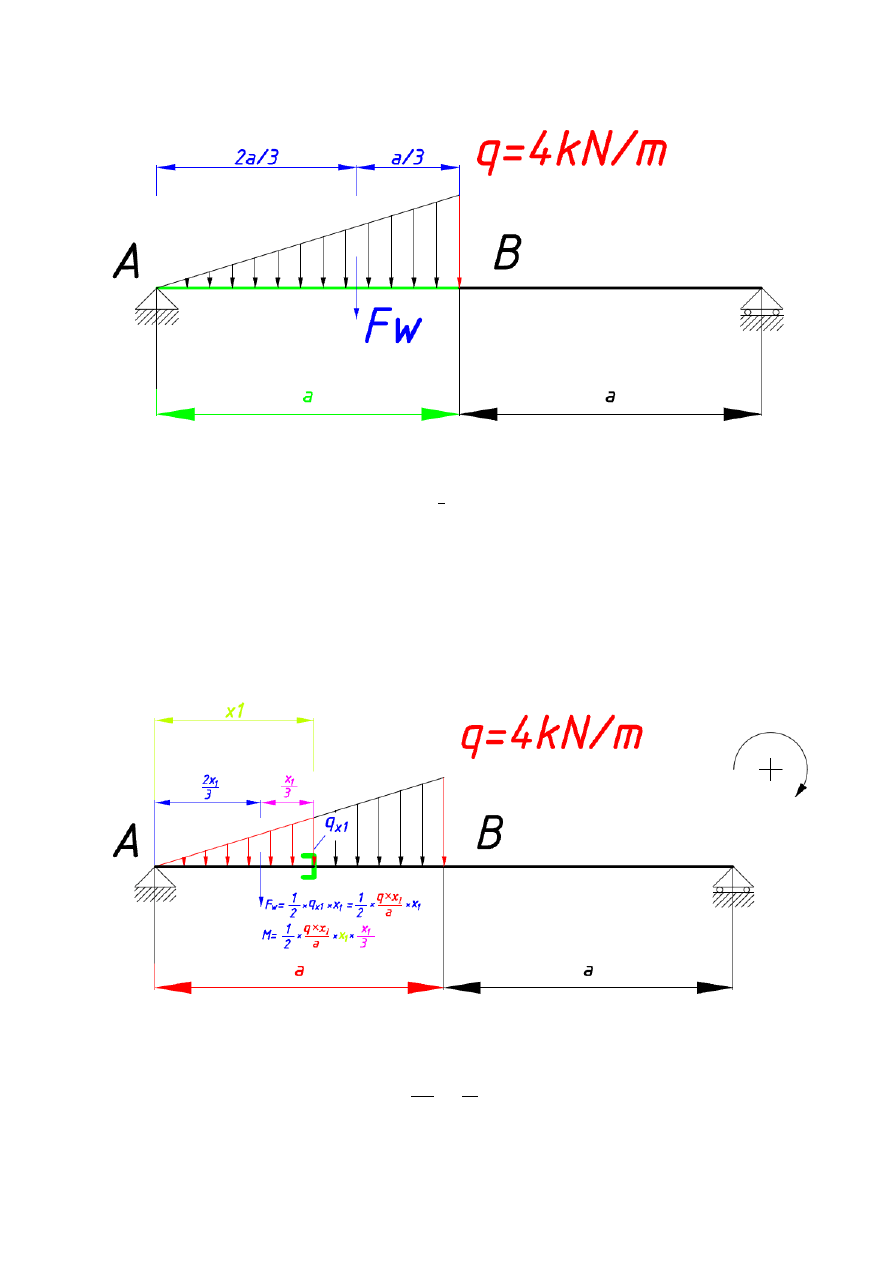
Uwaga !

W powyższym zadaniu mamy do czynienia z obciążeniem ciągłym zmieniającym się linowo

od zera do „q”. Podczas wyznaczania wzoru na moment gnący należy pamiętać o tym, że

wartość siły wypadkowej działającej w pierwszym przedziale belki, gdzie występuje

obciążenie ciągłe, równa jest polu trójkąta P

Δ

=

. Siła wypadkowa F

w

leży w

odległości 2/3 od podpory A i 1/3 od punktu B (rys.10).

A więc:

-11-

Rys. 10 (Opracowanie własne)

F

w

=

Przy wyznaczaniu równania dla momentu gnącego w pierwszym przedziale (x

1

) należy

uwzględnić wartość obciążenia liniowego zmieniającego się od zera do „q”.

W naszym przypadku wartość momentu dla obciążenia rozłożonego liniowo i zmieniającego

się od 0 do „q” będzie wyglądać następująco (rys.11):

Rys. 11 (Opracowanie własne)

Korzystamy z następującej zależności:

,

-12-

po uproszczeniu otrzymujemy, że:

A zatem wartość momentu działającego w przedziale pierwszym dla w/w obciążenia wynosi:

Ze względu na przeciwny zwrot do przyjętego w analizowanym przykładzie, wartość

momentu dla obciążenia ciągłego, przyjmuje znak ujemny.

A więc:

LITERATURA:

1. Iwulski Z.: Wyznaczanie sił tnących i momentów zginających w belkach. Uczelniane

Wydawnictwa Naukowo-Dydaktyczne Kraków 2001

Opracował:

mgr inż. Artur Ulaszek