Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Notatki do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów”

Notatki do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów”

Arkusz 03: Siły przekrojowe

Arkusz 03: Siły przekrojowe

1. Siły przekrojowe: podstawy teoretyczne.

Podstawy teoretyczne do zagadnienia sił przekrojowych należy opracować na podstawie wykładu
i pierwszych ćwiczeń dotyczących tego tematu, a także następującej literatury: [1], [2].

• Definicja siły wewnętrznej.
• Twierdzenia o równoważności układów sił wewnętrznych i zewnętrznych.
• Siły przekrojowe (definicja, redukcja układu, znakowanie, podstawowe stany mechaniczne).

2. Związki różniczkowe dla sił przekrojowych – zasady sprawdzania wykresów

Jeżeli założymy, że rozważany pręt jest prostoliniowy i pozostaje w równowadze, to pomiędzy
funkcją gęstości obciążenia zewnętrznego, funkcją siły tnącej oraz funkcją momentu zginającego
zachodzą związki różniczkowe pokazane w ramce obok (znakowanie zgodnie z konwencją
przyjętą na zajęciach oraz w [1]).
Ze związków między tymi trzema wymienionymi wielkościami widać na przykład:
1) q

z

(x) f. stała → F

z

(x) f.

.

liniowa → M

y

(x) f. Kwadratowa; a także: 2) brak obciążenia ciągłego na

danym przedziale oznacza stałą wartość sił tnących oraz liniową funkcję momentu.

Z analizy matematycznej wiemy, że jeśli pochodna funkcji ma wartość 0 w pewnym punkcie, to w tym punkcie dla funkcji
pierwotnej może istnieć ekstremum lokalne (tzw. warunek konieczny istnienia ekstremum). Spojrzawszy na nasze związki
różniczkowe, widać, że gdy siła poprzeczna zeruje się, moment może osiągnąć wartość ekstremum lokalnego.

Zasady sprawdzające poprawność wykresów sił przekrojowych:

•

Moment dodatni jest narysowany po stronie włókien rozciąganych.

•

Zgodność ze związkami różniczkowymi.

•

Extremum momentu: M

y

(x) = extr. <=> F

z

(x)=0.

•

Moment w przegubie jest równy 0.

•

Zwrot obciążenia ciągłego ustala wypukłość wykresu momentu („wiatr w żagiel”).

•

Siła lub moment skupiony powoduje skok na wykresie odpowiedniej wielkości (siły lub momentu) o wartości
równej wartości bezwzględnej tego obciążenia skupionego. Uwaga: zachowana jest równoległość wykresu po
obu stronach skoku, przy założeniu, że nie ma tam innych obciążeń.

•

Przyłożona siła skupiona (pionowa) powoduje brak gładkości na wykresie momentu w punkcie przyłożenia tej siły

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

dF

z

( x)

dx

=

q

z

( x)

dM

y

( x)

dx

= F

z

(x)

dM

y

2

(x)

dx

2

=

q

z

( x)

Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

(powstaje „strzałka”).

•

Niepodparty koniec belki, w którym nie przyłożono momentu skupionego => M

y

= 0 w tym punkcie.

Zadanie 1
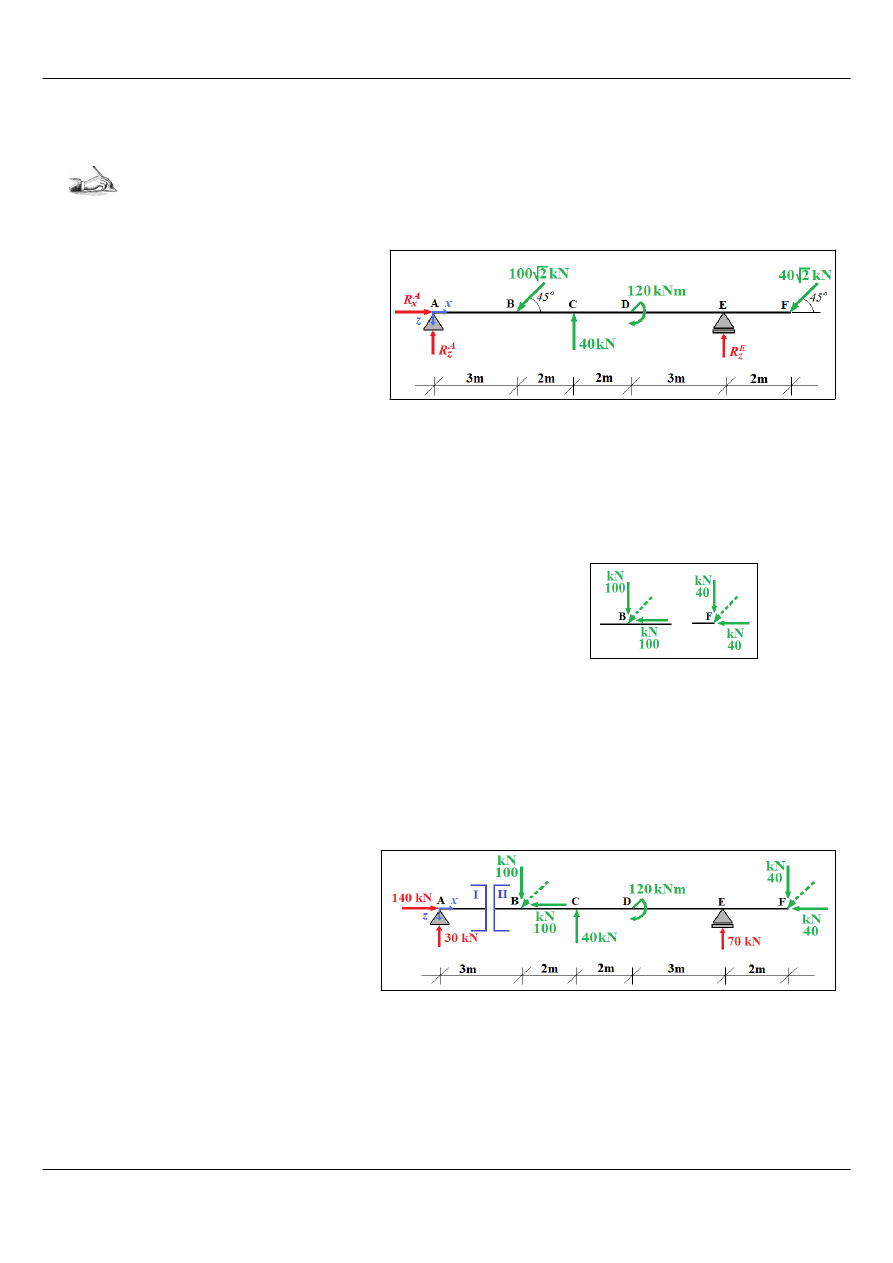
Dla zadanej konstrukcji (Rysunek 1) określić siły przekrojowe. (Treść zadania częściowo zaczerpnięta
z książki [4] str.21.)

(1) Sprawdzenie statycznej wyznaczalności

Konstrukcja ma dwa miejsca podparte, w których
generują się trzy reakcje w postaci sił. Równań
równowagi dostępnych dla przypadku płaskiego
jest także trzy, a więc stopień statyczniej
niewyznaczalności wynosi zero, a konstrukcja jest
statycznie wyznaczalna.

(2) Wyznaczenie reakcji

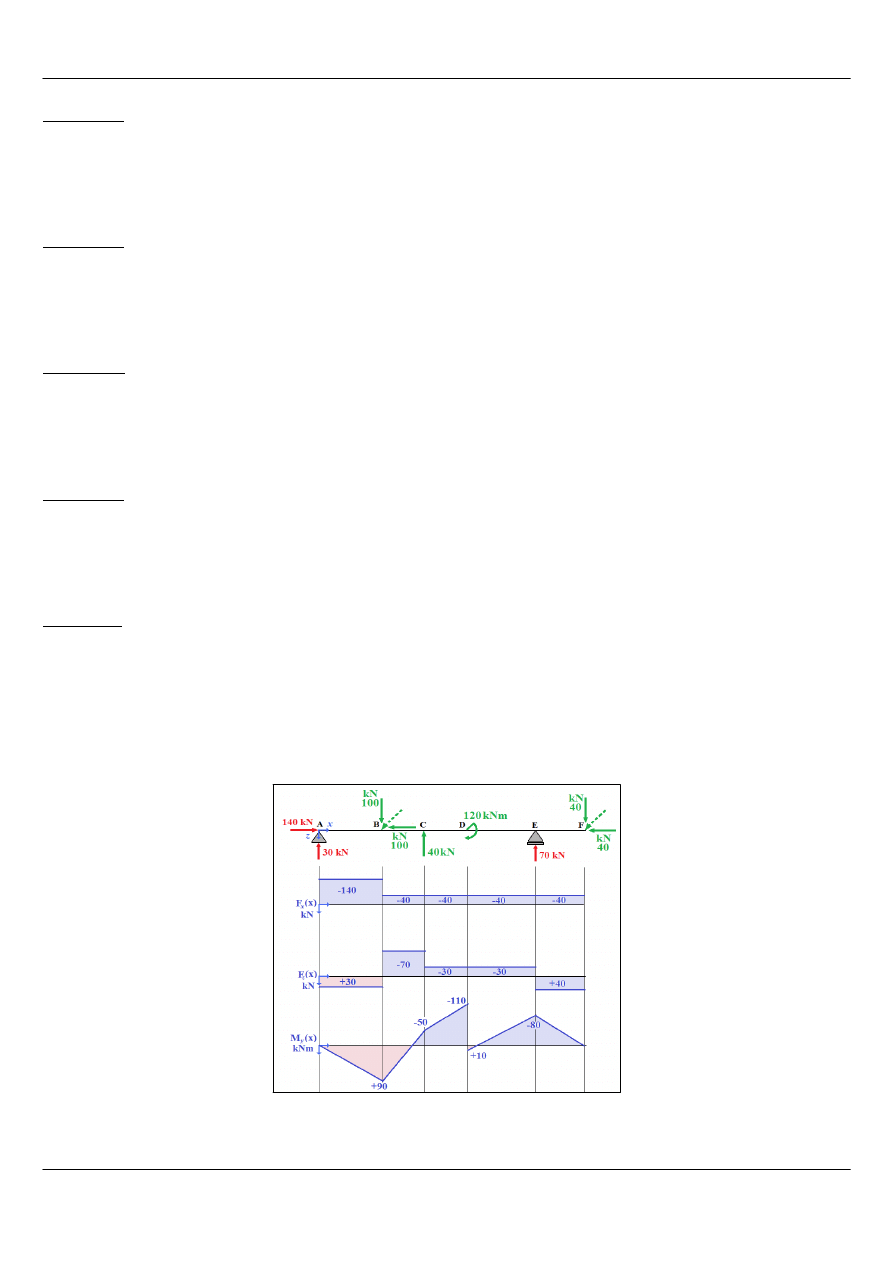
Przyjęto układ współrzędnych zaznaczony na rysunku. W drugim kroku określono punkty charakterystyczne. Następnie
narysowano i odpowiednio oznaczono występujące reakcje. Dla ułatwienia rozłożono siły nachylone pod kątem na
składowe równoległe do osi układu współrzędnych (Rysunek 2). Ostatnim etapem było rozpisanie i rozwiązanie układu
równań równowagi.

Σ X =0

⇔ R

x

A

100

40

= 0

⇔ R

x

A

= 140

[

kN

]

Σ M

y , A

=0

⇔

100

⋅3+ 40⋅5 120+ R

z

E

⋅10 40⋅12 = 0

⇔ R

z

E

= 70

[

kN

]

Σ Z =0

⇔

R

z

A

+ 100 40 70+ 30 = 0

⇔ R

z

A

= 30

[

kN

]

Warto dokonać sprawdzenia poprawności obliczeń przez dodatkowe równanie
sumy momentów.

(3) Siły przekrojowe

Po wyliczeniu reakcji znamy już wszystkie obciążenia zewnętrzne (czynne i bierne) przyłożone do konstrukcji. Siły
przekrojowe będą wyliczane w każdym przedziale charakterystycznym osobno. Po wyborze przedziału do rozważań,
dokonane zostanie jego myślowe przecięcie i tym
samym podział konstrukcji na dwie części: I i II.
Rysunek 3Rysunek 3 przedstawia schemat
konstrukcji wraz z układem sił zewnętrznych oraz
przykładowym podziałem na części I i II
dokonanym dla przedziału AB. W rozważaniach,
dla dokładnego zilustrowania, siły przekrojowe
będą obliczane dla zredukowanego układu sił
zewnętrznych obu części po kolei. Obliczenia w
[m], [kN] i [kNm].

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

Rysunek 1: Konstrukcja dla zad. 1.

Rysunek 2: Rozkład sił

nachylonych na składowe

równoległe do osi

Rysunek 3: Schemat konstrukcji do obliczeń sił przekrojowych

(przedział AB)

Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Przedział AB:

x

∈ (0 , 3)

F

x

(x) = [140]

I

= [ 100 40]

II

= 140

F

z

( x) =

[ 30]

I

= [100 40 70+ 40]

II

= 30

M

y

(x) = [ 30⋅x ]

I

= [ 100⋅(3 x)+ 40⋅(5 x) 120+ 70⋅( 10 x) 40⋅(12 x)]

II

= 30 x

M

y

(0

P

) = 30⋅0 = 0 oraz M

y

(3

L

) = 30⋅3 = 90

Przedział BC:

x

∈ (3 , 5)

F

x

(x) =

[140 100]

I

= [ 40]

II

= 40

F

z

( x) = [ 30+ 100]

I

= [ 40 70+ 40]

II

= 70

M

y

(x) =

[ 30⋅x+ 100⋅( x 3)]

I

= [+ 40⋅(5 x) 120+ 70⋅(10 x) 40⋅(12 x)]

II

= 70 x+ 300

M

y

(3

P

) = 90 oraz M

y

(5

L

) = 50

Przedział CD:

x

∈ (5 , 7)

F

x

(x) =

[140 100]

I

= [ 40]

II

= 40

F

z

( x) = [ 30+ 100 40]

I

= [ 70+ 40]

II

= 30

M

y

(x) =

[ 30⋅x+ 100⋅( x 3) 40⋅( x 5)]

I

= [ 120+ 70⋅(10 x) 40⋅(12 x)]

II

= 30 x+ 100

M

y

(5

P

) = 50 oraz M

y

(7

L

) = 110

Przedział DE:

x

∈ (7 , 10)

F

x

( x) =

[140 100]

I

= [ 40]

II

= 40

F

z

( x) = [ 30+ 100 40]

I

= [ 70+ 40]

II

= 30

M

y

( x) =

[ 30⋅x+ 100⋅( x 3) 40⋅( x 5)+ 120]

I

= [+ 70⋅(10 x) 40⋅(12 x)]

II

= 30 x+ 220

M

y

(7

P

) = + 10 oraz M

y

(10

L

) = 80

Przedział EF:

x

∈ (10 , 12)

F

x

(x) =

[140 100]

I

= [ 40]

II

= 40

F

z

( x) = [ 30+ 100 40 70]

I

= [+ 40]

II

= + 30

M

y

(x) =

[ 30⋅x+ 100⋅( x 3) 40⋅( x 5)+ 120 70⋅( x 10)]

I

= [ 40⋅(12 x)]

II

= 40 x 480

M

y

(10

P

) = 80 oraz M

y

(12

L

) = 0

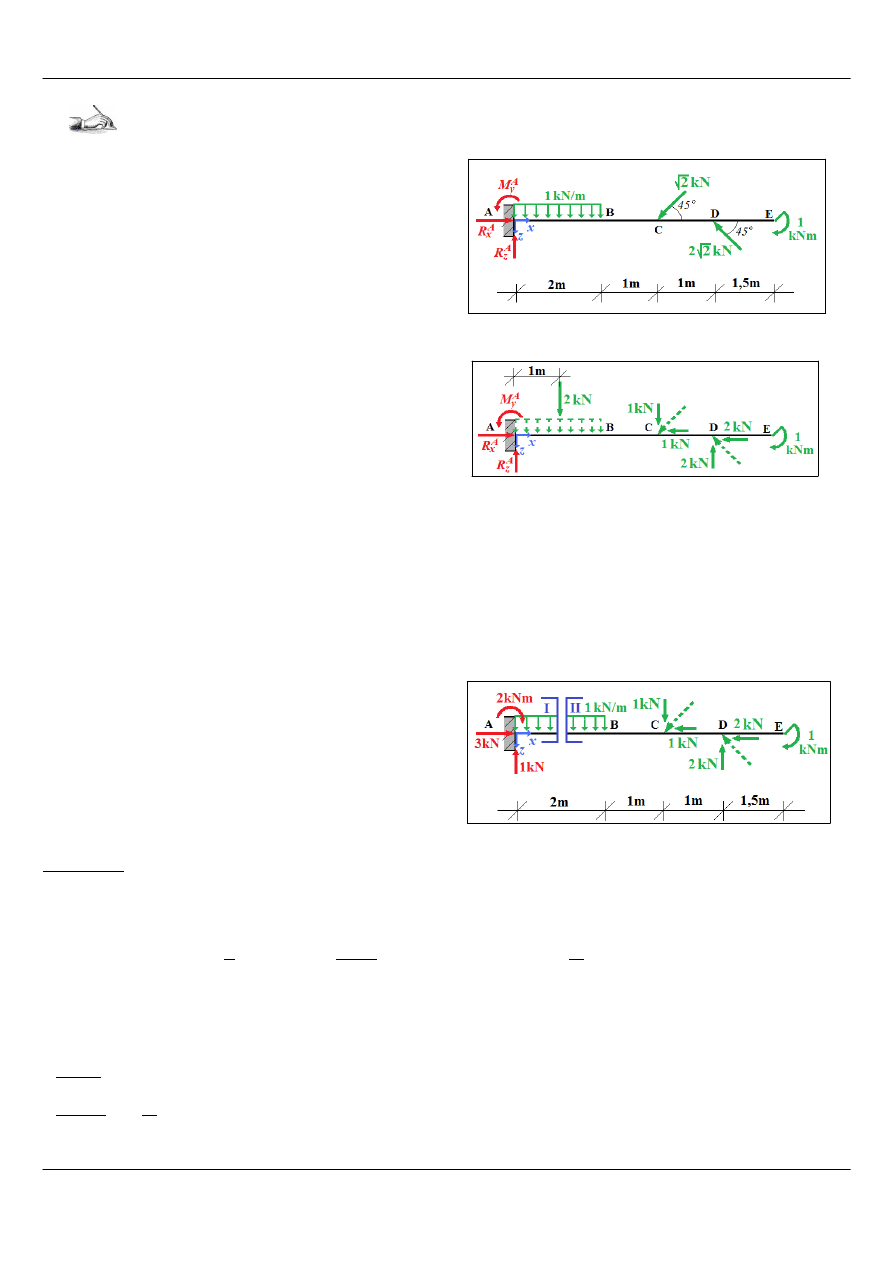
Wykresy sił przekrojowych przestawiają się następująco:

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

3

Rysunek 4: Siły przekrojowe w konstrukcji zad. 1

Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Zadanie 2
Dla zadanej konstrukcji (Rysunek 5) określić siły przekrojowe.

(1) Sprawdzenie statycznej wyznaczalności

Konstrukcja jest statycznie wyznaczalna (trzy teakcje, trzy
równania równowagi).

(2) Wyznaczenie reakcji

Przyjęto układ współrzędnych zaznaczony na rysunku.
W drugim kroku określono punkty charakterystyczne.
Następnie narysowano i odpowiednio oznaczono
występujące reakcje. Dla ułatwienia rozłożono siły
nachylone pod kątem na składowe równoległe do osi
układu współrzędnych i zamieniono obciążenie ciągłe na
skupione (Rysunek 6). Ostatnim etapem było rozpisanie
i rozwiązanie układu równań równowagi.

Σ X =0

⇔

R

x

A

1

1

= 0

⇔ R

x

A

= 3

[

kN

]

Σ Z =0

⇔

R

z

A

+ 1⋅2+ 1 2 = 0

⇔ R

z

A

= 1

[

kN

]

Σ M

y , A

=0

⇔ M

y

A

2

⋅1 1⋅3+ 2⋅4 1 = 0

⇔ M

y

A

= 2

[

kN

]

W związku z ujemną wartością momentu na utwierdzeniu, jaką otrzymano w wyniku obliczeń, zmieniono założony
wcześniej zwrot momentu (Rysunek 7). Warto dokonać sprawdzenia poprawności obliczeń przez dodatkowe równanie
sumy momentów.

(3) Siły przekrojowe

Znając już wszystkie obciążenia zewnętrzne, siły
przekrojowe wyliczamy w każdym przedziale
charakterystycznym osobno. Rysunek 7 przedstawia
konstrukcję z siłami zewnętrznymi oraz podziałem na
części I i II dla przedziału AB. Siły przekrojowe będą
obliczane dla zredukowanego układu sił zewnętrznych
części I i II. Obliczenia w [m], [kN], [kN/m] i [kNm].

Przedział AB:

x

∈ (0 , 2)

F

x

(x) =

[3]

I

= [ 1 2]

II

= 3

F

z

( x) = [ 1+ 1⋅x ]

I

= [1⋅(2 x)+ 1 2]

II

= x+ 1

F

z

(0

P

) = 1 oraz F

z

( 2

L

) = 1

M

y

(x) = [ 2 1⋅x+ 1⋅x⋅

x
2

]

I

= [ 1⋅( 2 x)⋅

(2 x)

2

1

⋅(3 x)+ 2⋅(4 x) 1]

II

=

x

2

2

+ x+ 2

M

y

(0

P

) = 2 oraz M

y

(2

L

) = 2

Dokonajmy sprawdzenia zgodnie z wzorami różniczkowymi:

dF

z

(x)

dx

= ( x+ 1)' = 1 =

q

z

( x)

dM

y

( x)

dx

= ( x

2

2

+ x+ 2)' = x+ 1 = F

z

( x)

.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

4

Rysunek 6: Zamiana na obciążenia ekwiwalentne do

obliczenia reakcji

Rysunek 7: Schemat konstrukcji do obliczeń sił

przekrojowych (przedział AB)

Rysunek 5: Konstrukcja dla zad. 2.

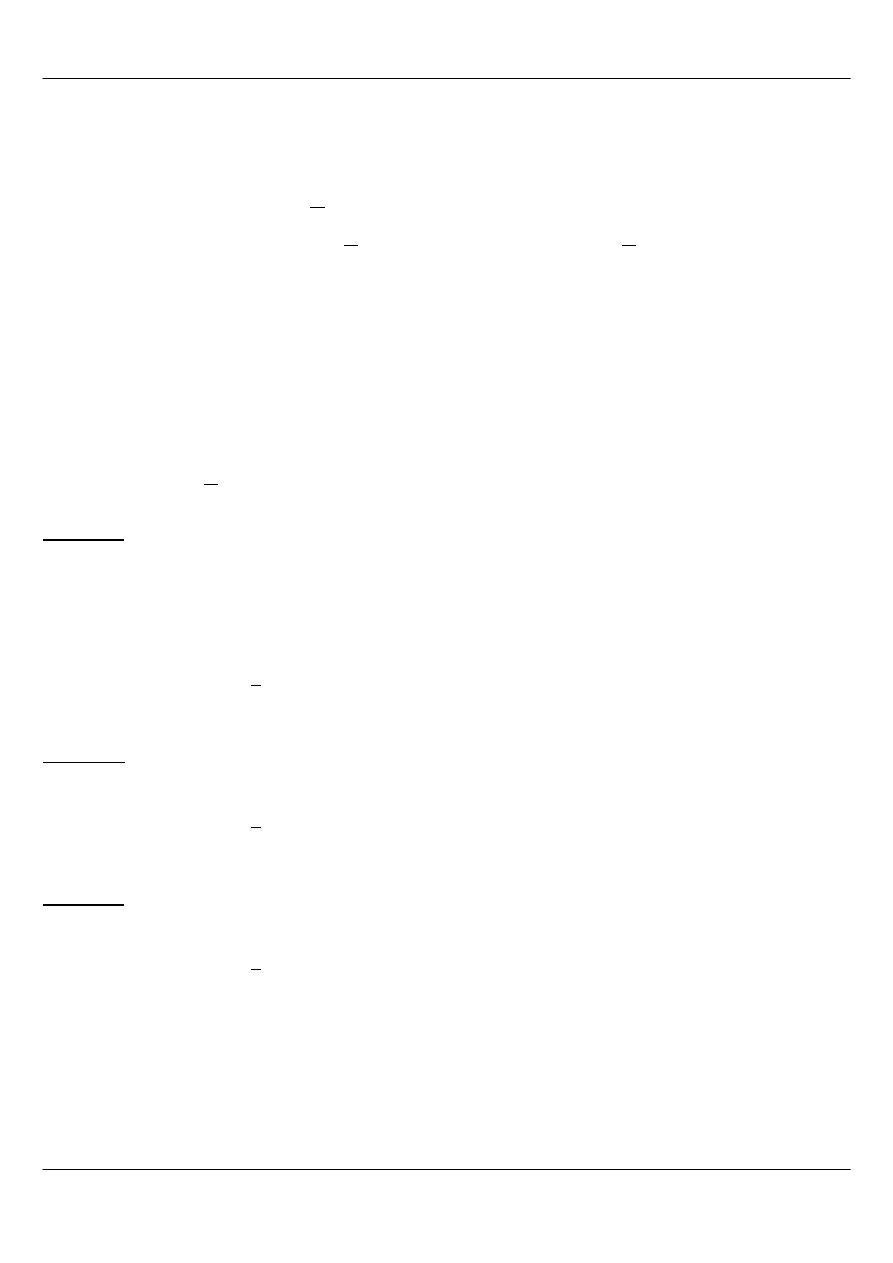
Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Można także skorzystać ze związków różniczkowych dla obliczenia sił przekrojowych w danym przedziale:

q

z

(x) = 1

F

z

( x) =

∫

q

z

( x)dx =

∫

1 dx

= x+ C

z warunków brzegowych: F

z

(0

P

) = 1 ⇒

0

+ C = 1 ⇒ C = 1 ⇒ F

z

(x) = x+ 1

M

y

(x) =

∫

F

z

(x) dx =

∫

( x+ 1)dx = x

2

2

+ x+ C

z warunków brzegowych: M

y

( 0

P

) = 2 ⇒

0

2

2

+ 0+ C = 2 ⇒ C = 2 ⇒ M

y

(x) = x

2

2

+ x+ 2

(Nawiasem, dodajmy: Gdyby w innych przedziałach także było obciążenie ciągłe, można by było w podobny sposób i dla
nich obliczyć funkcje sił przekrojowych. Z tym, że wtedy za warunki brzegowe należy przyjąć znane z poprzedniego
przedziału charakterystycznego wartości F

z

i M

y

na jego końcu i uwzględnić ewentualną obecność obciążenia skupionego

punkcie w rozważanym jako brzegowy.)

Jeszcze jedno zjawisko możemy zaobserwować dla przedziału AB, mianowicie istnienie wartości ekstremum lokalnego
momentu dla tego przedziału:

F

z

( x

extr

) = 0 ⇔

x

extr

+ 1 = 0 ⇔ x

extr

= 1

M

y

(x

extr

) = M

y

(1) =

1

2

2

+ 1+ 2 = 2,5 = M

extr

Przedział BC:

x

∈ (2 , 3)

Rozważając siły przekrojowe w przedziale, w którym nie występuje już obciążenie ciągłe, możemy zamiast niego
stosować równoważne mu obciążenie skupione (patrz: Rysunek 6):

F

x

(x) =

[3]

I

= [ 1 2]

II

= 3

F

z

( x) = [ 1+ 1⋅2]

I

= [+ 1 2]

II

= 1

M

y

(x) =

[ 2 1⋅x+ 1⋅2⋅(x 2

2

)]

I

= [ 1⋅(3 x)+ 2⋅(4 x) 1]

II

=

x

+ 4

M

y

(2

P

) = 2 oraz M

y

(3

L

) = 1

Przedział CD:

x

∈ (3 , 4)

F

x

(x) =

[3 1]

I

= [ 2]

II

= 2

F

z

( x) = [ 1+ 1⋅2+ 1]

I

= [ 2]

II

= 2

M

y

(x) =

[ 2 1⋅2+ 1⋅2⋅( x 2

2

)+ 1⋅( x 3)]

I

= [+ 2⋅(4 x) 1]

II

= 2x+ 7

M

y

(3

P

) = 1 oraz M

y

(4

L

) = 1

Przedział DE:

x

∈ (4 , 5,5)

F

x

(x) =

[3 1 2]

I

= [0]

II

= 0

F

z

( x) = [ 1+ 1⋅2+ 1 2]

I

= [0]

II

= 0

M

y

(x) =

[ 2 1⋅2+ 1⋅2⋅( x 2

2

)+ 1⋅( x 3) 2⋅( x 4)]

I

= [ 1]

II

= 1

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

5

Arkusz 03: Siły przekrojowe. Arkusz przeznaczony do ćwiczeń z przedmiotu „Podstawy wytrzymałości materiałów” na II roku dziennych studiów
Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

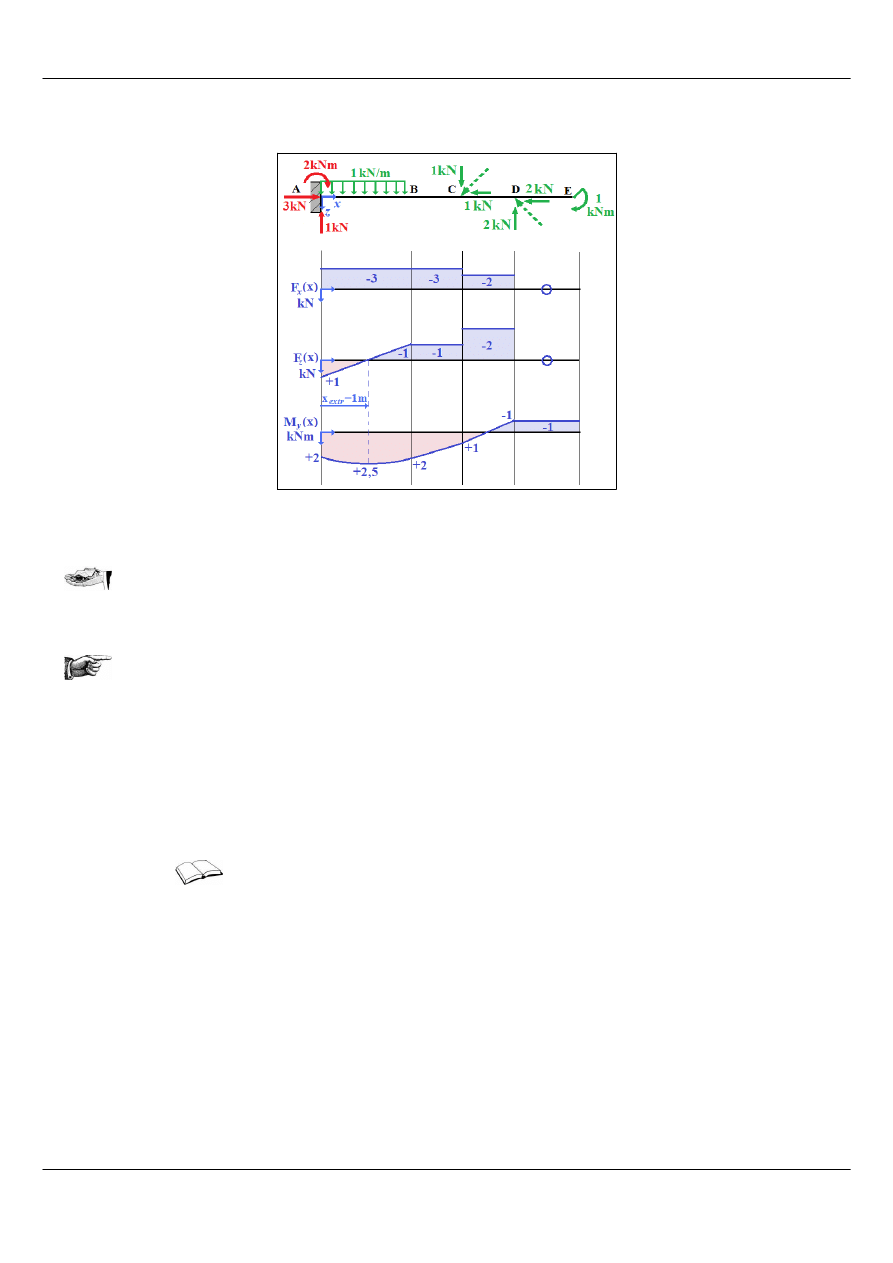
Wykresy sił przekrojowych przestawiają się następująco:

Jako ugruntowujące wiedzę warto rozwiązać kilka zadań z książki [3] (polecam zad. nr: 3, 7, 11, 15, 18, 21,
33, 51, 67) lub z innego zbioru zadań.

• Poprawne wyznaczanie reakcji w układach statycznie wyznaczalnych z obciążeniem skupionym i ciągłym.
Należy wiedzieć, jak sprawdzić poprawność obliczeń.
• Wyznaczanie sił przekrojowych z obu stron rozważanego przekroju, w konstrukcji obciążonej obciążeniem
skupionym i ciągłym.
• Umiejętność sprawdzenia wykresów, zgodnie z zasadami ich poprawności.
• Znajomość związków różniczkowych, umiejętność ich zastosowania.

3. Literatura

[1] Piechnik S. "Mechanika techniczna ciała stałego", Wydawnictwo PK, Kraków 2007
[2] Bodnar A. „Wytrzymałość materiałów. Podręcznik dla studentów wyższych szkół technicznych”, wydanie drugie

poszerzone i poprawione, Kraków 2004

[3] Iwulski Z. „Wyznaczanie sił tnących i momentów zginających w belkach: zadania z rozwiązaniami”, Uczelniane

Wydawnictwa Naukowo-Dydaktyczne AGH, Kraków 2001 (lub wersja elektroniczna: Biblioteka Główna AGH,
Kraków 2003).

[4] Grabowski J., Iwanczewska A. „Zbiór zadań z wytrzymałości materiałów”, Oficyna Wydawnicza Politechniki

Warszawskiej, Warszawa 2006

[5] Programy komputerowe do obliczeń statycznych.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

6

Rysunek 8: Siły przekrojowe w konstrukcji zad. 2