2

ĆW. 3. Badanie Obwodów RLC

I.

CEL ĆWICZENIA



Poznanie istoty łączenia poszczególnych elementów RLC w obwodach

elektrycznych,



Określenie pojemności zastępczej oraz rezystancji zastępczej obwodów.

II.

ZESTAW OPRZYRZĄDOWANIA DO ĆWICZENIA



Dekada kondensatorów



Mostek RLC



Dekady rezystorów



Zestaw przewodów łączeniowych

III.

SPOSÓB POSTĘPOWANIA

1.

Wyznaczyć wartości impedancji zastępczej dla układów R-R, gdzie:

R1 = 30 Ω, R2 = 6 Ω - połączonych szeregowo i równolegle korzystając z

mostka RLC ( instrukcja obsługi w załączniku ).

2.

Wyznaczyć wartości pojemności zastępczej, dobroci i stratności

dla układów C-C gdzie: C1 = 0,22 μF, C2 = 0,33 μF - połączonych

szeregowo i równolegle korzystając z mostka RLC dla częstotliwości

pomiaru: 100 Hz, 120 Hz, 1 kHz, 10 kHz (zmiana przyciskiem FREQ).

3.

Wyznaczyć wartości impedancji zastępczej dla układu RC

gdzie: R1 = 8 Ω, C1 = 0,22 μF - połączonych szeregowo korzystając z

mostka RLC dla częstotliwości pomiaru: 100 Hz, 120 Hz, 1 kHz, 10 kHz

(zmiana przyciskiem FREQ).

4.

Wyznaczyć wartości impedancji zastępczej dla układu RL

gdzie: R1 = 8 Ω, L1 = 1 mH - połączonych szeregowo korzystając z

mostka RLC dla częstotliwości pomiaru: 100 Hz, 120 Hz, 1 kHz, 10 kHz

(zmiana przyciskiem FREQ).

3

IV.

WSTĘP TEORETYCZNY

4.1. Analiza obwodów złożonych z elementów RLC połączonych szeregowo

i równolegle

4.1.1. Prawa Kirchhoffa dla obwodów prądu przemiennego.

Prawa Kirchhoffa sformułowane dla prądu stałego, stosuje się także do wartości

chwilowych przebiegów w obwodach prądu przemiennego.

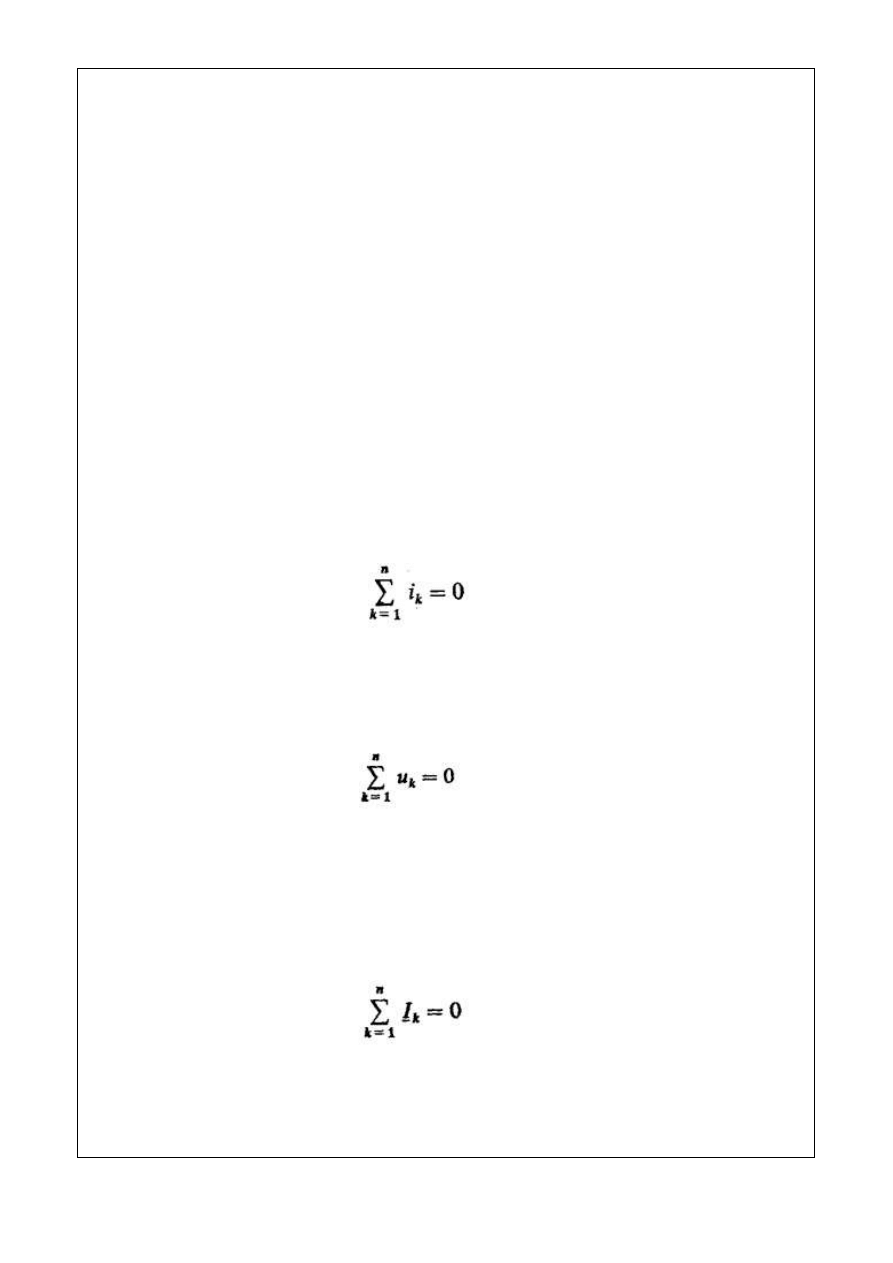
Pierwsze prawo Kirchhoffa: suma wartości chwilowych prądów w dowolnym węźle

obwodu elektrycznego jest równa zeru. Pojęcie węzła może być rozszerzone do obszaru

zamkniętego, obejmującego dowolną część obwodu

(4.1)

Drugie prawo Kirchhoffa: suma wartości chwilowych napięć na elementach źródłowych i

rezystancyjnych w dowolnym oczku zamkniętym jest równa zeru

(4.2)

Sumowanie wartości chwilowych przebiegów sprowadza się do sumowania sinusoid. Może

ono być wykonane przez sumowanie geometryczne wektorów lub analitycznie - za pomocą

rachunku symbolicznego.

W zapisie symbolicznym prawa Kirchhoffa przyjmują postać:

pierwsze prawo Kirchhoffa:

(4.3)

suma geometryczna prądów w dowolnym węźle obwodu elektrycznego jest równa zeru;

4

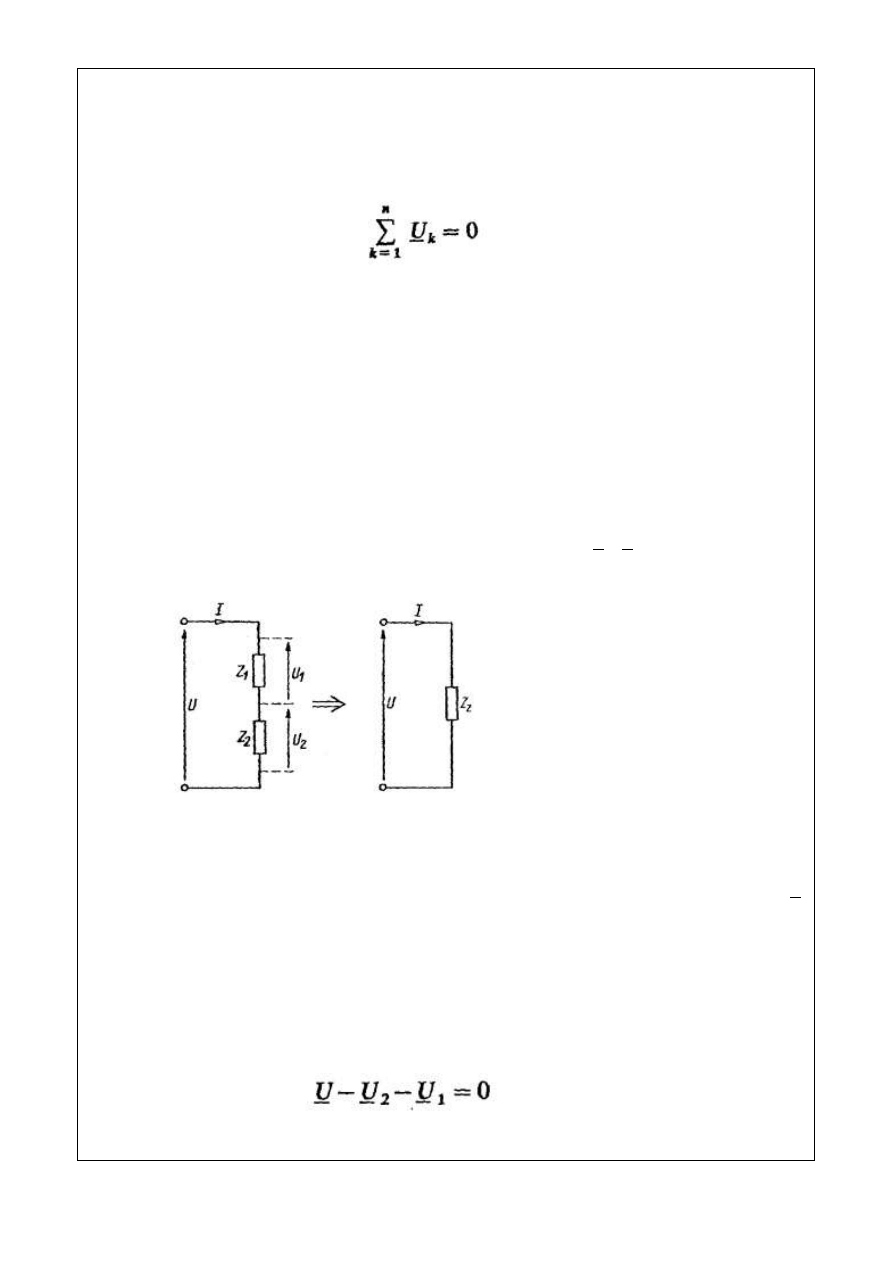
drugie prawo Kirchhoffa:

(4.4)

suma geometryczna napięć na elementach źródłowych i rezystancyjnych w dowolnym oczku

zamkniętym obwodu elektrycznego jest równa zeru.

Sumowanie geometryczne na wykresach wektorowych można wykonywać na zasadzie

równoległoboku lub wieloboku.

4.2.

Łączenie szeregowe i równolegle impedancji.

Korzystając z praw Kirchhoffa, można wyprowadzić wzory na impedancję zastępczą

połączenia szeregowego i równoległego odbiorników o impedancjach Z

1

i Z

2

.

Rys. 4.1. Połączenie szeregowe odbiorników

Na rysunku 4.1 pokazano połączenie szeregowe odbiorników. Odbiornik o impedancji Z

z

jest równoważny lub zastępczy, jeżeli jego odpowiedź na wymuszenie jest identyczna z

odpowiedzią układu szeregowego na to samo wymuszenie. Zgodnie z drugim prawem Kirchhoffa

dla obwodu szeregowego, przedstawionego na rys. 4.1, zachodzi równość

5

a zatem:

(4.5)

po uwzględnieniu prawa Ohma w postaci zespolonej:

U = Z I

lub

I = Y U

otzrymamy

(4.6)

Jest to odpowiedź obwodu szeregowego na wymuszenie I. Odpowiedzią odbiornika

równoważnego jest

(4.7)

Przez porównanie zależności (4.6) i (4.7) eliminujemy napięcie oraz prąd i otrzymujemy

wzór na impedancję równoważną

(4.8)

który możemy uogólnić na połączenie szeregowe dowolnej liczby odbiorników

(4.9)

Na rysunku 3.2 pokazano połączenie równolegle odbiorników o impedancjach Z

1

i Z

2

oraz

odbiornik równoważny o impedancji Z

z

.

6

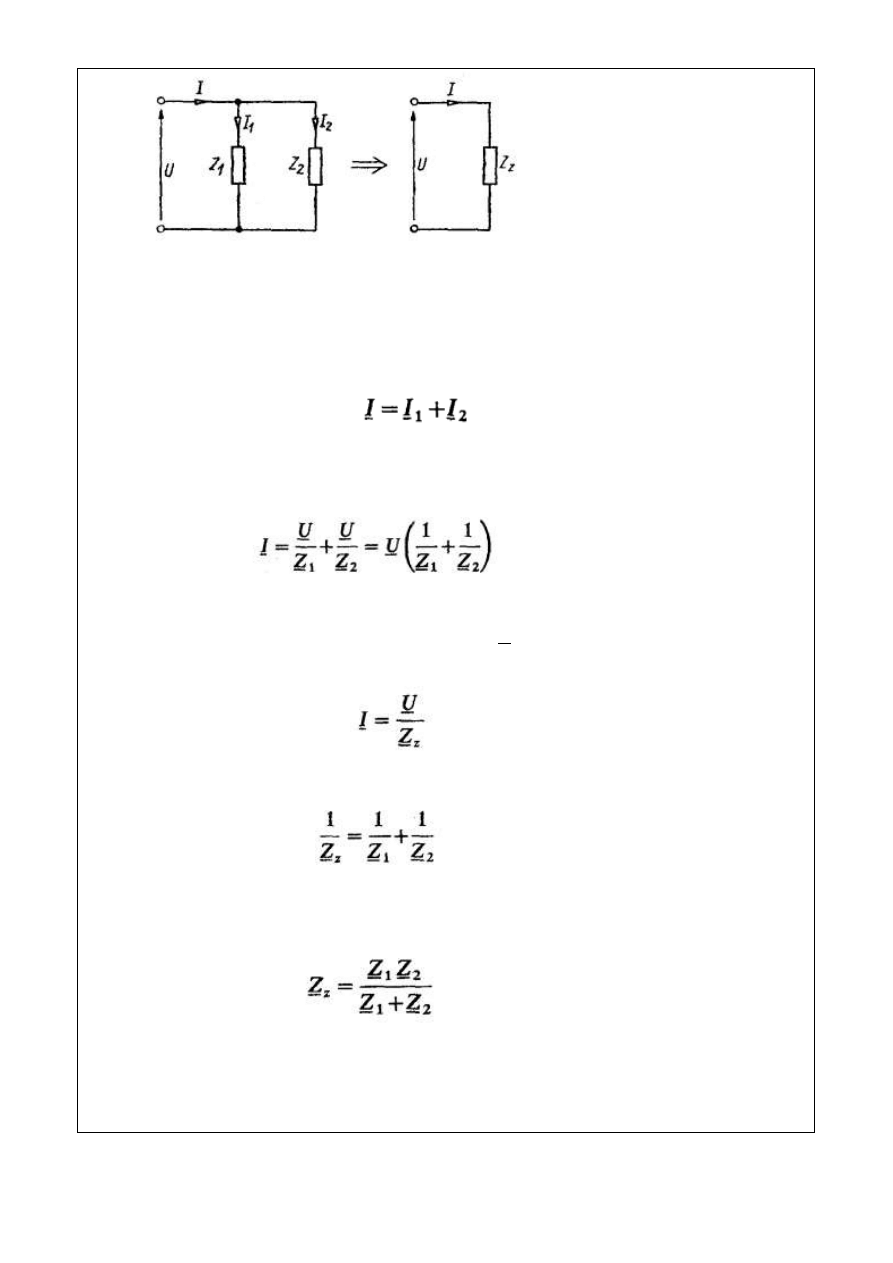
Rys. 4.2. Połączenie równoległe odbiorników

Zgodnie z pierwszym prawem Kirchhoffa

(4.10)

a po uwzględnieniu prawa Ohma w postaci zespolonej

(4.11)

Odpowiedzią odbiornika równoważnego na wymuszenie U jest

(4.12)

Z porównania odpowiedzi wynika

(4.13)

oraz

(4.14)

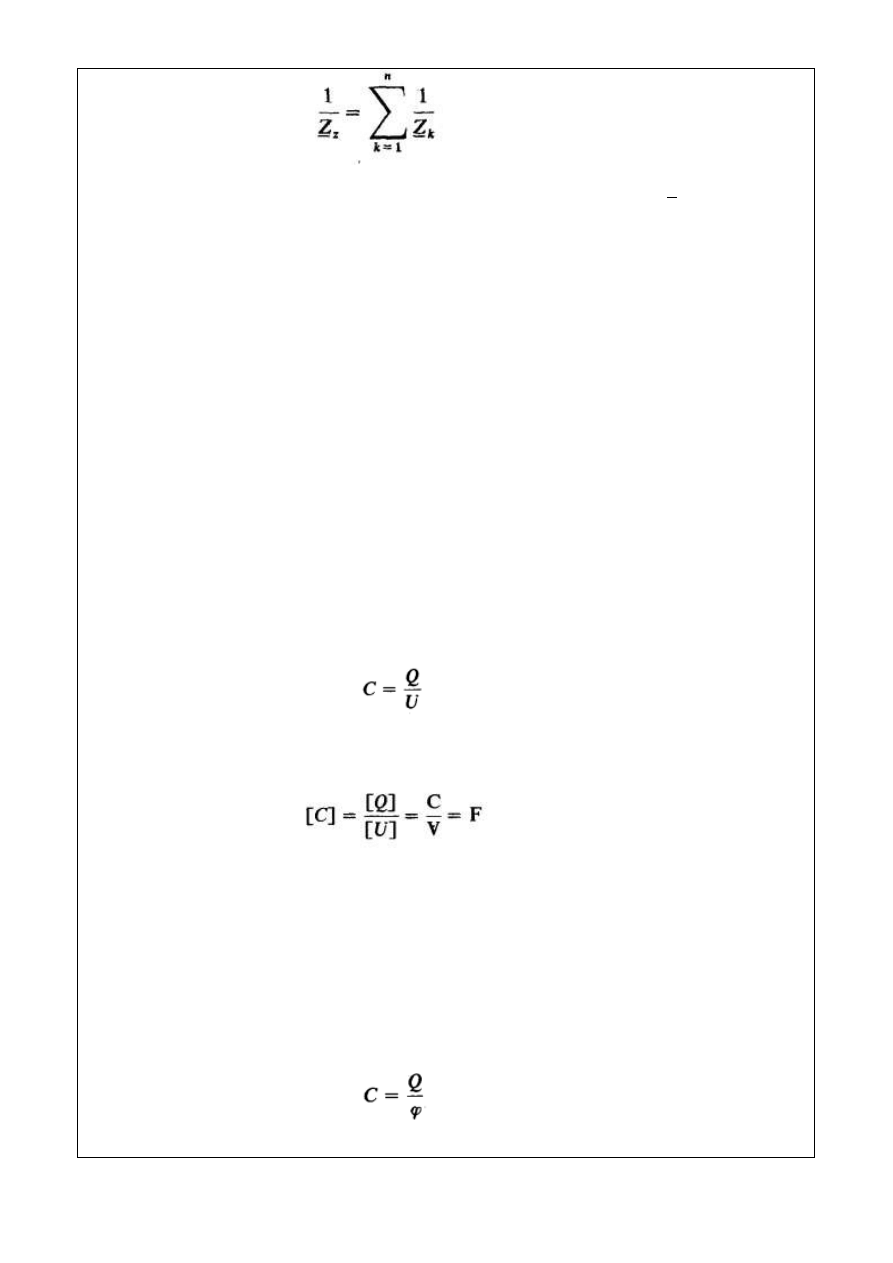
Wzór uogólniony na połączenie równoległe dowolnej liczby odbiorników ma postać

7

(4.15)

Podobnie jak w przypadku układu szeregowego odbiornik o impedancji Z jest równoważny

lub zastępczy, jeżeli jego odpowiedź na wymuszenie jest identyczna z odpowiedzią układu

równoległego na to samo wymuszenie.

4.3. Pojemność elektryczna. Kondensatory

Kondensatorem nazywamy urządzenie składające się z dwóch przewodników, zwanych

okładzinami lub elektrodami, rozdzielonych dielektrykiem.
Jeżeli do okładzin kondensatora doprowadzimy napięcie elektryczne U, to na okładzinach zacznie
się gromadzić ładunek elektryczny Q, przy czym na jednej okładzinie zgromadzi się ładunek
dodatni, a na drugiej - ujemny. Ładunek zgromadzony na jednej z okładzin nazywamy ładunkiem
kondensatora[1].

Doświadczalnie stwierdzono, że pomiędzy przyłożonym napięciem a ładunkiem

kondensatora istnieje związek, a mianowicie ładunek jest wprost proporcjonalny do napięcia, czyli:

Q = C ∙ U

(4.16)

gdzie: C – pojemność kondensatora.

Pojemnością kondensatora nazywamy więc stosunek ładunku kondensatora do napięcia

występującego pomiędzy jego okładzinami, czyli

(4.17)

Jednostką pojemności jest 1 farad (1 F). Jeżeli równaniu wielkości (4.17) przyporządkujemy
równanie jednostek, to

Pojemność równa jednemu faradowi jest bardzo duża, dlatego w praktyce stosuje się

jednostki mniejsze: μF = 10

- 6

F oraz pF = 10

- 12

F.

Pojemność jest własnością kondensatora określającą jego zdolność do gromadzenia ładunku

elektrycznego. Cechę posiadania pojemności przypisujemy nie tylko kondensatorom, ale również
przewodnikowi odosobnionemu.
Pojemnością przewodnika odosobnionego nazywamy stosunek ładunku nagromadzonego
na przewodniku do jego potencjału względem obranego punktu w polu elektrycznym, któremu
przypisujemy potencjał równy zeru, czyli

(4.18)

8

gdzie: Q oznacza ładunek zgromadzony na przewodniku, a φ - jego potencjał.

Z pojęcia pojemności przewodnika odosobnionego korzystamy np. przy wyznaczaniu

pojemności przewodu linii elektrycznej względem ziemi[1].

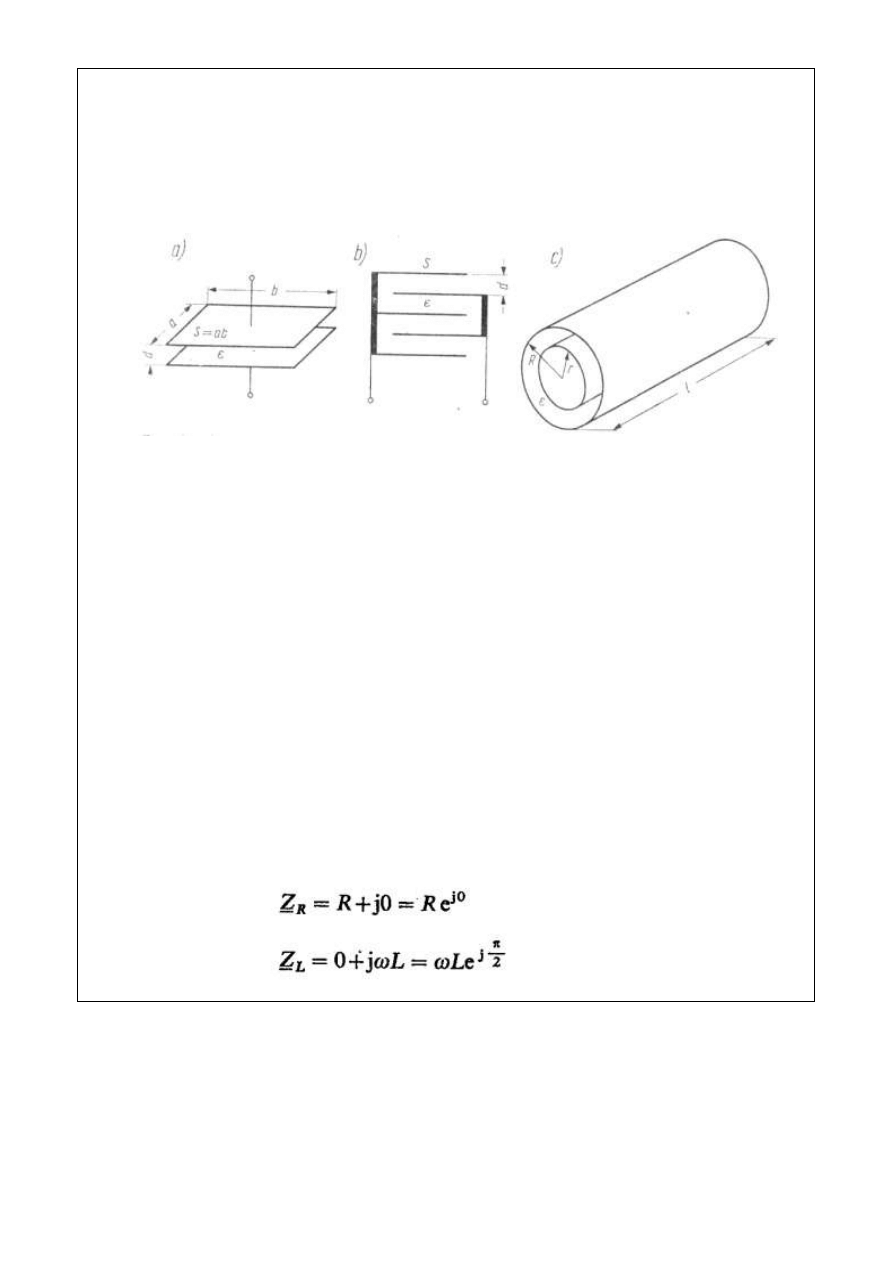
Pojemność kondensatora zależy od jego budowy[2]. Na rysunku 4.3 przedstawiono

kondensator płaski dwuelektrodowy, płaski wieloelektrodowy oraz kondensator cylindryczny.

Rys. 4.3. Rodzaje kondensatorów: a) płaski dwuelektrodowy; b) płaski wieloelektrodowy;

c) cylindryczny [2]

Pojemność kondensatora płaskiego dwuelektrodowego wynosi:

C = ε ∙ S / d

(4.19)

Natomiast dla kondensatora n – elektrodowego:

C = (n – 1) ∙ ε ∙ S / d

(4.20)

Pojemność kondensatora cylindrycznego:

C = 2π ∙ ε ∙ l / ( ln R / r )

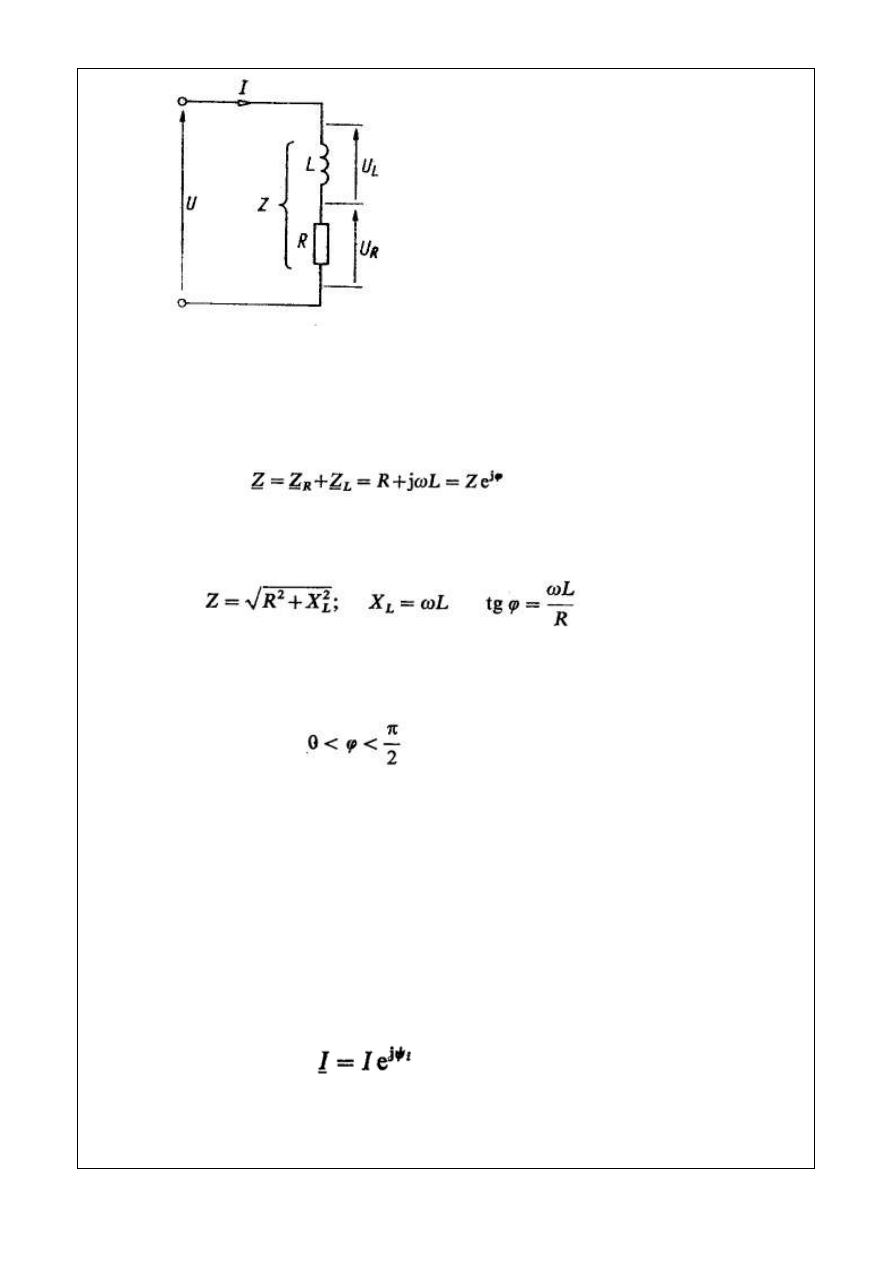
4.2.1. Obwód RL szeregowy.

Obwód ten (rys. 4.4) powstał przez połączenie szeregowe impedancji

(4.21)

9

Rys. 4.4. Obwód RL szeregowy

Impedancja wypadkowa jest sumą składowych

przy czym

Kąt φ jest dodatni, a jego wartość zawiera się w granicach

Tangens kąta p dąży do zera, gdy wartość L jest dostatecznie mała (obwód z rezystancją R)

oraz do nieskończoności, gdy wartość R jest dostatecznie mała (obwód z indukcyjnością L).

Mówi się, że obwód ma charakter indukcyjny, jeżeli prąd jest opóźniony w fazie w stosunku

do napięcia o kąt mniejszy od π/2, a większy od zera.

Przy założeniu, że przebiegiem wymuszającym jest prąd

odpowiedzi układu będą kolejno

10

(4.21)

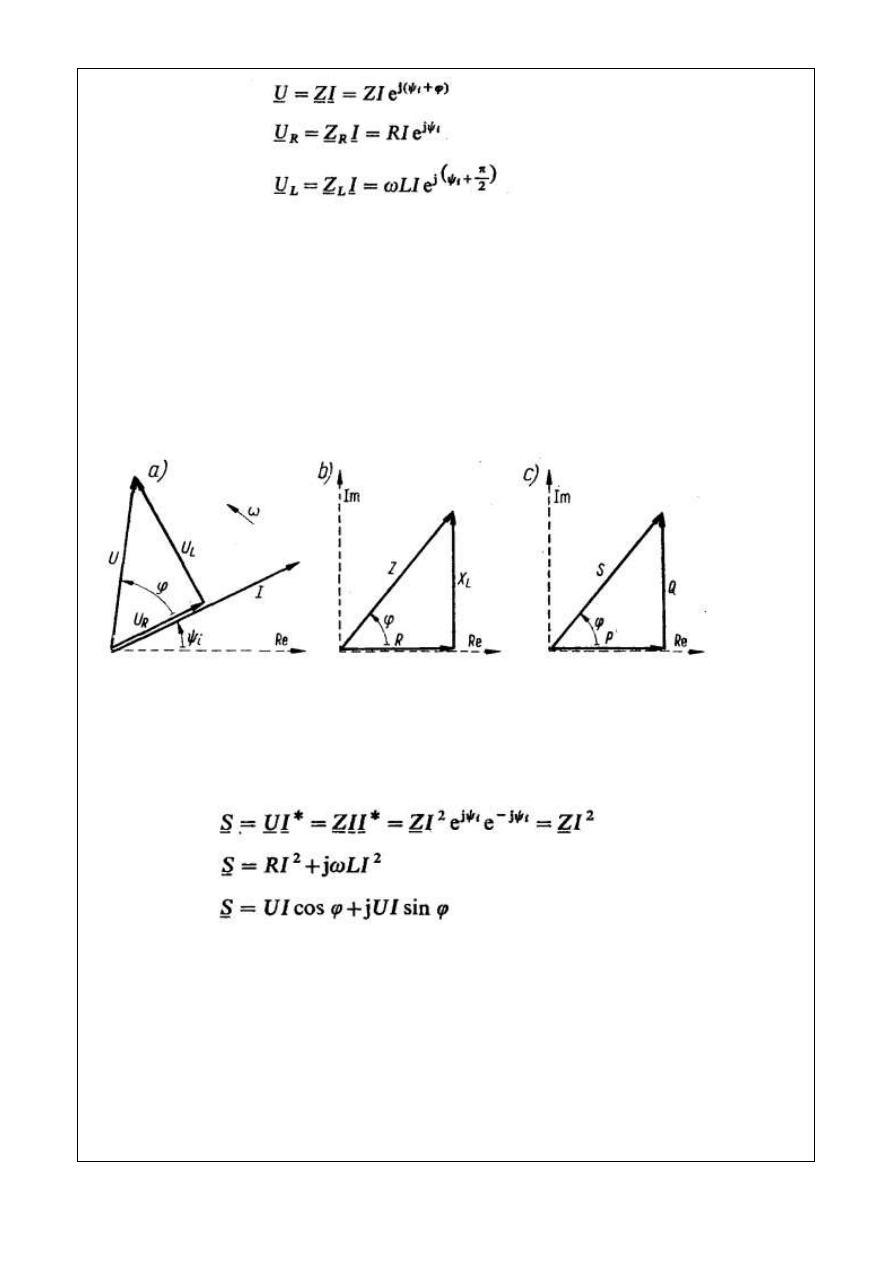
Na rysunku 4.4 przedstawiono wykres wektorowy napięć i prądu w obwodzie z rys. 4.3.

Wykres zaczynamy rysować począwszy od prądu. W fazie z prądem rysujemy napięcie na

rezystancji, a pod kątem prostym do wektora prądu rysujemy wektor napięcia na „indukcyjności;

pamiętamy, że napięcie to jest przyspieszone w stosunku do prądu.

Łatwo zauważyć, iż napięcie U

R

jest składową czynną napięcia zasilającego

Rys. 4.5. Wykres wektorowy przebiegów (a), trójkąt oporów (b) i trójkąt mocy (c) obwodu RL

szeregowego z rys. 4.3

(4.22)

Ze wzoru (4.22) wynika, że trójkąt mocy jest trójkątem oporów w innej skali.

11

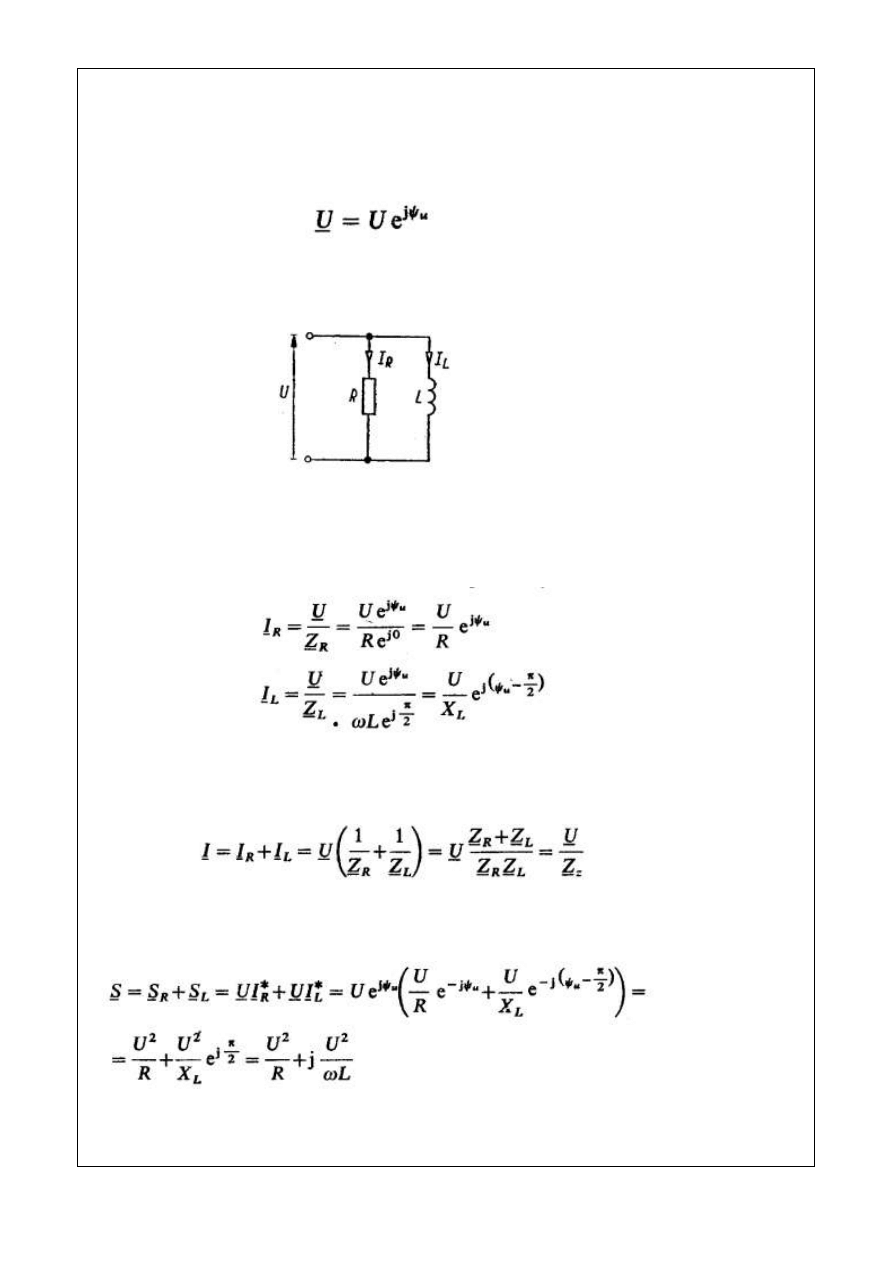
4.3. Obwód RL równoległy

Obwód RL równoległy (rys. 4.6). Przyjmujemy, że przebiegiem wymuszającym jest

napięcie

o czym należy pamiętać podczas rysowania wykresów wektorowych.

Rys 4.6. Obwód RL równoległy

Odpowiedzi układu w postaci prądów gałęziowych określają zależności

(4.23)

Suma prądów gałęziowych jest równa prądowi dopływającemu

Moc pozorna układu jest sumą mocy w gałęziach

(4.24)

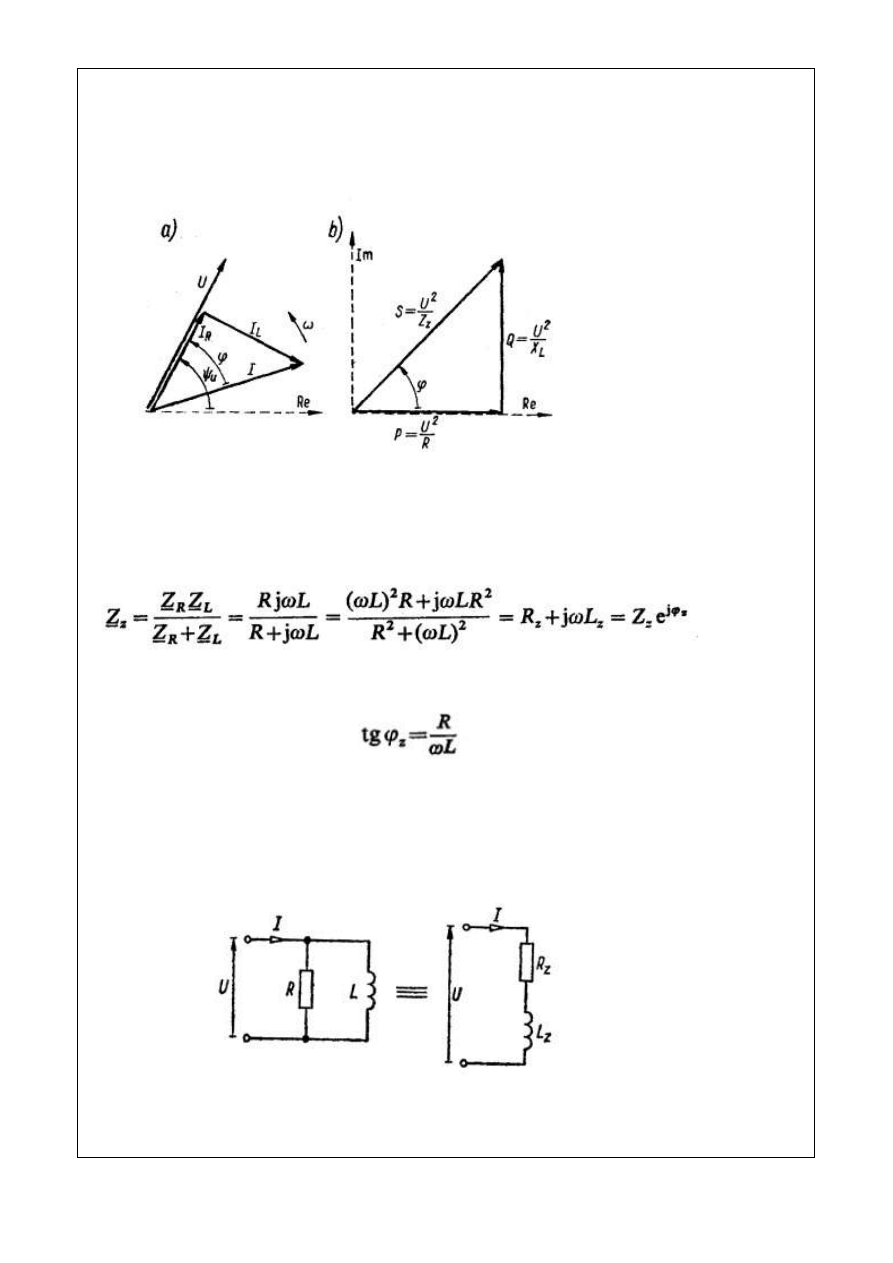
Wykres wektorowy przebiegów w omawianym obwodzie przedstawiono na rys. 4.7.

12

Wykres zaczynamy rysować, począwszy od napięcia. W fazie z napięciem rysujemy wektor prądu

płynącego przez rezystancję, a pod kątem prostym do wektora napięcia, rysujemy wektor prądu

płynącego przez indukcyjność. Prąd ten jest opóźniony w stosunku do napięcia. Suma

geometryczna prądów jest równa prądowi dopływającemu.

Rys. 4.7. Wykres wektorowy przebiegów (a) i trójkąt mocy (b) obwodu RL równoległego z rys. 4.6

Łatwo zauważyć, że prąd I

R

jest składową czynną prądu I. Uwzględniając fakt równoległego

połączenia elementów, można obliczyć impedancję zastępczą układu

(4.25)

przy czym

Kąt φ

z

zawiera się w granicach od zera do π/2. Tangens kąta φ

z

dąży do zera, gdy wartość L

jest dostatecznie duża (obwód o dużym prądzie w rezystancji R) lub do nieskończoności, gdy

wartość R jest dostatecznie duża (obwód o dużym prądzie w indukcyjności L).

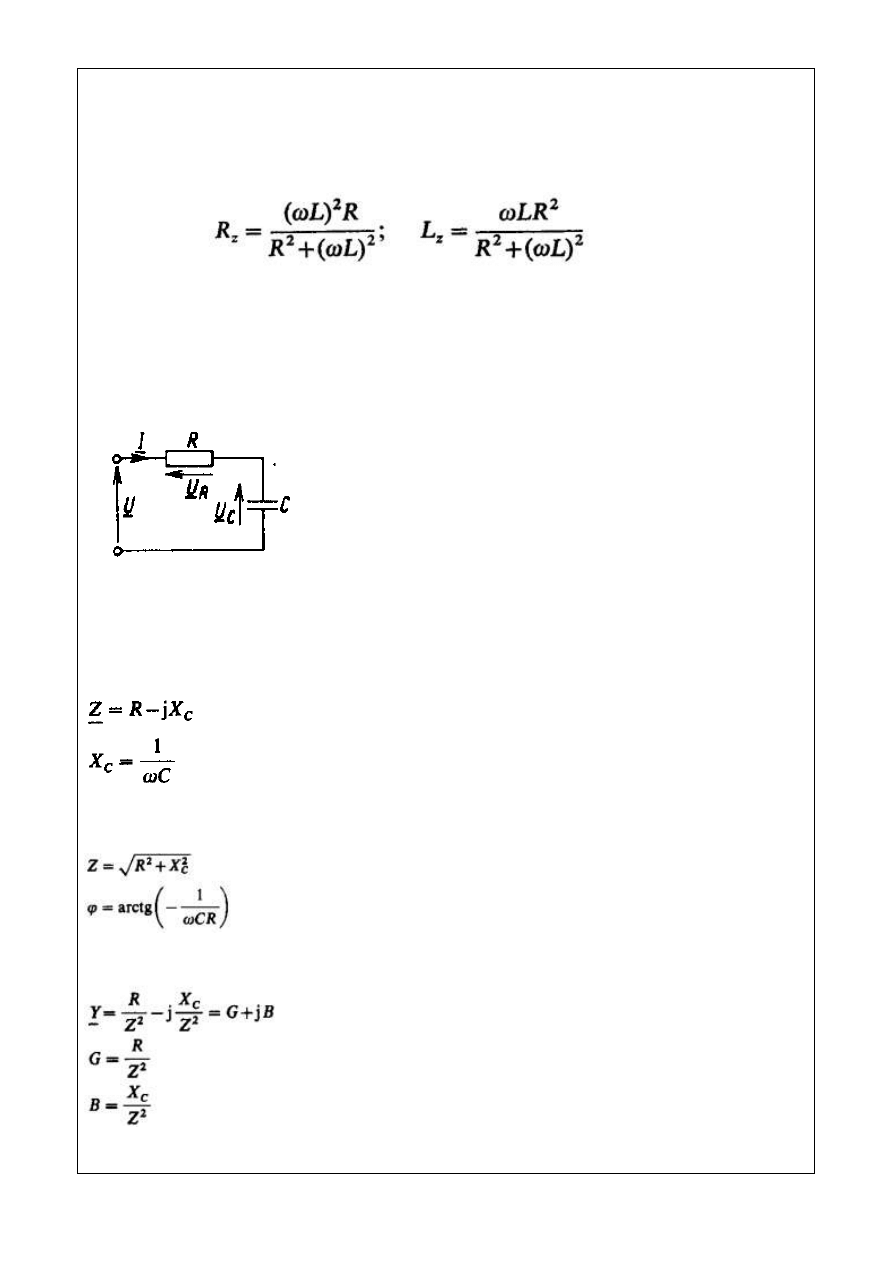
Rys. 4.8. Równoważność układów RL równoległego i szeregowego

13

Z analizy wzorów wynika, że przy określonej częstotliwości między obwodem szeregowym

i równoległym zachodzi równoważność (rys. 4.8). Każdy obwód RL równoległy można zastąpić

układem szeregowym o elementach

(4.26)

i odwrotnie.

4.4. Obwód RC Szeregowy i Równoległy

4.4.1 Obwód RC szeregowy

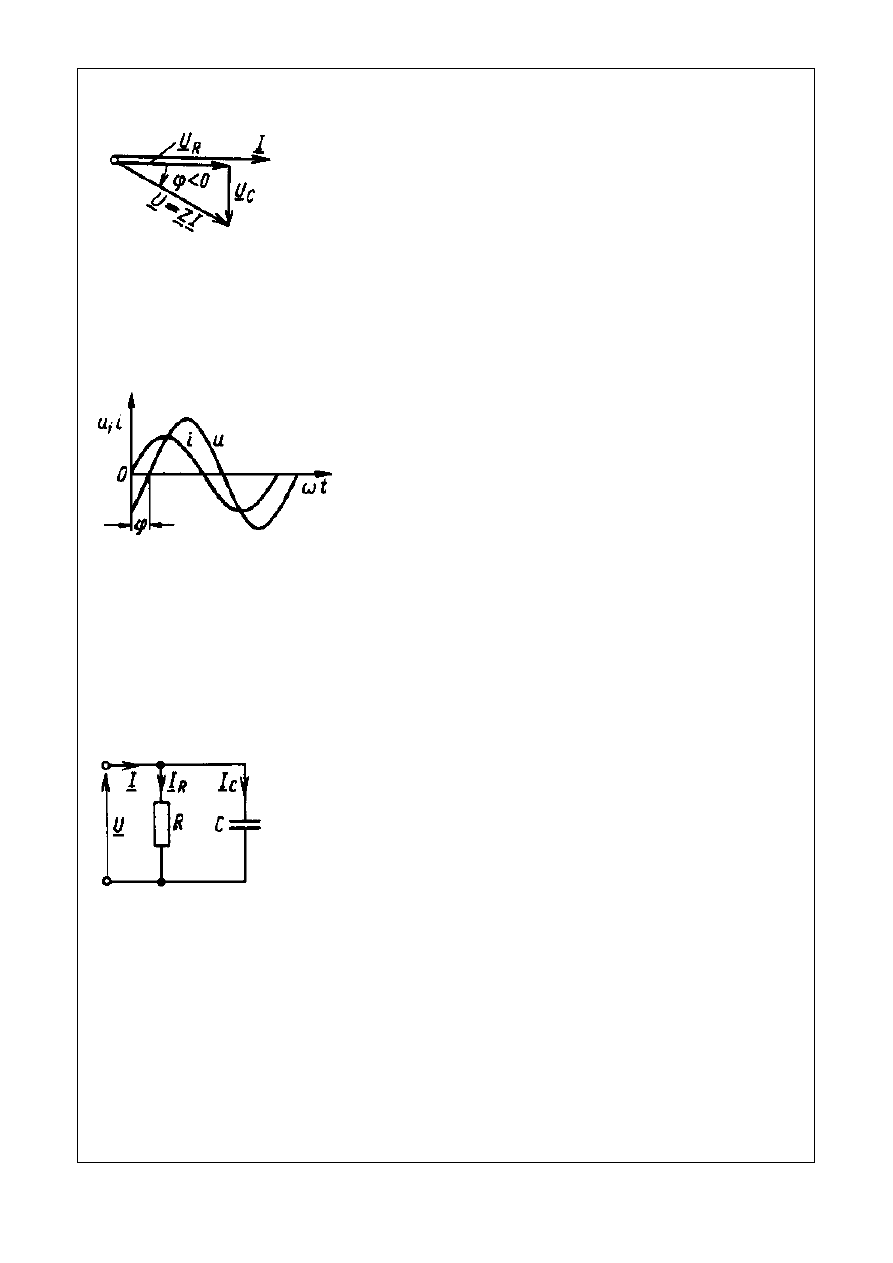
Rys 4.9. Obwód RC szeregowy

Impedancja zespolona obwodu z rys. 4.9

(4.27)

Moduł i argument impedancji obwodu z rys. 4.9

(4.28)

Admitancja zespolona obwodu z rys. 4.9

(4.29)

14

Wykres wektorowy obwodu

Rys 4.10. Wykres wektorowy obwodu z rys. 4.9

Wykres Czasowy obwodu

Rys. 4.11. Wykres Czasowy obwodu z rys. 4.9

Obwód RC równoległy

Schemat obwodu

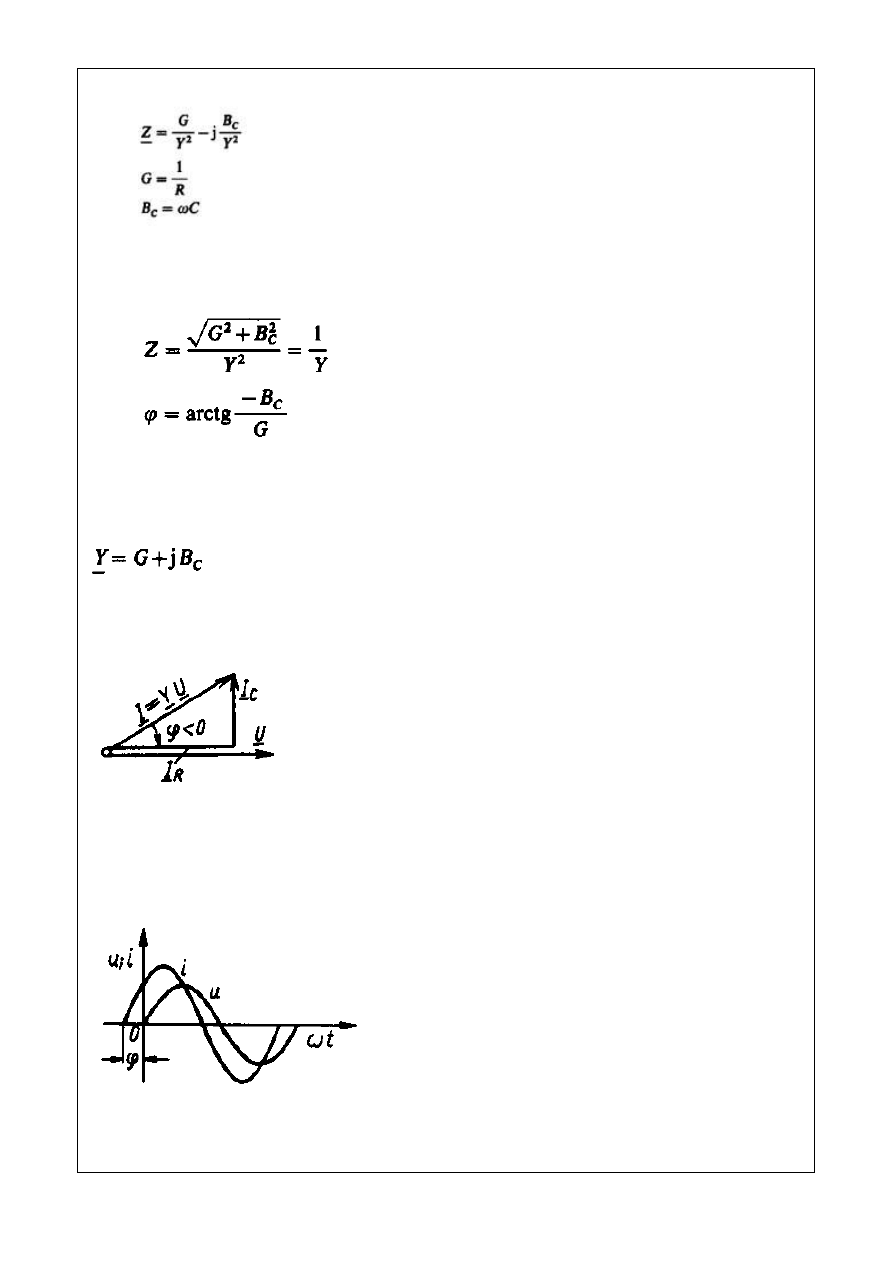
Rys 4.12. Obwód RC równoległy

15

Impedancja zespolona obwodu z rys. 4.12

(4.30)

Moduł i argument impedancji obwodu z rys. 4.12

(4.31)

Admitancja zespolona obwodu z rys. 4.12.

Wykres wektorowy obwodu

Rys 4.13. Wykres wektorowy obwodu z rys. 4.12

Wykres Czasowy obwodu

Rys. 4.14. Wykres Czasowy obwodu z rys. 4.12

16

V.

OPRACOWANIE WYNIKÓW

1. Zestawić wyniki odczytane za pomocą miernika RLC z wynikami samodzielnych obliczeń,

2. Zinterpretować otrzymane wyniki.

0

VI.

ZAGADNIENIA DO ZALICZENIA ĆWICZENIA



Definicja pojemności,



Rozwiązanie układu kondensatorów połączonych szeregowo,



Rozwiązanie układu kondensatorów połączonych równolegle,



Wzory na pojemność zastępczą układu szeregowo i równolegle połączonych

kondensatorów.

VII. LITERATURA

1. B. Miedziński „Elektrotechnika podstawy i instalacje elektrotechniczne” PWN Warszawa 2000

2. H. Rawa „Elektryczność i magnetyzm w technice” PWN Warszawa 2001

3. G. Łomnicka-Przybyłowska „Pomiary elektryczne. Obwody prądu zmiennego” PWN

Warszawa 2000

4. S. Bolkowski „Teoria obwodów elektrycznych” WNT, Warszawa 2001

5. A Chwaleba M. Poniński, A Siedlecki „Metrologia elektryczna” WNT Warszawa 2000