J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
1
P
rzykłady analizy płyt – zadania z płyt prostokątnych
Ćwiczenie 14
Hipotezy wytrzymałościowe
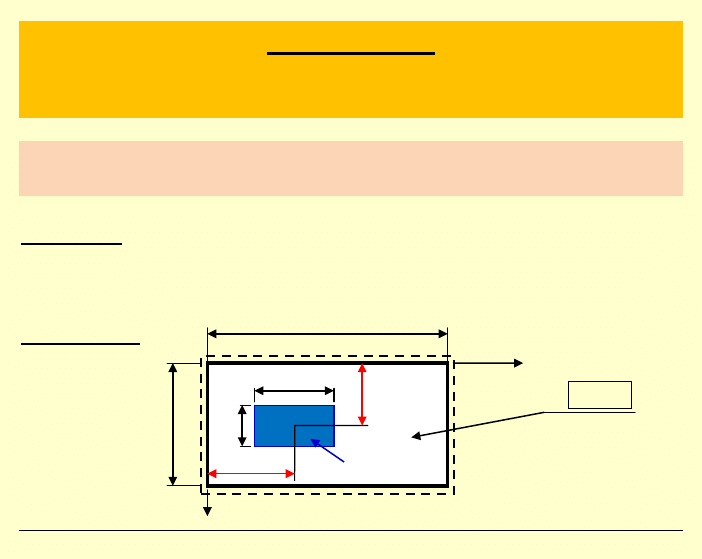
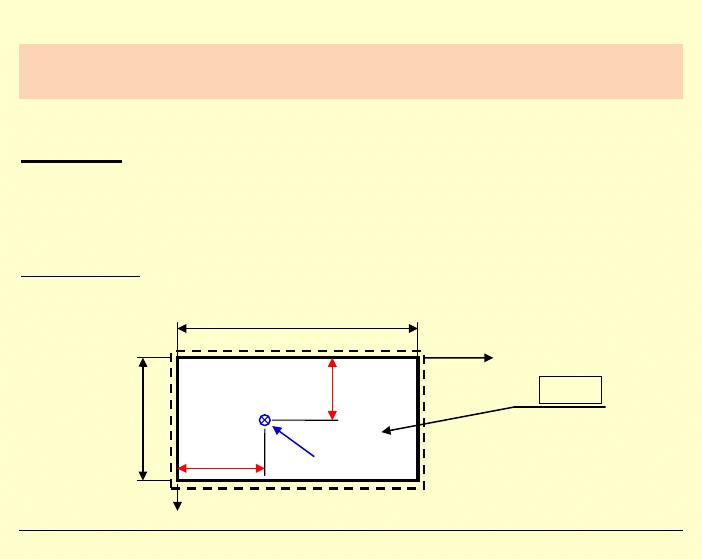
PŁYTA PROSTOKĄTNA, SWOBODNIE PODPARTA,
OBCIĄŻONA FRAGMENTARYCZNIE
Przykład:
u v
×
Wyznaczyć powierzchnię ugięcia płyty swobodnie
podpartej
, obciążonej równomiernie na prostokącie
(wypadkowa z obciążenia wynosi: P q u v
= ⋅ ⋅ )
1
x
Rzut z góry:
2
x
b
a
, ,
E
h
ν
q
const
=
u
v
ξ
η
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
2
Obciążenie:
(
)
1
2
1
2
1
1
,
sin
sin
mn
m
n
m x
n x
q x x
a
a
b
π
π
∞
∞
=
=
=
∑∑
gdzie:
(
)
2
2
1
2
1
2
2
2
4
,
sin
sin
u
v
mn
u
v
m x
n x
a
q x x
ab
a
b
ξ
η
ξ
η
π
π
+
+
−
−
=
∫ ∫
Dla
P
q
u v
=
⋅
zachodzi:
2
2
1
2
1
2
2
2
4
sin
sin
u
v
mn
u
v
m x
n x
P
a
dx dx
abuv
a
b
ξ
η
ξ
η
π
π
+
+
−
−
=
∫ ∫
Zatem:
2
2
1
1
2
2
4
cos
cos
u
v
mn
u
v
m x
m x
P
a
b
a
abuv m n
a
a
ξ
η
ξ
η
π
π
π π
+
+
−
−
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
3
Ostatecznie:
2
4
2
2
2
2
cos
cos
cos
cos
mn
u
u
v
v
m
m
m
m
P
a
mnuv
a
a
b
b
π ξ
π ξ
π η
π η
π
+
−
+
−
=
−
−
Przywołując z trygonometrii:
cos
cos
2sin
sin
2
2
α β
α β
α
β
+
−
−
= −
mamy:
2
2
2
u
u
m
m
m
a
a
π ξ
π ξ
πξ
α β
+
+
−
+ =
=
oraz:
2
2
u
u
m
m
m u
a
a
π ξ
π ξ
π
α β
+
−
−
− =
=
S
tąd:
2
16
sin
sin
sin
sin
2
2
mn
P
m
n
m u
n v
a
mnuv
a
b
a
b
πξ
πη
π
π
π
=
i podobnie
dla drugiej
pary
argumentów
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
4
Sprawdzenie w przypadku:
2
a
ξ
=
,
2
b
η
=
,
u
a
=
, v
b
= , P qab
=
:
Wówczas:
2
2
2
2
16
16
sin
sin
2
2
mn
P
m
n
q
a
mnab
mn
π
π
π
π
=
=
,
gdy:
,
1,3,5...
m n
=
lub:
0
mn
a
=
, gdy któraś z wartości:
m
lub
n
jest parzysta!
Uwaga: M
ożna porównać to rozwiązanie z zadaniem dla płyty
prostokątnej obciążonej równomiernie na całej powierzchni!
(
)
1
2
1
2
2
4
2
2
1
1
1
,
sin
sin
mn
m
n
a
m x
n x
w x x
D
a
b
m
n
a
b
π
π
π
∞
∞
=
=
=
+
∑∑
Ostatecznie:
gdzie:
,
m n
–
liczby całkowite nieparzyste:
1,3,5...
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
5
PŁYTA PROSTOKĄTNA, SWOBODNIE PODPARTA,
OBCIĄŻONA SIŁĄ SKUPIONĄ
Przykład:
P
Wyznaczyć powierzchnię ugięcia i ugięcie maksymalne
płyty swobodnie podpartej, obciążonej siłą skupioną
,
przyłożoną w punkcie o współrzędnych:
1
x
ξ
=
i
2
x
η
=
Rzut z góry:
1
x
2
x
b
a
, ,
E
h
ν
P
ξ
η
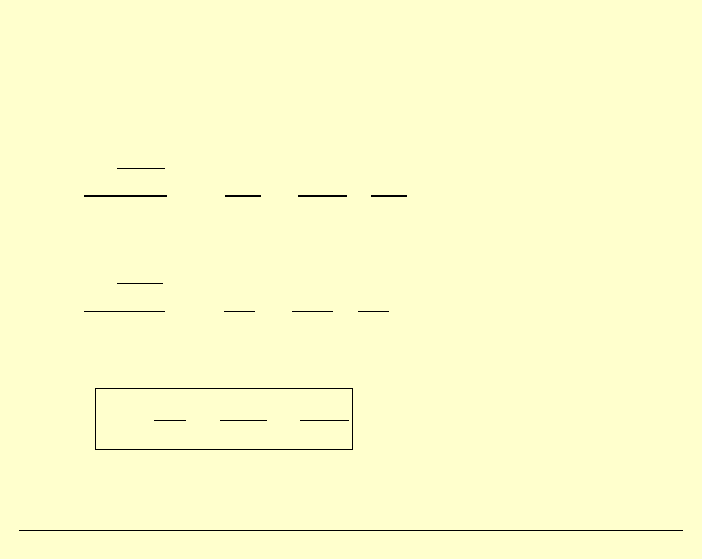
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
6
Z poprzedniego zadania otrzymamy wyrazy
mn
a
dla:
0
u
→
,
0
v
→
:
1)
0
0
sin
2
lim
lim
cos
2
2
2
u
u
m u
m
m u
m
a
u
a
a
a
π
π
π
π
→
→
=
=
2)
0
0
sin
2
lim
lim
cos
2
2
2
u
v
m v
n
n v
n
b
v
b
b
b
π
π
π
π
→
→
=
=
Zatem:
4
sin
sin
mn
P
m
m
a
ab
a
b
πξ
πη
=

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
7
(
)
1
2
1
2
2
4
2
2
1
1
sin
sin
4
,
sin
sin
m
n
m
n
m x
n x
P
a
b
w x x
abD
a
b
m
n
a
b
πξ
πη
π
π
π
∞
∞
=
=
=
+
∑∑
Powierzchnia ugięcia:
Szereg ten
również jest szybkozbieżny!
Obliczamy
ugięcie w środku płyty (od siły położonej centrycznie),
tj. dla:
1
2
a
x
ξ
= =
,
2
2
b
x
η
=
=
:
2
4
2
2
1
1
4
1
max
m
n
P
w
abD
m
n
a
b
π
∞
∞
=
=
=
+
∑∑
, gdzie:
,
1,3,5...
m n
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
8
Dla płyty kwadratowej (a b
= ):
(
)
2
2
4
2
2
1
1
4
1
max
m
n
Pa
w
D
m
n
π
∞
∞
=
=
=
+
∑∑
, gdzie:
,
1,3,5...
m n
=
Biorąc pod uwagę jedynie pierwsze cztery wyrazy szeregu
otrzymamy (dla
,
1,3
m n
=
):
(
) (
)
2
3
2
2
4
2
2
1
4
1
1
max
1
9
m
Pa
w
D
m
n
π
=
=
+
+
+
∑
2
2
4
4
1
1
1
1
max
0,01121
4
100
100
324
Pa
Pa
w
D
D
π
=
+
+
+
=
Jeśli przyjmie się, iż
2
P
qa
=
to w
porównaniu z ugięciem dla
q
const
=
na całej powierzchni płyty jest to ugięcie 3 razy większe!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
9
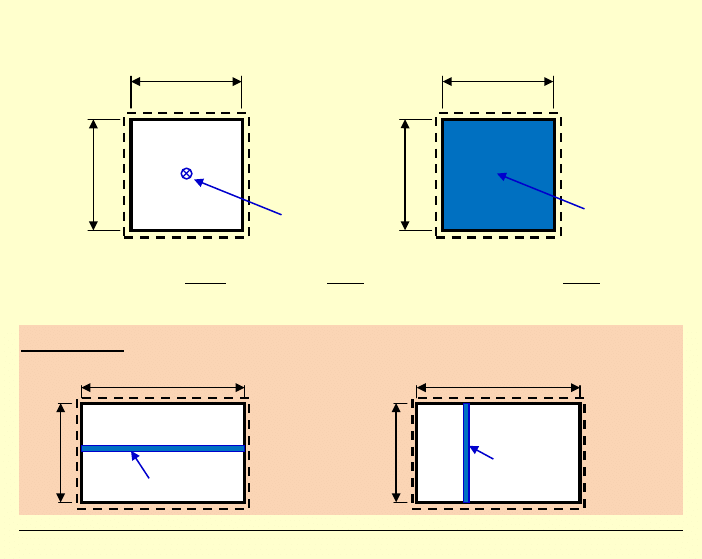
Porównanie ugięć płyty a a
×
pod rozważanymi obciążeniami:
Dyskusja!
Przypadek szczególny: ścianki działowe na stropie
a
a
2
P
qa
=
a
a
q
const
=
2
4
max
0,01121
0,01121
Pa
qa
w
D
D
=
=
4
max
0, 00406
qa
w
D
=
b
a
u
a
=
0
v
→
q
b
a
q
0
u
→
v
b
=
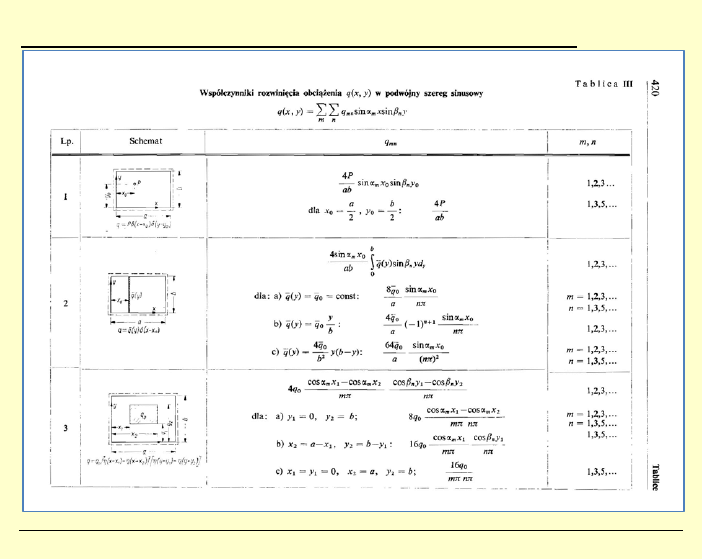
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
10
Zbigniew
Kączkowski – „Płyty. Obliczenia statyczne.”
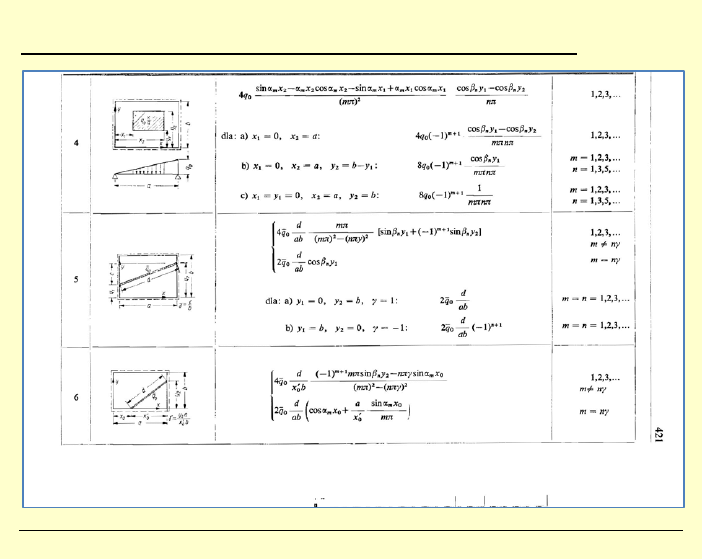
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
11
Zbigniew Kączkowski – „Płyty. Obliczenia statyczne.”

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
12
HIPOTEZY WYTRZYMAŁOŚCIOWE
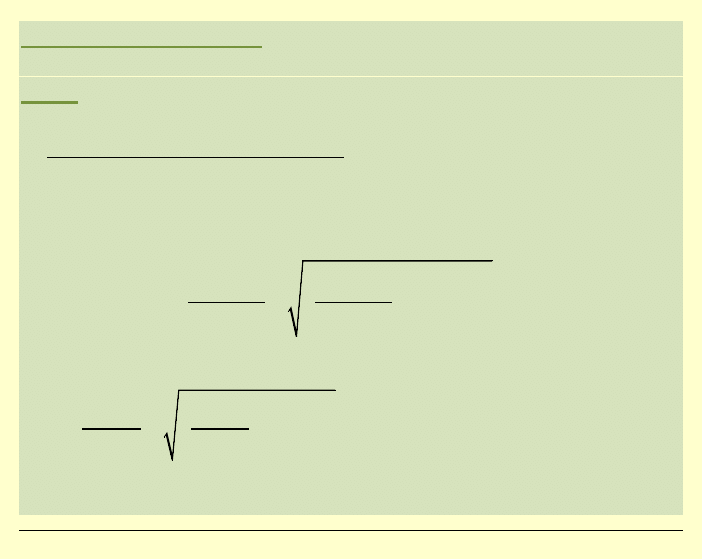
Zadanie 1:
Określić, czy dany stan jest bezpieczny wg dwóch
hipotez wytrzymałościowych: Treski i HMH.
[
]
18
6
0
6
2
0
0
0
5
MPa
σ
=
−
W przypadku, gdy stan jest bezpieczny, określić wymagany zapas
bezpieczeństwa stosownie dla obu hipotez wytrzymałościowych,
zakładając jednoparametrowy wzrost wszystkich składowych
tensora naprężenia. Przyjąć
0
28MPa
σ
=
.
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
13
Rozwiązanie zadania 1:
Ad 1)
Hipoteza Treski
1)
Obliczenie naprężeń głównych
1
σ
:
,
2
σ
i
3
σ
Ponieważ
0
xz
yz
zx
zy
MPa
τ
τ
τ
τ
=
=
=
=
mamy:
3
5MPa
σ
= −
Wówczas:
( )
2
2
1/2
2
2
x
y
x
y
xy
σ
σ
σ
σ
σ
τ
+
−
=
±
+
podstawiając wartości liczbowe:
( )
2
2
1/2
18
2
18 2
6 [
]
2
2
MPa
σ
+
−
=
±
+
10 10 [
]
MPa
=
±
Zatem:
1
20MPa
σ
=
oraz
2
0MPa
σ
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
14
2)
Ekstremalne naprężenia styczne
max
τ
:
1
3
max
2
σ σ
τ
−
=
podstawiając wartości liczbowe:
( )
[
]
max
20
5
25
12,5
2
2
MPa
MPa
MPa
τ
− −
=
=
=
3)
Ocena bezpieczeństwa stanu naprężeń:
Stan jest bezpieczny
, gdyż:
max
12,5MPa
τ
=
0
0
28
14
2
2
MPa
MPa
σ
τ
≤
=
=
=
4) Obliczenie zapasu
bezpieczeństwa wg Treski:
,
bezp T
z
,
max
0
bezp T
z
τ
τ
⋅
=
,
12,5
14
bezp T
z
MPa
MPa
→
⋅
=
Zatem:
,
14
/ 12,5
bezp T
z
MPa
MPa
=
=
1,120
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
15
Ad 2)
Hipoteza HMH (Hubera–Misesa–Hencky’ego)
1) Sprawdzenie warunku
obszaru bezpiecznego, wyrażonego
w
naprężeniach głównych:
(
) (
) (
)
2
2
2
2
2
1
3
2
1
3
0
2
σ
σ
σ
σ
σ σ
σ
−
+
−
+
−
≤ ⋅
podstawiając wartości liczbowe:
(
)
( )
(
)
( )
(
)
2
2
2
0
20
5
0
20
5
−
+ − −
+
− −
(
) ( )
2
2
2
20
5
25
= −
+ −
+
1050
=
( )
2
2
0
2
2 28
1568
σ
⋅
= ⋅
=
Zatem: 1050 1568
≤
, tak więc stan jest bezpieczny!
Uwaga:
Warunek stanu bezpiecznego można także wyrazić
w
układzie
Oxyz
:
(
) (
)
(
)
2
2
2
2
2
0
6
2
y
x
z
y
x
z
xy
σ
σ
σ
σ
σ
σ
τ
σ
−
+
−
+
−
+ ⋅
≤ ⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
16
(
) (
)
(
)
2
2
2
2
2
0
6
2
y
x
z
y
x
z
xy
σ
σ
σ
σ
σ
σ
τ
σ
−
+
−
+
−
+ ⋅
≤ ⋅
podstawiając wartości liczbowe:
(
)
( )
(
)
( )
(
)
( )
2
2
2
2
2 18
5
2
18
5
6 6
L
=
−
+ − −
+
− −
+ ⋅
1050
=
( )
2
2
0
2
2 28
1568
P
σ
= ⋅
= ⋅
=
Zatem:
1050 1568
≤
, tak więc stan jest bezpieczny!
2) Obliczenie zapasu
bezpieczeństwa wg HMH:
,
bezp HMH
z
(
)
2
,
bezp HMH
z
L
P
⋅ =
(
)
2
,
1050 1568
bezp HMH
z
→
⋅
=
Zatem:
(
)
2
,
1568 / 1050
bezp HMH
z
=
=
1, 49333
Tak więc:
,
1, 49333
bezp HMH
z
=
= 1,22202
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
17
Uwaga:
Można wg hipotezy HMH zastępczo wprowadzić pojęcie
naprężeń zredukowanych
z
σ
:
(
) (
) (
)
2
2
2
2
1
3
2
1
3
1
2
z
σ
σ
σ
σ
σ
σ σ
=
⋅
−
+
−
+
−
lub:
(
) (
)
(
)
2
2
2
2
1
6
2
z
y
x
z
y
x
z
xy
σ
σ
σ
σ
σ
σ
σ
τ
=
⋅
−
+
−
+
−
+ ⋅
Wówczas warunek stanu
bezpiecznego można zapisać w postaci:
0
z
σ
σ
≤
W niniejszym przypadku, mamy:
1
1
1050
22,913
2
2
z
L
MPa
σ
=
⋅ =
⋅
=
0
28MPa
σ
≤
=
Zapas
bezpieczeństwa wg HMH
,
bezp HMH
z
policzymy wg wzoru:
,
0
bezp HMH
z
z
σ
σ
⋅
=
,
22,913
28
bezp HMH
z
MPa
MPa
→
⋅
=
Zatem:
,
28
/ 22,913
bezp T
z
MPa
MPa
=
=
1, 22202

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
18
Zadanie 2:
[
]
12
21
k MPa
σ
σ
=
=
Ile powinny wynosić naprężenia
,
aby spełnione były warunki plastyczności wg dwóch hipotez
wytrzymałościowych: Treski i HMH.
[
]
12
0
8
0
0
0
0
k
k
MPa
σ
=
Przyjąć
0
15MPa
σ
=
.
Rozwiązanie zadania 2:
Ad 1)
Hipoteza Treski
1)
Obliczenie naprężeń głównych
1
σ
:
,
2
σ
i
3
σ
Ponieważ
13
23
31
32
0MPa
σ
σ
σ
σ
=
=
=
=
, mamy:
3
0MPa
σ
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
19
Wówczas:
( )
2
2
11
22
11
22
1/2
12
2
2
σ
σ
σ
σ
σ
σ
+
−
=
±
+
podstawiając wartości liczbowe:
( )
2
2
1/2
12 8
12 8
[
]
2
2
k
MPa
σ
+
−
=
±
+
2
10
4
[
]
k
MPa
=
±
+
2)
Ekstremalne naprężenia styczne
max
τ
:
Ekstremalnymi naprężeniami stycznymi mogą być wielkości:
2
3
max,1
2
σ
σ
τ
−
=
,
3
1
max,2
2
σ
σ
τ
−
=
,
1
2
max,3
2
σ σ
τ
−
=
podstawiając wartości liczbowe:
[
]
2
max,1
1
5
4
2
k
MPa
τ
= − ⋅
+
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
20
[
]
2
max,2
1
5
4
2
k
MPa
τ
= + ⋅
+
[
]
2
max,3
4
k
MPa
τ
=
+
W poszczególnych przypadkach granicznymi wartościami
bezwz
ględnymi naprężeń
[
]
k MPa , przy których warunek
plastyczności jest równością, są odpowiednio:
przypadek 1:
1
24,920
k
MPa
=
przypadek 2:
2
4,583
k
MPa
=
przypadek 3:
3
7, 228
k
MPa
=
3)
Ocena bezpieczeństwa stanu naprężeń:
Stan jest bezpieczny wtedy, gdy:
[
]
4,583 ; 4,583
k
MPa
∈ −

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 14 • KMBiM WILiŚ PG
21
Ad 2)
Hipoteza HMH (Hubera–Misesa–Hencky’ego)
1)
Sprawdzenie warunku obszaru bezpiecznego:
Skorzystamy z warunku stanu bezpiecznego w
układzie
1 2 3
Ox x x
:
(
) (
) (
)
2
2
2
2
2
22
11
33
22
11
33
12
0
6
2
σ
σ
σ
σ
σ
σ
σ
σ
−
+
−
+
−
+ ⋅
≤ ⋅
podstawiając wartości liczbowe:
(
) (
) (
)
( )
2
2
2
2
8 12
0 8
12 0
6
L
k
= −
+
−
+
−
+ ⋅
2
224
6 k
=
+ ⋅
( )
2
2
0
2
2 15
450
P
σ
= ⋅
= ⋅
=
Zatem:
2
224
6
450
k
+ ⋅
≤
2
6
450
224
226
k
→ ⋅
≤
−
=
Tak więc:
[
]
2
226 / 6
6,137
k
MPa
≤
=
2)
Ocena bezpieczeństwa stanu naprężeń:
Stan jest bezpieczny wtedy, gdy:
[
]
6,137 ; 6,137
k
MPa
∈ −
Document Outline
Wyszukiwarka
Podobne podstrony:
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
35) TSiP 2010 11 ćw11
36) TSiP 2010 11 ćw12
24) TSiP 2010 11 ćw06
31) TSiP 2010 11 ćw10
29) TSiP 2010 11 ćw08
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
więcej podobnych podstron