J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
1
P
rzykłady analizy płyt –
pasmo płytowe, płyty prostokątne
Ćwiczenie 11
PASMO
PŁYTOWE
Równanie różniczkowe ugięcia płyty
(
)
1
2
,
w x x :
(
)
4
4
4
1
2
4
2
2
4
1
1
2
2
,
2
q x x
w
w
w
x
x x
x
D
∂
∂
∂
+ ⋅
+
=
∂
∂ ∂
∂
,
gdzie:
(
)
3
2
12 1
E h
D
ν
⋅
=
⋅ −
← sztywność płytowa
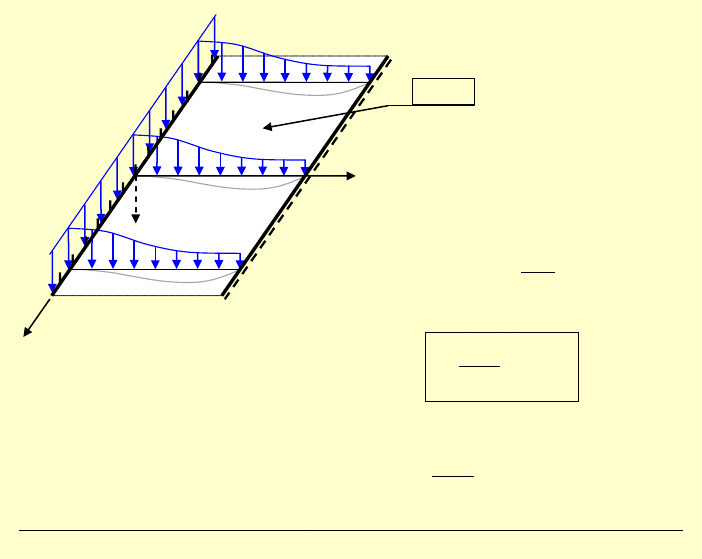
Przyjmujemy, że obciążenie jest funkcją jednej zmiennej –
( )
1
q x ,
a
płyta jest nieograniczona w kierunku osi
2
x .
Jest to więc przypadek symetrii translacyjnej!
Zakładamy, że szerokość pasma
a
jest
stała →
a
const
=
!
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
2
Wynika stąd równanie pasma płytowego:
( )
4
1
4
1
w
D
q x
x
∂
⋅
=
∂
Można więc stosować symbol pochodnej zwyczajnej i całkować
bezpośrednio funkcje jednej zmiennej:
( )
3
1
1
1
3
1
d w
D
q x dx
C
dx
⋅
=
+
∫
itd.
z powyższych założeń wynika,
że dla każdego
2
x
linie ugięcia są takie same,
zatem:
2
0
w
x
∂
=
∂
( )
1
q x
1
x
(
)
2
x
→ ±∞
w
, ,
E
h
ν
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
3
Przypadek szczególny:
( )
( )
4
1
1
4
1
d w x
D
q x
q
dx
⋅
=
=
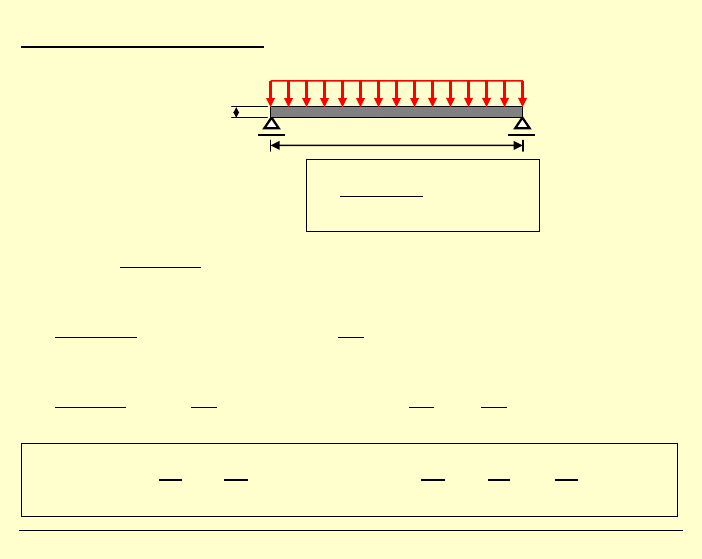
P
asmo swobodnie podparte, obciążone
równomiernie
Równanie pasma płytowego:
Dalej:
( )
3
1
1
1
1
1
3
1
d w x
D
qdx
C
qx
C
dx
⋅
=
+
=
+
∫
( )
(
)
2
2
1
1
1
1
1
1 1
2
2
1
2
d w x
x
D
qx
C dx
q
C x
C
dx
⋅
=
+
=
+
+
∫
( )
2
3
2
1
1
1
1
1 1
2
1
1
2 1
3
1
2
6
2
dw x
x
x
x
D
q
C x
C
dx
q
C
C x
C
dx
⋅
=
+
+
=
+
+
+
∫
( )
3
2
4
3
2
1
1
1
1
1
1
1
2 1
3
1
1
2
3 1
4
6
2
24
6
2
x
x
x
x
x
D w x
q
C
C x
C dx
q
C
C
C x
C
⋅
=
+
+
+
=
+
+
+
+
∫
q
const
=
h
const
=
a
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
4
Warunki brzegowe:
1°
1
0
0
x
w
=
=
; 2°
1
0
x
a
w
=
=
3°
1
2
2
1
0
0
x
w
x
=
∂
=
∂
; 4°
1
2
2
1
0
x
a
w
x
=
∂
=
∂
Realizując warunki brzegowe dla:
( )
4
3
2
1
1
1
2
1
1
3
1
4
24
6
2
q x
C x
C
x
D w x
C
x
C
⋅
⋅
⋅
⋅
=
+
+
+
⋅ +
, mamy:
z 1°
→
1
2
3
4
0
0
0
0
0
24
6
2
C
C
q
C
C
⋅
⋅
⋅
=
+
+
+
⋅ +
→
4
0
C
=
z 3°
→
1
2
0
0
0
2
q
C
C
⋅
=
+
⋅ +
→
2
0
C
=
z 4°
→
2
1
0
0
2
q a
C a
⋅
=
+
⋅ + →
1
2
q a
C
⋅
= −
z 2°
→
4
3
2
3
0
0
0
24
2
6
2
q a
q a
a
a
C a
⋅
⋅
⋅
=
+ −
⋅
+
+
⋅ + →
3
3
24
q a
C
⋅
=
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
5
Zatem:
( )
4
3
2
1
1
1
2
1
1
3
1
4
24
6
2
q x
C x
C
x
D w x
C
x
C
⋅
⋅
⋅
⋅
=
+
+
+
⋅ +
więc:
( )
4
3
3
1
1
1
1
24
12
24
q x
qa x
qa
x
D w x
⋅
⋅
⋅
⋅
=
−
+
Lub, w innej postaci:
( )
4
3
4
1
1
1
1
2
24
x
x
x
qa
w x
D
a
a
a
=
⋅
− ⋅
+
⋅
Zauważmy, że:
4
3
4
1
1
1
1
2
2
24
2
2
2
a
qa
a
a
a
w x
D
a
a
a
=
=
⋅
⋅
− ⋅
⋅
+
⋅
⋅
4
3
4
1
1
1
2
2
24
2
2
2
a
qa
w
D
=
⋅
− ⋅
+
⋅
4
1
1
1
2
24
16
8
2
qa
D
=
⋅
− ⋅ +
⋅
Tak więc:
4
5
2
384
a
qa
w
D
=
⋅
;
(
)
4
2
3
5
1
2
32
a
qa
w
E h
ν
= ⋅
⋅ −
⋅
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
6
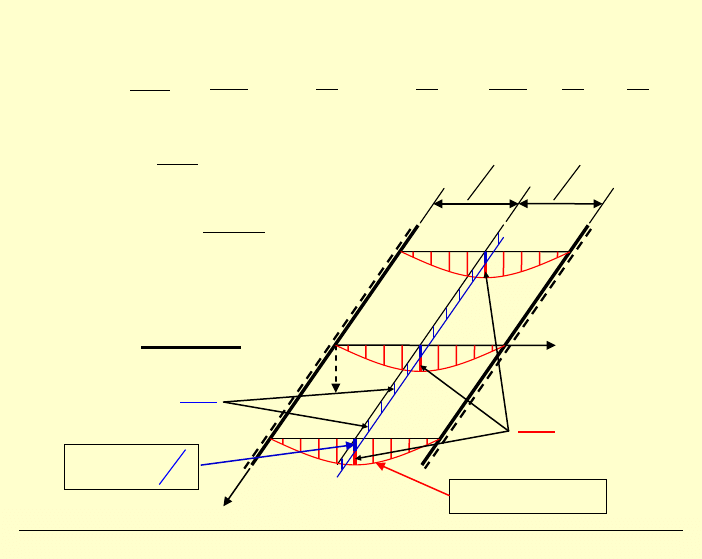
Momenty w paśmie płytowym:
2
11
2
1
w
M
D
x
∂
= − ⋅
∂
2
2
1
1
12
12
24
x
x
qa
a
a
= −
⋅
⋅
− ⋅
2
2
1
1
2
x
x
qa
a
a
= −
⋅
−
2
22
11
2
1
w
M
D
M
x
ν
ν
∂
= − ⋅ ⋅
= ⋅
∂
(
)
2
12
1
2
1
0
w
M
D
x x
ν
∂
= − ⋅ −
⋅
=
∂ ∂
Wykresy:
2
8
qa
2
8
qa
ν
⋅
1
x
(
)
2
x
→ ±∞
w
(
)
11
2
M
x
const
=
(
)
22
1
2
a
M
x
=
2
a
2
a
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
7
/
Dyskusja!
1) Różnica sztywności między belką, a pasmem płytowym
Sztywność belki o szerokości b=1m, w stosunku do sztywności
pasma płytowego ( EJ / D ):
(
)
2
3
2
3
1
1
12
EJ
E h
D
E h
ν
ν
−
= ⋅ ⋅
= −
⋅ ⋅
więc:
(
)
2
1
pasma
belki
w
w
ν
= −
⋅
(przy tej samej szerokości
a
i obciążeniu)
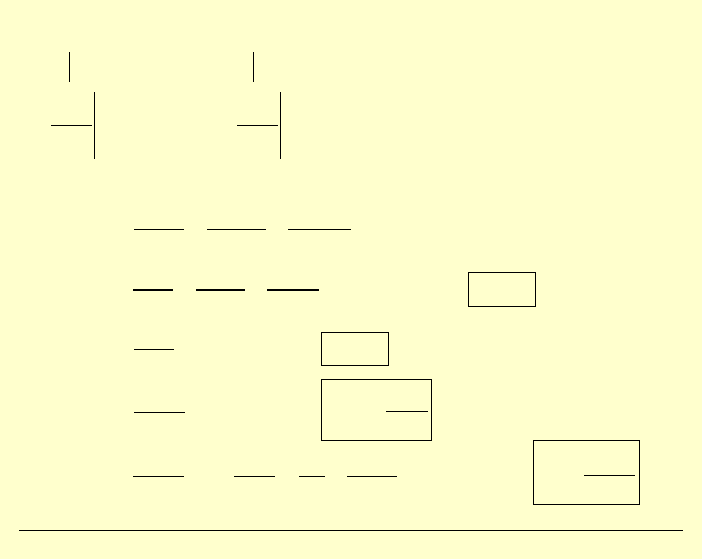
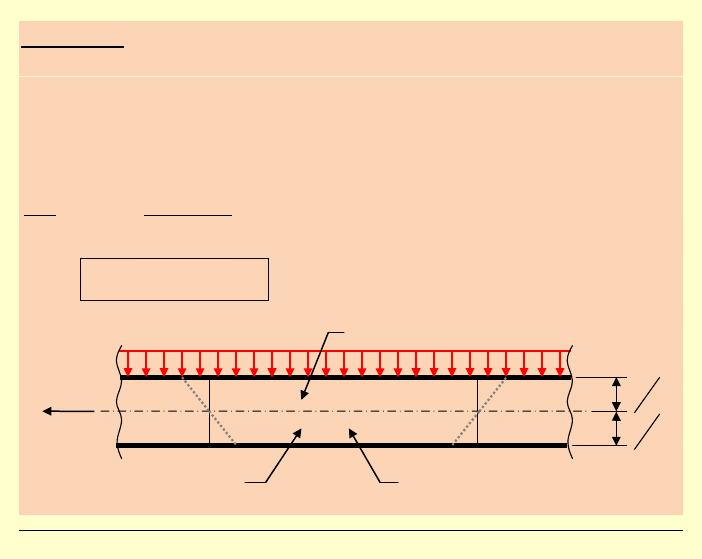
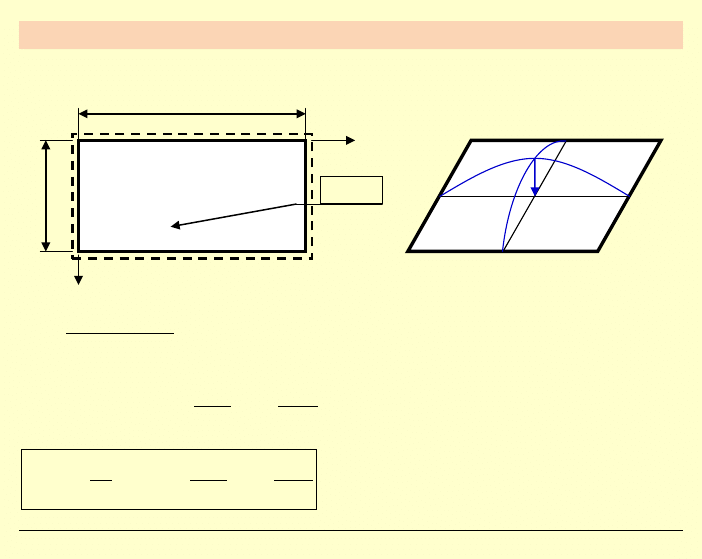
Uzasadnienie fizyczne:
2
x
2
h
2
h
deformacja dla
0
ν
≠
← klinowanie się pasków
rozciąganie
(zwężenie przekroju)
ściskanie (rozszerzenie przekroju)
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
8
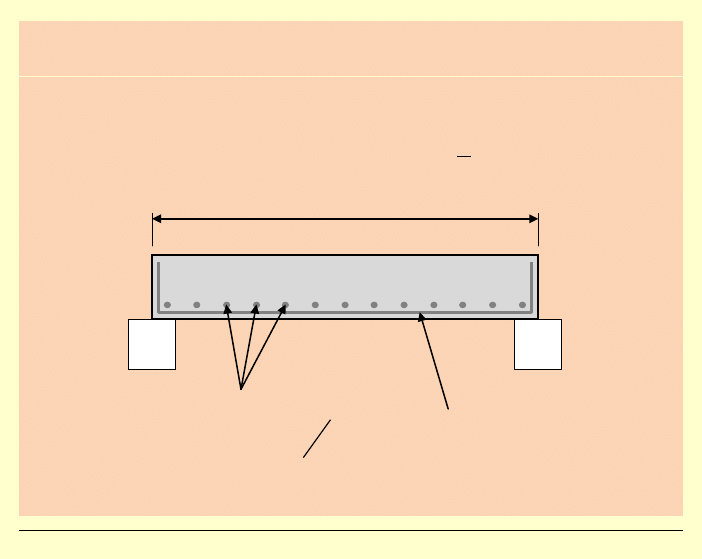
2)
Pasmo żelbetowe
Przyjmuje się, iż dla pasma żelbetowego
1
5
ν
≈
.
a
zbrojenie na moment
22
M
(
)
1
20%
:
5
odpowiada
ν
→
=
zbrojenie na moment
11
M
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
9
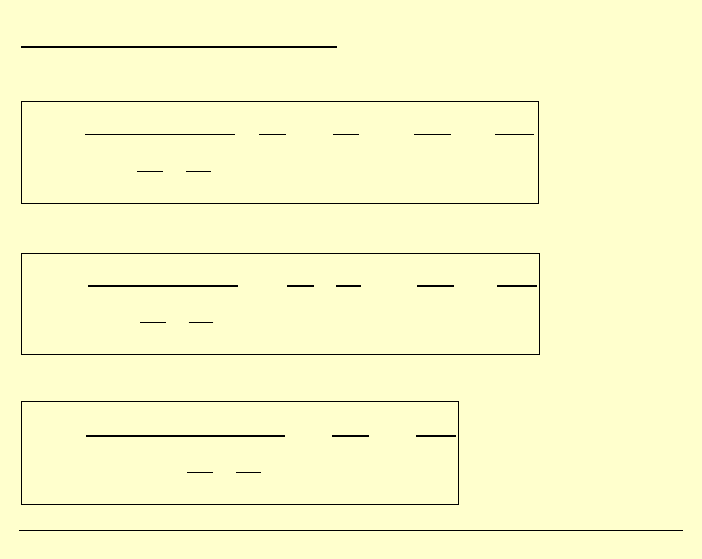
PŁYTA PROSTOKĄTNA
Płyta swobodnie podparta , obciążenie podwójnie sinusoidalne:
(
)
3
2
12 1
E h
D
ν
⋅
=
⋅ −
← sztywność płytowa
(
)
1
2
1
2
0
,
sin
cos
x
x
q x x
q
a
b
π
π
=
⋅
⋅
← funkcja obciążenia
4
1
2
0
1
sin
cos
x
x
w
q
D
a
b
π
π
∇
=
⋅ ⋅
⋅
← równanie płytowe
a
b
2
x
1
x
, ,
E
h
ν
0
q

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
10
Warunki brzegowe (pary warunków brzegowych):
1°
(
)
1
2
0 ;
0
w x
x
=
= ;
(
)
1
2
;
0
w x
a x
=
=
2°
(
)
1
2
;
0
0
w x x
=
= ;
(
)
1
2
;
0
w x x
b
=
=
3°
(
)
,11
1
2
0 ;
0
w
x
x
=
= ;
(
)
,11
1
2
;
0
w
x
a x
=
=
4°
(
)
,22
1
2
;
0
0
w
x x
=
= ;
(
)
,22
1
2
;
0
w
x x
b
=
=
Przyjmujemy rozwiązanie równania płyty w postaci:
(
)
1
2
1
2
,
sin
cos
x
x
w x x
C
a
b
π
π
= ⋅
⋅
Rozwiązanie to spełnia wszystkie
(
)
1
2
,
w x x
warunki brzegowe!
Różniczkowanie funkcji
i porównanie wyrazów przy tych
samych funkcjach trygonometrycznych:
2
4
4
4
4
0
4
2
2
4
2
2
2
1
1
q
C
C
a
a b
b
a
b
D
π
π
π
π
⋅
+
+
=
⋅
+
=
→
0
2
4
2
2
1
1
q
C
D
a
b
π
=
⋅
+
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
11
(
)
11
,11
,22
M
D
w
w
ν
= − ⋅
+ ⋅
Momenty w paśmie płytowym:
0
1
2
11
2
2
2
2
2
2
1
1
sin
sin
1
1
q
x
x
M
a
b
a
b
a
b
π
π
ν
π
=
⋅
+ ⋅
⋅
⋅
⋅
+
(
)
22
,22
,11
M
D
w
w
ν
= − ⋅
+ ⋅
0
1
2
22
2
2
2
2
2
2
1
1
sin
sin
1
1
q
x
x
M
a
b
a
b
a
b
π
π
ν
π
=
⋅
⋅
+
⋅
⋅
⋅
+
(
)
12
12
1
M
D
w
ν
= − ⋅ −
⋅
(
)
0
1
2
12
2
2
2
2
1
cos
cos
1
1
q
x
x
M
a
b
a b
a
b
ν
π
π
π
⋅ −
=
⋅
⋅
⋅ ⋅
⋅
+
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 11 • KMBiM WILiŚ PG
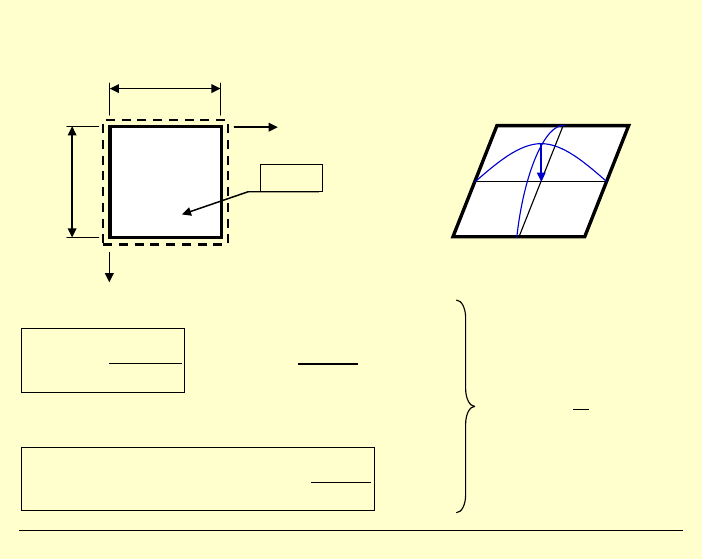
12
Przypadek szczególny:
płyta kwadratowa, a b
=
Maksymalne ugięcie płyty:
4
0
2
max
4
q
a
w
D
π
⋅
=
⋅
4
0
0,00257
q
a
D
⋅
≈
⋅
Maksymalne moment
y zginające w płycie:
(
)
2
0
11
22
2
max
max
1
4
q
a
M
M
ν
π
⋅
=
= +
⋅
0
q
1
x
2
x
b
a
, ,
E
h
ν
dla:
1
2
a
x
=
Document Outline
Wyszukiwarka
Podobne podstrony:
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
36) TSiP 2010 11 ćw12
24) TSiP 2010 11 ćw06
31) TSiP 2010 11 ćw10
29) TSiP 2010 11 ćw08
37) TSiP 2010 11 ćw14
34) TSiP 2010 11 ćw13
25) TSiP 2010 11 ćw07
30) TSiP 2010 11 ćw09
więcej podobnych podstron