J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

1

Pasmo tarczowe – kontynuacja

Ćwiczenie 10

Repetytorium z tarcz

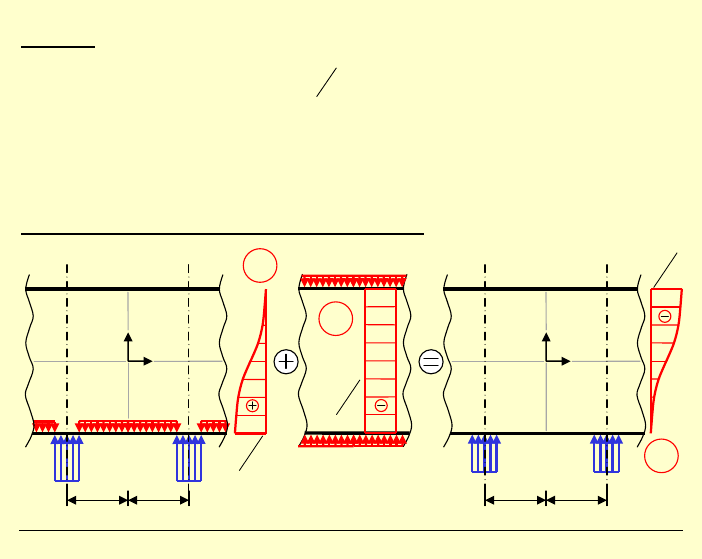
Przypadek szczególny

z zakresu zagadnień pasm tarczowych –

tarcza bardzo wysoka

b

→ ∞

, tzn.

Zbadamy graniczne wartości stałych

n

c i

n

d przy b

→ ∞.

Przywołajmy wzory na naprężenia

11

σ

:

(

)

(

)

2

11

1

1

1

1

1

1

cos

cos

cos

n

n

n

n

n

n

n

n

n

n

x b

n

n

n

a

x

a

a

c

x

a

a

d

x

σ

α

α

α

∞

∞

∞

=

=

=

=

=

⋅

−

+

⋅ ⋅

+

−

⋅ ⋅

∑

∑

∑







oraz:

(

)

(

)

2

11

1

1

1

1

1

1

cos

cos

cos

n

n

n

n

n

n

n

n

n

n

x

b

n

n

n

a

x

a

a

c

x

a

a

d

x

σ

α

α

α

∞

∞

∞

=−

=

=

=

=

⋅

−

+

⋅ ⋅

−

−

⋅ ⋅

∑

∑

∑





gdzie:

2

2

n

n

n

n

b

c

sh 2

b

b

α

α

α

=

+

oraz

2

2

n

n

n

n

b

d

sh 2

b

b

α

α

α

=

−

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

2

Wzory na

n

c

i

n

d

mają więc następującą strukturę:

1

,

lim

1

n

n

x

c d

sh x

x

→∞

=

±

Z twierdzenia de l’Hôspitala mamy:

lim

2

x

x

x

e

e

x

−

→∞

−

lim

2

x

x

H

x

e

e

−

→∞

+

→

= ∞

Zatem, przy b

→ ∞ mamy

0

n

c

→ oraz

0

n

d

→

Mamy stąd bardzo interesujący wynik:

(

)

( )

11

2

1

0

1

2

x

b

p x

a

σ

= − =

−

Często, dla obciążeń samorównoważących się:

0

0

a

=

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

3

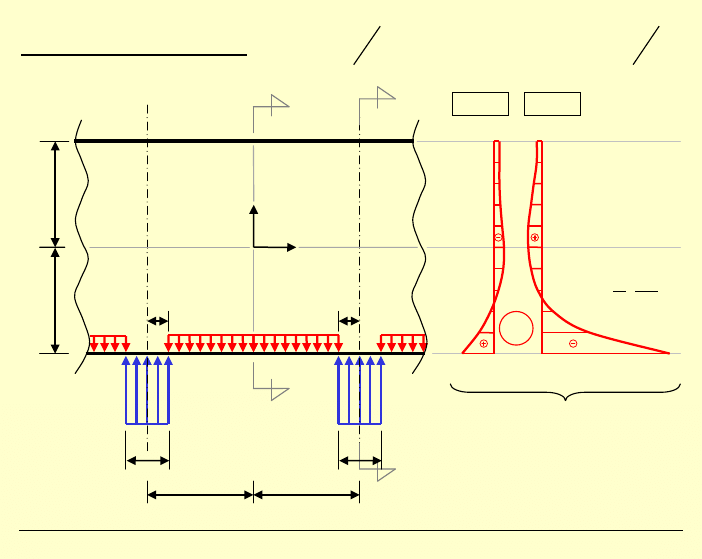
Przykład numeryczny b l

=

:

,

5

l

c

=

→

'

1

4

q

q

=

(

)

q

const

=

kN

m









/ 5

l

/ 5

l

4q

4q

q

g

×

l

1

x

2

x

l

b

l

=

b

l

=

2c

2c

A

A

B

B

0, 088

0,156

1, 002

0, 088

0,186

2

q kN

g m





×  





4, 002

B

B

−

11

σ

A

A

−

porównanie ze wzorem

dla:

b

l

= = ∞

→ bardzo dobre przybliżenie

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

4

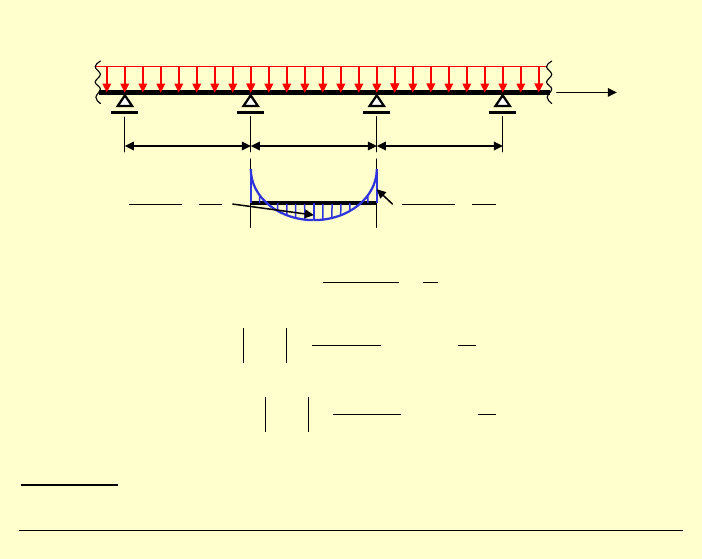
Porównanie z

teorią belek:

Wskaźnik wytrzymałości:

( )

2

2

2

2

6

3

g

l

W

gl

⋅

=

= ⋅

Naprężenia w przęśle:

2

,

2

3

0, 25

6 2

g d

ql

q

gl

g

σ

⋅

=

=

⋅

⋅

Naprężenia w podporze:

2

,

2

3

0,50

3 2

g d

ql

q

gl

g

σ

⋅

=

=

⋅

⋅

Wniosek:

b

l

=

Stosowanie teorii belek w przypadku tarcz o proporcjach

wymiarów jak powyżej (

) nie ma sensu!

2l

2l

2l

∞

q

( )

2

2

2

24

6

q

l

ql

⋅

=

( )

2

2

2

12

3

q

l

ql

⋅

=

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

5

q

Uwagi:

1)

Przyłożenie obciążenia

kN

m









na górnym lub na dolnym brzegu

(ewentualnie między górnym, a dolnym brzegiem tarczy)
nie

wpływa na rozkład naprężeń

11

σ

i

12

σ

, a

wpływa jedynie

na

naprężenia

22

σ

.

Wynika to z następującego rozumowania:

22

σ

q

g

l

q

1

x

2

x

g

×

l

q

g

22

σ

q

q

l

1

x

2

x

g

×

l

22

σ

q

g

11

0

σ

=

12

0

σ

=

→ bo są to kier. główne

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

6

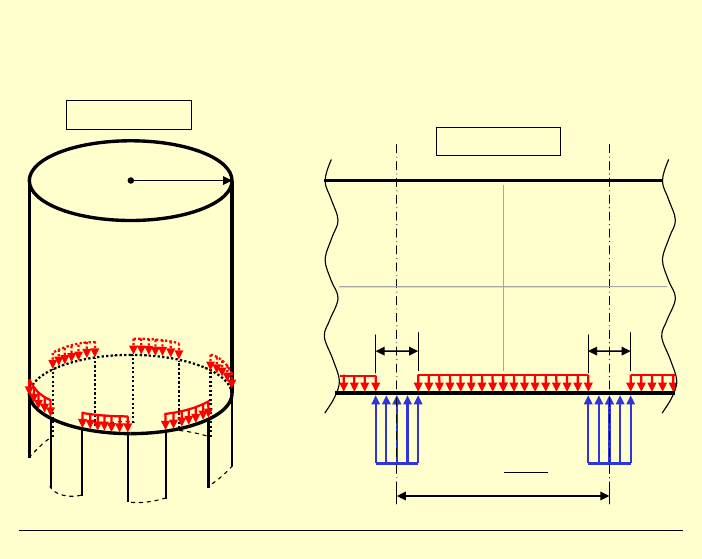
2)

Podobnie rozwiązuje się tarcze zakrzywione w planie

→ zbiorniki i silosy

:

Rozwini

ęcie

:

Konstrukcja

2c

2c

2

2

R

l

n

π

=

R

n podpór

(

)

6

tutaj n

=

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

7

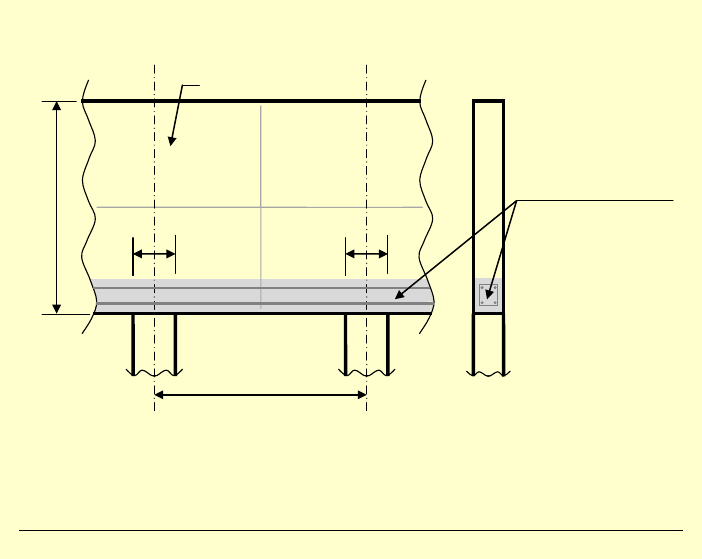
3)

Przykład „bezwładności” myślenia inżynierskiego:

→ Inżynierowie nie znający teorii tarcz projektowali belki jakoby

dźwigające ścianę żelbetową. W rzeczywistości mamy tu do

czynienia z tarczą zginaną o wymiarach

2

2

b

l

×

!

2c

2c

2l

2b

zbędna (błędna)

belka żelbetowa

ściana betonowa

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

8

REPETYTORIUM Z TARCZ

Zadanie 1:

Przeanalizować stan naprężenia w tarczy.

Funkcja naprężeń Airy’ego dana jest wzorem:

( )

2

2

,

sin

F r

C r

ϕ

ϕ

= ⋅ ⋅

, gdzie:

C

const

=

,

0

C

>

Rozwiązanie zadania 1:

Składowe stanu naprężenia obliczamy ze wzorów:

2

2

2

1

1

rr

F

F

r

r

r

σ

ϕ

∂

∂

= ⋅

+

⋅

∂

∂

,

2

2

F

r

ϕϕ

σ

∂

=

∂

,

1

r

F

r r

ϕ

σ

ϕ





∂

∂

= −

⋅





∂

∂





Obliczamy pomocnicze pochodne funkcji

( )

,

F r

ϕ

:

(

)

2

2

2

( , )

sin

2

sin

F r

C r

r C

r

r

ϕ

ϕ

ϕ

∂

∂

→

=

⋅ ⋅

=

⋅ ⋅

∂

∂

(

)

2

2

2

2

( , )

2

sin

2

sin

F r

r C

C

r

r

ϕ

ϕ

ϕ

∂

∂

→

=

⋅ ⋅

= ⋅ ⋅

∂

∂

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

9

(

)

2

2

2

2

( , )

sin

2

sin

cos

sin 2

F r

C r

C r

C r

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

∂

∂

→

=

⋅ ⋅

= ⋅ ⋅ ⋅

⋅

= ⋅ ⋅

∂

∂

(

)

2

2

2

2

( , )

sin 2

2

cos 2

F r

C r

C r

ϕ

ϕ

ϕ

ϕ

ϕ

∂

∂

→

=

⋅ ⋅

= ⋅ ⋅ ⋅

∂

∂

(

)

2

1

( , )

1

sin 2

sin 2

sin 2

F r

C r

C r

C

r r

r r

r

ϕ

ϕ

ϕ

ϕ

ϕ





∂

∂

∂

∂





→ −

⋅

= −

⋅ ⋅ ⋅

= −

⋅ ⋅

= − ⋅









∂

∂

∂

∂









Składowe stanu naprężenia:

2

2

2

1

1

rr

F

F

r

r

r

σ

ϕ

∂

∂

= ⋅

+

⋅

∂

∂

(

)

(

)

2

2

2

1

1

2

sin

2

cos 2

r C

C r

r

r

ϕ

ϕ

= ⋅

⋅ ⋅

+

⋅ ⋅ ⋅ ⋅

2

2

sin

2

cos 2

rr

C

C

σ

ϕ

ϕ

= ⋅ ⋅

+ ⋅ ⋅

→

2

2

cos

rr

C

σ

ϕ

= ⋅ ⋅

2

2

F

r

ϕϕ

σ

∂

=

∂

→

2

2

sin

C

ϕϕ

σ

ϕ

= ⋅ ⋅

1

r

F

r r

ϕ

σ

ϕ





∂

∂

= −

⋅

→





∂

∂





sin 2

r

C

ϕ

σ

ϕ

= − ⋅

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

10

Zatem:

2

2

cos

rr

C

σ

ϕ

= ⋅ ⋅

,

2

2

sin

C

ϕϕ

σ

ϕ

= ⋅ ⋅

,

sin 2

r

C

ϕ

σ

ϕ

= − ⋅

tak więc:

→ dla

0

ϕ

= ° zachodzi:

2

rr

C

σ

=

,

0

ϕϕ

σ

=

,

0

r

ϕ

σ

=

→ dla

90

ϕ

= ° zachodzi:

0

rr

σ

= ,

2C

ϕϕ

σ

=

,

0

r

ϕ

σ

=

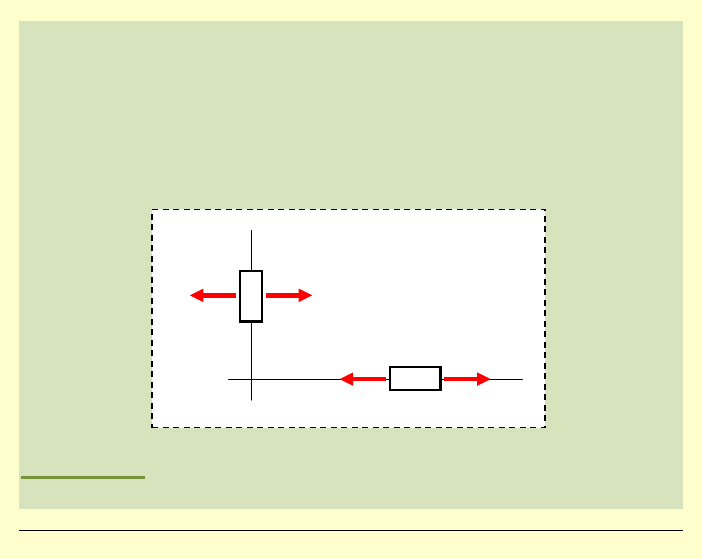
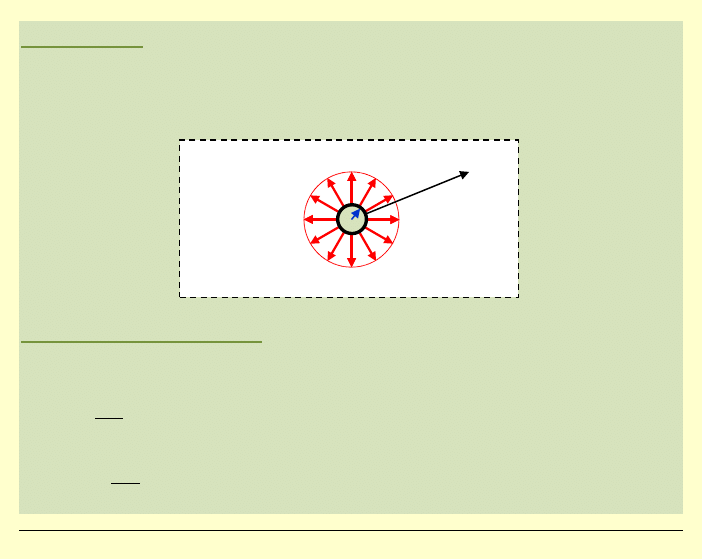
Odpowiedź:

Jest to więc równomierne rozciąganie naprężeniem

o

wartości równej

σ

=2C w kierunku

ϕ

=0° !

2C

2C

2C

2C

90

ϕ

= °

0

ϕ

= °

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

11

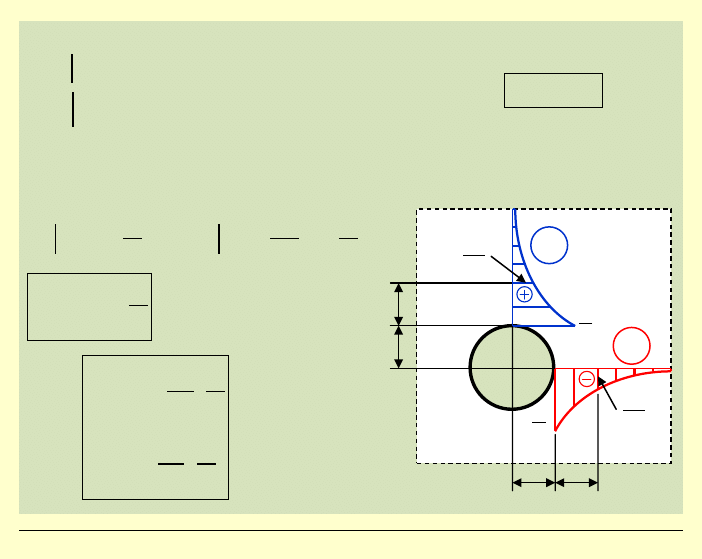
Zadanie 2:

kN

m









Wyznaczyć stan naprężeń w blasze z otworem,

poddanej działaniu ciśnienia wewnętrznego p

(gdzie: p –

obciążenie ciągłe na jednostkę długości brzegu otworu)

Rozwiązanie zadania 2:

Rozwiązanie ogólne, w przypadku obrotowej symetrii:

(

)

(

)

2

3

4

2

2

3

4

2

2

1 2ln

2

3 2ln

rr

C

C

C

r

r

C

C

C

r

r

ϕϕ

σ

σ



=

+

+

⋅ +







= −

+

+

⋅ +



r

g

×

p

a

J. Górski, M. Skowronek,

M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 10 • KMBiM WILiŚ PG

12

Zauważmy, że gdy współrzędna

r

→ ∞

, to naprężenia dążą do zera:

(

)

(

)

3

4

3

4

0

2

1 2ln

0

0

2

3 2ln

0

rr r

r

C

C

r

C

C

r

ϕϕ

σ

σ

→∞

→∞



= +

+

⋅ +

=





= +

+

⋅ +

=



→ stąd:

3

4

,

0

C C

=

Pozostałą w obliczeniach stałą

2

C

C

≡ wyznaczamy z warunku

brzegowego:

rr r a

p

g

σ

=

= −

2

2

rr r a

C

p

a

g

σ

=

→

=

= −

2

2

p

C

a

g

= − ⋅

Stąd:

2

2

2

2

rr

a

p

r

g

a

p

r

g

ϕϕ

σ

σ



= −

⋅









=

⋅



a

a

a

a

ϕϕ

σ

rr

σ

p

g

4

p

g

4

p

g

p

g