
Definicja współczynników dla stateczno
ś
ci - nie modyfikowa
ć
!
σ
0.1 0.2
,
12
..
:=
Pr
ę
t sztywno-sztywny:
α σ
( )
σ
sin
σ
( )
σ
cos
σ
( )
⋅
−
2 1
cos
σ
( )
−
(
)
⋅
σ
sin
σ
( )
⋅
−
⋅
:=
β σ
( )
σ
σ
sin
σ
( )
−
2 1
cos
σ
( )
−
(
)
⋅
σ
sin
σ
( )
⋅
−
⋅
:=
υ σ
( )
σ
2
1
1 cos
σ
( )
⋅
−
2 1
cos
σ
( )
−
(
)
⋅
σ
sin
σ
( )
⋅
−
⋅
:=
δ σ
( )
σ
3
sin
σ
( )
2 1
cos
σ
( )
−
(
)
⋅
σ
sin
σ
( )
⋅
−
⋅
:=
Pr
ę
t sztywno-przegubowy:
α
I
σ
( )
σ
2
sin
σ
( )
sin
σ
( )
σ
cos
σ
( )
⋅
−
⋅
:=
δ
I
σ
( )
σ
3
cos
σ
( )
sin
σ
( )
σ
cos
σ
( )
⋅
−
⋅
:=
Pr
ę
t wspornikowy:
α
III
σ
( )
1
− σ
⋅
tan
σ
( )
⋅
:=
Koniec definicji współczynników.
Dane :
kN
m
2
E
2.1 10
8
⋅
:=
l1
5.8
:=
m
I1
11260 10
8
−
⋅
:=
m
4
l2
5.0
:=
m
I2
869 10
8
−
⋅
:=
m
4
K11
σ
1
σ
2
,
(
)
α
I
σ
2
( )
α σ
2
( )
+
(
)
E I1
⋅
l1
⋅
3 E
⋅
I2
⋅
l2
+
:=
K12
σ
1
σ
2
,
(
)
α
I
σ
2
( )
υ σ
2
( )
−
(
)
E I1
⋅
l1
2
⋅
:=
K13
σ
1
σ
2
,
(
)
α
I
σ
2
( )
−
E I1
⋅
l1
2
⋅
:=
K21
σ
1
σ
2
,
(
)
α
I
σ
2
( )
υ σ
2
( )
−
(
)
E I1
⋅
l1
2
⋅
:=
K22
σ
1
σ
2
,
(
)
σ
1
2
−
δ
I
σ
2
( )
+
δ
I
σ
1
( )
+
δ σ
2
( )
+
E I1
⋅
l1
3
⋅
:=
K23
σ
1
σ
2
,
(
)
σ
1
2
δ
I
σ
2
( )
−
E I1
⋅
l1
3
⋅
:=
K31
σ
1
σ
2
,
(
)
α
I
σ
2
( )
−
E I1
⋅
l1
2
⋅
:=
K32
σ
1
σ
2
,
(
)
σ
1
2
δ
I
σ
2
( )
−
E I1
⋅
l1
3
⋅
:=
K33
σ
1
σ
2
,
(
)
σ
1
2
−
δ
I
σ
2
( )
+
E I1
⋅
l1
3
⋅
:=
K
σ
1
σ
2
,
(
)
K11
σ
1
σ
2
,
(
)
K21
σ
1
σ
2
,
(
)
K31
σ
1
σ
2
,
(
)
K12
σ
1
σ
2
,
(
)
K22
σ
1
σ
2
,
(
)
K32
σ
1
σ
2
,
(
)
K13
σ
1
σ
2
,
(
)
K23
σ
1
σ
2
,
(
)
K33
σ
1
σ
2
,
(
)
:=
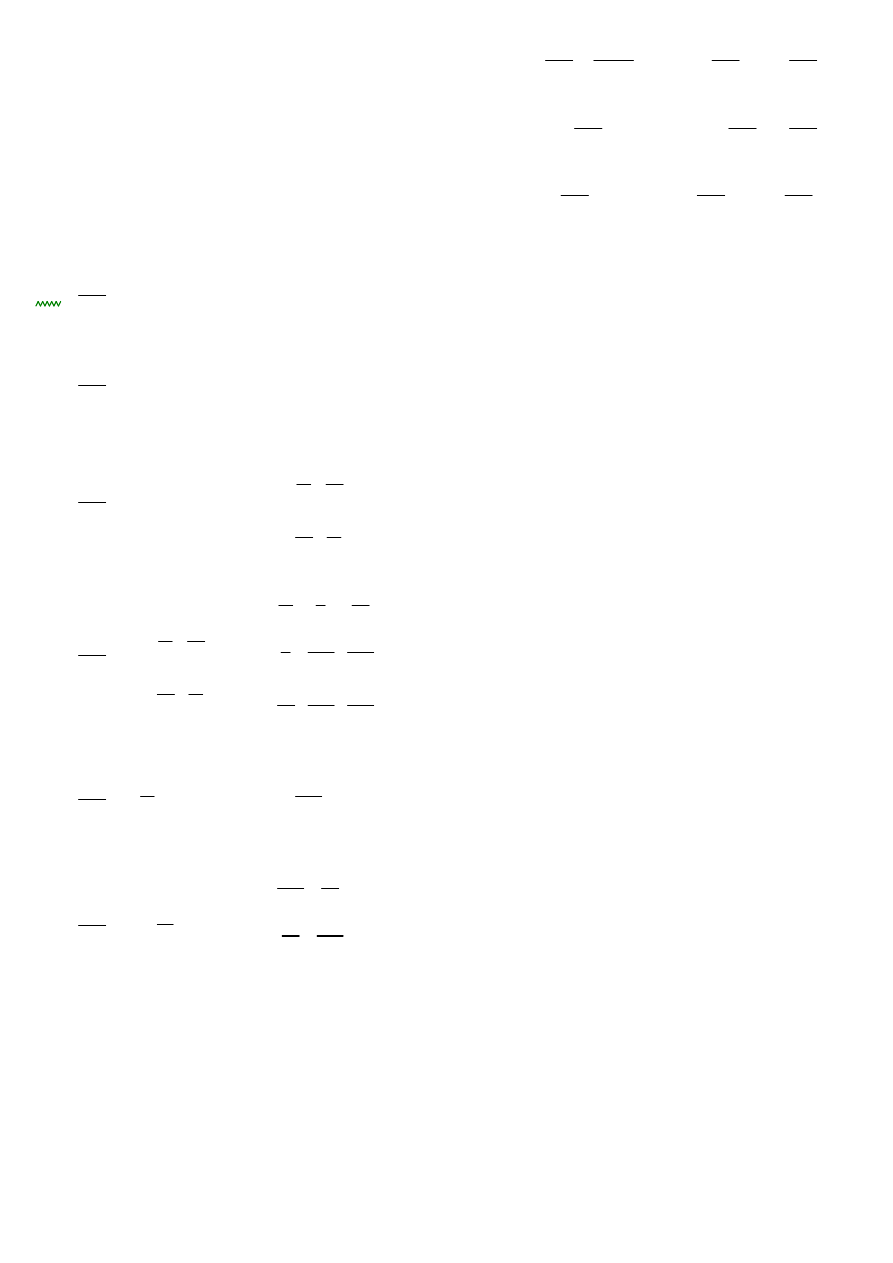
KI
3
4
+
(
)
E I1
⋅
l1
⋅
3 E
⋅
I2
⋅
l2
+
3
6
−
(
)
E I1
⋅
l1
2
⋅
3
−
E I1
⋅
l1
2
⋅
3
6
−
(
)
E I1
⋅
l1
2
⋅
3
3
+
12
+
(
)
E I1
⋅
l1
3
⋅
3
−
E I1
⋅
l1
3
⋅
3
−
E I1
⋅
l1
2
⋅
3
−
E I1
⋅
l1
3
⋅
3
E I1
⋅
l1
3
⋅
:=
K1
E I2
⋅
l2
2
0
0
0
0
0
0
0
0
0
⋅
:=
K1G
0
0
0
0
0
0
0
0
0
:=
K2
E I2
⋅
l2
2
3 l2
⋅
0
0
0
0
0
0
0
0
⋅
:=
K2G
0
0
0
0
0
0
0
0
0
:=
K3
E I1
⋅
l1
2
0
0
0
0
0
0
0
0
0
⋅
:=
K3G
0
0
0
0
1
l1
1
−
l1
0
1
−
l1
1
l1
:=
K4
E I1
⋅
l1
2
3 l1
⋅
3
3
−
3
3
l1
3
−
l1
3
−
3
−
l1
3
l1
⋅
:=
K4G
l1
5
1
5
1
−
5
1
5
6
5 l1
⋅
6
−
5 l1
⋅
1
−
5
6
−
5 l1
⋅
6
5 l1
⋅
:=
K5
E I1
⋅
l1
2
0
0
0
0
3
l1
0
0
0
0
⋅
:=
K5G
0
0
0
0
6
5 l1
⋅
0
0
0
0
:=
K6
E I1
⋅
l1
2
4 l1
⋅
6
−
0
6
−
12
l1
0
0
0
0
⋅
:=
K6G
2 l1
⋅
15
1
−
10
0
1
−
10
6
5 l1
⋅
0
0
0
0
:=
KII
K1
K2
+
K3
+
K4
+
K5
+
K6
+
:=
Sprawdzenie :
KII
29633.216
2108.740
−
2108.740
−
2108.740
−
2181.455
363.576
−
2108.740
−
363.576
−
363.576
=
=
KI
29633.216
2108.740
−
2108.740
−
2108.740
−
2181.455
363.576
−
2108.740
−
363.576
−
363.576
=
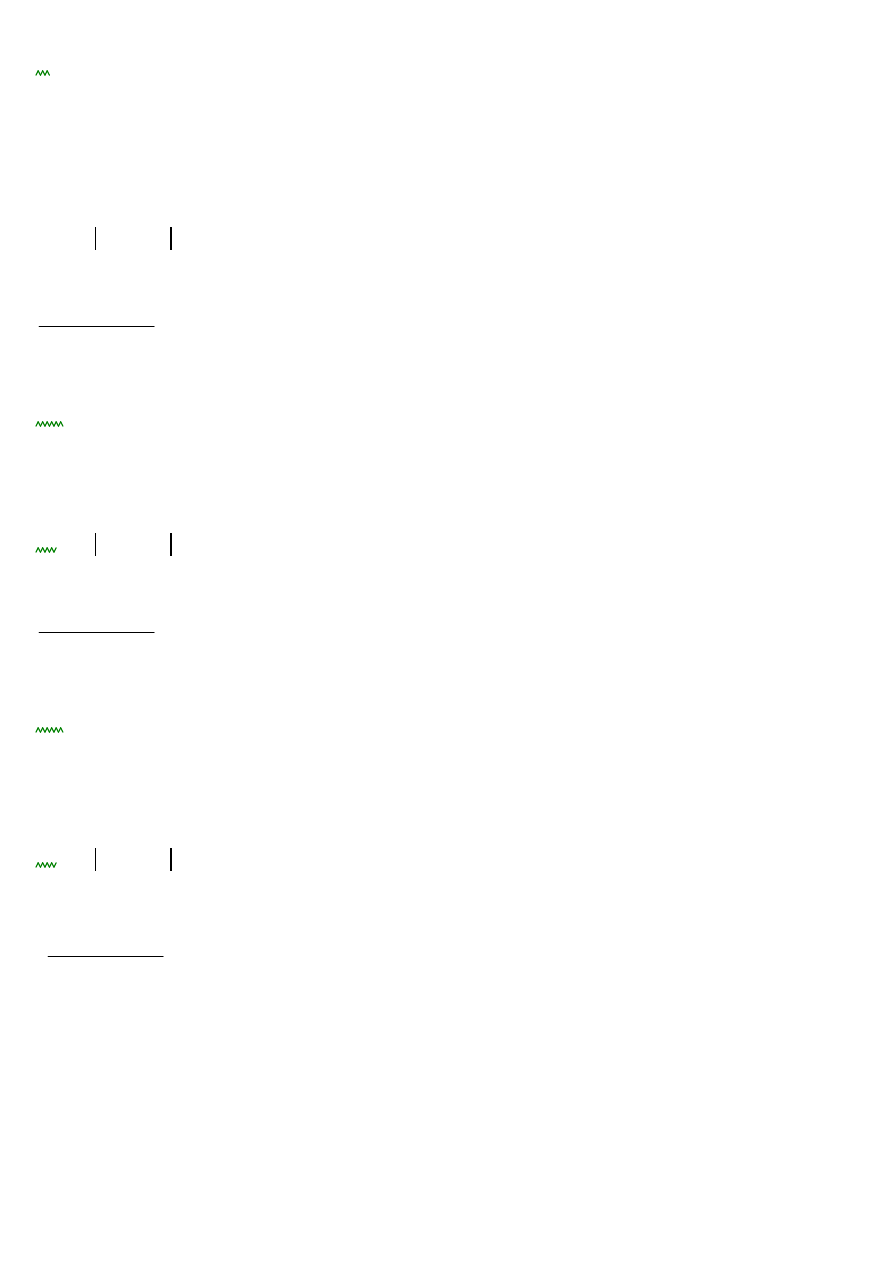
1). S1, S2 = 0
S
0
:=
KG
K3G K5G
+
:=
KG
0.000
0.000
0.000
0.000
0.379
0.172
−
0.000
0.172
−
0.172
=
M S
( )
KII S KG
⋅
−
:=
root M S
( ) S
,
(
)
746.968
=
746.968
746.622
−
746.622
100
⋅
%
0.046 %
=
2). S1 = 0, S2
KG
K4G K6G
+
:=
KG
1.933
0.100
0.200
−
0.100
0.414
0.207
−
0.200
−
0.207
−
0.207
=
M S
( )
KII S KG
⋅
−
:=
root M S
( ) S
,
(
)
717.375
=
717.375
716.490
−
716.490
100
⋅
%
0.124 %
=
3). S1, S2
KG
K1G K2G
+
K3G
+
K4G
+
K5G
+
K6G
+
:=
KG
1.933
0.100
0.200
−
0.100
0.793
0.379
−
0.200
−
0.379
−
0.379
=
M S
( )
KII S KG
⋅
−
:=
root M S
( ) S
,
(
)
366.014
=
366.014
365.862
−
365.862
100
⋅
%
0.042 %
=
Wyszukiwarka
Podobne podstrony:
Mathcad, projekt nr 1c
Mathcad Projekt 3 nr 3
Projekt nr 1piątek
Projekt nr 1, Projekt nr 1 EC przeciwprężna
Dane Projekt nr 1 MK
Mathcad Projekt metal
Projekt nr 1 przyklad z zajec
BO projekt nr 1, Guzek
Projekt Nr 3 Wał Strona Tytułowa
Zarządzanie projektem innowacyjnym Projekt nr II
Hydrologia projekty PROJEKT nr 2 HYDROLOGIA
Projekt Nr 2 Strona Tytułowa
Mathcad projekt
Projekt nr 1 przyklad
Projekt Nr 3 Wał
Projekt nr 1 z wytrzymnki
Mathcad Projekt belki kablobetonowej
Cwiczenie projektowe nr 1 z TRB masy ziemne
więcej podobnych podstron