Określenie Modułu Younga poprzez pomiar 

ugięcia belki

Grupa laboratoryjna 2:

Skibowski Krzysztof

Jaskólski Kamil

Kordulasińska Monika

Krzemińska Anna

Sienicka Monika

Olczykowski Łukasz

Toczek Tomasz

Krasowski Wojciech

1. Cel ćwiczenia

Celem ćwiczenia jest doświadczalne określenie modułu Younga za pomocą 

pomiaru krzywizny linii ugięcia belki zginanej. Przy wykonaniu obliczeń 
wytrzymałościowych konstrukcji znajomość wartości modułu Younga materiału jest 
konieczna, albowiem jego wartość decyduje o wielkości odkształceń obciążonej 
konstrukcji.

2. Przebieg ćwiczenia

2.1. Wymiary próbki

B=2,95 cm

H= 0,8 cm

Wymiary próbki zostały wykonane przy użyciu suwmiarki.

Następnie określamy pozostałe wielkości potrzebne do określenia modułu Younga. 

•

Odległość między podporami A i D wynosi 

300 mm. Jest to wielkość 

odczytana z podziałki umieszczonej na maszynie wytrzymałościowej

•

Odległość między podporami B i C 

d=189 mm dokładność suwmiarki 0,02

•

Odległość między czujnikiem lewym a prawym 

l=100 mm wielkość zmierzona 

suwmiarką o dokładności 0,02

•

Odległość pomiędzy podporami A i B oraz C i D 

e= 55,5 mm

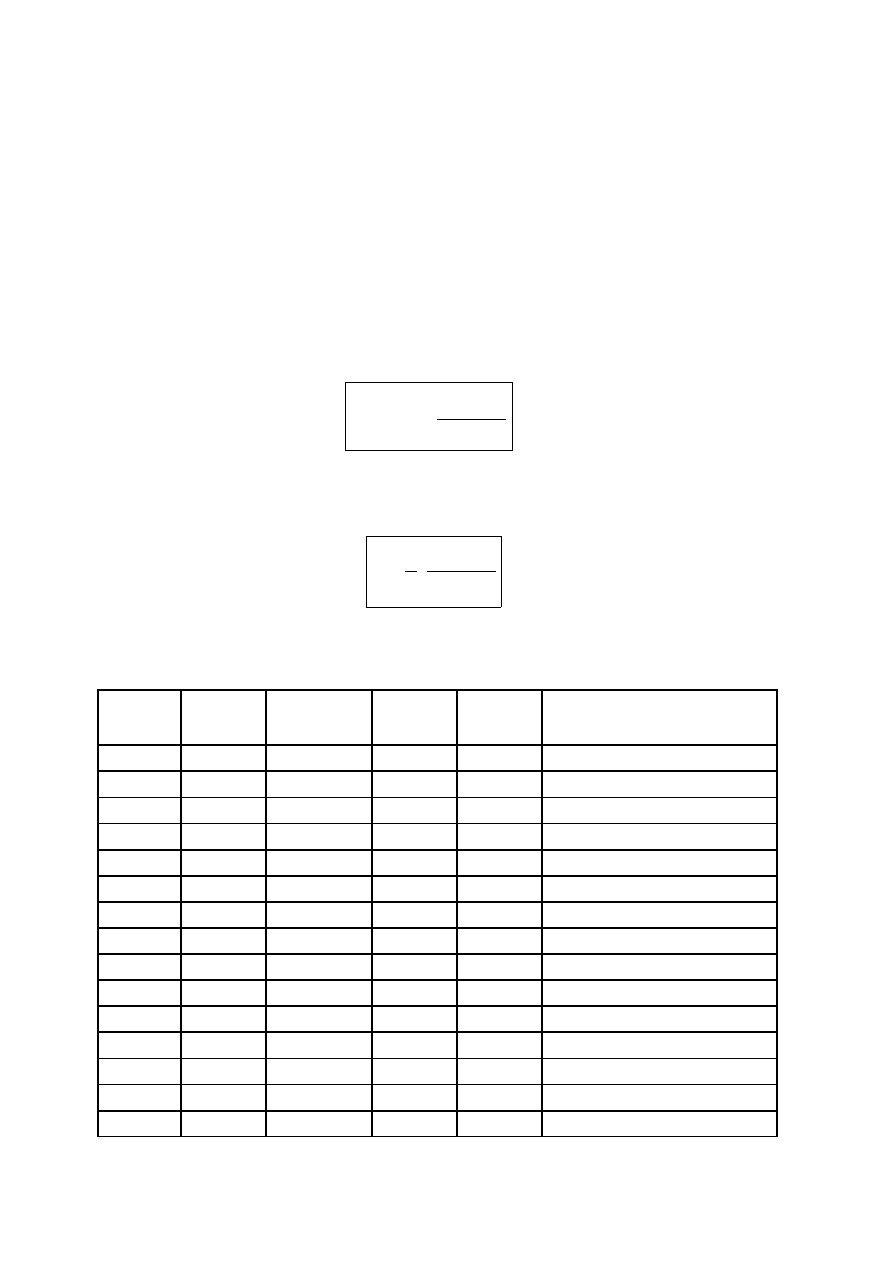
o wielkość e obliczamy ze wzoru:

 

mm

d

AD

e

5

,

55

2

=

−

=

2.2. Obciążanie i odciążanie próbki

Próbkę umieszczamy na podporach maszyny wytrzymałościowej. Następnie 

poddajemy próbkę odciążeniu siłą P na każdym kroku zwiększając ją o 0,1 KN 
dochodząc aż do wielkości 1,9 KN. Następnie próbkę odciążamy zmniejszając siłę P o 
0,1 KN dochodząc do 0. Przy każdym kroku siły odczytujemy z czujników wartości f

l

, 

f

s

, f

p

. 

Skala 2KN=200kg

o

wartość 

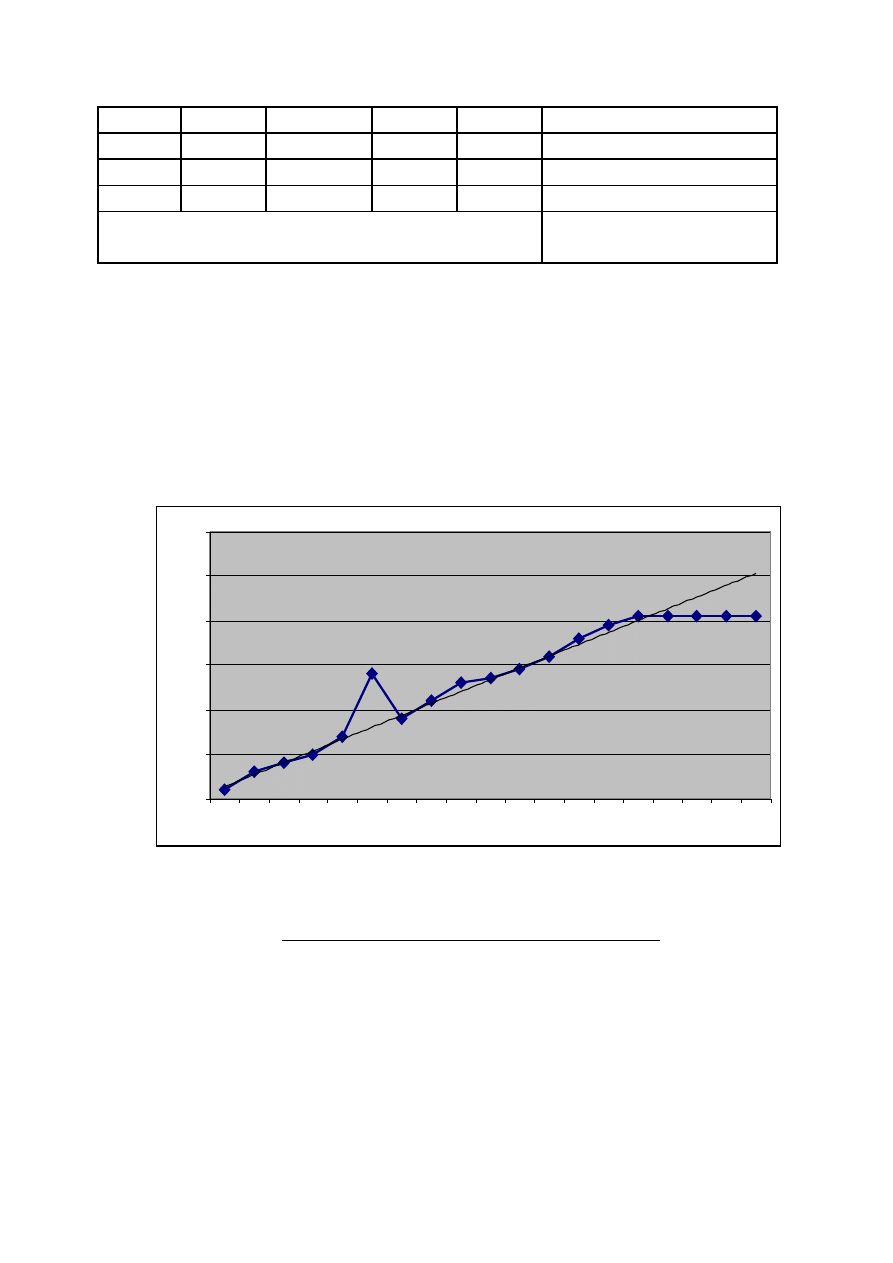
f obliczamy ze wzoru:

o

wartość 

E obliczamy ze wzoru:

OBCIĄŻANIE

P[kN]

F

lewy 

[mm]

F

środkowy 

[mm]

f

prawy 

[mm]

f [mm]

E [GPa]

0,1

0,11

0,12

0,11

0,01

275,5892479

0,2

0,22

0,25

0,22

0,03

183,7261653

0,3

0,33

0,37

0,33

0,04

206,6919359

0,4

0,44

0,49

0,44

0,05

220,4713983

0,5

0,54

0,61

0,54

0,07

196,8494628

0,6

0,65

0,79

0,65

0,14

118,1096777

0,7

0,76

0,85

0,76

0,09

214,3471928

0,8

0,86

0,97

0,86

0,11

200,4285439

0,9

0,97

1,10

0,97

0,13

190,7925562

1,0

1,07

1,21

1,08

0,135

204,1401836

1,1

1,18

1,33

1,19

0,145

209,0677053

1,2

1,29

1,45

1,29

0,16

206,6919359

1,3

1,39

1,57

1,39

0,18

199,036679

1,4

1,49

1,69

1,50

0,195

197,8589472

1,5

1,58

1,79

1,59

0,205

201,6506692

2

p

l

s

f

f

f

f

+

−

=

3

2

4

3

h

b

f

l

e

P

E

⋅

⋅

⋅

⋅

⋅

=

1,6

1,64

1,85

1,65

0,205

215,0940471

1,7

1,71

1,92

1,72

0,205

228,5374251

1,8

1,77

1,98

1,78

0,205

241,980803

1,9

1,82

2,03

1,83

0,205

255,424181

E

śr

 =

208,7625662

   

Obliczamy średnią arytmetyczną z wyznaczonych wielkości E. Wartość ta wynosi:

E

śr

 = 208,7625662 [GPa]

2.4. Wykres wielkości f w funkcji P

0

0,05

0,1

0,15

0,2

0,25

0,3

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9

Błąd obliczeniowy =  (Odchyłka górna + Odchyłka dolna) / 2

Średnia wszystkich E

Odchyłka górna: 66,826682

Odchyłka dolna: 90,652889

Odchyłka średnia: 78,739785

F

[

m

m

]

P [kN]

Błąd obliczeniowy = 78,739785/ 208,7625662 = 0,3771739