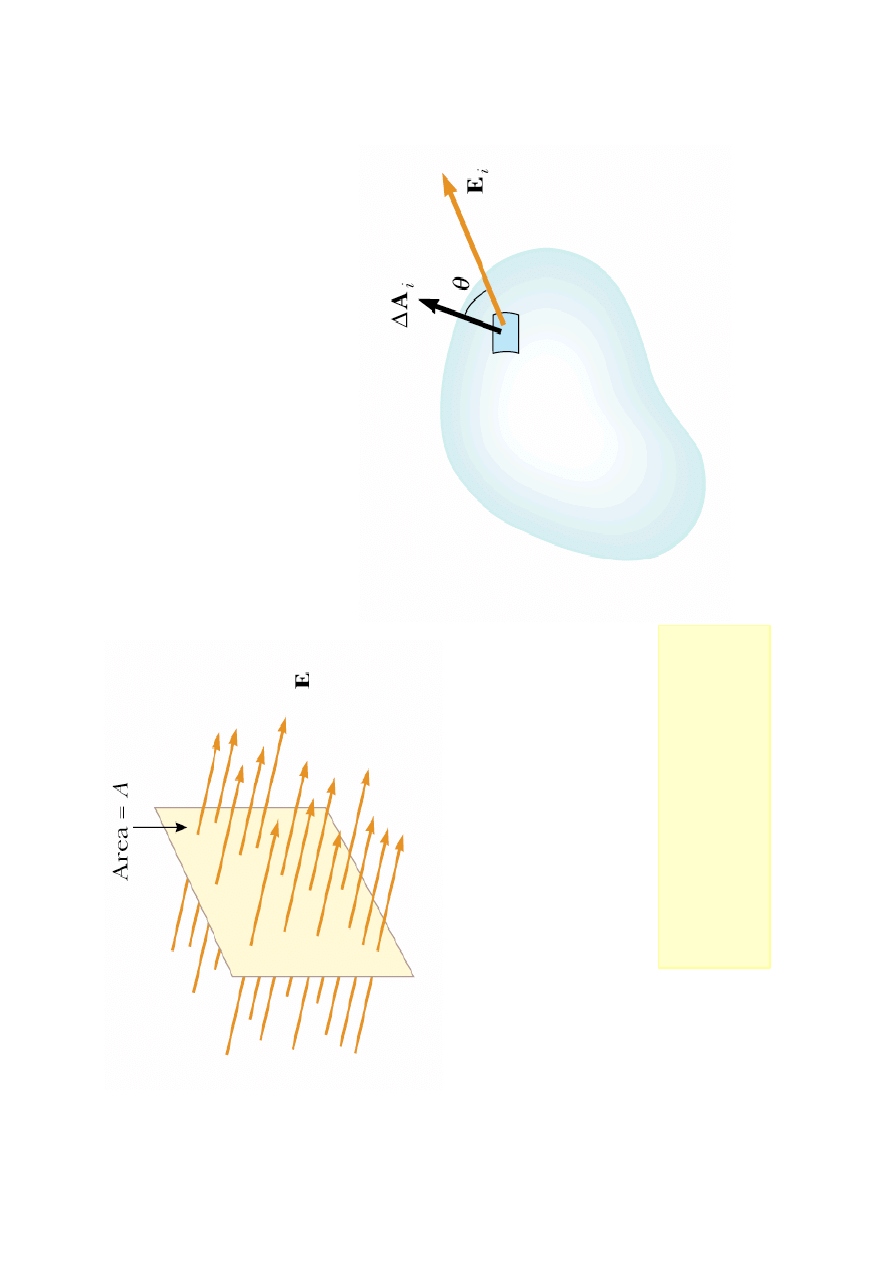
A
E
Φ
E
=
[N
⋅m
2
/C
]
S
tr
um
ie
ń
po
la
e
le
kt
ry
cz
ne
go
j
e
st
pr
op
or
cj
on
al
ny
d
o
li
cz
b
y
li
ni
i
po
la
e
le
kt
ry
cz
ne
go
p
rz
e
ch
od
z
ąc
yc
h
p
rz
e
z
po
w
ie
rz
ch
ni
ę
uo
gó
ln
io
na
d
ef
. s
tr
um
ie
ni
a
S
tr
um
ie
ń
Po
la
E
le
kt
ry
cz
ne
go
i
i
i
i
∆
cos
θ
∆A
E
∆Φ
E
A
E
v
v
⋅
=
=
∫
⋅
=
ia
powierzchn
A
E
r
r
d
Φ
E
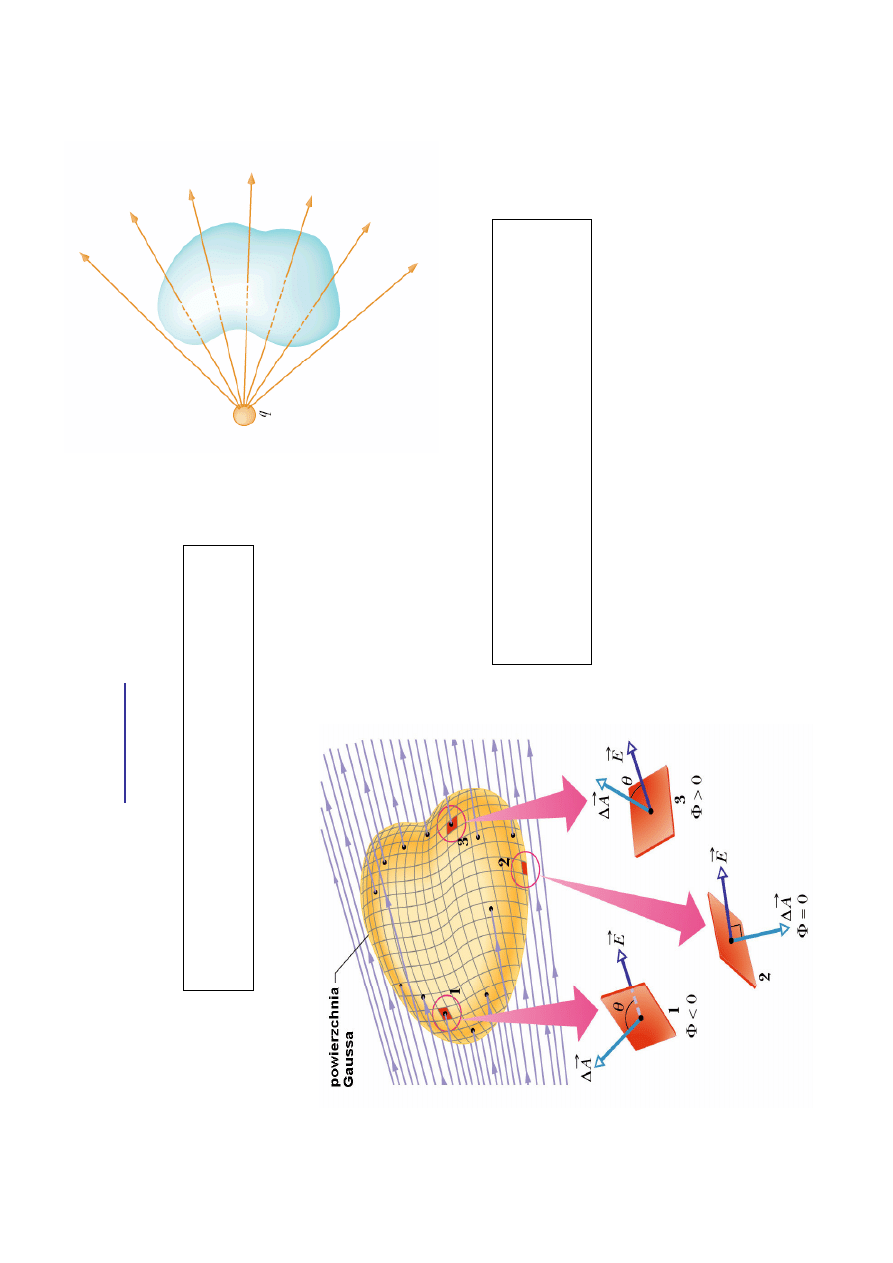
Z
am
kn
ię
ta
p
ow
ie
rz
ch
ni
a
w
ze
w
nę
tr
zn
ym
p
ol
u
(ż
ad
ny
ch
ła
d
un
kó
w
w
ew
ną
tr
z
po
w
ie
rz
ch
ni
)
Pr
zy
kł
ad
:
K
aż
d
a
lin
ia
s
ił
po
la
w
ch
od
zą
ca
d
o
w
nę
tr
za
b
ęd
zi
e
je
r
ów
ni
eż
op
us
zc
za
ć
W
yp
ad
ko
w
y
st
ru
m
ie
ń
pr
ze
z
za
m
kn
ię
tą
po
w
ie
rz
ch
ni
ę
w
ew
ną
tr
z
kt
ór
ej
n
ie
m
a
ła
d
un
kó
w
w
yn
os
i
Z
E
R
O
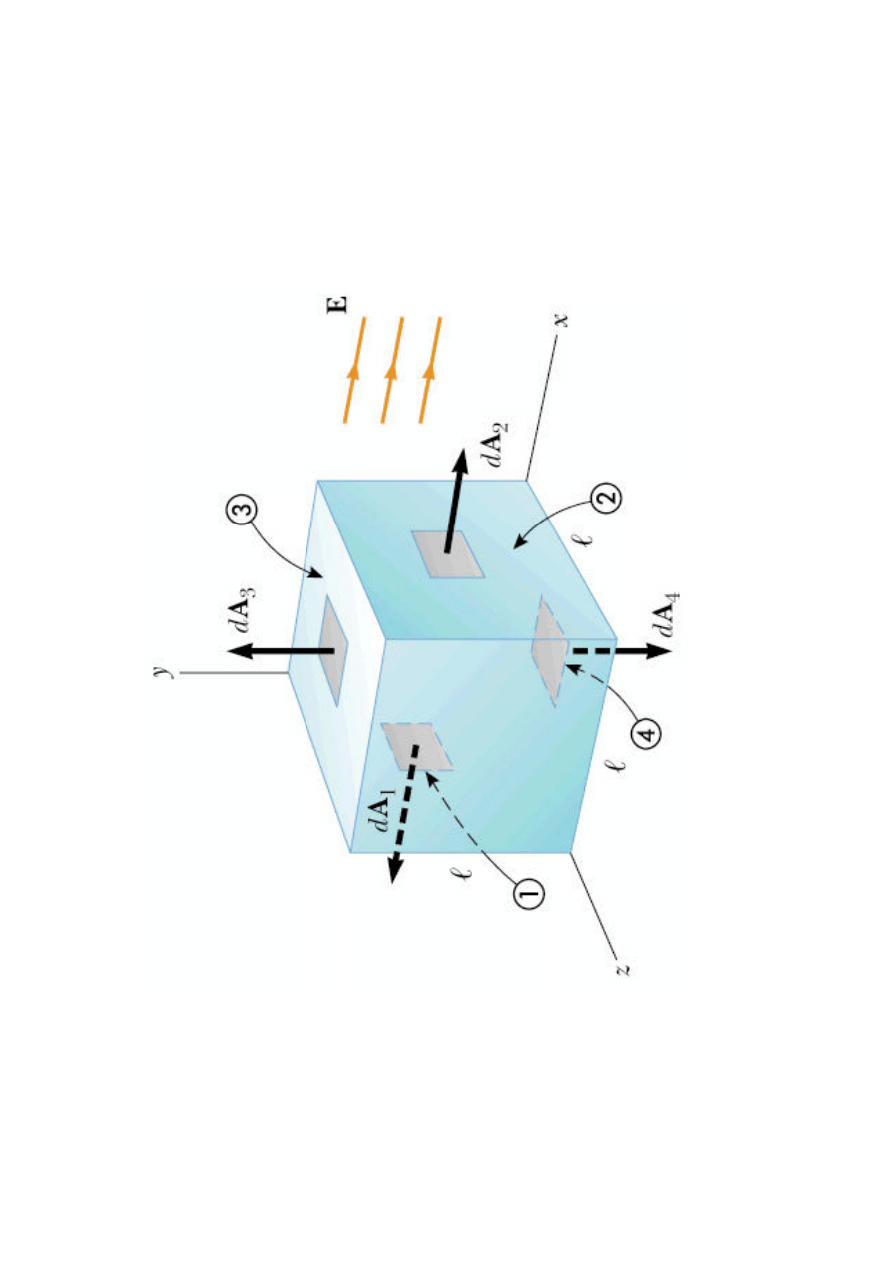
st
ru
m
ie
ń
po
la
e
le
kt
ry
cz
ne
go
p
op
rz
ez
s
ze
śc
ia
n
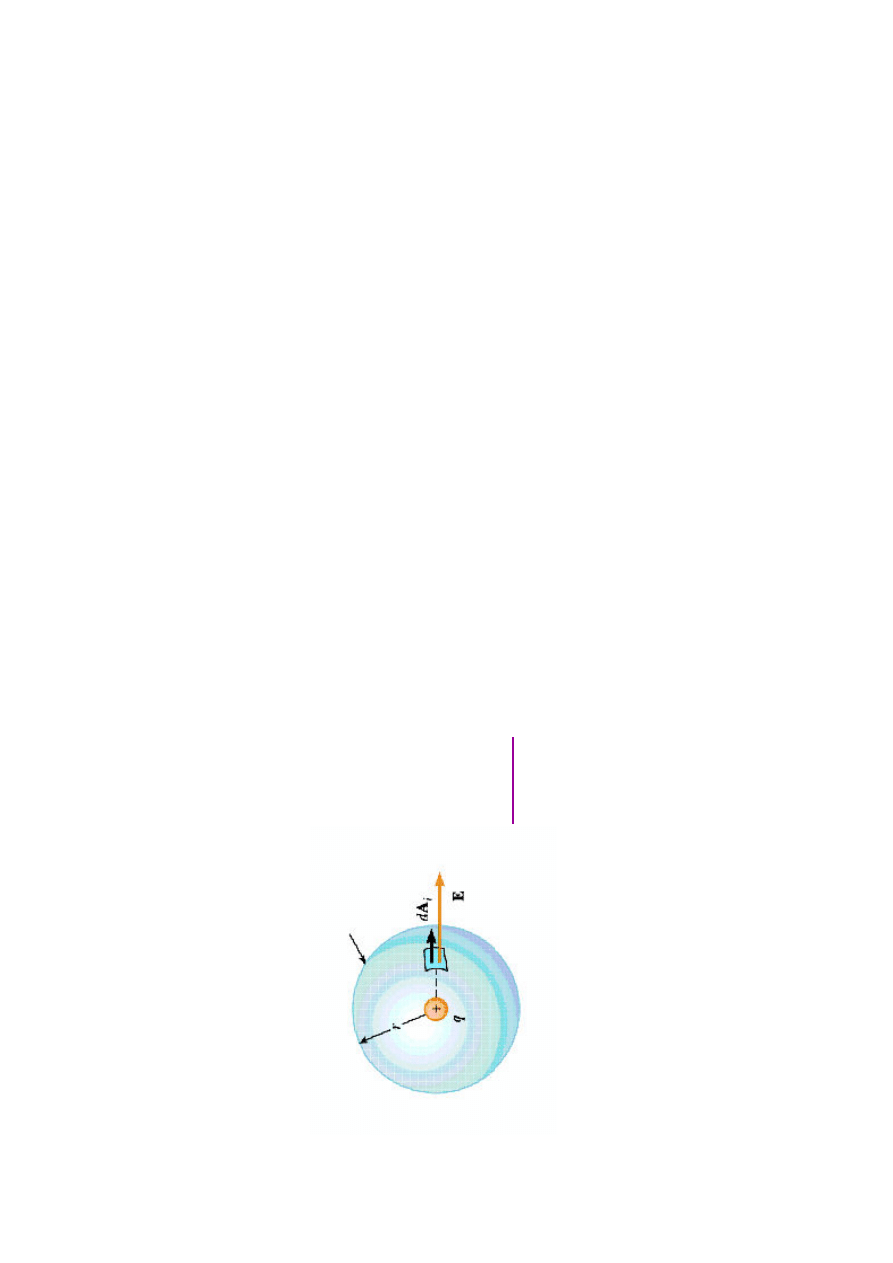
w
e
źm
y
po
je
d
yn
cz
y
ła
d
un
e
k
q
i
ot
oc
zm
y
go
s
ym
e
tr
yc
zn
ie
po
w
ie
rz
ch
ni
ą
sf
e
ry
cz
ną
o
pr
om
ie
ni
u
r
Py
ta
ni
a:
J
ak
s
ię
zm
ie
ni
s
tr
um
ie
ń
je
śl
i
pr
om
ie
ń
sf
e
ry
–z
m
ni
e
js
zy
m
y
o
po
ło
w
ę
?
–z
w
ię
ks
zy
m
y
d
w
uk
ro
tn
ie
?
•
I
le
w
yn
os
i
st
ru
m
ie
ń
po
la
e
le
kt
ry
cz
ne
go
Φ
E
od
ła
d
un
ku
1.
0
C
um
ie
sz
cz
on
e
go
w
c
e
nt
ru
m
p
ow
.
sf
e
ry
cz
ne
j
o
pr
om
ie
ni
u
1.
0
m
?
C
o
b
ęd
zi
e,
j
eś
li
po
w
. z
am
kn
ię
ta
o
ta
cz
a
ła
d
un
ek
(
źr
ód
ło
p
ol
a
)?
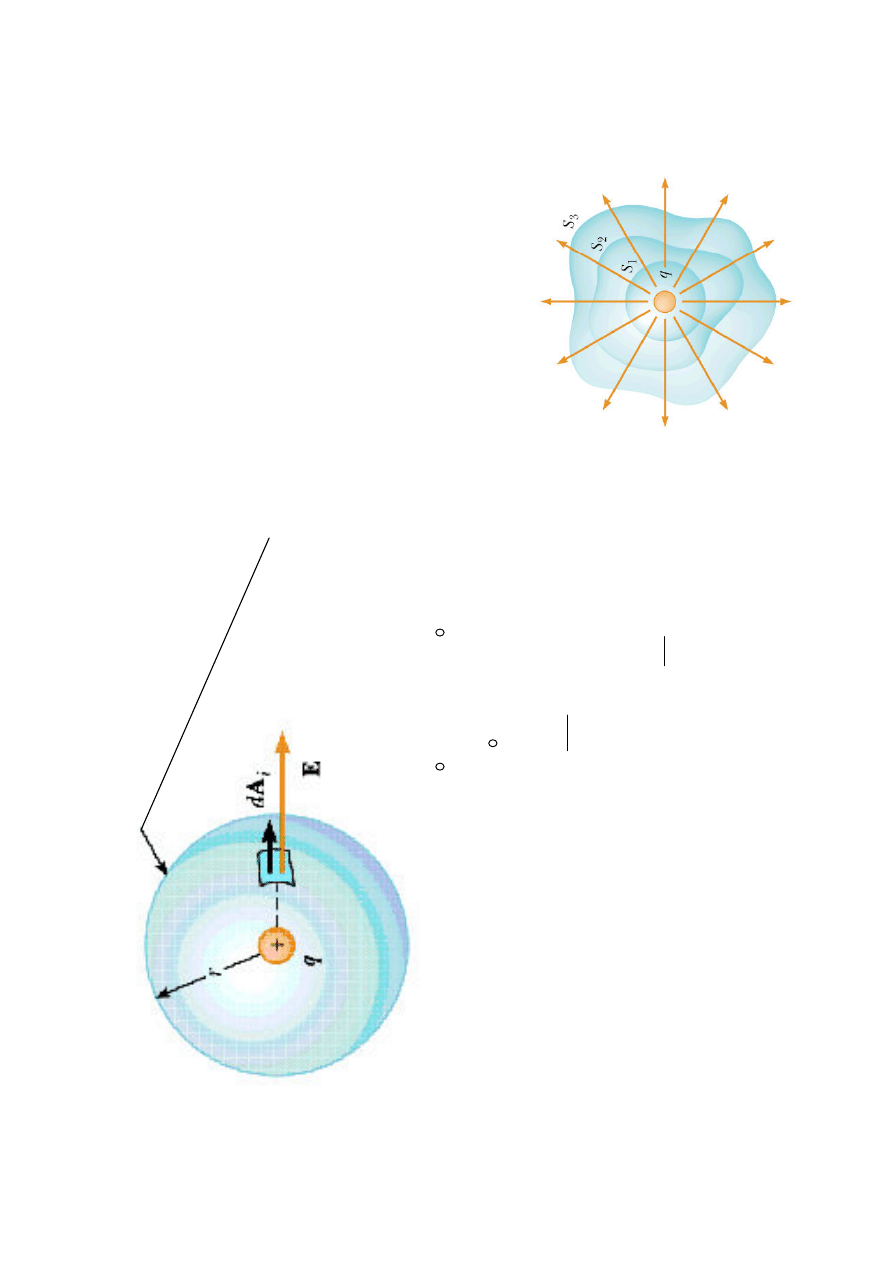
U
og
ól
ni
aj
ąc
n
a
d
ow
ol
ną
po
w
ie
rz
ch
ni
ę
za
m
kn
ię
tą
...
0
E
E
E
ε
q
q
k
4
π
Φ
r
4
π
r
q
k
Φ
dA
E
Φ
dA
E
d
Φ
2
2
=
=
=
=
=
⋅
=
∫
∫
∫
)
(
A
E
E
r
r
..l
ic
z
ym
y
st
ru
m
ie
ń
po
la
e
le
kt
ry
cz
ne
go
w
yp
ły
w
aj
ąc
y
po
pr
ze
z
tę
po
w
ie
rz
ch
ni
ę

Pr
a
w
o
G
a
us
sa
•
Pr
aw
o
G
au
ss
a
w
ią
że
s
tr
um
ie
ń
po
la
e
le
kt
ry
cz
ne
go
,
Φ
E
pr
ze
z
za
m
kn
ię
tą
po
w
ie
rz
ch
ni
ę
(„
ga
us
ow
sk
ą
”)
z
w
yp
ad
ko
w
ym
ła
d
un
ki
e
m
q
w
ew
n
,
kt
ór
y
je
st
z
am
kn
ię
ty
w
e
w
ną
tr
z
te
j
po
w
ie
rz
ch
ni
:
wewn
wewn
E
q
k
4
π
ε
d
Φ
o
q
=
=
⋅
=
∫
A
E
r
r
•
Φ
E
ni
e
z
a
le
ży
od
•
Po
ło
że
ni
a
ła
d
un
kó
w
w
e
w
ną
tr
z
po
w
ie
rz
ch
ni
(
ga
us
ow
sk
ie
j)
.
•
K
sz
ta
łt
u
za
m
kn
ie
te
j
po
w
ie
rz
ch
ni
(
ga
us
ow
sk
ie
j)
.
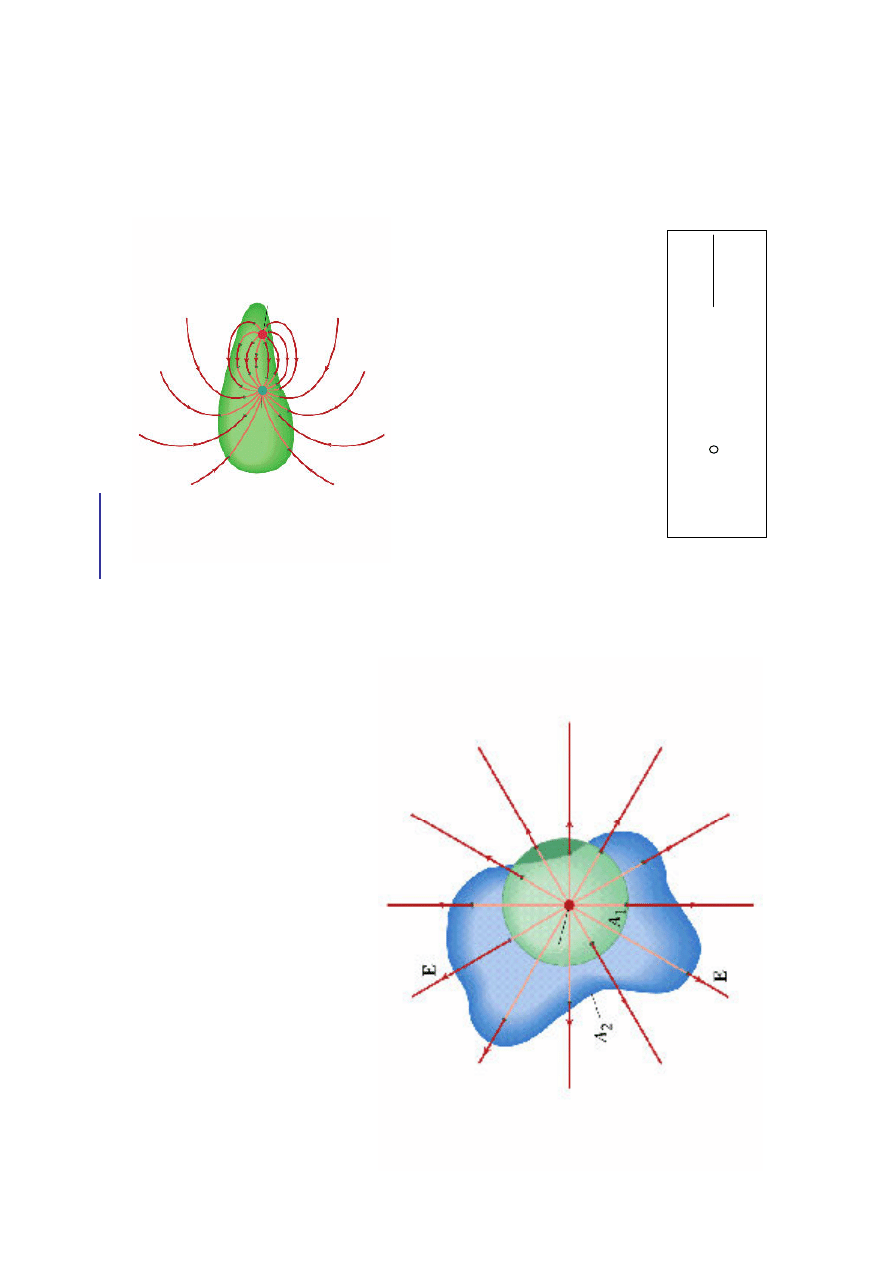
o
wewn
E
ε
q
d
Φ
=
⋅
=
∫
A
E
r
r
Po
w
ie
rz
ch
ni
a
za
m
kn
ię
ta
o
ta
cz
aj
ąc
a
d
ow
ol
ne
ła
d
un
ki
q
W
yp
ad
ko
w
y
st
ru
m
ie
ń
po
la
e
le
kt
ry
cz
ne
go
n
ie
za
le
ż
y
an
i
od
k
sz
ta
łt
u
po
w
ie
rz
ch
ni
z
a
m
y
k
a
ją
ce
j
go
,
an
i
od
r
oz
m
ie
sz
cz
e
ni
a
ł
a
d
un
k
u(
ów
)
w
e
w
ną
tr
z
te
j
po
w
ie
rz
ch
ni
.
-
2
q
+
q
A
T
a
po
w
ie
rz
ch
ni
a o
ta
cz
a w
yp
ad
ko
w
y
ła
d
un
ek
q
w
ew
n
=
(-
2
q
)
+
(+
q
)
C
zy
m
j
e
st
p
ra
w
o
G
a
us
sa
?
Pr
aw
o
G
au
ss
a
je
st
p
o
pr
os
tu
c
za
sa
m
i
ła
tw
ie
j
uż
yć
d
o
ok
re
śl
e
ni
a
an
al
it
yc
zn
e
j
fo
rm
y
po
la
e
le
kt
ry
cz
ne
go
ni
ż
pr
aw
o
C
ou
lo
m
b
a,
s
zc
ze
gó
ln
ie
j
e
śl
i
m
am
y
d
o
cz
yn
ie
ni
a
b
ar
d
zo
s
ym
e
tr
yc
zn
ym
ro
zk
ła
d
e
m
ła
d
un
kó
w
(
sy
m
.
sf
e
ry
cz
na
,
w
al
co
w
a,
p
ła
sz
cz
yz
na
s
ym
.,
sy
m
. l
in
io
w
a)
.
Pr
aw
o
G
au
ss
a
ni
e
m
ów
i
na
m
n
ic
n
ow
e
go
.
N
ie
j
e
st
n
ow
ym
pr
aw
e
m
f
iz
yk
i,
l
e
cz
j
e
d
yn
ie
n
ow
ym
s
po
so
b
e
m
w
yr
aż
en
ia
pr
aw
a
C
ou
lo
m
b
a
S
to
su
ją
c
pr
a
w
o
G
a
us
sa
•
m
am
y
m
oż
li
w
oś
ć
w
yb
or
u
d
og
od
ne
j
d
o
ob
li
cz
e
ń
po
w
ie
rz
ch
ni
za
m
kn
ię
te
j
(p
ow
.
G
a
us
ow
sk
ie
j)
.
•
na
jw
yg
od
ni
e
j,
j
e
śl
i
po
w
ie
rz
ch
ni
a
ga
us
ow
sk
a
od
po
w
ia
d
a
sy
m
e
tr
ii
pr
ob
le
m
u.
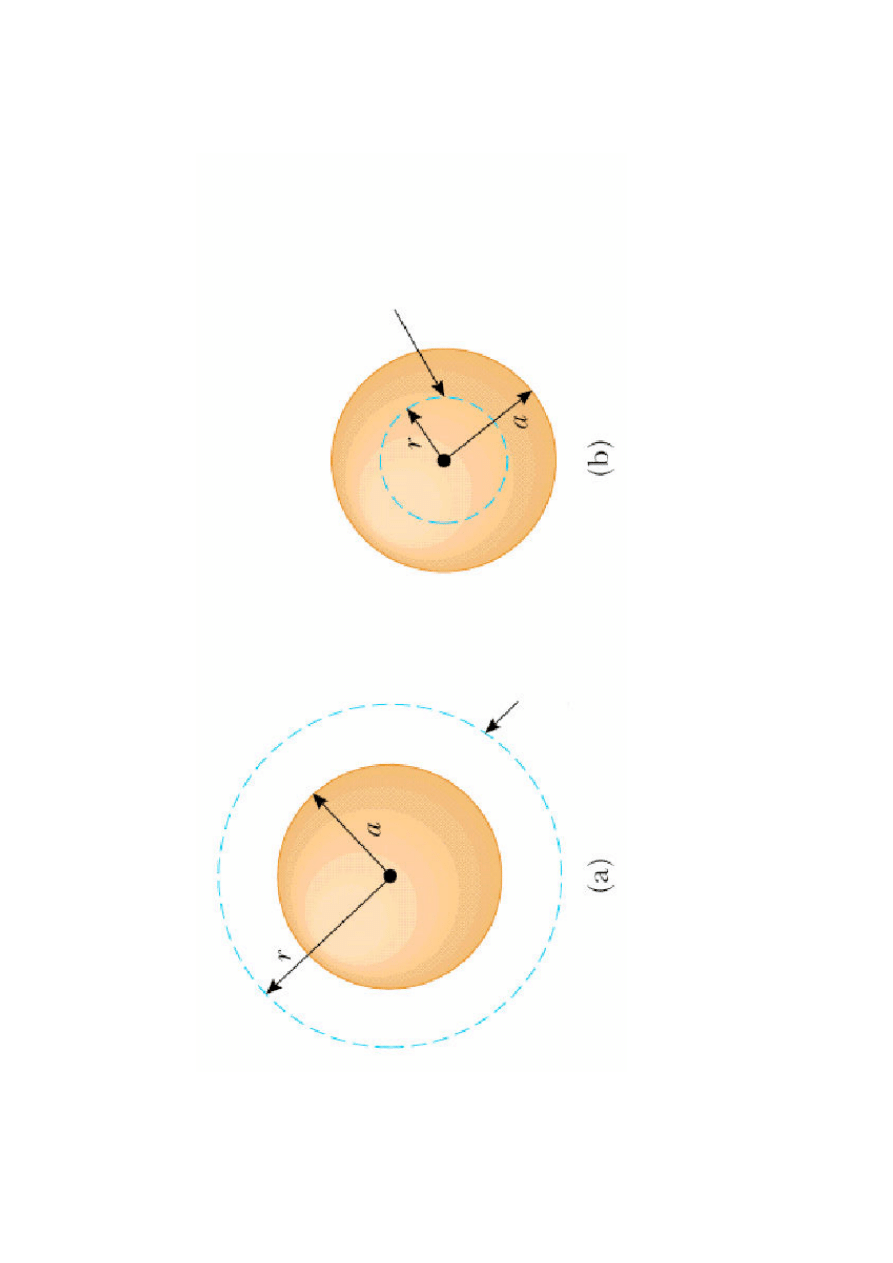
Pr
zy
kł
ad
:
sf
er
yc
zn
e
sy
m
et
ry
cz
ny
r
oz
kł
ad
ła
d
un
ku
p
o
w
.
G
au
ss
a
(s
fe
ra
)
p
o
w
.
G
au
ss
a
(s
fe
ra
)
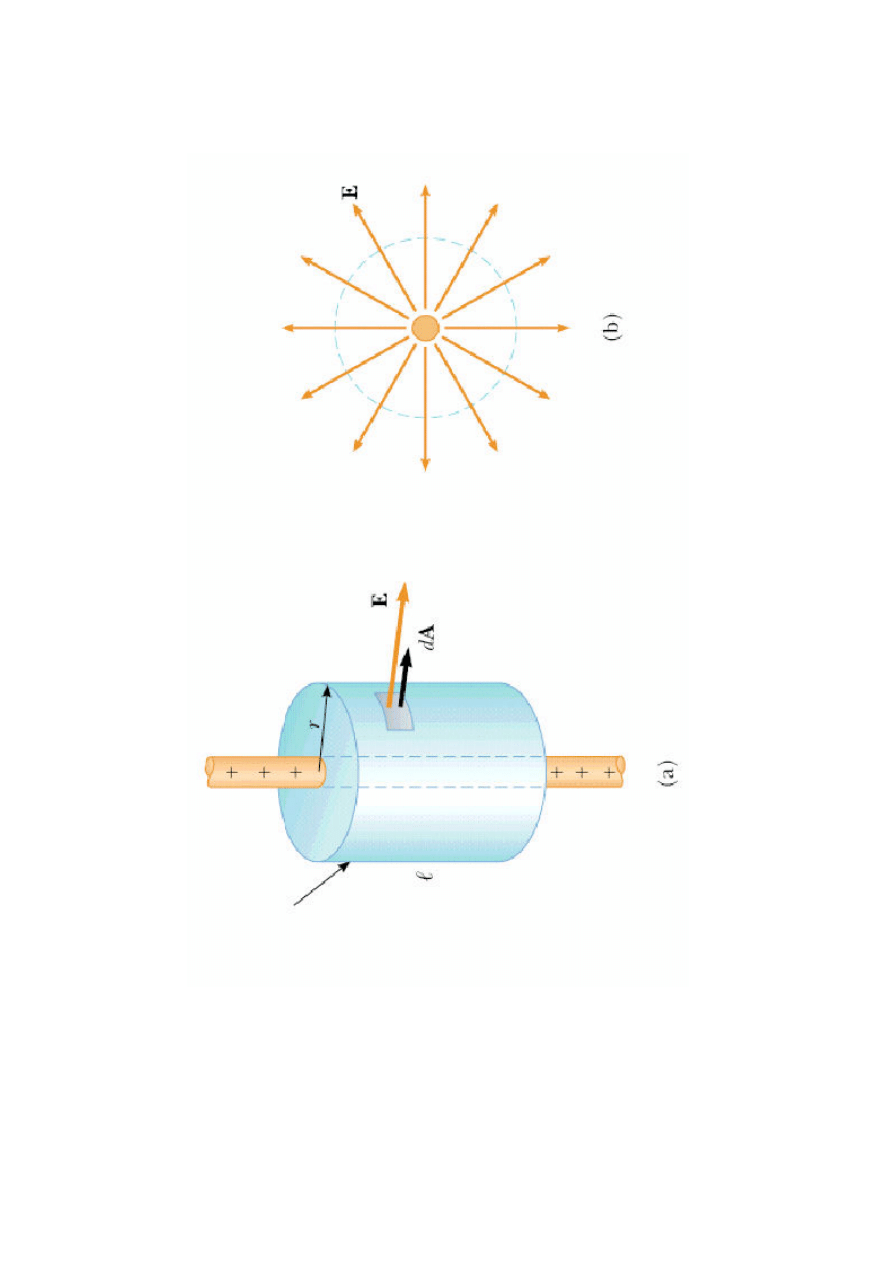
Pr
zy
kł
ad
:
cy
lin
d
ry
cz
ni
e
sy
m
et
ry
cz
ny
r
oz
kł
ad
ła
d
un
ku
p
o
w
ie
rz
ch
n
ia
G
au
ss
a
(c
y
li
n
d
er
)
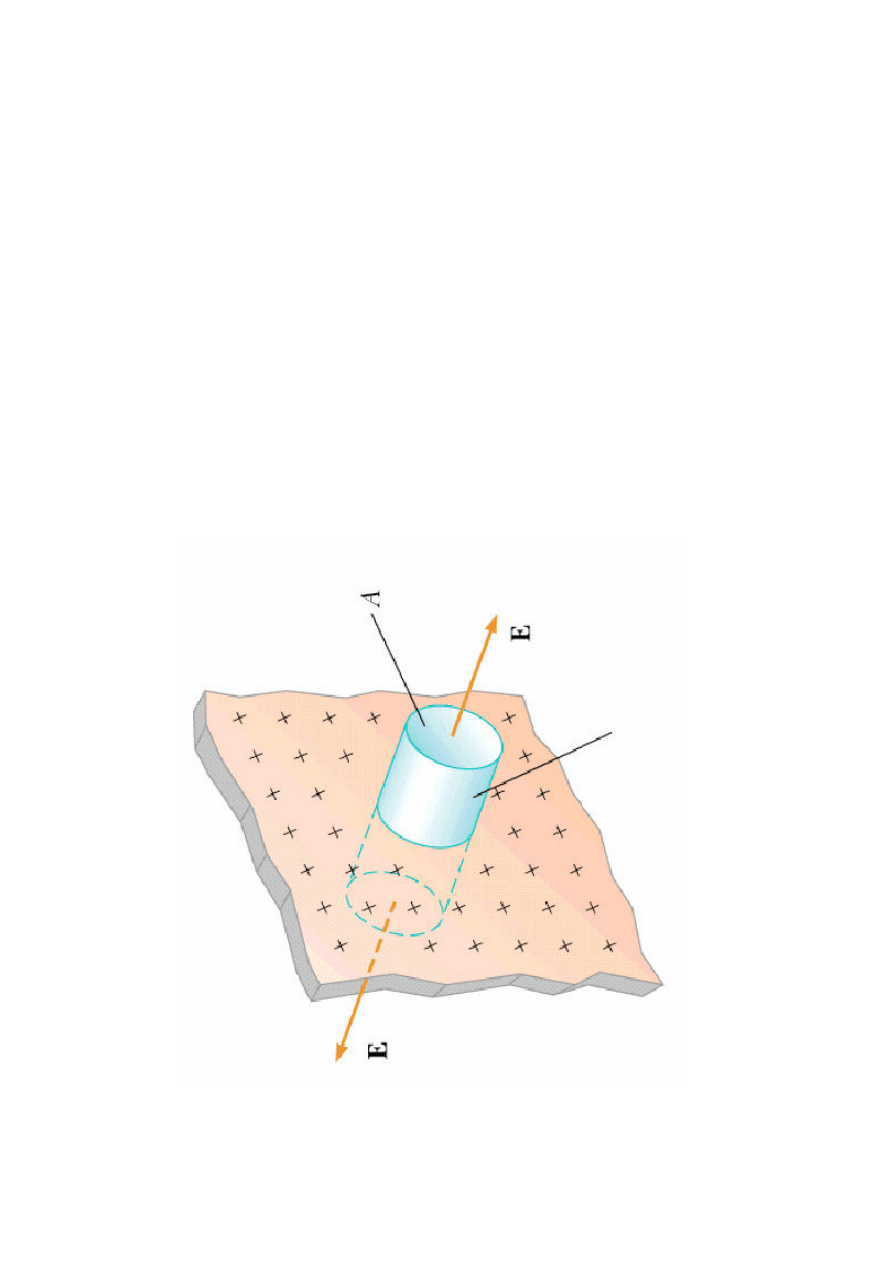
Pr
zy
kł
ad
:
na
ła
d
ow
an
a
pł
as
zc
zy
zn
a
iz
ol
at
or
a
p
o
w
.
G
au
ss
a
(c
y
li
n
d
ry
cz
n
a)
πσ
2
=
A
E
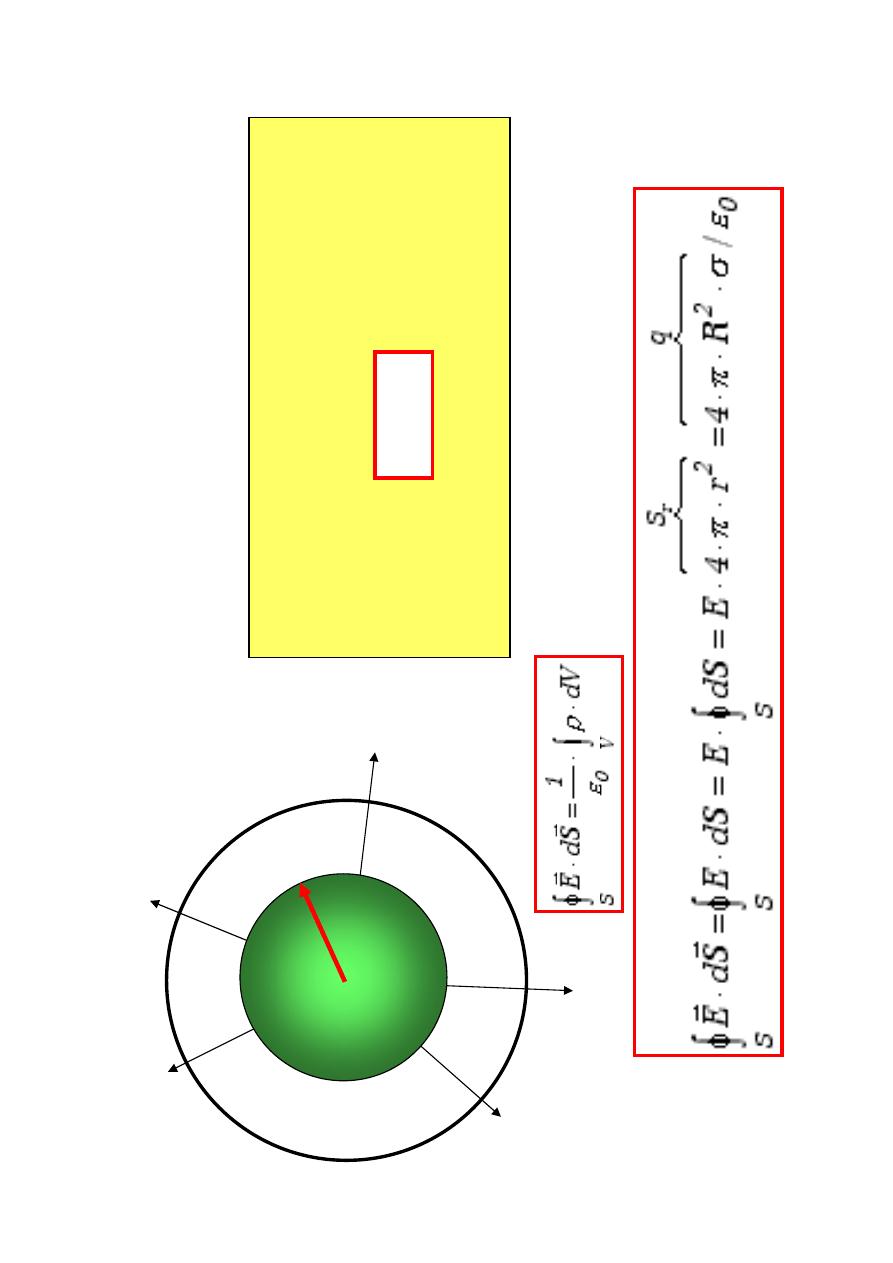
J
e
d
n
o
ro
d
n
ie
n
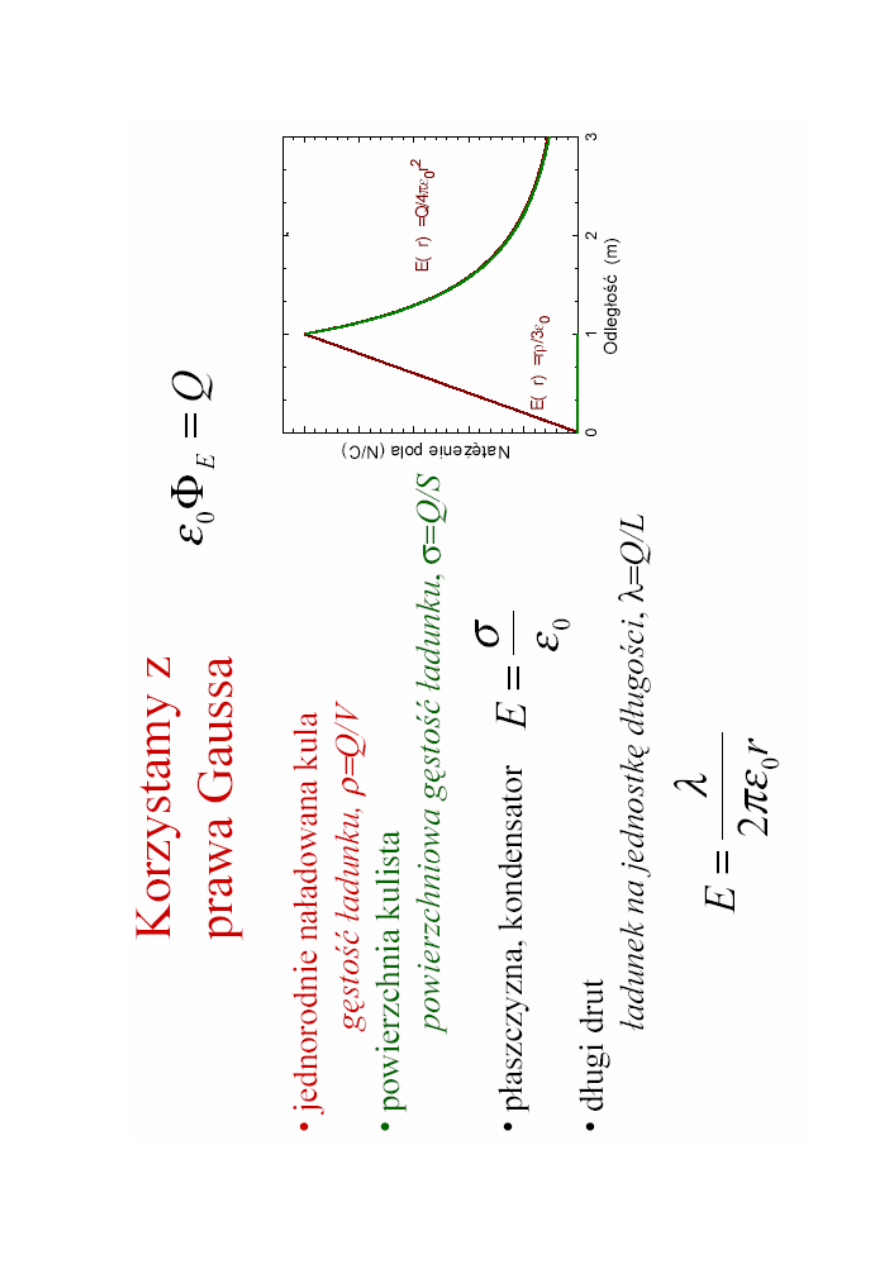
a
ła
d
o
w
a
n
a
p
o
w
ie
rz
c
h
n
ia
k
u
li
R
G
ę
s
to
ś
ć
p
o
w
ie
rz
c
h
n
io
w
a
σσσσ
D
la
p
u
n
k
tó
w
n
a
z
e
w
n
ą
tr
z
s
fe
ry
:
D
la
p
u
n
k
tó
w
w
e
w
n
ą
tr
z
s
fe
ry
:
E
=
0
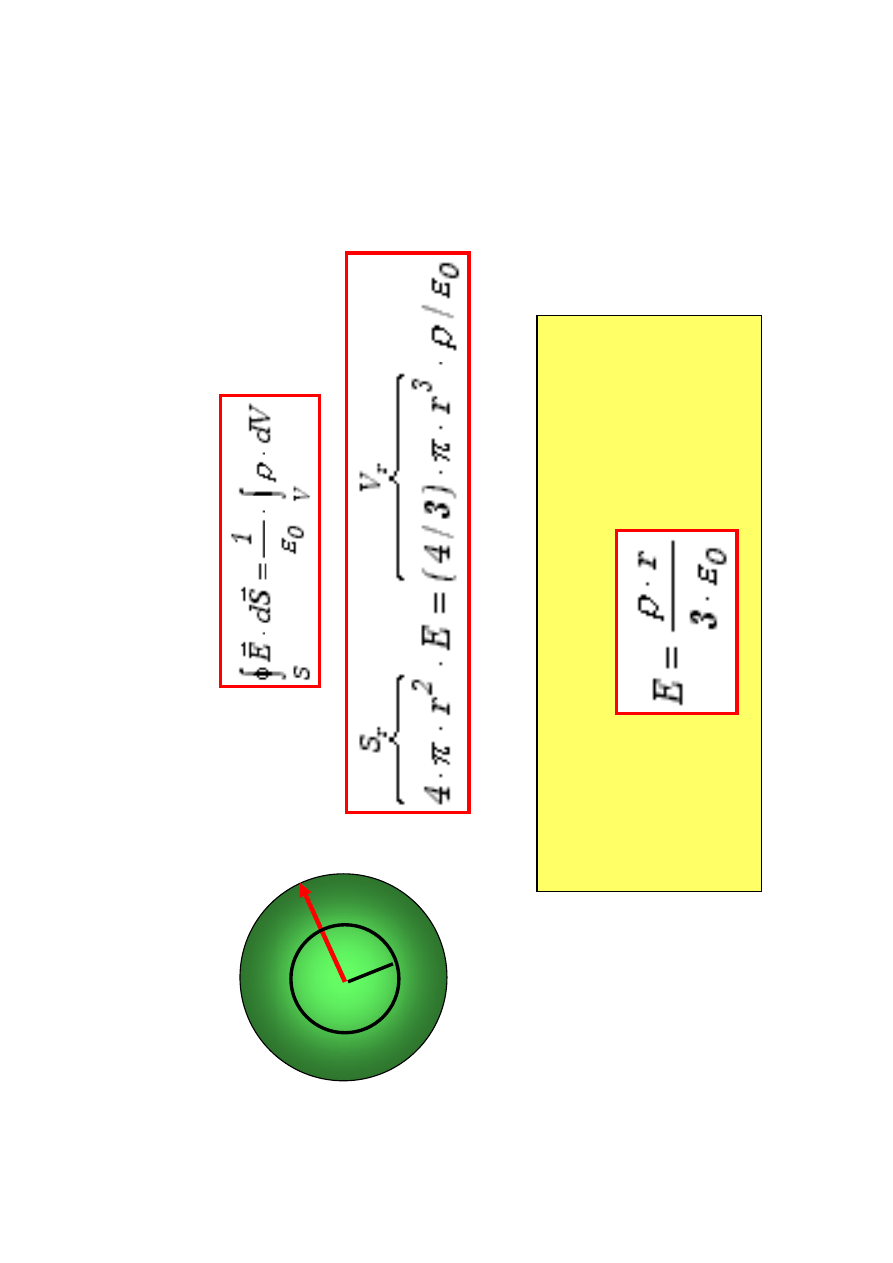
J
e
d
n
o
ro
d
n
ie
n
a
ła
d
o
w
a
n
a
k
u
la
R
G
ę
s
to
ś
ć
o
b
ję
to
ś
c
io
w
a
ρρρρ
D
la
p
u
n
k
tó
w
w
e
w
n
ą
tr
z
k
u
li
:
r
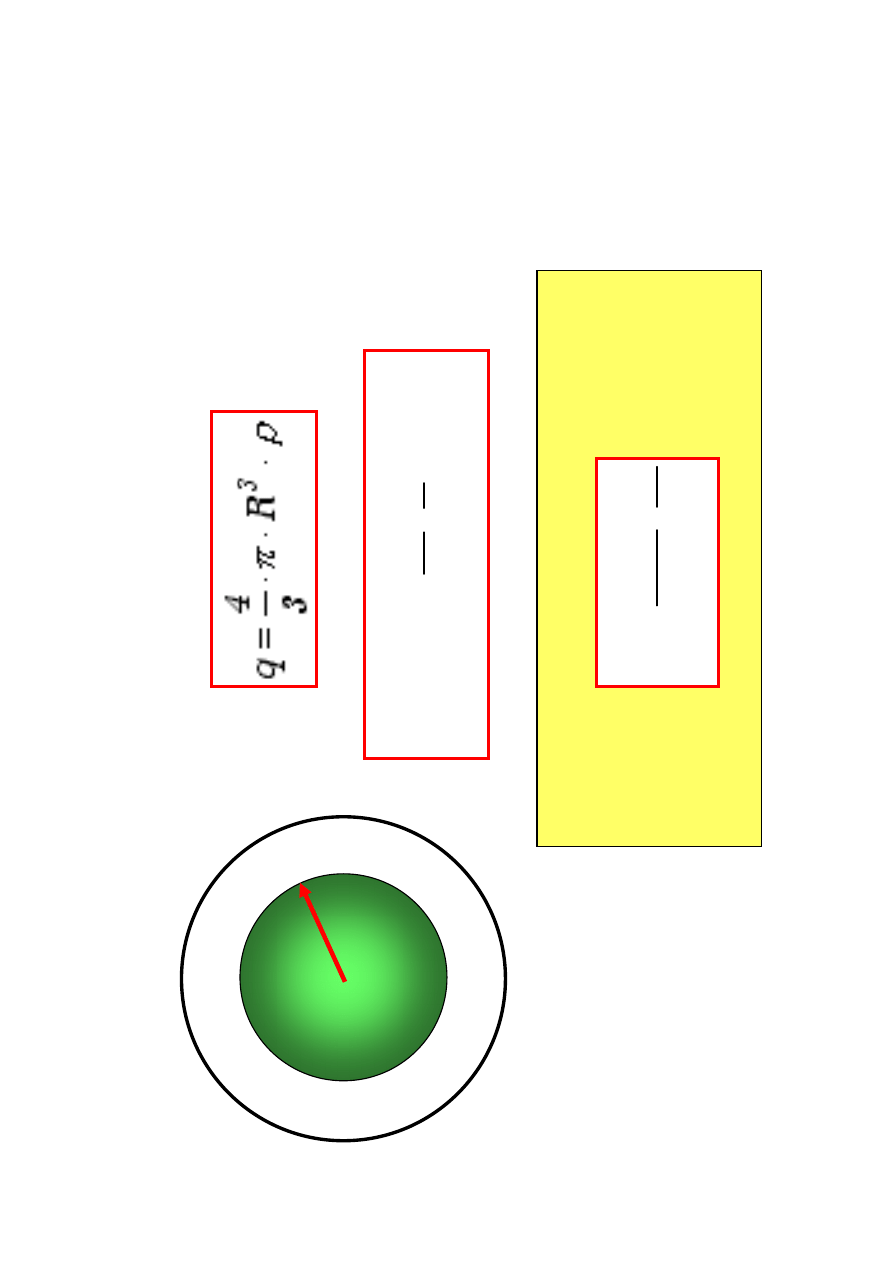
J
e
d
n
o
ro
d
n
ie
n
a
ła
d
o
w
a
n
a
k
u
la
R
ρρρρ
ππππ
εεεε
ππππ
⋅⋅⋅⋅
⋅⋅⋅⋅
====
⋅⋅⋅⋅
3
0
2
3
4
1
4
R
r
E
D
la
p
u
n
k
tó
w
n
a
z
e
w
n
ą
tr
z
k
u
li
:
2
0
3
1
3
r
R
E
⋅⋅⋅⋅
====
εεεε
ρρρρ
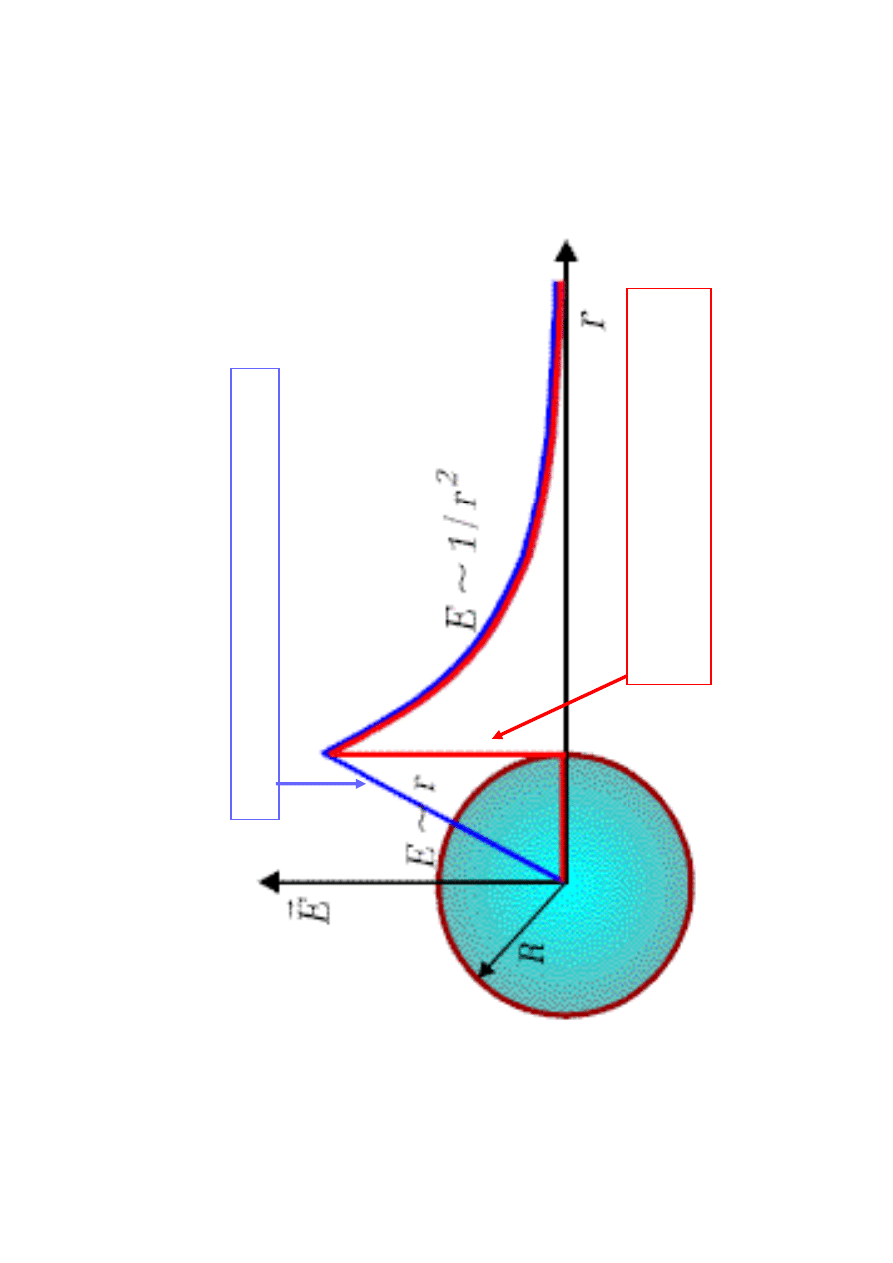
P
o
le
ł
a
d
u
n
k
u
s
fe
ry
c
z
n
ie
-s
y
m
e
tr
y
c
z
n
e
g
o
J
e
d
n
o
ro
d
n
ie
n
a
ła
d
o
w
a
n
a
k
u
la
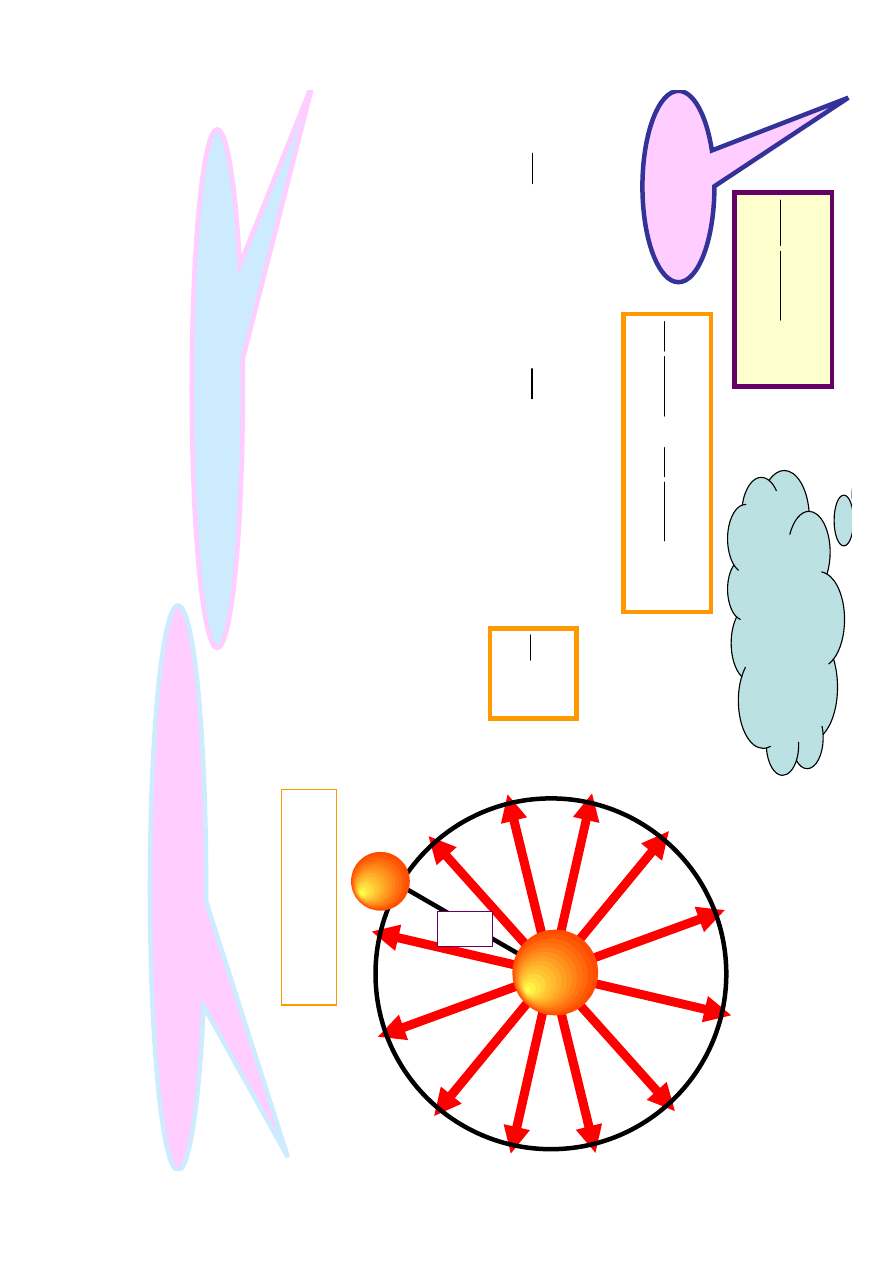
J
e
d
n
o
ro
d
n
ie
n
a
ła
d
o
w
a
n
a
p
o
w
ie
rz
c
h
n
ia
k
u
li
O
r
an
y
!
N
ie
p
a
m
ię
ta
m
p
.
C
o
u
lo
m
b
a!
0
ε
Q
Φ
=
N
ie
m
art
w
s
ię
,
ja
p
am
ię
ta
m
p
.
G
au
ss
a!
0
|
|
ε
Q
A
E
=
=
Φ
0
2
4|
|
ε
π
Q
r
E
=
=
al
e
prz
ec
ie
ż.
..
F
=
q
E
2
r
ε
4
π
1
F
0
=
C
o
u
lo
m
b
!
2
0
0
2
4
1
4
1
|
|
r
Q
Q
r
E
πε
ε
π
=
=
cz
yl
i..
.
ro
zw
aż
am
y
po
w
.
sfe
ry
cz
n
ą
w
o
k
ó
ł
ła
d
u
n
k
u
Q
o
pro
m
ie
n
iu
r
ró
w
n
y
m
o
d
le
g
ło
śc
i
m
ię
d
zy
q
i
Q
:
r
Q
q
E
⊥
A
w
sz
ęd
zi
e
C
zy
r
ze
cz
yw
iś
ci
e
p
.
G
a
us
sa
je
st
r
ów
no
w
aż
ne
p
.
C
ou
lo
m
b
a
?
Q
0
ε
Q
Φ
zewn
=
2
0
4
1
|
|
r
Q
E
πε
=
0
E
=
N
a
z
ew
n
ą
tr
z
..
.w
ię
c
ja
k
p
o
p
rz
ed
n
io
W
ew
n
ą
tr
z
0
Φ
wewn
=
ła
d
u
n
ek
w
ew
n
ąt
rz
po
w
.
sfe
ry
cz
n
ej
=
0
Pr
zy
kł
ad
z
as
to
so
w
an
ia
p
. G
au
ss
a:
J
a
k
w
y
g
lą
d
a
p
o
le
e
le
k
tr
y
c
z
n
e
w
p
o
b
liż
u
n
a
ła
d
o
w
a
n
e
j
p
o
w
ło
k
i
k
u
lis
te
j?
zewn
Φ
P
o
n
o
w
n
ie
ro
zw
aż
am
po
w
.
sfe
ry
cz
n
ą
w
sp
ó
łś
ro
d
k
o
w
ą
z
n
ał
ad
o
w
an
ą
ła
d
u
n
k
ie
m
Q
po
w
ło
k
ą
k
u
li
st
ą:
wewn
Φ

•
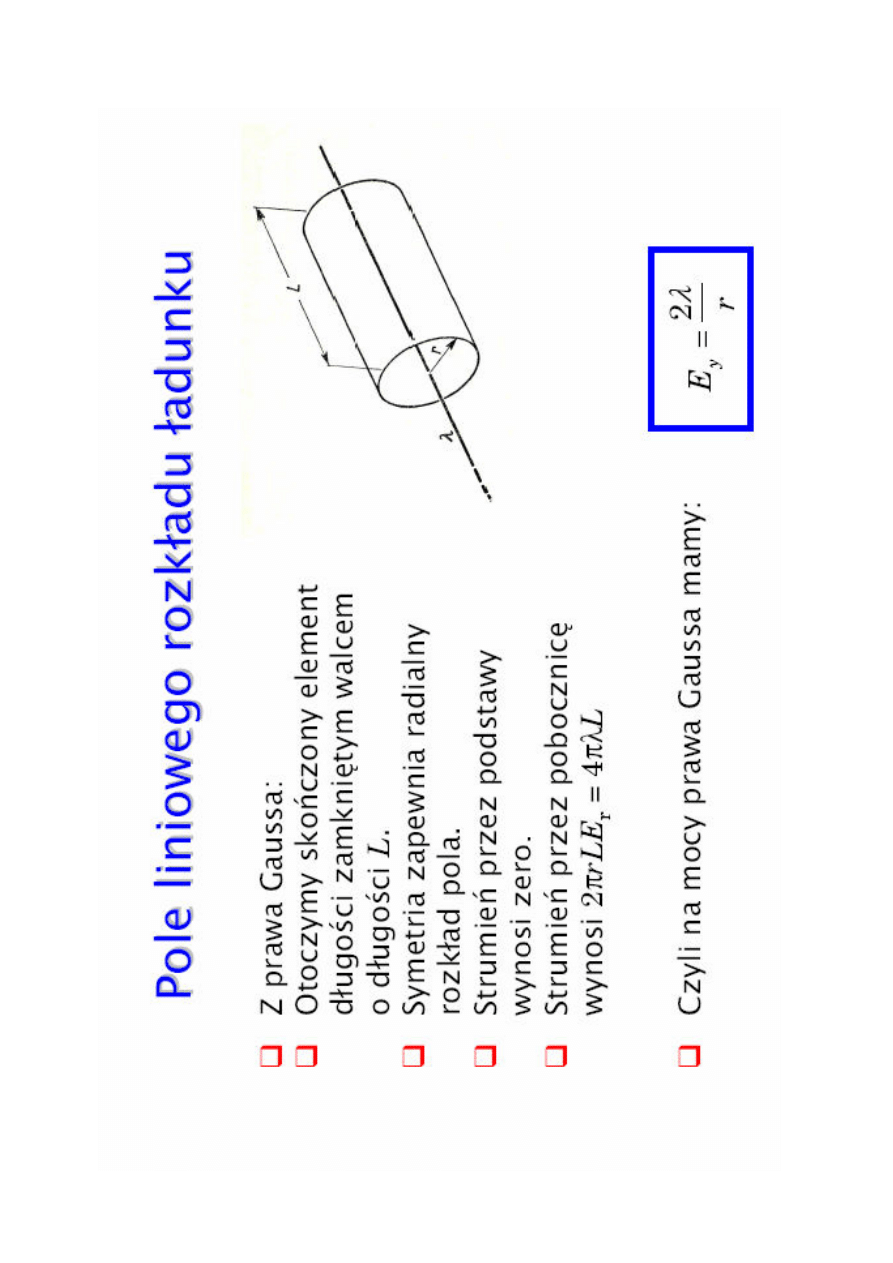
S
tr
um
ie
ń
po
pr
ze
z
ze
w
nę
tr
zn
e
d
e
nk
o
cy
li
nd
ra
A
w
yn
os
i
E
A
,
po
ni
e
w
aż
E
⊥
A
(p
an
uj
e
ró
w
no
w
ag
a
).
•
W
k
on
se
kw
e
nc
ji
,
st
ru
m
ie
ń
pr
ze
z
śc
ia
nk
i
b
oc
zn
e
c
yl
in
d
ra
j
e
st
Z
E
R
O
•
Po
le
w
e
w
ną
tr
z
pr
ze
w
od
ni
ka
j
e
st
Z
E
R
O
(ł
ad
un
ki
w
yp
ch
nę
ły
s
ię
na
p
ow
ie
rz
ch
ni
ę
),
w
ię
c
i
st
ru
m
ie
ń
pr
ze
z
po
w
ie
rz
ch
ni
ę
cy
li
nd
ra
w
e
w
ną
tr
z
pr
ze
w
od
ni
ka
je
st
Z
E
R
O
o
o
o
o
E
ε
σ
ε
A
q
A
ε
q
E
ε
q
EA
d
Φ
wewn
wewn
wewn
=
=
=
=
=
=
∫
A
E
r
r
Pr
ze
w
od
ni
ki
a
p
ra
w
o
G
a
us
sa
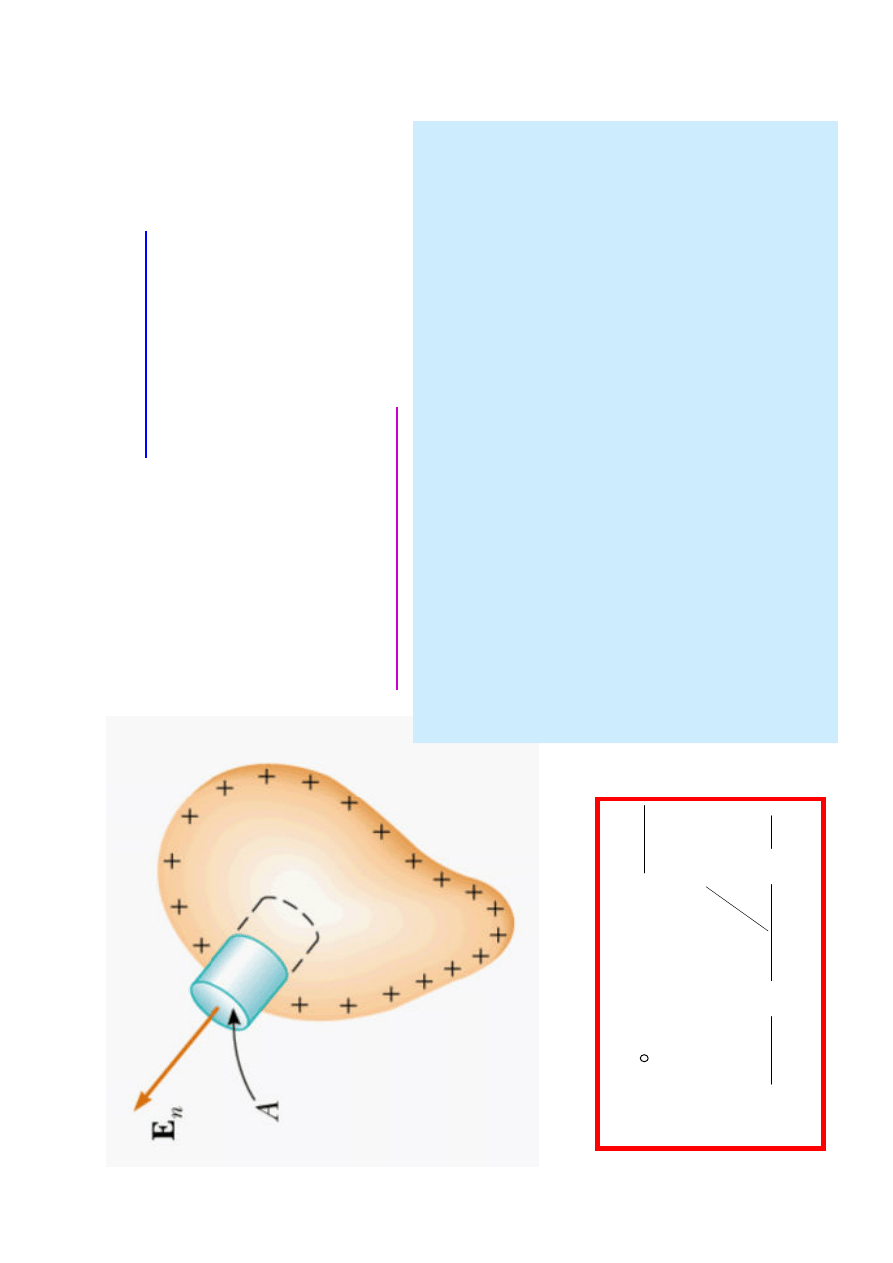
•
W
w
ar
un
ka
ch
r
ów
no
w
ag
i
e
le
kt
ro
st
at
yc
zn
e
j
po
le
e
le
kt
ry
cz
ne
w
e
w
ną
tr
z
pr
ze
w
od
ni
ka
j
e
st
Z
E
R
O
•
Ł
ad
un
e
k
w
yp
ad
ko
w
y,
j
e
śl
i
je
st
,
to
z
na
jd
uj
e
si
ę
na
z
e
w
nę
tr
zn
e
j
po
w
ie
rz
ch
ni
pr
ze
w
od
ni
ka
.
•
Po
le
e
le
kt
ry
cz
ne
w
b
ez
po
śr
e
d
ni
e
j
b
li
sk
oś
ci
pr
ze
w
od
ni
ka
j
e
st
p
ro
st
op
ad
łe
d
o
je
go
po
w
ie
rz
ch
ni
i
p
ro
po
rc
jo
na
ln
e
d
o
gę
st
oś
ci
po
w
ie
rz
ch
ni
ow
e
j
ła
d
un
ku
.
•
G
ę
st
oś
ć
ła
d
un
ku
j
e
st
n
aj
w
ię
ks
za
w
p
ob
li
żu
ob
sz
ar
ów
p
ow
ie
rz
ch
ni
o
n
aj
m
ni
e
js
zy
m
pr
om
ie
ni
u
kr
zy
w
iz
ny
.

Wyszukiwarka
Podobne podstrony:
Zeszyty Dla Elektryk w cz2
Praktyczny kurs elektroniki cz2
Zeszyty Dla Elektryk w cz2
Praktyczny kurs elektroniki cz2
GSM w elektronice cz2
cw2 elektr aparat w lab metrol cz2
Cwiczenia cz2 Z1 struktura elektronowa i rozbudowa powłok treść zadań
Napęd Elektryczny wykład
Podstawy elektroniki i miernictwa2
elektryczna implementacja systemu binarnego
urządzenia elektrotermiczn
Podstawy elektroniki i energoelektroniki prezentacja ppt
Elektryczne pojazdy trakcyjne
elektrofizjologia serca
Zakażenia grzybicze skóry cz2
więcej podobnych podstron