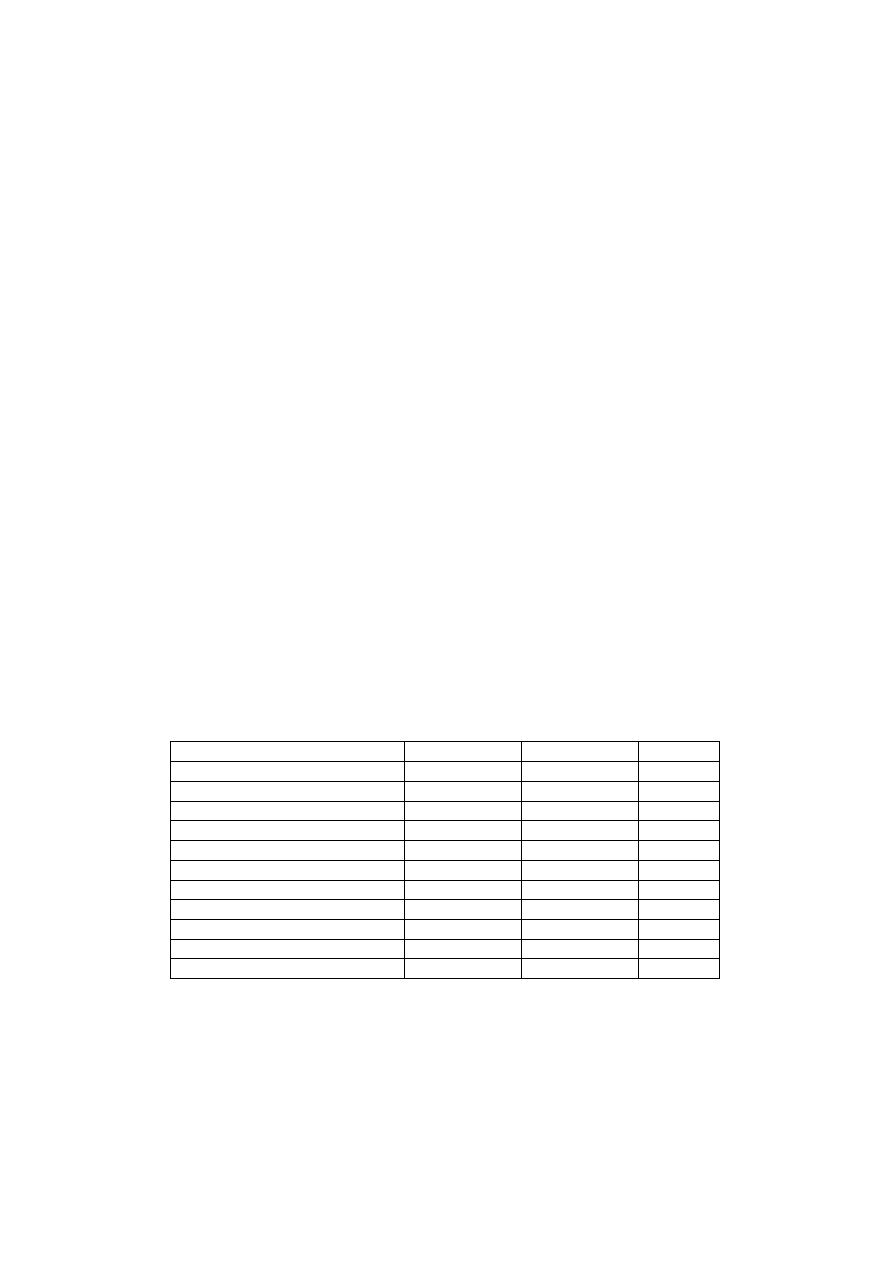
P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

1

WSTĘP

1. Sygnały i obwody

1.1. Klasyfikacja sygnałów
1.2. Opis albo reprezentacja sygnałów.
a) reprezentacji w dziedzinie (w domenie) czasu - przebieg (wykres w funkcji

czasu); mówimy

b) reprezentacji w dziedzinie (w domenie) częstotliwości - widmo amplitudy i

widmo fazy; mówimy o opisie widmowym

c) reprezentacja statystyczna
ad.a). Przebieg charakteryzują : kształt (sinusoidalny, piłokształtny, prostokątny,
wykładniczy itd. i opisujące go parametry), wartości chwilowe, powtarzalność czy
też nie, itp.; Z kolei kształt sygnału można opisać za pomocą parametrów, np.
sinusoidalny: amplituda, częstotliwość, faza początkowa, tłumienie, przesunięcie –
offset, wartość skuteczna itd.),
ad.b)

Opis widmowy sygnału jest w ogólnym przypadku zespoloną funkcją

częstotliwości i opiera się na przekształceniu Fouriera. Widmem sygnału jest zbiór
prostych drgań harmonicznych powstałych z rozkładu sygnału.
ad.c)
Opisuje się je też za pomocą właściwości statystycznych: średnia, średnia moc,
gęstość prawdopodobieństwa, rozkład (np. normalny Gaussa).

----------------------------------------------------------------------------------------------------

Tablica. Klasyfikacja zakresów częstotliwości podana przez Institute of Electrical and
Electronic Engineers (IEEE):

Nazwa zakresu

Częstotliwość

Długość fali

ELF (Extreme Low Frequency)

30-300 Hz

10000-1000 km

VF (Voice Frequency)

300-3000 Hz

1000-100 km

VLF (Very Low Frequency)

3-30kHz

100-10 km

LF (Low Frequency)

30-300 kHz

10-1 km

MF (Medium Frequency)

300-3000 kHz

1-0.1 km

HF (High Frequency)

3-30 MHz

100-10 m

VHF (Very High Frequency)

30-300 MHz

10-1 m

TV

UHF (Ultra High Frequency)

300-3000 MHz 100-10 cm

TV

SHF (Super High Frequency)

3-30 GHz

10-1 cm

EHF (Extreme High Frequency)

30-300 GHz

1-0.1 cm

Submilimeter wave

300-3000GHz

1-0.1 mm

W praktyce funkcjonuje uproszczony podział częstotliwości na fale radiowe (RF) do 4
GHz i mikrofale (MW) (systemy radarowe) – powyżej 4 GHz.

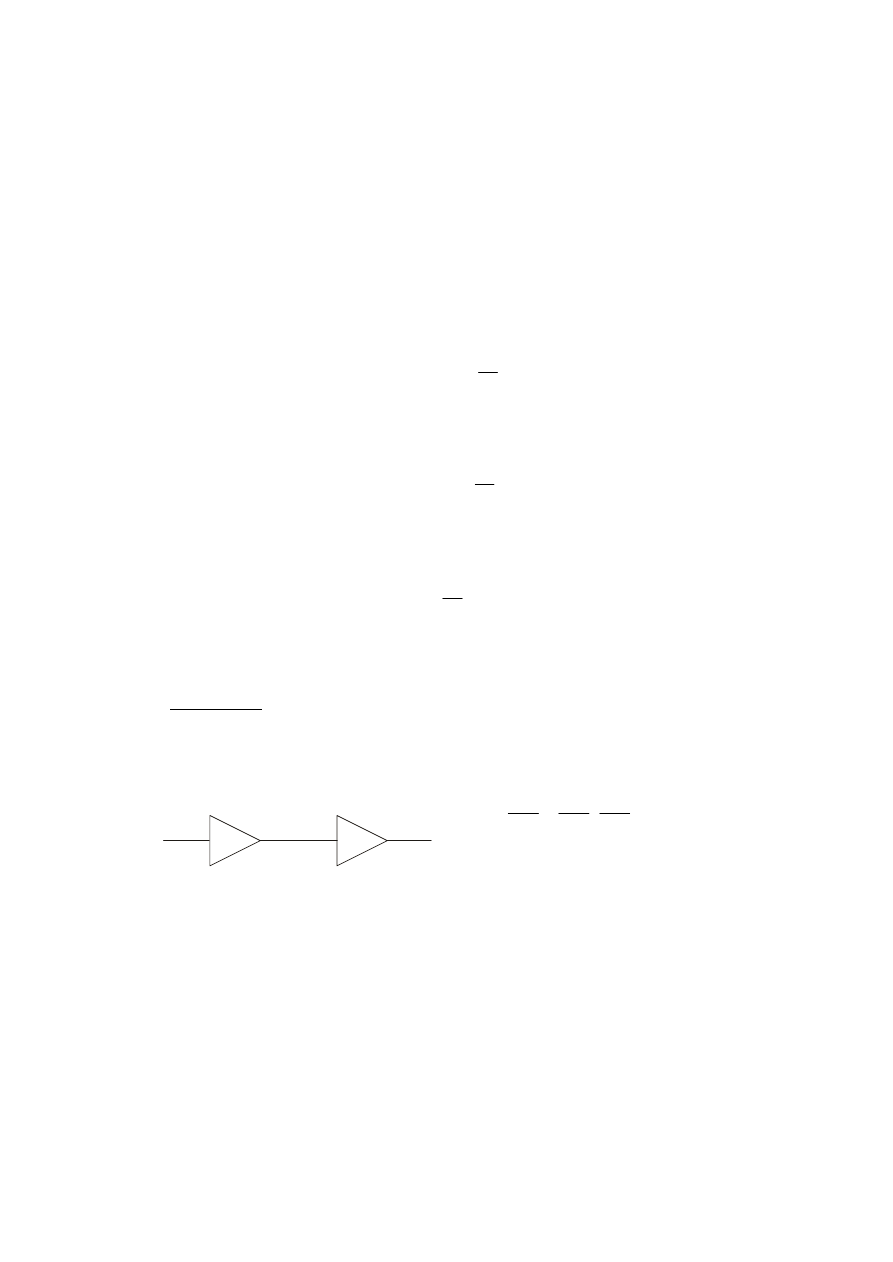
P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

2

1.3. Generowanie, wzmacnianie, przekształcanie i transmisja sygnałów

Wzmacnianie sygnałów.
Współczynnik wzmocnienia układu (wzmacniacza) jest stosunkiem mocy sygnału
wyjściowego do mocy sygnału wejściowego, przy danej częstotliwości lub w
wyznaczonym zakresie częstotliwości.

1

P

P

G

o

p

=

(1.1)

Alternatywnym sposobem opisu wzmocnienia mocy jest stosunek logarytmiczny,
w jednostkach zwanych bel, lub decybel . Równanie wyrażające moc w decybelach
ma postać:

dB

P

P

G

i

o

p









=

log

10

(1.2)

Przyjęto, że, wzmocnienie napięciowe jest wyznaczane w decybelach wynosi

.

log

20

dB

V

V

G

i

o

v









=

(1.5)

Przykład 1.1.
Dwa wzmacniacze o wzmocnieniach napięciowych 20 i 40 są połączone
kaskadowo. Jaki jest ich wspólny współczynnik wzmocnienia wyrażony w V/V i
w dB.
Obliczenie wzmocnienia wzmacniaczy

1

2

u

u

we

wy

we

wy

u

K

K

U

U

U

U

U

U

K

⋅

=

⋅

=

=

800

40

20

2

1

=

⋅

=

⋅

=

u

u

u

K

K

K

Wzmocnienie kaskady w decybelach

)

(

2

)

(

1

2

1

2

1

)

(

log

20

log

20

)

log(

20

)

log(

20

dB

u

dB

u

u

u

u

u

u

dB

u

K

K

K

K

K

K

K

K

+

=

+

=

⋅

=

=

dB

dB

dB

U

U

K

we

dB

u

26

)

20

(log

20

)

/

log(

20

)

(

1

≈

=

=

dB

dB

dB

U

U

K

wy

dB

u

32

)

40

(log

20

)

/

log(

20

)

(

2

≈

=

=

dB

K

K

K

dB

u

dB

u

dB

u

58

32

26

)

(

2

)

(

1

)

(

=

+

=

+

=

20

40

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

3

C. Transmisja (przenoszenie) sygnałów

Sygnał wejściowy ulega zniekształceniu w układzie elektronicznym. Istnieją trzy
podstawowe rodzaje zniekształceń: a) amplitudowe (tłumieniowe), b) fazowe i c)
nieliniowe;
a) – układ wzmacnia w różnym stopniu sygnał o różnych częstotliwościach

zmieniając proporcje sygnału wejściowego; zniekształcenia wprowadzone
przez układ są przedstawiane za pomocą zależności amplitudy sygnałów
wyjściowych w funkcji częstotliwości, przy założeniu niezmienności
amplitudy sygnałów wejściowych (charakterystyka częstotliwościowa),

b) – sygnały o różnych częstotliwościach pojawiają się na wyjściu w różnym

czasie,

c) – zmianie ulega kształt przebiegu sygnału; w wyniku odkształcenia przebiegu

okresowego w sygnale wyjściowym są obecne się składowe, których nie było
w sygnale wejściowym.

1.4. Elementy analizy układów liniowych

1.4.1. Transmitancja operatorowa:
Układ liniowy o elementach skupionych i stacjonarnych (współczynniki nie są
funkcjami czasu) może być opisany za pomocą funkcji operatorowej o postaci
ogólnej:

)

)...(

)(

(

)

)...(

)(

(

...

...

)

(

)

(

)

(

2

1

2

1

1

1

1

1

1

1

n

n

m

m

o

n

n

n

n

o

m

m

m

m

p

s

p

s

p

s

a

z

s

z

s

z

s

b

a

s

a

s

a

s

a

b

s

b

s

b

s

b

s

X

s

Y

s

K

−

−

−

−

−

−

=

+

+

+

+

+

+

+

+

=

=

−

−

−

−

(1.6)

gdzie: Y(s) i X(s) – odpowiednio wyrażenia w liczniku i mianowniku
transmitancji, m < n.

b

i

, a

j

– liczby rzeczywiste,

z

i

, p

j

– zera i bieguny funkcji (przy wartościach zmiennej zespolonej z

i

, p

j

,

licznik oraz mianownik są równe zeru.
Transmitancja operatorowa układu jest jednoznacznie określona rozkładem zer i
biegunów na płaszczyźnie zmiennej zespolonej S i stałym współczynnikiem b

m

/a

n

.

(Zera i bieguny są albo rzeczywiste albo występują parami jako wielkości
sprzężone – gdy są zespolone.

Sygnałami wejściowymi i wyjściowymi w układach elektronicznych są przebiegi
prądów i napięć na wejściu i wyjściu układu. Przykładami transmitancji są:

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

4

)

(

)

(

)

(

1

2

s

U

s

U

s

K

u

=

- transmitancja lub wzmocnienie napięciowe,

)

(

)

(

)

(

1

2

s

I

s

I

s

K

i

=

- transmitancja lub wzmocnienie prądowe,

)

(

)

(

)

(

1

2

s

I

s

U

s

K

z

=

- transimpedancja wzmocnienie napięciowo-prądowe,

)

(

)

(

)

(

1

2

s

U

s

I

s

K

y

=

- transadmitancja lub wzmocnienie prądowo-napięciowe.

1.4.2. Transmitancja widmowa (częstotliwościowa):

W przypadku sygnałów sinusoidalnych, operatorową funkcję przejścia układu (dla
stanu ustalonego)

)

(

)

(

)

(

s

X

s

Y

s

K

=

(1.7)

gdzie:

)}

(

{

)

(

t

x

L

s

X

=

- operatorowa funkcja sygnału wejściowego,

)}

(

{

)

(

t

y

L

s

Y

=

- operatorowa funkcja sygnału wyjściowego.

można

przekształcić

w

transmitancję

częstotliwościową

przez

formalne

podstawienie s = jω.

)

(

)

(

)

(

ω

ω

ω

j

X

j

Y

j

K

=

(1.8)

Transmitancja częstotliwościowa opisuje właściwości układu w dziedzinie
częstotliwości.

Postać ogólna, analogiczna do wyrażenia (1.8) jest następująca:

)

)...(

)(

(

)

)...(

)(

(

)

(

...

)

(

)

(

)

(

...

)

(

)

(

)

(

)

(

)

(

2

1

2

1

1

1

1

1

1

1

n

n

m

m

o

n

n

n

n

o

m

m

m

m

p

j

p

j

p

j

a

z

j

z

j

z

j

b

a

j

a

j

a

j

a

b

j

b

j

b

j

b

j

X

j

Y

j

K

−

−

−

−

−

−

=

+

+

+

+

+

+

+

+

=

=

−

−

−

−

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

ω

(1.9)

Inne postaci transmitancji częstotliwościowej:

)]

(

sin

)

(

[cos

|

)

(

|

)

(

ω

ϕ

ω

ϕ

ω

ω

j

j

K

j

K

+

=

(1.10a)

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

5

)

(

|

)

(

|

)

(

)

(

)

(

ω

ϕ

ω

ω

ω

ω

j

e

j

K

jQ

P

j

K

=

+

=

(1.10b)

Transmitancja częstotliwościowa umożliwia wyznaczyć dwie podstawowe
charakterystyki częstotliwościowe układu:
- charakterystykę amplitudową:

)

(

)

(

|

)

(

|

2

2

ω

ω

ω

Q

P

j

K

+

=

,

(1.11)

- charakterystykę fazową:

)

(

)

(

)

(

ω

ω

ω

ϕ

P

Q

arctg

=

.

(1.12)

Charakterystyka amplitudowa określa zmienność wzmocnienia (tłumienia)

amplitudy sygnałów sinusoidalnych o różnych częstotliwościach. Charakterystykę
amplitudową przedstawia się zazwyczaj w skali decybelowej tj. logarytmicznej
przy podstawie 10.

Charakterystyka fazowa określa przesuniecie fazy sygnału wyjściowego

względem fazy sygnału wejściowego przy różnych częstotliwościach.
Właściwości fazowe układu określa się za pomocą opóźnienia

ω

ω

ϕ

ω

τ

d

d

)

(

)

(

−

=

(1.13)

1.4.3. Rozkład Fouriera

Fourier wykazał, że dowolny, powtarzalny przebieg f(t) można zastąpić

przez sumę (nieskończonej ilości) przebiegów sinusoidalnych o częstotliwościach
będących wielokrotnością częstotliwości przebiegu podstawowego, tj. jego
harmonicznymi.

)

cos(

...

)

3

cos(

)

2

cos(

)

cos(

)

(

1

3

1

3

2

1

2

1

1

1

n

n

o

t

n

A

t

A

t

A

t

A

A

t

f

ϕ

ω

ϕ

ω

ϕ

ω

ϕ

ω

+

+

+

+

+

+

+

+

+

=

(1.14)

gdzie

T

f

1

1

=

. A

T

f

π

π

ω

2

2

1

1

=

=

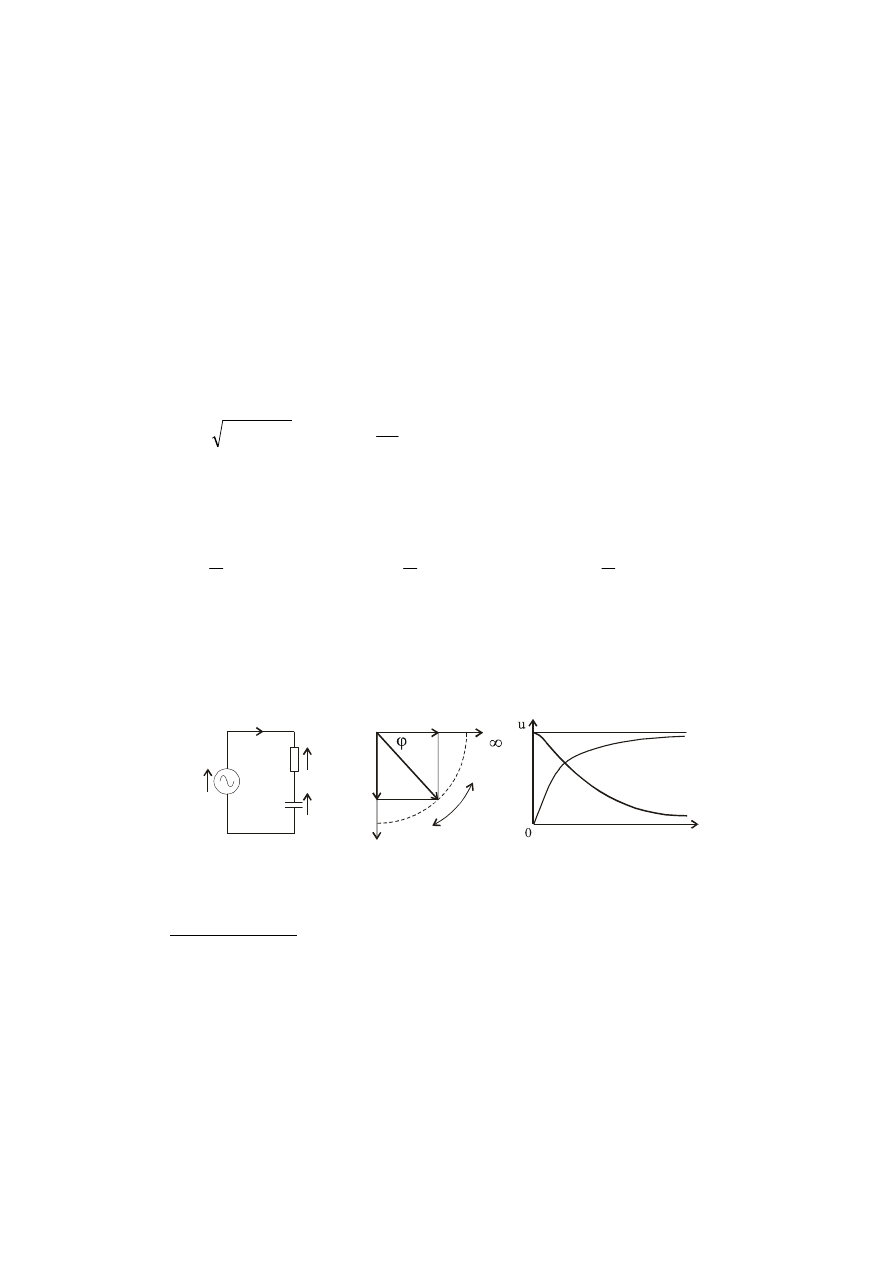
P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

6

Fourier pokazał też sposób obliczenia amplitud, częstotliwości oraz faz

poszczególnych składowych, (Analiza Fouriera), których sumowanie daje
wyjściowy przebieg okresowy (Synteza Fouriera).

1.4.4. Synteza Fouriera – odwrotny proces polegający na znalezieniu przebiegu z
sumowania poszczególnych przebiegów sinusoidalnych.

t

n

y

n

x

t

n

A

n

n

n

n

1

1

1

cos

sin

)

cos(

ω

ω

ϕ

ω

+

=

+

(1.15)

gdzie:

2

2

n

n

n

y

x

A

+

=

,

n

n

n

y

x

tg

1

−

=

ϕ

Amplitudy x

n

, y

n

, a zatem i amplitudy i fazy wszystkich składowych

harmonicznych, występujących w równaniu (1.15) wyznacza się z następujących
zależności:

∫

=

T

n

dt

t

n

t

f

T

x

0

1

)

sin(

)

(

2

ω

,

∫

=

T

n

dt

t

n

t

f

T

y

0

1

)

cos(

)

(

2

ω

,

∫

=

T

o

dt

t

f

T

A

0

)

(

1

(1.16)

1.5. Analiza obwodów RC, RL i RLC przy wymuszeniu sygnałem sinusoidalnym

1.5.1. Szeregowy obwód RC zasilany z źródła napięcia przemiennego

R

C

U

R

U

C

I

U

f = 0

f =

U

U

R

U

C

0

f

U

L

U

R

U

f

Wykres wskazowy:

Wektor prądu przyjęto jako odniesienie gdyż jest wspólny dla obu elementów R i
C; w fazie z prądem jest napięcie na oporniku a napięcie na kondensatorze jest
opóźnione w fazie o 90

o

el względem prądu.

Rys. a) Schemat obwodu, b) wykres wskazowy, c) odpowiedź częstotliwościowa

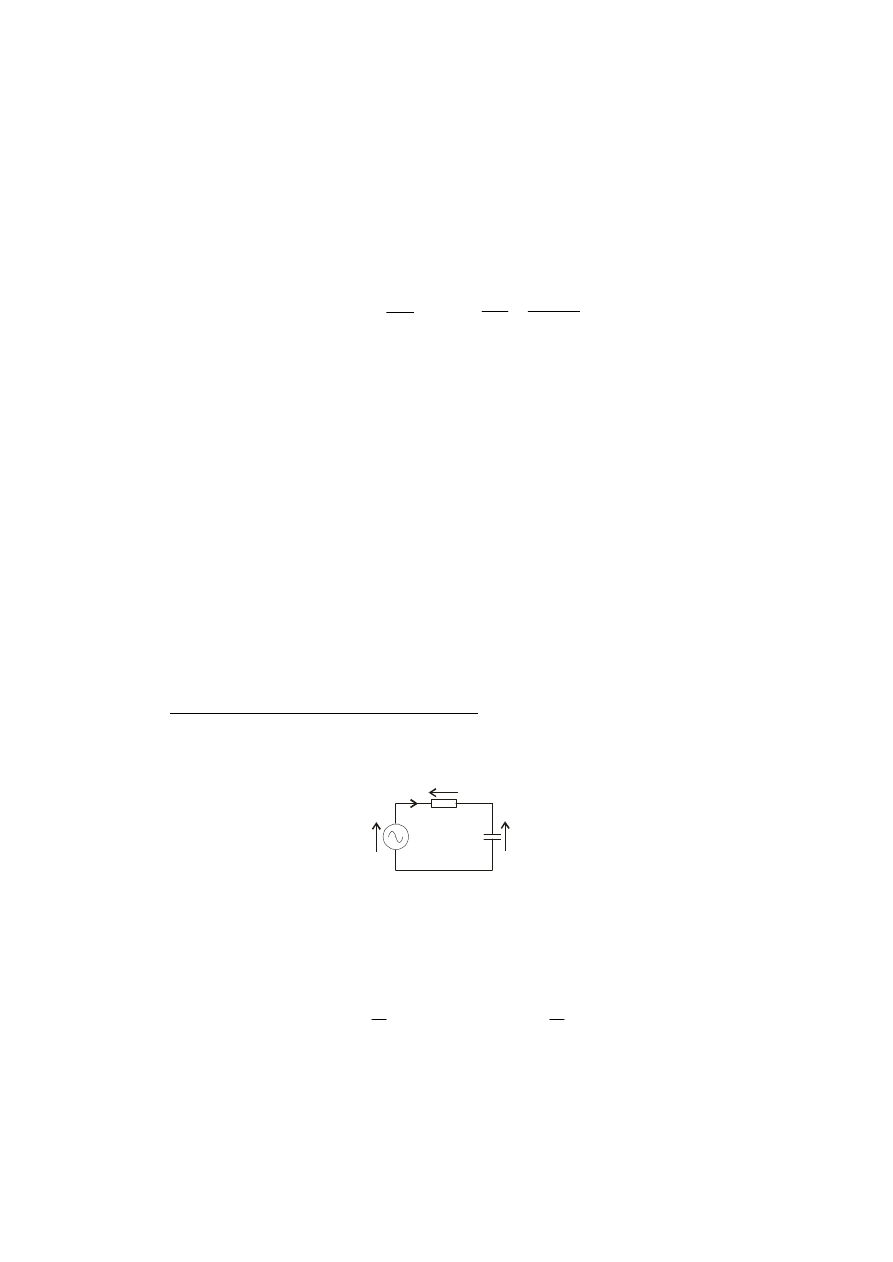
P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

7

ϕ

cos

|

|

|

|

we

R

U

u

=

ϕ

sin

|

|

|

|

we

C

U

u

=

R

X

ar

C

ctg

=

ϕ

,

C

f

C

X

C

⋅

=

=

π

ω

2

1

1

Jeśli przyjąć, że napięcie źródła ma stałą amplitudę w całym pasmie

częstotliwości, to miejscem geometrycznym wierzchołka trójkąta napięć jest okrąg
o promieniu |U

we

|.

Uproszczona interpretacja właściwości obwodu jest następująca:

A: Przy

∞

=

f

, jest:

0

=

C

X

,

0

=

C

u

,

0

=

ϕ

,

we

R

u

R

i

u

=

⋅

=

, kondensator

może być uważany za zwarty a cały sygnał wejściowy odkłada się na rezystorze.
Obwód ma charakter filtru górnoprzepustowego albo charakter filtru w.cz.
Na podstawie odpowiedzi częstotliwościowej z rys. c) widać, że ze wzrostem
częstotliwości napięcie na rezystancji staje się bliskie napięciu wejściowemu.

B: Przy

0

=

f

(zasilanie d.c.), jest:

∞

=

C

X

,

we

C

u

u

=

o

90

=

ϕ

,

0

=

i

,

0

=

R

u

,

kondensator może być uważany za rozwarty a cały sygnał wejściowy odkłada się
na kondensatorze. Obwód ma charakter filtru dolnoprzepustowego albo filtru m.
częstotliwości. Na podstawie odpowiedzi częstotliwościowej z rys.c) widać, że ze
zmniejszaniem się częstotliwości wzrasta napięcie na kondensatorze aż staje się
równe sygnałowi wejściowemu.

Analiza wzmocnienia napięciowego układu RC

I. Wzmocnienie napięciowe układu przyjmując za sygnał wyjściowy napięcie na
kondensatorze.

C

R

U =U

C

wy

U

=U

we

U

R

I

Równania obwodu w postaci czasowej (różniczkowe)

C

R

we

u

u

u

+

=

,

C

wy

u

u

=

∫

+

=

idt

C

iR

u

we

1

∫

=

idt

C

u

wy

1

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

8

A. Zapis operatorowy (Laplace’a)

)

(

1

)

(

)

(

s

I

Cs

s

RI

s

U

we

+

=

)

(

1

)

(

s

I

Cs

s

U

wy

=

τ

s

sRC

s

I

Cs

s

RI

s

I

Cs

s

U

s

U

s

K

we

wy

u

+

=

+

=

+

=

=

1

1

1

1

)

(

1

)

(

)

(

1

)

(

)

(

)

(

B. Zapis symboliczny

)

1

(

)

(

C

j

R

i

jX

i

iR

u

C

we

ω

−

=

−

+

=

)

1

(

)

(

C

j

i

jX

i

u

u

C

C

wy

ω

−

=

−

=

=

0

1

1

1

1

1

1

)

(

ω

ω

ω

ω

ω

ω

ω

j

RC

j

RC

j

j

C

j

R

i

C

j

i

u

u

j

K

we

wy

u

+

=

+

=

+

−

−

=











 −













−

=

=

, (1.16)

gdzie:

τ

π

ω

1

1

2

0

=

=

=

RC

f

o

.

Aby zilustrować właściwości układu przy zmianach częstotliwości można
wyznaczyć a następnie wykreślić: albo charakterystykę amplitudowo-fazową albo
amplitudową oraz fazową rozdzielnie.


W tym celu, w drugim przypadku, można zastosowano uproszczoną metodę
graficzną wyznaczając asymptoty przebiegów (dobierając odpowiednie wartości
częstotliwości f względem częstotliwości charakterystycznej f

o

).

)

(

)

(

)

(

1

)

(

1

1

)

1

)(

1

(

1

)

(

2

2

ω

ω

ω

ω

ω

ω

ω

ω

ω

jQ

P

RC

RC

j

RC

RC

j

RC

j

RC

j

j

K

u

+

=

+

⋅

−

+

=

+

−

−

=

(1.17)

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

9

2

0

2

0

2

2

2

2

2

1

1

1

1

)

(

1

1

)

(

1

)

(

1

1

)

(









+

=









+

=

+

=









+

+









+

=

f

f

RC

RC

RC

RC

j

K

u

ω

ω

ω

ω

ω

ω

ω

(1.18)

]

[

)]

(

[

]

)

(

1

))

(

1

)(

(

[

)

(

0

2









−

=

−

=

+

+

−

=

f

f

tg

arc

RC

tg

arc

RC

RC

RC

tg

arc

ω

ω

ω

ω

ω

ϕ

(1.19)

Charakterystyka częstotliwościowa – amplitudowa, logarytmiczna (decybelowa)

2

0

2

0

1

log

20

1

log

20

1

1

log

20









+

−

=









+

=

f

f

f

f

K

dB

u

(1.20)

































−

≈









+

−

−

≈









+

−

−

≈









+

−

=







 =

+

−

=

dB

f

f

dB

f

f

dB

f

f

f

f

K

dB

u

40

100

1

log

20

1

log

20

20

10

1

log

20

1

log

20

3

1

log

20

1

log

20

0

0

1

log

20

1

log

20

2

0

0

2

0

0

2

0

0

2

0

































=

=

=

≈

0

0

0

100

10

0

:

f

f

f

f

f

f

f

dla

przy częstotliwości granicznej

g

f

f

=

0

, rzeczywista wartość wzmocnienia jest

mniejsza o -3dB od wartości wynikającej z przebiegu asymptot podczas, gdy
pozostałe obliczone wartości są dobrze aproksymowane przez asymptoty.

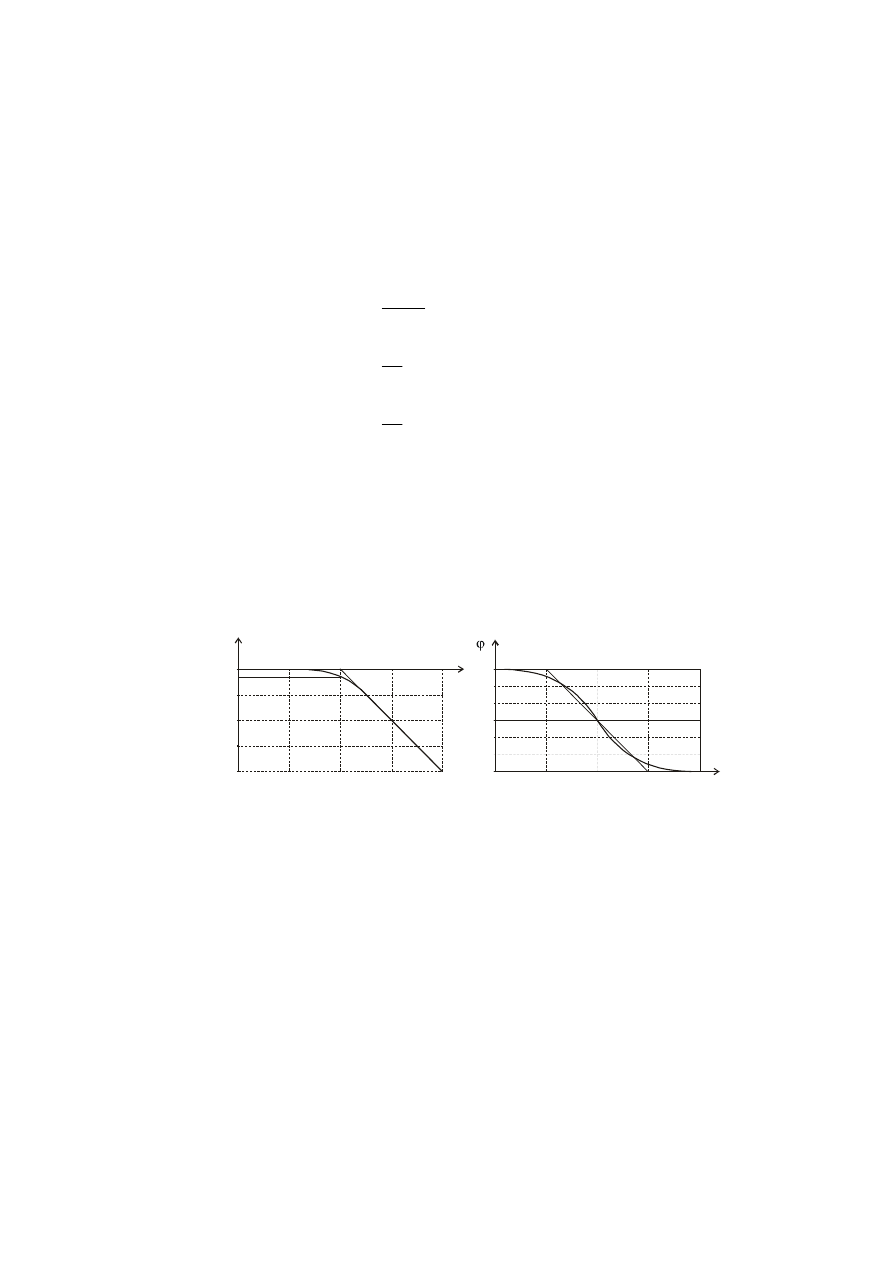
P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

10

Charakterystyka fazowa zwykle jest przedstawiana we współrzędnych liniowych.





















−

=







 ∞

−

−

=









−

=









≈

−

=

0

0

0

0

0

0

90

tg

45

tg

0

0

tg

f

arc

f

f

arc

f

f

arc

ϕ























∞

=

=

=

f

f

f

f

dla

0

0

:

Charakterystyka rzeczywista jest aprosymowana odcinkami (tzw. aproksymacja
odcinkowo liniowa): poziomą półprostą, odcinkiem prostej przechodzącym przez

punkt

0

45

−

=

ϕ

,

0

f

f

=

i nachylonym

dek

/

45

0

−

oraz przy wysokich

częstotliwościach poziomą półprostą.

0,01 0,1 1 10 100

|K |dB |K |

u

u

0 1

-20 0,1

f/f

o

-3 ~ 0,707

-40 0,01

a) b)

0,01 0,1 1 10 100

f/f

o

0

o

-90

o

-45

o

Rys.

II. Wzmocnienie napięciowe układu przyjmując za sygnał wyjściowy napięcie na
oporniku.

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

11

C

R

U

=U

we

U =U

R

wy

U

C

I

Równania obwodu w postaci czasowej (różniczkowe)

C

R

we

u

u

u

+

=

,

R

wy

u

u

=

∫

+

=

idt

C

iR

u

we

1

R

i

u

wy

⋅

=

A. Zapis operatorowy (Laplace’a)

)

(

1

)

(

)

(

s

I

Cs

s

RI

s

U

we

+

=

)

(

)

(

s

I

R

s

U

wy

⋅

=

τ

s

sRC

s

I

Cs

s

RI

s

RI

s

U

s

U

s

K

we

wy

u

1

1

1

1

1

1

)

(

1

)

(

)

(

)

(

)

(

)

(

+

=

+

=

+

=

=

B. Zapis symboliczny

)

1

(

)

(

C

j

R

i

jX

i

iR

u

C

we

ω

−

=

−

+

=

R

i

u

u

R

wy

⋅

=

=

ω

ω

ω

τ

ω

ω

ω

0

1

1

1

1

1

1

1

1

)

(

j

j

RC

j

C

j

R

i

iR

u

u

j

K

we

wy

u

−

=

−

=

−

=











 −

=

=

,

gdzie

τ

ω

1

1

0

=

=

RC

Wzmocnienie obwodu można wyznaczyć za pomocą rachunku zespolonego (jw.),
po czym wykreślić charakterystykę częstotliwościową modułu oraz fazy ilustrujące
właściwości wzmacniacza w funkcji częstotliwości. W tym celu można
zastosowano uproszczoną metodę graficzną wyznaczając asymptoty przebiegów
(po dobraniu odpowiednich wartości ω).

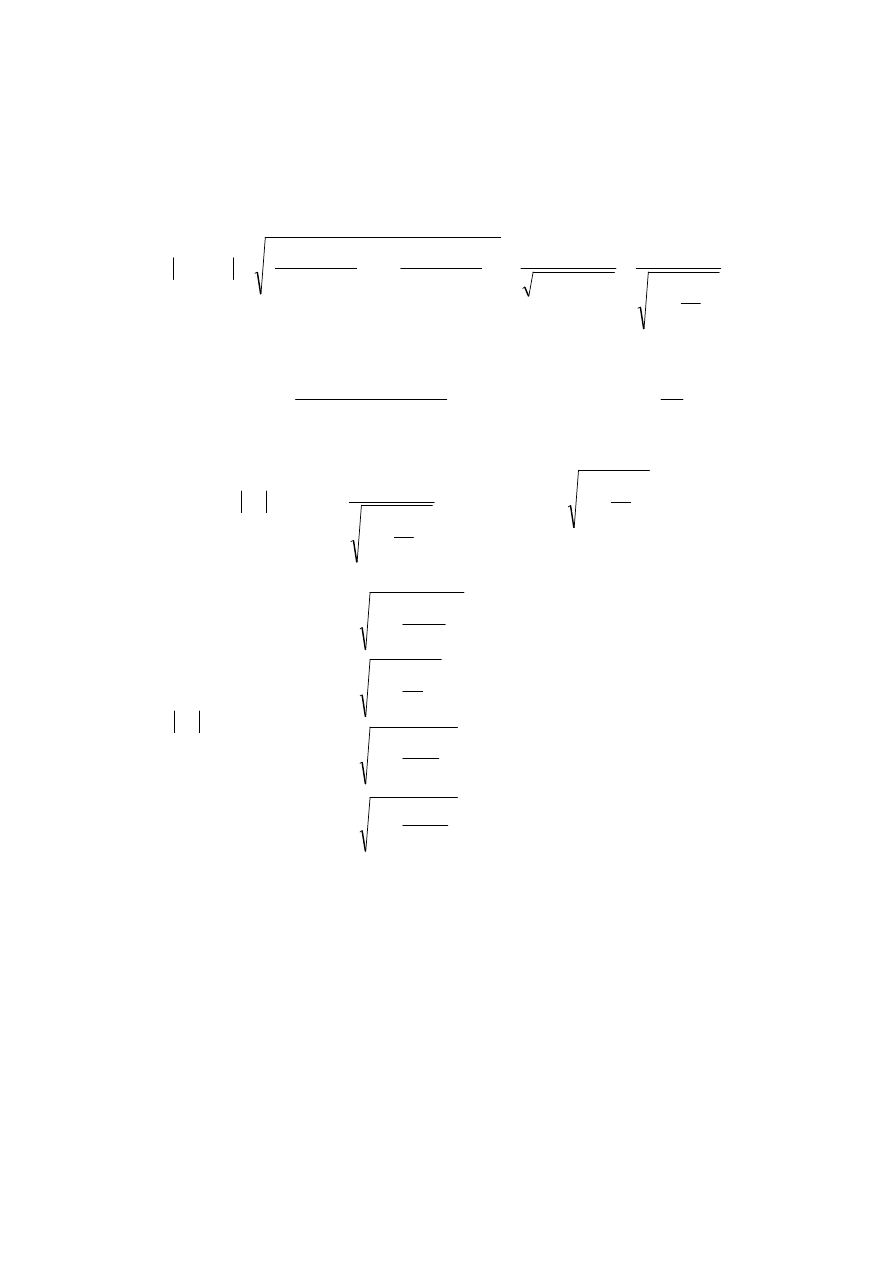
P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

12

2

0

2

2

2

2

2

1

1

)

(

1

1

)

(

1

)

(

1

1

)

(









+

=

+

=









+

+









+

=

f

f

RC

RC

RC

RC

j

K

u

ω

ω

ω

ω

ω

]

[tg

)]

[tg(

]

)

(

1

))

(

1

)(

(

[tg

)

(

0

2









−

=

−

=

+

+

−

+

ω

ω

ω

ω

ω

ω

ω

ϕ

arc

RC

arc

RC

RC

RC

arc

Charakterystyka częstotliwościowa - amplitudowa

2

0

2

0

1

log

20

1

log

20

1

1

log

20









+

−

=









+

=

f

f

f

f

K

dB

u

































−

≈









+

−

−

≈









+

−

−

≈









+

−

=







 =

+

−

=

dB

f

f

dB

f

f

dB

f

f

f

f

K

dB

u

40

100

1

log

20

1

log

20

20

10

1

log

20

1

log

20

3

1

log

20

1

log

20

0

0

1

log

20

1

log

20

2

0

0

2

0

0

2

0

0

2

0

































=

=

=

≈

0

0

0

100

10

0

:

f

f

f

f

f

f

f

dla

przy częstotliwości granicznej

0

f

, rzeczywista wartość wzmocnienia jest mniejsza

o -3dB od wartości wynikającej z przebiegu asymptot podczas, gdy pozostałe
obliczone wartości są dobrze aproksymowane przez asymptoty.

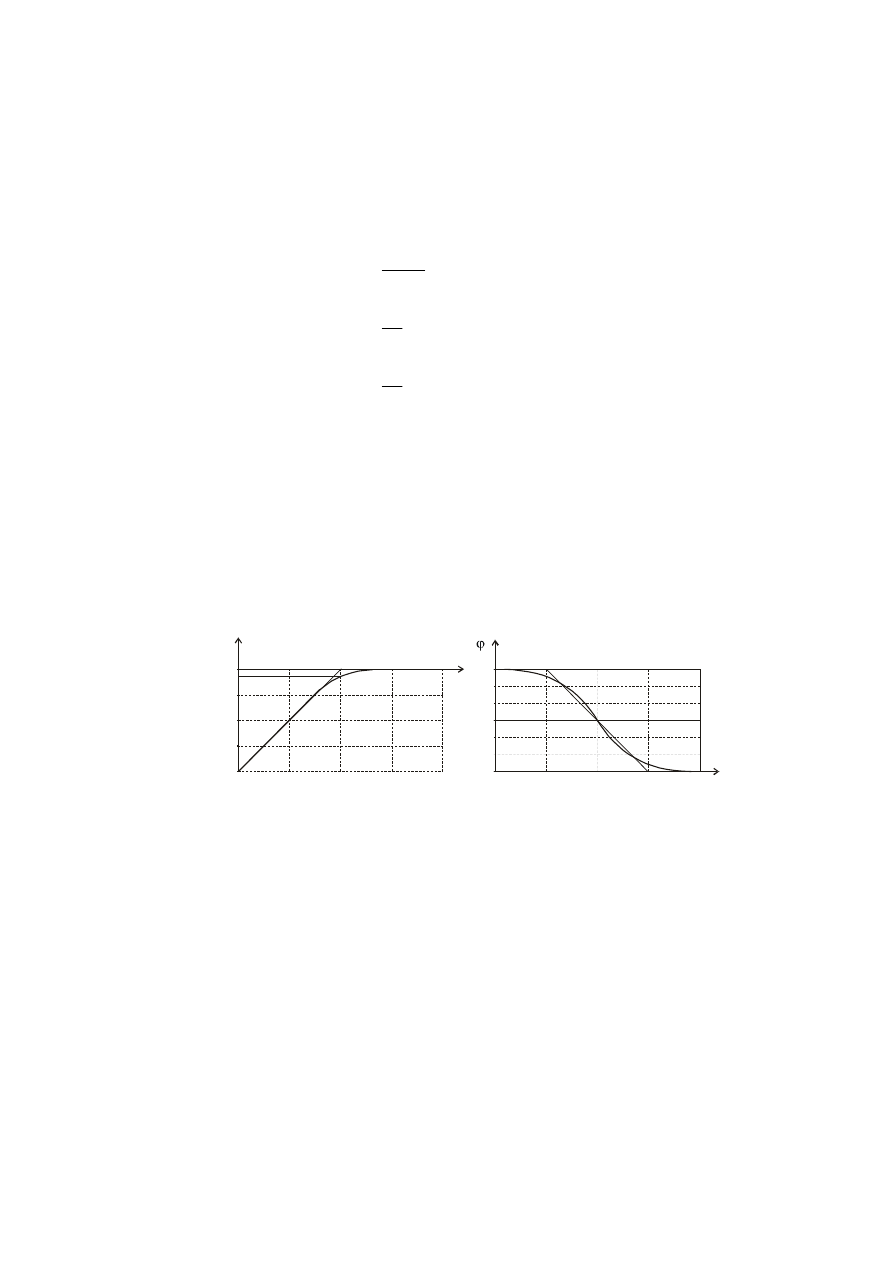
Charakterystyka częstotliwościowa – fazowa zazwyczaj jest przedstawiana we
współrzędnych liniowych.

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

13





















−

=







 ∞

−

−

=









−

=









≈

−

=

0

0

0

0

0

0

90

tg

45

tg

0

0

tg

f

arc

f

f

arc

f

f

arc

ϕ























∞

=

=

=

f

f

f

f

dla

0

0

:

Charakterystyka rzeczywista jest aprosymowana odcinkami (tzw. aproksymacja
odcinkowo liniowa): poziomą półprostą, odcinkiem prostej przechodzącym przez

punkt

0

45

−

=

ϕ

,

0

f

f

=

i nachylonym

dek

/

45

0

−

oraz przy wysokich

częstotliwościach poziomą półprostą.

0,01 0,1 1 10 100

|K |dB |K |

u

u

0 1

-20 0,1

f/f

o

-3 ~ 0,707

-40 0,01

a) b)

0,01 0,1 1 10 100

f/f

o

90

o

0

o

45

o

Rys.

................................................................................................................................

P1 SYGNAŁY I OBWODY 31

J.Piłaciński: Materiały pomocnicze do wykładu

14

R

L

C

C

R

R

L

R

I

I

L

I

I

R

U

R

U

C

U

U

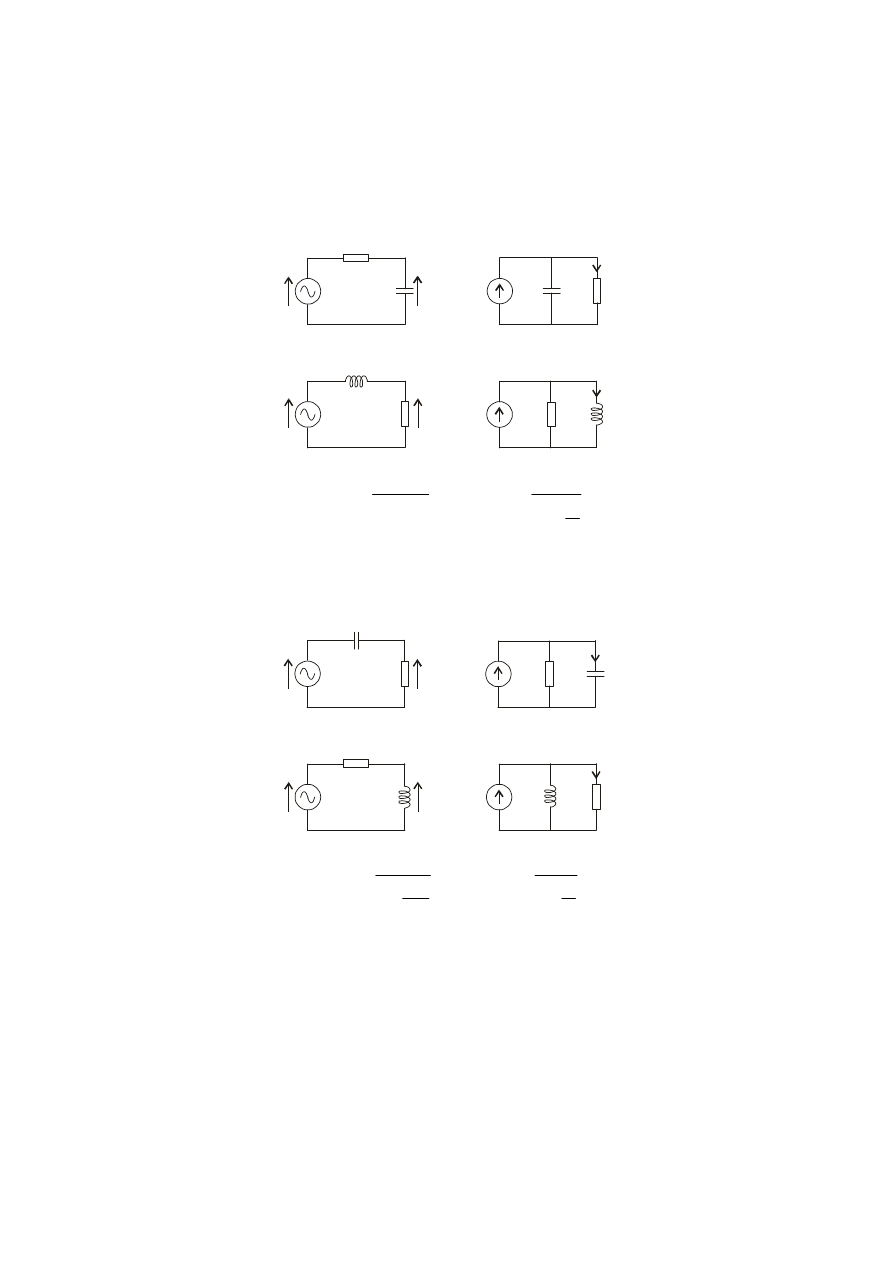
a) b)

c) d)

sRC

s

K

u

+

=

1

1

)

(

;

R

L

s

s

K

u

+

=

1

1

)

(

Rys. Obwody RC i RL realizujące jednobiegunową funkcję dolnoprzepustową

L

L

C

C

R

R

R

R

U

I

R

I

U

L

U

I

U

R

c) d)

a) b)

RC

s

s

s

K

u

1

)

(

+

=

;

L

R

s

s

s

K

u

+

=

)

(

Rys. Obwody RC i RL realizujące jednobiegunową funkcję górnoprzepustową