P R A C E N A U K O W E P O L I T E C H N I K I W A R S Z A W S K I E J
z. 64
Transport
2008
Jolanta
ŻAK
Wydział Transportu Politechniki Warszawskiej
Zakład Logistyki i Systemów Transportowych
ul. Koszykowa 75, 00-662 Warszawa
logika1@it.pw.edu.pl
MODELOWANIE USŁUG TRANSPORTOWYCH W OBSZARZE
DZIAŁANIA CENTRUM LOGISTYCZNO-DYSTRYBUCYJNEGO
Streszczenie
W artykule przedstawiono podej
ście do modelowania usług logistycznych w obszarze działania centrum
logistyczno-dystrybucyjnego. Zaproponowano formalizacj
ę opisu zapotrzebowań odbiorców i produkcji
okre
ślonego towaru oraz zapis charakterystyk sieci transportowej. Na potrzeby rozwiązania problemu
sformułowano zadanie optymalizacyjne modelowania usług transportowych w obszarze działania centrum
logistyczno-dystrybucyjnego oraz przykład jego rozwi
ązania
Słowa kluczowe: modelowanie usług, optymalizacja, sie
ć transportowa, centrum logistyczno-dystrybucyjnego
1. WPROWADZENIE
Przedmiotem analizy w niniejszym artykule jest centrum logistyczno-dystrybucyjne
w aspekcie modelowania realizacji usług transportowych na okre
ślonym obszarze.
Szczególnej uwadze po
święcony jest problem wybory lokalizacji centrum, która zapewni
optymaln
ą obsługę logistyczną dla danego rejonu sieci transportowej, spełniając przy tym
z
jednej strony wymagania klientów, za
ś z drugiej strony możliwości techniczno-
ekonomiczne dostawców usług logistycznych. Analizuj
ąc literaturę [1], [2], [3], [5] centrum
logistyczne definiowane jest jako samodzielny podmiot gospodarczy, który jest zlokalizowany
w pobli
żu dużych ośrodków gospodarczo-przemysłowych, jak również w pobliżu dróg, co
najmniej dwu ró
żnych gałęzi transportu, dysponujący: wydzielonym terenem powiązanym
z otoczeniem komunikacyjnym (głównie sieci
ą dróg), infrastrukturą, (drogi, place, parkingi,
budowie in
żynierskie i budynki), wyposażeniem, personelem i organizacją, świadczący usługi
logistyczne w ramach dora
źnych zleceń lub ciągłych umów z firmami zewnętrznymi.
Nale
ży podkreślić fakt, że centra logistyczne powinny być projektowane w taki sposób
aby stanowiły sie
ć usług multimodalnych oferowanych przez jednego uniwersalnego
operatora. Oznacza to,
że obok dużych centrów logistycznych powinien również następować
rozwój centrów ni
ższej rangi, organizowanych i obsługiwanych przez operatorów
gał
ęziowych (np. duże firmy samochodowo-spedycyjne), tzw. centrów logistyczno-
dystrybucyjnych [2], [3].
Wielko
ść, struktura oraz lokalizacja centrum musi być dostosowana do konkretnych
zada
ń logistycznych będących funkcją liczby i charakteru potrzeb klientów działających na
badanym obszarze. Charakter centrum logistycznego zale
ży m. in. od liczby oraz rodzaju
Jolanta
Żak
klientów, a tym samym od wielko
ści zapotrzebowania na usługę logistyczną [7]. Usługę
logistyczn
ą można zdefiniować jako zorganizowane przez specjalistyczną firmę zewnętrzną
transportowanie i magazynowanie produktów wraz z pełn
ą ich formalno-prawną obsługą.
W kompleksowej usłudze logistycznej mo
żna wyróżnić cztery podstawowe elementy
składowe:
• magazynowanie i obsługę zapasów;
• transportowanie i obsługę ładunku;
• badanie rynku i tworzenie marketingowego systemu informacji;
• finansowanie transakcji, obsługę bankową i ubezpieczeniową kontraktów.
Zatem zadaniem centrum logistyczno-dystrybucyjnego jest obsługa logistyczna danego
obszaru, która jest konsekwencj
ą lokalizacji tego centrum oraz jego rejonu ciążenia. Nie jest
to zadanie łatwe do rozwi
ązania, ponieważ należy przy tym uwzględnić szereg takich
aspektów jak, np. wielko
ść strumieni ładunków znajdujących się w rejonie obsługi, istniejącą
sie
ć transportową w otoczeniu potencjalnych miejsc lokalizacji centrum logistyczno-
dystrybucyjnego, itp.
2. OPIS PROBLEMU
Dla potrzeb formalnego opisu zagadnienia modelowania zakładamy,
że na pewnym
terytorium wyró
żnione są miejscowości charakteryzujące się bądź intensywnością produkcji
ró
żnorodnych towarów, bądź intensywnością zużycia różnorodnych towarów. Zmienną
r numerujemy towary ró
żnych rodzajów produkowane (zużywane) w obszarze działania
centrum logistyczno-dystrybucyjnego. Zbiór R wszystkich rodzajów towarów b
ędzie zbiorem
postaci:
R={1,2, ..., r, ...,R}.
Zakładamy ponadto,
że w danej miejscowości można towar jedynie produkować,
wzgl
ędnie tylko zużywać. Zanumerujemy indeksem i miejscowości, w których ma miejsce
produkcja towarów natomiast indeksem j miejscowo
ści, w których występuje zużycie
towarów. Dla jednoznaczno
ści przyjmujemy, że i∈I, I={1,2,...,i,...,I} natomiast j∈J,
J={1,2,...,j,...,J}. Wykorzystuj
ąc wprowadzone oznaczenia możemy wyróżnić dwa zbiory
miejscowo
ści:
P={i:
0
δ ri >
, i
∈I, r∈R}
O={ j:
0
r
j
α >
, r
∈R, j∈J}
gdzie:
δ ri
- intensywno
ść produkcji towaru r-tego rodzaju w miejscowości i;
α rj
- intensywno
ść zapotrzebowania na towar r-tego rodzaju w miejscowości j.
Zakładamy,
że dla każdego i∈I określony jest zbiór numerów towarów produkowanych
w tej miejscowo
ści, a więc dla każdego i∈I określony jest zbiór R
i
. Analogicznie dla ka
żdej
miejscowo
ści j∈J określony jest zbiór numerów towarów zużywanych w tej miejscowości,
a wi
ęc dla każdego j∈J określony jest zbiór R
j
.
Przyjmujemy,
że numery miejscowości m, w których potencjalnie może być usytuowane
centrum logistyczno-dystrybucyjnego (CL) tworz
ą zbiór M. Z punktu widzenia przydatności
danej miejscowo
ści do budowy CL każdą m-tą potencjalną miejscowość charakteryzują dwie
wielko
ści [4]:
178
Modelowanie usług transportowych w obszarze działania centrum logistyczno-dystrybucyjnego
•
κrm - koszt eksploatacji jednostki pojemności magazynu na jednostkę czasu dla
r-tego rodzaju towaru w m-tej miejscowo
ści, m∈M, r∈R;
•
0
m
κ
-koszt stały utrzymania magazynu w m-tym centrum, m
∈M.
Miejscowo
ści, w których znajdować się mogą centra charakteryzować będzie wielkość
pojemno
ści magazynu w położonego w miejscowości m P
m
.
Dostawy towarów realizowane s
ą różnymi środkami transportowymi. Zbiór środków
transportowych, które w obszarze centrum logistyczno-dystrybucyjnego mog
ą być stosowane
do realizacji przewozów, b
ędzie zbiorem postaci S={1,2,...,s,...,S}.
3. CHARAKTERYSTYKA SIECI TRANSPORTOWEJ
Sie
ć transportowa w obszarze centrum logistyczno-dystrybucyjnego zdefiniowana jest
jako S=(G, F
G
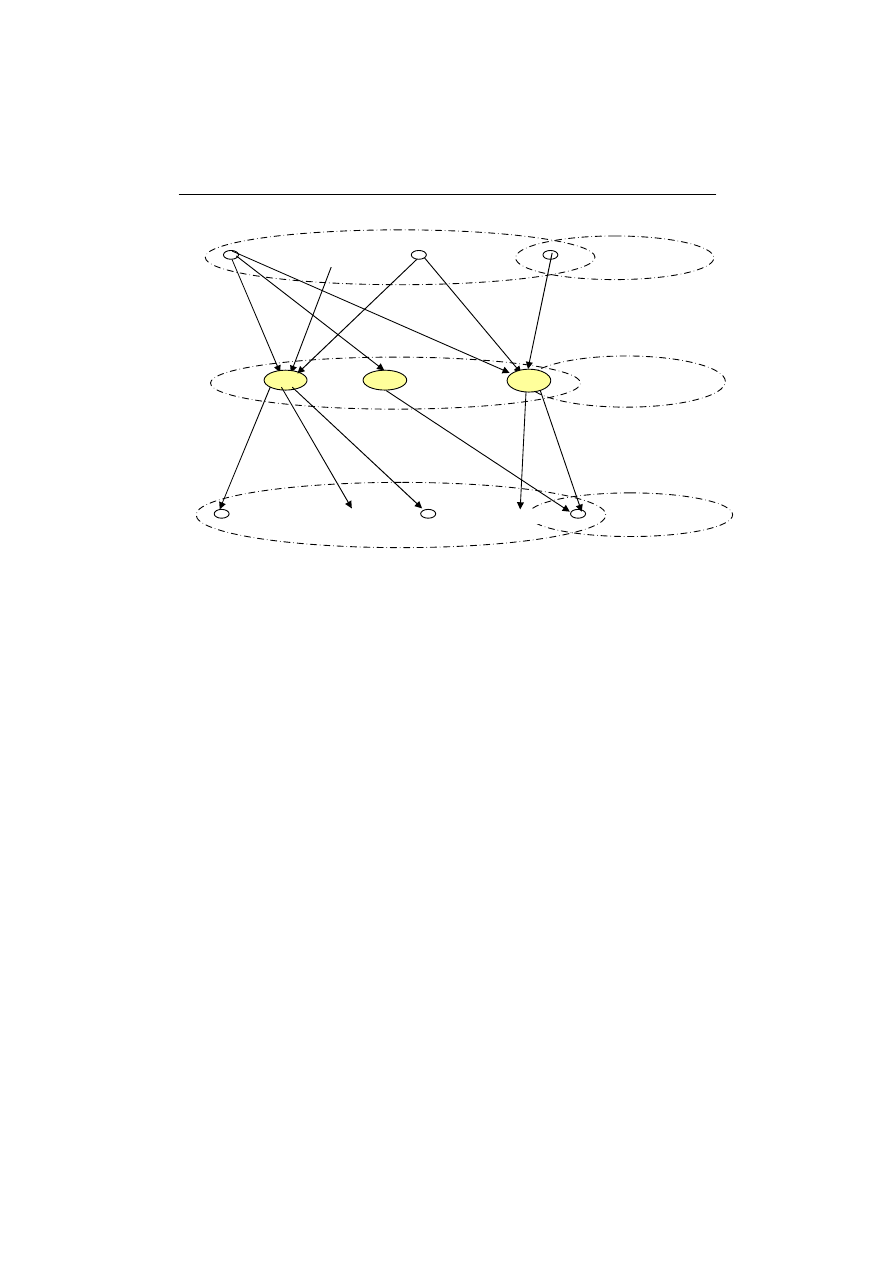
), przy czym G jest grafem G=(W,U), gdzie W=I
∪
∪
∪
∪
J
∪
∪
∪
∪
M (rys.1), a U zbiorem
bezpo
średnich połączeń transportowych, oraz funkcjami F
G
okre
ślonymi na zbiorach węzłów
I, M, J oraz bezpo
średnich połączeń transportowych U.
Bezpo
średnie połączenia transportowe (i,m),(m,j)∈U charakteryzują:
•
s
r,
m
i,
t
⎟⎠
⎞
⎜⎝
⎛
s
r,
j
m,
t
- czas transportu z miejscowo
ści i do centrum m towaru r-tego
rodzaju, s-tym typem
środków transportu (analogicznie dla relacji (m, j));
•
m
i,
π
⎟
⎠
⎞
⎜
⎝
⎛
j
m,
π
- intensywno
ść maksymalna przepływu towaru z miejscowości i do
miejscowo
ści m (analogicznie dla relacji (m, j)) ;
•
s
r,
m
i,
k
⎟⎟⎠
⎞
⎜⎜⎝
⎛
s
r,
j
m,
k
- koszt transportu jednostki towaru r-tego rodzaju z i do m , s-tym
rodzajem
środków transportu (analogicznie dla relacji (m, j)) ;
•
s
r,
0,
m
i,
k
⎟⎟⎠
⎞
⎜⎜⎝
⎛
s
r,
0,
j
m,
k
- koszt straty transportu pojedynczej dostawy towaru r-tego
rodzaju z miejscowo
ści i do miejscowości m, s-tym rodzajem środków transportu
(analogicznie dla relacji (m, j)).
Przyjmujemy,
że charakter strumieni towaru przepływających między miejscowościami
w obszarze CL jest okre
ślony. Zakładamy, że transport towaru r-tego rodzaju, s-tym rodzajem
środków transportu na ustalonym połączeniu transportowym (i,m) jest realizowany w postaci
dostaw o wielko
ści
s
r,
m
i,
Q
powtarzaj
ących się co odcinek czasu
s
r,
m
i,
T
, ponadto przyjmujemy,
że wielkość
s
r,
m
i,
T
odcinka czasu jest okre
ślona. Do pełnego opisu zagadnienia przyjmujemy,
że pierwsza dostawa, od chwili początkowej
s
r,
0
t
realizowana jest w chwili
s
r,
m
i,
ϕ
(w przypadku, gdy czas realizacji dostawy jest mierzony w i- tej miejscowo
ści). Dla dalszych
rozwa
żań wygodnie jest przyjąć, iż rozpatrywany system logistyczno-dystrybucyjny
funkcjonuje dostatecznie długo przed chwil
ą
s
r,
0
t
, wówczas zamiast wielko
ści
s
r,
m
i,
ϕ
stosujemy wielko
ść
s
r,
m
i,
ψ
o interpretacji odcinka czasu jaki upływa od chwili realizacji
ostatniej dostawy do chwili
s
r,
0
t
(mierzony w miejscowo
ści i).
179
Jolanta
Żak
Rys.1. Struktura sieci transportowej
Źródło: opracowanie własne.
Oczywi
ście, zachodzi równość:
s
r,
m
i,
s
r,
m
i,
T
s
r,
m
i,
ψ
ϕ
−
=
,
(2.1)
przy czym dla ka
żdego i
∈
I spełnione s
ą warunki:
0<
s
r,
m
i,
ϕ
≤
s
r,
m
i,
T
; (2.2)
0<
s
r,
m
i,
ψ
≤
s
r,
m
i,
T
.
(2.3)
Dla celów obliczeniowych niezb
ędna jest orientacja w czasie strumienia dostaw
wpływaj
ącego do centrum m. Oznaczymy przez
s
r,
m
i,
χ
odcinek czasu jaki upływa od ostatniej
dostawy do centrum m, do chwili pocz
ątkowej t
0
. Mi
ędzy wielkościami
s
r,
m
i,
ψ
oraz
s
r,
m
i,
χ
zachodz
ą zależności [4]:
⎪
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎪
⎨
⎧
<
−
−
≥
−
=
s
r,
m
i,
t
s
r,
m
i,
ψ
gdy
),
s
r,
m
i,
t
s
r,
m
i,
(
ψ
s
r,
m
i,
T
mod
s
r,
m
i,
T
s
r,
m
i,
t
s
r,
m
i,
ψ
gdy
),
s
r,
m
i,
t
s
r,
m
i,
(
ψ
s
r,
m
i,
T
mod
s
r,
m
i,
χ
(2.4)
⎪
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎪
⎨
⎧
≥
+
+
<
+
+
=
s
r,
m
i,
T
T
r,
m
i,
t
s
r,
m
i,
χ
gdy
,
s
r,
m
i,
T
-
)
T
r,
m
i,
t
s
r,
m
i,
(
χ
s
r,
m
i,
T
mod
s
r,
m
i,
T
T
r,
m
i,
t
s
r,
m
i,
χ
gdy
),
T
r,
m
i,
t
s
r,
m
i,
(
χ
s
r,
m
i,
T
mod
s
r,
m
,i
ϕ
(2.5)
J
j
1
DOSTAWCY
CENTRUM
LOGISTYCZNO DYSTRYBUCYJNE
1
i
ODBIORCY
L
L
I
L
L
L
m
l
1
L
M
180
Modelowanie usług transportowych w obszarze działania centrum logistyczno-dystrybucyjnego
Posta
ć analityczną intensywności strumienia dostaw r-tego towaru, s-tym środkiem
transportowym, wypływaj
ącego od dostawcy i do centrum m, wyraża wzór:
∑
=
+
−
=
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
T
1
t
s
r,
m
i,
ψ
s
r,
m
i,
nT
t
1
δ
s
r,
m
i,
T
s
r,
m
i,
Q
(t)
s
r,
m
i,
x
(2.6)
gdzie
1
δ jest funkcją delta-Kroneckera, ∈
n
N
+
.
Analogicznie posta
ć analityczną funkcji określającej wielkość dostawy r-tego towaru,
s-tym
środkiem transportowym wypływającej od i-tego dostawcy.
∑
=
+
−
=
⎟⎟
⎟
⎠
⎞
⎜⎜
⎜
⎝
⎛
⎟⎠
⎞
⎜⎝
⎛
T
1
t
s
r,
m
i,
ψ
s
r,
m
i,
nT
t
1
δ
s
r,
m
i,
Q
t
s
r,
m
i,
Q
(2.7)
na poł
ączeniu (i,m)∈U wygodnie jest charakteryzować strumień towaru r-tego rodzaju jego
intensywno
ścią , wyrażoną wzorem:
s
r,
m
i,
T
s
r,
m
i,
Q
s
r,
m
i,
x
=
(2.8)
Pełn
ą charakterystykę strumienia stanowią następujące trzy wielkości:
s
r,
m
i,
Q
,
s
r,
m
i,
T
,
s
r,
m
i,
ψ
oczywi
ście przy założeniu, że wielkości te są zdeterminowane.
Analogicznie zakładamy,
że transport towaru r-tego rodzaju na ustalonym połączeniu
transportowym (
m, j) jest realizowany w postaci dostaw o wielko
ści
s
r,
j
m,
Q
powtarzaj
ących się
co odcinek czasu
s
r,
j
m,
T
. Do pełnego opisu trzeba jeszcze doda
ć, że pierwsza dostawa od chwili
pocz
ątkowej
s
r,
0
t
jest realizowana w chwili
s
r,
j
m,
ϕ
(gdy czas realizacji dostawy jest mierzony
w centrum
m). Dla dalszych rozwa
żań wygodniej jest przyjąć, iż rozpatrywany system
zaopatrzenia funkcjonuje ju
ż dostatecznie długo przed chwilą
s
r,
0
t
. Wówczas zamiast
wielko
ści
s
r,
j
m,
ϕ
mo
żna stosować wielkość
s
r,
j
m,
ψ
oznaczaj
ącą czas jaki upływa od chwili
realizacji ostatniej dostawy do chwili t
0
(mierzony w
m-tym centrum).
Pełn
ą charakterystykę strumienia r-tego rodzaju towaru, s-tym środkiem transportu na
poł
ączeniu (m,j), przy założeniu , że wielkości są zdeterminowane stanowią następujące trzy
wielko
ści
s
r,
j
m,
Q
,
s
r,
j
m,
T
,
s
r,
j
m,
ψ
.
4. SFORMUŁOWANIE PROBLEMU OPTYMALNEJ ORGANIZACJI USŁUG
TRANSPORTOWYCH W OBSZARZE CENTRUM
Nale
ży wyznaczyć optymalną organizację systemu, a więc wielkości
( )
t
s
r,
m
i,
x
( )
⎟⎠
⎞
⎜⎝
⎛
t
s
r,
j
m,
x
dla przypadku zdeterminowanego, tzn., gdy w zadanym okresie (0,
s
r,
j
m,
T
) znane s
ą
181
Jolanta
Żak
zapotrzebowania odbiorców
0
r
j
α ≥
, mo
żliwości źródeł dostaw
0
r
i
δ ≥
dla wszystkich par
(
i,r),(( j,r)).
Żądamy przy tym, aby:
•
zapasy były przechowywane w potencjalnym magazynie o zało
żonej pojemności
Pm
≥0 dla wszystkich potencjalnych CL m=1,2,...,M;
•
przewozy transportowe nie przekraczały znanych przepustowo
ści π
i,m
≥0, (π
m,j
≥0),
poł
ączeń transportowych na wszystkich relacjach (i,m), (m,j).
Organizacj
ę będziemy uważali za optymalną wtedy, gdy suma kosztów utrzymania
zapasów i kosztów transportu b
ędzie minimalna.
Wszystkie powy
ższe wymagania możemy zapisać w następujący sposób:
• warunek nieujemności zmiennych decyzyjnych ∀ (i,m,r,s), ∀ t∈(0,
s
r,
m
i,
T
)
( )
0
t
s
r,
m
i,
x
≥
(3.1)
• warunek nie przekraczania możliwości źródeł dostaw∀ (i,m,r,s)
( )
r
i
δ
s
r,
m
i,
T
1
t
t
s
r,
m
i,
x
≤
∑
=
(3.2)
• warunek nie przekraczania zapotrzebowania odbiorców ∀ (j,m,r,s)
( )
r
j
α
s
r,
j
m,
T
1
t
t
s
r,
j
m,
x
≤
∑
=
(3.3)
• warunek nie przekraczania pojemności istniejącego magazynu
( )
∑
=
∑
∈
∑
=
≤
I
1
i
i
r
s
r,
m
i,
T
1
t
m
P
t
s
r,
m
i,
x
r
h
R
(3.4)
∀ i gdzie
r
h
jest współczynnikiem mianowanym przeliczenia ró
żnych jednostek
miary towaru na jednostk
ę miary pojemności magazynu;
• warunek nie przekraczania możliwości transportowych
( )
∑
=
≤
R
1
r
m
i,
π
t
s
r,
m
i,
x
r
g
(3.5)
∀ t∈(0,
s
r,
m
i,
T
)
∀ (i,m) gdzie
r
g jest współczynnikiem mianowanym przeliczenia
ró
żnych jednostek miary towaru na jednostkę miary przepustowości relacji (i,m).
Jako kryterium optymalno
ści w rozważanym przypadku przyjmuje się minimalizację
cz
ęści kosztów utrzymania systemu zależnych od organizacji działania systemu. Zatem
funkcj
ę kryterium możemy zapisać jako:
( )
( )
0
m
κ
T
1
t
I
1
i
i
R
r
J
1
j
r
h
r
m
k
t
j
R
r
s
r,
j
m,
x
r
h
r
m
k
t
s
r,
m
i,
x
I
1
i
J
1
j
j
R
r
s
r,
j
m,
x
s
r,
j
m,
k
i
R
r
s
r,
m
i,
x
s
r,
m
i,
k
s)
(m,
F
+
∑
=
⎟⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎝
⎛
∑
=
∑
∈
∑
=
∑
∈
−
∑
=
+
∑
=
∑
∈
+
∑
∈
=
(3.6)
która b
ędzie minimalizowana.
5. ROZWI
ĄZANIE PRZYKŁADOWEGO ZADANIA OPTYMALIZACYJNEGO
Dla weryfikacji podanego powy
żej podejścia dokonano wyboru lokalizacji centrum dla
obszaru na którym zidentyfikowano 22 dostawców i 20 odbiorców. Z analizy wst
ępnych
danych wyselekcjonowano 10 potencjalnych miejsc lokalizacji centrum. Dostawy towarów
182
Modelowanie usług transportowych w obszarze działania centrum logistyczno-dystrybucyjnego
realizowane s
ą czterema typami środków transportowych. Zatem wyróżnione w punktach
drugim i trzecim zbiory b
ędą miały postać:
•
M ={m: m=1,2,...,10};
•
I = { i: i=1,2,...,22};
•
J = { j: j=1,2,...,20};
•
S = {s: s=1,2,3,4}.
Zakładamy,
że przewożony jest jeden rodzaj towaru. Należy znaleźć optymalną, ze
wzgl
ędu na koszty, organizację usług transportowych w obszarze CL. Oczywiście
poszukujemy takiej lokalizacji centrum, aby funkcja kryterium zapisania formuł
ą (3.6) przy
spełnieniu ogranicze
ń (3.1), ( 3.2), ( 3.3), ( 3.4), ( 3.5) osiągała wartość minimalną.
Rozwi
ązania problemu dokonane jest dwuetapowo. W pierwszym etapie wykorzystano
program komputerowy
Algorytm jola działaj
ący w środowisku DEPHI 7.0 którym obliczono
wła
ściwy (optymalny) dobór środków transportowych do relacji.
W drugim etapie wykorzystano program firmy LINDO SYSTEMS INC - pakiet
LINGO 7.0 którym obliczono optymaln
ą lokalizację centrum uwzględniającą dobór środków
transportowych do relacji [6]. Rozwi
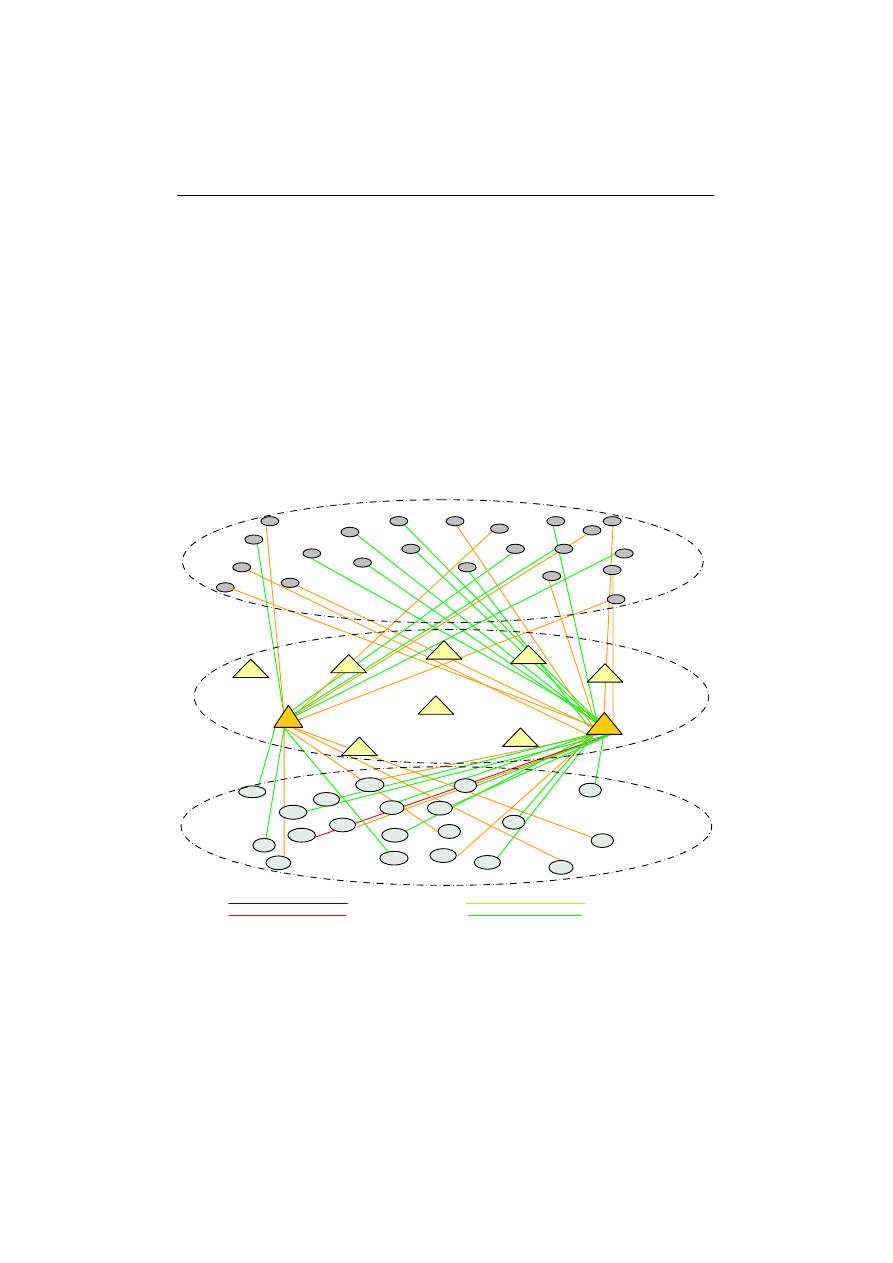
ązanie graficzne przedstawiono na rys 2.
Rys. 2. Ilustracja rozwi
ązania zadania.
Źródło: opracowanie własne.
W wyniku przeprowadzonych oblicze
ń wytypowane zostały 2 lokalizacje centrum
spo
śród potencjalnych 10 dla badanego obszaru. Wykorzystano trzy spośród czterech danych
typy
środków transportowych, oczywiście w różnych relacjach różne. Funkcja celu (koszty
17
Potencjalne
lokalizacje CL
1
13
3
4
7
8
9
10
11
12
15
2
14
16
18
19
20
21
22
5
8
2
9
4
7
5
6
1
1
2
3
8
10
9
4
5
7
10
DOSTAWCY
ODBIORCY
6
2
20
19
18
17
16
15
14
13
12
11
2. typ
środka transportowego
4. typ
środka transportowego
3. typ
środka transportowego
1. typ
środka transportowego
6
7
3
183
Jolanta
Żak
zwi
ązane z transportem i magazynowaniem) dla danego rozwiązania wynoszą
F (m, s)= 80266,68 PLN na dob
ę.
6. WNIOSKI
Zaproponowane w artykule podej
ście pozwala na wyznaczanie optymalnej ze względu
na koszty, organizacji usług logistycznych w obszarze działania centrum logistyczno-
dystrybucyjnego. Mo
żna również przeprowadzić analizę poprawności lokalizacji istniejących
centrów logistycznych dla wybranego obszaru usług.
Dodatkowym atutem proponowanego podej
ścia jest możliwość wyznaczenia lokalizacji
projektowanego lub oceny istniej
ącego centrum logistycznego dla wybranego obszaru usług
transportowych, uwzgl
ędniając właściwy dobór środków transportowych, jak również
ustalenie wielko
ści przepływów towarów między centrami logistycznymi.
Dwuetapowa metoda rozwi
ązania posiada tę zaletę, że pozwala na wykorzystanie
pierwszej cz
ęści tj.
wyznaczania wła
ściwego doboru środków transportowych do realizacji zadania
transportowego niezale
żnie od rozwiązania problemu lokalizacji. Umożliwia to rozwiązywanie
problemów zwi
ązanych tylko z właściwym doborem środków transportowych.
Jedyna uci
ążliwość metody związana jest z drugim etapem rozwiązywania zadania
polega ona na wprowadzeniu bardzo du
żej liczby danych wejściowych.
LITERATURA
[1]
Fijałkowski J.: Transport wewn
ętrzny w systemach logistycznych, Oficyna Wydawnicza
Politechniki Warszawskiej, Warszawa 2000.
[2]
Jacyna M.: Multicriteria Evaluation of Traffic Flow Distribution in a Multimodal Transport
Corridor, Taking into Account Logistics Base Service, Archives of Transport, Polish Academy
of Sciences, Com. of Transport, vol.10 iss.1-2, Warsaw 1999.
[3]
Jacyna M., Wasiak M.: Wieloaspektowa ocena organizacji centrów logistycznych w
hierarchicznym systemie dystrybucji, Wyd. Prace Naukowe, Akademii Morskiej w Gdyni.
Gdynia 2003.
[4]
Piasecki S, Kaszubowski Z: Optymalizacja systemów zaopatrzenia, PWN 1982.
[5]
Mundur L. (red): Metodyka lokalizacji i kształtowania centrów logistycznych w Polsce,
Kolejowa Oficyna Wydawnicza, Warszawa 2000.
[6]
Żak J.: Metoda lokalizacji centrum logistycznego w wybranym obszarze usług transportowych,
Rozprawa doktorska, Wydział Transportu PW 2005.
TRANSPORTATION SERVICES MODELING FOR LOGISTICS CENTER SURROUNDINGS
Abstract
Article presents an approach to modeling logistics services for logistics centre surroundings. Formal
description of customer demands, production supply and transportation system structure is proposed. In order to
solve the problem author provides formulation of transportation services modeling optimization task for logistics
centre surroundings likewise the computational example.
Keywords: services modeling, optimization, transportation network, logistics centre, distributional centre.
Recenzenci: Mirosława D
ąbrowa-Bajon, Marianna Jacyna
184