1

Optoelektronika I ETE6621W

Prowadzący dr inż. Marek Tłaczała

Wyk. 1. 26.02.2004

dr hab. inż. Marek Tłaczała
konsultacje: Wt, Czw 14

15

-16

00

www.wemif.pwr.wroc.pl/zpp/dydaktyka

Lit:

Z. Bielecki, A. Rogalski- Detekcja sygnałów optycznych
Hill, Boot- Optoelektronika

Pasmo promieniowania:

λ

=0,01

÷

1000

µ

m

h

ν

=0,001

÷

100eV

ν

=3*10

16

÷

3*10

11

Hz

Pasmo widzialne (od ultrafioletu do podczerwieni):

λ

=0,38

÷

0,78

µ

m

h

ν

=3,3

÷

1,65eV

]

[

24

,

1

]

[

eV

h

m

υ

µ

λ

=

WSTĘP DO OPTOELEKTRONIKI

Optoelektronika jest techniką systemów i przyrządów, które emitują, modulują, transmitują lub
wykrywają światło.
Badanie i wykorzystywanie zjawisk rozchodzenia się, obróbki i oddziaływania promieniowania, a
także emisji oraz detekcji promieniowania optycznego do konstrukcji i budowy układów
optoelektronicznych czyli takich, które pracują z dwoma rodzajami sygnałów: optycznym i
elektrycznym, a także z akustycznym i magnetycznym.

Właściwości optoelektroniki:
1. Budowa źródeł światła i detektorów
2. Zakres częstotliwości (foton (brak ładunku), nie elektron)

•

Szybkość transmisji

•

Gęstość zapisu (1/

λ

2

)

•

Szybkość obróbki

•

Czas dostępu

3. Obojętność toru informatycznego na zakłócenia

•

Pełna izolacja międzykanałowa

•

Pełna izolacja galwaniczna 10

16

Ω

, 10

6

V, 10

-4

pF

•

Brak sprzężenia między odbiornikiem a nadajnikiem

4. Obciążalność funkcjonalna

•

Modulacja AM, FM

•

Faza i polaryzacja

•

Kierunek rozprzestrzeniania się fali

5. Możliwość przedstawiania końcowej informacji w postaci obrazów RGB
6. Kompatybilność z innymi technologiami (np. z technologią krzemową), taniość i dostępność
surowca
7. Wysoka pojemność informatyczna kanału, mała tłumienność, duża dobroć układu,
jednokierunkowość sprzężenia

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

2

Dobroć układu- parametr opisujący element optoelektroniczny i jest to iloczyn mocy dysponowanej
danego elementu i kwadratu częstotliwości odniesiony do 1/c

2

.









=

2

2

2

1

m

W

Pf

c

Q









=

2

3

10

m

W

Q

el

1W/1GHz









=

2

10

10

m

W

Q

oe

10mW/300THz

7

10

=

el

oe

Q

Q

Dziedziny optoelektroniki

1. optoelektronika światłowodowa

•

technika światłowodowa

•

optoelektronika zintegrowana

•

optotelekomunikacja

2. optoelektronika obrazowa
3. optoelektronika fotowoltaiczna
4. optoelektronika informatyczna
5. optoelektronika laserowa
6. optoelektronika oświetleniowa

Ad. 1 Optoelektronika światłowodowa
Technika światłowodowa

1. Światłowodowa optyka gradientowa: soczewki światłowodowe, multipleksery wielofalowe.
2. Obrazowody światłowodowe: obrazowody wiązkowe, płytki światłowodowe, noktowizory,

korektory obrazu, TV wysokiej jakości 50 linii/mm.

3. Czujniki światłowodowe: detektory pól fizycznych i wielkości chemicznych.
4. Transmisja dużej mocy optycznej: dla laserów NdYAG, CO

2

, noże chirurgiczne, spawanie

przemysłowe.

Optoelektronika zintegrowana

1. Układy i systemy planarne dla fal optycznych będące analogiem układów elektronicznych typu

VLSI.

2. Operowanie sygnałem optycznym wielowymiarowym, np. informacja obrazowa.
3. Elementy i układy podstawowe: lasery i fotodetektory planarne, światłowody planarne,

sprzęgacze planarne, elementy optyczne, soczewki, filtry, pryzmaty, siatki dyfrakcyjne,
zwierciadła, konwertery modów, deflektory, modulatory, konwolutory, korelatory, pamięci
optyczne, mikroprocesory optyczne, elementy nieliniowe.

Głównym

celem

rozwoju

OZ

jest

budowa

całkowicie

optycznego

regeneratora

dla

optotelekomunikacji oraz budowa komputerów optycznych.

Optotelekomunikacja

1. Systemy transmisyjne dalekosiężne wzmacniakowe lądowe i morskie; zwiększenie:

•

przepływności informacyjnej,

•

odległości międzywzmacniakowej,

•

niezawodności działania i czasu życia,

•

odporności na działanie środowiska.

2. Lokalne sieci światłowodowe:

•

miejskie,

•

obiektowe: budynki biurowe, szpitale, okręty, samoloty...

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

3

•

informatyczne: połączenia wewnętrzne i komputerowe,

•

przemysłowe – dla bardzo trudnych warunków środowiskowych,

•

wojskowe.

Ad 2. Optoelektronika obrazowa

1. Poligrafia optoelektroniczna
2. Grafika komputerowa
3. Sztuczna wizja
4. Obróbka obrazów
5. Wyświetlacze

Ad. 3. Optoelektronika fotowoltaiczna

1. Słoneczna Optoelektronika - energetyczna.
2. Problemy konwersji różnych form energii optycznej na energię elektryczną (magazynowaną).

Ad. 4. Optoelektronika informatyczna

1. Dziedzina korzystająca głównie z osiągnięć optoelektroniki zintegrowanej i holografii.
2. Cyfrowe układy optyczne o pasmach terabitowych.
3. Masowe pamięci optyczne.

Celem jest budowa komputera optycznego.

Ad. 5. Optoelektronika laserowa

1. Lasery półprzewodnikowe i dielektryczne miniaturowe dla OZ, TŚ i optotelekomunikacji.
2. Lasery do zastosowań medycznych i przemysłowych (mikroobróbka materiałów).
3. Lasery do zastosowań metrologicznych.
4. Elementy, układy i systemy laserowe.

Kierunki rozwoju: stabilizacja laserów, lasery bardzo dużej mocy, nowe materiały i nowe pasma
pracy.

Stan rozwoju nauki i techniki w dziedzinie optoelektroniki

1. Światłowodowe soczewki gradientowe o znacznie większych aperturach i jakości lepszej od

soczewek klasycznych, refrakcyjna szerokopasmowa korekcja aberracji.

2. Wiązkowe obrazowody koherentne o rozdzielczości optycznej do 150 par linii/mm.
3. Ekrany telewizyjne o powierzchni kilku metrów kwadratowych.

Niebieska optoelektronika
Półprzewodnikowe diody laserowe emitujące niebieskie światło pozwalają na czterokrotne
zwiększenie ilości informacji na dyskach optycznych (DVD-RAM). Obecnie do zapisu i odczytu
informacji z tych dysków stosuje się lasery czerwone. Pojedyncze kryształy azotku galu (wg PAN)
uzyskuje się wykorzystując olbrzymie ciśnienie (porównywalne z potrzebnym do produkcji
sztucznego diamentu). Tak uzyskane monokryształy są podstawą struktury lasera. W innych ośrodkach
światowych laser buduje się na szafirze. Monokryształy azotku galu mają jednak w stosunku do
szafiru, co najmniej 10 tyś. razy mniej defektów struktury. Defekty struktury, które pojawiają się przy
tworzeniu struktury laserowej na szafirze, prowadzą do strat optycznych - zabijają emisje światła.
Defekty rozpraszają też światło, które podróżując w krysztale musi ulec wzmocnieniu. Struktura
podłoża musi być bardzo wysokiej jakości, by dawać jak najmniej strat optycznych. Oprócz dysków
optycznych niebieskie diody znajdą zastosowanie w drukarkach laserowych ultra-wysokiej
rozdzielczości, diagnostyce medycznej, a także w monitoringu środowiska.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

4

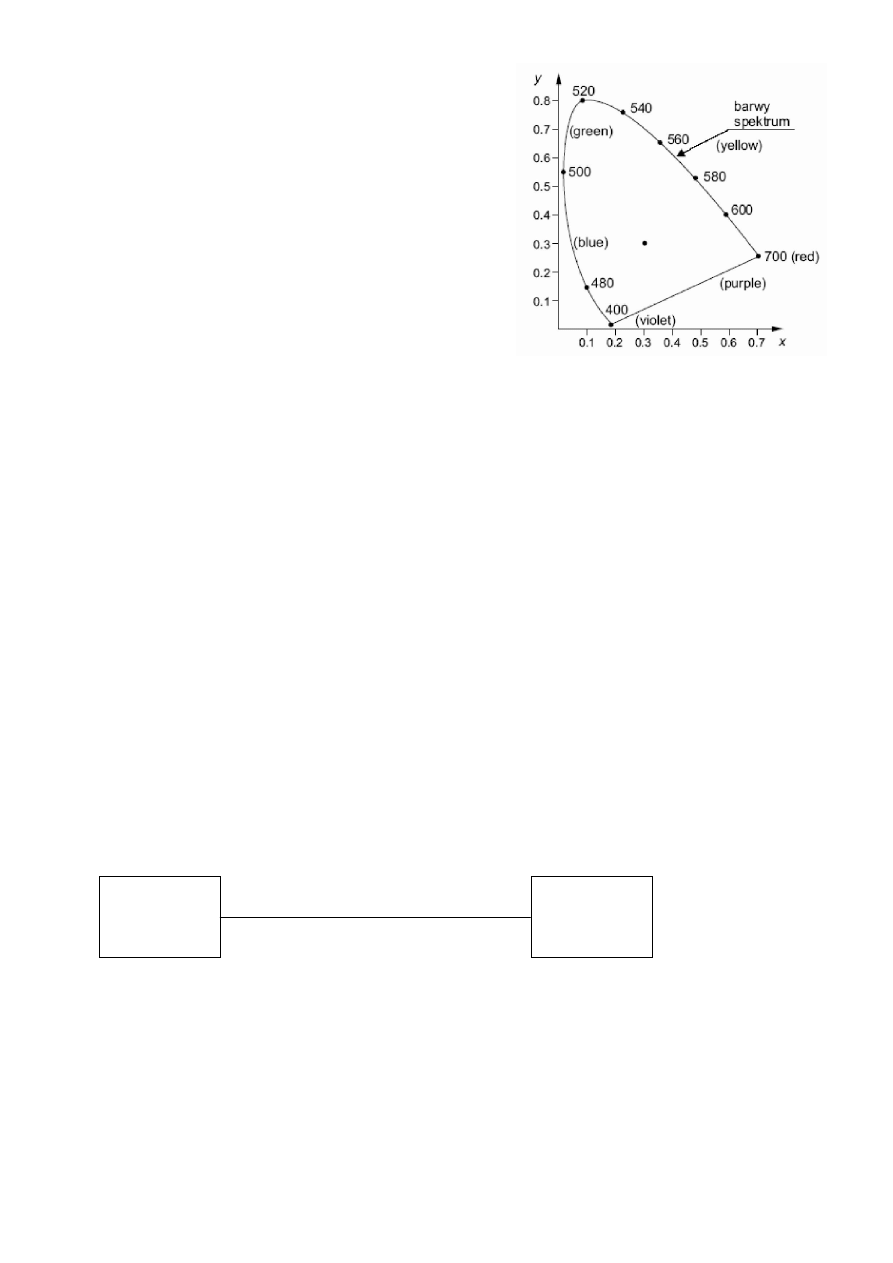
Diagram chromatyczności.
Diagram chromatyczności został zaprojektowany na
bazie trzech podstawowych kolorów, z ludzkiej
perspektywy widzenia. Wcale nie jest konieczne
określenie natężenia wszystkich trzech bazowych
kolorów, ponieważ jasność światła (suma wszystkich
natężeń) nie ma wpływu na odcień. Możemy po prostu
używać ułamkowych natężeń dwóch podstawowych
kolorów. Suma wszystkich trzech natężeń musi się
równać jeden, więc bardzo łatwo można policzyć trzeci
ułamek.

Żeby

uniknąć

ujemnych

ułamków

dla

podstawowych kolorów, Międzynarodowa Komisja ds.
Iluminacji opublikowała w roku 1931 standardowy
diagram chromatyczności.

Zalety światła białego:

•

Oszczędność 80-90% energii

•

Stopniowa degradacja źródła światła

•

Czas życia ponad 100tys. godzin (ponad 11 lat)

Zastosowania Optoelektroniki

•

telekomunikacja światłowodowa

•

czujniki dla potrzeb metrologii, automatyki i robotyki

•

komputerowe sieci odporne na zakłócenia

•

przekształcanie informacji obrazowych z obszaru widma niewidzialnego na widzialne

•

wzmacnianie kontrastowości i jaskrawości obrazu

•

mikroobróbka laserowa układów elektronicznych

•

obróbka tworzyw za pomocą wysokoenergetycznych wiązek laserowych

•

tworzenie nowych narzędzi i metod chirurgicznych

•

technika holograficzna

•

przetwarzanie energii promieniowania słonecznego na energię elektryczną

•

konstrukcja płaskich monitorów (ciekłokrystaliczne i diodowe)

•

magazynowanie danych (cd-rom, dvd)

•

światła sygnalizacyjne i ostrzegawcze o dużej jasności i niezawodności

Wyk. 2. 04.03.2004

`

tor transmisyjny

Nadajnik, podstawą jest źródło światła (generatory sygnałów, lasery LP, diody elektroluminescencyjne
LED). W skład nadajnika wchodzi również szereg innych układów optoelektronicznych (np.
modulatory, pryzmaty, soczewki). Torem transmisyjnym może z kolei być światłowód, powietrze.
Odbiornikiem zazwyczaj jest detektor (w najprostszym przypadku dioda półprzewodnikowa
spolaryzowana w kierunku zaporowym). Nadajnik wykorzystuje zjawisko generacji (do produkcji
nadajników wykorzystuje się pierwiastki grupy AIIIBV, dla I okna telekomunikacyjnego GaAs, dla II
i III okna In

x

Ga

1-x

As/InP), tor zjawisko rozchodzenia się światła, odbiornik absorpcje (do produkcji

wykorzystuje się pierwiastki grupy AIIIBV, lub AIIBVI).

Nadajnik

N

Odbiornik

O

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

5

Oznaczenia:
E

g

(szerokość przerwy wzbronionej), n (współczynnik załamania materiału),

α

(absorpcja), R(odbicie),

T (przepuszczanie),

χ

(przechwyt fotonów w zależności od koncentracji centrów).

CHARAKTERYSTYKI OPTYCZNE CIAŁA STAŁEGO
Równanie fali elektromagnetycznej płaskiej:























 −

=

ν

πν

x

t

i

E

E

o

2

exp

, rozpisując to dalej otrzymamy























 −

=

x

c

n

t

i

E

E

o

*

exp

ω

ω

, gdzie n*- zespolony współczynnik załamania, rozpisując n* mamy:







−









−

=

x

c

x

c

n

t

i

E

E

o

ωκ

ω

ω

exp

exp

(1)

ω

- częstotliwość, t- czas,

κ

- współczynnik pochłaniania (tłumienia) w danym materiale,

Pierwszy czynnik (1) określa fazę, drugi zależność wygaszania fali i głębokość wnikania.

2

E

I

=











−

=

x

c

E

I

o

ωχ

2

exp

2

)

exp(

x

I

I

o

α

−

=

Właściwości przewodników są selektywne, co oznacza że zależą one od częstotliwości.

Współczynnik absorpcji

λ

πχ

α

4

=

[1/cm]

Prędkość rozchodzenia się promieniowania w półprzewodniku, którego zespolony współczynnik
załamania:

n

*

=n-i

κ

wiąże się z prędkością światła w próżni c wzorem:

v=c/n

*

Czyli

1/v=n/c-i

κ

/c

Ostatni człon we wzorze jest czynnikiem tłumiącym. Po przejściu fali przez materiał o grubości x i
przewodności pozostaje jedynie ułamek mocy:

α

czyli:

gdzie

κ

jest to część urojona zwana współczynnikiem ekstynkcji.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

6

x

α

- głębokość na której tłumienie maleje e-razy

=

=

α

Znając współczynnik

α

możemy wyznaczyć grubość obszaru czynnego. Jeżeli

α

zależy od I to mamy

do czynienia z optyką nieliniową, jeżeli natomiast zależy od kierunku to mamy do czynienia z
ośrodkiem anizotropowym.

Współczynnik załamania n:
Prędkość rozchodzenia się światła w półprzewodniku na podstawie równań Maxwella możemy
określić jako:

Biorąc po uwagę zależność

i przyrównując części rzeczywiste i urojone obu równań otrzymamy:

Po rozwiązaniu tych równań ze względu na i

κ

otrzymujemy, że:

Współczynnik załamania n określa stosunek prędkości rozprzestrzeniania się fali w próżni do
prędkości fali w danym ośrodku (materiale)

.

=

Dla ośrodka izotropowego (jednorodnego) n nie zależy od kierunku rozchodzenia się fali i polaryzacji,
dla ośrodka anizotropowego n zależy od kierunku rozchodzenia się fali i polaryzacji. Zmieniać wartość
współczynnika n możemy poprzez zmianę koncentracji nośników (np. modulatory Macha-Zehndera)

Współczynnik odbicia

R:

Padające światło na p-p częściowo się odbija. Opisuje to zależność:

Pozostała część która wnika nazywamy współczynnikiem transmisji T=1-R.
Dla materiału przezroczystego, czyli gdy

κ

=0:

Gdy =0 to =1 i półprzewodnik odbija całkowicie promieniowanie.
Gdy materiał nie jest przezroczysty ani całkiem odbijający, to występują straty promieniowania
spowodowane absorpcją:

Najogólniej R jest to stosunek natężenia fali padającej do fali odbitej:

=

)

exp(

)

1

(

1

α

−

−

=

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

7

αν

χ

=

, gdzie

χ

- charakterystyka opisująca wpływ centrów rozproszenia, N- przekrój skuteczny na

wychwyt fotonów.

∫

=

ν

ν

α

σ

)

(

,

σ

- przekrój poprzeczny całkowity czynny na wychwyt fotonów

α

- opisuje procesy absorpcyjne w ciele stałym (np. w

półprzewodniku).

α

(

ν

)-

α

zależy od

ν

Wszystkie

charakterystyki

optyczne

są

funkcją

długości

promieniowania.

Całość

dotyczy

wymiany

energii

w

półprzewodnikach.
Podsumowując: n,

α

,

χ

, R,

κ

=f(

ν

)=f(

λ

)

Fonon- skwantowane drgania sieci krystalicznej. Energia fononu zależy od wektora falowego. Każde
dwa atomy o masach M

1

i M

2

oddalone są od siebie w odległości a oddziaływają na siebie i drgają. Z

tymi drganiami związana jest energia i częstotliwość drgań.


M

1

M

2

Częstotliwość drgań wynosi:

5

,

0

2

1

2

1

2

1

)

sin(

4

1

1

1

1















−









+

±









+

=

±

ν

,

gdzie:

a

f

-

oddziaływanie międzyatomowe miedzy dwoma sąsiednimi atomami

M

1

, M

2

- masy atomów

k- wektor falowy

a- odległość miedzy atomami

0

→

0

→

−

ν

w punkcie najwyższej symetrii

Γ

(000)

~

−

ν

(przy założeniu że k jest bardzo małe) mamy fonony

akustyczne A (o czest. akustycznej)
Rozróżniamy dwa rodzaje fononów akustycznych podłużne LA i
poprzeczne TA.

Inne rozwiązanie ma postać:

5

,

0

2

1

1

1

2





















+

=

+

ν

, częstotliwość zależy tylko od mas M

1

i M

2

.

Gdy

+

ν

to wówczas częstotliwości są dużo większe

≈

częstotliwości optycznej i wtedy mamy do

czynienia z fononami optycznymi O. Wyróżniamy fonony optyczne podłużne LO i poprzeczne TO.
Powyżej zera bezwzględnego każdy atom drga, co powoduje, że wpływa na widmo promieniowania.
Fotony generują fonony, co jest zjawiskiem niekorzystnym, choć zjawisko fononowe jest
wykorzystywane w detektorach.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

8

Wykład 3

11.03.2004

Widmo ekscytonowe
Ekscytron (wzbudzenie atomu) należy do stanu ładunkowo obojętnego i nie odpowiada za żaden
transport energii (jest elektrycznie obojętny). Ogólnie ekscytron to para elektron swobodny i dziura
swobodna miedzy którymi występuje oddziaływanie kulombowskie. Poruszający się ekscytron ma
energie kinetyczną:

)

(

2

*

*

2

+

=

h

,

k- wektor falowy związany z ruchem środka ciężkości
ekscytonu

Jonizacja atomu powoduje powstanie ekscytronu, a energia
jonizacji takiego układu wynosi:

2

2

4

*

1

2

ε

h

−

=

,

przy czym jest liczbą całkowitą ≥1, wskazującą różne stany ekscytonowe, a m

r

*

jest masą

zredukowaną

*

*

*

1

1

1

+

=

,

przy czym

i

są masami efektywnymi (zredukowanymi) elektronu i dziury.

Jeżeli natężenie lokalne pół jest większe od natężenia pola kulombowskiego wewnątrz ekscytronu,
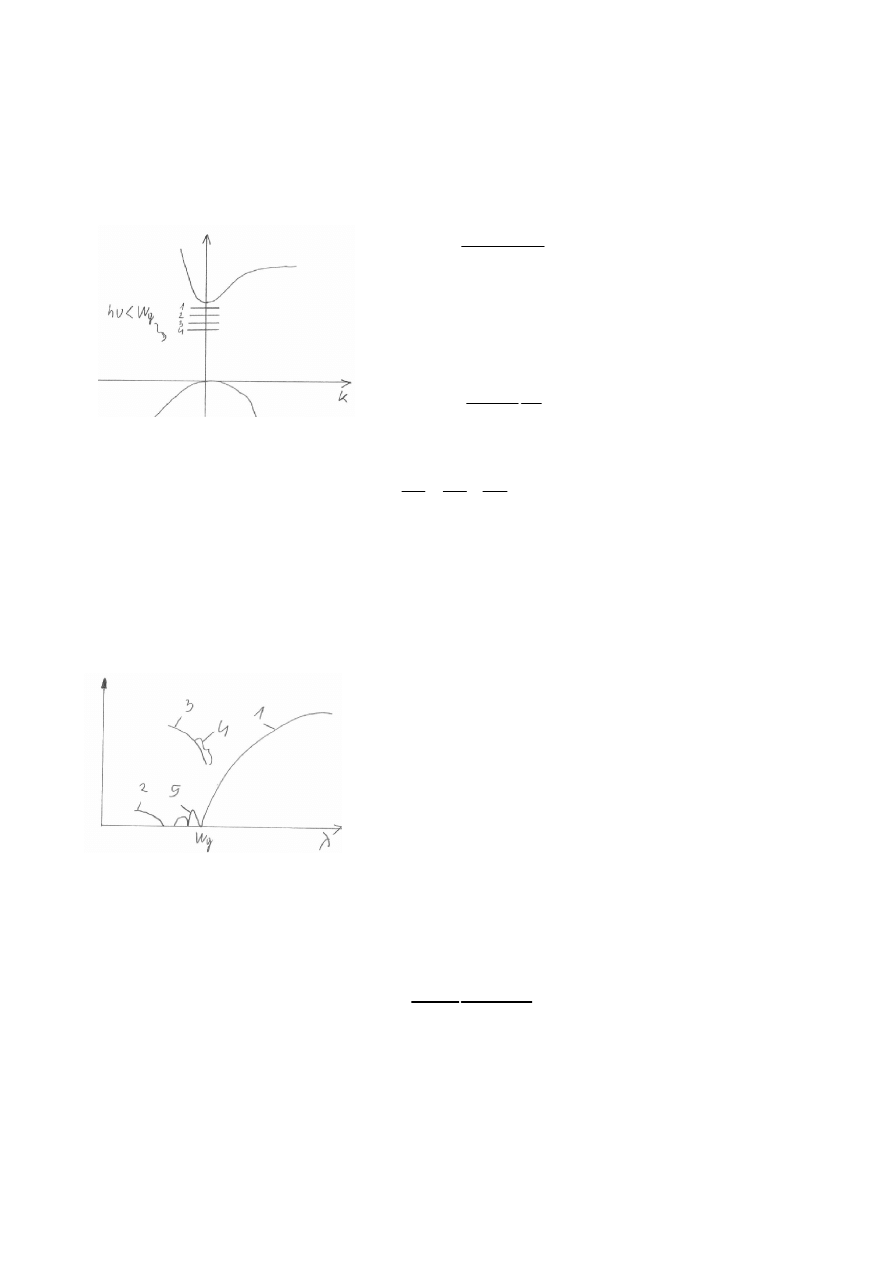
wówczas ekscytron rozpadnie się. Absorpcja zachodzi gdy h

υ

≥W

g

, a poziomy ekscytonowe mogą

powstać gdy h

υ≈

W

g

≤W-E

ex

. Para ekscytonowa nie jest odpowiedzialna za transport ładunku, ale może

się poruszać i dawać pewną sumę energii, którą można nazwać optyczną. Pojawienie się widma
ekscytonowego mówi o tym, że półprzewodnik ma bardzo dobrą, niezaburzoną strukturę.

Rodzaje absorpcji:
1- absorpcja podstawowa
2- absorpcja fononowa
3- pochłanianie na domieszkach
4- absorpcja na swobodnych nośnikach
5- piki ekscytonowe

ABSORPCJA
W procesie absorpcji foton o znanej energii wzbudza elektrony z niższych do wyższych stanów
energetycznych. Absorpcję wyrażamy poprzez współczynnik absorpcji

α

(h

υ

)

który jest

zdefiniowany jako względna szybkość zmniejszania się natężenia światła wzdłuż jego drogi
poruszania się

))

(

(

)

(

1

ν

ν

α

=

Przykładem absorpcji jest oddziaływanie foton-półprzewodnik. Do mechanizmów absorpcji
zaliczamy: przejścia elektronowe i wzbudzenie drgań sieci krystalicznej (generacja stanów
fononowych).

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

9

Rodzaje absorpcji:
1. Absorpcja podstawowa
Absorpcja podstawowa obejmuje przejścia międzypasmowe
oraz ekscytonowe, tzn. wzbudzenia elektronów z pasma
walencyjnego

do

pasma

przewodnictwa.

Absorpcja

podstawowa, charakteryzująca się gwałtownym wzrostem
wartości współczynnika absorpcji, może służyć do wyznaczania
wartości przerwy energetycznej półprzewodnika. Jednak, ze
względu na to, że przejścia podlegają pewnym regułom wyboru,
bezpośrednia ocena wartości przerwy energetycznej z krawędzi
absorpcji nie zawsze jest możliwa, gdyż muszą być również
wzięte pod uwagę procesy towarzyszące absorpcji. Współczynnik absorpcji

α

(h

υ

) dla danej energii

fotonu h

υ

jest proporcjonalny do prawdopodobieństwa P

pk

przejścia ze stanu podstawowego do stanu

końcowego i do gęstości dostępnych (pustych) stanów końcowych n

k

Ponadto proces ten musi być

sumowany po wszystkich możliwych przejściach pomiędzy stanami odległymi od siebie o energię h

υ

∑

=

)

(

ν

α

2. Absorpcja na drganiach sieci krystalicznej

(pochłanianie na fononach, pochłanianie fononowe).

3. Pochłanianie na domieszkach

(domieszkowe).

4. Absorpcja na swobodnych nośnikach.

Skąd to się bierze?

)

(

)

(

ν

ν

α

=

gdzie: P

pk

- prawdopodobieństwo przejścia ze stanu początkowego do końcowego

N(h

υ

)- kombinowana gęstość stanów energetycznych końcowych, uwzględnia liczbę zajętych

stanów początkowych i liczbę stanów pustych oddalonych o h

υ

.

P

pk

=|M

pk

|

2

=|V

pk

|

2

, gdzie ostatnia część to kwadrat z elementów macierzy

opisującej wszystkie możliwe przejścia. Jeżeli w punkcie najwyższej symetrii

Γ

(000) jest różne od 0 to zakładając że P

pk

=const≠ , to mamy przejścia

dozwolone proste.

0

=

−

=

∆

→

przejścia proste

Przejściami rządzą dwa prawa:

I. prawo zachowania energii

0

1

=

∑

∞

=

=

II. prawo zachowania wektora falowego (albo kwazipędu)

0

1

=

∑

∞

=

=

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

10

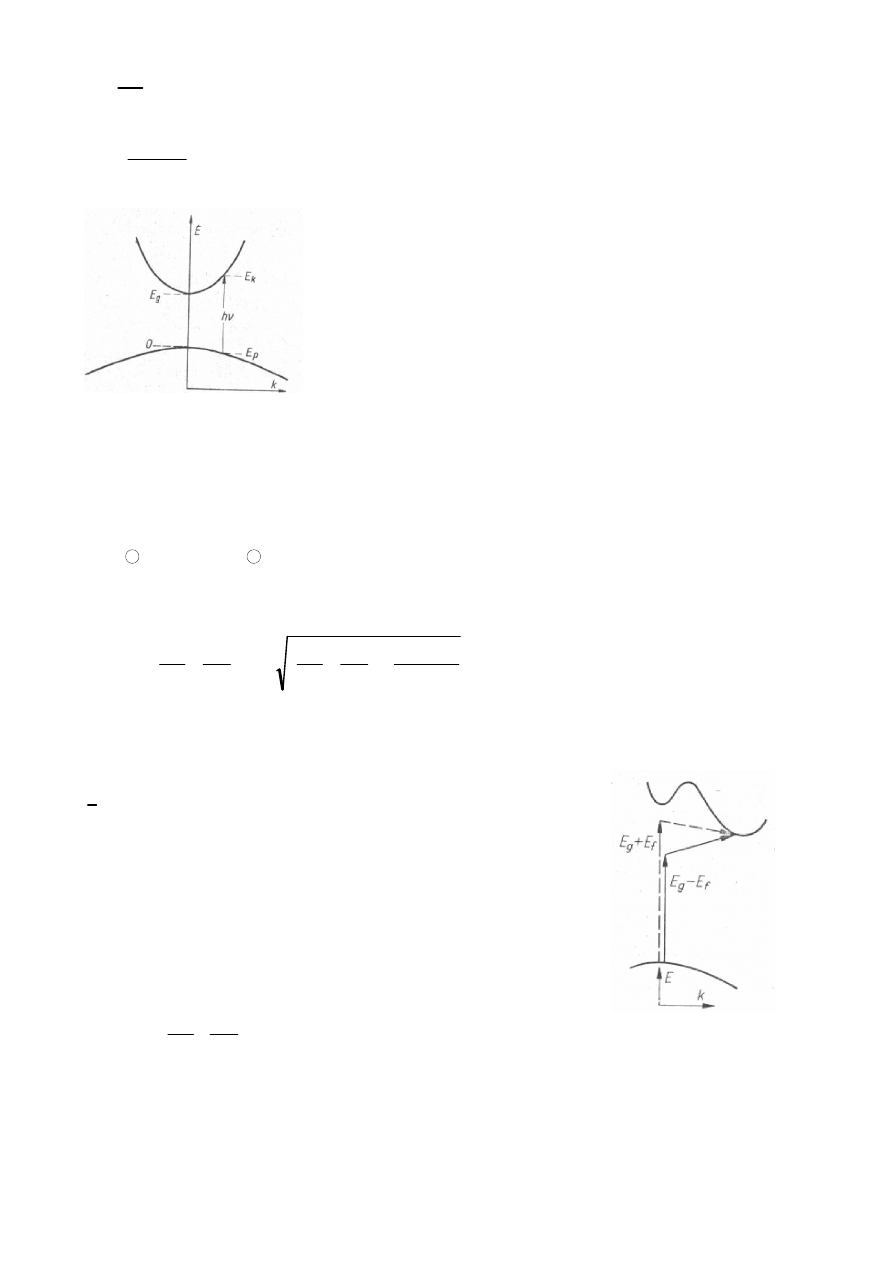
Przy przejściach absorpcyjne pomiędzy dwiema dolinami oddzielonymi przerwa energetyczną E

g

(przy założeniu, że wszystkie przejścia zachowujące pęd elektronu są dozwolone P

pk

jest niezależne od

k) każdy stan wyjściowy o energii E

p

związany jest ze stanem końcowym o energii E

k

. Wartości tych

stanów opisują wzory:

-energia początkowa:

*

2

2

2

h

−

=

-energia końcowa:

*

2

2

2

h

=

Po pochłonięciu fotonu zgodnie z zasadą zachowania energii w pasmach parabolicznych mamy:

*

2

2

*

2

2

2

2

h

h

+

=

−

ν









+

=

−

*

*

2

2

1

1

2

h

ν

Podstawiając za

*

*

*

1

1

1

=

+

otrzymamy

*

2

2

2

h

=

−

ν

(1)

Rozkład gęstości stanów.
W przestrzeni wektora falowego stany dozwolone są rozłożone w sposób równomierny.
Powierzchnie stałej energii są w przybliżeniu sferyczne, tak więc objętość w przestrzeni wektora
pomiędzy powierzchniami o energii

oraz

(lub między a

) wynosi

π

Ponieważ

pojedynczy stan zajmuje w przestrzeni pędów objętość

π

(przy czym

jest objętością

pojedynczego kryształu) oraz każdemu poziomowi energetycznemu odpowiadają dwa stany
(różne spiny), więc liczba stanów w przedziale energii między

oraz

υ

υ υ

wynosi:

( )

3

2

8

4

2

π

π

ν

ν

=

,

skracając otrzymamy

( )

2

2

π

ν

ν

=

(2)

Po zróżniczkowaniu (1) otrzymamy:

*

2

)

(

h

=

ν

(3)

5

,

0

)

(

'

−

=

ν

(4)

Wstawiając do równania (2) zależności z (3) i (4) otrzymamy:

5

,

0

)

(

"

)

(

−

=

ν

ν

α

, gdzie A”- stała materiałowa

Przejścia proste wzbronione:

W niektórych materiałach reguły kwantowe wyboru wzbraniają przejść dla k=0, ale zezwalają na przejścia przy
k≠0, przy czym prawdopodobieństwo tych przejść wzrasta z k

2

(P

pk

~ k

2

, dla

Γ

000 V

pk

=0 i P

pk

Γ

000

=0) . W

modelu obok prawdopodobieństwo przejścia wzrasta proporcjonalnie do (

υ

). Ponieważ gęstość stanów biorących udział w przejściach prostych jest

proporcjonalna do (

υ

więc współczynnik absorpcji zależy od

energii fotonów w następujący sposób:

2

3

)

(

'

)

(

−

=

ν

ν

α

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

11

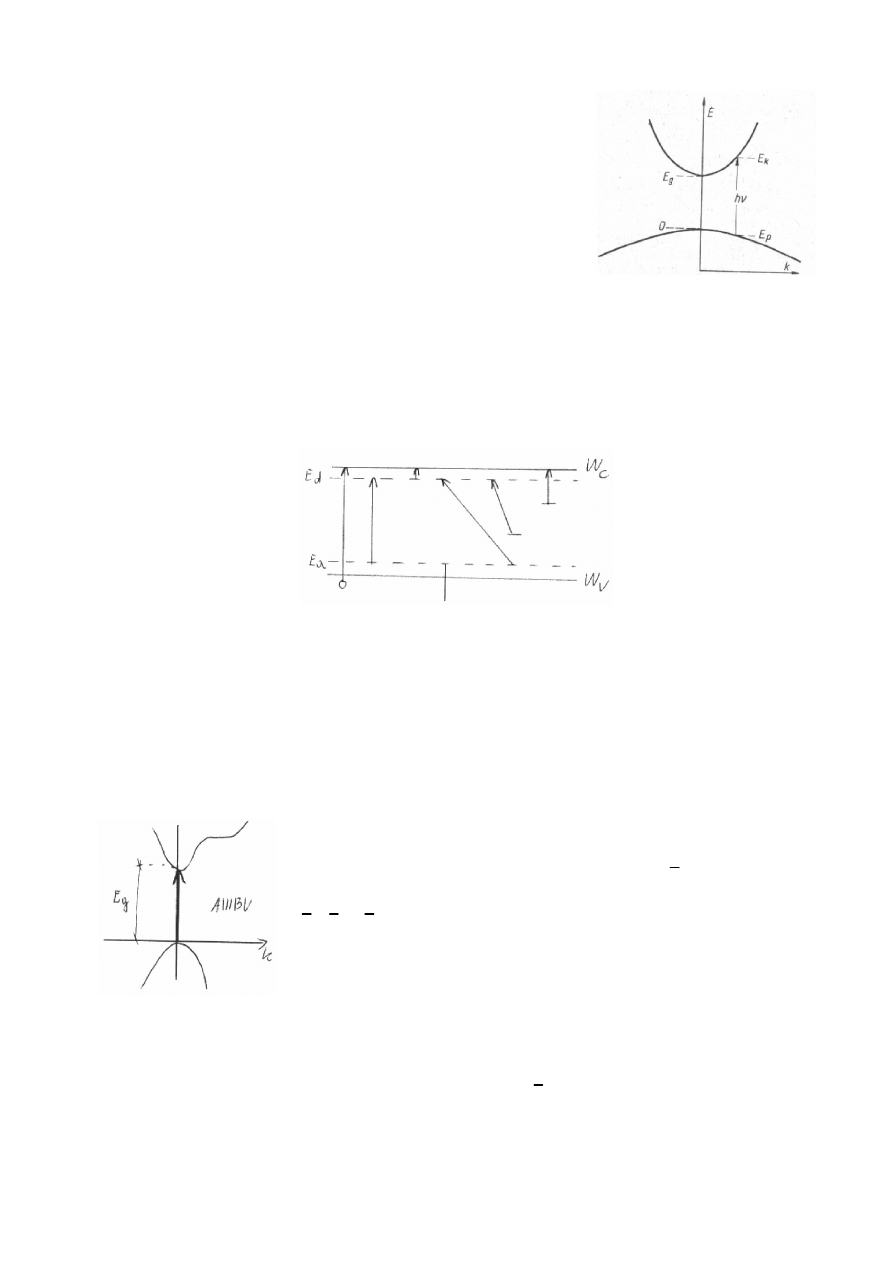
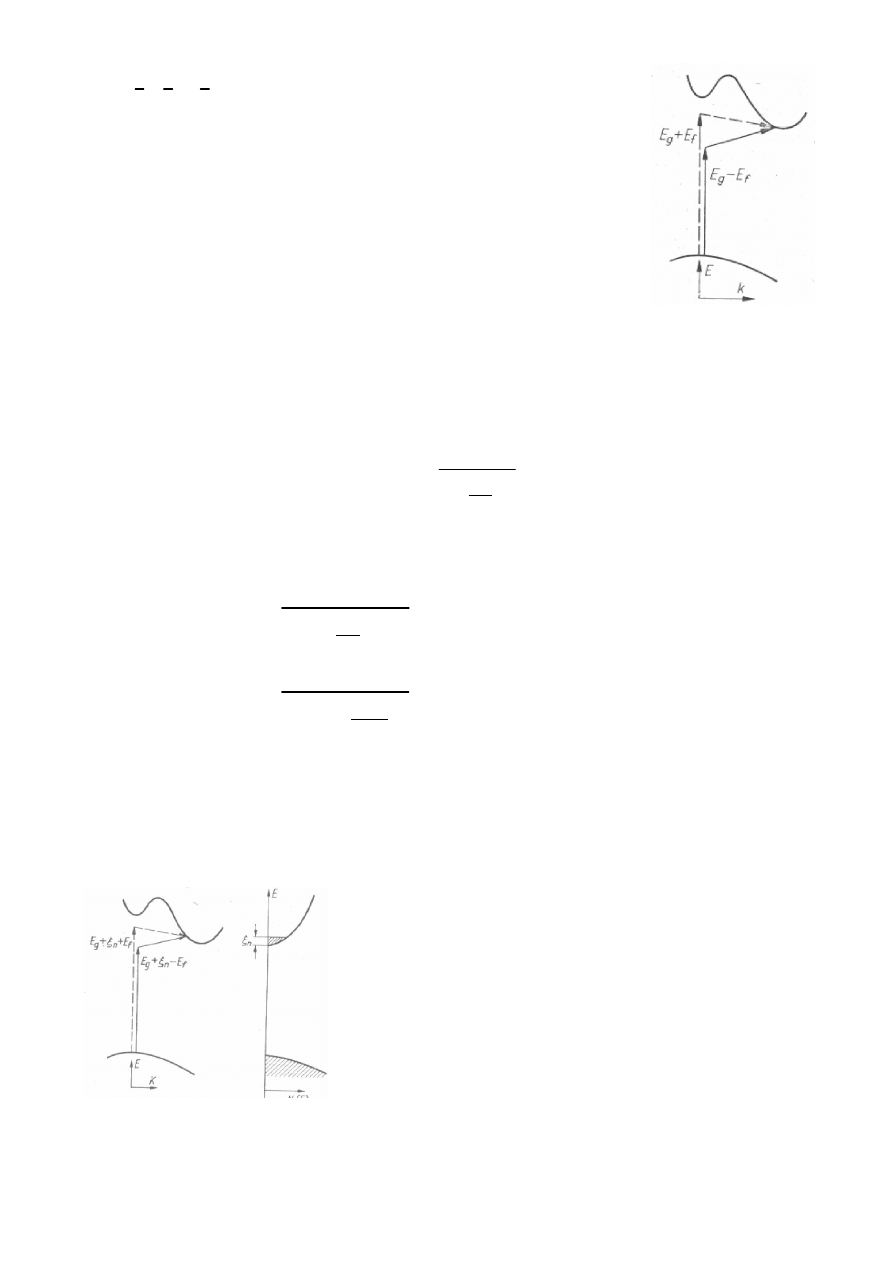
Przejścia skośne:

Gdy

0

≠

−

=

∆

→

przejścia skośne

Jeżeli w przejściu elektron zmienia zarówno energię jak i pęd, to musi
ono przebiegać dwustopniowo, gdyż foton nie może spowodować zmiany
pędu elektronu. Zachowanie padu zawdzięczamy oddziaływaniu z fononem,
co ilustruje rysunek z boku. Fonon jest kwantem drgań sieci. W
przejściach tych spośród szerokiego dostępnego widma fononów
mogą brać udział jedynie fonony o odpowiednim pędzie. Są to zwykle
fonony podłużne lub poprzeczne akustyczne. Każdy z nich ma
charakterystyczną energię

Tak więc w celu uzupełnienia przejścia

z

do

fonon musi być wyemitowany lub zaabsorbowany.

Przejścia skośne mogą następować ze wszystkich zajęt ych stanów
z pasma walencyjnego do wszystkich pustych stanów w paśmie przewodnictwa. Współczynnik
absorpcji jest proporcjonalny do iloczynu gęstości stanów wyjściowych i końcowych,
całkowanego po wszystkich możliwych kombinacjach stanów odległych od siebie o ±

współ-

czynnik

α

jest również proporcjonalny do prawdopodobieństwa oddziaływania elektronów z

fononami, które jest z kolei funkcją liczby fononów N

f

o energii E

f

. Liczba fononów jest dana

przez statystykę Bosego-Einsteina:

1

exp

1

−

=

Prawdopodobieństwo całkowite takiej absorpcji jest iloczynem prawdopodobieństwa P

pk

i

prawdopodobieństwa zabsorbowania fononu P

fon

(jest ono 4-5 razy mniejsze niż dla przejść

prostych). Absorpcję wyraża się wówczas zależnością:

1

exp

)

(

'

"

)

(

2

−









+

−

=

ν

ν

α

–

dla przejść z absorpcja fononu







 −

−

−

−

=

exp

1

)

(

'

"

)

(

2

ν

ν

α

–

dla przejść z emisją fononu

W półprzewodniku występują różne rodzaje fononów (podłużne akustyczne oraz dwa rodzaje
poprzecznych akustycznych), które mogą brać udział w przejściach skośnych. Wszystkie one biorą
udział w przejściach, ale z różnymi prawdopodobieństwami. Gdy półprzewodnik jest silnie
domieszkowany, poziom Fermiego znajduje się wewnątrz pasma (pasma przewodnictwa w materiale typu
n),

na głębokości

ξ

n

.

Ponieważ stany poniżej

ξ

n

są pełne, więc przejścia podstawowe do

stanów poniżej E

g

+

ξ

n

są zakazane i krawędź absorpcji przesuwa

się w stronę większych energii o wartość zbliżoną do

ξ

n

. Prze-

sunięcie krawędzi absorpcji spowodowane wypełnieniem pasm jest
nazywane efektem Bursteina-Mossa. W silnie domieszkowanych
półprzewodnikach z przerwą energetyczną skośną, jest możliwe
spełnienie zasady zachowania pędu dzięki procesom rozpraszania,
takim jak rozpraszanie elektron-elektron lub rozpraszanie na
domieszkach.

W

tych

przypadkach

prawdopodobieństwo

rozproszenia

jest

proporcjonalne

do

liczby

centrów

rozpraszających N i udział fononów jest zbyteczny.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

12

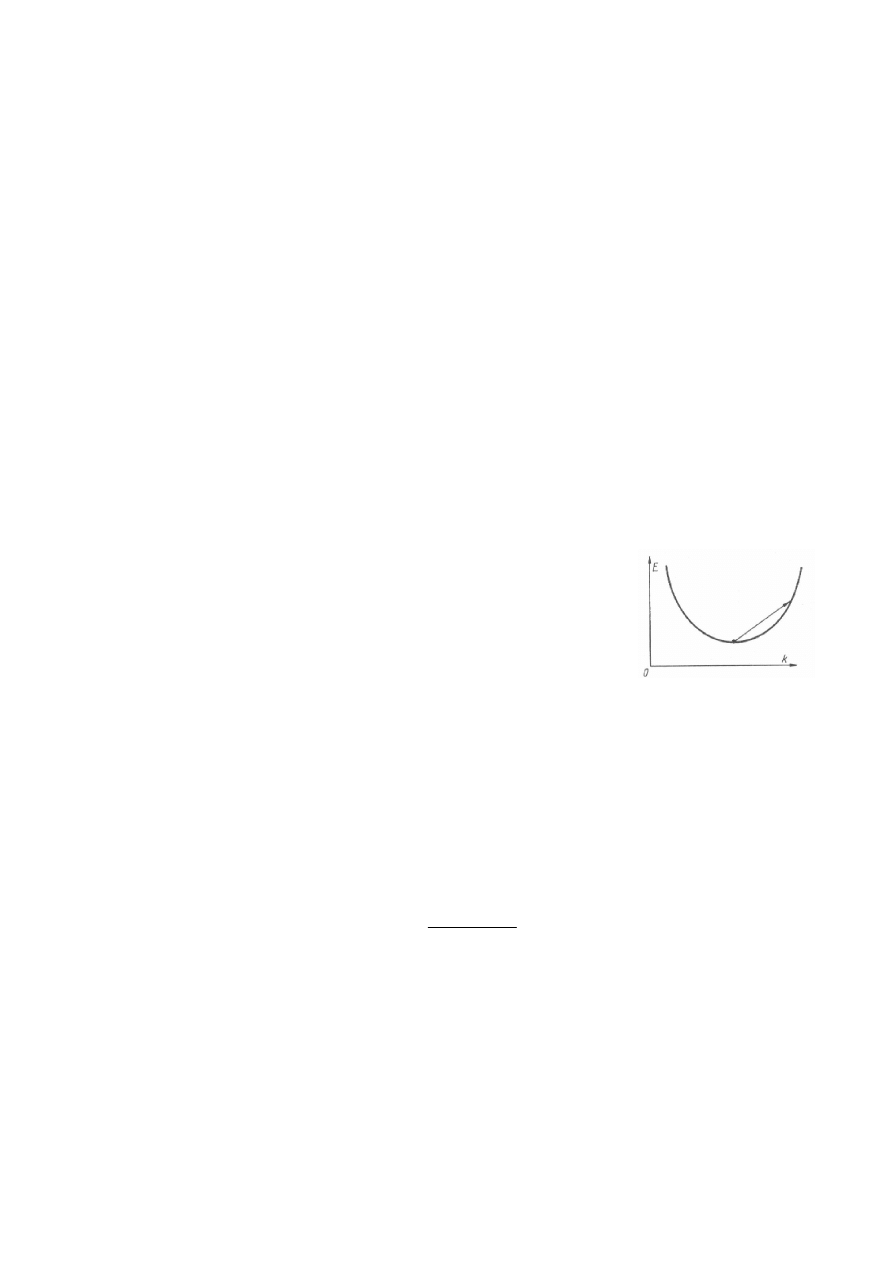
Absorpcja ekscytonowa
Proces tworzenia się ekscytonów powoduje zwykle pojawienie się wąskich linii na krawędzi absorpcji
półprzewodników z przerwą energetyczną prostą i stopni na krawędzi absorpcji półprzewodników z
przerwą energetyczną skośną. W materiałach z przerwą prostą ekscytony swobodne pojawiają
się przy energii fotonu

. W punkcie

= 0 jest to bardzo wyraźne przejście,

poszerzające się wraz z temperaturą. Ponieważ ekscytony mogą być kreowane z pewną
energią kinetyczną, oczywiste jest, że mogą one być również wytwarzane przez fotony o
większej energii i w ten sposób zwiększają współczynnik absorpcji w obszarze przejść
międzypasmowych. W materiałach o przerwie skośnej są potrzebne fonony w celu spełnienia
zasady zachowania pędu. Dlatego też wzrost współczynnika absorpcji otrzymujemy przy energii

(przejścia z absorpcją fononu) oraz przy

przejścia z emisją

fononu. W każdej z gałęzi akustycznych i optycznych widma fononowego występują dwa
rodzaje fononów poprzecznych i jeden rodzaj podłużnych. Ponieważ w przejściach może brać
udział więcej niż jeden fonon, więc mogą one być absorbowane lub emitowane w różnych
kombinacjach. Dlatego też można otrzymać dużą liczbę stopni w krawędzi absorpcji.

Ogólnie możemy zapisać:

α

(h

υ

)=B(h

υ

-E

g

±E

fon

-E

ex

-

ξ

n

)

m

, gdzie B- stała materiałowa

Absorpcja na swobodnych nośnikach
Przez nośnik swobodny rozumiemy nośnik, który może swobodnie poruszać się wewnątrz pasma,
tzn. nośnik, który może oddziaływać ze swoim otoczeniem. Absorpcje, na nośnikach
swobodnych charakteryzuje widmo monotoniczne, często pozbawione wszelkiej struktury, które
wzrasta proporcjonalnie do

λ

p

przy czym p zawiera się między 1,5 a

3,5,

λ

=c/

υ

jest długością fali fotonu. Aby zaabsorbować foton,

elektron musi przejść do wyższego stanu energetycznego wewnątrz
tej

samej

doliny.

Takie

przejście

wymaga

dodatkowego

oddziaływania w celu spełnienia zasady zachowania padu. Zmiana
pędu może być dokonana przez oddziaływanie z siecią, czyli z
fononami, lub przez rozpraszanie na zjonizowanych domieszkach.
Zderzenia z siecią półprzewodnika powodujące rozpraszanie na fononach akustycznych powodują
wzrost absorpcji proporcjonalny do

λ

1,5

. Natomiast rozpraszanie na fononach optycznych daje

zależność proporcjonalna do

λ

2,5

, podczas gdy rozpraszanie na zjonizowanych domieszkach daje

zależność proporcjonalną do

λ

3

lub

λ

3,5

. W ogólności występują wszystkie trzy metody

rozpraszania i w rezultacie współczynnik absorpcji

α

s

na nośnikach swobodnych jest średnią

ważoną trzech składników

α

s

=A

λ

1,5

+B

λ

2,5

+C

λ

3,5

przy czym

i C są stałymi. Dominujący rodzaj rozpraszania zależy od koncentracji

domieszek. Wykładnik p we wzorze

λ

p

powinien wzrastać

domieszkowaniem lub z

kompensacją. Klasyczny wzór na współczynnik absorpcji na nośnikach swobodnych ma postać:

τ

π

λ

α

3

2

2

2

8

*

=

,

przy czym

jest koncentracją nośników,

współczynnikiem załamania, a

τ

– czasem

relaksacji. Prawdopodobieństwo rozpraszania zależy od domieszki np. dla GaAs

α

s

=(S-siarka)>

α

s

(Se-selen)>

α

s

(Te-tellur)

Rekombinacja:
Zjawisko rekombinacja R (promieniowania) jest procesem odwrotnym do absorpcji

α

(R=

α

-1

).

Elektron zajmujący wyższy stan energetyczny, aniżeli to jest możliwe w stanie równowagi,
może przejść na niższy energetycznie pusty stan, przy czym cała lub większość różnicy energii
między

oboma

stanami

może

być

wyemitowana

w

postaci

promieniowania

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

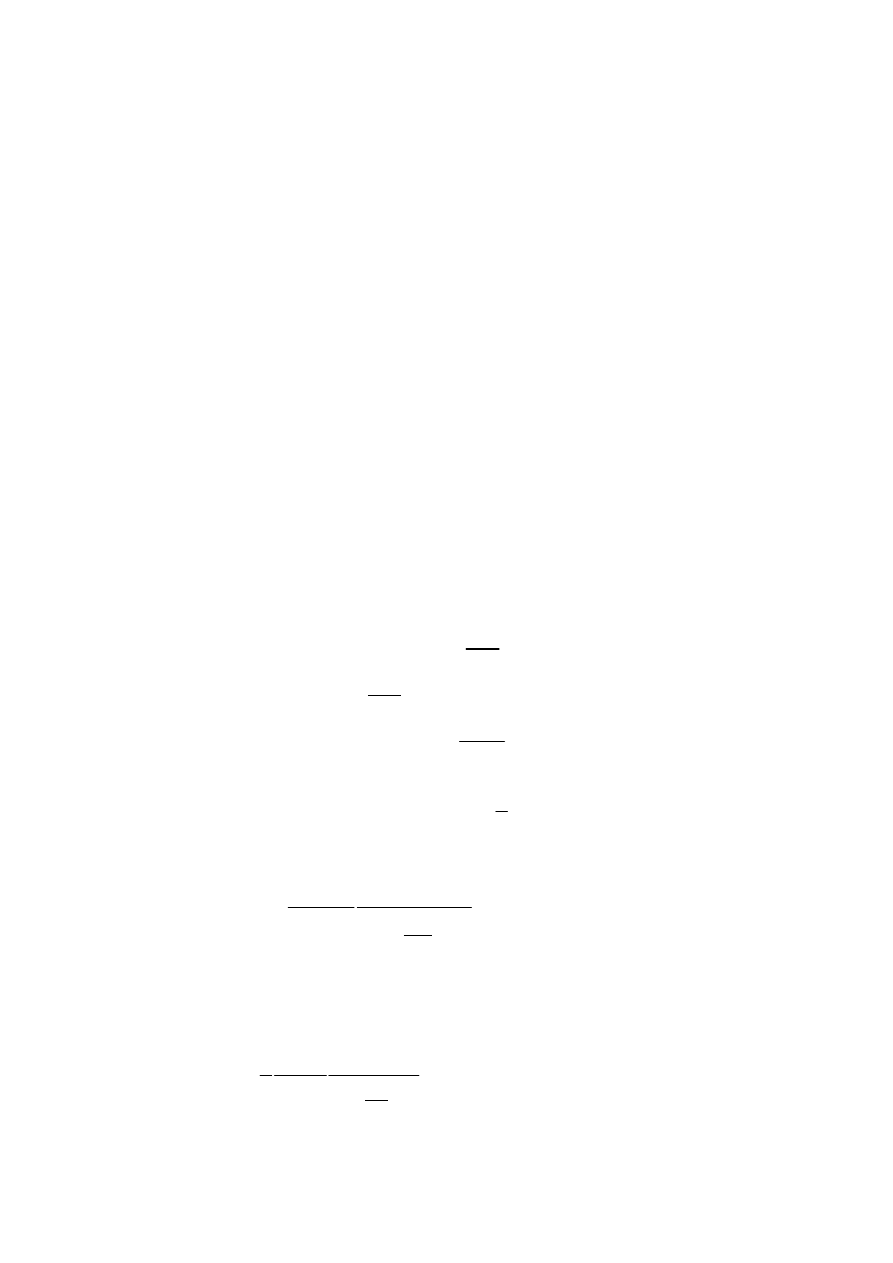
13

elektromagnetycznego. Duża ilość przejść promienistych w jednostce czasu na jednostkę
objętości powinna być proporcjonalna do iloczynu koncentracji dziur i elektronów:

Φ

=Bnp, gdzie

Φ

- całkowita liczba przejść, B- stała

LUMINESCENCJA
Podstawowym warunkiem wystąpienia emisji jest to, aby układ nie był w stanie równowagi. Takie
odchylenie od równowagi wymaga jakiegoś wzbudzenia. Proces emisji światła jest ogólnie nazywany
luminescencją. Wzbudzenie za pomocą prądu elektrycznego (wstrzykiwanie nośników bądź przebicie)
prowadzi do elektroluminescencji. Wzbudzenie optyczne (przez absorpcję fotonu) powoduje
fotoluminescencję

,

zaś

wzbudzenie

strumieniem

elektronów-

katodoluminescencję

.

Tryboluminescencja

jest związana ze wzbudzeniem mechanicznym, Termoluminescencja z kolei nie

jest jednakże prostym wzbudzeniem termicznym, które jest nazywane żarzeniem, ale wymaga
wzbudzenia w niskiej temperaturze, aby „zamrozić" nośniki w stanach pułapkowych, z których mogą
być one następnie uwolnione termicznie. W chemiluminescencji, światło jest wzbudzone na skutek
reakcji chemicznych. Fluorescencja jest luminescencją pojawiającą się tylko w trakcie wzbudzenia,
natomiast fosforescencja jest luminescencją, która trwa przez pewien okres po wyłączeniu
wzbudzenia.

TW. VAN ROOSBROECKA-SHOCKLEYA
W stanie równowagi termodynamicznej szybkość generacji optycznej par elektron-dziura jest równa
szybkości ich rekombinacji promienistej. Jeśli rozważymy równowagę szczegółową obu procesów
dla różnych częstotliwości fotonów , to możemy zapisać, że szybkość emisji o częstotliwości

w

przedziale d wynosi (przy założeniu że wydajność kwantowa jest równa 1):

ν

ν

ρ

ν

ν

ν

)

(

)

(

)

(

=

przy czym

jest prawdopodobieństwem zaabsorbowania fotonu o energii

na jednostkę czasu, zaś

ρ

(

υ

)- gęstością fotonów o częstotliwości

w przedziale

Prawdopodobieństwo absorpcji jest

związane ze średnim czasem życia fotonu w półprzewodniku zależnością:

)

(

1

)

(

ν

τ

ν

=

Średni czas życia może być obliczony ze średniej drogi swobodnej 1/

α

(

υ

) fotonu poruszającego się z

prędkością v=c/n (zakładając stały współczynnik załamania):

)

(

1

)

(

ν

α

ν

τ

=

Tak więc:

)

(

)

(

ν

α

ν

=

Tak więc twierdzenia van R-S ma postać: R(

υ

)d

υ

=G(

υ

)d

υ

Prawdopodobieństwo zależy od rodzaju ośrodka i szybkości absorpcji i wówczas:

1

exp

1

8

)

(

3

3

2

−













=

π

ν

ν

ρ

przy czym pierwszy czynnik jest stałą materiałową

Fizyczne podstawy rekombinacji:
R(

υ

)d

υ

=G(

υ

)d

υ

=P(

υ

)

ρ

(

υ

)d

υ

1

exp

1

8

)

(

3

3

2

−













=

π

α

υ

, skracając co się da otrzymamy

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

14

1

exp

1

8

)

(

2

2

2

−













=

π

α

υ

Całkowita rekombinacja w stanie równowagi może być obliczona z innej zależności:

∫

=

)

(

Powyższe równanie stanowi podstawowy związek miedzy spodziewanym widmem emisyjnym a
obserwowanym widmem absorpcyjnym. Powyższy wzór jest słuszny nie tylko dla przejść pasmo-
pasmo, ale również dla przejść pomiędzy każdymi zbiorami stanów. Powyższe wzory są słuszne
jedynie w przypadku równowagi termodynamicznej. W przeciwnym razie całkowita szybkość
rekombinacji promienistej R

c

jest proporcjonalna do koncentracji elektronów n i pustych stanów p:

2

=

Powyższy wzór mówi, że czas życia nośników maleje ze wzrostem ich koncentracji, oraz że całkowita
szybkość rekombinacji staje się równa R, gdy iloczyn

osiąga wartość samoistna . Ze wzrostem

pobudzenia (generowania nadmiarowych elektronów i dziur) niekoniecznie będzie wzrastać natężenie
promieniowania, gdyż zachodzą dodatkowe efekty. Dla materiału samoistnego czas życia nośników

(związany z emisją promienistą) wynosi

2

=

τ

, a stała materiałowa

2

=

. Im krótszy czas życia

nośników tym lepsza wydajność rekombinacji.

τ

↑

wraz ze wzrostem szerokości przerwy wzbronionej,

natomiast B jest większa (ok. czterokrotnie) dla materiałów z prosta strukturą przejść.
Widmo natężenia promieniowanie można wyznaczyć znając daną charakterystykę absorpcji i
współczynnik załamania.

Rekombinacja objętościowa.
I. Rekombinacja promienista
1. Rekombinacja prosta (międzypasmowa)- bezpośrednie przejście elektronu z pasma przewodnictwa
do pasma walencyjnego, przy czym uwolniona energia jest uniesiona przez emitowany foton. Przy
braku pola elektrycznego nadmiarowe pary są generowane w całej objętości półprzewodnika (proces
mało prawdopodobny).
2. Rekombinacja Shockleya-Reada-Halla (SRH)- proces rekombinacji pary elektron-dziura przy
udziale centrów rekombinacyjnych (atomy zanieczyszczeń i defekty struktury wprowadzające do
przerwy energetycznej zlokalizowane głęboko poziomy). Proces jest dwustopniowy.

Rekombinacja niepromienista:
1. Rekombinacja bezpośrednia (zderzeniowa) Augera- energia wyzwolona w wyniku rekombinacji
pary elektron-dziura jest przekazywana innemu nośnikowi, a następnie stopniowo rozpraszana dzięki
emisji fononów. Polega na zderzeniu 3 nośników (np. 2 elektrony i 1 dziura) i jest mało
prawdopodobna przy niewielkich koncentracjach. Możliwe są rozmaite typy procesów Augera, w
zależności od dozwolonych przejść i koncentracji nośników w półprzewodniku (rek. międzypasmowa,
z pasma donorowego do dziury w paśmie walencyjnym, rek. elektronu z pasma przewodnictwa z
dziurą związaną z akceptorem, elektronu z poziomu donorowego na poziom akceptorowy).
2.

Rekombinacja powierzchniowa- związana jest z urwaniem periodycznej sieci krystalicznej

(poziomy Tamma), powierzchniowa warstwa jest zubożona w elektrony (dla typu n) lub wzbogacona
w dziury (dla p), dla dodatniego ładunku prędkość rekombinacji zależy od wartości potencjału
powierzchniowego, a więc od stopnia zakrzywienia pasm energetycznych.
3. Rekombinacja przez defekty i wtrącenia

Rekombinacja niepromienista jest bardziej efektywna od promienistej, dlatego tez musimy brać to pod
uwagę przy projektowaniu układu opto…

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

15

Podsumowanie:
Absorpcja i rekombinacja

1. Na proces absorpcji składają się zarówno mechanizmy, z którymi związane jest wzbudzenie

elektronu w inny stan energetyczny, z którego to elektron na drodze rekombinacji, najczęściej
promienistej, może wrócić do stanu równowagi, a także procesy rozpraszania takie jak np.
rozpraszanie na fononach, defektach, swobodnych nośnikach ładunku, które w procesie
odwrotnym nie są odpowiedzialne za rekombinację promienistą.

2. Struktura widma absorpcyjnego jest bardzo złożona. Dlatego też interpretacja widma jest

bardzo trudna i wymaga uwzględnienia wszystkich mechanizmów i typów absorpcji.

3. Na podstawie analizy widma absorpcji możemy określić zarówno strukturę energetyczną

półprzewodnika (szerokość przerwy zabronionej, charakter przejść optycznych, strukturę
energetyczną pasma podstawowego i pasma przewodnictwa) jak i wielkości energetyczne
związane z widmami fononowymi i ekscytonowymi.

4. Na podstawie analizy widma absorpcji możemy także sprecyzować wymogi odnośnie

charakterystyk materiału stosowanego na przyrządy optoelektroniczne:

•

czystość materiału - decyduje o rozpraszaniu na domieszkach, a także o pobudzaniu
domieszek, czyli powstawaniu poziomów wzbudzonych w procesie rekombinacji
decydujących o długości fali emitowanego promieniowania (w danym przypadku
niepożądane). Decyduje to o czystości spektralnej widma emitowanego.

•

struktura - defekty są przede wszystkim centrami rozpraszania, a także źródłem emisji fotonu o
niepożądanej energii. Dla opracowania przyrządów potrzeba monokrystalicznych materiałów.

•

koncentracja domieszek musi być stosunkowo duża (przy otrzymywaniu materiału określonego
typu), aby zapewnić odpowiednio dużą kombinowaną gęstość stanów początkowych i
końcowych. Od góry koncentracja ograniczona jest mechanizmem rozpraszania na nośnikach
ładunku.

•

wybór materiału - decyduje o barwie emitowanego przez półprzewodnik światła.

•

temperatura - powinno być zrozumiałym, dlaczego w większości przypadków przyrządy o
dużej wydajności kwantowej pracują w niskich temperaturach i dlaczego poszukuje się
materiałów półprzewodnikowych np. do wytwarzania laserów o dużej mocy, emitujących
wiązkę koherentną i pracujących w temperaturze pokojowej.

MATERIAŁY DLA OPTOELEKTRONIKI

Podstawowe materiały na diody elektroluminescencyjne

Kolor

Materiał

Typ przejścia

Podczerwień

GaAs

proste

Czerwony

GaP(Zn,O)
GaAs

0,6

P

0,4

Al

0,3

Ga

0,7

As

skośne
proste
proste

Pomarańczowy

GaAs

0,35

P

0,65

Ga

0,7

In

0,3

P

skośne
proste

Żółty

GaAs

0,15

P

0,85

:N

GaInN:Mg
GaP:N

++

skośne
proste
skośne

Zielony

GaP:N
(In,Ga)N:Mg

skośne
proste

Niebieski

(In,Ga)N:Mg

proste

Fioletowy

GaN:Mg

proste

Ultrafiolet

GaN:Mg

proste

Biały

GaN + luminofor

proste

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

16

Podstawowe właściwości związków półprzewodnikowych AIIIBV

Związek półprzewodnikowy

Temp. top.

[°C]

Eg

[eV]

µ

n

[cm

2

/Vs]

µ

p

[cm

2

/Vs]

Współczynnik

załamania n

AlN

GaN

InN

2400
1700
1100

5,88

3,4

1,95

--

300

--

-
-
-

2,2
2,4
2,9

AlP

GaP

InP

2000
1467
1070

2,45
2,26
1,35

80

190

4600

30

120
150

3,0

3,45
3,45

AlAs

GaAs

InAs

1770
1238

942

2,16
1,43
0,36

280

9500

33000

--

450
460

3,2

3,65
3,52

AlSb

GaSb

InSb

1060

710
525

1,58
0,72
0,18

200

4000

78000

550

1400

750

3,4
3,8
4,0

Masa cząsteczkowa AlBV < GaBV < InBV.
Mä

⇒

E

g

æ, T

top

æ,

µ

n

ä

Podstawowe właściwości związków półprzewodnikowych AIIBVI

Związek półprzewodnikowy

Temp. top.

[°C]

Eg

[eV]

µ

n

[cm

2

/Vs]

µ

p

[cm

2

/Vs]

Typ

przewodnictwa

ZnS (S)

ZnS (W)

CdS
HgS

1020
1780
1750
1480

3,67
3,74
2,53
1,78

--

140
340
700

--

5

110

--

n
n
n
n

ZnSe
CdSe
HgSe

1520
1264

790

2,73
1,85
0,12

260
720

20000

15
75

--

n
n
n

ZnTe
CdTe
HgTe

1239
1041

670

2,23
1,51
0,08

530

1200

25000

30
60

200

p

n,p
n,p

ZnS - podstawa luminoforów wytwarzanych na skalę przemysłową, tworzy szereg roztworów stałych z CdS, CdSe, ZnSe.
Domieszkowanie miedzią -luminofory zielone i niebieskie, domieszkowanie magnezem - żółte.
CdS - fotorezystory o bardzo dużej fotoczułości w widzialnym zakresie widma.
CdHgTe - detektory podczerwieni.

Postęp w technice mikrofalowej i optoelektronice wiąże się z rozwojem metod wytwarzania
półprzewodnikowych struktur niskowymiarowych, takich jak; studnie kwantowe QW druty kwantowe
QWW i kropki kwantowe QD. Struktury te umożliwiają obserwację nowych zjawisk fizycznych,
które wykorzystuje się do wytwarzania przyrządów półprzewodnikowych nowej generacji. Obniżenie
wymiarowości oznacza, że nośniki są fizycznie ograniczone w jednym lub wielu kierunkach, a ich
ruch może odbywać się w płaszczyźnie (QW), wzdłuż jednego kierunku (QWW) albo w ogóle nie jest
możliwy (QD). Takie struktury przyjęto określać jako dwuwymiarowe (2D) w przypadku studni
kwantowych, jednowymiarowe (1D) dla drutu kwantowego lub zerowymiarowe (0D) w przypadku
kropki kwantowej. Redukcja wymiaru struktur prowadzi do jakościowej zmiany rozkładu gęstości
dozwolonych stanów energetycznych nośników i ich częściowej lub pełnej kwantyzacji. Modyfikacja
gęstości stanów, związana ze zmniejszeniem rozmiarów struktur, wpływa na znaczne polepszenie
właściwości optycznych i elektrofizycznych tych struktur, w porównaniu z właściwościami
materiałów objętościowych. Stosowanie struktur niskowymiarowych modyfikuje w znacznym stopniu
właściwości statyczne i dynamiczne nośników. W konsekwencji obserwuje się istotne zmiany
wynikowych charakterystyk przyrządów elektronowych, w których zastosowano struktury o obniżonej
wymiarowości.
Sterowanie

strukturą

energetyczną

materiałów

wieloskładnikowych

i

gęstością

stanów

energetycznych, określane jako inżynieria szerokości pasma zabronionego, jest uwarunkowane

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

17

możliwościami kontroli procesu wytwarzania jednorodnych struktur niskowymiarowych o grubościach
porównywalnych z długością fali de Broglie'a swobodnych nośników. Determinuje to warunki procesu
ich osadzania. Konstrukcja i technologia zaawansowanych optoelektronicznych i mikrofalowych
struktur przyrządowych wymaga opanowania umiejętności osadzania pojedynczych jednorodnych
warstw atomowych na dużych powierzchniach.
Postęp w optoelektronice i technice mikrofalowej wiąże się również z zastosowaniem heterostruktury,
tj. dwóch różnych materiałów półprzewodnikowych tworzących wspólną strukturę monokrystaliczną.
Kontrola procesu wzrostu heterostruktur, powtarzalne sterowanie grubością poszczególnych warstw
epitaksjalnych i ich składem oraz otrzymywanie heterostruktur o ostrych granicach metalurgicznych są
podstawą sterowania rozkładem gęstości stanów energetycznych. Niejednorodności grubości i składu
oraz chropowate granice rozdziału heterostruktur wpływają na zaburzenie rozkładu gęstości stanów i
powodują utratę przez strukturę jej właściwości kwantowych.
Do wytwarzania heterostruktur z różnych materiałów półprzewodnikowych niezbędna jest znajomość
mechanizmów

wzrostu

struktur

epitaksjalnych,

w

tym

struktur

wieloskładnikowych

i

niskowymiarowych. Pierwszorzędnej wagi nabiera również optymalizacja procesów krystalizacji i
umiejętność ich charakteryzacji. Chodzi tu przede wszystkim o określenie korelacji między
parametrami heterostruktur, charakterystykami wyjściowymi struktur przyrządowych a parametrami
procesów ich wzrostu. Podstawowym procesem wytwarzania heterostruktur jest epitaksja. Metodami,
które spełniają kryteria wytwarzania nowoczesnych, zaawansowanych heterostruktur przyrządowych
są epitaksja z zastosowaniem wiązek molekularnych (MBE - molecular beam epitaxy) oraz epitaksja z
zastosowaniem związków metaloorganicznych (MOVPE - metalorganic vapour phase epitaxy). Dalszy
postęp w technologii struktur przyrządowych, a szczególnie w technologii optoelektroniczno-
mikrofalowych układów scalonych, jest związany z opracowaniem powtarzalnej technologii tzw.
podłoży aktywnych. Podłoże aktywne zawiera wiele struktur epitaksjalnych, składa się z różnych
materiałów i obszarów czynnych, zawierających struktury o obniżonej wymiarowości. Dzięki temu
można w nich wytwarzać przyrządy dyskretne i realizować optyczne oraz elektryczne połączenia
między nimi. Ważnym aspektem projektowania i optymalizacji procesów technologicznych jest
stosowanie takiej sekwencji warstw epitaksjalnych, aby kolejne etapy wzrostu złożonej struktury
podłoża aktywnego nie wpływały na właściwości warstw już wytworzonych. Podłoża aktywne
powinny spełniać wymagania odnośnie do:

•

jednorodności grubości i składu na podłożach wyjściowych o średnicy 3 cali (lepiej niż 2%, co

odpowiada np. kontroli grubości na poziomie 1-2 nanometrów),

•

gładkości granicy rozdziału (interfejsu) w heterostrukturze,

•

jednorodności właściwości optycznych i elektrycznych na całej powierzchni struktury,

•

doskonałości właściwości strukturalnych,

•

kompatybilności z technologią wytwarzania przyrządów dyskretnych i układów scalonych,

•

możliwości ich strukturyzacji przestrzennej (np. wytwarzania struktur typu mesa),

•

możliwości realizacji połączeń optycznych i elektrycznych zarówno wewnętrznych, jak i

zewnętrznych.

λ

(

υ

)

→

inżynieria pasma zabronionego:

•

E

g

(szerokość pasma zabronionego)

•

Struktury z efektami kwantowymi

•

Lokalne pole w nanostrukturze (

δ

-doping)

Zmieniając skład materiału Al

x

Ga

1-x

As możemy zmieniać szerokość przerwy wzbronionej, a nawet

dopasować materiał do podłoża. Wcześniejsza struktura jest materiałem stosowanym dla długości fal
w zakresie 1,3

÷

1,55

µ

m.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

18

Wykład 6

1.04.2004

–

ły grupy AIIIBV są najczęściej stosowanymi związkami w przemyśle przy produkcji różnego

rodzaju urządzeń. Są to związki przyszłościowe z których najczęściej stosowane są następujące
związki: GaAs, InP, AlGaAs, InGaAs, GaInNAs, GaInNAAs,Sb
–Za ich pomocą możemy wytwarzać następujące struktury: kwantowe, naprężone, z balansem
naprężeń, gradientowe (materiały w których w sposób płynny zmieniamy zawartość jednego
pierwiastka)
–Technologia: MOVPE, MBE, strukturyzacja powierzchni, kontakty i międzypołączenia nanostruktur.
–Zastosowania mikroelektronika, optoelektronika, medycyna
Istotą tego wszystkiego jest to że materiały grupy AIIIBV mogą krystalizować (struktura kubiczna,
blendy cynkowej, heksagonalna)
Najnowszą strukturą jest GINES (GaAsNAs).

EPITAKSJA
Epitaksją

nazywa się proces wzrostu warstw monokrystalicznych na podłożu monokrystalicznym.

Często epitaksję opisuje się jako zorientowany krystalograficzny wzrost warstwy monokrystalicznej,
zachodzący na powierzchni zorientowanego krystalograficznie monokryształu podłożowego. Szybkość
zarodkowania warstw epitaksjalnych w początkowej fazie osadzania i szybkość ich wzrostu zależą od
temperatury, przesycenia (lub przechłodzenia) w fazie, z której jest realizowany proces wzrostu oraz
od natury stosowanego podłoża.
Podłoże

- jego właściwości strukturalne, orientacja, właściwości mechaniczne, stan i sposób

przygotowania powierzchni przed procesem epitaksji silnie wpływają na proces krystalizacji osadzanej
warstwy i jej charakterystyki. W wyniku krystalizacji struktura i orientacja krystalograficzna warstwy
znajdują się w określonej relacji do struktury i orientacji kryształu podłożowego. Najczęściej struktura
i orientacja warstwy epitaksjalnej odtwarzają dokładnie strukturę i orientację podłoża.

Wymagania stawiane procesowi epitaksji:
1. Struktura

•

Monokrystaliczna

•

Orientacja

•

Zgodność struktury do podłoża

•

Bezdefektowe

2. Właściwości mechaniczne

•

Stabilne mechanicznie

•

Płaszczyzny najlepszej łupliwości

3. Parametry elektryczne

•

Półizolacyjne (dla technologii planarnej

ρ

=10

7

Ω

cm)

•

Przewodzące (dla technologii krawędziowej)

4. Właściwości cieplne

•

Przewodność cieplna

5. Geometryczne

•

Określona grubość: (300

÷

400) ±15

µ

m

•

Średnica

•

Płaskorównoległość ±10

µ

m

6. Powierzchnia

•

Polerowana (do gładkości optycznej

∆ρ

<10nm)

•

Koncentracja defektów EPD na poziomie 10

4

cm

-2

(dla mikrofal) dla laserów 0!!

Utleniona powierzchnia nazywa się epi-ready.

Jeżeli podłoże oraz osadzany na nim materiał są takie same (np. krzem na krzemie, arsenek galu na
arsenku galu) lub mają taką samą strukturę krystaliczną i prawie takie same parametry sieciowe, to

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

19

mamy do czynienia z homoepitaksją. Wzrost warstwy jednego materiału na podłożu z innego
materiału, gdy różnią się one się strukturą krystalograficzną i parametrami sieciowymi, nazywa się
heteroepitaksją.

W początkowej fazie badania procesów epitaksji uważano, że wzrost

monokrystalicznych warstw epitaksjalnych jest możliwy tylko w przypadku takich materiałów, dla
których różnica parametrów sieciowych

∆

a

o

/a

o

(gdzie: a

0

- parametr sieci podłoża,

∆

a

o

- różnica

parametrów sieciowych podłoża i warstwy osadzanej na tym podłożu) nie przekracza k0,1%.
W większości zaawansowanych struktur przyrządowych i układów scalonych stosuje się podłoża
aktywne. Podłoże aktywne zawiera wiele struktur epitaksjalnych, wytworzonych najczęściej z różnych
materiałów. Zawiera też obszary aktywne ze strukturami niskowymiarowymi. Dzięki temu można
wytwarzać przyrządy dyskretne i realizować optyczne oraz elektryczne połączenia między nimi.
Ważnym aspektem projektowania i optymalizacji procesów technologicznych jest takie osadzanie
warstw epitaksjalnych, aby kolejne etapy wzrostu złożonej struktury podłoża aktywnego nie wpływały
na właściwości warstw już wytworzonych. Obszary czynne często są wytwarzane z wykorzystaniem
heterostruktur lub heterozłączy.
Heterozłącze

jest to układ dwóch różnych materiałów półprzewodnikowych tworzących wspólną

strukturę monokrystaliczną. Do wielu zastosowań wytwarza się heterozłącza, w których różnica
parametrów sieci jest duża, np. w heterostrukturach GaAs/Si- 4,1%, InGaAs/GaAs- 7%, GaN/Al

2

O

3

-

14%. Taka różnica parametrów sieciowych i jednocześnie występująca często różnica
współczynników rozszerzalności termicznej podłoża i warstwy epitaksjalnej powodują dużą
koncentrację defektów, które są generowane na granicy podłoże-warstwa epitaksjalna, a następnie
propagowane ku powierzchni osadzanej warstwy. Wymienione niedopasowania są przyczyną naprężeń
rozciągających lub ściskających, które powstają na granicy rozdziału heterostruktury. Proces
heteroepitaksji musi więc być odpowiednio kontrolowany i sterowany, dotyczy to zarówno procesu
zarodkowania, rozrostu zarodków, jak i ich zrastania się (koalescencji) w celu minimalizacji
niedoskonałości struktury. W praktyce stosuje się rozwiązania pośrednie, np. zarodkowanie i
wytwarzanie niskotemperaturowych warstw buforowych, osadzanie naprężonych warstw supersieci
(SLS) lub warstw dopasowujących parametry sieciowe, które są stosowane bądź w relaksacji
naprężeń, bądź jako warstwy pośrednie między podłożem a warstwą buforową (np. AlN osadzany na
podłożu szafirowym przed naniesieniem GaN).
Supersieć

jest to struktura krystaliczna, najczęściej półprzewodnikowa, w której na nośniki ładunku

elektrycznego, oprócz periodycznego w przestrzeni konfiguracyjnej pola elektrycznego atomów sieci
krystalicznej

φ

l

oddziałuje również pewne dodatkowe pole elektryczne, którego potencjał

φ

sl

jest

również periodyczny w przestrzeni konfiguracyjnej, lecz z okresem d znacznie większym niż okres
zmian potencjału

φ

l

który zależy od parametrów sieci krystalicznej. Warunkiem koniecznym, aby pole

elektryczne periodycznej supersieci oddziaływało na nośniki ładunku, jest spełnienie nierówności:
L>>d, w której: L- średnia droga swobodna nośnika ładunku w krysztale, d- okres zmian potencjału

φ

sl

.

Stosuje się wiele klasyfikacji supersieci heterozłączowych, ze względu na charakter zmian energii E

c

i

E

V

wartość powinowactwa elektronowego lub sposób wytwarzania. Szczególnym przypadkiem są

struktury supersieciowe, które można klasyfikować ze względu na mechanizm transportu nośników
ładunku. Rozróżnia się dwa przypadki:
1. Układ heterostruktur, w którym dwa materiały o różnej przerwie zabronionej występują
przemiennie, przy czym warstwy z półprzewodnika o węższej przerwie zabronionej (np. związek
potrójny InGaAs) są przedzielone grubymi warstwami półprzewodnika o szerszej przerwie
zabronionej (np. GaAs). Nośniki ładunku w materiale z mniejszą szerokością pasma zabronionego nie
mogą (np. na drodze tunelowania) przenikać przez otaczające go bariery GaAs. W takiej strukturze
nośniki ładunku są silnie zlokalizowane w jednowymiarowych, kwantowych studniach potencjału.
Do najważniejszych właściwości takiej struktury można zaliczyć: kwantowy efekt rozmiarowy,
podział głównych pasm energetycznych na podpasma, dwuwymiarowy charakter gazu elektronowego
lub dziurowego (2DEG, 2DHG).
2. Warstwy półprzewodnika z szerokim pasmem zabronionym mają niewielkie grubości i możliwe jest
tunelowanie nośników ładunku przez bariery potencjału między warstwami półprzewodnika z wąską

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

20

przerwą. W strukturze tej występuje sprzężenie studni potencjału, a zjawiska w niej zachodzące są
wywołane przez oddziaływania i transport w całej strukturze.
Ze względu na wartość powinowactwa elektronowego półprzewodników supersieci można podzielić
na:
1. Supersieci heterozłączowe pierwszego rodzaju (np. GaAs-Al

x

Gai_

x

As) utworzone z

półprzewodników, których przerwy energetyczne pokrywają się całkowicie (oddziaływania pomiędzy
nośnikami poszczególnych warstw supersieci zachodzą między pasmami tego samego typu); są to
supersieci kontrawariantne.
2. Supersieci heterozłączowe drugiego rodzaju (np. InAs-GaSb) wykonane z półprzewodników,
których przerwy energetyczne znajdują się blisko siebie, ale się nie pokrywają lub pokrywają jedynie
w niewielkim stopniu. W tego typu strukturach następuje oddziaływanie nośników różnych
półprzewodników z różnych pasm energetycznych.
3. Supersieci „politypowe" (np. GaSb-AISb-InAs) - struktury wielowarstwowe utworzone z co
najmniej trzech różnych półprzewodników. Oddziaływania między nośnikami mają w tym przypadku
bardziej zróżnicowany i skomplikowany charakter.

Niezbędnymi

warunkami

otrzymania

dobrej

jakości

krystalicznej

struktury

supersieci

heterozłączowych są zgodność typu struktury krystalograficznej półprzewodników tworzących daną
supersieć i dobre dopasowanie stałych sieciowych tych półprzewodników.
W układach wielokrotnych studni kwantowych stosuje się materiały, które różnią się nie tylko
wartościami przerwy wzbronionej, ale w których wraz ze zmianą składu zwiększa się różnica stałych
sieciowych

∆

a. Wiąże się to z generacją naprężeń i defektów na granicy heterostruktury. W warstwach

o grubości większej od tzw. grubości krytycznej pojawia się relaksacja naprężeń i generacja defektów,
głównie dyslokacji niedopasowania. Ze względu na rodzaj fazy, z której prowadzi się kontrolowany
wzrost warstw krystalicznych, do podstawowych metod epitaksji zalicza się:

•

epitaksję z fazy ciekłej– LPE

•

epitaksję z fazy gazowej– VPE

•

epitaksję z wiązek molekularnych– MBE

•

epitaksję ze związków metaloorganicznych– MOVPE.

Wyk. 7 15.04.2004

Epitaksja
Podłoże - wymagania
Z definicji epitaksji wynika, że powinny być spełnione poniższe warunki:

•

Struktura krystalograficzna podłoża i warstwy należą do tej samej grupy przestrzennej, czyli
oba materiały krystalizują w tej samej strukturze.

•

Wymiary komórek elementarnych podłoża i warstwy są do siebie zbliżone. Dopuszczalna
różnica parametrów komórek zależy od właściwości materiałów (odporności na stres,
współczynniki rozszerzalności termicznej itp.).
Przyjmuje się jednak pewne graniczne wartości różnic zwanych niedopasowaniem sieciowym

ε

, które definiowane jest jako stosunek różnicy parametru sieci warstwy i parametru sieci

podłoża do średniego parametru warstwy i podłoża:

gdzie:

a

L

- parametr sieci warstwy,

a

S

- parametr sieci podłoża,

a

av

- wartość średnia parametru sieci, a

av

=(a

L

+a

S

)/2.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

21

W technice epitaksji z fazy ciekłej LPE

:

o

dla

ε

nie większe niż 10

-3

osadzanie nie powoduje powstawania nowych defektów w

rosnącej warstwie,

o

dla

ε

nie mniejsze niż 10

-3

w warstwie przejściowej między podłożem a osadzaną

warstwą generowane są dyslokacje lub utrudnione jest zarodkowanie.

W technikach MOVPE i MBE, w których możliwe jest uzyskanie dużo wyższych przesyceń
niż w LPE, granicą jest

ε

nie większe niż 10

-1

.

•

Zarodki najchętniej lokują się w miejscach energetycznie najbardziej korzystnych, tzn. na
defektach sieci i zanieczyszczeniach. Mogą to być zerwane wiązania w krysztale np. stopnie
atomowe na powierzchni, defekty sieci. Ogólnie rzecz biorąc, defekty są odtwarzane przez
rosnąca warstwę. Podłoże powinno być więc możliwie bezdefektowe i mieć czystą
powierzchnię.

•

Konieczna jest stabilność temperaturowa podłoża w temperaturach epitaksji.

•

Możliwie zbliżone współczynniki liniowej rozszerzalności termicznej podłoża i warstwy.

•

Stabilność chemiczna podłoża w obecności reagentów.

Odwzorowywane są defekty, a w szczególności defekty śrubowe, na których proces zarodkowania
zachodzi szczególnie chętnie, ze względu na najniższą potrzebną energię formowania zarodka.
Praktycznie rzecz biorąc zawsze obserwuje się w warstwach epitaksjalnych defekty śrubowe. Rosną
one aż do powierzchni warstwy.
W technikach osadzanie z fazy gazowej często stosowanym zabiegiem jest użycie podłoży skośnych,
tzn. pochylonych. Powierzchnia podłoża nie ma dokładnej orientacji np. (100) dla GaAs, ale orientację
(100) z odchyłką o 2-4 stopni kątowych w stronę osi [110].
Co to daje? Przy takim cięciu monokryształu na powierzchni podłoża uwidaczniają się stopnie
atomowe. Charakteryzują się one zerwanymi, niewysyconymi wiązaniami chemiczno-krystalicznymi.
Osiadające na powierzchni podłoża aglomeraty np. GaAs czy też pojedyncze atomy galu lub arsenu
migrują po powierzchni (przy sprzyjających warunkach - odpowiednia temperatura i czas) w stronę
krawędzi stopni atomowych i tam podłączają się do kryształu podłoża. Zarodziowanie, które odbywa
się w ten sposób, przyspiesza wzrost warstwy nawet o rząd.

Sterowanie procesem
Kinetyka wzrostu
Epitaksja selektywna oraz epitaksja na profilowanym podłożu
Dla szeregu zastosowań (mikrosystemy, optoelektronika, układy scalone) potrzebne jest wytworzenie
struktur przestrzennych, takich jak np. rowki (V- i U-rowki), wyspy mesa czy światłowody planarne.
Robi się to po to, aby można było sprzęgać układy mikroelektroniczne z optoelektronicznymi i
mikromechanicznymi, a także z czujnikami różnego rodzaju.
Na rys. 1 przedstawiono schematycznie procesy selektywnej epitaksji i epitaksji na profilowanym
podłożu. Różnica między tymi technikami polega na tym, że epitaksja selektywna odbywa się na
podłożu zamaskowanym dielektrykiem i warstwa osadzana jest w oknach, zaś w przypadku epitaksji
na profilowanym podłożu wytrawiane są różne kształty w podłożu (najczęściej prostokąty). Następnie
usuwana jest maska i warstwa osadzana jest na dnie zagłębienia, na zboczach i na powierzchni
podłoża.

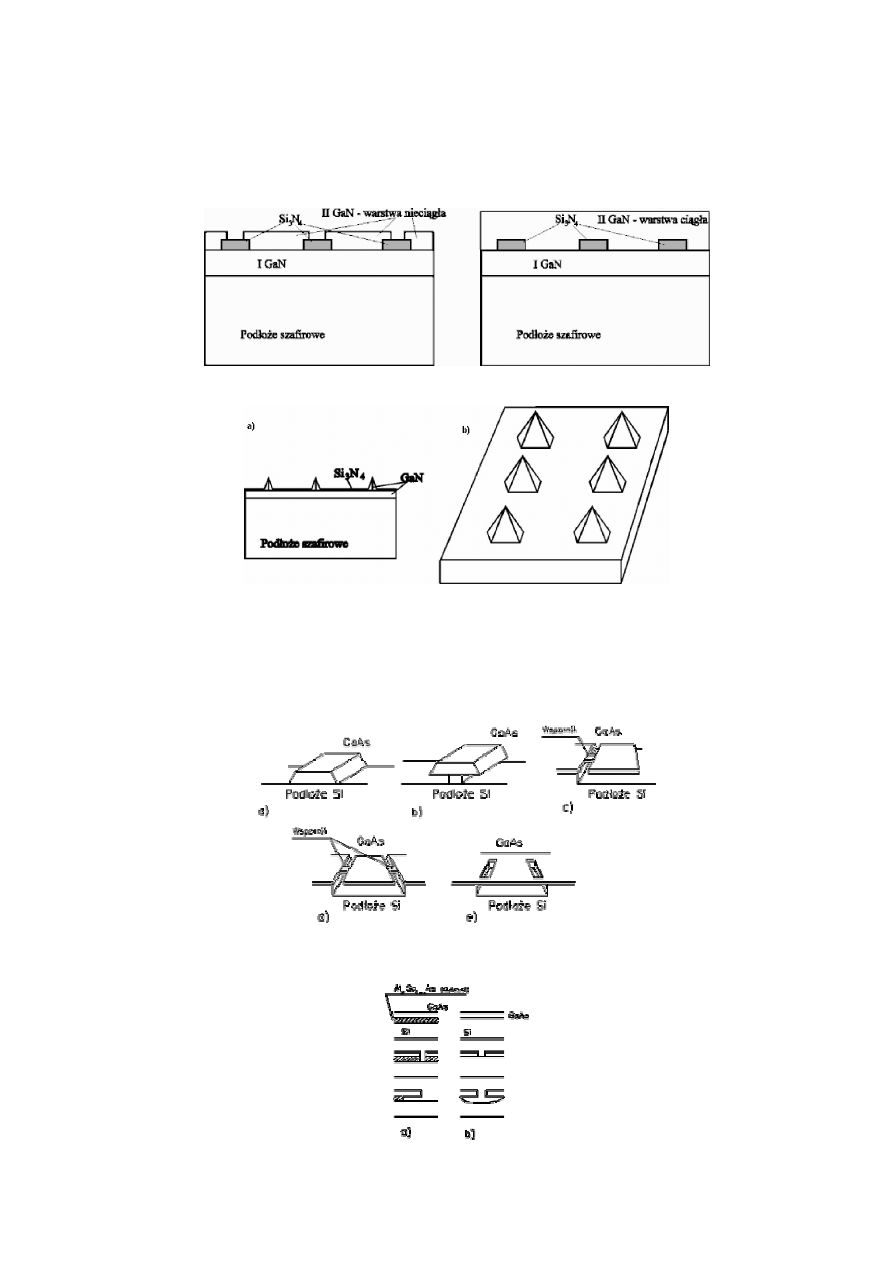
Rys.1. Schematyczne przedstawienie procesu epitaksji selektywnej a) i epitaksji na podłożu
profilowanym b).

W technice heteroepitaksji stosuje się czasem pewien rodzaj epitaksji selektywnej - metodę ELOG
(Epitaxy Lateral OverGrowth), której zasada pokazana została na rys. 2. Stosowana ona jest przy
osadzaniu warstw heteroepitaksjalnych o dużym niedopasowaniu do podłoża (duże różnice stałych
sieciowych, inna struktura krystaliczna - typ komórki elementarnej) i pozwala na zmniejszenie

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.

22

wpływu podłoża na osadzane warstwy oraz obniżenie koncentracji defektów i dyslokacji śrubowych,
które propagują się od warstwy przejściowej do powierzchni.
Metody osadzania selektywnego lub na podłożu profilowanym umożliwiają otrzymywanie różnych
struktur. Na rys. 3 pokazano metodę otrzymywania ostrzy z azotku galu do zastosowań w elektronice
próżniowej (zimna emisja polowa - płaskie panele wyświetlaczy). Można też wytworzyć różnego
rodzaju struktury przedstawione na rys. 4 i 5, które mogą być wykorzystane przy konstrukcjach
mikromechanicznych.

Rys.2 Schemat technologii ELOG z zastosowaniem epitaksji selektywnej do wytwarzania wysokiej
jakości warstw epitaksjalnych azotku galu

Rys.3 Wytwarzanie ostrzy z GaN: schemat procesu wzrostu ostrzy a) i matryca ostrzy b)

Struktury przedstawione na rys. 4b-e uzyskuje się w następujący sposób: na podłożu Si osadza się
warstwę GaAs, na niej zaś warstwę Al

x

Ga

1-x

As (0,4<x<1) i znowu GaAs. Za pomocą fotolitografii

otwiera się okna w warstwie GaAs i trawi selektywnie (Al,Ga)As aż do powierzchni krzemu (rys. 5a).
Następnie osadza się dalej GaAs. Można też wykorzystać właściwości trawionego selektywnie krzemu
w układzie jak na rys. 5b. Uzyskuje się w ten sposób obszary o wymiarach 200x250

µ

m.

Rys.4. Przykłady heterostruktur GaAs/Si osadzanych selektywnie: a) pasek mesa, b) pasek mesa z
podtrawianiem, c) wisząca płaszczyzna z jednym wspornikiem, d) wisząca płaszczyzna z dwoma
wspornikami, e) wisząca płaszczyzna z czterema wspornikami.

Rys.5. Propozycja kroków technologicznych w wytwarzaniu wiszących płaszczyzn.

Generated by Foxit PDF Creator © Foxit Software

http://www.foxitsoftware.com For evaluation only.