Pakiet MATLAB

Krzysztof Wlaźlik, Damian Wojdan

Akademia Górniczo Hutnicza

im. Stanisława Staszica w Krakowie

Wydział Fizyki i Informatyki Stosowanej

Fizyka Komputerowa

http://fatcat.ftj.agh.edu.pl/˜wojna/ksn/

Streszczenie

Tematem pracy jest pakiet MATLAB. Jest to potężne narzędzie
stosowane do przeprowadzania obliczeń i symulacji w wielu dzie-
dzinach nauki. Autorzy przedstawili podstawy pracy z progra-
mem, jak również wskazali na bardziej zaawansowane sposoby jego
wykożystania.

Kilka słów na początek

Poniższe opracowanie napisane zostało przez studentów Wydziału Fi-

zyki i Informatyki Stosowanej AGH. Zgodnie z zaleceniami pracę pisali-
śmy tak aby była ona zrozumiała dla przeciętnego studenta naszego wy-
działu, mamy nadzieje, że tak właśnie jest. Naszą intencją było również
zainteresowanie Matlabem osób, które nie miały z nim wcześniej doczynie-
nia. Materiały zamieszczone w tej pracy pochodzą z internetu, literatury
jak i z własnych doświadczeń studenckich. Praca w głównej mierze ma
charakter teoretyczny jednak pod koniec przedstawiliśmy przykładowy
program napisany przez nas w MATLAB-ie.

Wersja elektroniczna znajduje się pod adresem:

http://fatcat.ftj.agh.edu.pl/˜wojna/ksn/

Krzysztof Wlaźlik Damian Wojdan

Spis treści

1

Wstęp

4

1.1

Historia pakietu MATLAB

. . . . . . . . . . . . . . . . .

4

1.2

MATLAB - dlaczego warto spróbować ? . . . . . . . . . .

4

2

Podstawy MATLAB’a

6

2.1

Obsługa programu . . . . . . . . . . . . . . . . . . . . . .

6

2.2

Typy danych . . . . . . . . . . . . . . . . . . . . . . . . .

6

2.3

Operatory . . . . . . . . . . . . . . . . . . . . . . . . . . .

7

2.4

Macierze . . . . . . . . . . . . . . . . . . . . . . . . . . . .

8

2.4.1

Macierze dwuwymiarowe . . . . . . . . . . . . . . .

8

2.4.2

Macierze wielowymiarowe . . . . . . . . . . . . . .

9

2.5

Operacje na plikach

. . . . . . . . . . . . . . . . . . . . .

11

2.6

Moduły . . . . . . . . . . . . . . . . . . . . . . . . . . . .

11

2.6.1

Skrypty . . . . . . . . . . . . . . . . . . . . . . . .

11

2.6.2

Funkcje . . . . . . . . . . . . . . . . . . . . . . . .

12

3

Wizualizacja wyników

13

3.1

Grafika 2D

. . . . . . . . . . . . . . . . . . . . . . . . . .

13

3.1.1

Układ kartezjański . . . . . . . . . . . . . . . . . .

13

3.1.2

Układy nie kartezjańskie . . . . . . . . . . . . . . .

14

3.1.3

Opis układu . . . . . . . . . . . . . . . . . . . . . .

14

3.2

Grafika 3D

. . . . . . . . . . . . . . . . . . . . . . . . . .

15

4

Potęga MATLAB’a

18

4.1

TOOLBOX-y . . . . . . . . . . . . . . . . . . . . . . . . .

18

4.2

Przykład: Symbolic Math Toolbox . . . . . . . . . . . . .

19

5

Tworzenie GUI

21

6

Zakończenie

23

3

Rozdział 1

Wstęp

1.1

Historia pakietu MATLAB

Historia pakietu MATLAB sięga do lat siedemdziesiątych ubiegłego

wieku, kiedy to powstały fortranowskie biblioteki do obliczeń macierzo-
wych LINPACK i EISPACK. Jeden z autorów tych bibliiotek, Cleve Mo-
ler, chcąc ułatwić kożystanie z tych bibliotek bez znajomości fortrana
napisał program w formie prostego, interaktywnego języka poleceń - stąd
nazwa MATLAB-a od MATrix LABoratory. Program ten rozprowadzany
na zasadach public domain stał się pierwowzorem MATLABA.

W 1983 C. Moller oraz S. Bangert i J. Little postanowili rozwinąć

powyższy projekt - zastąpili Fortran językiem C i dodali zintegrowaną
grafikę. Założyli oni firmę The MathWorks Inc., która do dziś zajmuje się
rozwojem i sprzedażą pakietu Matlab. W 1985 roku pojawiła się pierwsza
wersja programu.

1.2

MATLAB - dlaczego warto spróbować ?

Obecnie MATLAB to pakiet przeznaczony do wykonywania obliczeń

numerycznych oraz graficznej prezentacji otrzymanych wyników. Dostępny
jest na różnych platformach sprzętowych oraz systemowych (np. Win-
dows, Macintosh, UNIX). MATLAB łączy w sobie interakcyjne środowi-
sko programowe oraz język programowania wysokiego poziomu. Głównym
przeznaczeniem pakietu są obliczenia naukowo - techniczne, inżynierskie
oraz wizualizacje dwu i trójwymiarowe. Program ten pozwala na wyko-
nywanie skomplikowanych obliczeń numerycznych z końcową wizualizacją
otrzymanych wyników. MATLAB łączy analizę numeryczną, obliczenia
macierzowe, przetwarzanie sygnałów, obliczenia symboliczne i grafikę w
łatwe do użycia środowisko.

4

Możliwości MATLAB’a są ogromne - jak mawia jeden z naszych ko-

legów ¨Nie ma takiej rzeczy, której nie dałoby się zrobić w Matlabie”.
Zakres zastosowań pakietu obejmuje bardzo różnorodne dziedziny nauki
i techniki. Można tu wymienić choćby elektronikę, telekomunikację, auto-
matykę, ekonomię, ale również zagadnienia z meteorologii, biologii i medy-
cyny. W dziedzinach algorytmów numerycznych algebry liniowej, analizy
matematycznej i numerycznej, czy całkowania numerycznego i oczywi-
ście rachunku macierzowego bardzo ważną role odgrywa dostęp do ich
najnowszych implementacji, jest to jedna z bardzo znaczących zalet MA-
TLAB’a. Wielką zaletą programu jest przyjazny interfejs użytkownika,
który początkującym ułatwia się z pakietem a zaawansowanym użytkow-
nikom pozwala na szybkie i sprawne tworzenie programów. Matlab ofe-
ruje ponadto liczne toolkity czyli rozszerzenia programu udostępniające
dodatkowe funkcje jak np. obliczenia statystyczne czy obsługę sieci neuro-
nowych. Możliwa jest również rozszerzalność pakietu przez importowanie
własnych aplikacji napisanych w języku C lub Fortranie stanowi ważny i
pożyteczny model pracy z pakietem.

Rozdział 2

Podstawy MATLAB-a

2.1

Obsługa programu

Praca w środowisku MATLAB-a przypomina pracę w typowym sys-

temie operacyjnym jak Linux czy DOS. Polega na wydawaniu poleceń,
które po zatwierdzeniu są wykonywane przez interpreter. Poniżej przed-
stawiamy kilka podstawowych komend input/output udostępnianych przez
program:

• Duże i małe litery są rozróżniane !
• Zmienna nie musi być zadeklarowana, jej implementacja rozpoczyna

się razem z nadaniem wartości.

• who - wyświetlenie listy zmiennych zadeklarowanych przez użytkow-

nika.

• clear nazwa-zmiennej - po wywołaniu tej komendy następuje usu-

niecie zmiennej o podanej nazwie, gdy nie podano nazwy zmiennej
to usuwane są wszystkie zmienne które dotychczas zdefiniował użyt-
kownik.

• dir - wyswietla zawartość aktualnego katalogu.
• chdir nazwa-katalogu - przechodzi do katalodu nazwa-katalogu.
• save nazwa-pliku - umożliwia zapisanie wszystkich zmiennych na

dysku .

• load nazwa-pliku - wczytuje wcześniej zapisane dane z pliku.
• Jeśli po poleceniu brak jest średnika to wynik jego wykonania zo-

stanie wyświetlony na ekranie.

2.2

Typy danych

MATLAB dopuszcza użycie następujących typów danych

1. Double - liczby podwójnej precyzji podstawowy typ danych dla

6

zmiennych MATLAB-a (wszystkie obliczenia w Matlabie są pro-
wadzone w trybie podwójnej precyzji dla zmiennych numerycznych
i łańcuchowych).

2. Char - znaki i łańcuchy znaków łańcuch znakowy definiuje się za

pomocą apostrofów i przechowywany jest w pamięci w postaci wek-
tora liczb całkowitych reprezentujących kody ASCII poszczególnych
znaków.

3. Sparse - dotyczy dwuwymiarowych macierzy rzadkich podwónej

precyzji (macierz rzadka to taka macierz,w której zapamiętywane
są tylko elementy niezerowe redukuje to zapotrzebowanie pamięci).

4. Cell - typ komórkowy - elementy tablic komórkowych mogą zawierać

inne tablice.

5. Struct - typ strukturalny - tablice strukturalne odwołują się do nazw

pól, które mogą zawierać inne tablice.

6. Uint8 - typ przeznaczony do efektywnego wykorzystania pamięci;

możiwe są takie operacje, jak zmiana wymiarów lub kształtu tablicy,
ale niedozwolone są żadne operacje matematyczne.

7. UserObject - typ definiowany przez użytkownika.

2.3

Operatory

Operatory arytmetyczne:

Operator
Macierzowy

Opis

Operator Ta-
blicowy

Przykład
macierzowy

Przykład ta-
blicowy

+

dodawanie

+

A+B

A+B

-

odejmowanie -

A-B

A-B

*

mnożenie

.*

A*B

A.*B

/

dzielenie

./

A*B

A./B

’

sprzężenie

A’

.’

transpozycja

A.’

Operatory logiczne:

Symbol

Op.Relacji

Symbol

Op.logiczny

<

mniejszy

&

AND

(ko-

niunkcja)

<=

mniejszy

lub

równy

!

OR

(alterna-

tywa)

>=

większy

lub

równy

∼

NOT

(nega-

cja)

>

większy

xor

wyłącznie OR

==

równy

∼=

nierówny

2.4

Macierze

Macierze są podstawowym typem danych wykorzystywanym w MATLAB-

ie. W pamięci przchowywane są w dwojaki sposób: gęsty - przechowuje
całą macierz i x j w pamięci albo rzadki - zapamiętywane są tylko wartości
niezerowe wraz z ich położeniami.Należy pamiętać, że MATLAB traktuje
liczby i wektory jako macierze, tzn. liczby są traktowane jak macierze
1x1, a wektory jak macierze 1xN.

2.4.1

Macierze dwuwymiarowe

Tworząc macierz musimu pamietać o tym że:

• elementy w wierszu macierzy muszą być oddzielane spacją lub prze-

cinkami

• średnik lub znak nowego wiersza kończy wiersz macierzy i powoduje

przejście do następnego

• cała lista elementów musi być ujęta w nawiasy kwadratowe.
• obowiązuje zasada indeksowania macierzy począwszy od 1

Najprostrz macierz tworzymy wymieniając jej elementy w nawiasach

kwadratowych:

>>M=[1 2 .2 4 ; 5.1 8 2 1]

W efekcie otrzymamy macierz następującej postaci:

M=
1.0000 2.0000 0.2000 4.0000
5.1000 8.0000 2.0000 1.0000

Odwołania do macierzy i kilka podstawowych komend (obliczanie rzędu

macierzy, wektrów wasnych ipt.):

• x(j:k)

- elementy wektora wierszowego x o numerach od j do k

• A(i,:)

- wszystkie elementy w wierszu i macierzy A

• A(i,j:l)

- wszystkie elementy w wierszu i macierzy A o numerach od j do l

• A(i:k,j:l)

- wszystkie elementy w kolumnach od j do l wierszy od i do l

• A(x,j:l)

- wszystkie elementy w kolumnach od j do l w wierszach macierzy
A o numerach określonych przez elementy wektora x

• A(:,:)

- cała dwuwymiarowa macierz A

• A(:)

- cała macierz A w postaci wektora kolumnowego.

• disp(A)

- wyświetla zawartość macierzy A w oknie poleceń

• size(A)

- wyświetla rozmiar dwuwymiarowej macierzy A (liczbę wierszy i
kolumn) w postaci dwuelementowego wektora wierszowego;

• [n m]=size(A)

- przypisuje zmiennej n liczbę wierszy, a zmiennej m liczb¸

e kolumn;

• n=size(A,1)

- przypisuje zmiennej n liczbę wierszy macierzy A.

• m=size(A,2)

– przypisuje zmiennej m liczbę kolumn macierzy A.

• length(x)

- zwraca długość wektora x lub dłuższy z wymiarów macierzy

• det(A)

- zwraca wyznacznik macierzy kwadratowej A.

• inv(A)

- zwraca macierz odwrotną do macierzy A.

• eye(n)

- tworzy macierz jednostkową nxn

• tril(A)

- utworzenie z macierzy A macierzy trójktnej dolnej.

• triu(A)

- utworzenie z macierzy A macierzy trójkątnej górnej.

2.4.2

Macierze wielowymiarowe

MATLAB umożliwia nam definiowanie macierzy wielowymiarowych.

Do tego typu macierzy odwołujemy się tak samo jak do macierzy dwu-
wymiarowych podając odpowiednią liczbę indeksów.

1. Pierwszy indeks - wiersz macierzy (wymiar 1).
2. Drugi indeks - kolumna macierzy (wymiar 2).
3. Trzeci indeks - strona macierzy (wymiar 3).
4. Czwarty indeks - książka macierzy (wymiar 4).
5. Piąty indeks - tom macierzy (wym5).

Implementacja takiej macierzy może się odbyć w następujący sposób:

>>D(:,:,1)=[1 3 0; 5 7 2]
>>D(:,:,2)=[4 7 8; 1 0 5]

czego efektem będzie macierz trójwymiarowa.

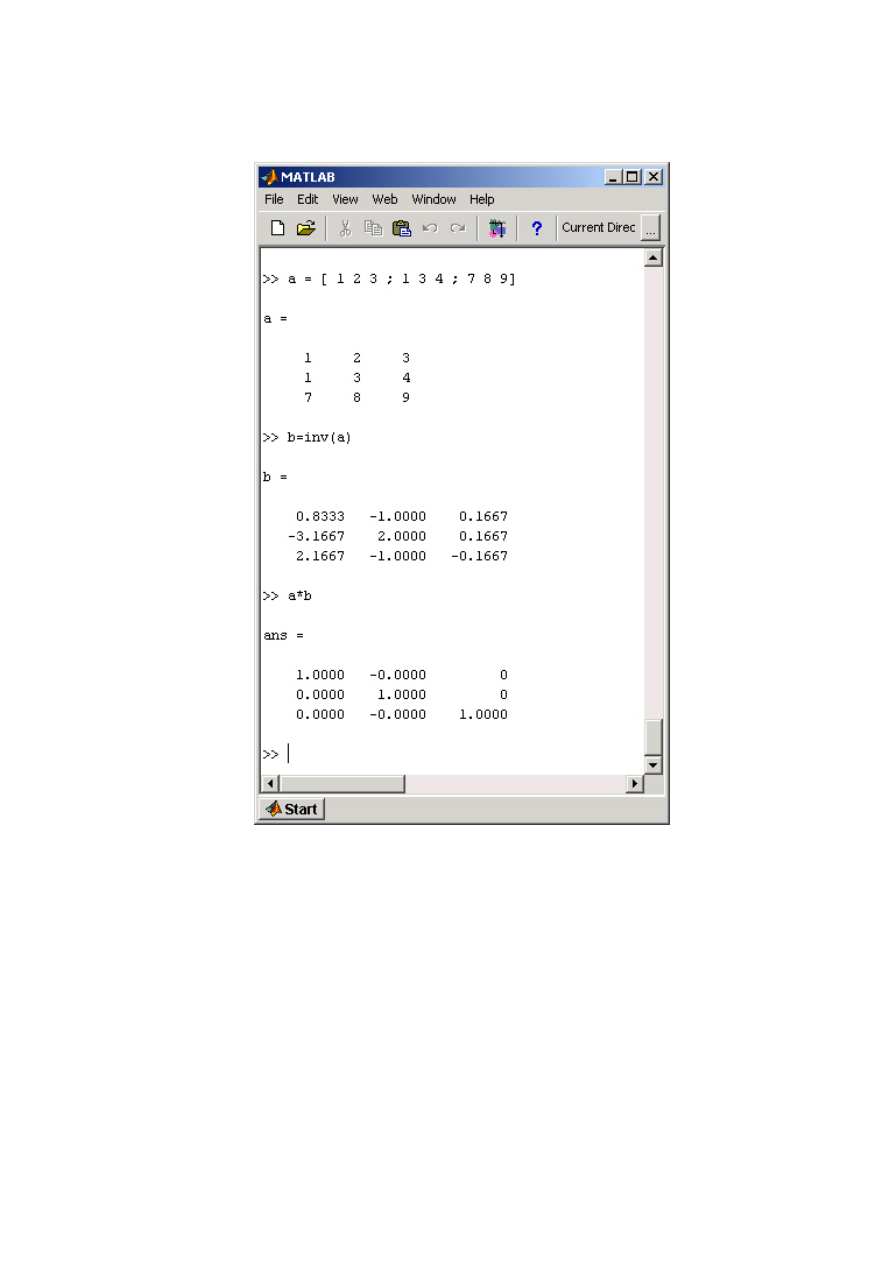
Rysunek 2.1: Przykład operacji na macierzach.

2.5

Operacje na plikach

MATLAB wspiera operacje na plikach - podstawowe komendy tego

typu to:

id-pliku = fopen(nazwa-pliku, typ-dostępu)

Funkcja fopen otwiera plik wskazany łańcuchem nazwa-pliku w sposób
określony przez zmienną typ-dostępu (np. ’r’ - do odczytu, ’w’ - do za-
pisu ’r+’ - do zapisu i odczytu) i zwraca unikatowy identyfikator pliku
(zmienną id-pliku). Identyfikator ten powinien być używany we wszyst-
kich operacjach wejścia i wyjścia wykonywanych na danym pliku. Jeżeli
operacja otwarcia pliku zakończy się sukcesem zmienna id pliku będzie
nieujemną liczbą całkowitą, w przeciwnym wypadku przyjmie wartość 1.

Druga postać wywołania funkcji fopen jest następująca:

[id-pliku, informacja]

= fopen(nazwa-pliku, typ-dostępu)

Informacja jest łańcuchem znakowym, który może być pomocny w usta-
leniu błędu. Jest on zwracany kiedy operacja otwarcia pliku zakończy się
niepowodzeniem.

Zamknięcie pliku o podanym identyfikatorze:

fclose(id-pliku)

Zamknięcie wszystkich otwartych plików:

fclose(all)

2.6

Moduły

2.6.1

Skrypty

Skrypt jest plikiem tekstowym o rozszerzeniu .m (m-plikiem), zawiera-

jącym polecenia i instrukcje Matlaba. Polecenia w pliku muszą być zgodne
z semantyką MATLAB-a. Skrypty nie pobierają żadnych argumentów
wejściowych ani nie zwracają argumentów wyjściowych mogą tylko opero-
wać na zmiennych dostępnych w przestrzeni roboczej MATLAB-a. Umiesz-
czanie komentarza w pliku skryptu (pierwsze 3 linie) daje nam możliwość
uzyskania pomocy na temat skryptu. Wywołujemy: help nazwa skryptu.

Funkcje obsługi wejścia skryptu

1. x=input(tekst) - wyświetla łańcuch tekst, oczekuje na wpisanie

przez użytkownika danej liczbowej i przypisuje ją zmiennej liczbowej
x, zamiast danej liczbowej można wpisać wyrażenie MATLAB-a,
którego funkcja obliczy,

2. x=input(tekst,s) - wyświetla łańcuch tekst, oczekuje na wpisanie

przez użytkownika łańcucha znakowego i przypisuje go zmiennej x,

3. pause - zatrzymuje wykonywanie skryptu do momentu naciśnięcia

dowolnego klawisza,

4. pause(n) - zastępuje wykonywanie skryptu na n sekund.

2.6.2

Funkcje

MATLAB udostępnia użytkownikom zintegrowany proceduralny ję-

zyk programowania. Zatem MATLAB jest programem, który nie tylko
daje użytkownikom możliwości wykorzystywania funkcji napisanych przez
innych (biblioteki i funkcje standardowe), ale pozwala na samodzielne ich
tworzenie. By zdefiniować funkcję, należy podobnie jak przy skryptach
umieścić ją w pliku z rozszerzeniem .m. Należy jednak pamiętać, by na-
zwa tego pliku była identyczna z nazwą zdefiniowanej funkcji. Podobne,
jak w skryptach, zastosowanie komentarza umożliwi wyświetlenie infor-
macji o funkcji poleceniem help. Tworząc funkcje należy pamiętać o tym
że, pierwszy wiersz m-pliku musi zawierać definicję nowej funkcji:

1. słowo kluczowe function,
2. nazwę funkcji musi być taka sama, jak nazwa pliku,
3. wartości funkcji (lista argumentów wyjściowych),
4. parametry funkcji (lista argumentów wejściowych).

Rozdział 3

Wizualizacja wyników

MATLAB udostępnia liczne metody wizualizacji otrzymanych wyników
obliczeń. Funkcje graficzne można podzielić na cztery podstawowe grupy:

1. przeznaczone do tworzenia wykresów dwu- i trójwymiarowych,
2. prezentujące wykresy ciągłe i dyskretne,
3. umożliwiające tworzenie grafiki wektorowej i rastrowej,
4. wysokiego i niskiego poziomu.

3.1

Grafika 2D

3.1.1

Układ kartezjański

Często gdy otrzymamy wyniki obliczeń warto umieścić je na wykresie.

Do rysowania prostych wykresów służy funkcja: plot. W zależności od
podanych parametrów wywołania:

• plot(x,y) - rysuje wykres elementów wektora y względem elemen-

tów wektora x,

• plot(y) - rysuje wykres elementów wektora y, przyjmując x = 1 :

length(y),

• plot(x,y,s) - rysuje wykres y(x) z określeniem dokładnego wyglądu

linii; s łańcuch zawierający kody,

• plot(x1,y1,x2,y2,...) - rysuje w jednym oknie wiele wykresów:

y1(x1), y2(x2),... ,

• plot(x1,y1,s1,x2,y2,s2,..) - rysuje w jednym oknie wiele wykre-

sów z określeniem dokładnego wyglądu linii każdego z nich.

Funkcja linspace pomaga w tworzeniu danych do wykresu:

• linspace(x1,x2,N) - generuje wierszowy wektor N liczb rozłożo-

nych równomiernie wprzedziale od x1 do x2,

• linspace(x1,x2) - generuje domyślnie 100 liczb z przedziału x1 do

13

x2,

• fplot(f,[x0,xk]) - f-łańcuch znakw zawierających nazwę funkcji

x0,xk-poczatek i koniec przedziału rysowania funkcji,

• [x,y]=fplot(...) - nie powoduje narysowania wykresu, tylko zwraca

wektor argu-mentw x i wektor wartoci funkcji y. Wykres uzyskanych
danych można narysowa za pomocą polecenia plot(x,y).

3.1.2

Układy nie kartezjańskie

Niekiedy jednak standardowy układ kartezjański nie wystarcza i po-

trzebujemy np. skali logarytmicznej, bądź układu współrzędnych biegu-
nowych. Wykresy w skali logarytmicznej można uzyskać dzięki loglog.
Funkcja rysuje wykres, używając skal logarytmicznych:

• loglog(x,y,s) - na obu osiach,
• semilogx(x,y,s) - tylko na osi x,
• semilogy(x,y,s) - tylko na osi y.

Wykresy we współrzędnych biegunowych realizuje funkcja polar(theta,r,s):

• theta - wektor kątów (w radianach) dla poszczególnych punktów,
• r - wektor odległości poszczególnych punktów od początku układu

współrzędnych.

Opcjonalnym argumentem funkcji jest łańcuch znaków s, określający

wygląd rysowanej linii, jak przy funkcji plot.

Pozostaje jeszcze wykres na płaszczyźnie liczb zespolonych:

• plot(z,s) - jeżeli z jest macierzą o elementach zespolonych, to zo-

stanie narysowany wykres Im(z)=f(Re(z)) ,

• poleceniem równoważnym powyższemu jest plot(Re(z),Im(z), s).

3.1.3

Opis układu

Aby zwiększyć czytelność i zrozumienie wykresów warto je opisywać.

Możemy to zrealizowac korzystają z jednej z funkcji:

• title(txt) - tekst opisujący dany wykres,
• text(x,y,txt) - umieszczenie tekstu w podanych współrzędnych x

i y ,

• xlabel(txt), ylabel(txt) - opis tekstowy osi układu,
• gird - bezparametrowe wywołanie, nakładamy siatkę na układ współ-

rzędnych.

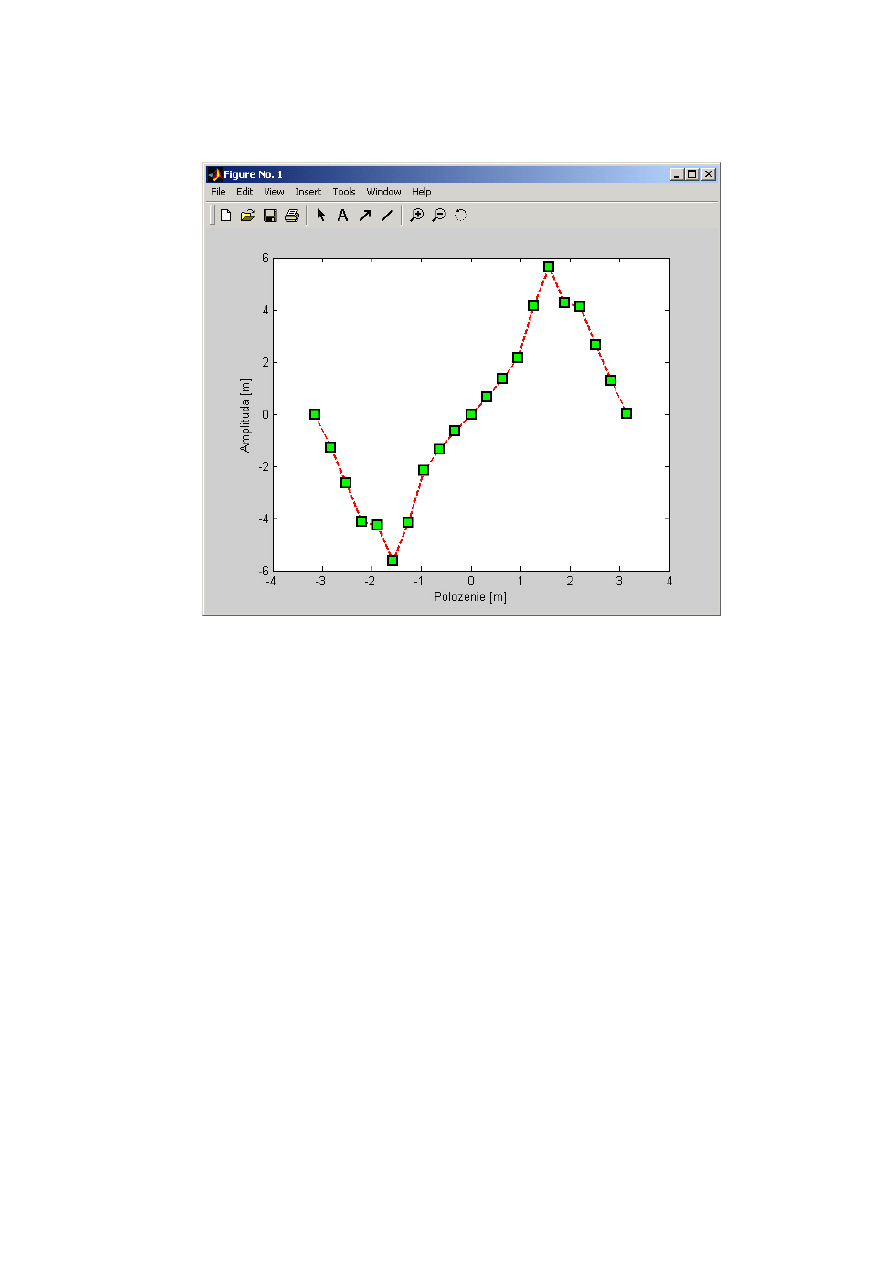
Rysunek 3.1: Przykładowy wykres 2D wykonany w MATLAB-ie.

3.2

Grafika 3D

MATLAB umożliwia również wizualizację trójwymiarową. Pakiet ten

udostępnia funkcje służące do rysowania krzywych przestrzennych (plot3 ),
siatek (mesh), powierzchni (surf ) oraz wykresów konturowych (contour ).
Polecenie:

plot3(x,y,z,s)

generuje trójwymiarową krzywą złożoną z punktów (xi, yi, zi), których
współrzędne zostały określone w wektorach x, y, z. Wektory muszą być
tej samej długości. Funkcja ta jest odpowiednikiem funkcji plot w grafice
dwuwymiarowej.
Powierzchnia rysowana jest w Matlabie jako wykres funkcji z=f(x,y), przy
czym współrzędne punktów (xi,yi) określone są za pomocą wektorów X i

Y, gdzie indeksy i j przyjmują wartości

i=1:length(X),

j=1:length(Y)

Ponieważ tworzymy wykres trójwymiarowy na dwuwymiarowej płasz-
czyźnie ekranu, na początek należy wygenerować specjalną siatkę na płasz-
czyźnie XY w tych węzłach, w których szukane są wartości funkcji w osi
z. Służy do tego funkcja meshgrid.

[x,y]=meshgrid(X,Y)

transformuje obszar opisany przez wektory X i Y (z przestrzeni 3D) na
dwie macierze x oraz y we współrzędnych ekranowych 2D.

[x,y]=meshgrid(X)

jest równoważne wywołaniu

meshgrid(X,X)

Funkcja mesh:

• mesh(x,y,z,c) - rysuje powierzchnię opisaną macierzami x,y,z w

postaci kolorowej siatki o polach wypełnionych kolorem tła elementy
macierzy c określają kolory linii poszczególnych pól.

• mesh(x,y,z) - rysuje powierzchnię, przyjmując c=z.
• mesh(z,c) - rysuje wykres wartoci elementów macierzy z, przyjmu-

jąc x=1:n, y=1:m, gdzie [m,n]=size(z).

• meshc(x,y,z,c) - rysuje siatkę identyczną jak funkcja mesh i umiesz-

cza pod nią wykres poziomicowy.

• meshz(x,y,z,c) - działa jak mesh, ale dodatkowo w dół od krawę-

dzi wykresu rysowane są linie określające płaszczyzny odniesienia.

Funkcje shpere i cylinder :

sphere(n)

tworzy kulę o promieniu 1 oraz środku w początku układu współrzędnych
z wykorzystaniem 2(n+1) punktów siatki tworzącej jej powierzchnią. Do-
danie polecenia:

surf(x+2,y-1,z+1)

utworzy wykres kuli o promieniu 1 ze środkiem w punkcie (2,-1,1). Funk-
cja:

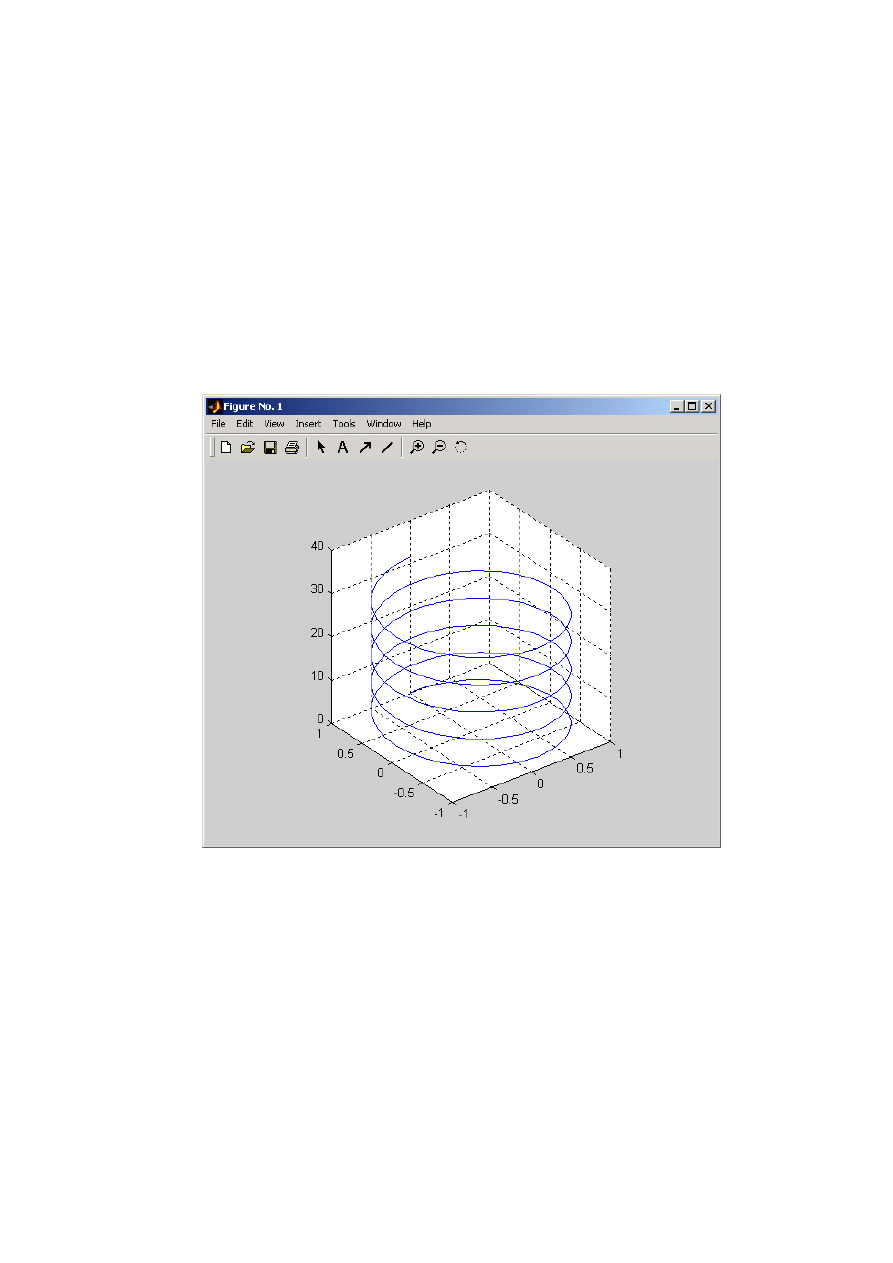
cylinder(r,n)

służy do tworzenia wykresów powierzchni obrotowych. Pobiera ona dwa
opcjonalne parametry wejściowe, parametr r oznacza wektor, który defi-
niuje promienie walca w kolejnych punktach wzdłuż osi z, a n oznacza
liczbę punktów siatki na obwodzie walca. Wartości domyślne dla tych
parametrów to r =[1 1] oraz n=20. Polecenie:

cylinder([1

0])

tworzy stożek o wysokości i promieniu podstawy równym 1.

Rysunek 3.2: Przykładowy wykres 3D wykonany w MATLAB-ie.

Rozdział 4

Potęga MATLAB-a

Powyższe rozdziały zawierały opis podstawowych oferowanych przez MATLAB-
a opcji. Tak naprawde potęgę programu budują jednak TOOLBOX-y,
czyli biblioteki ktore poszerzają zakres stosowania go do rozwiązywania
specjalistycznych problemów z określonych dziedzin (automatyka, elektro-
nika, telekomunikacja, matematyka etc.). Biblioteki te mogą być pisane
przez oddzielnych producentów oprogramowania jak również zwykłych
użytkowników.

4.1

TOOLBOX-y

Poniżej przedstawiamy listę wybranych TOOLBOX-ów z krótkim opi-

sem:

• Chemometrix Toolbox - przeznaczony do opracowywania danych

chemicznych,

• Financial Toolbox - przeznaczony do analiz i obliczeń finansowych

(planowanie stałych przychodów, badanie wydajności obligacji, kal-
kulacja przepływu gotówki, obliczanie stóp procentowych etc.).

• Fuzzy Logic Toolbox - środowisko do projektowania i diagnostyki

inteligentnych układów sterowania wykorzystujących metody logiki
rozmytej i uczenie adaptacyjne,

• Image Processing Toolbox - programowe narzędzia do przetwarzania

obrazów,

• Mapping Toolbox - przeznaczony do analizy informacji geograficz-

nych i wyświetlania map, z możliwością dostępu do zewnętrznych
źródeł geograficznych,

• Neural Network Toolbox - zbiór funkcji do projektowania i symulacji

sieci neuronowych,

• Higher-Order Spectral Analisis Toolbox - przeznaczony do analizy

18

sygnałów zakłóconych szumem niegaussowskim lub sygnałami ge-
nerowanymi przez procesy nieliniowe. Biblioteka ta znajduje zasto-
sowanie w biomedycynie, akustyce, ekonometrii, oceanografii, prze-
twarzaniu sygnałów mowy, technice radarowej i sonarowej,

• Symbolic Math Toolbox - zestaw funkcji do obliczeń symbolicznych

- rozszerza możliwości Matlaba o możliwość wykonywania obliczeń
symbolicznych,

• Parial Differential Equation Toolbox - zestaw funkcji do numerycz-

nego rozwiązywania równań różniczkowych cząstkowych metodą ele-
mentów skończonych,

• Simulink - pakiet służący do modelowania, symulacji i analizy ukła-

dów dynamicznych. Simulink dostarcza także graficzny interfejs użyt-
kownika umożliwiający konstruowanie modeli w postaci diagramów
blokowych,

• Spline Toolbox - zestaw bibliotek do aproksymacji i interpolacji

funkcjami sklejanymi,

• Wavelet Toolbox - biblioteka do analizy sygnałów oraz usuwania

szumów.

4.2

Przykład: Symbolic Math Toolbox

Symbolic Math Toolbox rozszerza możliwości MATLAB-a o możliwość

wykonywania obliczwń symbolicznych. Do tworzenia obiektów symbolicz-
nych służą komendy: sym oraz syms. Pierwszej z nich używamy chcąc
wprowadzić tylko jeden obiekt symboliczny, druga - pozwala na wprowa-
dzenie kilku na raz obiektów symbolicznych. Możemy to zrobić na kilka
sposobów:
x = sym(’x’) - wprowadzenie obiektu x,
syms x y z - wprowadzenie obiektów x y z (w praktyce najczęściej ko-
rzysta się z tego zapisu),
A = syms(’x’,’y’,’z’) - wprowadzenie obiektów x y z.

Gdy chcemy policzyć pierwiastek z pięciu to w głównym oknie MATLAB-

a wpisujemy sqrt(5). W odpowiedzi dostajemy ans = 2.2361. Jeżeli po-
traktujemy liczbę pięć jako obiekt symboliczny i wpiszemy a = sqrt(sym(5))
to nie otrzymamy wartości lecz wyrażenie a = 5

1/2

.

Tworzenie zmiennych symbolicznych oraz wyrażeń symbolicznych:
Gdy jako zmienne symboliczne wprowadzimy x = sym(’x’), t = sym(’theta’),
f= sym(’phi’) będziemy mogli tworzyć wyrażenia w których występują
te zmienne np. g = (sin(t))

2

+ (cos(f ))

2

. W odpowiedzi dostaniemy:

sin(theta)

2

+ cos(phi)

2

.

Całe wyrażenia możemy traktować jako obiekty symboliczne - np. c =
sym(’(sqrt(5)+sin(t))/cos(f )’). Mając tak zdefiniowane wyrażenie c mo-
żemy je wstawiać do innych wyrażeń i konstruować np. d = c*sin(t)+cos(f )/c.
Do wyrażenia d warto zastosować jeszcze komendę pretty(d). Gdy chcemy
zapisać trójmian kwadratowy korzystamy z komendy syms a b c x, a na-
stępnie f = a ∗ x

2

+ b ∗ x + c.

Funkcje do wykorzystania
W MATLAB-ie dostępne są niektóre elementarne funkcje takie jak sin()
czy exp(), które można bezpośrednio wykorzystać podając tylko odpo-
wiednie argumenty.

Uproszczenia wyrażeń algebraicznych - różne zapisy
Wprowadźmy trzy funkcje f(x), g(x) oraz h(x)
syms x
f = x

3

− 6 ∗ x

2

+ 11 ∗ x − 6

g = (x-1)*(x-2)*(x-3)
h = x*(x*(x-6)+11)-6
Są to takie same funkcje tylko inaczej zapisanei można przechodzić z jed-
nej postaci do drugiej. Jest kilka komend które mogą tego dokonać. Są to
np.: collect, expand, horner, factor, simplify, oraz simple:

• collect(f ) - zbiera współczynniki z tym samym x; gdy f = (1+x)*t

+ x*t to otrzymamy 2*x*t+t,

• expand(f ) - wymnaża wyrażenia w nawiasach; gdy f = cos(x+y)

otrzymamy cos(x)*cos(y)-sin(x)*sin(y),

• horner(f ) - doprowadza do postaci Hornera,
• factor(f ) - doprowadza do postaci iloczynów,
• simplify(f ) - upraszcza funkcję,
• simple(f ) - zapis w najkrótszej postaci; wyświetla różne rodzaje

zapisu.

Zastąpienie
Jeżeli w jakimś dużym wyrażeniu mamy pewien fragment który się powta-
rza, to stosując komendę r = subexpr(s) otrzymamy wyrażenie w prost-
szej postaci z nowym parametrem zamiast powtarzającego się fragmentu.
Można też samemu ustalić w jakim wyrażeniu co i czym ma być zastą-
pione. subs(r,a,10) oznacza: w obiekcie r zastąp obiekt a przez 10.

Rozdział 5

Tworzenie GUI

Standardowo MATLAB oferuje jeszcze jedno bardzo przydatne narzędzie
- GUIDE - czyli edytor gaficznego interfejsu użytkownika. Pozwala on na
budowanie okienkowych aplikacji przy użyciu standardowyvh kontrolek
takich jak np.:

• push button - przycisk, który wywołuje przypisaną do niego funk-

cję zwrotną,

• radio button - kontrolka do tworzenia pól wyboru opcji,
• edit text - pole tekstowe, do którego użytkownik może wpisywać

wartości,

• static text - statyczny tekst, czyli po prostu napis,
• frame - obiekt do grupowania elementów interfejsu,
• axes - niezwykle użyteczna kontrolka, na której można rysować

dowolne wykresy.

Wszystkie kontrolki można oprogramować używając standardowych po-
leceń MATLAB-a tak, aby powstał program spełniający nawet najwięk-
sze wymagania. Każda kontrolka posiada swoje właściwości, więc można
dowolnie ją skonfigurować do potrzeb aplikacji. Poniżej przedstawiamy
program napisany w ramach zajęć Pakiety Obliczeniowe na Wydziale Fi-
zyki i Informatyki Stosowanej. Program służy do demonstracji rozkładów
statystycznych, obliczania prawdopodobieństw na zadanym poziomie uf-
ności, oraz graficznej prezentacji wyników. Wykożystuje on możliwości
programu GUIDE oraz funkcje zawarte w Statistics Toolbox - biblio-
tece do obliczeń statystycznych.

21

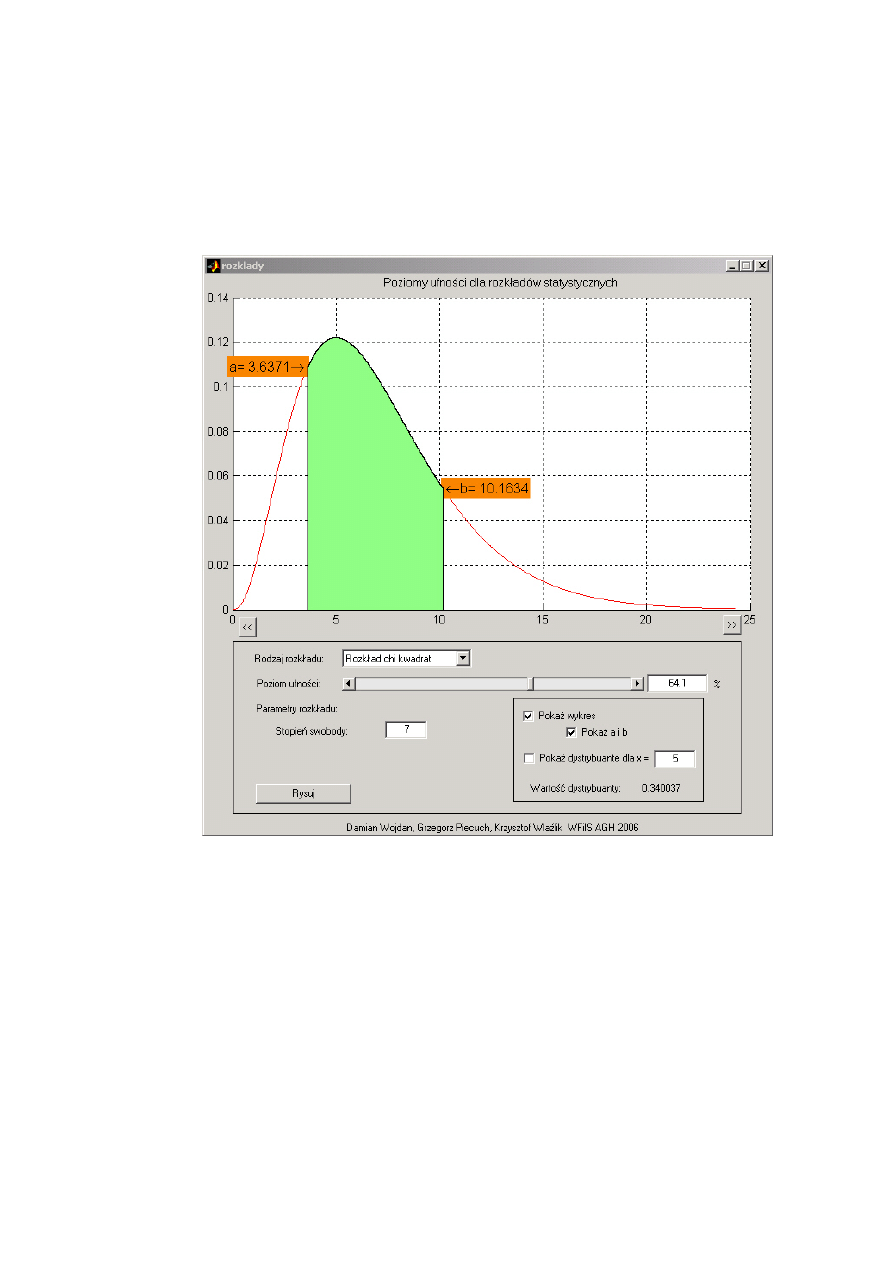
Rysunek 5.1: Przykład aplikacji stworzonej w GUIDE.

Rozdział 6

Zakończenie

MATLAB obecnie jest niemal standardem i podstawowym narzędziem
pracy naukowca, inżyniera i analityka finansowego. Wydajne i szybkie al-
gorytmy oraz doskonałe mechanizmy analityczne czynią z niego doskonałe
narzędzia zarówno dla matematyka, jak i dla ekonomisty lub genetyka. Ję-
zyk programowania MATLAB umożliwia tworzenie własnych aplikacji, a
ogromna ilość bibliotek zewnętrznych ułatwia zastosowanie tych aplikacji
do różnych celów. MATLAB jest dziś szeroko stosowany w laboratoriach
badawczych. Coraz częściej wykorzystuje się go również na uczelniach.

Mamy nadzieje, że nasze opracowanie sprawi, że czytające osoby nie zna-
jące MATLAB-a zainteresują się tym niezwykle ciekawym i potężnym na-
rzędziem. Nawet jeśli nie jesteś informatykiem czy naukowcem na pewno
zdarzyło Ci się stanąć przed problemem wymagającym nieco bardziej
skomplikowanych obliczeń. W takim przypadku MATLAB znakomicie
się nadaje udostępniając przyjazny dla użytkownika interfejs, intuicyjny
język programowania i doskonałą pomoc, w której znaleźć można opis
funkcji programu. Tak więc drogi czytelniku jeśli znajdziesz chwilę czasu
poświęć ją na naukę MATLAB-a a z pewnością Ci się to opłaci.

Bibliografia

[1] MATLAB i Simulink. Poradnik użytkownika. Wydanie II. Bogumiła
Mrozek, Zbigniew Mrozek. Wydawnictwo Helion.
[2] http://www.mathworks.com/access/helpdesk/help/techdoc/
[3] http://en.wikipedia.org/wiki/MATLAB
[4] System pomocy programu MATLAB.

23