1

MATLAB – PODSTAWY

ZNAKI SPECJALNE

=

– symbol przypisania

[ ]

– tworzenie tablic, argumenty wyjściowe funkcji, łączenie tablic

{ }

– indeksy struktur i tablic komórkowych

( ) – nawiasy do określania kolejności działań, do ujmowania indeksów
tablic, do ujmowania argumentów wejściowych funkcji

.

– kropka dziesiętna

...

– kontynuacja polecenia w następnej linii

,

– separator indeksów tablicy, argumentów funkcji, poleceń

;

– koniec wiersza macierzy, rezygnacja z wypisywania wyniku na ekranie

% –

początek komentarza w danej linii

:

– generowanie wektorów, indeksowanie macierzy

‘ – początek i koniec łańcucha znaków, operator transpozycji, operator

sprzężenia zespolonego

FUNKCJE SPECJALNE

pi

–

3.14159265...

realmin

– najmniejsza liczba rzeczywista

realmax –

największa liczba rzeczywista

Inf

–

nieskończoność

NaN

–

Not–a–Number

ans

–

zmienna

robocza

Inf – nieskończoność jest generowana przez dzielenie liczby różnej od 0 przez zero,
lub przez działanie na wartościach, które wykraczają po za największą możliwą
wartość rzeczywistą określoną przez funkcję realmax.

NaN jest generowana przy próbie wykonania działań typu 0/0 lub Inf–Inf

2

ZMIENNE LICZBOWE W MATLAB-IE

dzielą się na dwa typy:

typ całkowity ze znakiem (int8, int16, int32, int64) i
typ całkowity bez znaku (uint8, uint16, uint32, uint64)

typ rzeczywisty pojedynczej precyzji (single) oraz typ
rzeczywisty podwójnej precyzji (double)

Defaultowym (domyślnym) typem numerycznym dla zmiennych MATLAB-a jest typ
double!

Jeśli zmienna x ma wartość

>> x = 12.56
x =
12.5600

Instrukcja
>> int16(x)
ans =
13
konwertuje wartość x na liczbę całkowitą.

ans – oznacza zmienną utworzoną automatycznie przez MATLAB–a, gdy dane
wyrażenie nie zostało przypisane żadnej zmiennej. Por. z przykładem poniżej:

>> x = 12.56
x =
12.5600

>> y = int16(x)
y =
13

Typ

Zakres zmiennych typu rzeczywistego

single –3.40282e038

3.4283e+038

double –2.22507e+308

1.79769e+308

3

RÓŻNE FORMATY ZAPISU LICZBY RZECZYWISTEJ NA PRZYKŁADZIE

LICZBY

π

>>

format long, pi

ans =
3.14159265358979

>> format long e, pi
ans = 3.141592653589793e+000

ZMIENNE W MATLAB–ie

Zmiennym nadaje się nazwy. Nazwa może się składać:

• z liter, cyfr i znaku podkreślenia

• z dowolnej liczby znaków, ale tylko około 63 są rozróżnialne przez

MATLAB-a

Nazwa musi zaczynać się od litery !

UWAGA!

MATLAB rozróżnia wielkość liter w nazwie zmiennej !!!

Dla MATLAB-a zmienne A i

a

to dwie różne zmienne!

Format

Typ

Postać

short stałoprzecinkowy

3.1416

long stałoprzecinkowy

3.14159265358979

short e

zmiennoprzecinkowy

3.1416e+000

long e

zmiennoprzecinkowy

3.141592653589793e+000

rat ułamkowy

355/113

4

PODSTAWOWĄ STRUKTURĄ DANYCH W MATLAB-IE JEST TABLICA

Tablica (array) – to forma gromadzenia i przechowywania danych w pamięci
komputera. Tablicom nadaje się nazwy. Dane przechowywane w tablicy nazywają się
jej elementami. Położenie elementu w tablicy określone jest za pomocą indeksów.
MATLAB dopuszcza tablice wielowymiarowe!

Macierz (matrix) – jest szczególnym przypadkiem tablicy dwuwymiarowej!

– tablica A(5 x 5) – macierz

B = 10 – tablica B(1 x 1) – skalar

STANDARDOWE FUNKCJE MATEMATYCZNE

⎟

⎟

⎟

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎜

⎜

⎜

⎝

⎛

=

10

2

9

7

0

4

0

7

0

1

7

10

7

2

0

9

9

2

4

5

10

0

7

7

2

A

5

OPERATORY ARYTMETYCZNE W MATLAB–ie w odniesieniu do

MACIERZY

Operatory działań na macierzach:
A+B

A-B

A*B

A/B

A\B

A^B

A’

Operator

Opis

+ Dodawanie,

jednoargumentowy operator plus

- Odejmowanie,

jednoargumentowy operator minus

* Mnożenie macierzy
/

Prawostronne dzielenie macierzy

\

Lewostronne dzielenie macierzy

^ Potęgowanie macierzy
‘ Transponowanie

macierzy

Wyjaśnienie. Jeśli:

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

=

2

9

4

7

5

3

6

1

8

A

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

=

6

3

1

3

2

1

1

1

1

B

* Mnożenie macierzy

/

Prawostronne dzielenie macierzy

1

/

−

⋅

=

A

B

A

B

\

Lewostronne dzielenie macierzy

B

A

B

A

⋅

=

−1

\

Związek między działaniami na macierzach B/A I A\B

)'

'

'\

(

/

B

A

A

B

=

^ Potęgowanie macierzy – podniesienie macierzy A do potęgi p

Przypadki:

p liczba całkowita >0

C=A^p = A*A...*A

p liczba całkowita <0

C=(A-1)^p

A^p gdy p jest liczbą rzeczywistą lub p^A – potęgowanie wymaga wyznaczania
wartości i wektorów własnych
Gdy A i p są macierzami – błąd!

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

⋅

+

⋅

+

⋅

=

=

6

2

3

9

1

4

3

2

2

9

1

4

1

2

1

9

1

4

6

7

3

5

1

3

3

7

2

5

1

3

1

7

1

5

1

3

6

6

3

1

1

8

3

6

2

1

1

8

1

6

1

1

1

8

* B

A

C

n

j

i

b

a

c

n

k

kj

ik

ij

,...

2

,

1

,

,

1

=

=

∑

=

6

OPERATORY ARYTMETYCZNE W MATLAB–ie w odniesieniu do TABLIC.

NOTACJA KROPKOWA

Operatory działań na tablicach:
A+B

A-B

A.*B

A./B

A.\B

A.^B

A.’

Operator

Opis

+ Dodawanie,

jednoargumentowy operator plus

- Odejmowanie,

jednoargumentowy operator minus

.* Mnożenie tablic
./

Prawostronne dzielenie tablic

.\

Lewostronne dzielenie tablic

.^ Potęgowanie tablic
.’ Transponowanie

tablicy

‘ Sprzężenie zespolone

Wyjaśnienie. Jeśli

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

=

2

9

4

7

5

3

6

1

8

A

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

=

6

3

1

3

2

1

1

1

1

B

DZIELENIE TABLICOWE

PRAWOSTRONNE A./B LEWOSTRONE A.\B

SPOSOBY OKREŚLANIA TABLIC W MATLAB-ie

• Dane do tablicy są wprowadzane z klawiatury

• Tablica jest wczytywana z zewnętrznego pliku z danymi

• Tablicę może wygenerować użytkownik aplikacji wg ściśle określonego

algorytmu, za pomocą napisanej przez siebie funkcji

• Tablica może zostać wygenerowana za pomocą odpowiedniej funkcji MATLAB-a

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=

6

2

3

9

1

4

3

7

2

5

1

3

1

6

1

1

1

8

*

. B

A

D

n

j

i

b

a

c

ij

ij

ij

,...

2

,

1

.

=

=

ij

ij

ij

P

b

a

c

B

A

C

=

⇔

= /

.

ij

ij

ij

L

a

b

c

B

A

C

=

⇔

=

\

.

7

ZADAWANIE TABLICY Z KALWIATURY

• Wprowadź dane oddzielając elementy danego wiersza macierzy spacjami lub

przecinkami

• Użyj znaku średnika by zaznaczyć koniec wiersza

• Otocz wprowadzoną listę elementów nawiasami [ ]

Dla macierzy

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

=

2

9

4

7

5

3

6

1

8

A

napiszemy >>A = [8 1 6; 3 5 7; 4 9 2]

FUNKCJE MATLAB–a DO GENEROWANIA TABLIC

(n – liczba wierszy, m – liczba kolumn)

• magic(n) – generuje macierz magiczną

• pascal(n) – generuje macierz Pascala stopnia n

• eye(n,n) – generuje macierz jednostkową nxn

• ones(n,m) – generuje tablicę nxm złożona z samych jedynek

• zeros(n,m) – generuje tablicę nxm złożoną z samych zer

• rand(n,m) – generuje tablicę nxm o elementach będących liczbami

losowymi o rozkładzie równomiernym z przedziału (0,1)

• randn(n,m) – generuje tablicę nxm złożoną z liczb będących liczbami

losowymi o rozkładzie normalnym

PODSTAWOWE FUNKCJE DZIAŁAŃ NA TABLICACH

Y = sum(A)
gdy:
A – wektor, funkcja sum zwraca jako Y sumę elementów wektora
A – tablica, funkcja sum zwraca jako Y wektor sum w kolumnach tablicy

Y = prod(A)
gdy:
A – wektor, funkcja zwraca jako Y iloczyn elementów wektora
A – tablica, funkcja zwraca jako y wektor iloczynów elementów w kolumnach

Y = diag(A)
Funkcja zwraca jako Y wektor z przekątnej głównej macierzy A

Y = det(A) funkcja zwraca jako Y wartość wyznacznika macierzy kwadratowej

8

Y = tril(A)
Funkcja zwraca jako macierz dolną trójkątną z macierzy A

Y = triu(A)
Funkcja zwraca jako Y macierz górną trójkątną z macierzy A


Y = inv(A)
Funkcja zwraca pod nazwą Y macierz odwrotną do macierzy A

Y = max(A)
gdy:
A jest wektorem funkcja zwraca wartość Y będącą max elementem wektora A
A jest macierzą funkcja zwraca wektor wierszowy Y o elementach będących max z
poszczególnych kolumn


Y = min(A)
gdy:
A jest wektorem funkcja zwraca wartość Y będącą min elementem wektora A
A jest macierzą funkcja zwraca wektor wierszowy Y o elementach będących min z
poszczególnych kolumn tablicy A
Y = mean(A)
gdy:
A jest wektorem funkcja zwraca pod nazwą Y średnią arytmetyczną jego elementów
A jest macierzą - zwraca wektor wierszowy Y o elementach będących średnimi
arytmetycznymi elementów poszczególnych kolumn tablicy A

Y = sort(A) lub Y = sort(A,’ascend’)
gdy:
A jest wektorem funkcja zwraca jako Y wektor uporządkowany rosnąco
A jest macierzą - sortuje każdą kolumnę A rosnąco


Y = sort(A, ‘descend’)
j.w. tylko dla uporządkowania malejącego

NORMY:

Y = norm(A,p)

p =1 - max suma modułów w kolumnach

∑

=

≤

≤

=

n

i

ij

n

j

a

A

1

1

1

max

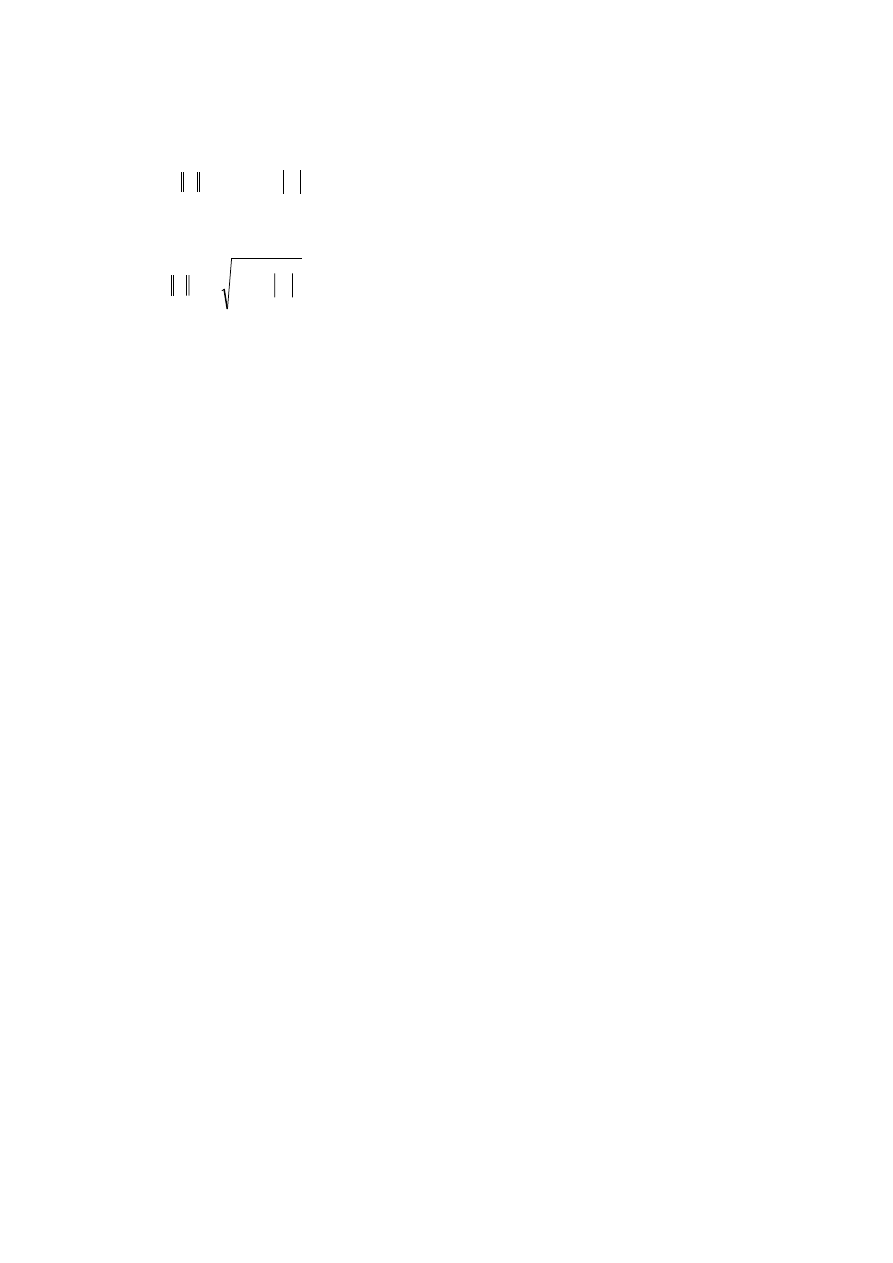
9

p = inf max suma modułów w wierszach A

p=‘fro’ – norma Frobeniusa

Jeśli

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

=

6

3

1

3

2

1

1

1

1

A

wówczas

>> A_1=norm(A,1)

A_1 =
10
>> A_inf=norm(A,'inf')

A_inf =
10

>> A_fro=norm(A,'fro')
A_fro =
7.9373

SZYBKIE TWORZENIE TABLIC – OPERATOR DWUKROPEK ( : )

Tworzenie wektora wierszowego:

>> a= 1:5

% Tworzenie wektora wierszowego (to jest komentarz)

a=
1 2 3 4 5

>> b=1:2:10

b =
1 3 5 7 9

>>c = 1:-2.5:-10

∑

=

≤

≤

=

n

j

ij

n

i

a

A

1

1

inf

max

∑∑

=

=

=

n

i

n

j

ij

fro

a

A

1

2

1

10

c =
1.0000 -1.5000 -4.0000 -6.5000 -9.0000

Transponowanie wektora wierszowego:
>> c=c'
c =
1.0000
-1.5000
-4.0000
-6.5000
-9.0000


>> n = (1:5)’

% Tworzy wektor wierszowy i transponuje

n =
1
2
3
4
5

>> potegi = [n n.^2 n.^3 2.^n ]

% Tablica kwadratów, sześcianów i potęg liczby 2 ...

% dla w/w tablicy n

potegi =
1 1 1 2
2 4 8 4
3 9 27 8
4 16 64 16
5 25 125 32

Utworzenie tablicy wartości lnx dla danego zakresu x:

>> x = (1:0.2:2)'
x =

1.0000
1.2000
1.4000

1.6000
1.8000

2.0000

>> lnx = log(x)

lnx =
0
0.1823

0.3365
0.4700

0.5878
0.6931

lub

11

>> lnx = [x log(x)]

lnx =
1.0000 0
1.2000 0.1823

1.4000 0.3365
1.6000 0.4700

1.8000 0.5878
2.0000 0.6931

ZNAK (: ) W WYRAŻENIACH INDEKSOWYCH

Wyrażenia indeksowe odnoszą się do części macierzy lub tablicy. Zapis:

A(1:k,j)

oznacza k pierwszych elementów z j-tej kolumny tablicy A.


sum(A(1:4,4))
oznacza sumę elementów leżących w 4. kolumnie tablicy A.


Dwukropek odnosi się do wszystkich elementów w wierszu lub kolumnie
macierzy / tablicy

Słowo kluczowe end odnosi się do ostatniego wiersza lub kolumny tablicy.

sum(A(:,end)) oznacza sumę wszystkich elementów leżących w ostatniej kolumnie
tablicy A.




Na przykład:

A =
1 5 7
3 5 9
1 3 4
0 6 7

>> s=sum(A(1:3,2))
s =

13 – suma trzech pierwszych elementów z drugiej kolumny macierzy A.

>> suma_3=sum(A(3:end,end))
suma_3 =
11 – suma elementów w ostatniej kolumnie macierzy A z wierszy od 3 do
ostatniego