TEMAT:
Równania Lagrange'a II rodzaju
i
i
i
d
L
L
Q
dt
q
q
Gdzie:
Q
i
- siła uogólniona
L - potencjał kinetyczny
i
q - współrzędna uogólniona
i
q - prędkość uogólniona
L
E U
Liczba stopni swobody układu
s
n
w
Gdzie:
s - liczba stopni swobody układu
n - liczba współrzędnych wyjściowych (opisujących ruch wszystkich brył w układzie)
w - liczba więzów kinematycznych
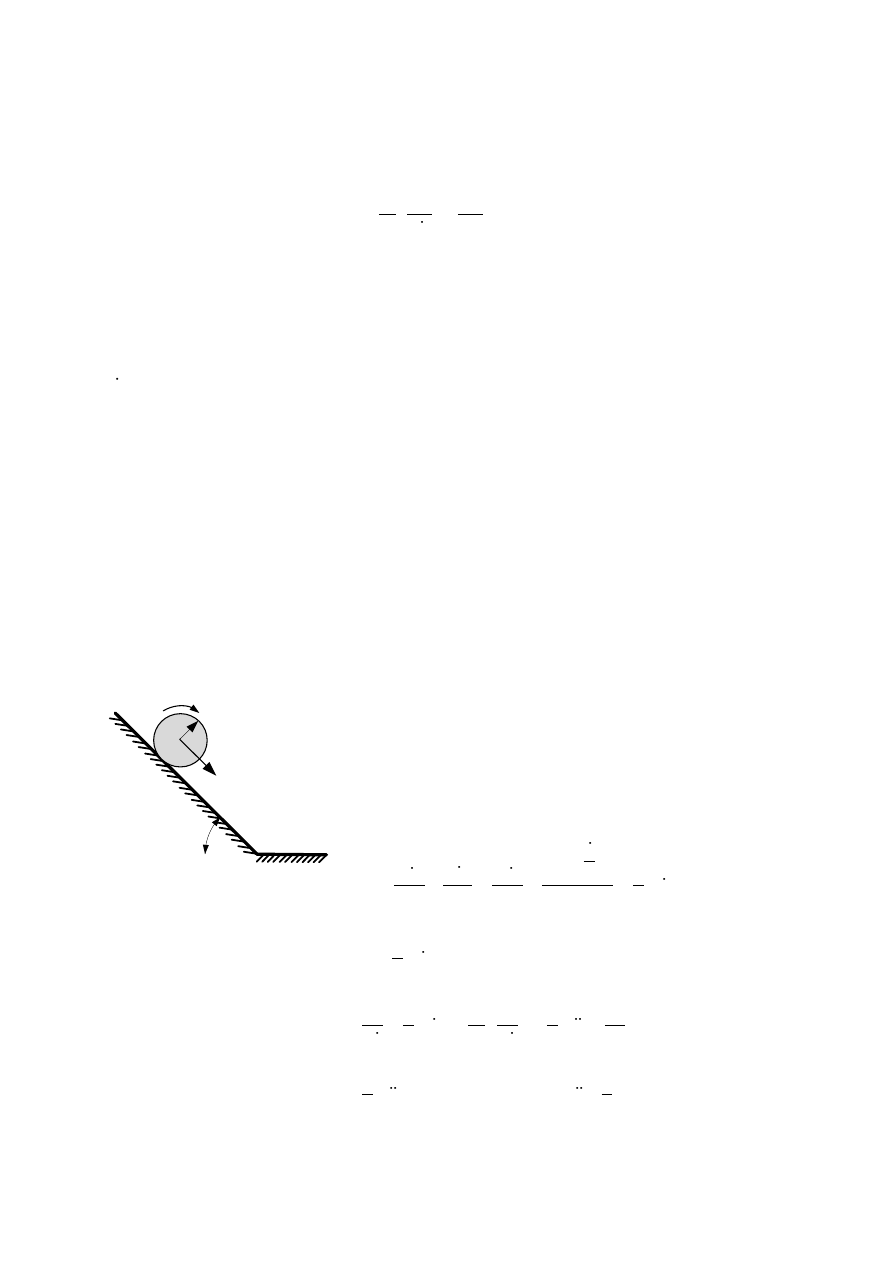
1. Wyznacz przyśpieszenia brył w układzie korzystając z równań Lagrange'a II rodzaju.
r
m
x
Współrzędne wyjściowe:
,
x
Równania więzów:
x
r
Liczba stopni swobody:
2 1 1
s
Współrzędna uogólniona:
q
x
Energia układu:
2
2
2
2
2
2
3
2
2
2
4
4
sin
x
mr
mx
I
mx
r
E
mx
U
mgx
2
3
sin
4
L
mx
mgx
Pochodne:
3
2
L
mx
x
3
2
d
L
mx
dt
x
sin
L
mg
x
Równanie ruchu:
3
sin
0
2
mx mg
2
sin
3
x
g
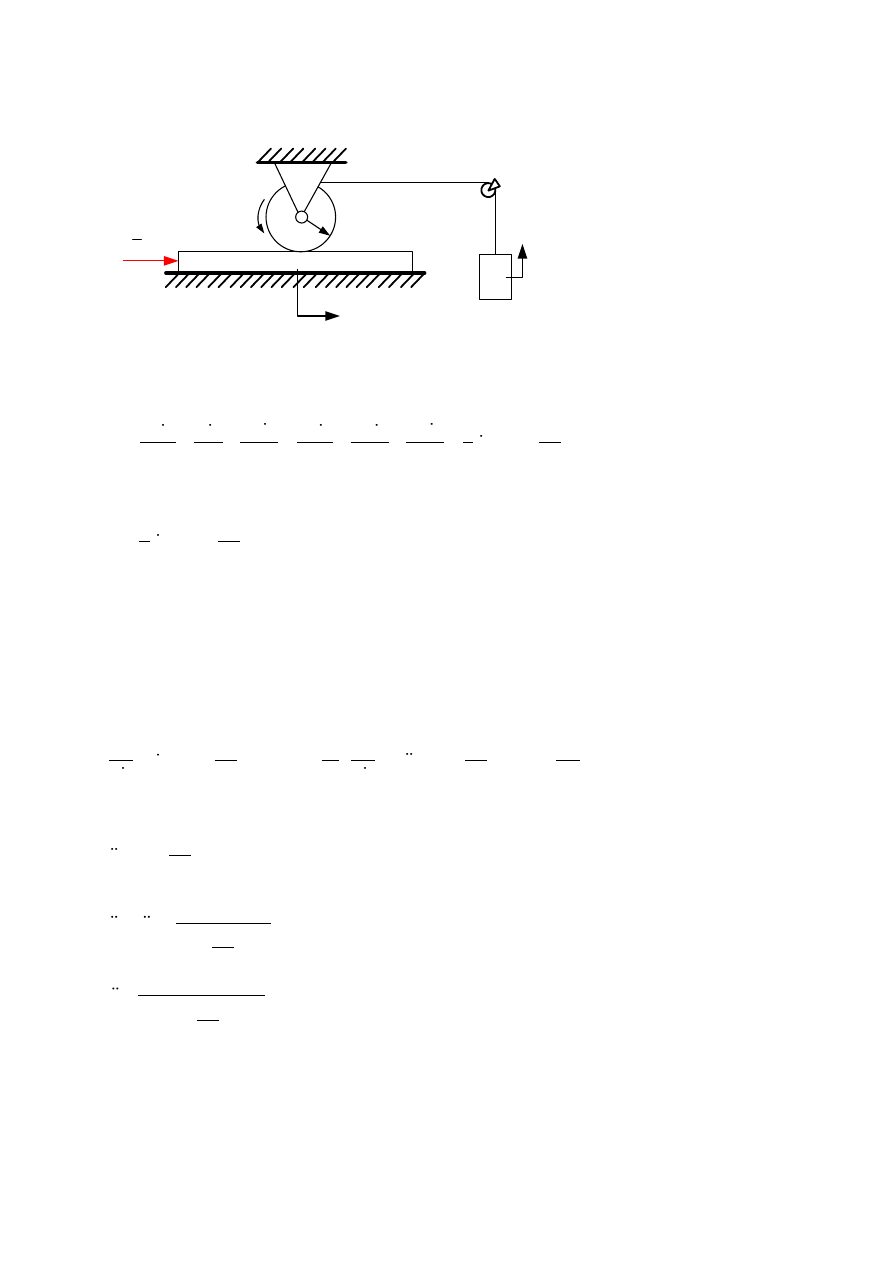
2. Wyznacz przyśpieszenia brył w układzie korzystając z równań Lagrange'a II rodzaju.
r
1
m
2
m
R
F
1
x
2
x
3
m
Współrzędne wyjściowe:
1
2
,
,
x x
Równania więzów:
1
2
x
R
x
R
Liczba stopni swobody:
3 2 1
s
Współrzędna uogólniona:
1
q
x
Energia układu:
2
2
2
2
2
2
2
3
2
3 1
1 1
1 1
2 1
2
1
1
3
3
3
3
1
1
2
2
2
2
4
2
2
2
m x
m x
m x
m x
m x
m
I
E
x
m
m
U
m gx
m gx
2
2
1
1
3
3
1
1
2
2
m
L
x
m
m
m gx
Praca wirtualna układu
1
1
x
W
F x
Q
F
Pochodne:
2
1
1
3
1
2
m
L
x
m
m
x
2
1
1
3
1
2
m
d
L
x
m
m
dt
x
3
1
L
m g
x
Równanie ruchu
:
2
1
1
3
3
2
m
x
m
m
m g
F
3
1
2
2
1
3
3
2
1
3
2
2
F
m g
x
x
m
m
m
F
m g
m
R m
m
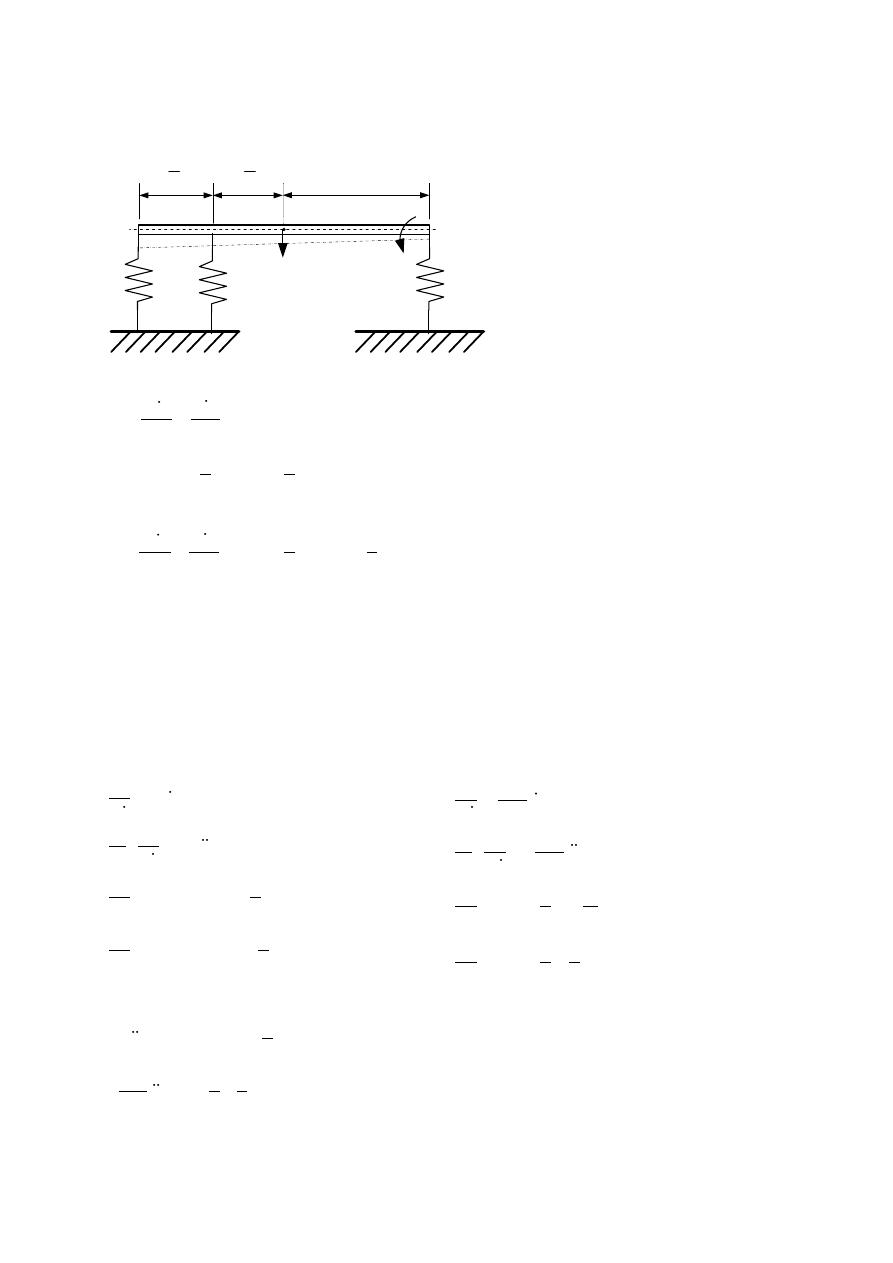
3. Wyznacz równania ruchu belki korzystając z równań Lagrange'a II rodzaju.
k
m
l
2
l
2
l
k
k
x
Współrzędne wyjściowe:
,
x
Równania więzów:
-
Liczba stopni swobody:
2
0
2
s
Współrzędne uogólnione:
1
2
q
x
q
Energia układu:
2
2
2
2
2
2
2
1
2
2
mx
I
E
l
U
mgx
k
x
x
l
x
l
2
2
2
2
2
1
2
2
2
2
mx
I
l
L
mgx
k
x
x
l
x
l
Praca wirtualna układu
1
2
0
0
0
0
x
W
x
x
Q
Q
Pochodne:
L
mx
x
d
L
mx
dt
x
2
3
2
L
l
mg
k x
x
l
x
l
x
L
l
mg
k
x
x
2
3
L
ml
2
3
d
L
ml
dt
2
2
2
2
2
4
9
2
4
L
l
l
k x
xl
l
xl
l
L
l
k x
l
Równanie ruchu
:
2
2
3
0
2
9
0
3
2
4
l
mx mg
k
x
ml
l
k x
l
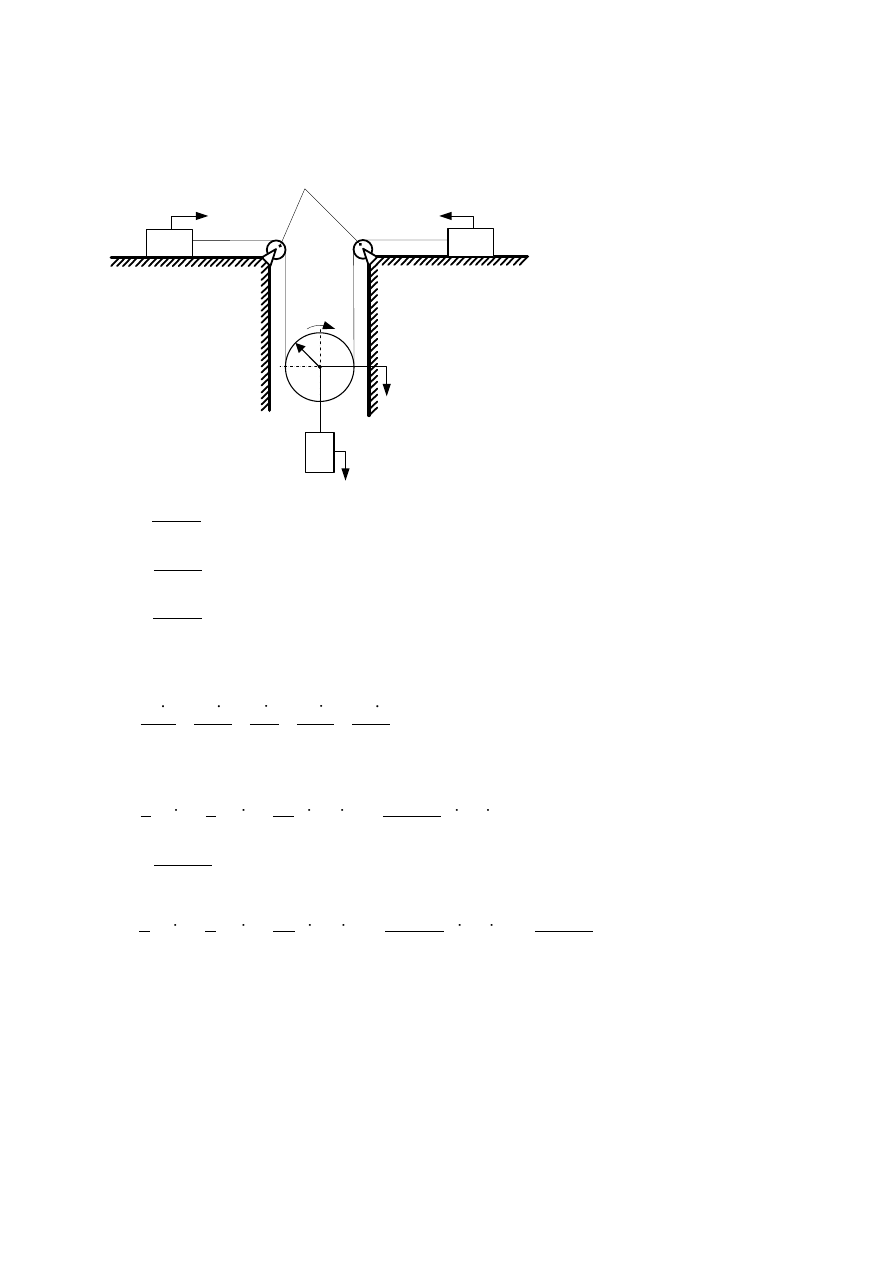
4. Wyznacz przyśpieszenie masy m
1
oraz m
2
, korzystając z równań Lagrange'a II
rodzaju.
bezmasowe krążki
1
m
4
m
2
m
3
m
2
x
4
x
3
3
x
1
x
r
Współrzędne wyjściowe:
1
2
3
4
3
,
,
,
,
x x x x
Równania więzów:
1
3
3
2
3
3
3
4
x
x
r
x
x
r
x
x
Liczba stopni swobody:
5 2 1
s
Współrzędna uogólniona:
1
1
2
2
q
x
q
x
1
2
3
2
1
3
1
2
4
2
2
2
x
x
x
x
x
r
x
x
x
Energia układu:
2
2
2
2
2
3
3 3
1 1
2
2
4
4
3
3
4
4
2
2
2
2
2
I
m x
m x
m x
m x
E
U
m gx
m gx
2
2
2
2
3
3
4
1 1
2
2
2
1
1
2
3
3
1
2
1
1
2
2
16
8
2
m
m
m
E
m x
m x
x
x
x
x
m
m
U
g x
x
2
2
2
2
3
3
4
3
3
1 1
2
2
2
1
1
2
1
2
1
1
2
2
16
8
2
m
m
m
m
m
L
m x
m x
x
x
x
x
g x
x
Praca wirtualna układu
1
1
2
2
1
1
2
2
x
x
W
gm x
gm
x
Q
gm
Q
gm
Pochodne:

3
3
4
1 1
2
1
1
2
1
8
4
m
m
m
L
m x
x
x
x
x
x
1
1
3
4
2
3
4
1
3
1
1
1
8
4
8
4
L
x
m
m
m
x
m
m
x
3
3
4
2
2
2
1
1
2
2
8
4
m
m
m
L
m x
x
x
x
x
x
1
1
4
2
4
4
2
1
1
3
1
8
4
8
4
L
x
m
m
x
m
m
x
1
1
3
4
2
3
4
1
3
1
1
1
8
4
8
4
d
L
x
m
m
m
x
m
m
dt
x
1
1
4
2
2
3
4
2
1
1
3
1
8
4
8
4
d
L
x
m
m
x
m
m
m
dt
x
3
3
1
2
m
m
L
g
x
3
3
2
2
m
m
L
g
x
Równanie ruchu
:
3
3
1
1
3
4
2
3
4
1
3
3
1
1
4
2
2
3
4
2
3
1
1
1
8
4
8
4
2
1
1
3
1
8
4
8
4
2
m
m
x
m
m
m
x
m
m
g
gm
m
m
x
m
m
x
m
m
m
g
gm
Wyszukiwarka
Podobne podstrony:
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
więcej podobnych podstron