1/3

Lista 7 – rozwi zania

(zasady dynamiki, praca, energia, moc, uderzenia, dynamika ruchu obrotowego)

Zad. 1.

W nieruchomej windzie na pasa era działaj dwie siły – ci ko ci

G i nacisku N, skierowane

w tym samym kierunku o przeciwnych zwrotach. Warunek równowagi dla takiego układu

mo na zapisa jako

0

=

+

−

N

G

.

Przyjmuj c, e

mg

G

=

siła nacisku wynosi

N

785

=

= mg

N

.

Je li winda porusza si z przyspieszeniem a na pasa era działa dodatkowo siła bezwładno ci

ma

F

b

=

, skierowana przeciwnie do zwrotu wektora przyspieszenia

a.

Podczas ruchu do góry, czyli zgodnie z dodatnio skierowan półosi Y, siła bezwładno ci

działa przeciwnie, co powoduje, e równanie równowagi przybiera nast puj c posta

0

=

−

+

−

b

wz

F

N

G

.

Siła nacisku wynosi zatem

N

1020

)

(

=

+

=

a

g

m

N

Podczas ruchu w dół siła bezwładno ci działa zgodnie z dodatnio skierowan półosi Y,

zatem

0

=

+

+

−

b

op

F

N

G

a siła nacisku wynosi

N

545

)

(

=

−

=

a

g

m

N

.

Zad. 2.

Korzystaj c z zale no ci na drog s oraz przyspieszenie w ruchu jednostajnie zmiennym,

przyspieszenie (opó nienie) a podczas hamowania wynosi

2

2

0

m/s

3

,

11

2

=

=

s

v

a

Siła bezwładno ci działaj ca na kierowc wynosi

N

900

2

2

0

=

=

=

s

mv

ma

F

b

Zad. 3.

Praca siły grawitacji wynosi

J

9810

=

∆

⋅

=

h

mg

W

Zad. 4.

Energia całkowita pojemnika w dowolnej chwili podczas spadku wynosi

k

p

c

E

E

E

+

=

. W

chwili upadku energia potencjalna wynosi

0

2

=

p

E

, zatem cała energia zgromadzona jest w

postaci energii kinetycznej

2

2

k

c

E

E

=

, któr mo na wyznaczy dwoma sposobami.

A) Nale y wyznaczy pr dko w chwili zderzenia podczas spadku swobodnego

gh

v

k

2

=

pr dko podstawi do wzoru na energi kinetyczn

J

883

2

2

2

=

=

=

mgh

mv

E

k

k

.

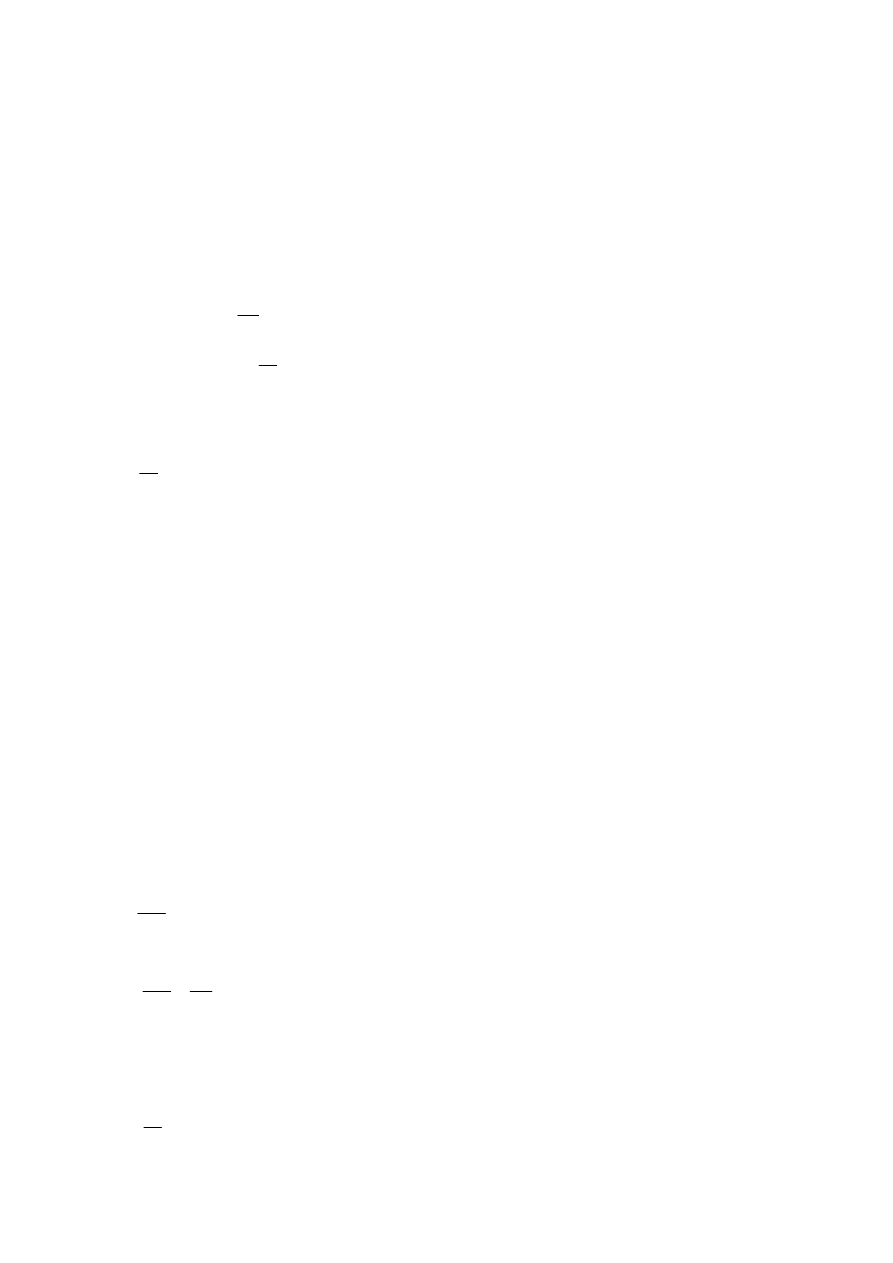
2/3

B) Przed rozpocz ciem spadku całkowita energia pojemnika była zgromadzona w postaci
energii potencjalnej

1

1

p

c

E

E

=

, poniewa pr dko pojemnika wynosiła 0. Zgodnie z zasad

zachowania energii mechanicznej, energia całkowita ciała jest zawsze stała

2

1

c

c

c

E

E

E

=

=

,

zatem

J

883

1

2

=

=

=

mgh

E

E

p

k

Zad. 5.

Przyjmuj c ruch po płaskiej drodze energia potencjalna samochodów wynosi

0

=

=

pc

pos

E

E

,

a energia całkowita skupiona jest w postaci energii kinetycznej.

(

)

kJ

469

2

2

=

+

=

os

os

os

kos

v

m

M

E

(

)

kJ

854

2

2

=

+

+

=

c

t

k

c

kc

v

m

m

M

E

Zad. 6.

Moc okre lona jest jako iloraz pracy i czasu, w którym praca ma by wykonana

kW

00

,

1

=

=

t

W

P

Zad. 7.

Moc w ruchu liniowym mo na wyrazi jako iloczyn siły tarcia T i pr dko ci v, z któr

porusza si samochód. Je li na samochód w kierunku Y nie działa inna siła czynna ni

grawitacji M·g, siła tarcia wyniesie

Mg

T

µ

=

.

Swobodny spadek odbywa si z przyspieszenie g z pr dko ci pocz tkow równ 0, wi c

wykorzystuj c wzory dla ruchu jednostajnie zmiennego

kW

18

,

8

=

=

=

Mgv

Tv

P

µ

Zad. 8.

W przypadku poruszania si samochodu po równi pochyłej sił oporu dla ruchu (zaniedbuj c
tarcie) jest składowa styczna siły grawitacji

α

sin

⋅

= mg

G

t

. Moc potrzebna do wykonania

ruchu wynosi zatem

kW

9

,

37

sin

=

⋅

⋅

=

⋅

=

v

mg

v

G

P

t

α

Zad. 9.

Sprawno

η

układu nap dowego wyra a si jako iloraz mocy obci enia P

obc

do mocy

silnika P

s

s

obc

P

P

=

η

Przyjmuj c moc obci enia jako

v

F

P

obc

⋅

=

otrzymuje si

kW

1

,

17

=

=

=

η

η

Fv

P

P

obc

s

Zad. 10.

W czasie pokonywania zakr tu na palet b dzie oddziaływa stycznie do podło a

przyspieszenie do rodkowe a

n

R

v

a

n

2

=

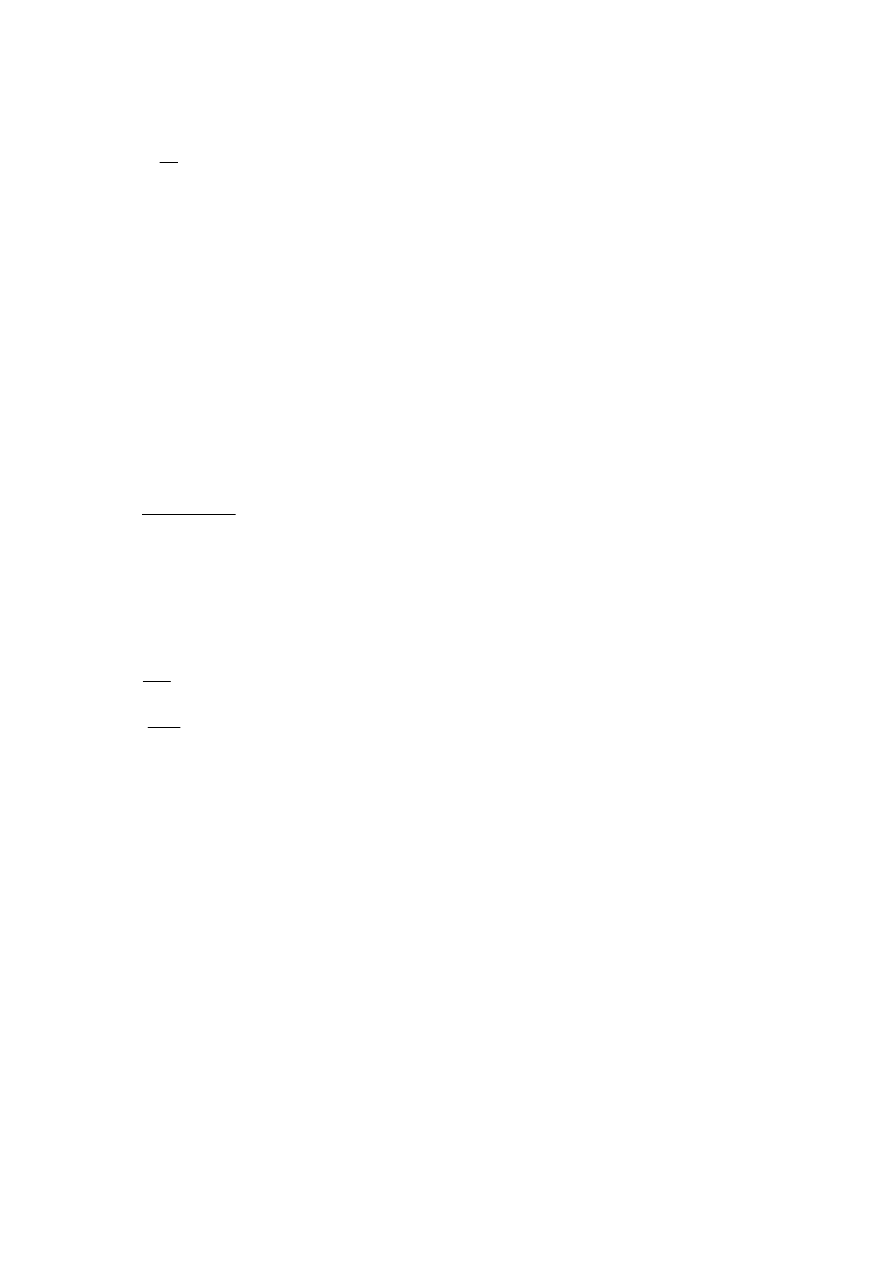
3/3

Powoduje ono powstanie siły bezwładno ci F

b

o zwrocie przeciwnym (od rodka krzywizny

zakr tu) o warto ci

kN

73

,

4

2

=

=

R

v

m

F

b

Tarcie mi dzy palet a powierzchni naczepy (uwzgl dniaj c wył cznie sił grawitacji w

kierunku Y) wyniesie

kN

96

,

1

=

= mg

T

µ

Siła bezwładno ci F

b

jest zatem wi ksza od siły tarcia T

T

F

b

> ,

co oznacza, e paleta przesunie si po powierzchni naczepy (przyjmuj c dostatecznie du y

zarys podparcia, który uniemo liwia przewrócenie si palety).

Zad. 11.

Przyjmuj c, e samochód ci arowy porusza si zgodnie z dodatnio skierowan półosi X a

samochód osobowy przeciwnie, zasad zachowania p du mo na przedstawi w postaci

równania

2

)

(

v

m

m

v

m

v

m

os

c

os

os

c

c

+

=

−

Pr dko samochodów po zderzeniu wyniesie

m/s

21

,

3

km/h

5

,

11

2

=

=

+

−

=

os

c

os

os

c

c

m

m

v

m

v

m

v

Zmiana pr dko ci samochodu ci arowego wynosi

m/s

13

,

5

km/h

5

,

18

2

−

=

−

=

−

=

∆

c

c

v

v

v

,

a samochodu osobowego

m/s

1

,

17

km/h

5

,

61

2

−

=

=

−

=

∆

os

os

v

v

v

.

Przyspieszenia, którym zostali poddani kierowcy obu pojazdów wynosz odpowiednio

2

m/s

13

,

5

=

∆

=

t

v

a

c

c

2

m/s

1

,

17

=

∆

=

t

v

a

os

os

Siła bezwładno ci podczas zderzenia, która działa na ka dego z kierowców wynosi

N

410

=

=

c

k

bc

a

m

F

N

1370

=

=

os

k

bos

a

m

F