
1/6
Lista 2 – rozwi zania
(moment siły, dowolny układ sił)
Zad. 1.
Moment siły r ki
F wzgl dem rodka ruby to iloczyn warto ci siły i odległo ci kierunku
działania siły od rodka, czyli długo ci klucza r. Pomijaj c znak momentu otrzymano
Nm
5
,
37
=
⋅
=
r
F
M
s
Zad. 2.
Moment siły
F musi pokona opór w rubie, zatem
op
M
d
F
=
⋅
2
, zatem pomijaj c znak
momentu siły otrzymano
N
200
2
=
=
d
M
F
op
Zad. 3.
Moment siły
G wzgl dem bieguna A to iloczyn warto ci siły i odległo ci kierunku działania
siły od punktu A
a
r
2
1
=
. Uwzgl dniaj c znak momentu siły otrzymano
kNm
4
,
2
2
1
−
=
⋅
−
=
a
G
M
A
Zad. 4.
Moment siły ci ko ci wzgl dem bieguna O to iloczyn warto ci siły mg i odległo ci tej siły
od punktu O. Uwzgl dniaj c znak momentu siły otrzymano
Nm
8
,
36
−
=
⋅
−
=
a
mg
M
O
Zad. 5.
Moment siły ci ko ci wzgl dem biegunów A i B to iloczyn warto ci siły
G i odległo ci od
tych biegunów. Uwzgl dniaj c znak momentu siły otrzymano
Nm
1320
Nm
3380
)
(
−
=
⋅
−
=
−
=
+
⋅
−
=
b
mg
M
b
a
mg
M
G
B
G
A
Zad. 6.
Moment główny sił ci ko ci wzgl dem rodka ci ko ci S statku jest równy sumie
momentów siły ci ko ci kontenera 1 i kontenera 2 wzgl dem punktu S. Uwzgl dniaj c znak
momentu siły otrzymano
kNm
343
5
,
2
4
2
1
2
1
−
=
⋅
−
⋅
=
+
=
d
g
m
d
g
m
M
M
M
S
S
S
Zad. 7.
Moment główny układu sił
F
1
,
F
2
i
F
3
to suma momentów wszystkich sił wzgl dem
bieguna O, zatem uwzgl dniaj c znaki momentów
Nm
0
,
40
3
3
2
2
1
1
3
2
1
=
⋅
−
⋅
+
⋅
−
=
+
+
=
r
F
r
F
r
F
M
M
M
M
O
O
O
O

2/6
Zad. 8.
Dla siły
F
A
Nm
0
,
60
1
1
−
=
⋅
−
=
r
F
M
A
A
O
Nm
0
2
=
A
O
M
Rami działania siły
F
A
wzgl dem bieguna O
3
wynosi
A
d
r
α
sin
3
3
=
Nm
105
sin
3
3
3
=
⋅
=
⋅
=
A
A
A
A
O
d
F
r
F
M
α
Dla siły
F
B
Nm
0
1
=
B
O
M
Nm
0
2
=
B
O
M
Rami działania siły
F
B
wzgl dem bieguna O
3
wynosi
(
)
B
B
d
d
r
α
sin
3
3
3
′
+
=
(
)
Nm
346
sin
3
3
3
3
−
=
′
+
⋅
−
=
⋅
−
=
B
B
B
B
B
O
d
d
F
r
F
M
α
Moment główny układu sił
F
A
i
F
B
Nm
0
,
60
1
1
1
−
=
+
=
B
O
A
O
AB
O
M
M
M
Nm
0
2
2
2
=
+
=
B
O
A
O
AB
O
M
M
M
Nm
241
3
3
3
−
=
+
=
B
O
A
O
AB
O
M
M
M
Zad. 9.
Moment główny układu sił to suma momentów wszystkich sił wzgl dem danego bieguna,
zatem
Nm
6
,
75
0
4
2
2
3
2
1
4
3
2
1
−
=
⋅
+
+
⋅
−
⋅
+
⋅
=
+
+
+
=
a
F
b
a
F
F
b
F
M
M
M
M
M
A
A
A
A
A
Zad. 10.
Para sił mo e by zrównowa ona wył cznie inn par sił, zatem
0
=
⋅
−
⋅
d
F
D
F
dk
k
. St d
N
1500
=
⋅
=
d
D
F
F
k
dk
Zad. 11.
Nm
0
3
2
5
4
3
1
=
⋅
−
⋅
+
⋅
−
⋅
−
=
a
F
a
F
a
F
a
F
M
B
Układ sił równoległych jest w równowadze (suma składowych y wynosi 0), dlatego nie ma
znaczenia biegun, wzgl dem którego wyznaczany jest moment, czyli
Nm
0
=
=
=
=
=
E
D
C
B
A
M
M
M
M
M
.
Zad. 12.
Para sił mo e zosta zrównowa ona tylko przez par sił, zatem
0
=
⋅
−
⋅
b
R
a
F
N
1000
=
=
b
a
F
R
N
1000
=
= R
R
A
N
1000
−
=
−
= R
R
B
Zad. 13.
Wyst puj tylko pionowe składowe reakcji
R
A
i
R
B
. Zwroty reakcji zgodne z dodatnimi
półosiami układu współrz dnych.
3/6
a)
Składowe y:
0
=
+
−
B
A
R
F
R
Moment główny wzgl dem A:
0
=
⋅
+
⋅
−
a
R
b
F
B
N
667
=
=
a
b
F
R
B
N
1330
)
1
(
=
−
=
a
b
F
R
A
b)
Składowe y:
0
=
+
−
B
A
R
qc
R
Moment główny wzgl dem A:
(
)
0
2
1
=
⋅
+
+
⋅
−
a
R
c
b
qc
B
N
500
2
1
=
+
=
a
c
b
qc
R
B
N
500
2
1
=
−
−
=
a
c
b
a
qc
R
A
Zad. 14.
W podporze A wyst puje tylko składowa pionowa
R
A
, a w B: pozioma
R
Bx
i pionowa
R
By
.
Siła
F rozkłada si na składow poziom F
x
(
α
cos
F
F
x
=
) i pionow
F
y
(
α
sin
F
F
y
=
).
Zwroty reakcji zgodne z dodatnimi półosiami układu współrz dnych.
a)
Składowe x:
0
=
+
−
Bx
x
R
F
Składowe y:
0
=
+
−
By
y
A
R
F
R
Moment główny wzgl dem A:
0
=
⋅
+
⋅
−
a
R
b
F
By
y
N
1730
cos
=
=
α
F
R
Bx
N
333
sin
=
=
a
b
F
R
By
α
kN
667
sin
=
−
=
a
b
a
F
R
A
α
b)
W ruchomej podporze A wyst puje reakcja pionowa do podło a, która przy nachyleniu
podło a pod pewnym k tem, powoduje wyst powanie składowej
R
Ax
(
β
sin
A
Ax
R
R
=
)
i pionow
R
Ay
(
β
cos
A
Ay
R
R
=
).
Składowe x:
0
=
+
−
Bx
x
Ax
R
F
R
Składowe y:
0
=
+
−
By
y
Ay
R
F
R
Moment główny wzgl dem A:
0
=
⋅
+
⋅
−
a
R
b
F
By
y
N
333
sin
=
=
a
b
F
R
By
α
N
770
cos
sin
=
−
⋅
=
a
b
a
F
R
A
β
α
N
1350
cos
sin
sin
cos
=
−
⋅
−
=
a
b
a
F
R
Bx
β
α
β
α
4/6
Zad. 15.
W podporze A wyst puje tylko składowa pionowa
R
A
, a w B: pozioma
R
Bx
i pionowa
R
By
.
Siła
F rozkłada si na składow poziom F
x
(
α
cos
F
F
x
=
) i pionow
F
y
(
α
sin
F
F
y
=
).
Zwroty reakcji zgodne z dodatnimi półosiami układu współrz dnych.
a)
Składowe x:
0
=
+
Bx
x
R
F
Składowe y:
0
=
+
+
y
By
A
F
R
R
Moment główny wzgl dem A:
0
=
⋅
+
⋅
+
c
F
a
R
M
y
By
kN
73
,
1
cos
−
=
−
=
α
F
R
Bx
kN
75
,
1
sin
1
−
=
−
−
=
a
c
F
M
a
R
By
α
kN
750
,
0
1
sin
1
=
−
+
=
a
c
F
M
a
R
A
α
b)
Składowe x:
0
=
+
−
Bx
x
R
F
Składowe y:
0
=
+
+
−
y
By
A
F
R
qd
R
Moment główny wzgl dem A:
(
)
(
)
0
2
1
=
+
+
⋅
+
⋅
+
+
⋅
−
e
d
b
F
a
R
d
b
qd
y
By
kN
73
,
1
cos
=
=
α
F
R
Bx
kN
500
,
0
sin
2
1
=
+
+
+
+
−
=
a
d
b
qd
a
e
d
b
F
R
By
α
kN
50
,
2
sin
2
1
=
−
+
+
+
−
−
=
a
a
e
d
b
F
a
d
b
a
qd
R
A
α
Zad. 16.
W podporach wyst puj tylko składowe pionowe
R
A
i
R
B
(brak składowych x sił czynnych).
Zwroty reakcji zgodne z dodatnimi półosiami układu współrz dnych.
a)
Składowe y:
0
=
−
+
qc
R
R
B
A
Moment główny wzgl dem A:
(
)
0
2
1
=
+
⋅
−
⋅
+
c
a
qc
a
R
M
B
kN
00
,
5
1
2
1
=
+
+
−
=
a
c
a
qc
M
a
R
B
kN
00
,
1
2
1
−
=
−
=
a
c
qc
M
a
R
A
b)
W podporze B wyst puj składowe: pozioma
R
Bx
i pionowa
R
By
. Siła
F
1
rozkłada si na
składow poziom
F
1x
(
1
1
1
cos
α
F
F
x
=
) i pionow
F
1y
(
1
1
1
sin
α
F
F
y
=
), a siła
F
2
na
F
2x
(
2
2
2
cos
α
F
F
x
=
) i pionow
F
2y
(
2
2
2
sin
α
F
F
y
=
).
Składowe x:
0
2
1
=
−
+
−
x
Bx
x
F
R
F
Składowe y:
0
2
1
=
+
+
−
y
By
y
A
F
R
F
R
Moment główny wzgl dem A:
(
)
0
2
1
=
+
⋅
+
⋅
+
⋅
−
c
a
F
a
R
b
F
y
By
y
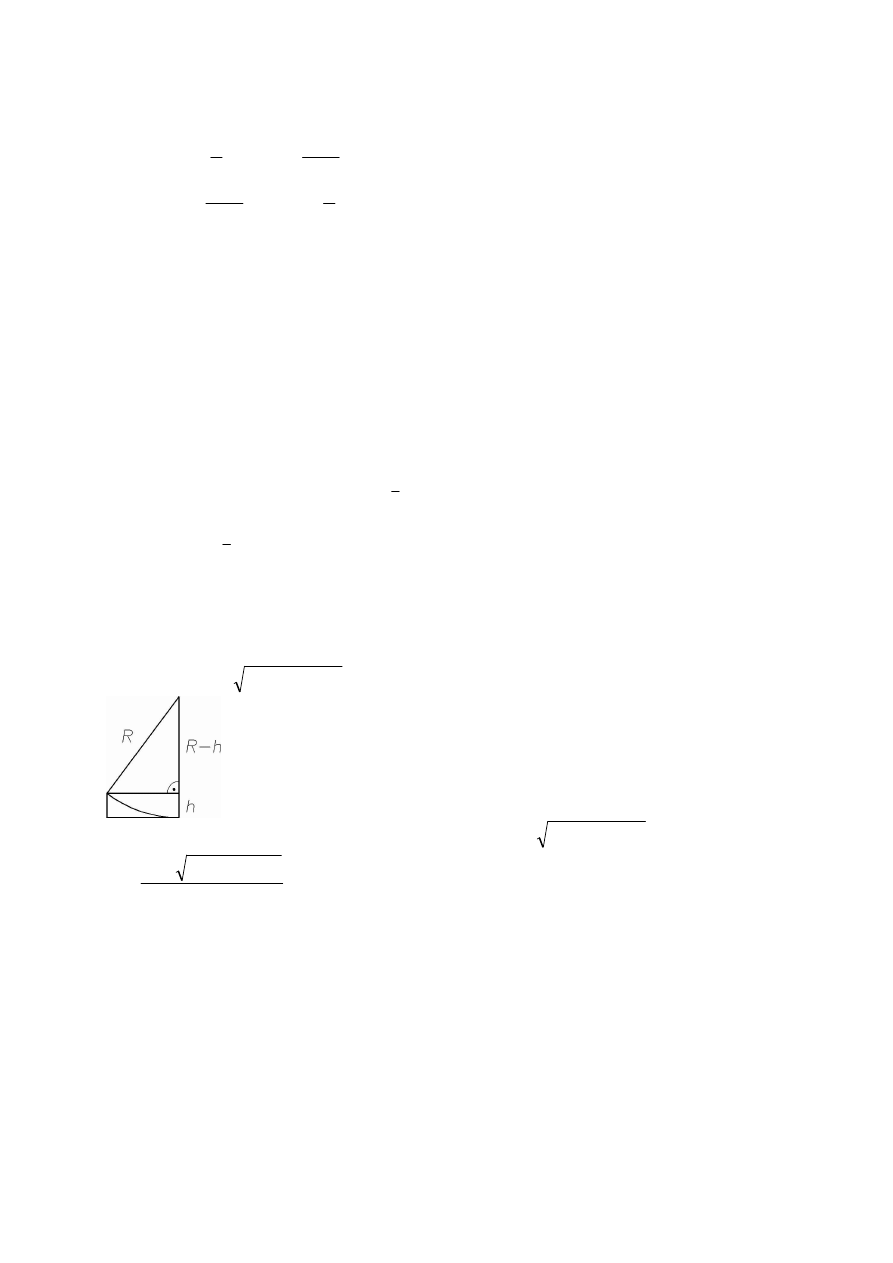
5/6
kN
33
,
4
cos
cos
2
2
1
1
=
+
=
α
α
F
F
R
Bx
kN
83
,
1
sin
sin
2
2
1
1
−
=
+
−
=
a
c
a
F
a
b
F
R
By
α
α
kN
33
,
1
sin
sin
2
2
1
1
=
+
−
=
a
c
F
a
b
a
F
R
A
α
α
Zad. 17.
Zwrot reakcji pionowej
R
A
zgodny z dodatni półosi układu współrz dnych, zwrot momentu
M
A
przeciwny do ruch wskazówek zegara.
a)
Składowe y:
0
=
+
−
A
R
F
Moment główny wzgl dem A:
0
=
+
⋅
A
M
a
F
kN
00
,
2
=
= F
R
A
kNm
0
,
10
−
=
−
= Fa
M
A
b)
Składowe y:
0
=
+
−
A
R
qb
Moment główny wzgl dem A:
(
)
0
2
1
=
+
−
⋅
A
M
b
a
qb
kN
00
,
6
=
= qb
R
A
(
)
kNm
0
,
24
2
1
−
=
−
⋅
−
=
b
a
qb
M
A
Zad. 18.
Na walec oddziałuj dwie siły: ci ko ci
G oraz F wzdłu ci gna, skierowana zgodne
z ujemn półosi układu współrz dnych.
Z warunków geometrycznych wynika, e rami działania siły
F wynosi
h
R
− , natomiast dla
siły ci ko ci
G:
(
)
2
2
h
R
R
−
−
.
Moment główny wzgl dem punktu styku:
(
)
(
)
0
2
2
=
−
−
⋅
−
−
⋅
h
R
R
mg
h
R
F
(
)
kN
68
,
3
2
2
=
−
−
−
⋅
=
h
R
h
R
R
mg
F
Zad. 19.
W ło ysku górnym wyst puje tylko składowa pozioma
R
A
, a w dolnym pozioma
R
Bx
i pionowa
R
By
. Zwroty reakcji zgodne z dodatnimi półosiami układu współrz dnych.
Składowe x:
0
=
+
Bx
A
R
R
Składowe y:
0
=
− mg
R
By
Moment główny wzgl dem B:
0
=
⋅
−
⋅
−
b
mg
a
R
A

6/6
kN
47
,
1
−
=
−
=
a
b
mg
R
A
kN
981
,
0
=
= mg
R
By
kN
47
,
1
=
=
a
b
mg
R
Bx
Zad. 20.
Wyst puj tylko pionowe składowe reakcji w lewej oponie
R
A
i w prawej oponie
R
B
. Zwroty
reakcji zgodne z dodatnimi półosiami układu współrz dnych.
Składowe y:
0
=
−
+
mg
R
R
B
A
Moment główny wzgl dem B:
0
=
⋅
−
⋅
−
b
mg
a
R
A
kN
420
,
0
−
=
−
=
a
b
mg
R
A
kN
40
,
1
=
+
=
a
b
a
mg
R
B
Data: 23.04.2010
Wyszukiwarka
Podobne podstrony:
Lista 7 rozw
Lista 3 rozw
Lista 6 rozw
lista 0 rozw
Lista 0 rozw
Lista 5 rozw
Lista 1 rozw
Lista 4 rozw
lista 3 4 rozw
Lista 7 rozw
lista 0 rozw
więcej podobnych podstron