1/6
Lista 3 – rozwi zania
( rodki ci ko ci, tarcie)
Zad. 1.
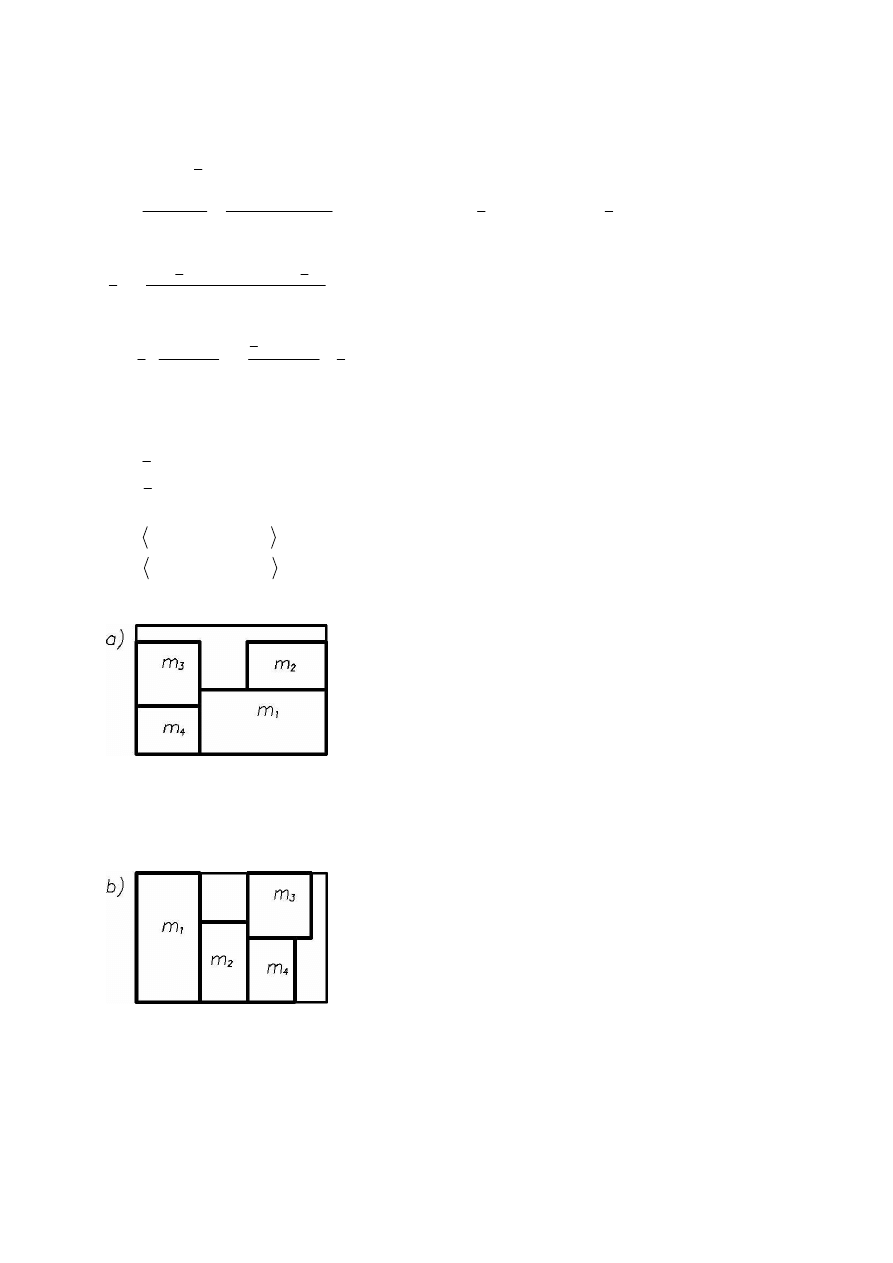
Podział elementu mo na wykona wg trzech wariantów. Jako jednostk mo na wybra
dowoln jednostk długo ci. Przyj to milimetr.
Wariant A
Element mo na podzieli na 5 prostok tów o wymiarach 10 × 15.
Elementy numerujemy od lewej. Wszystkie pola s równe i wynosz :
2
5
4
3
2
1
mm
150
15
10
=
⋅
=
=
=
=
=
A
A
A
A
A
mm
5
,
7
mm
25
mm
5
,
22
mm
25
mm
5
,
22
mm
15
mm
5
,
22
mm
5
mm
5
,
7
mm
5
5
5
4
4
3
3
2
2
1
1
=
=
=
=
=
=
=
=
=
=
y
x
y
x
y
x
y
x
y
x
cm
0
,
15
5
4
3
2
1
5
5
4
4
3
3
2
2
1
1
=
+
+
+
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
A
A
x
A
x
A
x
A
x
A
x
A
A
x
A
x
i
i
i
s
cm
5
,
16
5
4
3
2
1
5
5
4
4
3
3
2
2
1
1
=
+
+
+
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
A
A
y
A
y
A
y
A
y
A
y
A
A
y
A
y
i
i
i
s
Wariant B
Element dzielimy na 2 prostok ty o wymiarach 10 × 30 i 1 prostok t o wymiarach 10 × 15.
Elementy numerujemy od lewej. Pola wynosz odpowiednio:
2
2
2
3
1
mm
150
15
10
mm
300
30
10
=
⋅
=
=
⋅
=
=
A
A
A
mm
15
mm
25
mm
5
,
22
mm
15
mm
15
mm
5
3
3
2
2
1
1
=
=
=
=
=
=
y
x
y
x
y
x
cm
0
,
15
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
x
A
x
A
x
A
A
x
A
x
i
i
i
s
cm
5
,
16
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
y
A
y
A
y
A
A
y
A
y
i
i
i
s
Wariant C
Element dzielimy na kwadrat o wymiarach 30 × 30 i prostok t o wymiarach 10 × 15.
Pola wynosz odpowiednio:
2
2
2
1
mm
150
15
10
mm
900
30
30
=
⋅
=
=
⋅
=
A
A
mm
5
,
7
mm
15
mm
15
mm
15
2
2
1
1
=
=
=
=
y
x
y
x
2/6
cm
0
,
15
2
1
2
2
1
1
=
−
⋅
−
⋅
=
⋅
=
A
A
x
A
x
A
A
x
A
x
i
i
i
s
cm
5
,
16
2
1
2
2
1
1
=
−
⋅
−
⋅
=
⋅
=
A
A
y
A
y
A
A
y
A
y
i
i
i
s
Zad. 2.
Podział elementu mo na wykona wg dwóch wariantów.
Wariant A
Element mo na podzieli na 3 prostok ty o wymiarach (c+a) × a.
Elementy numerujemy od lewej. Pola wynosz odpowiednio:
a
a
c
A
A
⋅
+
=
=
)
(
3
1
a
b
A
⋅
=
2
Pocz tek układu współrz dnych przyjmujemy w lewy dolnym rogu (prostok ta,
obejmuj cego cały element). rodek ci ko ci prostok ta le y na przeci ciu przek tnych,
zatem
(
)
a
c
x
+
=
2
1
1
;
a
b
a
y
2
1
1
+
+
=
a
c
x
2
1
2
+
=
;
b
a
y
2
1
2
+
=
(
)
c
a
c
x
+
+
=
2
1
3
;
a
y
2
1
3
=
Współrz dne rodka ci ko ci
cm
5
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
x
A
x
A
x
A
A
x
A
x
i
i
i
s
cm
5
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
y
A
y
A
y
A
A
y
A
y
i
i
i
s
rodek ci ko ci wypada w rodku symetrii tego elementu.
Wariant B
Element mo na podzieli na 3 prostok ty, 2 z nich o wymiarach c × a i 1 o wymiarach
a
× (a+b+a).
Elementy numerujemy od lewej. Pola wynosz odpowiednio:
a
c
A
A
⋅
=
=
3
1
)
2
(
2
b
a
a
A
+
⋅
=
Pocz tek układu współrz dnych przyjmujemy w lewy dolnym rogu (prostok ta,
obejmuj cego cały element). rodek ci ko ci prostok ta le y na przeci ciu przek tnych,
zatem
a
x
2
1
1
=
;
a
b
a
y
2
1
1
+
+
=
a
c
x
2
1
2
+
=
;
(
)
b
a
y
+
= 2
2
1
2
c
a
c
x
2
1
3
+
+
=
;
a
y
2
1
3
=
Współrz dne rodka ci ko ci
cm
5
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
x
A
x
A
x
A
A
x
A
x
i
i
i
s
cm
5
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
A
A
A
y
A
y
A
y
A
A
y
A
y
i
i
i
s
rodek ci ko ci wypada w rodku symetrii tego elementu.
3/6
Zad. 3.
Osie wózka b d równomiernie obci one, gdy siła pochodz ca od masy przedmiotów b dzie
działa w połowie rozstawu osi, czyli składowa x rodka ci ko ci b dzie wypada w połowie
wózka
c
x
s
2
1
=
.
2
1
2
2
1
1
m
m
x
m
x
m
m
x
m
x
i
i
i
s
+
⋅
+
⋅
=
⋅
=
, jednocze nie
a
x
2
1
1
=
i
b
x
a
x
2
1
2
+
+
=
.
Po podstawieniach
(
)
2
1
2
1
2
2
1
1
2
1
m
m
b
x
a
m
a
m
c
+
+
+
⋅
+
⋅
=
i przekształceniach
mm
120
2
1
2
2
1
2
1
2
2
1
2
1
=
−
+
−
+
=
b
m
m
m
a
m
m
m
c
x
Zad. 4.
Teoretyczny rodek ci ko ci pustej palety znajduje si w punkcie:
mm
600
2
1
=
= m
x
s
mm
400
2
1
=
= n
y
s
Margines bł du poło enia rodka ci ko ci wypełnionej palety wynosi zatem:
mm
440
,
mm
360
mm
660
,
mm
540
=
=
s
s
y
x
a) Przykładowe rozwi zanie to:
dla którego poło enie rodka ci ko ci
mm
425
mm
620
=
=
s
s
y
x
b) Przykładowe rozwi zanie to:
dla którego poło enie rodka ci ko ci
mm
380
mm
615
=
=
s
s
y
x
4/6
Zad. 5.
Pocz tek układu współrz dnych przyjmujemy w lewy dolnym naro niku naczepy (platformy)
samochodu. rodek ci ko ci ka dego z pojemników le y na przeci ciu przek tnych
prostok ta, zatem
m
450
,
0
m
300
,
1
m
900
,
0
m
700
,
0
m
250
,
0
m
550
,
0
3
3
2
2
1
1
=
=
=
=
=
=
y
x
y
x
y
x
Współrz dne rodka ci ko ci
m
850
,
0
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
m
m
m
x
m
x
m
x
m
m
x
m
x
i
i
i
s
m
635
,
0
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
m
m
m
y
m
y
m
y
m
m
y
m
y
i
i
i
s
Zad. 6.
Pocz tek układu współrz dnych przyjmujemy w lewy dolnym naro niku stołu, przy czym
istotna jest tylko składowa pozioma x. rodek ci ko ci ka dego z pojemników, jak i stołu,
le y na przeci ciu przek tnych odpowiedniego prostok ta, zatem
mm
250
mm
150
mm
75
mm
25
mm
250
4
3
2
1
0
=
=
=
=
=
x
x
x
x
x
a) Współrz dna pozioma rodka ci ko ci bez uwzgl dniania stołu wynosi
mm
5
,
112
3
2
1
3
3
2
2
1
1
=
+
+
⋅
+
⋅
+
⋅
=
⋅
=
m
m
m
x
m
x
m
x
m
m
x
m
x
i
i
i
s
Punkt podparcia wypada w rodku lewej nogi (
mm
120
=
p
x
), czyli rodek ci ko ci le y
poza obrysem podparcia, dlatego stół si przewróci.
b) Współrz dna pozioma rodka ci ko ci z uwzgl dnieniem stołu wynosi
mm
7
,
122
3
2
1
0
3
3
2
2
1
1
0
0
=
+
+
+
⋅
+
⋅
+
⋅
+
⋅
=
⋅
=
m
m
m
m
x
m
x
m
x
m
x
m
m
x
m
x
i
i
i
s
Punkt podparcia wypada w rodku lewej nogi (
mm
120
=
p
x
), czyli rodek ci ko ci le y
mi dzy podporami i stół si nie przewróci.
Zad. 7.
Siła tarcia
T działa przeciwnie do ruchu, zatem
Składowe x:
0
=
+
−
x
F
T
Składowe y:
0
=
−
+
mg
N
F
y
Siła tarcia wynosi:
N
T
µ
=
, składowe
α
cos
F
F
x
=
i
α
sin
F
F
y
=
.
Po podstawieniu i przekształceniach
N
214
sin
cos
=
+
=
α
µ
α
µ
mg
F

5/6
Zad. 8.
Na ciało działa skierowana pionowo w dół siła grawitacji
G, któr mo na rozło y na
składow styczn
G
t
i normaln
G
n
. Siła tarcia
T działa w dół równi, poniewa przeciwstawia
si ruchowi ciała.
Składowe x (t – styczne, wzdłu równi):
0
=
+
−
−
F
G
T
t
Składowe y (n – normalne, prostopadle do równi):
0
=
+
−
N
G
n
Siła tarcia wynosi:
N
T
µ
=
, składowe
α
cos
mg
G
n
=
i
α
sin
mg
G
t
=
.
Po podstawieniu i przekształceniach
(
)
N
660
sin
cos
=
+
=
α
α
µ
mg
F
Zad. 9.
Na ciało działaj siły czynne: pozioma
F
w
oraz
F. Siła tarcia T działa przeciwnie do zwrotu
pr dko ci, poniewa przeciwstawia si ruchowi ciała. Warunki równowagi utworz układ
równa
=
−
−
=
=
−
−
=
0
0
mg
F
N
Y
F
T
F
X
y
x
w
Siła tarcia wynosi:
N
T
µ
=
, składowe
α
cos
F
F
x
=
i
α
sin
F
F
y
=
.
Po podstawieniu i przekształceniach
(
)
kg
297
cos
sin
=
+
−
=
α
α
µ
µ
µ
g
F
g
F
m
w
Zad. 10.
Na ciało działa skierowana pionowo w dół siła grawitacji
G, któr mo na rozło y na
składow styczn
G
t
i normaln
G
n
. Dodatkowo na ciało działa pozioma siła
F, któr mo na
rozło y na składow normaln
α
sin
2
g
m
F
n
=
i styczn
α
cos
2
g
m
F
t
=
. Siła tarcia
T działa
w dół równi, poniewa przeciwstawia si ruchowi ciała.
Składowe x (t – styczne, wzdłu równi):
0
=
+
−
−
t
t
F
G
T
Składowe y (n – normalne, prostopadle do równi):
0
=
+
−
−
N
F
G
n
n
Siła tarcia wynosi:
N
T
µ
=
, składowe
α
cos
1
g
m
G
n
=
i
α
sin
1
g
m
G
t
=
.
Po podstawieniu i przekształceniach
kg
398
sin
cos
sin
cos
1
2
=
−
+
=
α
µ
α
α
α
µ
m
m
Zad. 11.
Siła tarcia
T działa stycznie do tarczy hamulca, wywołuj c moment przeciwny do ruchu
wskazówek zegara.
Równowaga momentów:
0
2
1
2
1
2
1
=
⋅
−
⋅
+
⋅
B
H
H
d
mg
d
T
d
T
Siła tarcia wynosi:
F
T
µ
=
.
Po podstawieniu i przekształceniach
N
2040
1
2
1
=
⋅
=
H
B
d
d
mg
F
µ

6/6
Zad. 12.
Na transportowane przedmiot działa skierowana pionowo w dół siła grawitacji
G, któr
mo na rozło y na składow styczn
G
t
i normaln
G
n
. Siła tarcia
T b dzie zapobiega
zsuwaniu si przedmiotu w dół ta my, zatem
0
=
−
t
G
T
i
0
=
−
n
G
N
uwzgl dniaj c, e
N
T
µ
=
,
α
cos
mg
G
n
=
i
α
sin
mg
G
t
=
, otrzymuje si
268
,
0
tan
cos
sin
=
=
=
α
α
α
µ
Zad. 13.
Warto siły
F
d
dociskaj cej klocki hamulca do koła mo na wyznaczy z sumy momentów
dla d wigni:
(
)
0
=
⋅
−
−
⋅
k
d
k
d
l
F
l
l
F
. Siła tarcia wynosi:
d
F
T
µ
=
, a odpowiadaj cy jej
moment tarcia:
h
h
d
T
M
2
1
2
⋅
⋅
=
.
Po podstawieniu:
Nm
156
=
−
=
h
k
k
d
h
d
l
l
l
F
M
µ
Zad. 14.
Przy zaci gni tych hamulcach koła lizgaj si po podło u, dlatego wyst puje tarcie lizgowe.
Siła F
s
potrzebna do pokonania siły tarcia wynosi
N
2940
=
= mg
F
s
µ
.
W przypadku zwolnionego hamulca, koła samochodu tocz si po podło u, dlatego
N
1
,
98
=
= mg
f
F
t
t
.
Siła tarcia lizgowego jest wi ksza
30
=
=
t
s
F
F
ψ
Data: 23.04.2010
Wyszukiwarka
Podobne podstrony:
Lista 7 rozw
Lista 6 rozw
lista 0 rozw
Lista 2 rozw
Lista 0 rozw
Lista 5 rozw
Lista 1 rozw
Lista 4 rozw
lista 3 4 rozw
Lista 7 rozw
lista 0 rozw
więcej podobnych podstron