
dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
1
Zad.1
Zapisać wzory na interpolację Lagrange'a wprost i odwrotną dla dyskretnych argumentów i
wartości (1,2), (3,4), (4,5). Sprawdzić, czy te interpolanty są funkcjami wzajemnie
odwrotnymi.
Wzór interpolacyjny Lagrange'a (interpolacja wprost)
1
1
2
2
1
( )
( )
( )
( ) ...
( )
n
i
i
n
n
i
p x
f L x
f L x
f L x
f L x
=
=
=
+
+ +
∑
gdzie
1
1
2
1
1
1
2
1
1
1
(
)
(
) (
) ... (
) (
) ... (
)
( )
(
) (
) ... (
) (
) ... (
)
(
)
n
j
j
j i
i
i
n
i
n
i
i
i
i
i
i
i
n
i
j
j
j i
x
x
x
x
x
x
x
x
x
x
x
x
L x
x
x
x
x
x
x
x
x
x
x
x
x
=
≠
−
+
−
+
=
≠
−
−
⋅ −
⋅ ⋅ −
⋅ −
⋅ ⋅ −
=
=
−
⋅
−
⋅ ⋅
−
⋅
−
⋅ ⋅
−
−
∏
∏
dla danych z zadania
1
3
4
2
4
5
x
f
=
1
2
3
(
3)(
4)
(
1)(
4)
(
1)(
3)
( )
,
( )
,
( )
(1 3)(1 4)
(3 1)(3 4)
(4 1)(4 3)
x
x
x
x
x
x
L x
L x
L x
−
−
−
−
−
−
=
=
=
−
−
−
−
−
−
( )
2
2
2
1
1
2
2
3
3
7
12
5
4
4
3
( )
( )
( )
( )
2
4
5
1
6
2
3
x
x
x
x
x
x
p x
f L x
f L x
f L x
x
−
+
−
+
−
+
=
+
+
=
+
+
= +
−
Wzór na interpolację odwrotną Lagrange'a (funkcja musi być różnowartościowa!)
1
1
2
2
1
( )
( )
( )
( ) ...
( )
n
i
i
n
n
i
p y
x L y
x L y
x L y
x L y
=
=
=
+
+ +
∑
gdzie
1
1
2
1
1
1
2
1
1
1
(
)
(
) (
) ... (
) (
) ... (
)
( )
(
) (
) ... (
) (
) ... (
)
(
)
n
j
j
j i
i
i
n
i
n
i
i
i
i
i
i
i
n
i
j
j
j i
y
f
y
f
y
f
y
f
y
f
y
f
L y
f
f
f
f
f
f
f
f
f
f
f
f
=
≠
−
+
−
+
=
≠
−
−
⋅ −
⋅ ⋅ −
⋅ −
⋅ ⋅ −
=
=
−
⋅
−
⋅ ⋅
−
⋅
−
⋅ ⋅
−
−
∏
∏
Dla danych z zadania
1
2
3
(
4)(
5)
(
2)(
5)
(
2)(
4)
( )
,
( )
,
( )
(2 4)(2 5)
(4 2)(4 5)
(5 2)(5 4)
y
y
y
y
y
y
L y
L y
L y
−
−
−
−
−
−
=
=
=
−
−
−
−
−
−

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
2
( )
2
2
2
1
1
2
2
3
3
9
20
7
10
6
8
( )
( )
( )
( )
1
3
4
1
6
2
3
y
y
y
y
y
y
p y
x L y
x L y
x L y
y
−
+
−
+
−
+
=
+
+
=
+
+
= −
−
Dla interpolacji odwrotnej
1
1
x
y
y
x
= −
→
= +
otrzymujemy interpolację wprost i na
odwrót. Są to funkcje wzajemnie odwrotne.
Zad.2
Dokonać najlepszej aproksymacji (funkcją liniową, a następnie wykładniczą, ekspotencjalną
postaci
x
a be
+
dla danych z poprzedniego zadania.
Obliczenia dla aproksymacji liniowej
( )
p x
ax b
=
+
- postać aproksymacji
Funkcjonał błędu aproksymacji (suma kwadratów odchyłek pomiędzy wartością na prostej, a
wartością oryginalną)
(
) (
) (
) (
)
3
2
2
2
2
1
( , )
( )
2
3
4
4
5
i
i
i
B a b
p x
f
a b
a b
a b
=
=
−
=
+ −
+
+ −
+
+ −
∑
Optymalizacja funkcjonału
(
)
(
)
(
)
(
) (
) (
)
2
2
2 3 3
4
2 4 4
5
0
2
2
2 3
4
2 4
5
0
B
a b
a b
a b
a
B
a b
a b
a b
b
∂
=
+ − + ⋅ ⋅
+ − + ⋅ ⋅
+ − =
∂
∂
=
+ − +
+ − +
+ − =
∂
26
8
34
1
8
3
11
1
a
b
a
a
b
b
+
=
=
→
+
=
=
Końcowa postać aproksymacji ( )
1
p x
x
= +
- funkcja idealnie odtwarza wartości węzłowe
Obliczenia dla funkcji ekspotencjalnej
( )
x
p x
a be
= +
- postać aproksymacji
(
) (
)
(
) (
)
3
2
2
2
2
3
4
1
( , )
( )
2
4
5
i
i
i
B a b
p x
f
a be
a
be
a be
=
=
−
= + −
+ +
−
+ +
−
∑
(
)
(
) (
)
(
)
(
)
(
)
3
4
3
3
4
4
2
2
2
4
2
5
0
2
2
2
4
2
5
0
B
a be
a be
a be
a
B
e a be
e
a be
e
a be
b
∂
=
+ − +
+
− +
+
− =
∂
∂
=
+ − +
+
− +
+
− =
∂

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
3
(
)
(
) (
)
3
4
3
4
2
6
8
3
4
3
11
2
4
5
a
e e
e
b
e e
e
a
e
e
e b
e
e
e
+ + +
=
+ +
+
+ +
=
+
+
Dla przypomnienia:
2.7182
e
≈
3
77.4020
11
2.2800
77.4020
3391.7758
358.7695
0.0537
a
b
a
a
b
b
+
⋅ =
=
→
⋅ +
⋅ =
=
Końcowa postać aproksymacji ( )
2.2800 0.0537
x
p x
e
=
+
Sprawdzenie: wartości funkcji aproksymacyjnej w węzłach:
(1)
2.4261 ,
(3)
3.3595 ,
(4)
5.2144
p
p
p
=
=
=
Oczywiście jest różnica w stosunku do oryginalnych wartości (2,4,5), ale jest to wynik
aproksymacyjny, więc można spodziewać się takiej różnicy.
Zad.3
Wyprowadzić wzory różnicowe dla 3 węzłów
1
1
i
i
i
x
x
x
−
+
< <
na pierwszą pochodną
1
1
2
3
1
'
i
i
i
i
f
f
f
f
α
α
α
−
+
≈
+
+
oraz drugą pochodną
1
1
2
3
1
''
i
i
i
i
f
f
f
f
β
β
β
−
+
≈
+
+
Zastosować metodę interpolacji Lagrang'e oraz współczynników nieoznaczonych.
W celu łatwiejszych obliczeń przyjęte zostaną oznaczenia
1
1
2
1
,
i
i
i
i
h
x
x
h
x
x
−
+
= −
=
−
Układ współrzędnych zostanie przyjęty w punkcie o numerze "i", w którym należy znaleźć
wartości pochodnych numerycznych: pozostałe punkty będą więc leżeć w odległości -h1 oraz
h2 od środka. Dodatkowo zamiast indeksów dolnych: "i-1", "i" oraz "i+1" będą używane
oznaczenia: 1,2, 3.
Dane do
interpolacji Lagrange'a
1
2
1
2
3
0
h
h
x
f
f
f
f
−
=
Wielomiany Lagrange'a
(
)
( )(
)
(
)(
)
(
)(
)
(
)
(
)
2
1
2
1
1
2
3
1
1
2
2
2
2
1
2
( )
,
( )
,
( )
0
0
x x h
x
h
x
h
x
h x
L x
L x
L x
h
h
h
h
h
h
h h
−
+
−
+
=
=
=
−
− −
+
−
+
Interpolacja Lagrange'a i jej pochodne
1 1
2
2
3
3
( )
( )
( )
( )
p x
f L x
f L x
f L x
=
+
+
dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
4
(
)
(
)
2
2
1
1
1 1
2
2
3
3
1
2
3
1
1
2
1 2
2
1
2
2
2
2
'( )
'( )
'( )
'( )
x
h
x
h
h
x
h
p x
f L
x
f L
x
f L
x
f
f
f
h h
h
h h
h
h h
−
− +
+
=
+
+
=
−
+
+
+
(
)
(
)
1 1
2
2
3
3
1
2
3
1
1
2
1 2
2
1
2
2
2
2
''( )
''( )
''( )
''( )
p x
f L
x
f L
x
f L
x
f
f
f
h h
h
h h
h
h h
=
+
+
=
−
+
+
+
Wzory różnicowe = wartości pochodnych interpolacji w punkcie centralnym wzoru (x = 0)
(
)
(
)
2
2
1
1
2
1
2
3
1
1
2
1 2
2
1
2
'
'(0)
h
h
h
h
f
p
f
f
f
h h
h
h h
h
h h
−
≈
= −
+
+
+
+
(
)
(
)
2
1
2
3
1
1
2
1 2
2
1
2
2
2
2
''
''(0)
f
p
f
f
f
h h
h
h h
h
h h
≈
=
−
+
+
+
Metoda współczynników nieoznaczonych
Należy rozwinąć każdą z wartości funkcyjnych wzoru różnicowego
1
2
3
,
,
f
f
f rozwinąć w
szereg Taylora względem punktu centralnego wzoru (o numerze 2). Rozwinięcie obejmuje
wyrazy rzędu 0,1,2, czyli trzy pierwsze, dlatego, że na trzech wartościach funkcji oparty jest
wzór: są trzy niewiadome współczynniki, więc potrzeba trzech równań.
2
1
2
1 2
1
2
2
2
2
3
2
2
2
2
2
1
'
'' ...
2
1
'
'' ...
2
f
f
h f
h f
f
f
f
f
h f
h f
= −
+
+
=
= +
+
+
Następnie każde z rozwinięć należy pomnożyć przez odpowiedni współczynnik: według
założonego wzoru na pierwszą pochodną:
2
1
2
1 2
1
2
1
2
2
2
2
3
2
2
2
2
2
3
1
'
'' ...
/
2
/
1
'
'' ...
/
2
f
f
h f
h f
f
f
f
f
h f
h f
α
α
α
= −
+
+
⋅
=
⋅
= +
+
+
⋅
W dalszej kolejności należy dodać powyższe równania: po stronie prawej uzyskamy w ten
sposób postać wzoru różnicowego, a po lewej - zbiór wartości funkcji i jej pochodnych, z
uporządkowanymi współczynnikami:
(
)
(
)
2
2
1
1
2
2
3
3
2
1
2
3
2
1
1
2
3
2
1
1
2
3
1
1
'
''
2
2
f
f
f
f
f
h
h
f
h
h
α
α
α
α α α
α
α
α
α
+
+
=
+
+
+
−
+
+
+
Lewa strona powyższego wzoru ma być przybliżeniem pierwszej pochodnej:
(
)
(
)
2
2
2
2
1
2
3
2
1
1
2
3
2
1
1
2
3
1
1
'
'
''
2
2
f
f
f
h
h
f
h
h
α α α
α
α
α
α
≈
+
+
+
−
+
+
+

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
5
Pozostaje więc porównań współczynniki stojące po obydwu stronach powyższej równości
(przy odpowiednich pochodnych) i rozwiązać uzyskany w ten sposób układ równań.
(
)
(
)
2
1
1
1
2
1
2
3
2
1
1
1
2
3
2
1 2
2
2
1
1
2
3
1
3
2
1
2
0
1
1
1
0
2
2
h
h h
h
h
h
h
h
h h
h
h
h
h h
h
α
α α α
α
α
α
α
α
α
−
=
+
+
+
=
−
−
+
=
→
=
+
=
=
+
Końcowa postać wzoru
(
)
(
)
2
2
1
1
2
1
2
3
1
1
2
1 2
2
1
2
'
h
h
h
h
f
f
f
f
h h
h
h h
h h
h
−
≈ −
+
+
+
+
Dla drugiej pochodnej te same rozwinięcia wartości funkcyjnych będziemy mnożyć przez
współczynniki "beta":
2
1
2
1 2
1
2
1
2
2
2
2
3
2
2
2
2
2
3
1
'
'' ...
/
2
/
1
'
'' ...
/
2
f
f
h f
h f
f
f
f
f
h f
h f
β
β
β
= −
+
+
⋅
=
⋅
= +
+
+
⋅
(
)
(
)
2
2
1
1
2
2
3
3
2
1
2
3
2
1
1
2
3
2
1
1
2
3
1
1
'
''
2
2
f
f
f
f
f
h
h
f
h
h
β
β
β
β β β
β
β
β
β
+
+
=
+
+
+
−
+
+
+
Lewa strona powyższego wzoru ma być przybliżeniem drugiej pochodnej:
(
)
(
)
2
2
2
2
1
2
3
2
1
1
2
3
2
1
1
2
3
1
1
''
'
''
2
2
f
f
f
h
h
f
h
h
β β β
β
β
β
β
≈
+
+
+
−
+
+
+
(
)
(
)
1
1
1
2
1
2
3
1
1
2
3
2
1 2
2
2
1
1
2
3
3
2
1
2
2
0
2
0
1
1
1
2
2
2
h h
h
h
h
h h
h
h
h
h h
β
β β β
β
β
β
β
β
β
=
+
+
+
=
−
+
=
→
= −
+
=
=
+
Końcowa postać wzoru
(
)
(
)
2
1
2
3
1
1
2
1 2
2
1
2
2
2
2
''
f
f
f
f
h h
h
h h
h
h h
≈
−
+
+
+

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
6
Zad.4
Zastosować wzory z zad.3 do obliczenia pierwszej i drugiej pochodnej funkcji
sin( )
( )
x
f x
x
=
w punkcie
5
x
=
. Zastosować różne położenia węzłów
1
1
,
i
i
x
x
−
+
. Obliczyć błąd uzyskanych
wyników.
Analityczne wartości pochodnych
(
)
(
)
2
2
4
cos( ) sin( )
'( )
,
'(5)
0.0951
cos( )
sin( ) cos( )
cos( ) sin( ) 2
''( )
,
''(5)
0.1537
x
x
x
f x
f
x
x
x
x
x
x
x
x
x
x
f
x
f
x
−
=
=
−
−
−
−
=
=
Obliczenia dla konfiguracji
1
2
3
1
2
4,
5,
6
1
x
x
x
h
h
=
=
=
→
= =
,
1
1
2
2
3
3
( )
0.1892
,
(
)
0.1918 ,
( )
0.0466
f
f x
f
f x
f
f x
=
= −
=
= −
=
= −
Pochodne numeryczne (wg wzorów z poprzedniego zadania - obydwie metody dały te same
wzory) i ich błędy
( )
( )
( )
( )
2
2
2
2
'
' 5
0.0713 0.0951
'
0.0713 ,
0.2503
' 5
0.0951
''
'' 5
0.1478 0.1537
''
0.1478 ,
0.0384
'' 5
0.1537
f
f
f
e
f
f
f
f
e
f
−
−
≈
=
=
=
−
−
≈
=
=
=
Obliczenia dla konfiguracji
1
2
3
1
2
1
1
2
1
4 ,
5,
5
,
3
3
3
3
x
x
x
h
h
=
=
=
→
=
=
,
1
1
2
2
3
3
( )
0.2144
,
(
)
0.1918 ,
( )
0.1525
f
f x
f
f x
f
f x
=
= −
=
= −
=
= −
Pochodne numeryczne i ich błędy
( )
( )
( )
( )
2
2
2
2
'
' 5
0.0899 0.0951
'
0.0899 ,
0.0547
' 5
0.0951
''
'' 5
0.1679 0.1537
''
0.1679 ,
0.0924
'' 5
0.1537
f
f
f
e
f
f
f
f
e
f
−
−
≈
=
=
=
−
−
≈
=
=
=
Zad.5
Zastosować poznane kwadratury (Newtona - Cotesa oraz Gaussa) do obliczenia
0
sin( )
x dx
π
∫
dzieląc przedział całkowania na dwa podprzedziały. Obliczyć błędy uzyskanych wyników.
dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
7
Wynik analityczny
0
0
( )
sin( )
cos( )
2
b
a
I
f x dx
x dx
x
π
π
=
=
= −
=
∫
∫
Rozwiązania numeryczne (podział przedziału
[
]
0
π
na dwa podprzedziały 0
2
π
oraz
2
π π
).
- metoda prostokątów
( )
p
I
f a h
=
(0)
1.5708 ,
0.2146
2
2
2
p
p
I
I
I
f
f
e
I
π
π π
−
=
⋅ +
⋅ =
=
=
- metoda trapezów
(
)
0.5
( )
( )
t
I
f a
f b h
=
+
( )
0.5
(0)
0.5
1.5708 ,
0.2146
2
2
2
2
t
t
I
I
I
f
f
f
f
e
I
π
π
π
π
π
−
=
+
⋅ +
+
⋅ =
=
=
- metoda parabol (Simsona)
( ) 4
( )
6
2
S
h
a b
I
f a
f
f b
+
=
+
+
( )
3
(0) 4
4
2.0046
,
0.0023
12
4
2
12
2
4
S
S
I
I
I
f
f
f
f
f
f
e
I
π
π
π
π
π
π
π
−
=
+
+
+
+
+
=
=
=
- metoda Gaussa (2-punktowa)
( )
( )
(
)
2
1
2
1
1
2
G
b a
I
f x
f x
−
=
⋅
+ ⋅
, gdzie
1,2
1,2
2
2
b a
b
a
x
z
−
+
=
+
,
1
2
1
1
,
3
3
z
z
= −
=
dla
0
2
x
π
∈
:
(1)
(1)
1
2
0.3319
,
1.2388
x
x
=
=
dla
2
x
π π
∈
:
(2)
(2)
1
2
1.9027
,
2.8096
x
x
=
=
( )
( )
(
)
( )
( )
(
)
(1)
(1)
(2)
(2)
2
2
1
2
1
2
1
1
1
1
1.9969
,
0.0016
4
4
G
G
I
I
I
f x
f x
f x
f x
e
I
π
π
−
=
⋅
+ ⋅
+
⋅
+ ⋅
=
=
=

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
8
Zad.6
Zastosować metodę Eulera, Rungego-Kutty II i IV rzędu oraz wybraną metodę predyktor -
korektor do aproksymacji rozwiązania poniższego zagadnienia początkowego z krokiem 0.1
3
3
2
,
(0)
1
dy
x
y
y
dx
= −
=
Oszacować błędy otrzymanych wyników.
Wzory na kolejne wartości funkcji
- metoda Eulera
1
( ,
)
i
i
i
i
y
y
h f x y
+
= + ⋅
- metoda Rungego-Kutty II rodzaju
1
2
1
1
1
2
( ,
)
(
,
)
1
(
)
2
i
i
i
i
i
i
K
h f x y
K
h f x
h y
K
y
y
K
K
+
= ⋅
= ⋅
+
+
= +
+
- metoda Rungego-Kutty IV rodzaju
1
2
1
( ,
)
1
1
(
,
)
2
2
i
i
i
i
K
h f x y
K
h f x
h y
K
= ⋅
= ⋅
+
+
3
2
4
3
1
1
2
3
4
1
1
(
,
)
2
2
(
,
)
1
(
2
2
)
6
i
i
i
i
i
i
K
h f x
h y
K
K
h f x
h y
K
y
y
K
K
K
K
+
= ⋅
+
+
= ⋅
+
+
= +
+
+
+
Przyjmujemy
0
1
0
2
0
3
0
0
,
0.1 ,
0.1 ,
2
0.2
,
3
0.3
x
x
x
h
h
x
x
h
x
x
h
=
= + =
=
= +
=
= +
=
( )
3
3
0
1 ,
,
2
y
f x y
x
y
=
= −
Trzy kolejne wartości funkcji obliczone za pomocą
- metody Eulera
(
)
3
3
1
0
0
0
0.1
( ,
)
1 0.1 0
2 1
0.8
y
y
f x y
=
+
⋅
= +
⋅
− ⋅
=
(
)
3
3
2
1
1
1
0.1
( ,
)
0.8 0.1 0.1
2 0.8
0.6977
y
y
f x y
= +
⋅
=
+
⋅
− ⋅
=
(
)
3
3
3
2
2
2
0.1
( ,
)
0.6977 0.1 0.2
2 0.6977
0.6306
y
y
f x y
=
+
⋅
=
+
⋅
− ⋅
=
- metody R-K II

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
9
(
)
1
0
0
2
0
0
1
0
1
2
0.1 ( ,
)
0.2
,
0.1 (
0.05,
0.1)
0.1023
1
0.8488
2
K
f x y
K
f x
y
y
y
K
K
=
= −
=
+
−
= −
=
+
+
=
(
)
1
1
1
2
2
1
1
2
0.1 ( ,
)
0.1222
,
0.0759
1
0.7498
2
K
f x y
K
y
y
K
K
=
= −
= −
= +
+
=
(
)
1
2
2
2
3
2
1
2
0.1 ( ,
)
0.0835 ,
0.0565
1
0.6798
2
K
f x y
K
y
y
K
K
=
= −
= −
=
+
+
=
- metody R-K IV
1
2
3
4
1
0
1
2
3
4
0.2
,
0.1458
,
0.1594
,
0.1187
1
(
2
2
)
0.8452
6
K
K
K
K
y
y
K
K
K
K
= −
= −
= −
= −
=
+
+
+
+
=
1
2
3
4
2
1
1
2
3
4
0.1206
,
0.0964
,
0.1009
,
0.0817
1
(
2
2
)
0.7457
6
K
K
K
K
y
y
K
K
K
K
= −
= −
= −
= −
= +
+
+
+
=
1
2
3
4
3
2
1
2
3
4
0.0821 ,
0.0684
,
0.0705 ,
0.0589
1
(
2
2
)
0.6759
6
K
K
K
K
y
y
K
K
K
K
= −
= −
= −
= −
=
+
+
+
+
=
Dokładność metod można oszacować na dwa sposoby
- porównanie wartości obliczonych przy tym samym
h , ale za pomocą dwóch różnych
metod (o różnych dokładnościach), np.
oszacowanie błędu rozwiązania metody Eulera dla wartości
3
y
( )
(
)
3
3
(
)
3
0.6306 0.6798
0.0724
0.6798
E
R K II
R K II
y
y
e
y
−
−
−
−
≈
=
=
oszacowanie błędu rozwiązania metody R-K II dla wartości
3
y
(
)
(
)
3
3
(
)
3
0.6798 0.6759
0.0058
0.6759
R K II
R K IV
R K IV
y
y
e
y
−
−
−
−
−
≈
=
=
- porównanie wartości obliczonych tą samą metodą, ale przy pomocy dwóch różnych
odstępów
h , np. oszacowanie błędu rozwiązania
3
y dla h = 0.1 , przy pomocy h = 0.05, co
wymagałoby obliczenia sześciu wartości funkcji (dla otrzymania wartości dla tego samego
x
= 0.3).
Metoda predyktor - korektor polega na zastosowaniu dwóch rodzajów wzoru
- wzoru otwartego (predyktor) - przewidującego następną wartość funkcji na podstawie kilku
znanych wstecz,
dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
10
- wzoru zamkniętego w celu poprawienia uzyskanej wartości za pomocą korektora -
obliczającego wartość daną funkcji w oparciu o jej wcześniejsze przybliżenie.
Dla przykładu zostanie zastosowane podejście predyktor - korektor II rzędu, co wymaga
użycia następujących wzorów
- predyktor (k = 0) :
(0)
1
1
2
(23
16
5
),
( ,
)
12
i
i
i
i
i
i
i
i
h
y
y
f
f
f
f
f x y
+
−
−
= +
⋅
−
+
≡
- korektor (k > 0):
(
1)
( )
1
1
1
(5
8
)
12
k
k
i
i
i
i
i
h
y
y
f
f
f
+
+
+
−
= +
⋅
+
−
O zakończeniu obliczeń za pomocą korektora powinno decydować np. następujące kryterium
(
1)
( )
1
1
(
1)
1
k
k
i
i
dop
k
i
y
y
y
ε
+
+
+
+
+
−
≤
gdzie
dop
ε
- dopuszczalna wartość błędu (przyjmowana).
W bieżącym zadaniu zostanie obliczona - za pomocą podejścia pred.-kor. - wartość
3
y , w
oparciu o wartości
2
y oraz
1
y , otrzymane wcześniej za pomocą wzoru R-K IV.
(
)
(
)
( )
(
)
(0)
3
2
2
1
0
0.1
(23
16
5
)
12
0.1
0.7457
23
0.2, 0.7457
16
0.1, 0.8452
5
0,1
0.6658
12
y
y
f
f
f
f
f
f
=
+
⋅
−
+
=
=
+
−
+
=
(
)
(
) (
)
(
)
(1)
(0)
3
2
3
2
1
0.1
(5
8
)
12
0.1
0.7457
5
0.3, 0.6658
8
0.2, 0.7457
0.1, 0.8452
0.6775
12
y
y
f
f
f
f
f
f
=
+
⋅
+
−
=
=
+
+
−
=
(
)
(
) (
)
(
)
(2)
(1)
3
2
3
2
1
0.1
(5
8
)
12
0.1
0.7457
5
0.3, 0.6675
8
0.2, 0.7457
0.1, 0.8452
0.6762
12
y
y
f
f
f
f
f
f
=
+
⋅
+
−
=
=
+
+
−
=
oszacowanie błędu
(2)
(1)
3
3
(2)
3
0.6775 0.6762
0.0019
0.6775
y
y
e
y
−
−
≈
=
=
Zad.7
Zapisać i rozwiązać układ równań algebraicznych MRS dla zagadnienia brzegowego
( )
2
''
'
,
0,3
u
u
u
x
x
+ + =
∈
'(0)
1 ,
(3)
2
u
u
=
=
dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
11
Dla wszystkich pochodnych zastosować centralne wzory różnicowe 3-węzłowe.
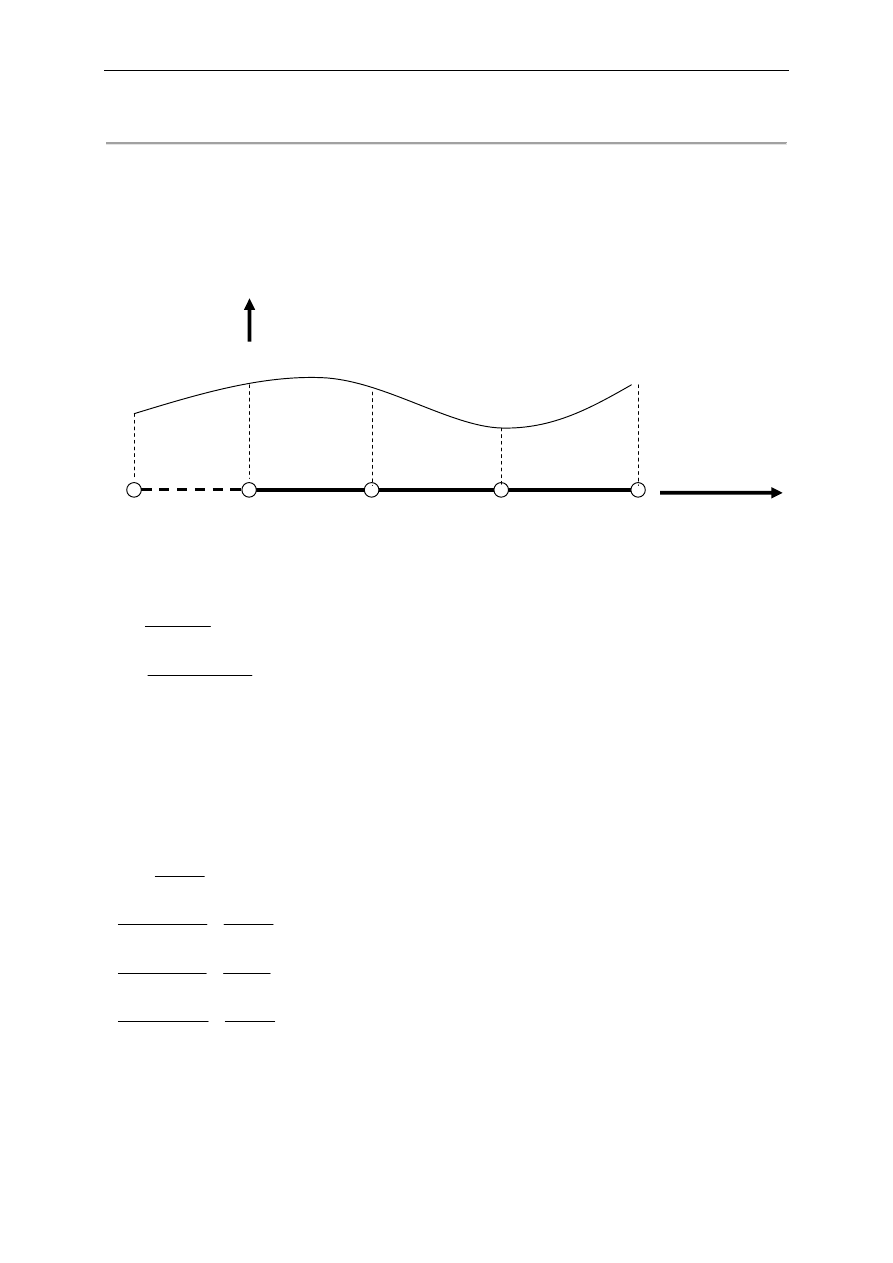
W temacie brak danych na temat liczby węzłów - zatem przyjęto 4 węzły w obszarze + 1
węzeł fikcyjny, potrzebny do dyskretyzacji różnicowej warunku na pierwszą pochodną w
lewym węźle brzegowym.
Rysunek do zadania
0
1
2
3
4
h =1
1
u
2
u
3
u
4
u
0
u
u
x
x = 0
x = 1
x = 2
x = 3
Wzory różnicowe centralne 3-węzłowe
1
1
1
1
2
'
2
2
''
i
i
i
i
i
i
i
u
u
u
h
u
u
u
u
h
+
−
−
+
−
≈
−
+
≈
Równania różnicowe wynikają z:
- zapisania warunku brzegowego na pierwszą pochodną '(0) 1
u
=
w węźle 1
- zapisania równań różnicowych (odpowiadających równaniu różniczkowemu) w węzłach
obszaru 1,2,3.
- zapisania warunku brzegowego na funkcję (3)
2
u
=
w węźle 3.
2
0
1
0
2
0
1
2
2
0
1
2
2
1
2
3
3
1
2
2
2
2
3
4
4
2
3
2
4
'
1
2
2 1
2
0
1
2 1
2
1
1
2 1
2
2
1
2 1
2
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
−
≈
=
→
= −
⋅
−
+
−
+
+ =
⋅
−
+
−
+
+ =
⋅
−
+
−
+
+ =
⋅
=
Po wprowadzeniu do równań 2-4 informacji z pierwszego i ostatniego otrzymujemy:

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
12
2
1
2
2
2
1
2
2
1
2
3
3
1
2
2
2
2
3
2
3
2
2 2
2
0
1
2 1
2
1
1
2 1
2
2
2
2
1
2 1
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
− −
+
− +
+
+ =
⋅
−
+
−
+
+ =
⋅
−
+
−
+
+ =
⋅
lub w zapisie macierzowym, co daje rozwiązania
1
1
2
2
3
3
1
2
0
1
7
1
3
1
1
4
2
2
1
1
1
0
1
2
u
u
u
u
u
u
−
−
=
→
=
−
Zad.8
Zapisać układ równań algebraicznych MRS po dyskretyzacji 4 węzłami fizycznymi (w
rozważanym obszarze i na jego brzegu) oraz odpowiednimi fikcyjnymi dla belki. Zastosować
centralne wzory różnicowe 5-cio węzłowe. Zapisać wzory różnicowe do obliczenia reakcji.
Należy zacząć od sporządzenia rysunku do zadania - poniżej. Na belce o długości L = 3 m
znajdują się cztery (n = 4) węzły (3,4,5,6, z czego 3 i 6 to węzły brzegowe), natomiast po
dwóch stronach brzegu dodatkowo jeszcze po dwa węzły fikcyjne (1,2 oraz 7,8). Moduł siatki
przy takim podziale wynosi
3
1
1
3
L
m
h
m
n
=
=
=
−
.
1
2
3
4
5
6
7
8
10 kN/m
100 kN
h =1 m
Sformułowanie (lokalne) problemu brzegowego
( )
4
4
( )
,
0, 3
100
'(0)
0
,
'''(0)
,
(0)
0
,
'(3)
0
d w
q x
x
dx
EJ
kN
w
w
w
w
EJ
=
∈
=
=
=
=

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
13
Warunki brzegowe (cztery, bo równanie różniczkowe jest czwartego rzędu) wynikają z
podparcia belki oraz z obciążenia brzegowego.
Zapisanie układ równań algebraicznych MRS wymaga
- zapisania dwóch warunków brzegowych w węźle brzegowym 3,
- zapisania równania różnicowego czwartego rzędu w węzłach belki (jedno równanie w
węzłach 3,4,5,6),
- zapisania dwóch warunków brzegowych w węźle brzegowym 6.
Przy obciążeniu liniowym warto zapisać sobie relację, wg której obciążenie może być
obliczane dla każdego punktu
( )
0,3
x
∈
:
10
( )
3
q x
x
=
Operatory różnicowe 5-cio węzłowe na kolejne pochodne
(z czego w zadaniu będą potrzebne wzory na pierwszą, trzecią i czwartą pochodną).
(
)
2
1
1
2
2
1
1
2
2
2
1
1
2
3
2
1
1
2
4
1
1
2
2
1
'
12
3
3
12
1
1
4
5
4
1
''
12
3
2
3
12
1
1
1
'''
2
2
1
''''
4
6
4
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
w
w
w
w
w
h
w
w
w
w
w
w
h
w
w
w
w
w
h
w
w
w
w
w
w
h
−
−
+
+
−
−
+
+
−
−
+
+
−
−
+
+
≈
−
+
−
≈
−
+
−
+
−
≈
−
+
−
+
≈
−
+
−
+
Układ równań
(
)
(
)
(
)
(
)
1
2
4
5
1
2
4
5
3
1
2
3
4
5
4
2
3
4
5
6
4
3
4
5
6
7
4
4
5
6
7
8
4
6
4
5
7
8
1 1
2
2
1
0
1 12
3
3
12
1
1
1
100
1
2
2
1
4
6
4
0
1
1
10 1
4
6
4
1
3
1
20 1
4
6
4
1
3
1
1
4
6
4
10
1
0
1 1
2
2
1
0
1 12
3
3
12
w
w
w
w
w
w
w
w
EJ
w
w
w
w
w
w
w
w
w
w
EJ
w
w
w
w
w
EJ
w
w
w
w
w
EJ
w
w
w
w
w
−
+
−
=
−
+
−
+
=
−
+
−
+
=
−
+
−
+
=
−
+
−
+
=
−
+
−
+
=
=
−
+
−
=

dr inż. Sławomir Milewski
slawek@L5.pk.edu.pl
Kr, 2011-01-15
Rozwiązania przykładowych zadań na kolokwium nr 2 z MatStos i MetNum
14
Dwa pierwsze równania to różnicowe reprezentacje warunków brzegowych w węźle 3 - czyli
pochodnej pierwszej i trzeciej. Cztery kolejne to równania różnicowe z obszaru (na czwartą
pochodną) - ich prawe strony to wartości obciążenia ciągłego w kolejnych węzłach (czyli dla
x = 0, x = 1, x = 2 i x = 3). Dwa ostatnie to warunki brzegowe w węźle 6.
Ten sam układ w postaci macierzowej wygląda następująco:
1
2
3
4
5
6
7
8
1
2
2
1
0
0
0
0
0
12
3
3
12
100
1
1
1
0
1
0
0
0
0
2
2
10
1
4
6
4
1
0
0
0
1
3
0
1
4
6
4
1
0
0
20
0
0
1
4
6
4
1
0
3
0
0
0
1
4
6
4
1
10
0
0
0
0
0
1
0
0
0
1
2
2
1
0
0
0
0
0
12
3
3
12
w
w
w
w
w
EJ
w
w
w
−
−
−
−
−
−
−
=
−
−
−
−
−
−
Obliczenie reakcji wymaga:
- obliczenia drugiej pochodnej ugięcia (moment zginający / EJ) w lewej podporze
- obliczenia drugiej (moment zginający / EJ) i trzeciej pochodnej (- siła poprzeczna / EJ)
ugięcia w prawej podporze
Reakcja w lewej podporze
1
1
2
3
4
5
2
1
4
5
4
1
1
12
3
2
3
12
EJ
R
w
w
w
w
w
=
−
+
−
+
−
Reakcje w prawej podporze
2
4
5
6
7
8
2
1
4
5
4
1
1
12
3
2
3
12
EJ
R
w
w
w
w
w
=
−
+
−
+
−
3
4
5
7
8
3
1
1
1
2
2
EJ
R
w
w
w
w
= −
−
+
−
+
Wyszukiwarka
Podobne podstrony:
mzm zad roz woj 2006
pochodna cząstkowa zad + roz
algebra zad i roz z i egzaminu 7XNKTHD5YLOFNFQHSHKURMSFNNMAGI6FPPJZWVY
kol2 zad fiz rozw id 239188 Nieznany
mzm zad roz woj 2006
AnalizaMat-kol2-przykladowe-zad
Fund zad kol2 GHor id 181430 Nieznany
AnalizaMat kol2 przykladowe zad
zwi roz zad wytrz
cyfry rzymskie roz zad
Fund zad do kol2
AnalizaMat kol2 przykladowe zad
więcej podobnych podstron