
Algorytmy ewolucyjne

Nomenclature
Individual – the single proposition (e.g. chromosome in GA) of problem solutions,
Population – the set of individuals,
Genome – complete set of genetic materials (space of all possible solutions),
Chromosome – a part of genome composed of genes,
Gene – smallest element of chromosome, which represents elementar information
(trait of the individual),
Locus – position of the gene in chromosome,
Alelle – set of all possible traits in a given gene (all versions of a gene),
Genotype – the information about individual included in chromosome
(construction\plan of the chromosome – e.g. in GA: information is encoded in
chromosome as a string of bits),
Fenotype – the individuals (chromosome) properties that are evaluated according
the fitness function, based on which the particular chromosome (solution) is
ranked against all the other chromosomes in population,
Reproduction – the process of generation of new population using GA operators:
crossover (the fragments of two chromosomes are swaped), and mutation
(modification of the value of gene).

Introduction to EA
Genetic algorithms are a part of evolutionary computing,
which is a rapidly growing area of artificial intelligence.
Idea of evolutionary computing was introduced in the 1960s by
A genetic algorithms are search algorithms that mimic the process
of natural evolution, based on the mechanics of natural selection
and natural genetics.
Idea of evolutionary computing was introduced in the 1960s by
I. Rechenberg in his work "Evolution strategies" (Evolutionsstrategie in
original). His idea was then developed by other researchers.
Bremermann H. J.: The evolution of intelligence. The nervous
system as a model of its environment. ONR report no. 1, Contract
No. 477(17), University of Washington, Seattle, 1958.
Genetic Algorithms (GAs) were invented by John Holland and
developed by him and his students and colleagues. This lead to
Holland's book "Adaption in Natural and Artificial Systems" published in
1975.

Introduction to EA
Genetic algorithm
(GA): (Simple Genetic Algorithm - SGA):
Holland, J. H.: Adaptation in natural and artificial systems.
University of Michigan Press, Ann Arbor, 1975.
Evolutionary strategy (ES):
Rechenberg I.: Evolutionsstrategie: optimierung technischer systeme nach
prinzipien der biologischen evolution. Frommann-Holzboog, Stuttgart 1973.
Genetic programming
Genetic programming
Fogel, L. J., Owens, A.J., Walsh, M.J. (1966): Artificial Intelligence through
Simulated Evolution, John Wiley.
Cramer Nichael Lynn (1985): A representation for the Adaptive Generation of
Simple Sequential Programs.
In Proceedings of an International Conference on Genetic Algorithms and the
Applications, Grefenstette, John J. (ed.), Carnegie Mellon University.
Koza J. R.: Genetic programming: A paradigm for genetically breeding populations
of computer programs to solve problems. Raport nr STAN-CS-90-134, Stanford
University, 1990.
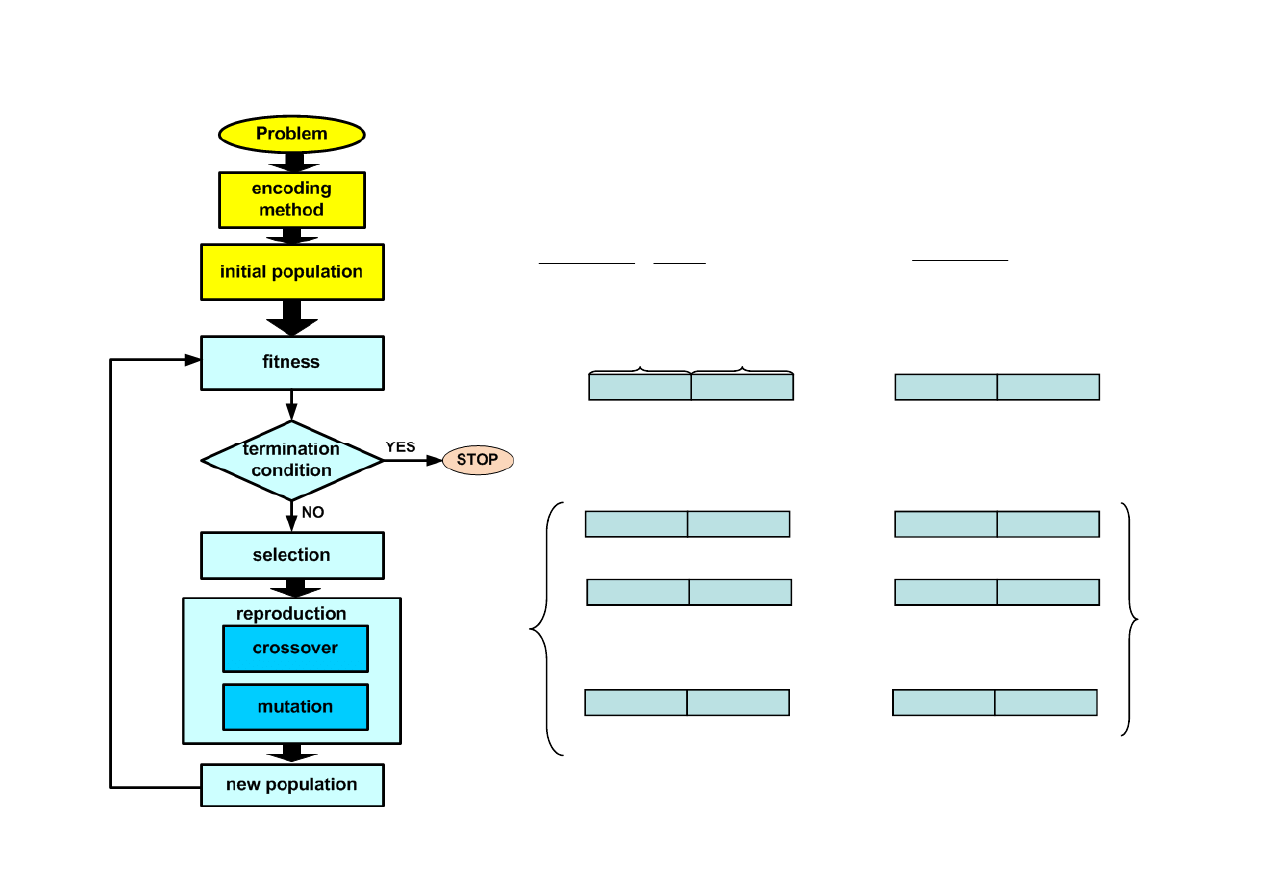
GA flowchart
)
3
cos(
)
2
sin(
2
1
x
x
y
+
=
minimum of the function:
]
20
:
1
.
0
:
10
[
,
2
1
∈
x
x
encoding of chromosomes:
bits
x
7
1
→
bits
x
7
2
→
∑
=
⋅
⋅
−
+
=
6
0
2
127
min
max
min
i
i
i
x
x
x
bx
x
0787
.
0
127
10
20
127
min
max
=
−
=
−
x
x
genome:16 384 individuals
1010111 0100101
0111001 1101111
initial populations (parents):
…
bits
x
7
1
→
bits
x
7
2
→
chromosome 1
chromosome n
26
.
1
)
91
.
12
,
85
.
16
(
2
1
=
=
=
x
x
f
3
.
0
)
74
.
18
,
49
.
14
(
2
1
=
=
=
x
x
f
0111001 1
0
00101
1010111 0101111
0101111 1001101
1110100 11
1
1001
1001001 0101111
001
1
001 0001101
32
.
1
)
43
.
15
,
49
.
14
(
2
1
−
=
=
=
x
x
f
28
.
0
)
1
.
16
,
7
.
13
(
2
1
=
=
=
x
x
f
09
.
0
)
53
.
19
,
13
.
19
(
2
1
=
=
=
x
x
f
21
.
0
)
7
.
13
,
85
.
16
(
2
1
−
=
=
=
x
x
f
89
.
0
)
7
.
13
,
18
.
15
(
2
1
−
=
=
=
x
x
f
02
.
1
)
02
.
11
,
97
.
11
(
2
1
−
=
=
=
x
x
f
reproduction
n
e
w
p
o
p
u
la
ti
o
n
…
…
o
ff
s
p
ri
n
g

Mutation plays very important role in GA
(genome)
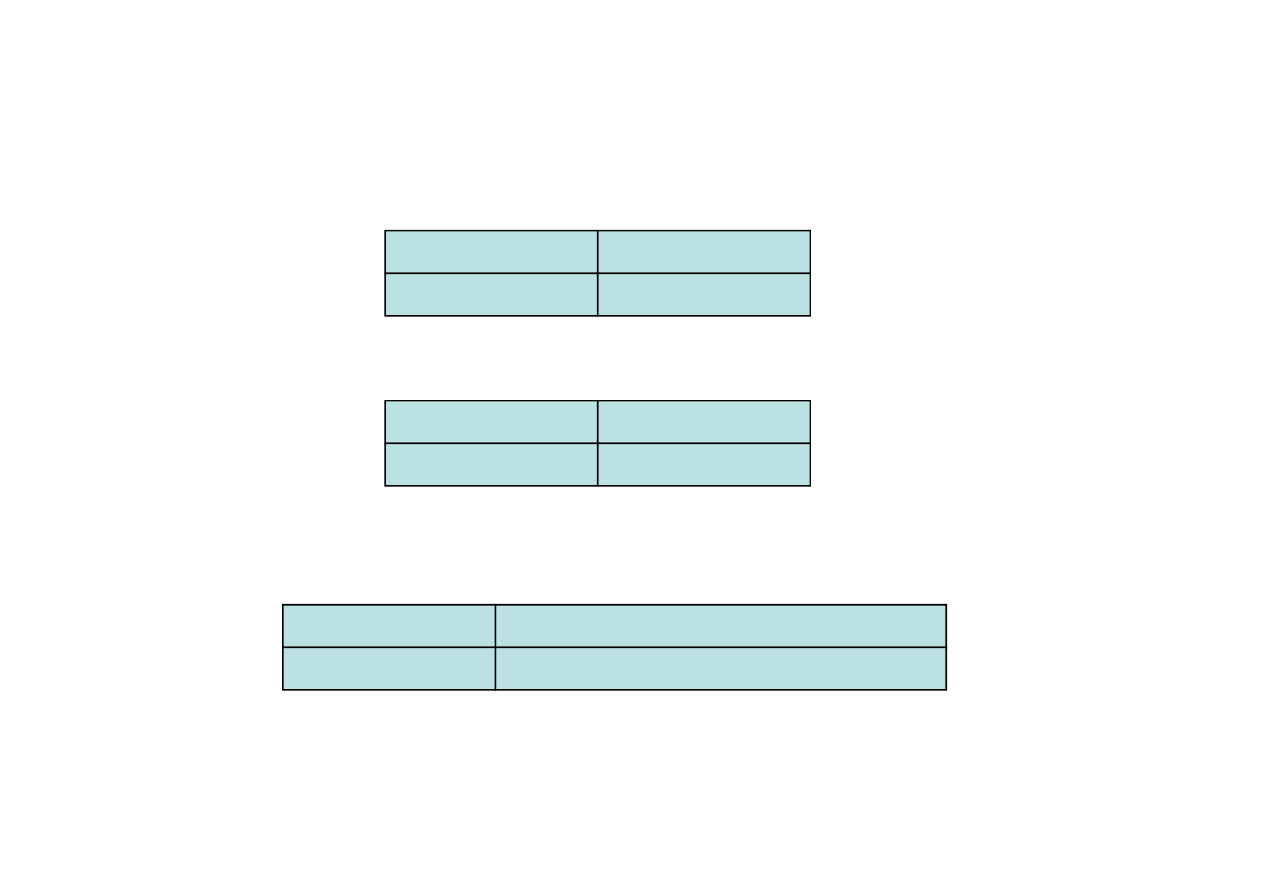
Chromosomes encoding
100111011111
Binary encoding
Chromosom A
011011100101
Chromosom B
Permutation encoding
1 8 5 3 2 7 6 4
Chromosom A
3 4 5 1 2 6 7 8
Chromosom B
Value encoding
0.12 1.456 2.314 0.777 1.17
Chromosom A
A B D S I O W R T H J K L S P Y
Chromosom B
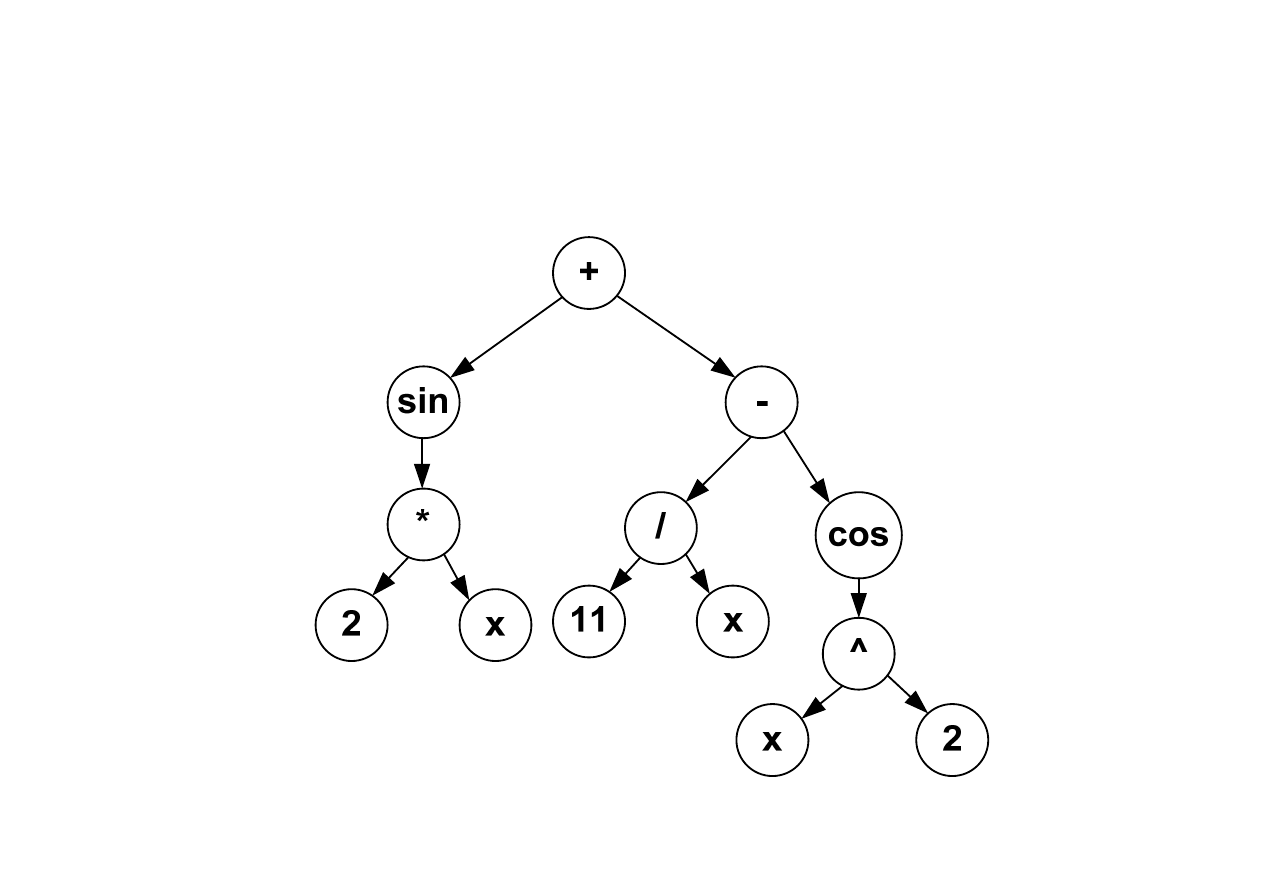
Tree encoding (drzewiasta struktura danych)
Chromosomes encoding
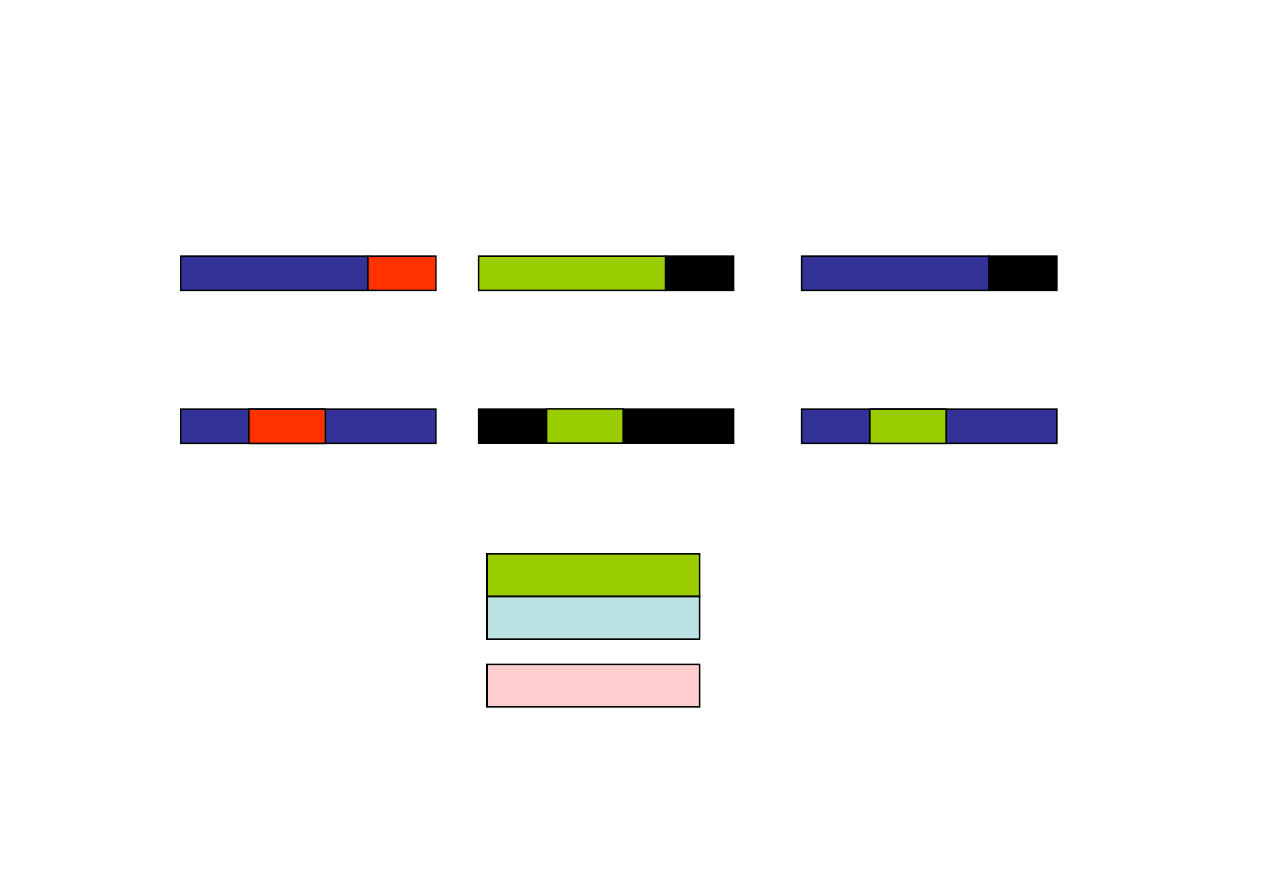
GA operators: crossover methods
single point crossover
+
=
parent A
parent B
offspring
+
=
two point crossover
parent A
parent B
offspring
+
=
arithmetical crossover
110111011111
011011110101
AND
parent A
parent B
010011010101
offspring
=
GA operators: crossover methods
scattered crossover (krzy
ż
owanie rozproszone)
1 0 1 0 1
a b c d e
parent A
parent B
Random binary vector:
a b c d e
parent B
1 b c 0 e
offspring
=
Random binary vector:
[ 1 0 0 1 0]

(
)
ParentA
ParentB
U
ParentA
Child
−
⋅
+
=
)
1
,
0
(
- intermediate crossover:
U(0,1) uniformly distributed random scalar
GA operators: crossover methods
[6.7 4.5 7.4 2.1]
[4.7 3.8 5.5 3.1]
[6.1 4.3 6.8 2.4]
parent A:
parent B:
child:
U(0,1) = 0.3

(
)
ParentB
U
ParentA
U
Child
⋅
−
+
⋅
=
)
1
,
0
(
1
)
1
,
0
(
1
- arithmetical crossover:
U(0,1) uniformly distributed random scalar
GA operators: crossover methods
(
)
ParentA
U
ParentB
U
Child
⋅
−
+
⋅
=
)
1
,
0
(
1
)
1
,
0
(
2
[6.7 4.5 7.4 2.1]
[4.7 3.8 5.5 3.1]
[5.3 4.0 6.1 2.8]
parent A:
parent B:
child 1:
U(0,1) = 0.3
[6.7 4.5 7.4 2.1]
[4.7 3.8 5.5 3.1]
[6.1 4.3 6.8 2.4]
parent A:
parent B:
child 1:
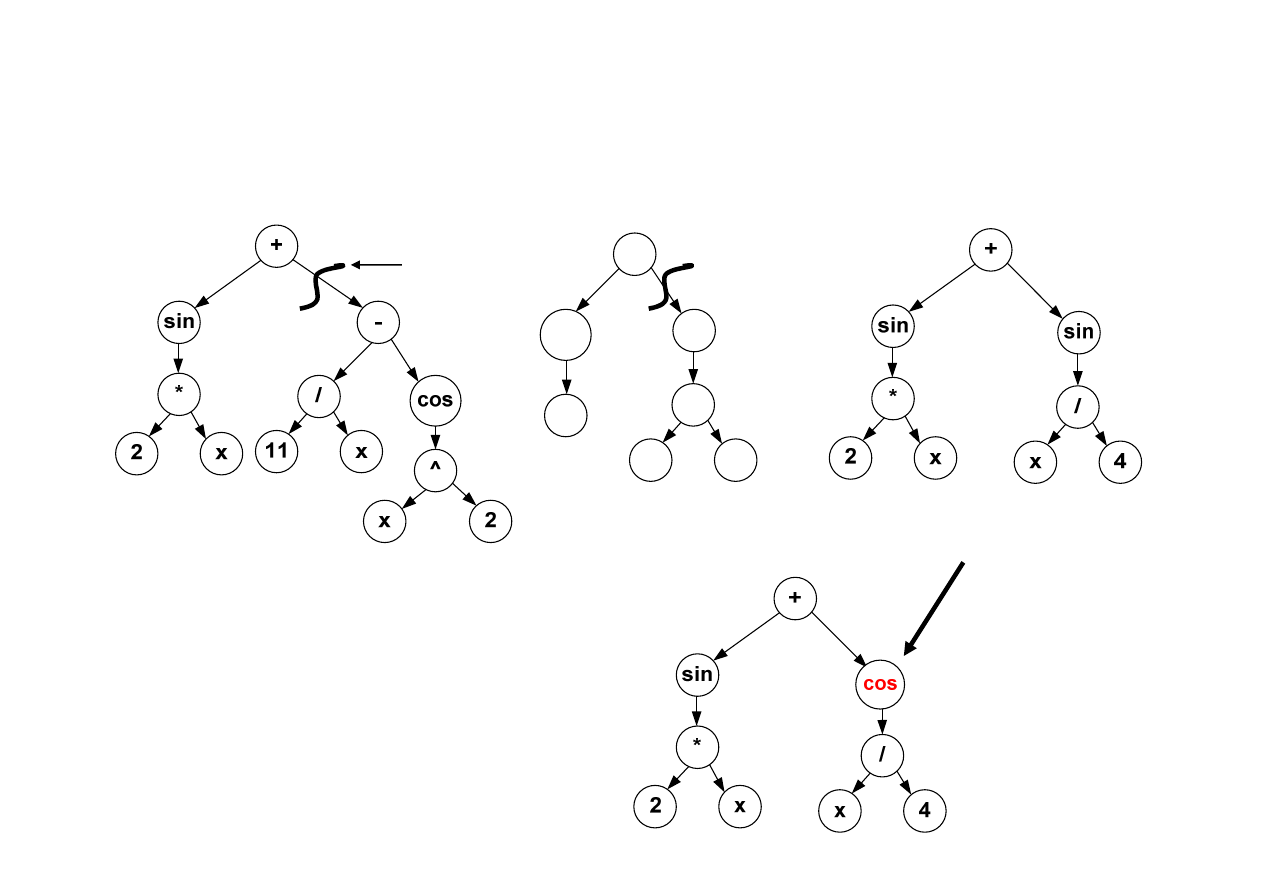
+
x
sin
/
cos
Parent A
Parent B
offspring
crossover point
+
=
GA operators: crossover methods
x
4
sin(2*x)+11/x-cos(x^2)
cos(x)+sin(x/4)
sin(2*x)+sin(x/4)
sin(2*x)+
cos
(x/4)
mutation
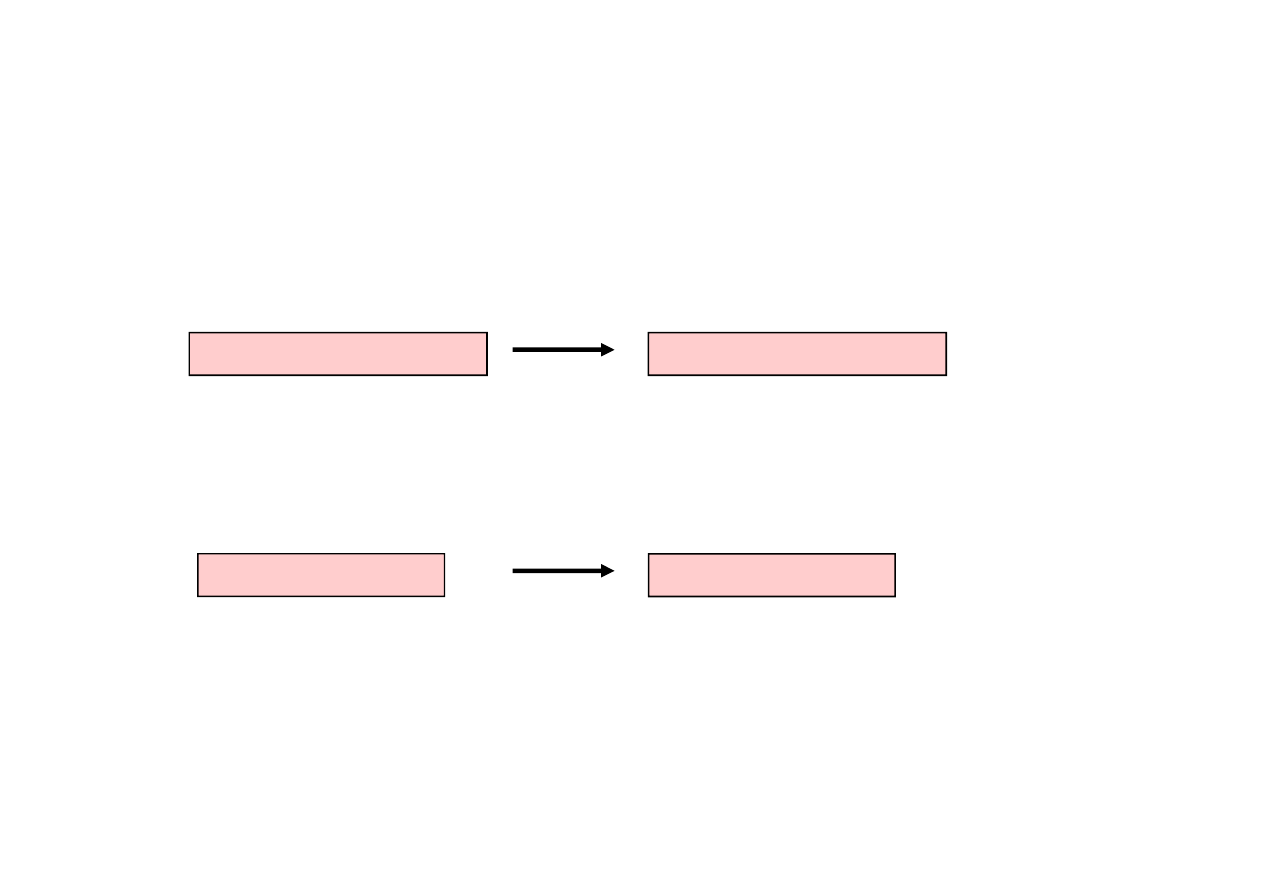
GA operators: mutation
Mutation – prevents falling all solutions in populations into a local
optimum of solved problem.
Bits inversion
1 1
0
1 1 1 0
1
1 1 1 1
1 1
1
1 1 1 0
0
1 1 1 1
offspring
mutation
Order changing
1 2
3
6 7 8
5
4 9
offspring
1 2
5
6 7 8
3
4 9
mutation

locus
locus
locus
Gene
U
Gene
Gene
⋅
+
=
)
1
,
0
(
'
- uniform mutation (mutacja jednorodna):
[6.7
4.5
7.4 2.1]
[6.1
5.8
6.8 2.4]
GA operators: mutation
Individual before mutation:
U(0,1) = 0.3
Individual after mutation:
locus
locus
locus
Gene
U
Gene
Gene
⋅
−
=
)
1
,
0
(
'
[6.7
4.5
7.4 2.1]
[6.1
3.2
6.8 2.4]
Individual before mutation:
U(0,1) = 0.3
Individual after mutation:

Selection methods:
Elitist selection
The most fit (the best fitness) members
of each generation
of each generation
are guaranteed to be selected.

Selection methods:
Roulette Wheel Selection
)
(x
f
y =
The fitness: maximum of the function
The fitness of N=6 chromosomes:
y = [1
40
4 2 6 3]
Probability(i) = y(i)/sum(y) * 100%
[2%
71%
7% 4% 11% 5%]
11%
2%
71%
7%
4%
11%
5%
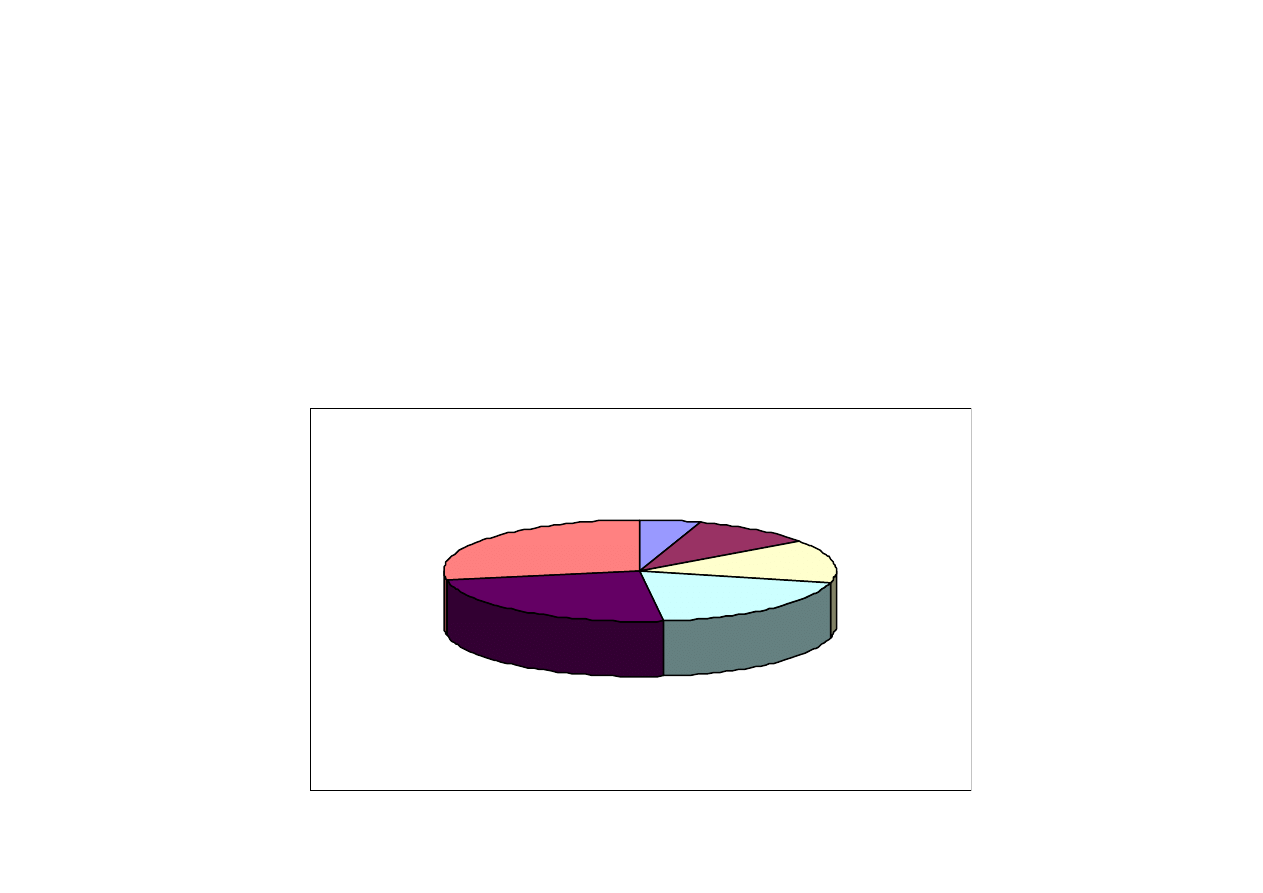
Selection methods:
Rank Selection
)
(x
f
y =
The fitness: maximum of the function
The fitness of N=6 chromosems:
y = [1 2 3 4 6
40
]
Probability(i) = n(i)/sum(n) * 100%
n = [1 2 3 4 5
6
]
[5% 10% 14% 19% 24%
28%
]
5%
10%
14%
19%
24%
28%

Selection methods:
Uniform Selection
The
N= 6
individuals are sorted from worst to the best:
n = [1 2 3 4 5 6 ]
U1(0,1)=[0.9 0.2 0.6 0.4 0.5 0.7]
The vectors of random scalars are generated:
U2(0,1)=[0.4 0.1 0.8 0.4 0.6 0.8]
The vectors of parents:
U1(0,1)*
6
= [5 1 4 2 3 4]
U2(0,1)=[0.4 0.1 0.8 0.4 0.6 0.8]
U2(0,1)*
6
= [2 1 5 2 4 5]
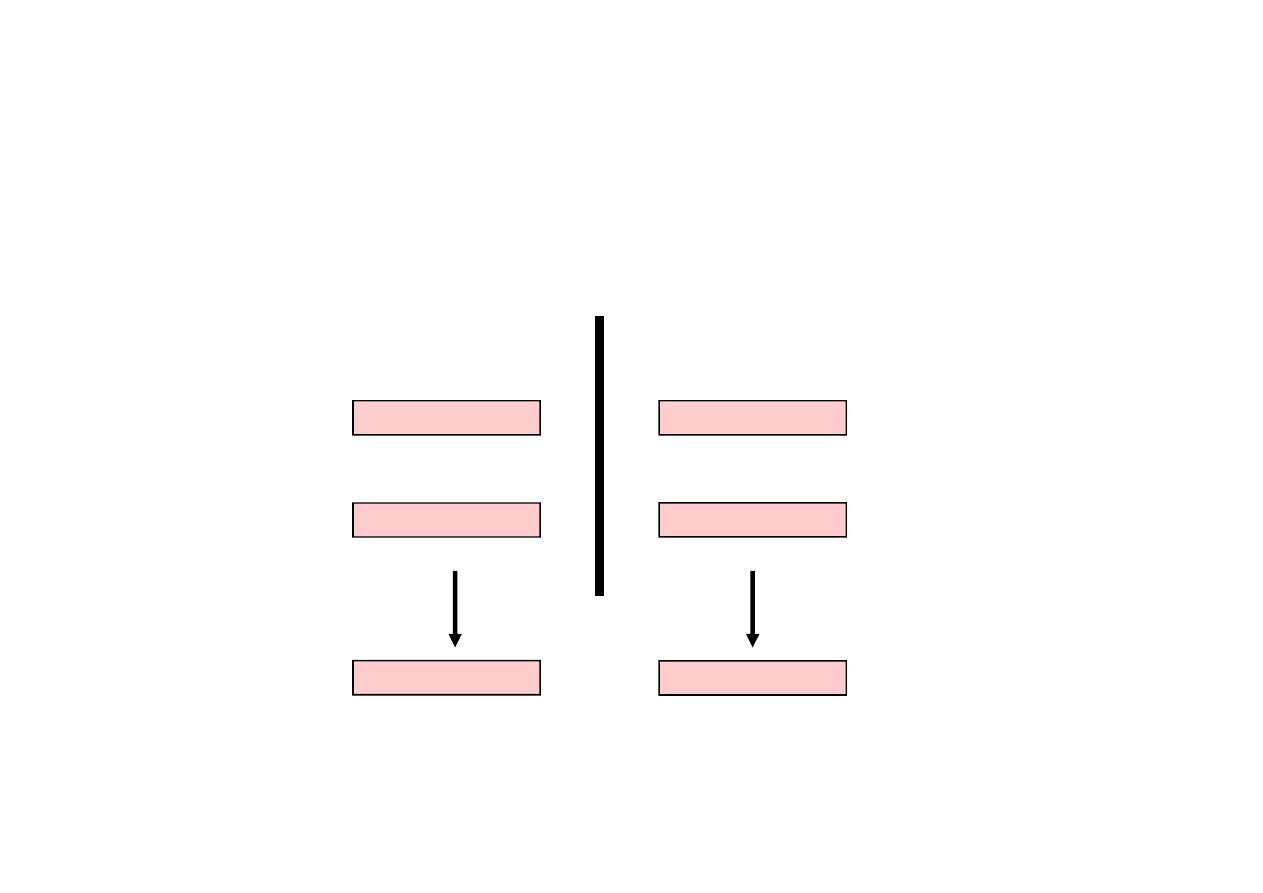
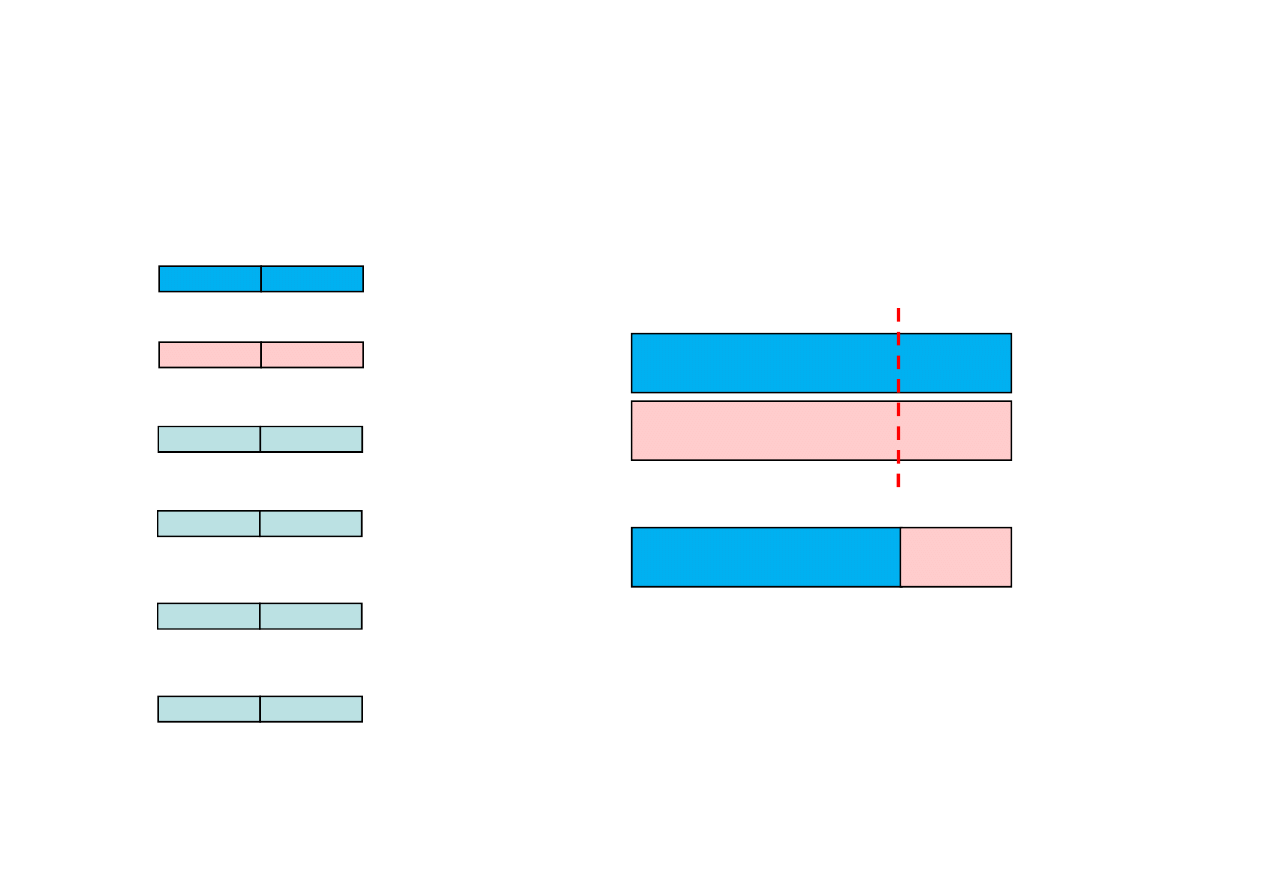
Selection methods:
Tournament Selection
)
(x
f
y =
The fitness: maximum of the function
The fitness of N=6 chromosems:
y = [1 40 4 2 6 3]
Chromosom 1
fitness: y = 1
Chromosom 3
fitness: y = 4
Tournament 1
Tournament 2
winner!
Chromosom 2
fitness: y = 40
Chromosom 4
fitness: y = 2
winner!
winner!
Chromosom 2
Chromosom 3
parents
Przykład: selekcja kołem ruletki
)
3
cos(
)
2
sin(
2
1
x
x
y
+
=
minimum funkcji:
0111001 1101111
0111001 1000101
1 0 0 1 0 0 1 0 1 0 1 1 1 1
30
.
0
)
68
.
19
,
14
.
16
(
2
1
−
=
=
=
x
x
f
bie
żą
ca populacja
1001001 0101111
5583
.
0
)
60
.
19
,
74
.
15
(
2
1
−
=
=
=
x
x
f
0 1 1 1 0 0 1 1 1 0 1 1 1 1
Parent A:
Parent B:
krzy
ż
owanie
jednopunktowe
1010111 0100101
0111001 1000101
0101111 1001101
0011001 0001101
18
.
1
)
37
.
16
,
14
.
16
(
2
1
=
=
=
x
x
f
27
.
1
)
45
.
16
,
21
.
19
(
2
1
=
=
=
x
x
f
73
.
1
)
00
.
17
,
60
.
19
(
2
1
=
=
=
x
x
f
39
.
1
)
92
.
16
,
98
.
15
(
2
1
=
=
=
x
x
f
0 1 1 1 0 0 1 1 1 0 1 1 1 1
1 0 0 1 0 0 1 0 1 0 1 1 1 1
Parent B:
Offspring:
5583
.
0
)
60
.
19
,
74
.
15
(
2
1
−
=
=
=
x
x
f
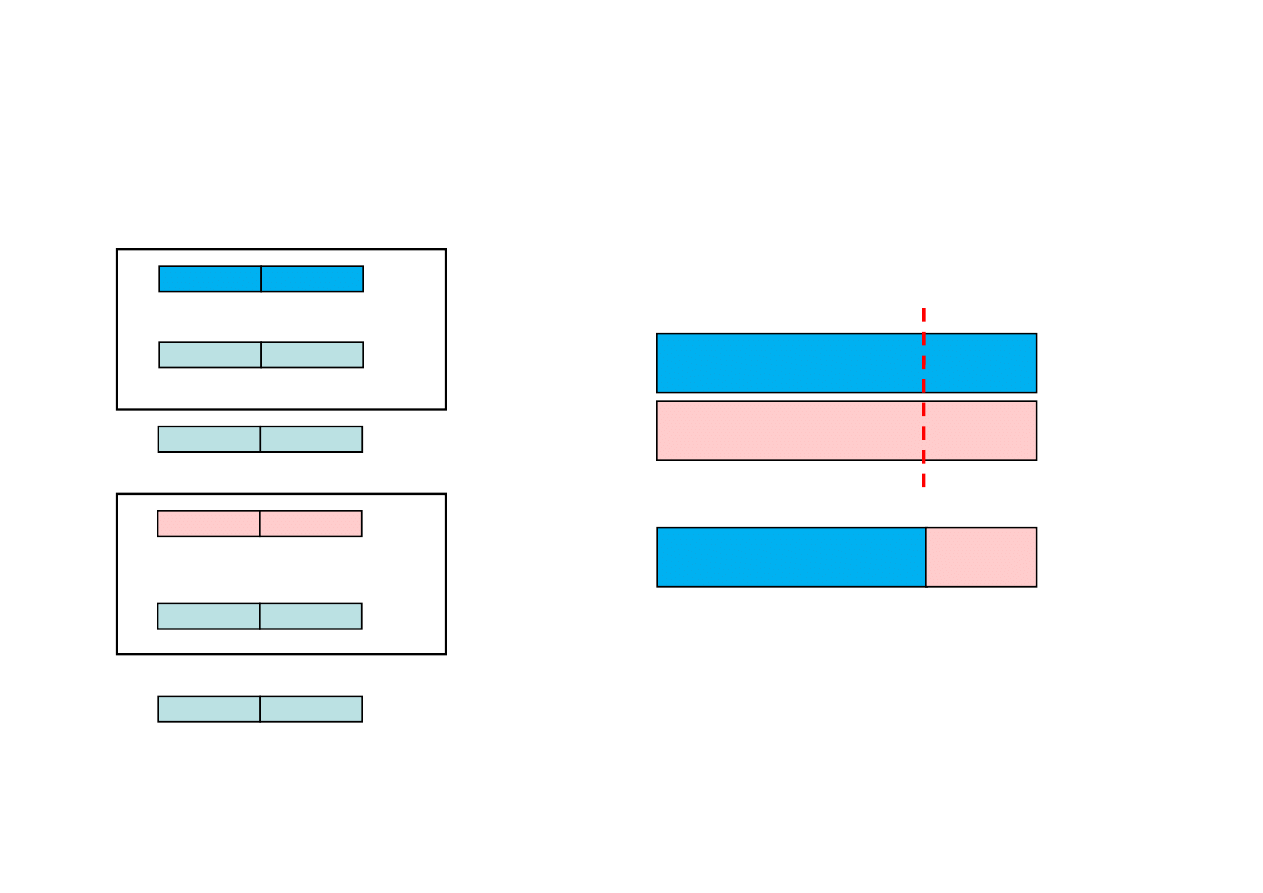
Przykład: selekcja turniejowa
)
3
cos(
)
2
sin(
2
1
x
x
y
+
=
minimum funkcji:
0111001 1101111
0111001 1000101
1 0 0 1 0 0 1 0 1 0 1 1 1 1
30
.
0
)
68
.
19
,
14
.
16
(
2
1
−
=
=
=
x
x
f
bie
żą
ca populacja
1001001 0101111
5583
.
0
)
60
.
19
,
74
.
15
(
2
1
−
=
=
=
x
x
f
1 0 1 0 1 1 1 0 1 0 0 1 0 1
Parent A:
Parent B:
krzy
ż
owanie
jednopunktowe
T
o
u
rn
a
m
e
n
t
1
1010111 0100101
0111001 1000101
0101111 1001101
0011001 0001101
18
.
1
)
37
.
16
,
14
.
16
(
2
1
=
=
=
x
x
f
27
.
1
)
45
.
16
,
21
.
19
(
2
1
=
=
=
x
x
f
73
.
1
)
00
.
17
,
60
.
19
(
2
1
=
=
=
x
x
f
39
.
1
)
92
.
16
,
98
.
15
(
2
1
=
=
=
x
x
f
1 0 1 0 1 1 1 0 1 0 0 1 0 1
1 0 0 1 0 0 1 0 1 0 0 1 0 1
Parent B:
Offspring:
69
.
0
)
45
.
16
,
74
.
15
(
2
1
=
=
=
x
x
f
T
o
u
rn
a
m
e
n
t
2
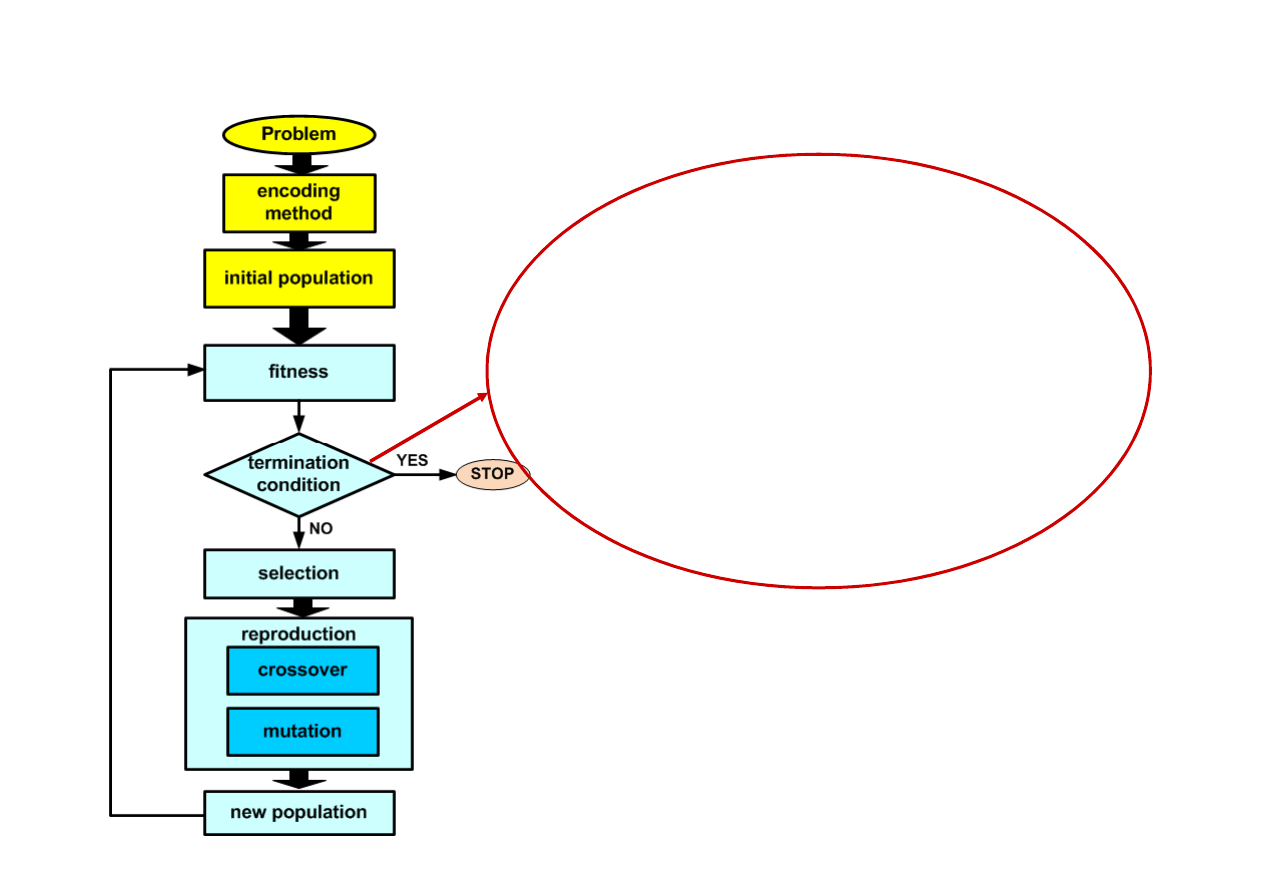
Termination condition
• a solution is found that satisfies
assumed criteria,
• fixed number of generations reached,
• allocate budjet reached (time),
• succesive iterations no longer produce
better results.
Wyszukiwarka
Podobne podstrony:
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
D20031152Lj id 130579 Nieznany
więcej podobnych podstron