
1
Ć
wiczenie 9
BADANIE WYTRZYMAŁOŚCI ZMĘCZENIOWYCH METALI
Opracował: dr inż. Maciej Kahsin
1. Wstęp
Obciążenie zmienne w czasie powoduje powstanie w materiale elementu
konstrukcyjnego zmiennego stanu naprężenia. Badania doświadczalne wykazują, że materiał
może ulec uszkodzeniu przy naprężeniu cyklicznym o wartości znacznie mniejszej od
wytrzymałości na rozciąganie R
m
, a nawet od granicy plastyczności R
e
. Zmęczeniem
materiału
określa się zmiany w materiale elementów konstrukcyjnych maszyn poddanych
działaniu obciążeń zmiennych w czasie, prowadzące do obniżenia wytrzymałości i w
konsekwencji do zniszczenia elementu konstrukcyjnego. Przebieg zmian obciążenia elementu
może mieć charakter okresowy, pseudookresowy jak i stochastyczny.
2. Cel ćwiczenia
Celem ćwiczenia jest zapoznanie się ze zjawiskiem zmęczenia materiału, wielkościami
opisującymi obciążenie i naprężenie cykliczne, z metodyką badań zmęczeniowych oraz z
urządzeniami do badań zmęczeniowych.
3. Podstawowe informacje o zmęczeniu materiałów
3.1. Fizykomechaniczne przyczyny zmęczenia materiałów
Na podstawie badań przyjmuje się, że główną przyczyną zmęczenia materiału są
mikropęknięcia, które propagują i łączą się w grupy pod wpływem obciążenia zmiennego w
czasie. W obszarze mikropęknięć powstaje lokalne spiętrzenie naprężeń, a po pewnym czasie
propagacja i łączenie się mikropęknięć przenosi się do skali makro. Proces postępuje tak
długo, aż osiągnięta zostanie pewna krytyczna długość pęknięcia, po której element
konstrukcyjny ulegnie gwałtownemu zniszczeniu. Makropęknięcia tworzą się najczęściej na
powierzchni materiału, tzn. tam gdzie występują słabsze ziarna materiału. Stan ten tłumaczy
się tym, że wewnętrzne ziarna materiału są powiązane z każdej strony, a ziarna na
powierzchni są powiązane jedynie „do wewnątrz”. Zniszczenie zmęczeniowe ma charakter
kruchy, gdyż nie pojawia się wyraźne odkształcenie plastyczne.
3.2. Złom zmęczeniowy
W przypadku metali, obserwując złom zmęczeniowy można wyróżnić dwie strefy
przełomu (rys. 1). Strefa pierwsza nazywa się strefą zniszczenia zmęczeniowego. Ma ona
często charakterystyczną gładką i błyszczącą (muszlową) powierzchnię. Strefa druga, bardziej
gruboziarnista, powstaje nagle w ostatnim etapie pracy elementu konstrukcyjnego. Tą część
przełomu nazywa się strefą doraźną. Strefa ta nie różni się zasadniczo od przełomów
uzyskiwanych w próbach statycznych.
Strefa pierwsza powstaje podczas stopniowego rozwoju pęknięcia zmęczeniowego. Obie
powierzchnie pęknięcia naciskają na siebie zgodnie z cykliczną zmianą obciążenia,
powodując jednoczesne wzajemne ścieranie i zgniatanie (stąd gładka i błyszcząca
powierzchnia strefy pierwszej). Stopień gładkości i pozornej drobnoziarnistości wzrasta wraz
ze wzrostem liczby cykli przeniesionych przez element, aż do całkowitego zniszczenia.

2
Rys. 1. Przełomy zmęczeniowe: a) z ogniskiem punktowym, b) z ogniskiem obwodowym
Stosunek udziału powierzchni strefy pierwszej do drugiej przełomu zmęczeniowego zwiększa
się wraz ze spadkiem wartości okresowo zmiennych naprężeń. Wraz ze wzrostem okresowo
zmiennych naprężeń stopień gładkości strefy pierwszej maleje. W strefie złomu
zmęczeniowego często można zauważyć wyraźne linie odpowiadające kolejnym położeniom
czoła pęknięcia. Linie te nazywane są liniami frontu szczeliny zmęczeniowej lub liniami
spoczynkowymi. Powstają one na skutek zatrzymywania się pęknięcia w jednej płaszczyźnie i
przeskoku do sąsiedniej płaszczyzny. Fakt ten można wytłumaczyć umocnieniem się
materiału w obszarze linii pęknięcia, gdy obciążenia zmęczeniowe zostaną na pewien czas
przerwane, a warunki fizykalne umożliwią odbudowę naruszonych ziaren w obszarze linii
spoczynkowej. Na podstawie układu linii spoczynkowych można ustalić ognisko (miejsce
zapoczątkowania złomu zmęczeniowego), jak i sposobu jego rozprzestrzeniania się.
3.3. Wielkości wpływające na zmęczenie materiału
Zmęczenie materiałów zależy od wielu czynników. Główne z nich to:
•
lokalne spiętrzenie naprężeń (zjawisko karbu),
•
stan powierzchni i warstwy powierzchniowej,
•
wady materiału (pęcherze, duże wtrącenia niemetaliczne, itp.),
•
efekt skali,
•
krótkotrwałe przeciążenia.
Wpływ powyższych czynników zostanie przedstawiony szerzej w dalszej części instrukcji.
4. Obciążenia i naprężenia zmienne w czasie
Zmienny stan obciążenia oddziaływujący na element konstrukcyjny wywołuje w nim
zmienny stan naprężenia. Jednym z najprostszych do przeanalizowania przypadków
obciążenia zmiennego w czasie jest osiowe rozciąganie lub/i ściskanie prostoosiowego pręta
pryzmatycznego siłą harmoniczną. Wartość siły wewnętrznej można opisać zależnością:
]
[
)
sin(
)
(
N
t
N
N
t
N
a
m
ω
+
=
,
(1)
gdzie: N
m
– średnia (stała) wartość normalnej siły wewnętrznej [N], N
a
– amplituda normalnej
siły wewnętrznej [N], ω – częstotliwość kołowa [s
−1
], t – czas [s].
Wykorzystując wielkość ω można określić okres zmian T oraz ich częstotliwość f ze
związków:
π
ω
2
1
=
=
T
f
,
(2)
W zależności od wartości sił N
m
i N
a
wzór (1) może opisywać w trakcie jednego cyklu
jednoosiowe ściskanie (N(t) ≤ 0), jednoosiowe rozciąganie (N(t) ≥ 0), lub rozciąganie i
ś
ciskanie, (N(t) zmienia znak w trakcie cyklu). Aby wyznaczyć zmianę naprężeń w
opisywanym przypadku rozciągania lub ściskania, wystarczy podzielić wzór (1) przez pole
przekroju poprzecznego pręta A, otrzymując zależność:
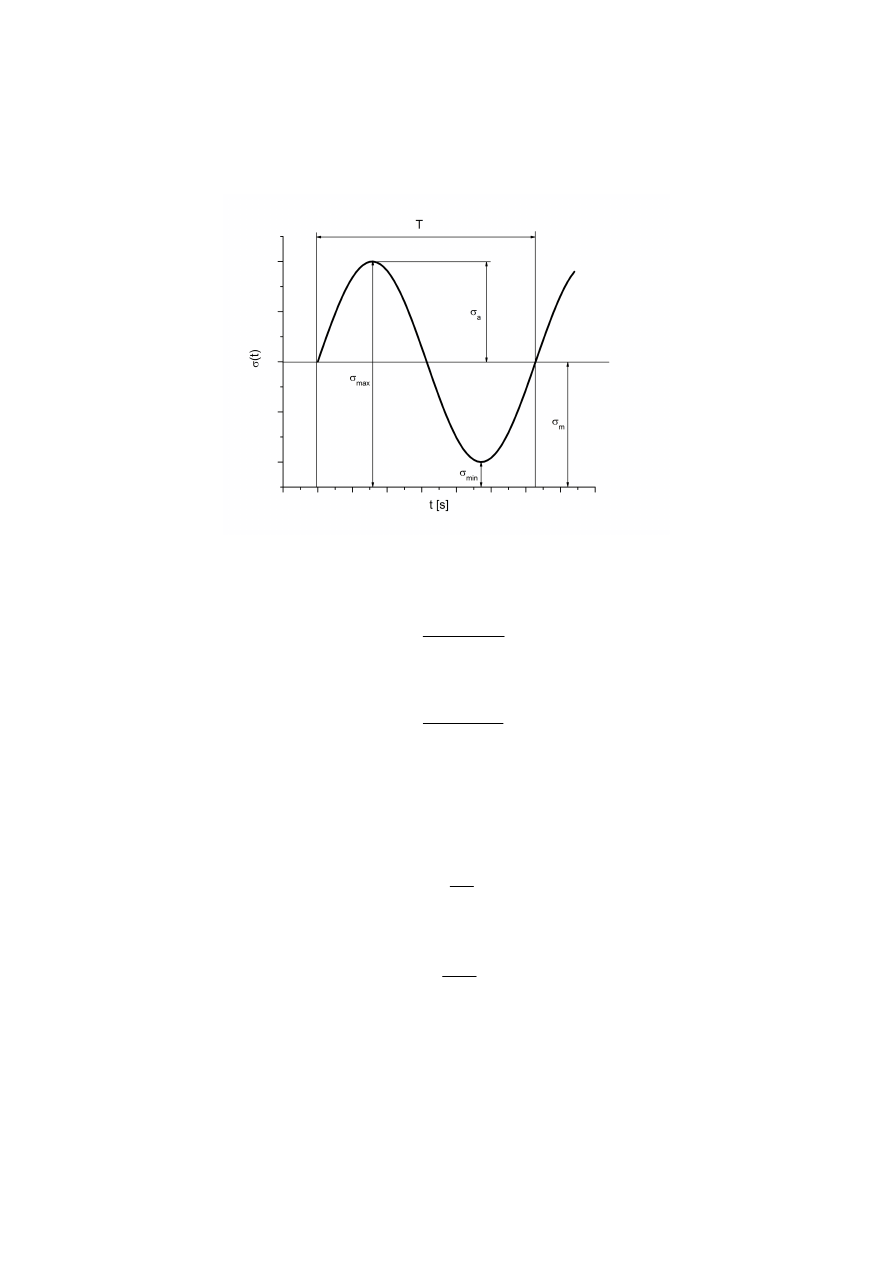
3
]
[
)
sin(
)
(
Pa
t
t
a
m
ω
σ
σ
σ
+
=
,
(3)
gdzie: σ
m
– średnia (stała) wartość naprężenia normalnego [Pa], σ
a
– amplituda naprężenia
normalnego [Pa].
Rys. 2. Przebieg zmiany naprężenia normalnego w trakcie osiowego rozciągania lub/i ściskania
Posługując się oznaczeniami z rys. 2 można wyznaczyć zależności:
− wartość naprężenia średniego (stałego):
2
min
max
σ
σ
σ
+
=
m
,
(4)
− wartość amplitudy naprężenia:
2
min
max
σ
σ
σ
−
=
a
,
(5)
− wartość maksymalna i minimalna naprężenia:
a
m
σ
σ
σ
±
=
min
max/
.
(6)
Dodatkowo w oparciu o wartości naprężenia średniego, amplitudowego, maksymalnego i
minimalnego definiowane są, współczynnik stałości obciążenia:
a
m
σ
σ
χ
=
(7)
oraz współczynnik amplitudy cyklu:
max
min
σ
σ
=
R
.
(8)
Wykorzystując definicje współczynnika stałości cyklu (7) i współczynnika amplitudy cyklu
(8) można wyróżnić następujące cykle:
1) cykl jednostronny dodatni, gdy: 0 < R < 1, 1 < χ < +∞ (tzn. rozciąganie σ
max
> 0,
σ
min
> 0, σ
m
> 0),
4
2) cykl tętniący dodatni, gdy: R = 0, χ = 1 (tzn. odzerowe rozciąganie σ
max
> 0,
σ
min
= 0,
2
max
σ
σ
=
m
),
3) cykl dwustronny dodatni, gdy:
−1 < R < 0, χ = 1 (tzn. rozciąganie (dominujące) i
ś
ciskanie σ
max
> 0, σ
min
< 0, σ
max
> |σ
min
|, σ
m
> 0),
4) cykl wahadłowy, gdy: R =
−1, χ = 0 (tzn. symetryczne rozciąganie i ściskanie,
σ
max
= +σ
a
, σ
min
=
−σ
a
, σ
m
= 0),
5) cykl dwustronny ujemny, gdy:
−∞ < R < −1, −1 < χ < 0 (tzn. rozciąganie i ściskanie
(dominujące) σ
max
> 0, σ
min
< 0, σ
max
< |σ
min
|, σ
m
< 0),
6) cykl tętniący ujemny, gdy: R = −∞, χ =
−1 (tzn. odzerowe ściskanie σ
max
= 0,
σ
min
< 0,
2
min
σ
σ
=
m
),
7) cykl jednostronny ujemny, gdy: 1 < R < +∞,
−∞ < χ < −1 (tzn. ściskanie σ
max
< 0,
σ
min
< 0, σ
m
< 0).
Przedstawiony powyżej opis można uogólnić na przypadki zginania, skręcania i ścinania,
oraz ich dowolną kombinację zgodnie z zasadami przedstawionymi na wykładzie z
wytrzymałości materiałów. Zagadnienia dotyczące stochastycznych przebiegów obciążenia i
naprężenie nie będą tu rozpatrywane.
5. Wyznaczanie wytrzymałości zmęczeniowej (Wykres Wöhlera
−
−
−
−
krzywa S
−
−
−
−
N
materiału)
Przy obliczeniach wytrzymałościowych elementów konstrukcyjnych pracujących pod
zmiennym w czasie obciążeniem, konieczna jest znajomość pewnych danych, które można
wyznaczyć na podstawie odpowiednich badań laboratoryjnych. Typowe badania
zmęczeniowe przeprowadza się na serii jednakowych próbek, wykonanych z tego samego
materiału. Zaleca się, aby materiał był nie tylko z tego samego wytopu, ale nawet z tego
samego wlewka. Warunki przeprowadzania badań zawarte są w normach: PN
−74/H−04327 i
PN
−76/H−04325. W zależności od wyznaczanych parametrów próbki powinny być jak
najprostsze (wyznaczenie wskaźników zmęczeniowych materiału) lub jak najlepiej
odwzorowujące
kształt
elementu
konstrukcyjnego
(wyznaczenie
wytrzymałości
zmęczeniowej elementu konstrukcyjnego). Kształt próbek nie jest zwykle normalizowany,
wyjątek stanowią niektóre próbki do zmęczeniowej próby obrotowego zginania opisane w
PN
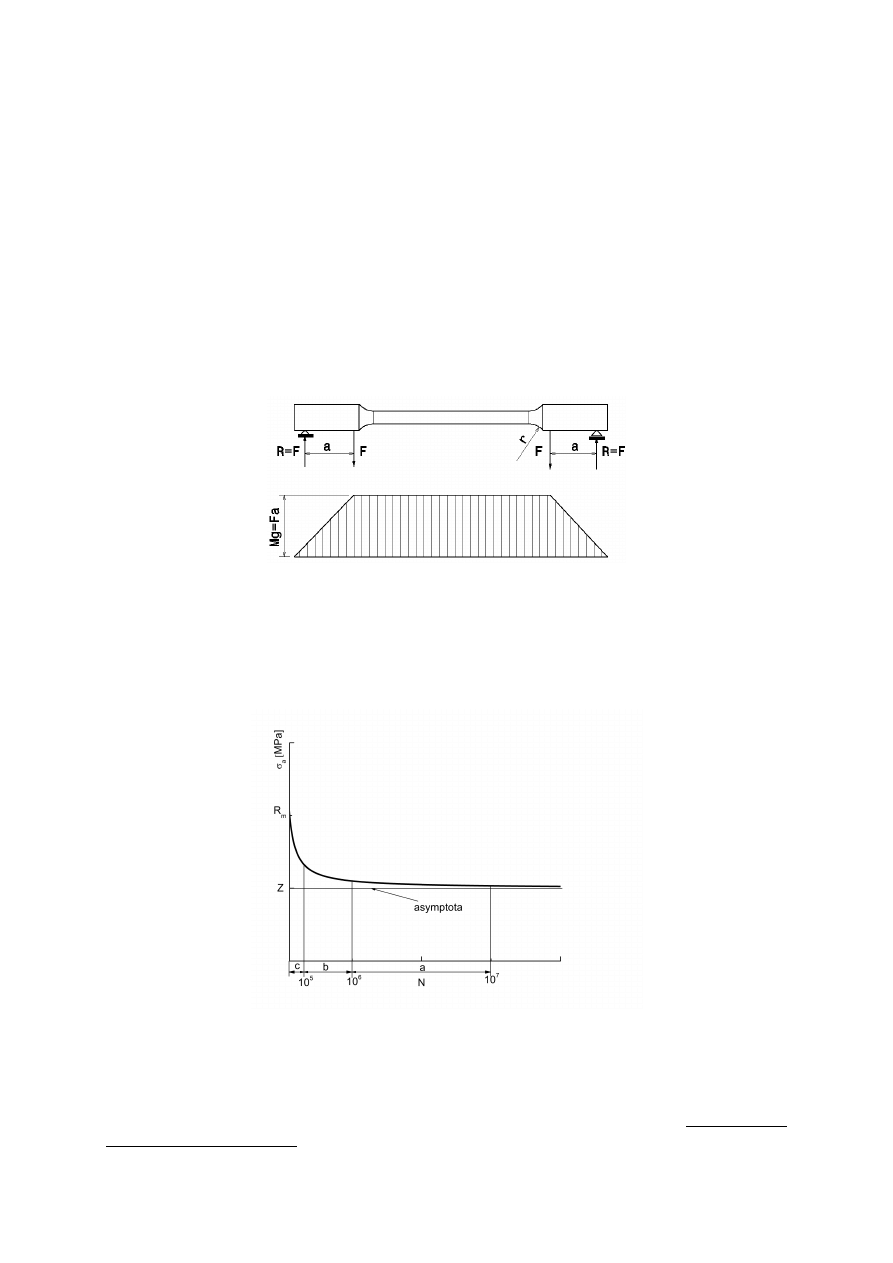
−76/H−04325 (rys. 3).
Rys. 3. Próbki do zmęczeniowej próby obrotowego zginania
Rodzaj
karbu
D
[mm]
d
[mm]
r
[mm]
t
[mm]
ω
[˚]
V
10
5
0,5:0,25
2,5
67˚30'
V
15
7,5
0,5:0,25
3,75
58˚30'
V
20
10
0,5:0,25
5
51˚52'
U
6
5
0,5
−
U
9
7,5
0,75
−
U
12
10
1
−
5
Najczęściej przeprowadzane próby zmęczeniowe to: rozciąganie i/lub ściskanie, zginanie,
skręcanie lub jakiejkolwiek kombinacji tych podstawowych sposobów obciążenia.
Ze względu na techniczną łatwość realizacji najczęściej wykonywaną próbą
zmęczeniową jest próba zginania (tzw. klasyczna próba zmęczeniowa). Schemat obciążenia
stosowany w tej próbie przedstawiono na rys. 4. Próbkę obciążoną statycznie wprawia się w
ruch obrotowy. Wówczas górne włókna próbki poddane są ściskaniu, a dolne rozciąganiu.
Przejście od rozciągania do ściskania odbywa się w trakcie jednego cyklu (cykl wahadłowy,
R
=
−1, χ = 0, σ
max
= +σ
a
, σ
min
=
−σ
a
, σ
m
= 0). Minimalna ilość próbek wykorzystanych w
trakcie badania powinna wynosić od 8 do 12 sztuk. Pierwsze przyłożone obciążenie powinno
wywoływać naprężenia maksymalne poniżej wartości R
m
. Kolejne próbki obciąża się tak, aby
osiągnąć mniejsze wartości obciążenia maksymalnego przy jednoczesnym zwiększeniu ilości
cykli do zniszczenia. Po przeprowadzonych próbach tworzony jest wykres σ
a
= f(N) (rys.5)
(tzw. wykres Wöhlera, lub krzywa S
−N).
Rys. 4. Schemat obciążenia próbki przy zmęczeniowej próbie zginania
Na podstawie wykresu (rys. 5) odczytuje się wartość nieograniczonej wytrzymałości
zmęczeniowej, lub inaczej
− rzeczywistej granicy zmęczenia Z
*
(* oznacza odpowiednie
oznaczenie literowe zależne od przypadku obciążenia zgodnie z tab.1 normy PN-76/H-04325.
W przypadku opisanej próby jest to Z
go
).
Rys. 5. Wykres Wöhlera
Wartość asymptotyczna naprężenia Z wyznacza asymptota (rys. 5). W praktyce wystarczającą
dokładność odczytu dla stali konstrukcyjnych stanowi wartość naprężenia dla liczby cykli
równej N = 10
7
, a dla metali i stopów nieżelaznych N = (2-10)·10
7
(np. stopy Al, Cu, dla
których na wykresie S
−N nie istnieje asymptota). Jest to tak zwana wytrzymałość
zmęczeniowa ograniczona.
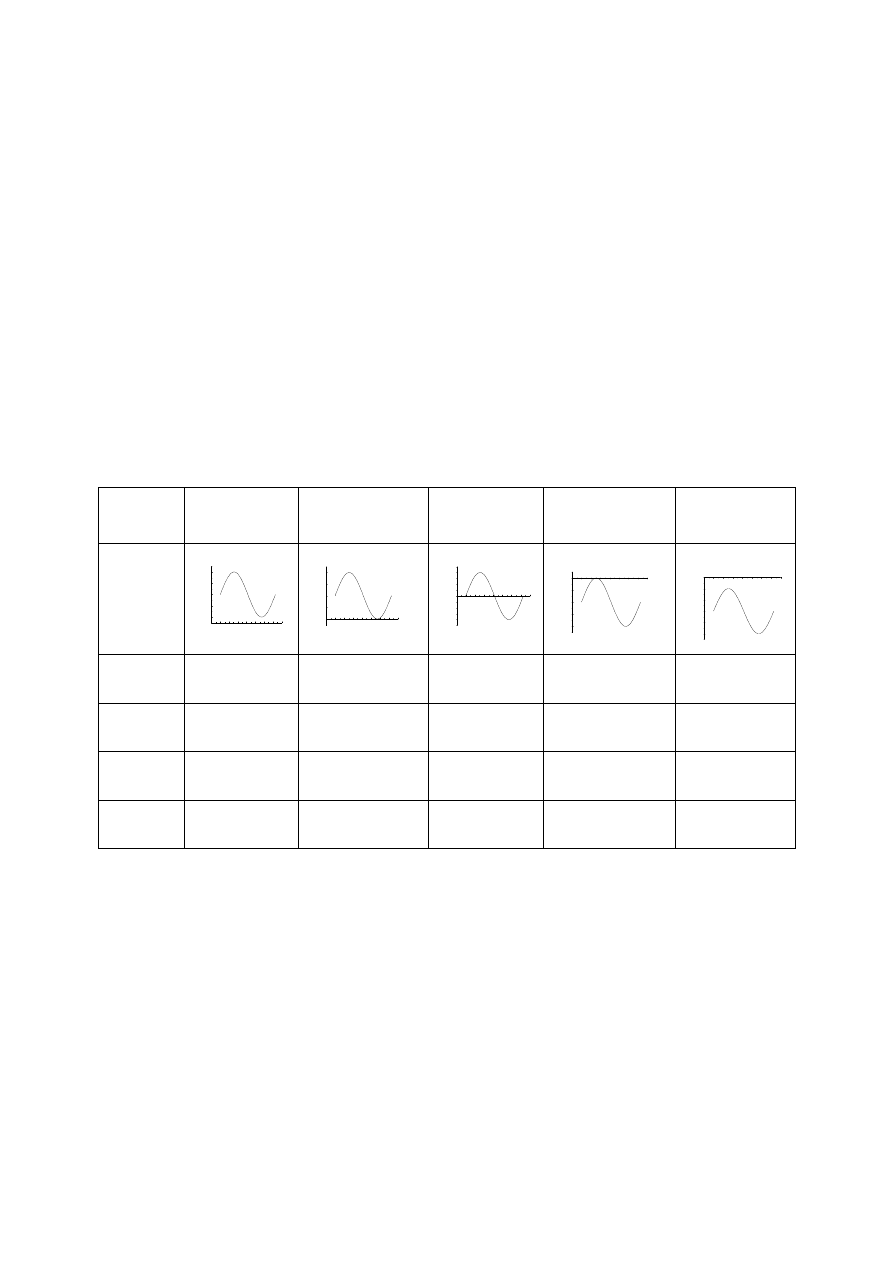
6
Na wykresie można wyróżnić trzy obszary:
− przedział właściwych przełomów zmęczeniowych (a),
− przedział przedwczesnych przełomów zmęczeniowych (b), nazywany również
zmęczeniem wysokocyklowym, gdy naprężenia są na tyle małe, że można pominąć
odkształcenia plastyczne,
− przedział przełomów okresowego przeciążenia (c), inaczej zwane zmęczeniem
niskocyklowym, zazwyczaj w zakresie N 10
2
÷10
4
i zwykle wiąże się ze znacznym
odkształceniem plastycznym.
6. Wyznaczanie wytrzymałości zmęczeniowej przy cyklach niesymetrycznych
(Wykres Smitha, wykres Haigha)
Dla innych przypadków obciążenia schemat uzyskania krzywej Wöhlera i odpowiedniej
wartości zmęczeniowej Z
*
przebiega w podobny sposób jak dla obustronnego zginania, przy
czym w trakcie prób utrzymywana jest stała wartość σ
m
(tj. zmienia się tylko wartość σ
a
).
Przebieg cykli oraz oznaczenia dla różnego rodzaju obciążenia przedstawiono w tab.1.
Tablica 1. Oznaczenia wytrzymałości zmęczeniowej w zależności od rodzaju cyklu i obciążenia
Cykl
jednostronny −
dodatni
odzewowo tętniący
−dodatni
wahadłowy
odzewowo tętniący
−ujemny
jednostronny − ujemny
Przebieg w
czasie
σ
lu
b
τ
t
σ
lu
b
τ
t
σ
lu
b
τ
t
σ
lu
b
τ
t
σ
lu
b
τ
t
Rozciąganie
Z
r
Z
rj
Z
rc
−
−
Ściskanie
−
−
Z
rc
Z
cj
Z
c
Zginanie
Z
g
Z
gj
Z
go
Z
gj
Z
g
Skręcanie
Z
s
Z
sj
Z
so
Z
sj
Z
s
Pomimo tego, że wytrzymałość zmęczeniowa jest stałą materiałową, to zależy ona
również od sposobu obciążenia. Np. dla cyklu obustronnego wytrzymałość przy zginaniu jest
o 15% do 30% wyższa niż przy rozciąganiu. Z badań laboratoryjnych wynikają zależności:
so
sj
rc
rj
go
gj
go
so
go
ro
Z
,
Z
Z
,
Z
Z
,
Z
Z
,
Z
Z
,
Z
⋅
≈
⋅
≈
⋅
≈
⋅
≈
⋅
≈
5
1
5
1
5
1
57
0
7
0
(9)
7
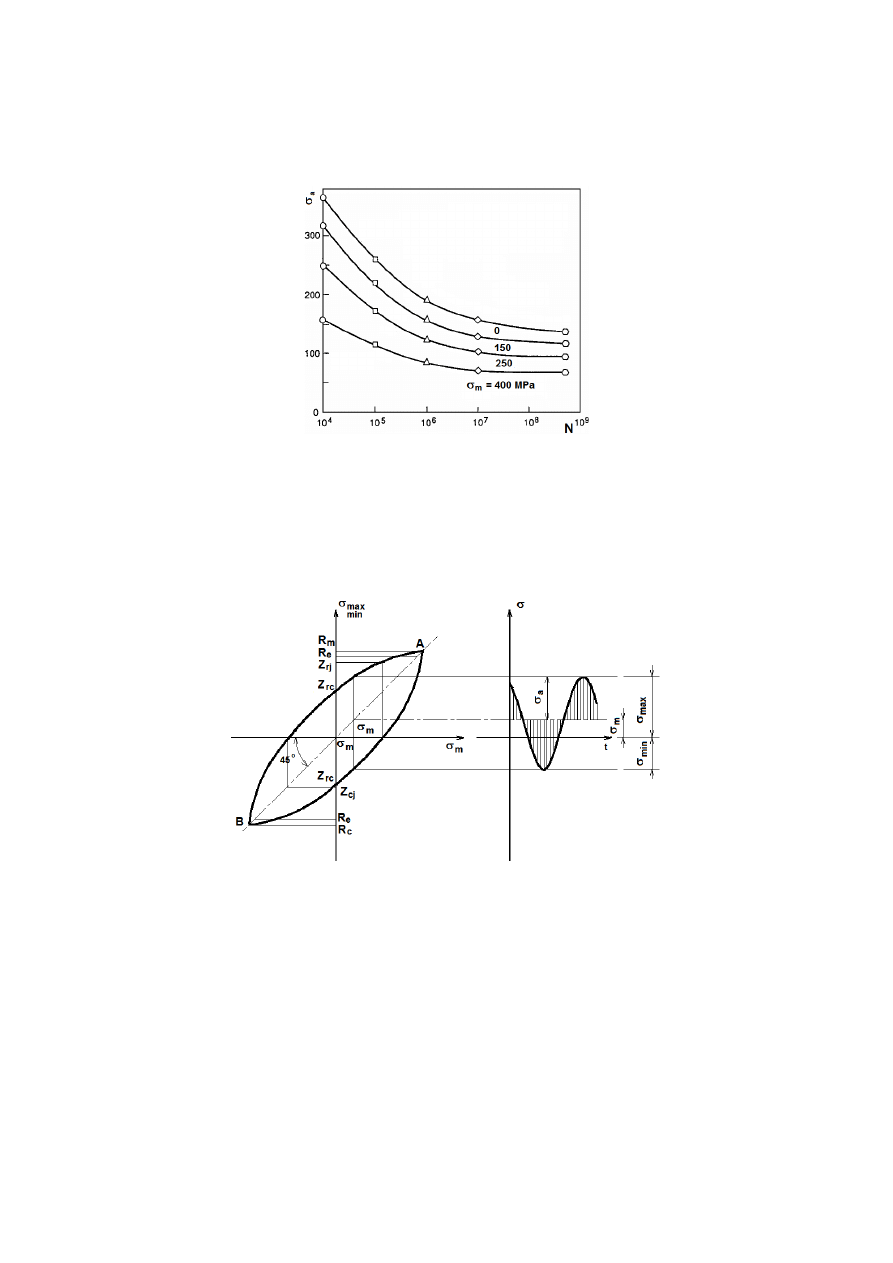
Badania wykazują, że istnieje wpływ wielkości naprężeń średnich na wartość
wytrzymałości zmęczeniowej. Dla większych wartości σ
m
(rys. 6) następuje obniżenie
wartości wytrzymałości zmęczeniowej.
Rys. 6. Krzywe S
−N stali konstrukcyjnej dla σ
m
= const przy rozciąganiu
Wyniki pomiarów przeprowadzonych dla σ
m
= const umożliwiają wyznaczenie wartości σ
min
,
σ
max
(dla danego σ
m
), przy których nie nastąpi zniszczenie próbki, a ich zestawienie można
zaprezentować w postaci wykresu Smitha (rys. 7). Wykres wykonywany jest we
współrzędnych σ
m
, σ
max/min
. Krzywe BA i AB wyznaczają odpowiednio maksymalną i
minimalną wartość naprężenia zmiennego dla danej wartości σ
m
.
Rys. 7. Wykres Smitha
Istnieje możliwość wykreślenia uproszczonego wykresu Smitha, który w przeciwieństwie do
pełnego wykresu Smitha nie wymaga przeprowadzenie dużej liczby kosztownych i
długotrwałych prób laboratoryjnych. Do konstrukcji wykresu uproszczonego wystarczy
znajomość wytrzymałości na rozciąganie R
m
, granicy plastyczności R
e
, oraz wytrzymałości
zmęczeniowej dla cyklu wahadłowego Z
rc
. Dodatkowo dla materiałów o symetrycznych
charakterystykach wytrzymałościowych, np. takich jak stale konstrukcyjne, wystarczy
wykreślenie połówki wykresu uproszczonego (tj. dla σ
m
≥ 0). Konstrukcję uproszczonego
wykresu Smitha przedstawiono na rys. 8. Z punktu widzenia obliczeniowych zastosowań
praktycznych, w większości przypadków dokładność uzyskana za pomocą odczytu z
uproszczonego wykresu Smitha jest wystarczająca i dlatego w praktyce można użyć tego
wykresu
do
wyznaczenia
przybliżonej
wartości
zmęczeniowego
współczynnika
bezpieczeństwa.
8
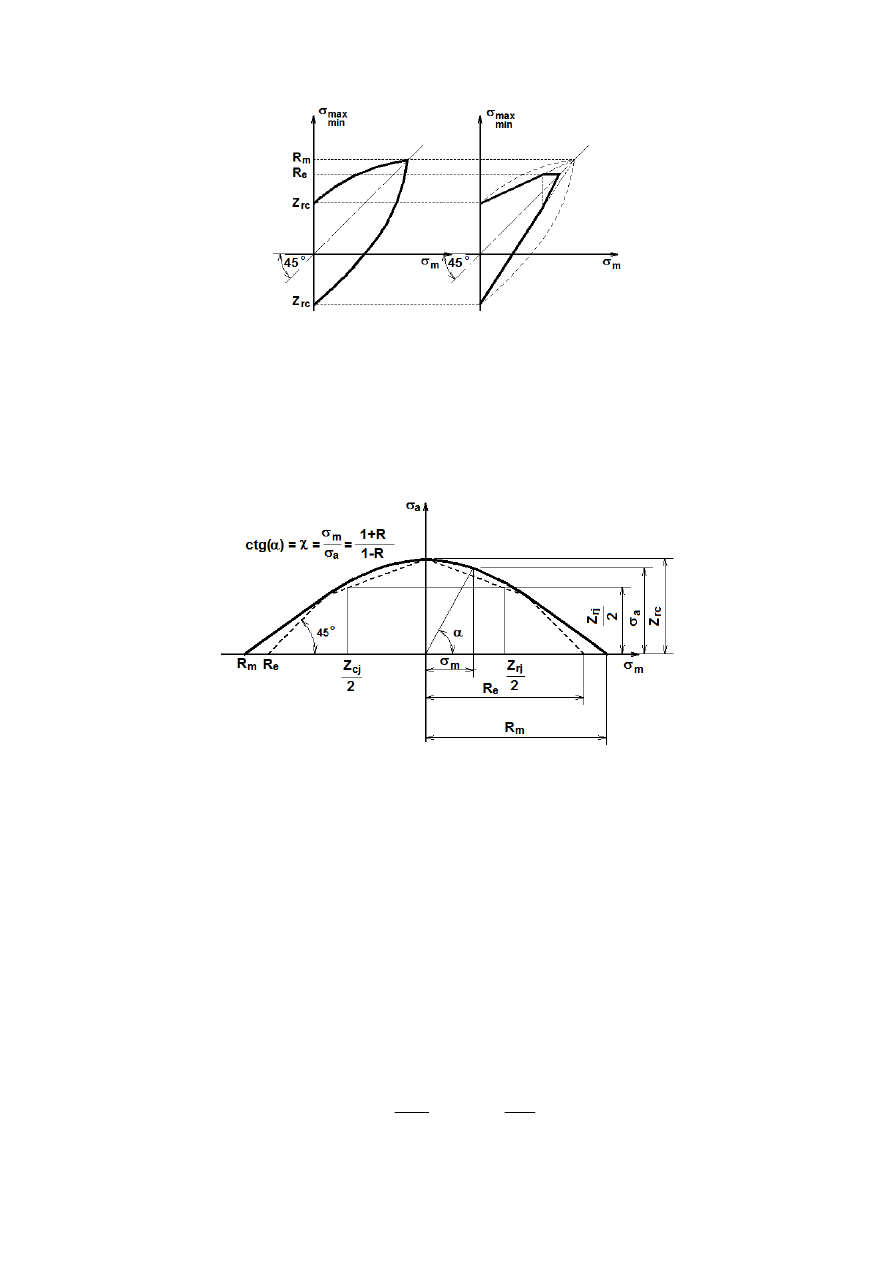
Rys. 8. Uproszczony wykres Smitha
Prostszy w konstrukcji od wykresu Smitha oraz umożliwiający łatwiejszą analizę
wytrzymałościową doboru naprężeń dopuszczalnych jest wykres Haigha (rys. 9). Każdemu
punktowi na krzywej odpowiada określona wartość współczynnika stałości obciążenia (7).
Podobnie jak wykres Smitha, wykres Haigha może zostać uproszczony, obrazuje to linia
przerywana na rys. 8. Wykres Haigha powstaje z części wykresu Smitha (rys. 8) obróconego
o 45
o
.
Rys. 9. Pełny i uproszczony (linie przerywane) wykres Higha
7. Zjawiska wpływające na zmęczenie materiału
Jak już wspomniano w punkcie trzecim, wytrzymałość zmęczeniowa elementu
konstrukcyjnego może zależeć od szeregu czynników. Poniżej omówione zostaną niektóre z
nich. Należy pamiętać, że w trakcie eksploatacji maszyn często dochodzi do nałożenia się
szeregu zjawisk wpływających na trwałość zmęczeniową danego elementu konstrukcyjnego.
7.1. Wpływ karbu
Uwzględnienie zjawiska karbu (koncentracji naprężeń) dla elementów konstrukcyjnych
działających pod zmiennym obciążeniem jest bardzo istotne. Dla niektórych prędkości zmian
naprężeń w elemencie konstrukcyjnym obserwuje się przesunięcie granicy plastyczności w
okolice granicy wytrzymałości na rozciąganie. Oznacza to, że materiał plastyczny może ulec
kruchemu pękaniu. Teoretyczny wpływ zjawiska karbu opisywany jest współczynnikiem
kształtu
α
k
definiowanym jako:
n
k
σ
σ
α
max
=
lub
n
k
τ
τ
α
max
=
(10)
9
gdzie:
σ
max
,
τ
max
– największe naprężenie związane z istnieniem zmiany kształtu przedmiotu,
σ
n
,
τ
n
– naprężenie nominalne obliczone za pomocą konwencjonalnych wzorów
wytrzymałościowych dla najbardziej osłabionego pola przekroju przedmiotu.
Doświadczenie pokazuje, że w rzeczywistości materiały nie są tak wrażliwe na zjawisko
karbu, jakby to wynikało z wartości współczynnika
α
k
.
W przypadku określania wpływu
koncentracji naprężeń na wytrzymałość zmęczeniową wprowadza się tzw. zmęczeniowy
współczynnik działania karbu lub krócej – współczynnik działania karbu
β
k
definiowanym
jako:
k
bk
k
Z
Z
=
β
,
(11)
gdzie: Z
bk
– wytrzymałość zmęczeniowa próbek gładkich bez karbu, Z
k
– wytrzymałość
zmęczeniowa próbek gładkich z karbem.
Współczynniki
α
k
i
β
k
określają tzw. współczynnik wrażliwości materiału na działanie karbu
lub krócej – współczynnik wrażliwości
η
definiowanym jako:
1
1
−
−
=
k
k
α
β
η
,
(12)
Dla materiałów o liniowej i idealnie sprężystej charakterystyce materiałowej
α
k
=
β
k
, więc
η
= 1 (np. szkło). Dla materiałów niewrażliwych na zjawisko karbu
β
k
= 1, więc
η
= 0 (np.
ż
eliwo szare). Dla większości stali konstrukcyjnych
η
∈(0,6 ÷ 0,8), przy czym większe η mają
stale o dużej wytrzymałości.
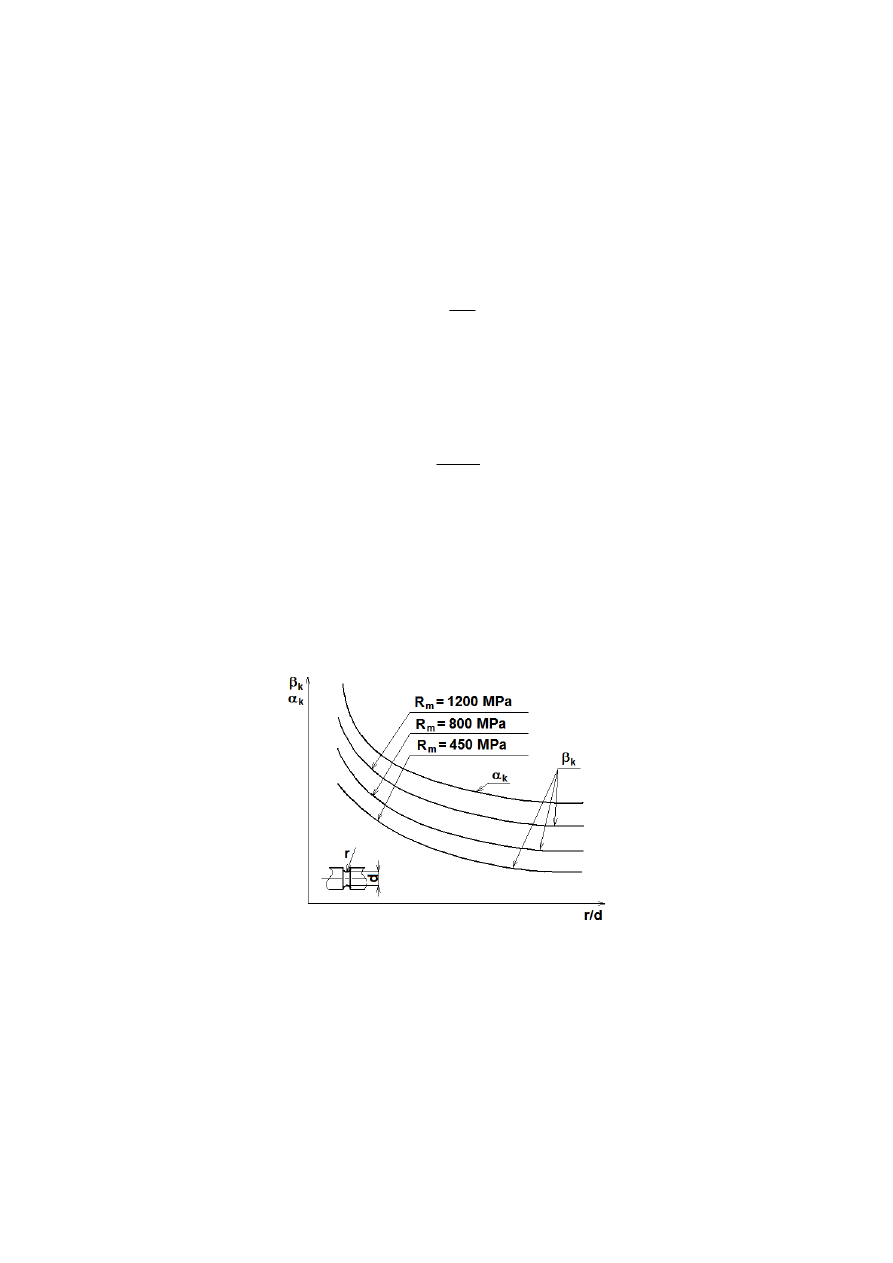
Na rys. 10 przedstawiono przebieg wartości współczynników
α
k
i
β
k
w zależności od
rozmiaru karbu dla próbek cylindrycznych wykonanych ze stali i próby obrotowego zginania.
Jak widać zawsze
α
k
>
β
k
, a materiały o większej wytrzymałości są bardziej wrażliwe na
działanie karbu.
Rys. 10. Wartość współczynników
α
k
i
β
k
w zależności od rozmiaru karbu dla próbek cylindrycznych
wykonanych ze stali i próby obrotowego zginania
7.2. Wpływ działania środowiska korozyjnego
Zjawiska zmęczenia korozyjnego wynikają na skutek działania korozji i zmiennych
naprężeń. Zmienne naprężenia w środowisku korozyjnym powodują powstanie ostrych
wżerów wypełnionych produktami korozji. Korozja zmęczeniowa prowadzi do znacznego
obniżenia wytrzymałości zmęczeniowej. Dla stali i agresywnego środowiska ciekłego
wytrzymałość zmęczeniowa maleje 1,5 do 10 razy. Przy zmęczeniu korozyjnym krzywa
zmęczenia przybiera charakterystyczny wygląd przedstawiony na rys. 11. Jak widać nie
istnieje asymptota, do której dąży wartość naprężenia wraz ze wzrostem liczby cykli.

10
Wielkością charakteryzującą wpływ środowiska na wytrzymałość zmęczeniową stali jest tzw.
współczynnik odporności cyklicznej
β
wyrażany w procentach i definiowany jako:
%
100
⋅
=
BP
B
Z
Z
β
,
(13)
gdzie: Z
B
– granica zmęczenia w danym środowisku, Z
BP
– granica zmęczenia w powietrzu.
Korozja zmęczeniowa może być silnie związana z temperaturą pracy danego elementu
konstrukcyjnego ze względu na zmianę aktywności środowiska korozyjnego w zależności od
temperatury.
Badanie korozji zmęczeniowej przebiega na podobnych stanowiskach jak w przypadku
badań zmęczenia materiałów w powietrzu. Wprowadzane są jedynie adaptacje umożliwiające
umieszczenie próbki w środowisku korozyjnym.
Rys. 11. Krzywe S−N dla gładkich szlifowanych próbek stalowych
7.3. Wpływ skali
Na podstawie badań ustalono, że wraz ze wzrostem wymiarów próbek (o takich samych
kształtach i wymiarach) wartość wytrzymałości zmęczeniowej spada. Fakt ten tłumaczy się
tym, że przy założeniu jednakowej gęstości rozłożenia pęknięć mikroskopowych w próbkach
o większej objętości będzie ich więcej, co zwiększa prawdopodobieństwo pęknięć
zmęczeniowych. Dodatkowo można stwierdzić, że elementy o małych wymiarach mają
zazwyczaj lepsze własności mechaniczne uzyskane w trakcie procesu technologicznego.
Wytrzymałość zmęczeniową ustala się na małych próbkach. Aby uwzględnić rzeczywiste
rozmiary elementu wprowadza się tzw. współczynnik skali
β
s
definiowany jako:
do
d
s
Z
Z
=
β
,
(14)
gdzie: Z
d
– wytrzymałość zmęczeniowa próbki o średnicy d, Z
do
– wytrzymałość zmęczeniowa
próbki o średnicy d
0
(d > d
0
).
11
7.4. Wpływ krótkotrwałych przeciążeń
W trakcie eksploatacji maszyny może zdarzyć się, że na skutek chwilowego przeciążenia
wartość naprężenia przekroczy czasowo wartość wytrzymałości zmęczeniowej materiału (tzn.
krótkotrwałe przeciążenie). Chwilowe przeciążenia obniżają wytrzymałość zmęczeniową
elementu konstrukcyjnego. Aby wyznaczyć zależność pomiędzy chwilowymi przeciążeniami,
a wytrzymałością zmęczeniową przeprowadza się specjalne próby. Pierwszą z próbek obciąża
się tak, aby wywołać naprężenia
σ
1
w zakresie pomiędzy wartością granicy wytrzymałości
(
σ
min
= Z
G
), a wartością ograniczonej wytrzymałości zmęczeniowej dla N
1
cykli (
σ
max
=
σ
w
1
).
Po osiągnięciu wartości N
1
cykli próbę kontynuuje się aż do 10
7
cykli przy naprężeniu
równym Z
G
. Jeżeli próbka nie pęknie uważa się, że amplituda przeciążenia nie miała wpływu
na zmianę wartości wytrzymałości zmęczeniowej. Jeżeli próbka pękła wcześniej niż N = 10
7
cykli, próbę powtarza się dla zmniejszonej amplitudy przeciążenia. Na skutek prób wyznacza
się wartość amplitudy przeciążenia
σ
F
1
, która nie spowoduje uszkodzenia próbki przy
naprężeniu Z
G
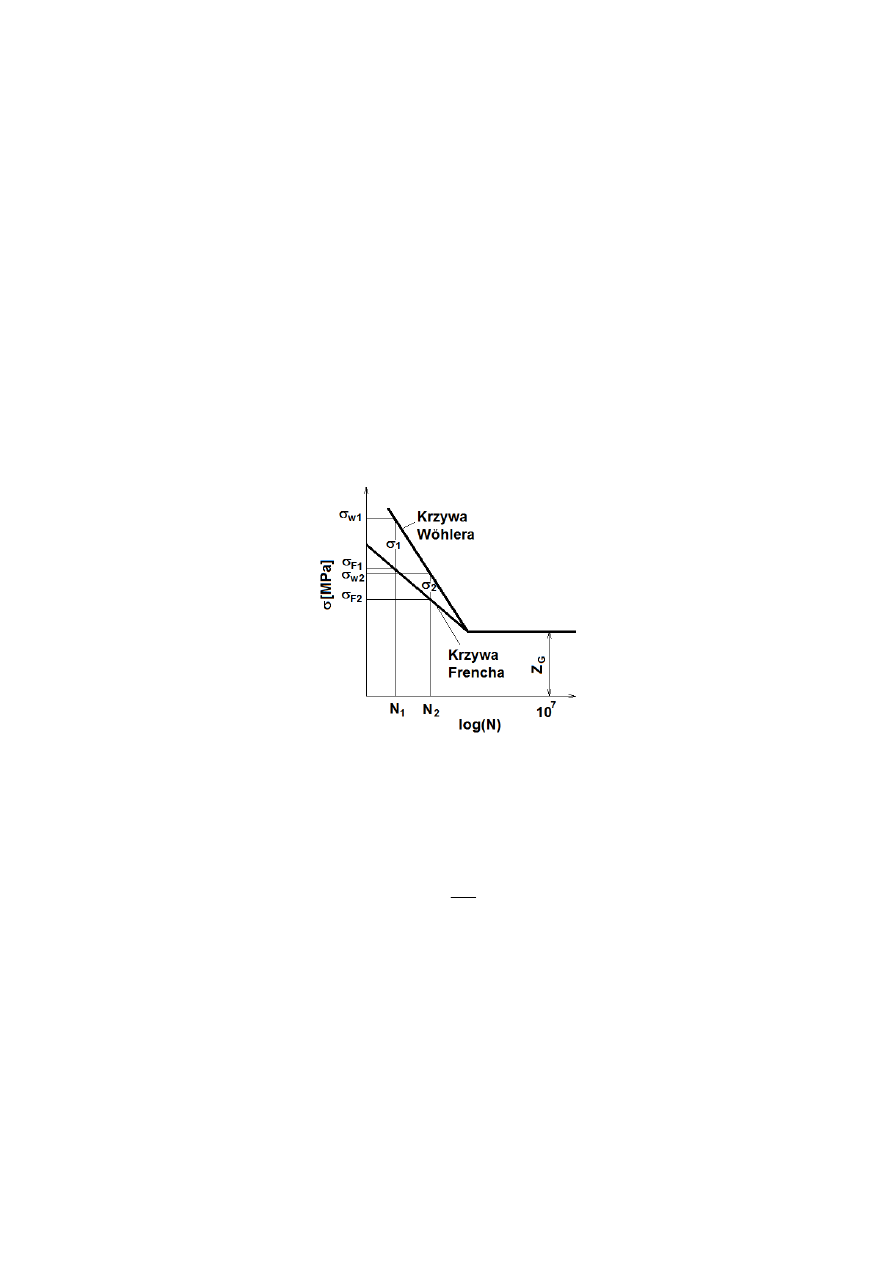
. Następnie bada się przeciążenia dla ilości cykli N
2
, itd. Zbiór wszystkich
wartości
σ
Fi
tworzy tzw. krzywą Frencha (rys. 12). Obszar pomiędzy krzywymi Wöhlera i
Frencha obejmuje przeciążenia obniżające granicę wytrzymałości. Obszar pod krzywą
Frencha obejmuje wszystkie przeciążenia nie mające wpływu na granicę zmęczenia.
Rys. 12. Krzywa Frencha i Wöhlera we współrzędnych logarytmicznych
7.5. Wpływ stanu powierzchni
Wytrzymałość zmęczeniowa elementu konstrukcyjnego jest tym większa, im gładsza jest
jego powierzchnia. Wpływ stanu powierzchni elementu opisuje współczynnik
β
p
określony
wzorem
p
gl
p
Z
Z
=
β
,
(15)
gdzie: Z
gl
– wytrzymałość zmęczeniowa próbki o gładkiej (polerowanej), Z
p
– wytrzymałość
zmęczeniowa próbki o danym stanie powierzchni.
Przykładowo dla:
− stali konstrukcyjnej szlifowanej
β
p
= 1 do 1,2,
− stali konstrukcyjnej skorodowanej wodą morską
β
p
= 3,7,
− żeliwa
β
p
= 1,0,
− duraluminium
β
p
= 1,1 do 1,2,
− stopów magnezu
β
p
= 1,25 do 1,4.
12
8. Schematy maszyn wytrzymałościowych do prób zmęczeniowych.
Poniżej przedstawione zostały schematy maszyn wytrzymałościowych oraz schematy
obciążeń próbek wykorzystywanych w celu wyznaczenia granicy zmęczenia.
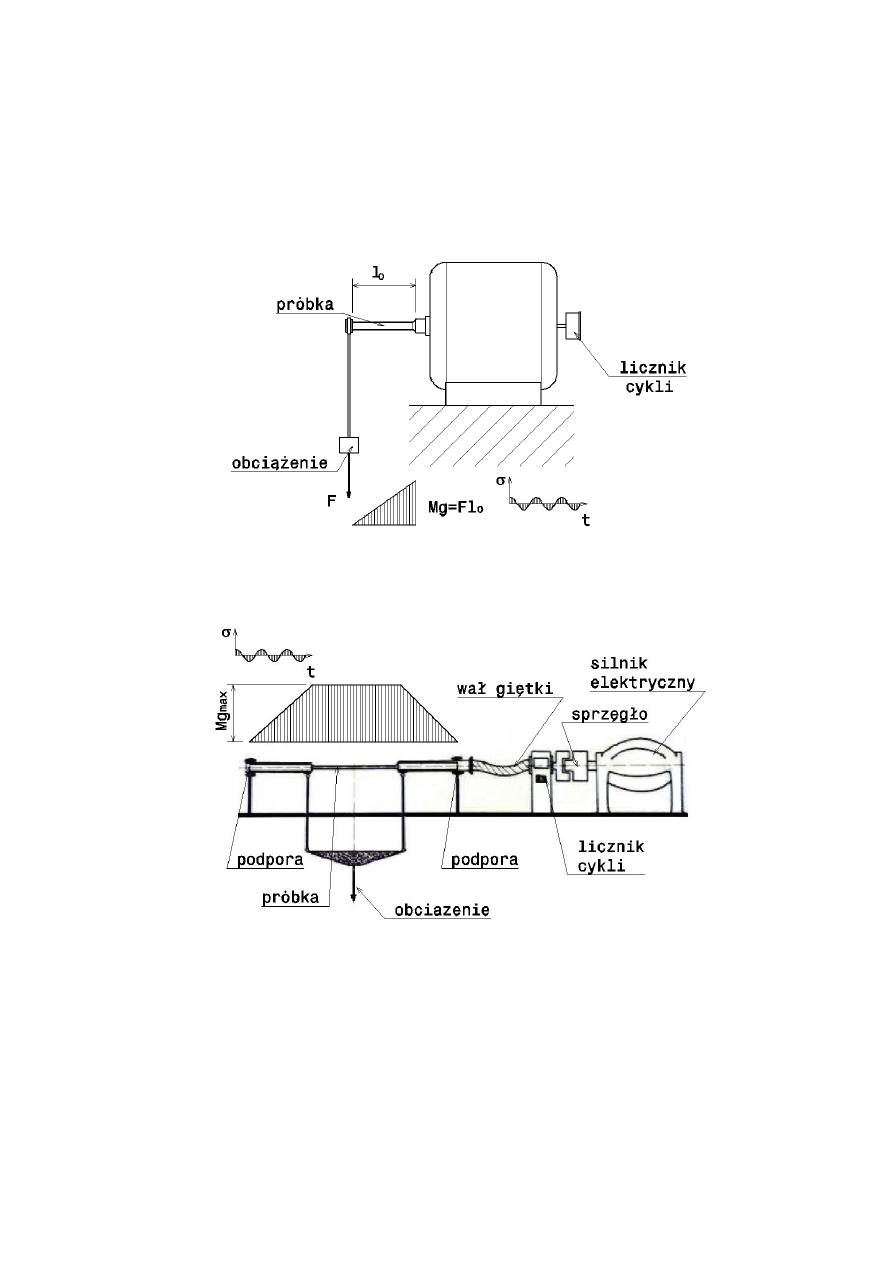
8.1. Zginanie
Rys.13. Maszyna wytrzymałościowa do badania granicy zmęczenia przy obustronnym zginaniu obrotowym
Rys. 14. Maszyna wytrzymałościowa do badania granicy zmęczenia przy obustronnym zginaniu
obrotowym
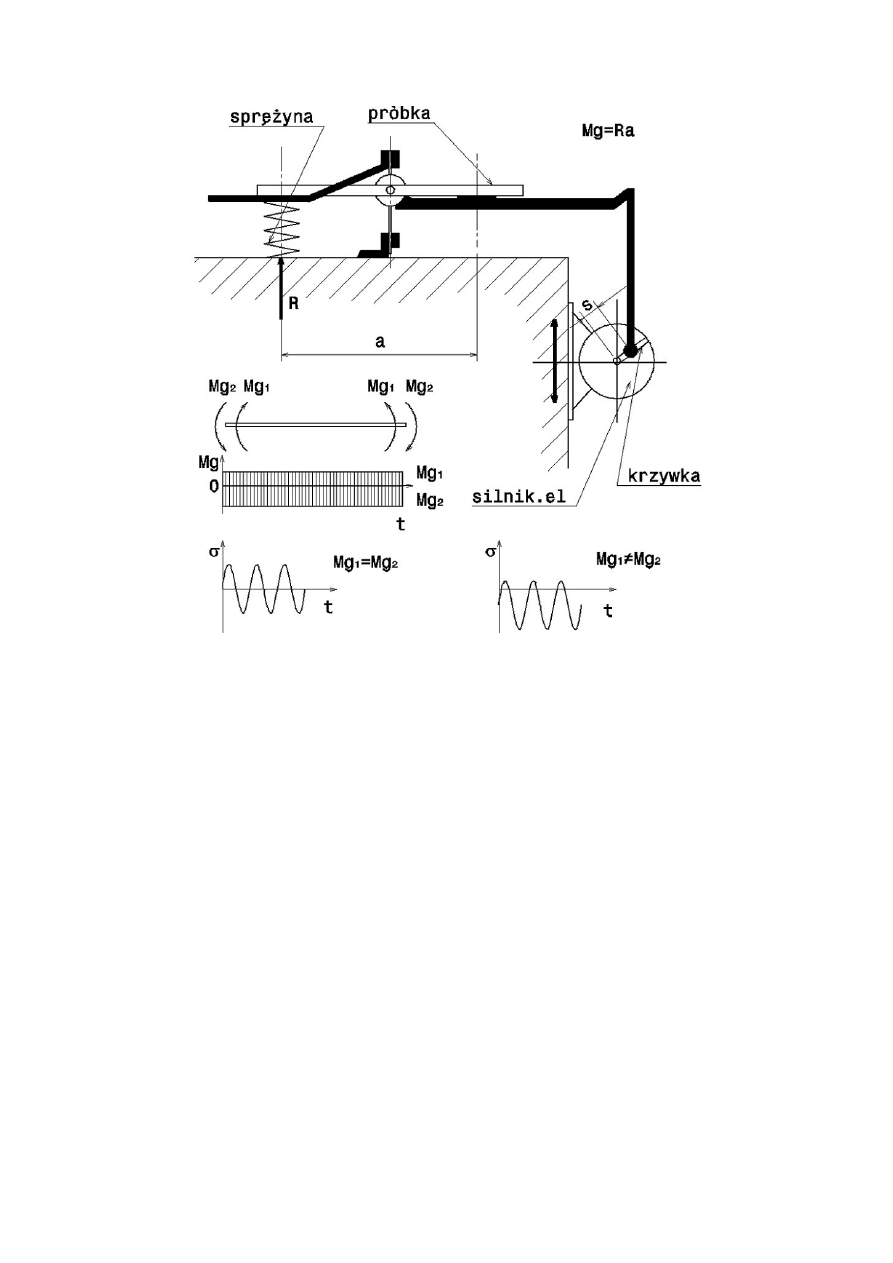
13
Rys. 15. Maszyna wytrzymałościowa do badania granicy zmęczenia przy zginaniu
14
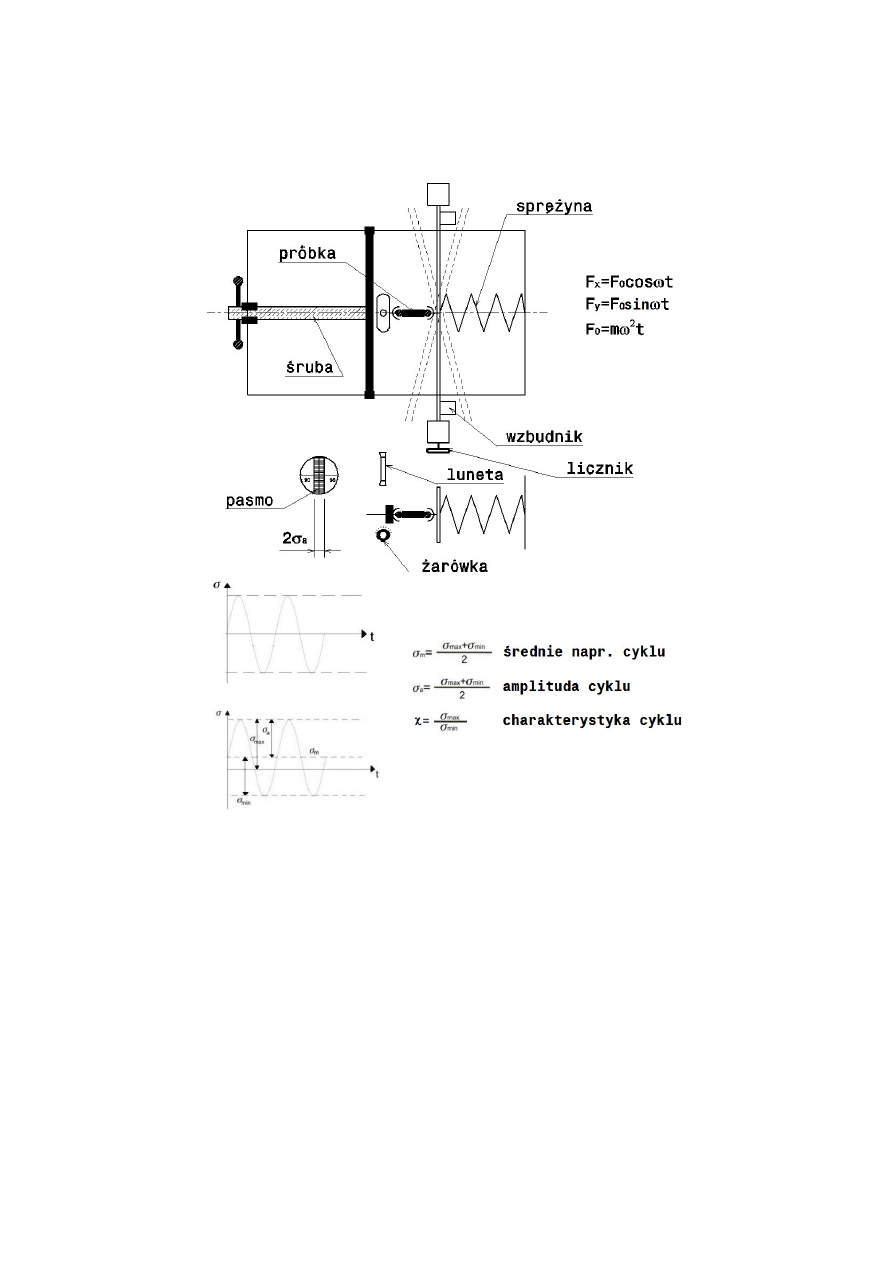
8.2. Rozciąganie i ściskanie
Rys. 16. Schemat maszyny wytrzymałościowej do badania granicy wytrzymałości zmęczeniowej przy
rozciąganiu i/lub ściskaniu
15
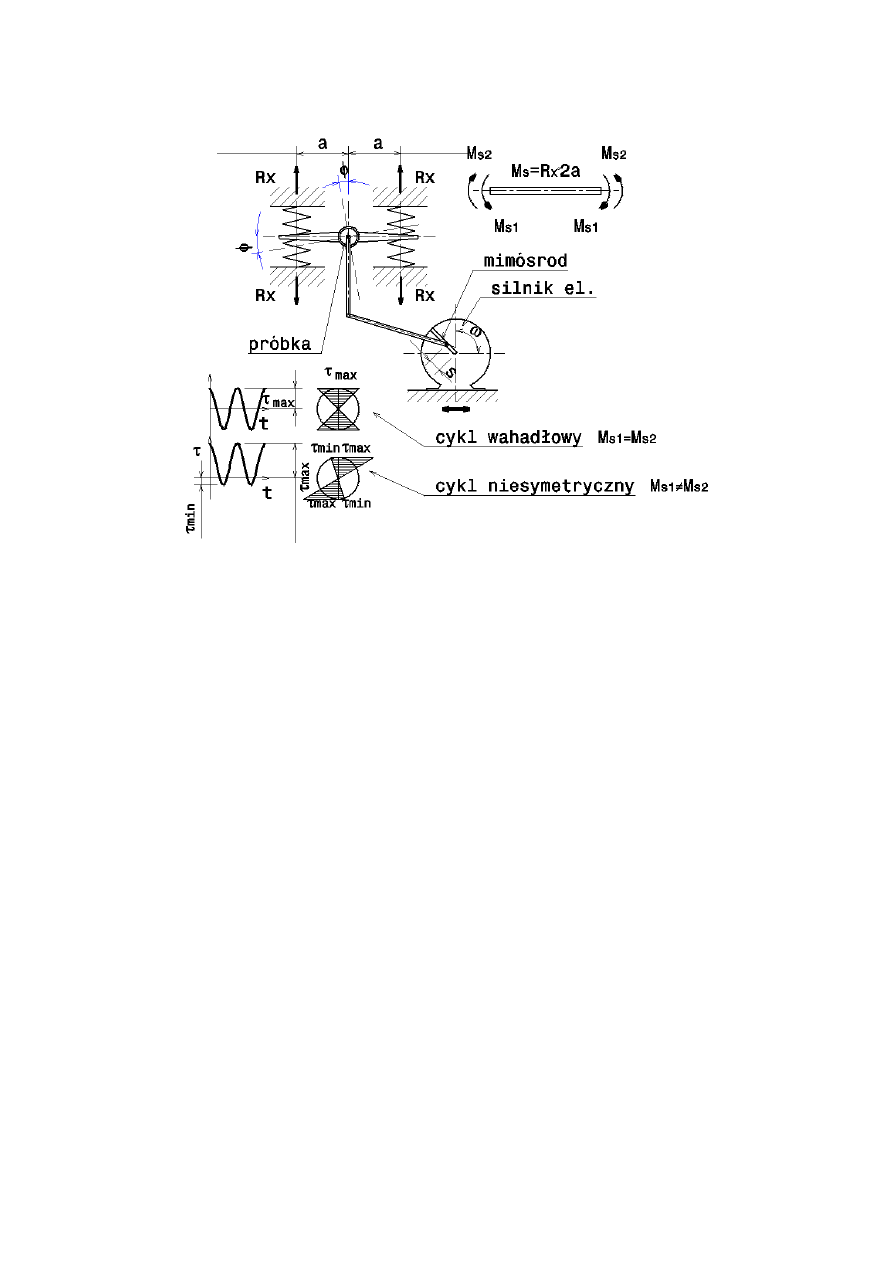
8.3. Skręcanie
Rys. 17. Schemat maszyny wytrzymałościowej do badania granicy wytrzymałości zmęczeniowej przy
skręcaniu
9. Wykonanie sprawozdania
W sprawozdaniu należy umieścić:
1) tytuł i cele ćwiczenia,
2) definicje wielkości charakterystycznych związanych z wytrzymałością zmęczeniową,
3) opis rodzajów cykli zmęczeniowych,
4) rysunki próbek
do zmęczeniowej próby obrotowego zginania
,
5) rodzaj badanego materiału (wyrobu),
6) opis sposobu tworzenia krzywej S−N i wyznaczania wielkości granicy zmęczenia
materiału, opis sposobu tworzenia wykresu Smitha,
7) opis zjawisk wpływających na zmęczenie materiału.
Literatura
[1] Bachmacz W.: Wytrzymałość materiałów. Badania doświadczalne. Skrypt Politechniki Częstochowskiej,
Częstochowa 1973.
[2] Banasik M.: Ćwiczenia laboratoryjne z wytrzymałości materiałów. PWN, Warszawa 1977.
[3] Boruszak A., Sykulski R., Wrześniowski K.: Wytrzymałość materiałów. Doświadczalne metody badań.
Wydawnictwo Politechniki Poznańskiej, Poznań 1977.
[4] Dyląg Z., Orłoś Z.: Wytrzymałość zmęczeniowa materiałów. Warszawa. WNT 1962.
[5] Jastrzębski P., Mutermilch J., Orłoś W.: Wytrzymałość materiałów. Warszawa. Arkady 1985.
[6] Katarzyński S., Kocańda S., Zakrzewski M.: Badania właściwości mechanicznych metali. WNT, Warszawa
1967.
[7] Łączkowski R.: Wytrzymałość materiałów. Gdańsk. WPG 1988.
[8] Mazurkiewicz S.: Laboratorium z wytrzymałości materiałów. Wydawnictwo Politechniki Krakowskiej,
Kraków 1978.
[9] Niezgodziński M.E., Niezgodziński T.: Wzory wykresy i tablice wytrzymałościowe. Warszawa. WNT
1996.
[10] Orłoś Z.: Doświadczalna analiza odkształceń i naprężeń. PWN, Warszawa 1977.

16
[11] Walczyk Z.: Wytrzymałość materiałów. Gdańsk. WPG 1998.
Wyszukiwarka
Podobne podstrony:
1080 PDF C09
1238 C09
lwm c08 (2)
LWM sciaga
mlipski sprawko?7 C09
lwm c04 (2)
Sprawozdanie LWM tensometria
C09
lwm c03 (2)
lwm pyt
C09
lwm wstep (2)
~$ipski sprawko?7 C09
c09
LWM, Politechnika Łódzka, II rok, wytrzymałość materiałów
lwm c lab 01 02
więcej podobnych podstron