W hybrydyzacji sp
2
dany atom i atomy z nim związane leżą w jednej płaszczyźnie. Cząsteczka zbudowana z trzech
atomów zawsze będzie płaska (łącząc liniami atomy wyjdzie nam trójkąt, który ma jedną płaszczyznę!).
Do zapamiętania:
amoniak NH
3
: układ tetraedryczny (zniekształcony, bo występują w.p.e. na atomie azotu, które odpychają się mocniej
niż wiązania, co powoduje deformację), kształt: piramida trygonalna, kąty między wiązaniami 107
o
.
woda H
2
O : układ tetraedryczny (zniekształcony j.w.), kształt: trójkąt równoramienny, kąty między wiązaniami 105
o
,
cząsteczka wody ma budowę płaską (bo trzy połączone atomy utworzą trojkąt i znajdą się w jednej płaszczyźnie).
W organicznej: węgiel, przy którym jest wiązanie potrójne lub dwa wiązania podwójne jest w hybrydyzacji sp, węgiel
przy którym znajduje się jedno wiązanie podwójne jest w hybrydyzacji sp
2
, a węgiel przy którym są wyłącznie cztery
wiązania pojedyncze jest w hybrydyzacji sp
3
(policz wiązania sigma!).
POLARNOŚĆ CZĄSTECZKI:
Aby cząsteczka byla polarna musi spełniać dwa warunki: musi mieć wiązania kowalencyjne spolaryzowane, aby na
jednym z atomów gromadził się cząstkowy ładunek dodatni, a na drugim ujemny (atom pierwiastka bardziej
elektroujemnego silniej przyciąga elektrony!). Dodatkowo cząsteczka nie może mieć budowy symetrycznej.
Co to znaczy? Cząsteczka nie ma budowy symetrycznej, jeśli da się ją przedzielić płaszczyzną (kreską) tak, by po
jednej stronie był ładunek dodatni, a po drugiej ujemny. Najlepiej zrozumieć na przykładach:
Cząsteczki niepolarne
to na przykład: gazy O
2
, Cl
2,
fosfor P
4
– ponieważ występują tu wiązania czysto kowalencyjne, a
więc ładunek elektronów w wiązaniach jest równo rozmieszczony (ta sama elektroujemność pierwiastków, więc żaden
atom nie przyciąga elektronów silniej, niż pozostałe). Inna cząsteczka niepolarna to np. metan CH
4
. Tutaj występują
wiązania kowalencyjne spolaryzowane, ale cząsteczka ma budowę symetryczną. Cztery wiązania C – H są oddalone
od siebie o tę samą odległość (kąt) i są sobie równoważne. Jeśli stworzymy „wektory wypadkowe wiązań” to one się
nam zrównoważą (atom węgla ciągnie z jednakową siłą elektrony we wszystkie strony, siłe te równoważą się). Inaczej
mozna powiedzieć, iż nie da się poprowadzić jednej płaszczyzny („kreski”) tak, by po jednej stronie tej kreski były
cząstkowe ładunki dodatnie (wodory) a po drugiej stronie węgiel z cząstkowym ładunkiem ujemnym.
Inny przykład to cząsteczka CO
2
, która w uproszczeniu wygląda tak: O=C=O. Widzimy zatem, że jeden atom tlenu
„ciągnie” elektrony w prawo, drugi zaś w lewo, przez co wektory tych sił się równoważą. Inaczej: nie da się
poprowadzić płaszczyzny („kreski”) która oddzielałaby jednocześnie ładunek dodatni i ujemny.
Przyklad cząsteczki niepolarnej w hybrydyzacji sp
2
to cząsteczka SO
3
. Można narysować trójkąt z podstawą na dole i
wierzchołkiem na górze, w środku którego znajduje się atom siarki. Wypadkowa dwóch „dolnych” wiązań będzie
skierowana w dół i będzie się równoważyć z wiązaniem z tlenem położonym u góry (w wierzchołku).
Cząsteczki polarne:
w hybrydyzacji sp to na przykład cząsteczka HCl. Wiązanie to jest silnie spolaryzowane,
elektrony są przesunięte w kierunku atomu chloru. Przez co na atomie wodoru tworzy się cząstkowy ładunek dodatni,
na chlorze cząstkowy ładunek ujemny. Cząsteczka nie jest symetryczna, można poprowadzić „kreskę” dzielącą
czasteczkę na dwa obszary:
+
H--
|
--Cl
--
.
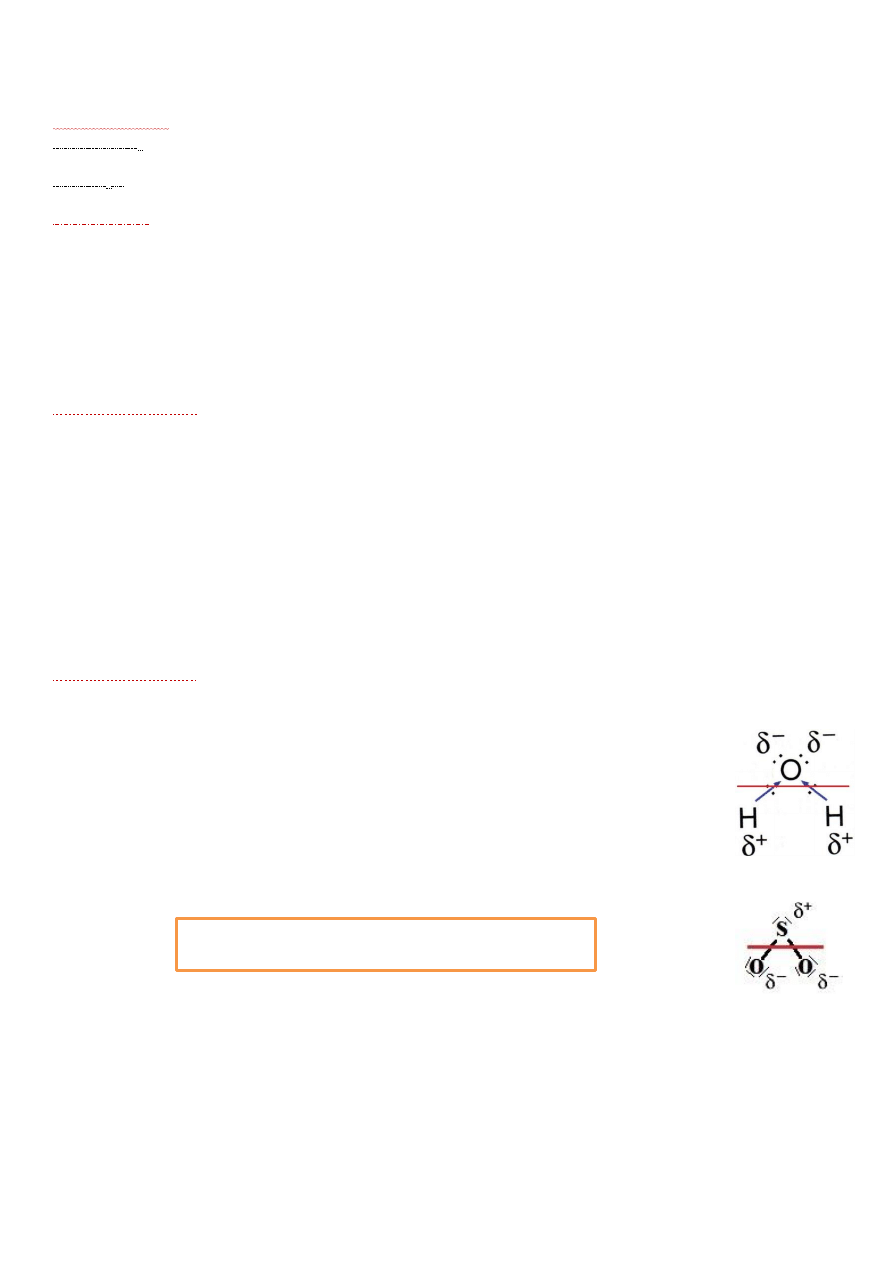
Najpopularniejszy przykład cząsteczki polarnej to cząsteczka wody. Podobnie jak w przypadku
metanu, cz. wody wykazuje hybrydyzację sp
3
, jednak tutaj mamy tylko dwa wodory, które będą
„ciągnąć” tlen w różne strony i nie ma symetrii. W cząsteczce możemy wyróżnić dwa bieguny -
dodatni i ujemny:
Za przykład cząsteczki polarnej w hybrydyzacji sp
2
może posłużyć cz. SO
2
. Widzimy sytuację
podobną do poprzedniej, tak samo możemy wyznaczyć dwa bieguny cżąsteczki – dodatni, który
gromadzi się na atomie siarki i ujemny, który gromadzi się po stronie atomów tlenu.
dipol – układ dwóch różnoimiennych ładunków rozsuniętych na
pewna odległość
każda grupa funkcyjna związana z atomem węgla wiązaniem C-N ma łączny stopień utlenienia –I na każde
wiązanie C-N
stopień utlenienia atomu azotu w związkach organicznych oblicza się, zastępując każde wiązanie C-N
atomem wodoru
Ustalanie produktów reakcji zachodzi raczej „na wyczucie”, ale tutaj także trzeba pamiętać o pewnych zasadach.
Przede wszystkim do zajścia reakcji redoks potrzebny jest utleniacz i reduktor.
Utleniacz – sam ulega redukcji, pobiera elektrony obniżając swój stopień utlenienia, powoduje utlenianie
innego związku
Reduktor – sam ulega utlenianiu, oddaje elektrony podwyższając swój stopień utlenienia, powoduje redukcję
innego związku
Druga sprawa to środowisko. Równanie reakcji musi miec swoje odzwierciedlenie w rzeczywistości.
Jeśli reakcja przebiega w środowisku kwasowym, to do wyrównywania ładunku i atomów używamy
cząsteczek wody i jonów H
+
.
Jeśli reakcja przebiega w środowisku obojętnym, to do wyrównywania ładunku i atomów używamy
cząsteczek wody i jonów H
+
lub OH
-
(chociaż dość często w produktach powstaje zasada, więc ja dla przykładu zawsze
„korzystałam” z jonów OH
-
).
Jeśli reakcja przebiega w środowisku zasadowym to do wyrównywania ładunku i atomów używamy
cząsteczek wody i jonów OH
-
.
Jeżeli reakcja przebiega w środowisku kwasowym, to nie możemy do wyrównania ładunku użyć jonów OH
-
, bo ich
tam po prostu nie ma (a dokładniej są w znikomych ilościach). Ewentualne jony OH
-
pochodzące np, z
autodysocjacji wody będą wiązane przez jony H
+
pochodzące od kwasu (którego użyliśmy do zakwaszenia
środowiska) w cząsteczki wody.
Przykład uzgadniania współczynników dla reakcji KMnO
4
+ HCl →
widzimy mangan na +VII stopniu utlenienia, który jest silnym utleniaczem i z chęcią będzie się redukować.
Patrzymy na środowisko – kwasowe, zatem mangan będzie się redukować do jonów Mn
2+
tworząc sól. Jedyny anion
tej soli, jaki może zaistnieć to Cl
-
, mamy zatem pierwszy produkt reakcji: MnCl
2
. Jeżeli mamy utleniacz, który się
redukuje, musimy mieć także reduktor, który się utleni – podwyższy swój stopień utlenienia. Jon K
+
(nie
zapominajmy, że mamy rozpuszczalną sól i mocny kwas, wszystko istnieje w formie całkowicie zdysocjowanej!) nie
może się dalej utlenić. Jony H
+
także. Dalej rozważamy Cl
-
- owszem, jon chlorkowy może przejść w wolny chlor
cząsteczkowy, podwyższając swój stopień utlenienia z –I na 0. Mamy kolejny produkt: Cl
2
. Dalsze produkty to już
tylko „produkty uboczne”. Jon potasu będzie także tworzyć sól z jonami chlorkowymi. Powstanie także woda (dla
nas – „dla wyrównania wodoru”).
Na przykładzie powyższej reakcji krok po kroku przedstawię jak robimy bilans jonowo-elektronowy.
Zapisujemy równanie reakcji w zapisie cząsteczkowym: KMnO
4
+ HCl → MnCl
2
+ Cl
2
+ H
2
O
i jonowym: MnO
4
-
+ Cl
-
+ H
+
→ Mn
2+
+ Cl
2
+ H
2
O
zapisujemy jony, które biorą udział w reakcji redukcji:
MnO
4
-
→ Mn
2+
Widzimy, że mangan przechodzi z +VII stopnia utlenienia, na +II, a więc musi pobrać 5 elektronów, zapisujemy:
MnO
4
-
+ 5e → Mn
2+
Liczymy teraz ładunek: po lewej stronie mamy -6, po prawej +2. Środowisko jest kwasowe, możemy korzystać z
jonów H
+
, a więc żeby wyrównać ładunek po obu stronach, po lewej stronie musimy dołożyć 8 H
+
:
MnO
4
-
+ 5e + 8 H
+
→ Mn
2+
Teraz zostaje nam do wyrównania wodór i tlen, uzupełniamy cząsteczkami wody, dodając ich po prawo 4:
MnO
4
-
+ 5e + 8 H
+
→ Mn
2+
+ 4 H
2
O
teraz zapisujemy jony, które biorą udział w reakcji utleniania:
Cl
-
→ Cl
2
od razu wyrównujemy ilości pierwiastka
(robimy to zawsze, gdy po jednej ze stron mamy „nierozdzielne” atomy, własnie
np. w postaci dwuatomowych cząsteczek):
2 Cl
-
→ Cl
2
widzimy, że każdy atom musiał oddać po jednym elektronie, w sumie 2 elektrony po prawo:
Często popełniany przez maturzystów błąd: azot w grupie nitrowej –NO
2
jest na +III stopniu utlenienia (cała grupa
ma łączny stopień utlenienia –I zgodnie z przedostatnim punktem powyżej lub: wiązanie C-N zastępujemy atomem
wodoru i otrzymujemy HNO
2
, azot jest na st. utl. x + 1 + (-2)*2 = 0, x = 3
W grupie aminowej –NH
2
azot jest na –III st. ut. (cała grupa na –I lub: zastępujemy wiązanie C-N atomem wodoru i
uzyskujemy: HNH
2
, azot jest na st. utl. x+1+1*2 = 0, x = -3
Hydroliza jest reakcją odwracalną! Dlatego w roztworze wodnym znajdują się w przypadku h. kationowej: wolne
cząsteczki NH
3
, jony NH
4
+
i H
3
O
+
oraz cząsteczki wody oczywiście. W przypadku przykładu h. anionowej w
roztworze znajdują się jony: CO
3
2-
, HCO
3
-
, OH
-
oraz cząsteczki wody.
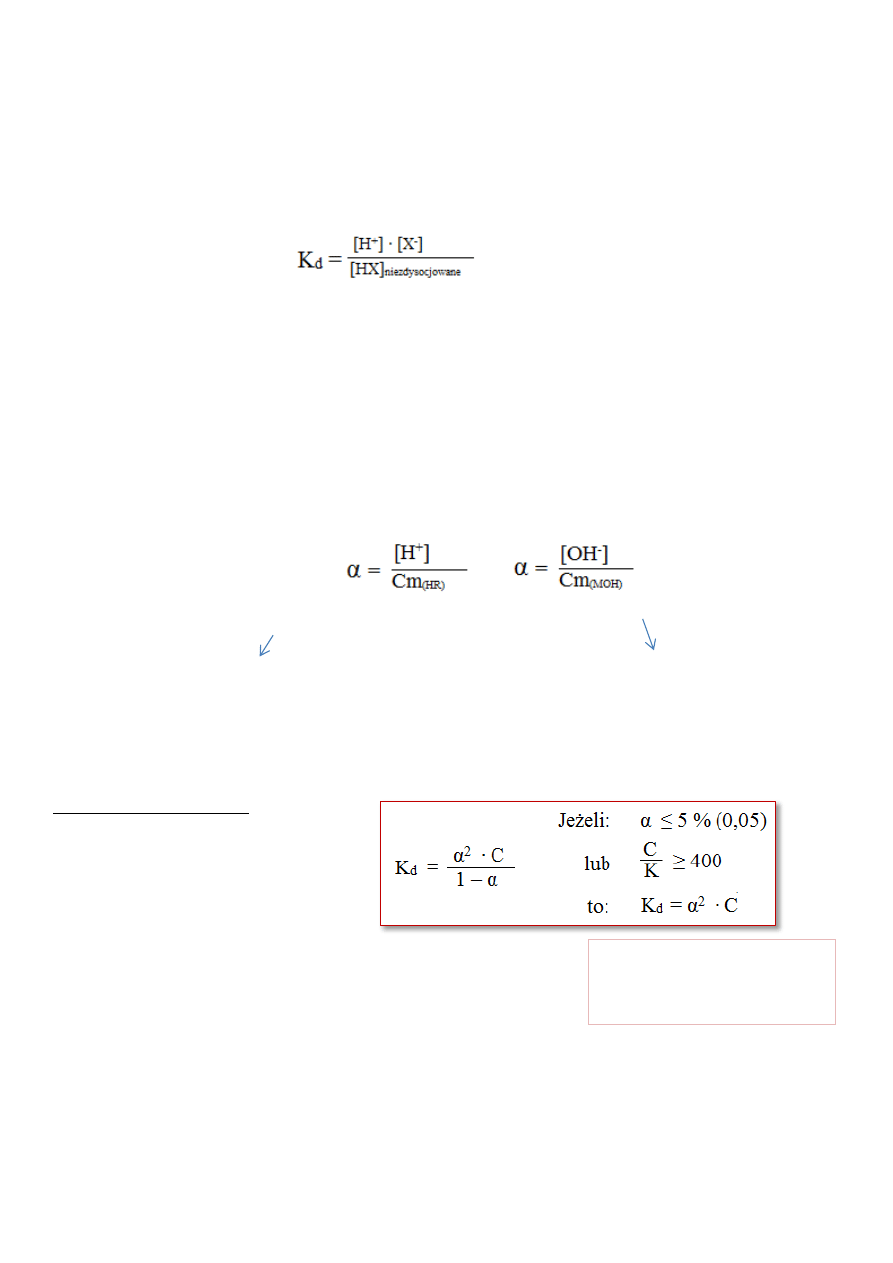
STAŁA I STOPIEŃ DYSOCJACJI
Moc elektrolitu jest określana stałą i stopniem dysocjacji.
Miarą mocy elektrolitu jest stała dysocjacji K
d
, która jest wielkością charakterystyczną dla danego elektrolitu
i nie zależy od poczatkowego stężenia elektrolitu, natomiast zależy od temperatury.
dla: HX ↔ H
+
+ X
-
=>
Dla kwasów i zasad dysocjujących etapowo, dla każdego etapu można wyznaczyć stałą dysocjacji, np.
H
3
PO
4
↔ H
+
+ H
2
PO
4
-
K
1
H
2
PO
4
-
↔ H
+
+ HPO
4
2-
K
2
K
1
>> K
2
>> K
3
HPO
4
2-
↔ H
+
+ PO
4
3-
K
3
Ze wzrostem temperatury stała dysocjacji rośnie, ponieważ temperatura powoduje szybsze poruszanie się cząsteczek,
co ułatwia dysocjację, wskutek czego rośnie liczba czasteczek zdysocjowanych a maleje niezdysocjowanych.
Im wyższa stała dysocjacji tym mocniejszy kwas! Czasem dla określenia mocy kwasu używa się również wielkości
pK
a
, która jest ujemnym logarytmem dziesiętnym ze stalej dysocjacji. W tym przypadku im mniejsza wartość pK
a
tym mocniejszy kwas (odpowiednio dla zasady pK
b
).
Stopień dysocjacji to stosunek cząsteczek zdysocjowanych do liczby cząsteczek wprowadzonych pierwotnie do
roztworu.
Stopień dysocjacji zalezy od: rodzaju elektrolitu, temperatury (ze wzrostem temp. α nieznacznie rośnie), stężenia
początkowego (ze wzrostem rozcieńczenia α rośnie).
Przyczyny tego są dwie: po pierwsze im więcej wody dostarczymy Wzrost temperatury powoduje szybsze poruszanie
do roztworu, tym dysocjacja będzie zachodzić z większym efektem, się cząsteczek, przez co ich zderzenia są częstsze i
co spowoduje większą ilość cząsteczek zdysocjowanych (większy efektywniejsze (elektrolitu i wody), a to prowadzi
licznik). do wzrostu efektywności dysocjacji. Ogólne stęzenie
(mianownik) się nie zmienia, ale rośnie licznik, czyli
ilość cząstek zdysocjowanych, co przekłada się na
wzrost stopnia dysocjacji.
Stałą i stopień dysocjacji można ze sobą powiązać.
Prawo rozcieńczeń Ostwalda:
Przykład zadania:
Oblicz stopień dysocjacji kwasu HF, jeśli w
jego 0,5-molowym wodnym roztworze stężenie jonów fluorkowych wynosi
0,018 mol ∙ dm
-3
.
Zapisujemy równanie dysocjacji kwasu HF: HF ↔ H
+
+ F
-
(kwas słaby, reakcja odwracalna!)
Z równania reakcji widzimy, że liczba jonów H
+
jest równa liczbie jonów F
-
, ponieważ reakcja pozostaje w
stechiometrii 1:1, a dysocjacja jest jednoetapowa. W przypadku np. kwasu H
2
S nie możemy powiedzieć, że jonów
H
+
jest 2 razy więcej niż jonów S
2-
, ponieważ jest to słaby kwas, który dysocjuje w dwóch etapach, a stała dysocjacji
drugiego etapu jest dużo niższa niż pierwszego).
Ponieważ stężenie jonów fluorkowych równa się stężeniu jonów wodorowych, możemy je zastąpić, podstawiając do
wzoru:
[HX]
niezdysocjowane
= Cm
początkowe
- [H
+
]
Stała dysocjacji lepiej charakteryzuje
moc elektrolitu, ponieważ nie zależy
od stężenia poczatkowego, a
wyłącznie od temperatury!
WODORKI
Dla grup 1-15: wzór EH
n
nazewnictwo: wodorek E-u (np. wodorek litu)
Dla grup 16-17: wzór H
n
E nazewnictwo: Eowodór (np. siarkowodór)
Większość wodorków otrzymuje się w bezpośredniej syntezie pierwiastka z wodorem.
wodorki jonowe – ciała stałe o jonowych sieciach krystalicznych zawierających kation metalu i anion
wodorkowy H
-
(jądro wodoru otoczone dubletem elektronowym), mają wysokie temperatury topnienia i
wrzenia, stopione przewodzą prąd elektryczny, są to wodorki litowców i wapniowców
wodorki metaliczne – zawieraja atomy wodoru w lukach sieci krystalicznej, sa to wodorki metali
prześciowych, np. Pd, Ti
wodorki kowalencyjne – pomiędzy wodorem a pierwiastkiem występuje wiązanie kowalencyjne, są to
wodorki berylu, magnezu, boru oraz pierwiastków grup 14-17
W wodorkach pierwiastek zawsze przyjmuje jak najniższą wartościowość!
Wodorki jonowe reagują z wodą tworząc wodorotlenek i wodór, np.:
NaH
-I
+ H
2
I
O → NaOH
I
+ H
2
0
(jonowo: NaH + H
2
O → Na
+
+ OH
-
+ H
2
)
jest to reakcja redoks, swój stopień utlenienia zmienia wodór: 2 H
-I
→ H
2
0
+ 2e
(dwójki w równaniu
2 H
I
+2e → H
2
0
sumarycznym się skrócą)
Wodorki fluorowców i siarkowców po rozpuszczeniu w wodzie ulegają dysocjacji jonowej. Wodne roztwory tych
wodorków to kwasy beztlenowe, z czego do mocnych kwasów zaliczamy roztwory: HCl, HBr, HI.
Moc kwasów beztlenowych rośnie w obrębie okresu w prawo, w obrębie grupy w dół.
H
2
S < HCl – kwas solny jest silniejszy od siarkowodorowego, ponieważ chlor ma większą elektroujemność od siarki,
co powoduje silniejszą polaryzację wiązania H-Cl. Im silniej spolaryzowane wiązanie tym łatwiej pod wpływem
wody „oderwać” H
+
.
HF << HCl < HBr < HI – w tym przypadku moc kwasu rośnie w dół grupy, chociaż elektroujemność maleje. Jednak
nad regułą elektroujemności (jak przypadek wyżej) stoi tutaj inna zależność: idąc w dół zauważymy, że promień
atomowy pierwiastka rośnie. Im większy promień atomowy, tym dalej „znajduje się” wodór (wiązanie tworzą
elektrony walencyjne znajdujące się najdalej od jądra), tym samym siła z jaką jądro przyciąga ten wodór jest słabsza
i łatwiej oderwać H
+
.
WODOROTLENKI
Wzór ogólny: M(OH)
n
. Wodorotlenki mają budowę jonową, zawierają w sieci krystalicznej jony M
n+
i OH
-
.
Sposoby otrzymywania:
tlenek metalu lekkiego + H
2
O → wodorotlenek – np. K
2
O + H
2
O → 2 KOH
metal lekki + H
2
O → wodorotlenek + H
2
– np. 2 K + 2 H
2
O → 2 KOH + H
2
reakcja strąceniowa (warunek: wodorotlenek musi być słabo rozpuszczalny w wodzie). Do roztworu soli
zawierającego kationy metalu dodajem r-r mocnej zasady, np.:
FeCl
3
+ 3 KOH → Fe(OH)
3
+ 3 KCl (jonowo: Fe
3+
+ 3 OH
-
→ Fe(OH)
3
)
Moc wodorotlenków rośnie w grupach i maleje w okresach. Im mniejsza elektroujemność metalu tym słabsze
oddziaływanie wiąząće między atomem tego metalu a atomem tlenu w grupie OH.
Wodorotlenki litowców i wapniowców to mocne elektrolity. Oznacza to, że dysocjują całkowicie (
α
= 100%). Cała
ilość rozpuszczonego wodorotlenku występuje w roztworze w formie jonów (nie ma rozpuszczonych cząsteczek
MOH). Słabe wodorotlenki jak Mg(OH)
2
dysocjują odwracalnie (w roztworze ustala się stan równowagi pomiędzy
formą zdysocjowaną – w jonach, a niezdysocjowaną – w cząsteczkach).
Ca(OH)
2
mimo, iż jest wodorotlenkiem słaborozpuszczalnym w wodzie, to jest mocnym elektrolitem, ponieważ
wszystko to, co się w wodzie rozpuści (co jest ponad osadem) występuje w formie jonów Ca
2+
i OH
-
(nie ma w
roztworze swobodnie „pływających” cząsteczek Ca(OH)
2
).
Ze względu na gęstość metale możemy podzielić na tzw. metale lekkie i ciężkie.
Do metali lekkich zaliczamy: metale I i II grupy oraz glin, itr, skand, tytan.
Do metali ciężkich zaliczamy pozostałe metale, np. rtęć, miedź, ołów, chrom, nikiel, złoto.
Przypomnijmy, że nie każdy wodorotlenek to zasada!
Zasada = wodorotlenek, którego roztwór zawiera jony OH
-
są to wodorotlenki metali I i II grupy bez Be i Mg
JAK TWORZYMY WZORY STRUKTURALNE CZĄSTECZEK?
Na początku nauki najważniejsza jest zasada: Każdy atom dąży do uzyskania trwałej konfiguracji najbliższego gazu
szlachetnego, dla wodoru jest to dublet (bo 2 elektrony), dla pozostałych pierwiastków oktet (bo 8 e.). Reguła ta jest
bardzo często spełniana podczas łączenia się atomów w cząsteczki, lecz nie zawsze.
Przyjrzyjmy się z bliska przykładom (rysunek z opisanymi graficznie przykładami stronę niżej)
H
2
SO
3
:
1. siarkę umieszczamy po środku, wodory obok atomów tlenu. Rozmieszczenia atomów nauczysz się wraz z
kolejnymi przykładami.
2. dla każdego atomu kropeczkami zaznaczamy liczbę elektronów walencyjnych. Uwaga – elektrony
sparowane podwójnie, niesparowane pojedynczo. W zapisie klatkowym widać ile mamy e. sparowanych i
niesparowanych.
3. Łączymy kropeczki pomiędzy wodorami a tlenami. Jest to wiązanie kowalencyjne spolaryzowane, które
można zaznaczać kreską bądź klinem (szersza jego część przy atomie bardziej elektroujemnym ukazuje
większe zagęszczenie chmury elektronowej w tym obszarze). Dla przykładu zaznaczyłam wyłącznie w tym
przypadku, dalej stosuję zwykłe kreski również dla w. kow. spol. Wodór ma już dublet, ponieważ w
wiązaniu kowalencyjnym ma „do dyspozycji” 2 elektrony. Tlen uzyskał na „współwłasność” od wodoru
jeden elektron. Ma ich teraz 7 (razem z 6 e. walencyjnymi). Tlen potrzebuje dwóch elektronów, aby osiągnąć
oktet. Każdy atom tlenu utworzy zatem z siarką wiązanie kowalencyjne (spolaryzowane) i tak każdy uzyska
brakujący elektron do uzyskania oktetu. Siarka posiadała 6 elektronów walencyjnych („swoich”), uzyskała
także „na współwłasność” od każdego atomu tlenu po jednym elektronie. Ma ich zatem już 8, czyli osiągnęła
oktet. Zatem trzeci, niepołączony z wodorem, tlen uzyska od siarki na „współwłasność” wolna parę
elektronową (wiąz. koordynacyjne). Wszystkie atomy mają oktet/dublet.
HNO
3
:
1. jak w przykładzie wcześniej jeden tlen umieszczamy „z” wodorem.
2. Rozpisujemy kropeczkami elektrony walencyjne dla każdego atomu. W przypadku atomu azotu: 1 para
elektronów sparowanych i 3 elektrony niesparowane (te w czerwonym kółeczku faktycznie powinny byc i są
niesparowane, ale umieściłam je blisko siebie, ponieważ występuje tu wiązanie podwójne z tlenem).
3. jak w przypadku poprzednim łączymy wodór i tlen wiązaniem kowalencyjnym (spolaryzowane ze względu
na znaczną róznicę elektroujemności). Tlen uzyskał w ten sposób jeden elektron od wodoru i ma ich teraz 7.
Łączy się następnie w. kowalencyjnym z azotem (jako, że atomowi tlenu brakuje do oktetu dwóch
elektronów będzie on zawsze łączył się dwoma wiązaniami kowalencyjnymi). Teraz sprawa pozostalych
dwóch atomów tlenu: jeden łączy się podwójnym wiązaniem z azotem. W ten sposób zarówno atom azotu
jak i tlen uzyskuja oktet (oktet możemy poznać po tym, że przy każdym atomie znajdują się teraz 4 kreseczki
oznaczające pary elektronowe – wiązania + wolne pary elektronowe). Co zatem zrobimy z trzecim atomem
tlenu? Uzyska on poprzez wiązanie kooordynacyjne 2 elektrony od azotu (azot udostępnia swoją w.p.e.
tlenowi, ale sam jej nie traci, „współużytkują” ją razem i jednocześnie).
Przykłady A, B i C:
Za pomocą tych przykładów chciałam pokazać, że wiązania jonowego nie zapisujemy kreseczkami! Różni się ono
od wiązania kowalencyjnego bardzo znacząco. Tutaj nie dochodzi do „współużytkowania” elektronów przez dwa
atomy. Jeden atom (pierwiastka mniej elektroujemnego) całkowicie traci elektron/y
i oddaje je atomowi pierwiastka bardziej elektroujemnego. W ten sposób tworzą się dwa jony (kation i anion), a
„wiązanie” jonowe to przyciąganie elektrostatyczne między nimi. Cząsteczki takie zapisujemy w formie jonów!
Tutaj przykład: dwie sole i wodorotlenek metalu I grupy.
CO:
1. Zaznaczamy na atomach elektrony walencyjne. Tutaj podobnie ze względu na podwójne wiązanie
zaznaczyłam niesparowane elektrony obok siebie (mozna o tym zapomnieć, jak już pisanie wzorów wejdzie
w nawyk).
2. Tlen potrzebuje do oktetu uzyskać od węgla dwa elektrony, łączy się więc z nim podwójnym wiązaniem (w.
kowalen.). Ale! Teraz liczymy ile elektronów ma węgiel (dwie kropeczki + dwa wiązania = 6 elektronów).
Powinien uzyskać jeszcze 2 elektrony.
3. W tym punkcie widzimy „rozwiązanie problemu”. Węgiel „dostaje” na współużytek od atomu tlenu jego
wolną parę elektr. (w. koordynacyjne).
Elektrony w ogniwie płyną obwodem zewnętrznym od anody do katody. Dlaczego? Otóż na anodzie zachodzi
utlenianie, a więc oddawanie elektronów. Płyną one obwodem do katody, gdzie zachodzi redukcja, czyli
przyjmowanie elektronów. Umownie przyjęto, że prąd płynie zawsze w kierunku przeciwnym do kierunku
elektronów, a więc od katody do anody.
Przykład zadania: Płytkę cynkową o masie 50g zanurzono w roztworze azotanu(V) srebra. Po zakończeniu reakcji
masa płytki wyniosła 51g. Oblicz, ile gram srebra wydzieliło się na płytce.
Wpierw porównujemy potencjały:
Zn|Zn
2+
-0,76V – anoda
Ag|Ag
+
0,8 V – katoda
układamy równanie reakcji zachodzącej w ogniwie: Zn + 2 Ag
+
→ Zn
2+
+ 2 Ag
z równania reakcji wynika, że reagują ze sobą: 1 mol cynku i 2 mole jonów Ag
+
→ oznacza to tyle co: gdy do
roztworu w postać jonów przechodzi 1 mol cynku, to jednocześnie z roztworu wydzielają się w formę metaliczną 2
mole jonów Ag
+
. Ponieważ płytka cynkowa była zanurzona w roztworze azotanu(V) srebra, to srebro wydziela się
właśnie na tej płytce. Zatem przyrost masy płytki (lub jej ubytek, to zależy co ma większą masę – to, co się wydziela
czy to, co się osadza) stanowi własnie to, co się osadziło minus to, co się wydzieliło do roztworu.
Możemy zatem obliczyć przyrost masy płytki, gdyby do roztworu przechodziła stechiometryczna ilość 1 mola
cynku: przejście 1 mola Zn – wydzielenie się 2 moli Ag
+
przejście 65,4g Zn – wydzielenie się 2∙107,9g Ag
+
Przy stechiometrycznej wymianie masa płytki przyrasta o: 2∙107,9g – 65,4g = 150,4g
Wzrost masy płytki o 150,4g = wydzielenie się 2 ∙ 107,9g Ag
+
wzrost masy płytki o 1g (51g-50g) = wydzielenie się Xg Ag
+
i wyliczamy z proporcji X: X = 1,43g Ag
+
Widzimy zatem, że na płytce wydzieliło się nam 1,43g srebra. Płytka w sumie przyrosła tylko o 1gram. Zatem 0,43g
cynku musiało przejść do roztworu.
Inny sposób obliczania przyrostu lub ubytku płytki stosujemy dla ogniw zbudowanych z dwóch płytek zanurzonych
w dwóch roztworach. Siłą rzeczy metal wydzielający się Z roztworu nie może osadzić się na metalu wydzielającym
się DO roztworu (niestety jony nie przeskoczą naczynia z roztworem). Przykładem może być ogniwo Daniella.
Jeśli mamy podane, że masa płytki cynkowej wzrosła o 5 gram, to osadziła się na niej miedź z roztworu, ale nic z
niej nie ubywało. Ubytek był natomiast na płytce cynkowej, ponieważ to cynk przechodzi do roztworu (ale w
osobnym półogniwie). W tym przypadku nie liczymy żadnego „przyrostu płytki”! tylko korzystamy z najzwyklejszej
proporcji: przejście do roztworu 1 mola Zn – wydzielenie się 1 mola Cu
przejście do roztworu 65g Zn – wydzielenie się 63,5 g Cu
przejście do roztworu X g Zn – wydzielenie się 5g Cu
X = 5,12g Zn
Przykład innego zadania: Na podstawie przedstawionych poniżej równań reakcji elektrodowych oraz wartości
potencjałów standardowych oceń, czy są możliwe następujące procesy:
A. redukcja jonów Fe
3+
przez jony Cr
3+
B. utlenienie jonów Fe
2+
przez jony MnO
4
-
I. Fe
3+
+ e ↔ Fe
2+
E
o
= 0,77 V
II. MnO
4
-
+ 8 H
+
+ 5e ↔ Mn
2+
+ 4 H
2
O E
o
= 1,52 V
III. Cr
3+
+ e ↔ Cr
2+
E
o
= -0,41 V
źródło: matura ZamKor marzec 2012
Odpowiedź do punktu A: Nie jest możliwym zredukowanie jonów Fe
3+
przez jony Cr
3+
. Porównajmy potencjały
standardowe: aby doszło do redukcji jonów Fe
3+
półogniwo I musi pełnić funkcję katody (bo na katodzie zachodzi
redukcja), a połączone półogniwo III. musi pełnić funkcję anody. Patrząc na potencjały standardowe stwierdzamy, że
jest to jak najbardziej możliwe, ponieważ półogniwo I ma potencjał wyższy od półogniwa III. Jednak gdyby
półogniwo III miało być anodą, to proces zachodzący w tym półogniwie byłby taki: Cr
2+
→ Cr
3+
+ e, ponieważ na
anodzie zachodzi utlenianie – oddawanie elektronów! A więć w półogniwie tym utleniają się jony Cr
2+
a nie jony
Cr
3+
. Zatem owszem, możliwa jest redukcja Fe
3+
w połączeniu z tym półogniwem ale przez jony Cr
2+
a nie Cr
3+
.
Odpowiedź do punktu B: Tak, możliowe jest utlenienie jonów Fe
2+
przez jony MnO
4
-
. Porównajmy potencjały
standardowe tych dwóch półogniw, I i II. W powstałym ogniwie, półogniwo I będzie pełnić funkcję anody, ponieważ
ma niższy potencjał, a półogniwo II będzie pełnić funkcję katody (wyższy potencjał). Zatem w półogniwie I zajdzie
reakcja: Fe
2+
→ Fe
3+
+ e (bo na anodzie utlenianie!, tutaj już jedna strzałka!). W półogniwie II reakcja zachodzi
względem redukcji: MnO
4
-
+ 8 H
+
+ 5e → Mn
2+
+ 4 H
2
O.
Sumarycznie: MnO
4
-
+ 8 H
+
+ Fe
2+
→ Fe
3+
+ Mn
2+
+ 4 H
2
O
CAŁOŚĆ SAMOUCZKA
ORAZ WSZELKIE PYTANIA
DOSTĘPNE POPRZEZ:
SAMOUCZEKCHEMICZNY@GMAIL.COM