1
Podstawy Konstrukcji Maszyn
Wykład 9
Przekładnie zębate część 2
Korekcje
Dr inż. Jacek Czarnigowski
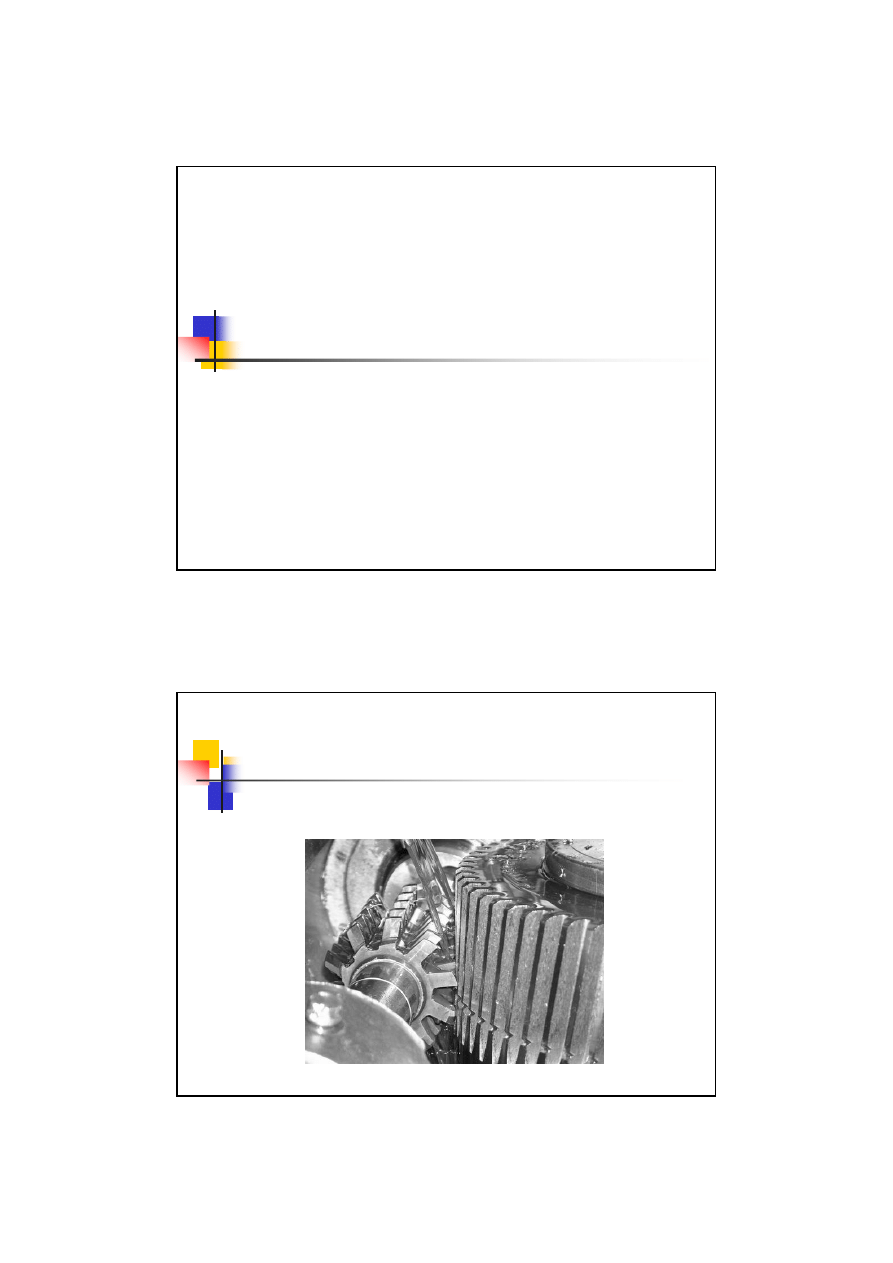
Obróbka kół zębatych
Metoda obwiedniowa
2
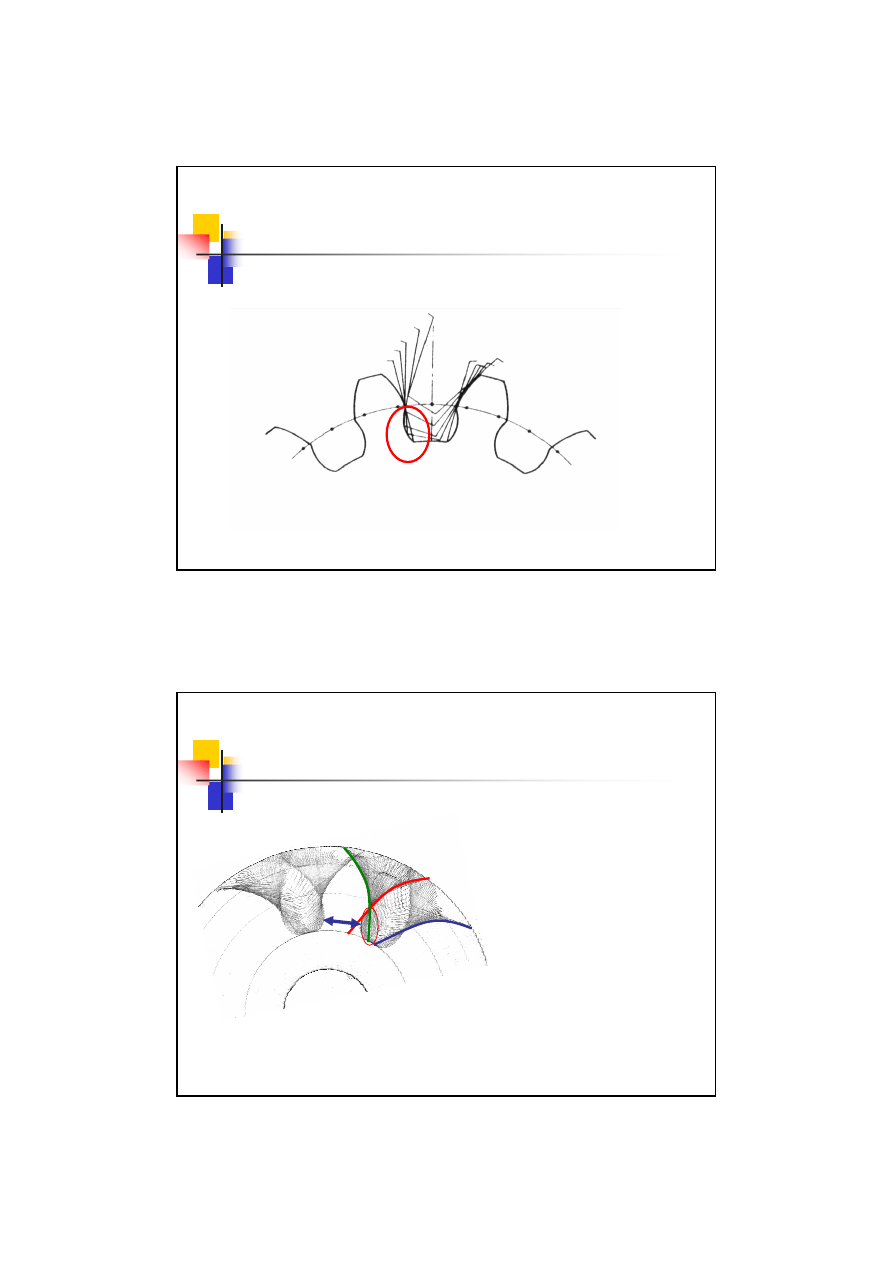
Podcięcie zębów
Podcięcie stopy zęba
Wstępuje gdy jest duża kątowa
odległość zębów, czyli przy
nacinaniu małej ich liczby.
Podcięcie zębów
Podcięcie zęba
Następuje skrócenie linii styku.
Osłabienie zęba:
- Mniejsza grubość,
- zjawisko karbu.
3
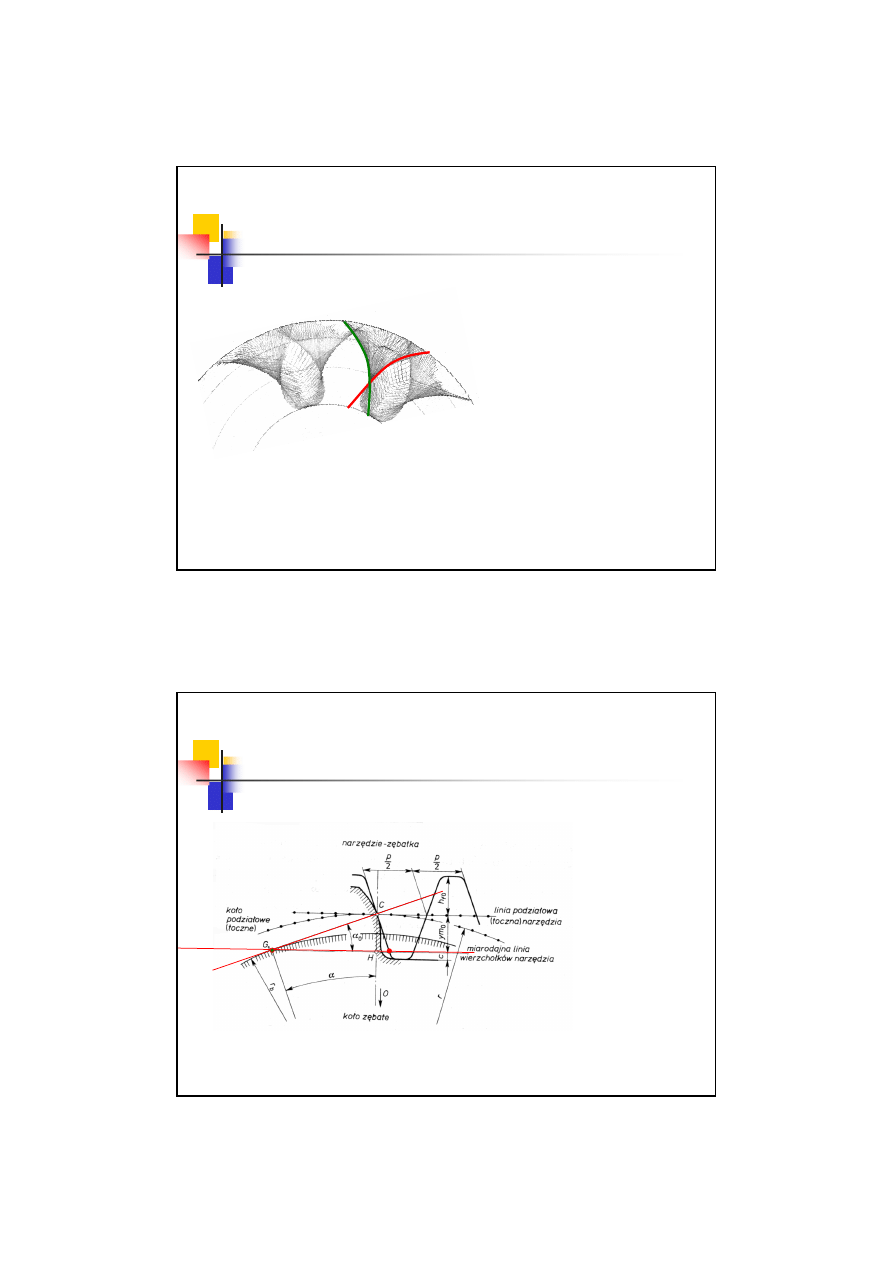
Podcięcie zębów
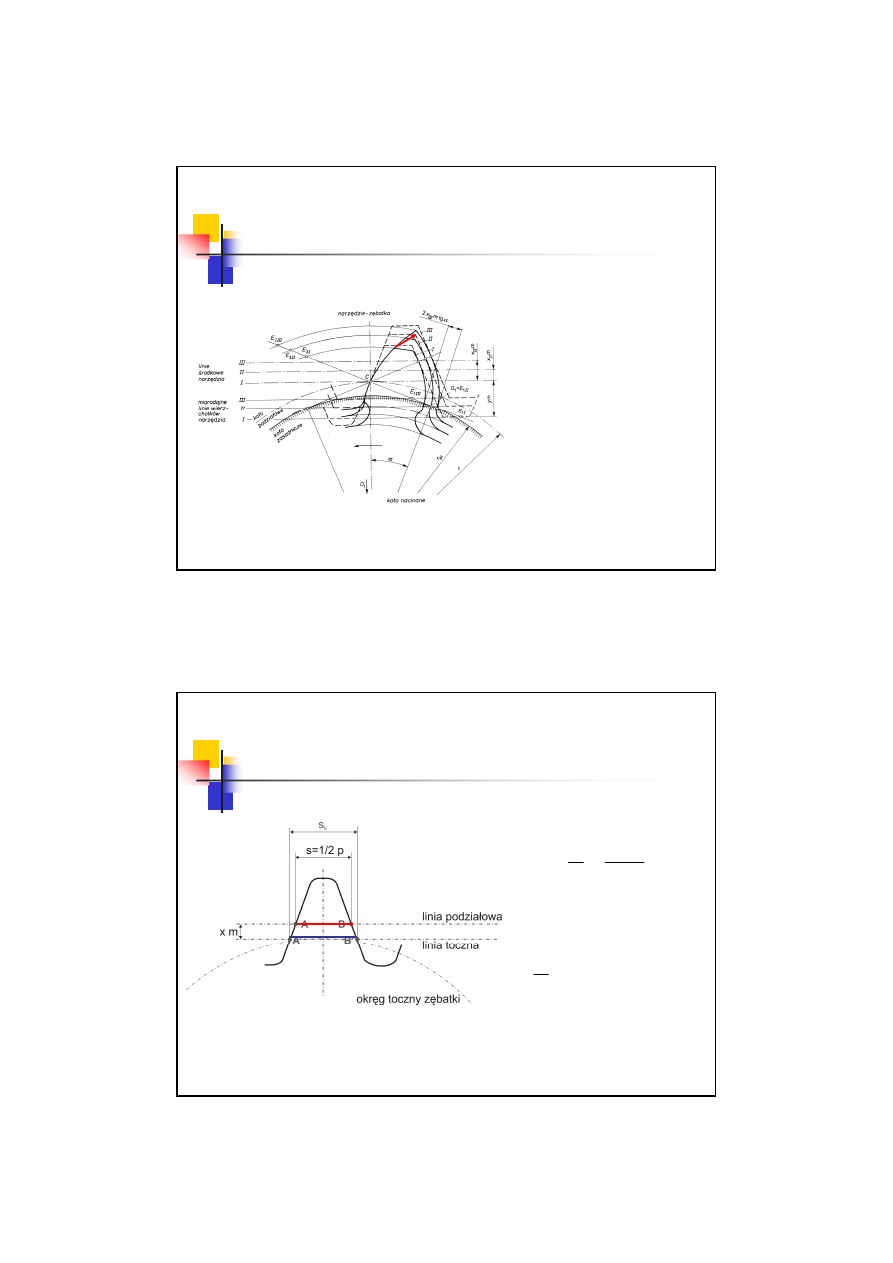
Podcięcie zęba – powstawanie
Podcięcie powstaje zatem wtedy, gdy linia ewolwentowa
tworzona przez zewnętrzny róg narzędzia podczas zazębiania
przetnie się z linią ewolwentową tworzoną przez ten sam róg
podczas wyzębiania
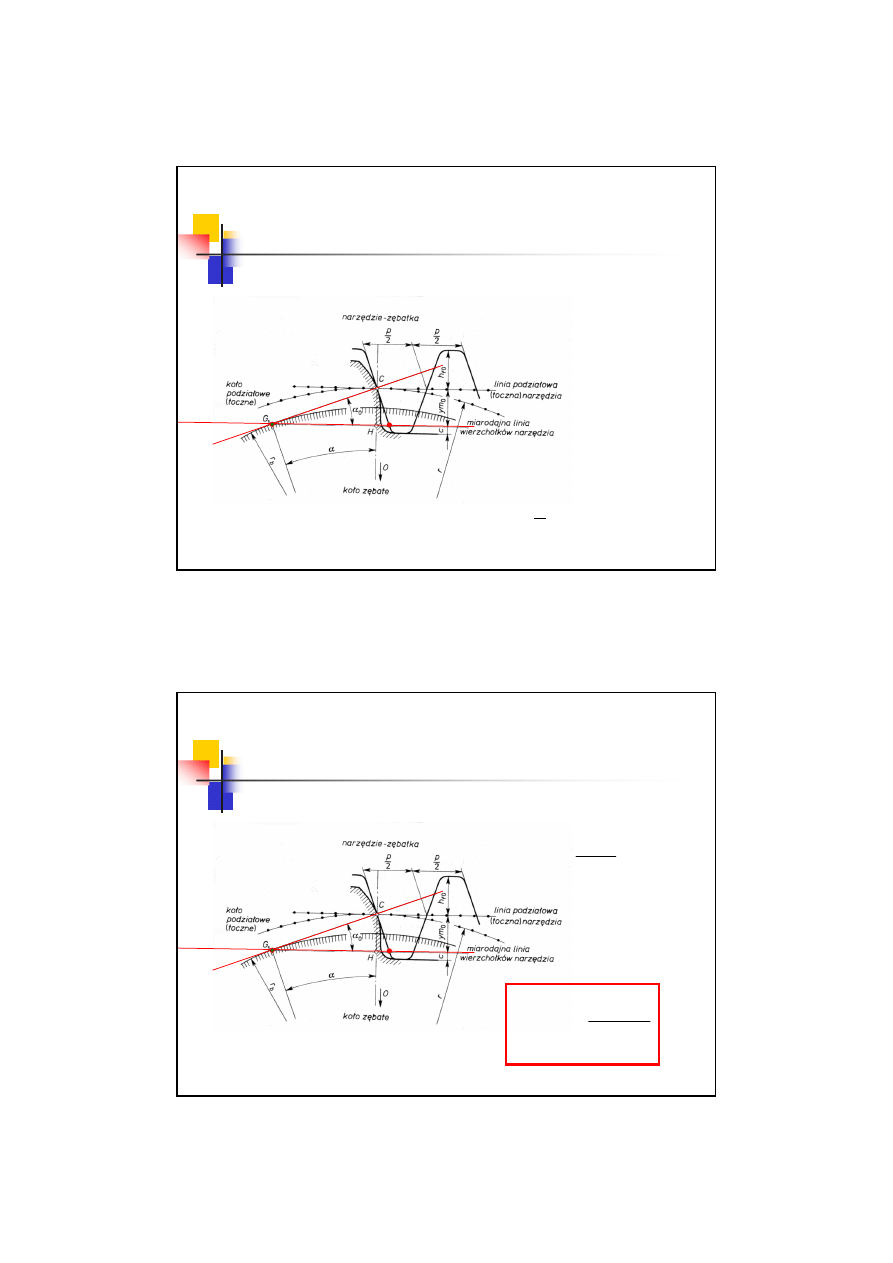
Podcięcie zębów
Graniczna liczba zębów
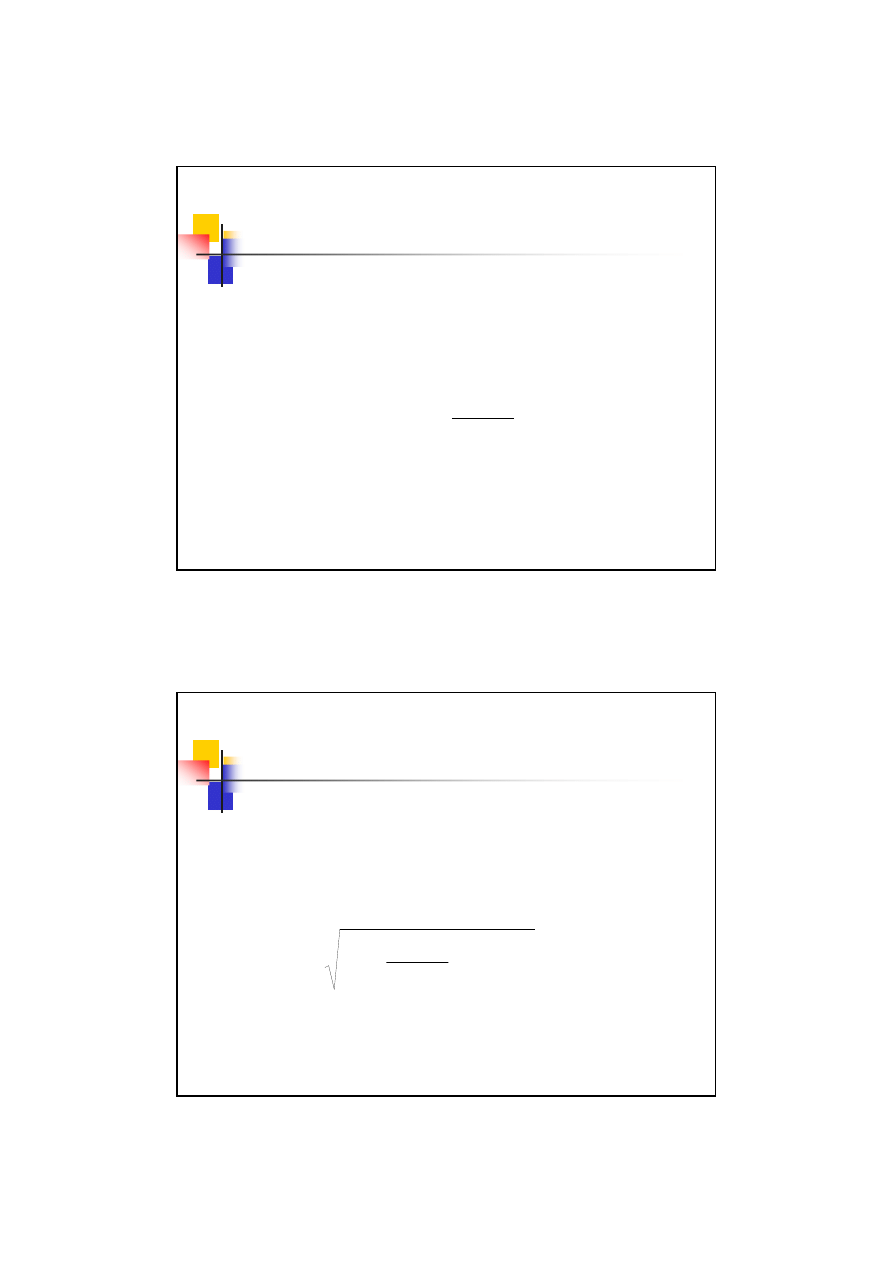
Graniczne dopuszczalne położenie narzędzia jest takie przy którym
prosta równoległa do linii toczne narzędzia
przechodząca przez ostatni
punkt prostoliniowy
krawędzi narzędzia przechodzi przez
punkt
styczności linii przyporu z okręgiem zasadniczym
4
Podcięcie zębów
Graniczna liczba zębów – metoda Maaga
α
sin
⋅
=
⋅
=
CG
m
y
CH
α
sin
⋅
=
r
CG
α
2
sin
⋅
=
⋅
r
m
y
z
m
r
⋅
=
2
1
Podcięcie zębów
Graniczna liczba zębów – metoda Maaga
α
2
sin
2
⋅
⋅
=
⋅
z
m
m
y
α
2
sin
2
⋅
=
=
y
z
z
gr
5
Podcięcie zębów
Graniczna liczba zębów – metoda Maaga
α
2
sin
2
⋅
=
<
y
z
z
gr
Podcięcie nastąpi jeżeli:
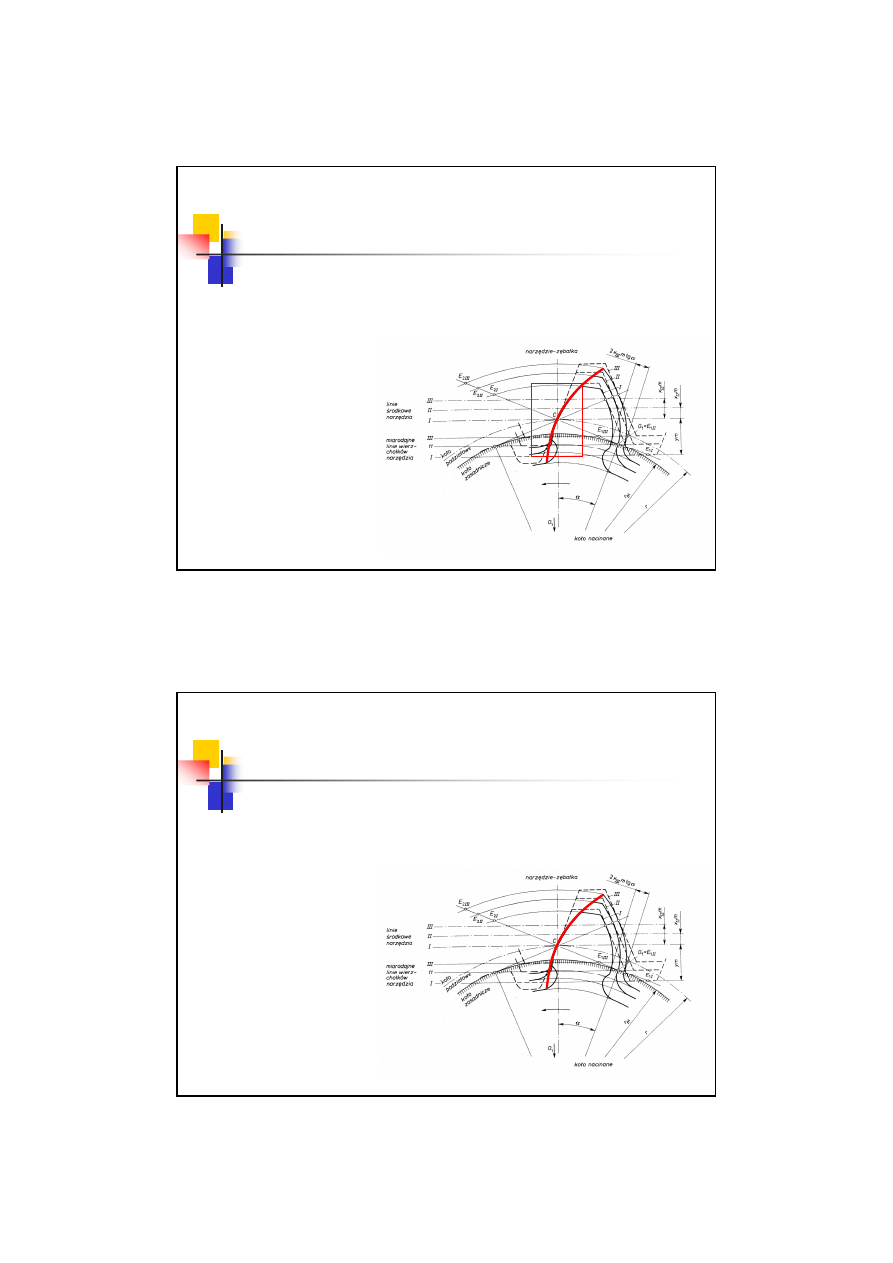
Podcięcie zębów
Graniczna liczba zębów – metoda
Fellowsa
(
)
o
o
o
gr
z
y
z
y
z
z
−
+
⋅
⋅
+
=
α
2
2
sin
4
Zmiana kształtu narzędzia powoduje, że zmieniają się proporcję w
poprzednim zapisie i rolę zaczyna odgrywać liczba zębów narzędzia:
z
o
6
Przesunięcie zarysu
Eliminacja podcięcia zęba
Czasami istnieje potrzeba wykonania koła zębatego o ilości zębów
mniejszej od granicznej.
Aby nie dopuścić do
podcięcia można
„skorzystać z innej części
ewolwenty”
Przesunięcie zarysu
Korekcja uzębienia
Odsunięta zostanie zatem linia toczna narzędzia od koła zasadniczego
wykonywanego koła.
Zabieg ten nazywany jest:
Przesunięciem zarysu
(Korekcją uzębienia)
Ile ?
7
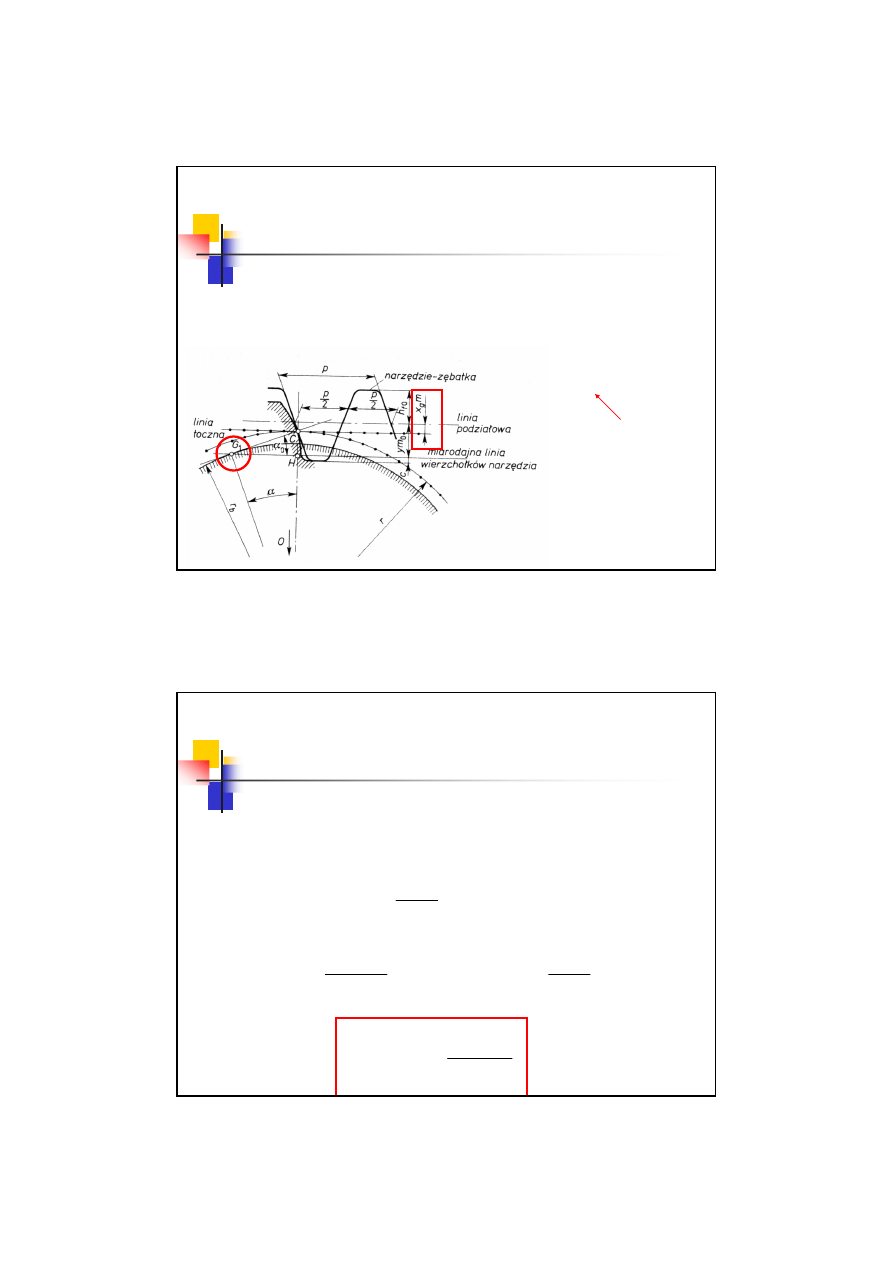
Przesunięcie zarysu
Korekcja uzębienia – wartość graniczna
Jakie powinno być przesunięcie aby uniknąć podcięcia?
m
x
X
gr
⋅
=
Współczynnik korekcji
α
2
sin
⋅
=
⋅
−
⋅
=
r
m
x
m
y
CH
gr
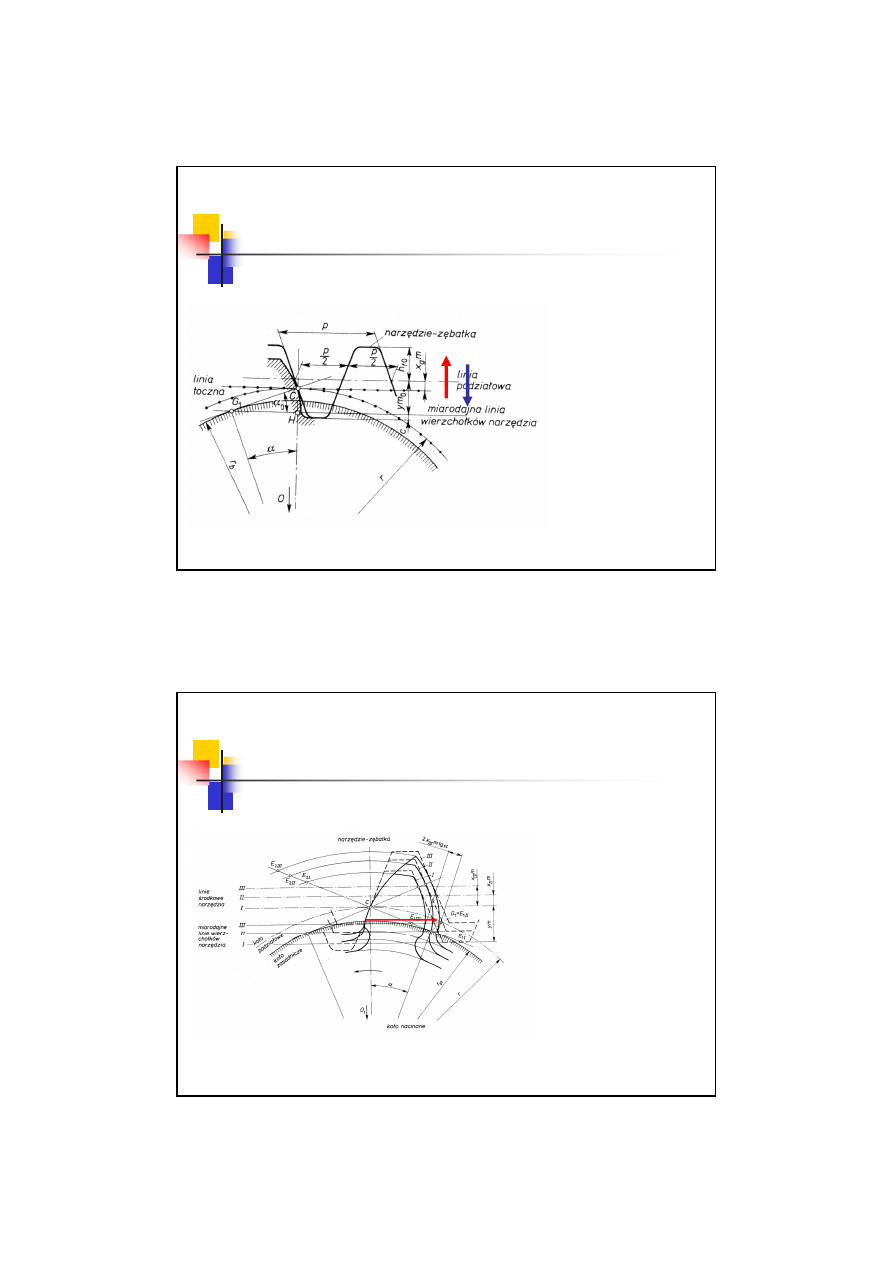
Przesunięcie zarysu
Korekcja uzębienia – wartość graniczna
Zatem:
(
)
α
2
sin
2
⋅
⋅
=
⋅
−
z
m
m
x
y
gr
gr
gr
z
y
y
z
⋅
=
⇒
⋅
=
2
sin
sin
2
2
2
α
α
Ponieważ:
Otrzymujemy:
gr
gr
gr
z
z
z
y
x
−
⋅
=
8
Przesunięcie zarysu
Korekcja uzębienia
0
>
x
Korekcja dodatnia
0
<
x
Korekcja ujemna
Przesunięcie zarysu
Korekcja uzębienia – zalety
Zwiększenie grubości zęba u
podstawy
Zmniejszenie naprężeń
stykowych w wyniku
zmniejszenia krzywizny
ewolwenty
Możliwość zmiany odległości
osi.
9
Przesunięcie zarysu
Korekcja uzębienia – wady
Zmniejszenie grubości zęba
na wierzchołku – możliwość
wykruszenia
Zwiększenie się poślizgu
międzyzębnego – wzrost
tocznego kąta przyporu
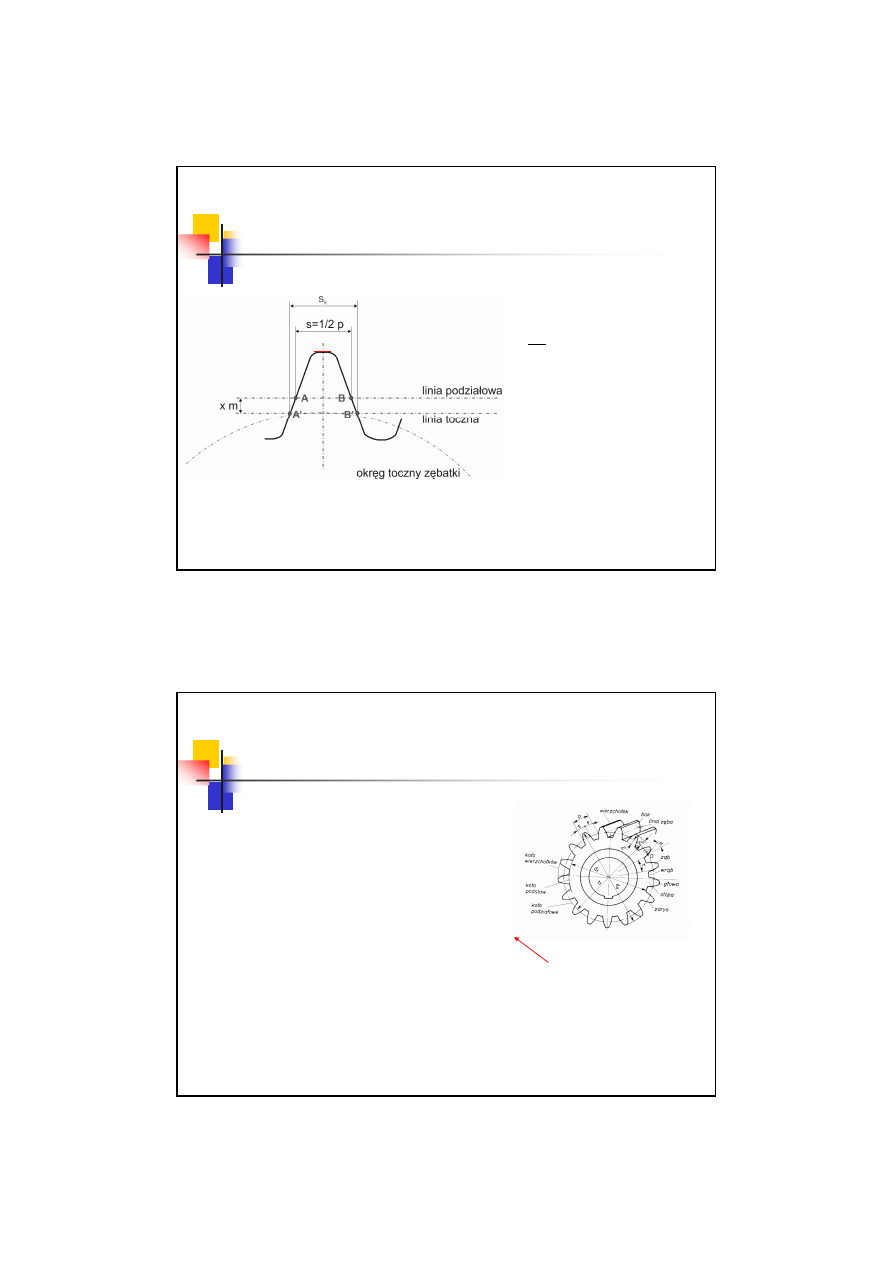
Grubość zęba
Na linii tocznej natomiast:
Grubość zęba na linii
podziałowej wynosi:
2
2
m
P
s
⋅
=
=
π
m
tg
x
s
k
⋅
⋅
⋅
+
=
α
π
2
2
10
Grubość zęba
Wartość ta nie może być za
mała:
Grubość na wierzchołku
zęba wynosi natomiast:
−
+
⋅
=
a
k
a
a
inv
inv
d
s
d
s
α
α
m
s
a
⋅
=
25
,
0
min
Jednolita struktura
materiału
m
s
a
⋅
=
4
,
0
min
Niejednolita struktura materiału (nawęglanie,
hartowanie powierzchniowe)
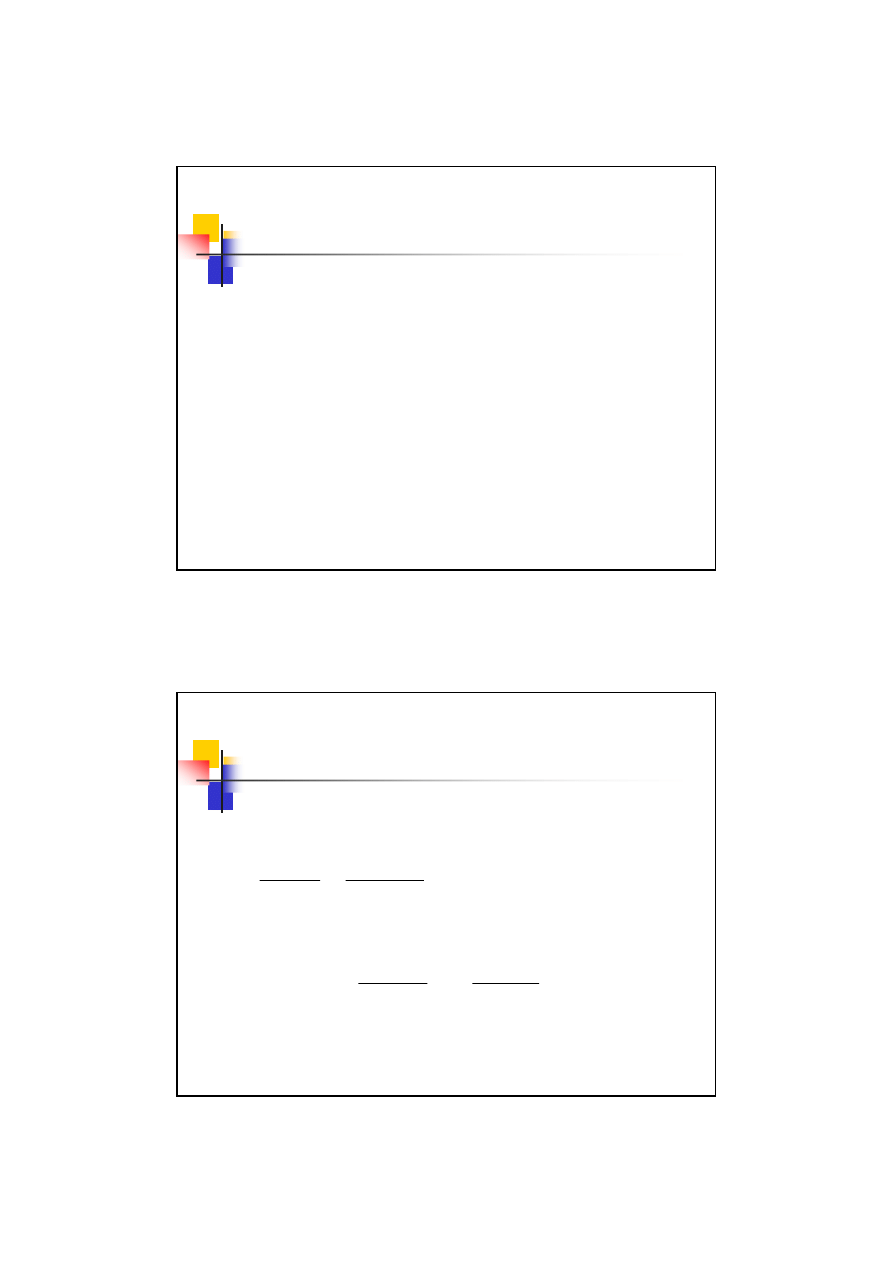
Podstawowe wymiary koła zębatego
Średnica podziałowa
z
m
d
⋅
=
Średnica głów
(
)
k
x
y
z
m
d
a
⋅
−
⋅
+
⋅
+
⋅
=
2
2
2
Współczynnik zeszlifowania głowy zęba
Średnica stóp
(
)
*
2
2
2
c
x
y
z
m
d
f
⋅
−
⋅
+
⋅
−
⋅
=
11
Przykład 9.1
– wymiary koła zębatego
z
1
=13
m
= 5
y
= 1
α
= 20
°°°°
c* = 0,25
W przekładni walcowej dane jest koło o zębach prostych obliczyć
graniczną liczbę zębów, graniczny współczynnik przesunięcia zarysu,
średnice koła, grubość zęba na okręgu podziałowym bez uwzględnienia
przesunięcia zarysu, grubość zęba na okręgu podziałowym oraz grubość
zęba u wierzchołka po uwzględnieniu przesunięcia zarysu. Założyć
obróbkę kół metodą Maaga.
Przykład 9.1
– wymiary koła zębatego
Graniczna liczba zę
ę
ę
ębów:
Graniczny współłłłczynnik przesunię
ę
ę
ęcia zarysu:
> z
1
= 13
17
097
,
17
20
sin
1
2
sin
2
2
2
≈
=
⋅
=
⋅
=
o
gr
y
z
α
2857
,
0
17
13
17
1
1
=
−
⋅
=
−
⋅
=
gr
gr
gr
z
z
z
y
x
Przyjmujemy współczynnik przesunięcia zarysu większy od granicznego
3
,
0
1
=
x
12
Przykład 9.1
– wymiary koła zębatego
Zatem wymiary koła wynoszą
mm
00
,
65
13
5
1
1
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
00
,
78
0
2
3
,
0
2
1
2
13
5
2
2
2
1
1
1
=
⋅
+
⋅
+
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
50
,
55
25
,
0
2
3
,
0
2
1
2
13
5
*
2
2
2
1
1
1
=
⋅
−
⋅
+
⋅
−
⋅
=
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
Przykład 9.1
– wymiary koła zębatego
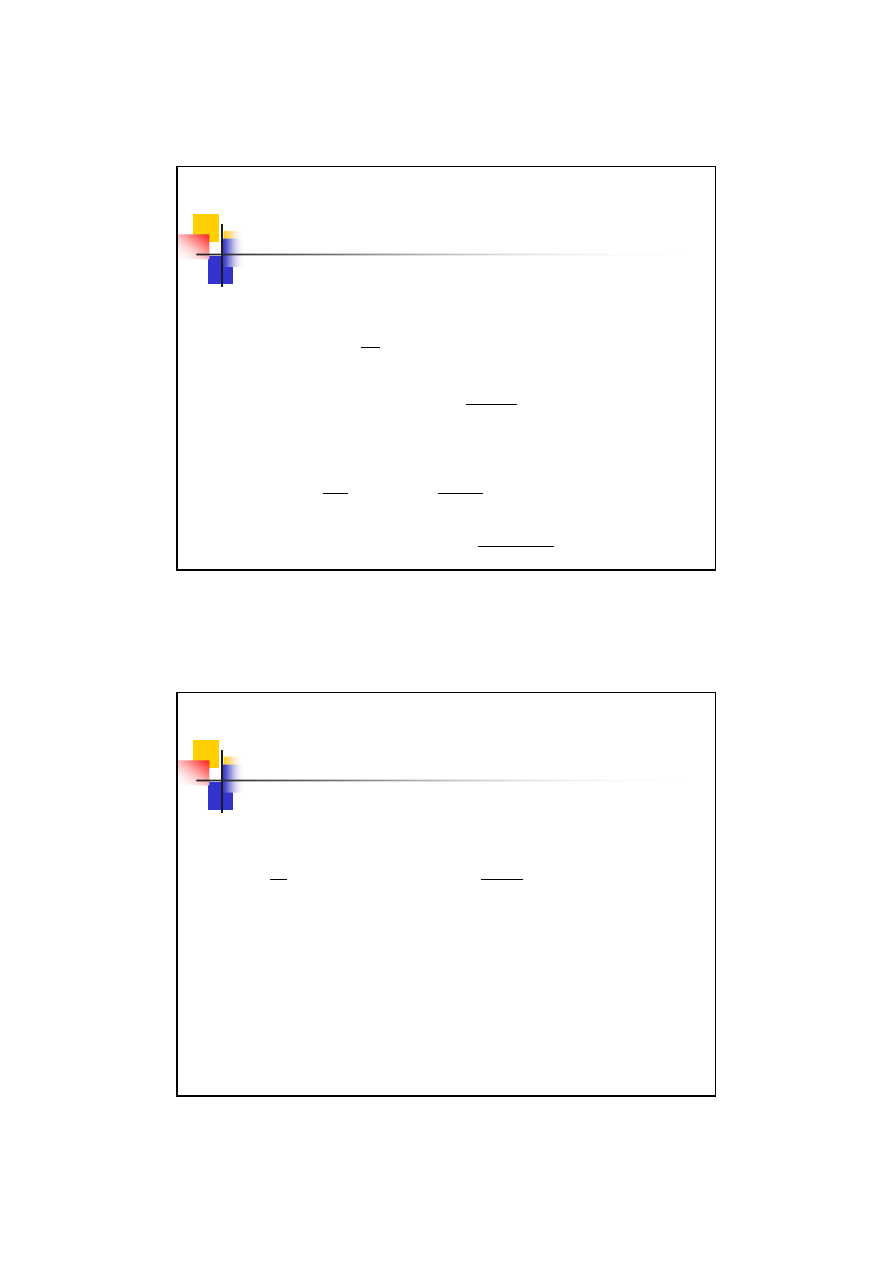
Grubość zęba mierzona na okręgu podziałowym:
mm
854
,
7
2
5
2
=
⋅
=
⋅
=
π
π
m
s
Na linii tocznej natomiast:
mm
946
,
8
5
20
3
,
0
2
2
2
2
1
=
⋅
⋅
⋅
+
=
⋅
⋅
⋅
+
=
o
k
tg
m
tg
x
s
π
α
π
13
Przykład 9.1
– wymiary koła zębatego
Grubość zęba o wierzchołka to:
gdzie:
−
+
⋅
=
a
k
a
a
inv
inv
d
s
d
s
α
α
014904
,
0
180
20
20
=
⋅
−
=
−
=
o
o
o
tg
tg
inv
π
α
α
α
123010
,
0
180
46
,
38
46
,
38
1
1
1
=
⋅
−
=
−
=
o
o
o
a
a
a
tg
tg
inv
π
α
α
α
mm
08
,
61
20
cos
00
,
65
cos
=
⋅
=
⋅
=
o
b
d
d
α
o
a
b
a
d
d
46
,
38
00
,
78
08
,
61
arccos
arccos
1
1
1
=
=
=
α
Przykład 9.1
– wymiary koła zębatego
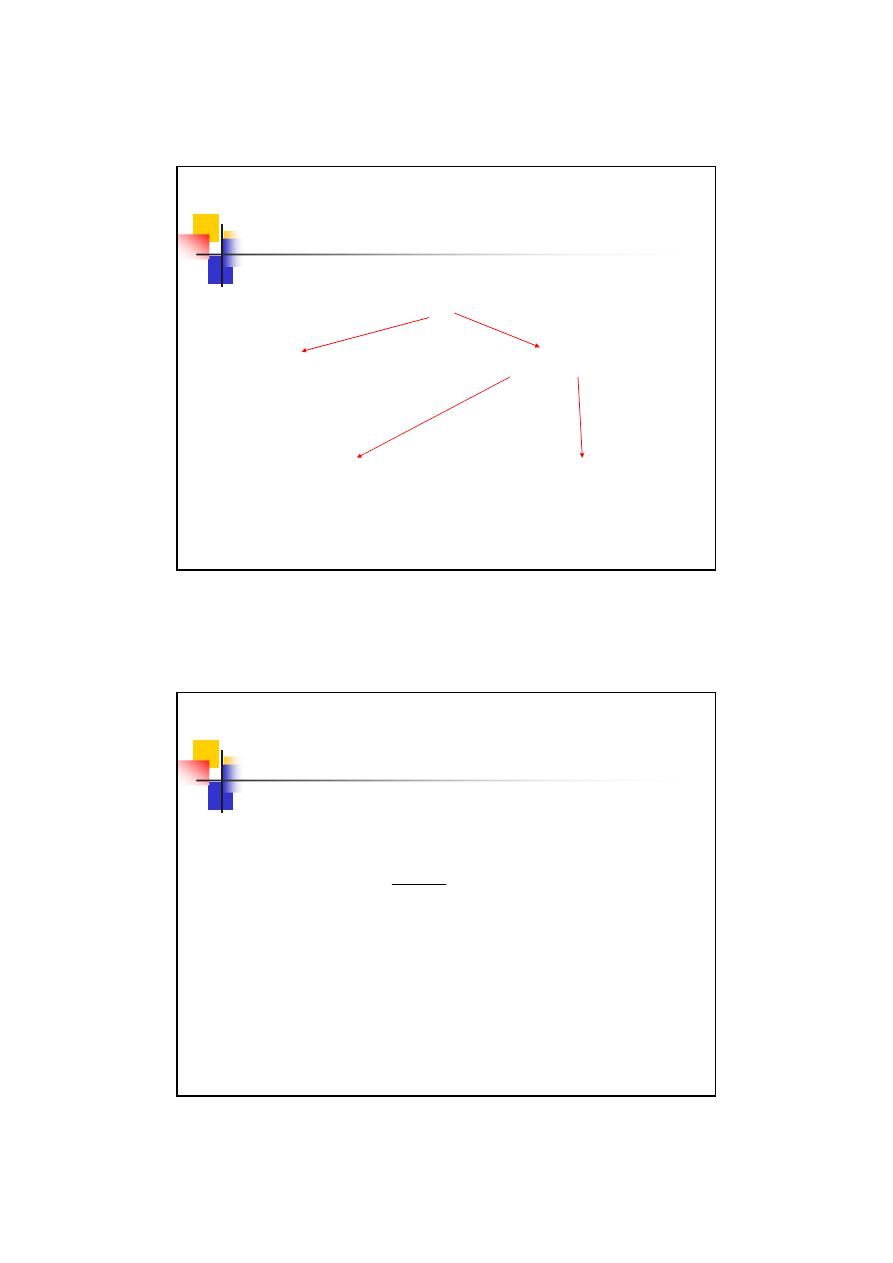
Zatem grubość zęba o wierzchołka to:
Zatem porównując do wartości dopuszczalnych:
mm
303
,
2
123010
,
0
014904
,
0
00
,
65
946
,
8
00
,
78
=
−
+
⋅
=
−
+
⋅
=
a
k
a
a
inv
inv
d
s
d
s
α
α
mm
25
,
1
5
25
,
0
25
,
0
mm
303
,
2
min
=
⋅
=
⋅
=
>
=
m
s
s
a
a
Jednolita struktura materiału
Niejednolita struktura materiału (nawęglanie, hartowanie powierzchniowe)
mm
00
,
2
5
4
,
0
4
,
0
mm
303
,
2
min
=
⋅
=
⋅
=
>
=
m
s
s
a
a
14
Rodzaje zazębień
Zazębienie
Zerowe
Korygowane
Bez przesunięcia osi
P-0
Z przesunięciem osi
P
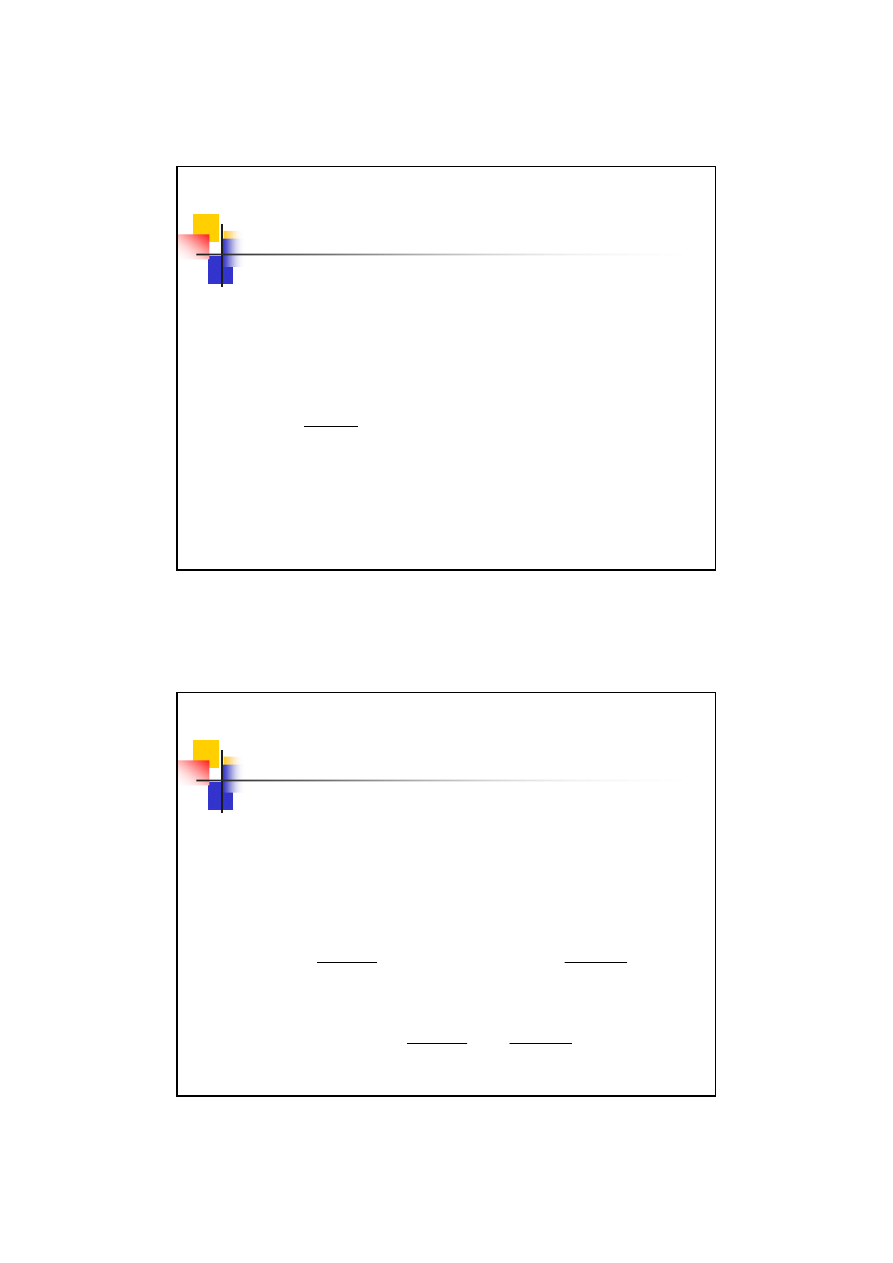
Zazębienie zerowe
Oba koła nie są korygowane
m
z
z
a
a
w
⋅
+
=
=
2
2
1
α
α
=
w
d
d
w
=
0
2
1
=
=
x
x
15
Zazębienie P-0
Oba koła są korygowane ale tak, aby odległość osi pozostała bez zmian
m
z
z
a
a
w
⋅
+
=
=
2
2
1
α
α
=
w
d
d
w
=
0
2
1
=
+
x
x
Uzyskuje się to poprzez zastosowanie korekcji dodatniej dla jednego koła
i korekcji ujemnej o tej samej wartości bezwzględnej dla koła drugiego.
Stosowana jest gdy jedno z kół ma za mało zębów w stosunku do wartości
granicznej.
gr
z
z
<
1
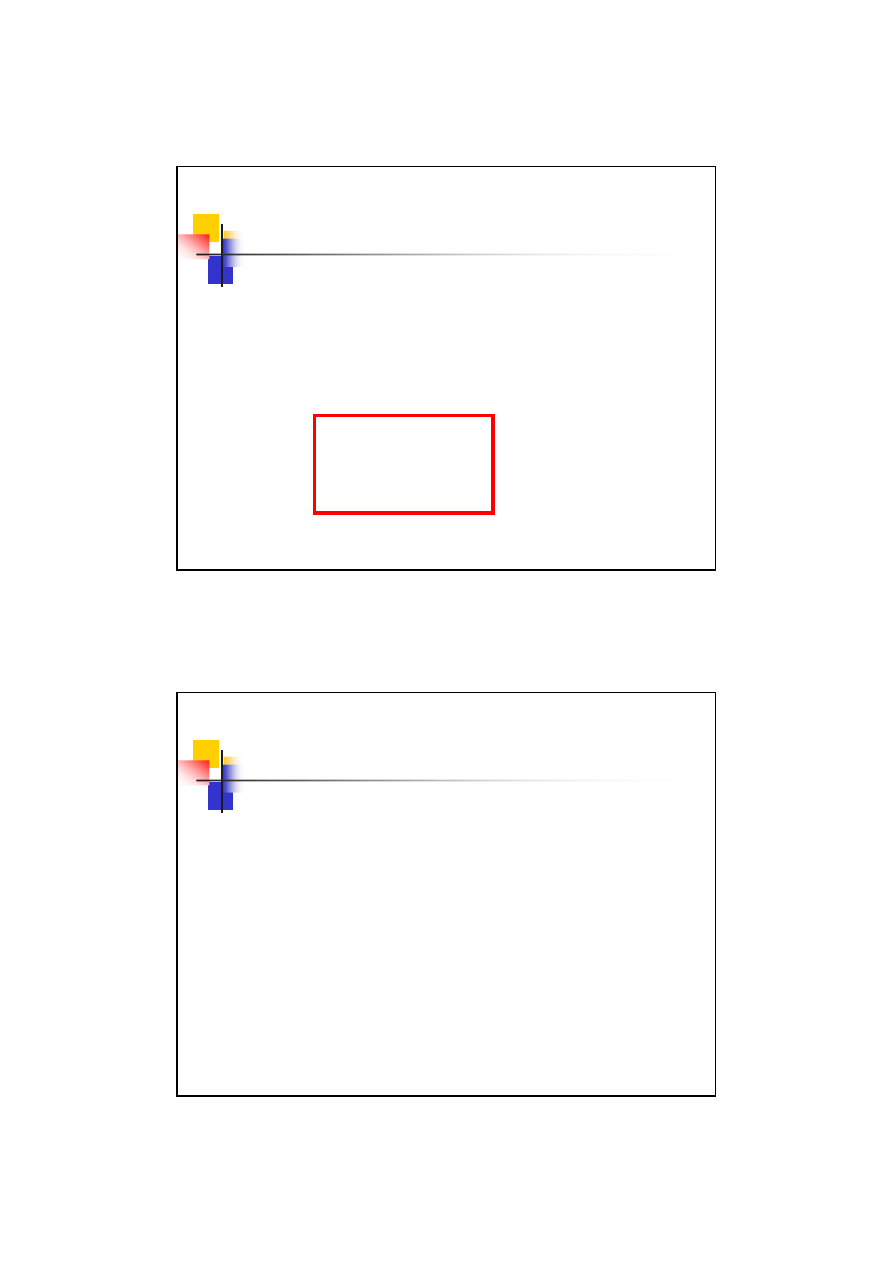
Zazębienie P-0
2
1
x
x
−
=
W takim przypadku musimy jednak pamiętać aby nie uszkodzić drugiego
koła – aby korekcja nie doprowadziła do podcięcia podstawy zęba.
Rozważmy przypadek graniczny:
gr
gr
gr
z
z
z
y
x
x
1
1
1
−
⋅
=
=
gr
gr
gr
z
z
z
y
x
x
2
2
2
−
⋅
=
=
0
2
1
2
1
=
−
⋅
+
−
⋅
=
+
gr
gr
gr
gr
z
z
z
y
z
z
z
y
x
x
16
Zazębienie P-0
gr
z
z
z
⋅
=
+
2
2
1
Zatem:
Stąd do przeprowadzenia
korekcji P-0
konieczne jest spełnienie dwóch
warunków:
gr
z
z
<
1
gr
z
z
z
⋅
≥
+
2
2
1
Konieczność korekcji
Możliwość wykonania
Przykład 9.2
– korekcja P-0
z
1
=13
z
2
=37
m
= 2,5
y
= 1
α
= 20
°°°°
c* = 0,25
Obliczyć wymiary kół zębatych oraz liczbę przyporu dla przekładni:
17
Przykład 9.2
– korekcja P-0
17
097
,
17
20
sin
1
2
sin
2
2
2
≈
=
⋅
=
⋅
=
o
gr
y
z
α
Sprawdźmy, czy korekcja jest potrzebna:
gr
z
z
<
1
Sprawdźmy, czy można wykonać korekcję P-0:
34
17
2
2
50
37
13
2
1
=
⋅
=
⋅
>
=
+
=
+
gr
z
z
z
Oba warunki spełnione zatem można wykonać korekcję P-0
Przykład 9.2
– korekcja P-0
gr
x
x
≥
1
Graniczny współczynnik korekcji:
Przyjmujemy wartość korekcji:
29
,
0
1
2
−
=
−
=
x
x
Zatem:
2857
,
0
17
13
17
1
1
=
−
⋅
=
−
⋅
=
gr
gr
gr
z
z
z
y
x
29
,
0
1
=
x
18
Przykład 9.2
– korekcja P-0
Zatem wymiary koła wynoszą
mm
50
,
32
13
5
,
2
1
1
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
95
,
38
0
2
29
,
0
2
1
2
13
5
,
2
2
2
2
1
1
1
=
⋅
+
⋅
+
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
70
,
27
25
,
0
2
29
,
0
2
1
2
13
5
,
2
*
2
2
2
1
1
1
=
⋅
−
⋅
+
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
mm
50
,
92
37
5
,
2
2
2
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
05
,
96
0
2
29
,
0
2
1
2
37
5
,
2
2
2
2
2
2
2
=
⋅
+
⋅
−
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
80
,
84
25
,
0
2
29
,
0
2
1
2
37
5
,
2
*
2
2
2
2
2
2
=
⋅
−
⋅
−
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
Przykład 9.2
– korekcja P-0
Odległość osi:
mm
50
,
62
2
37
13
5
,
2
2
2
1
=
+
⋅
=
+
⋅
=
z
z
m
a
Średnice zasadnicze:
mm
54
,
30
20
cos
50
,
32
cos
0
1
1
=
⋅
=
⋅
=
α
d
d
b
mm
92
,
86
20
cos
50
,
92
cos
0
2
2
=
⋅
=
⋅
=
α
d
d
b
19
Przykład 9.2
– korekcja P-0
Kąty głów:
Liczba przyporu:
0
1
1
1
36
,
38
94
,
38
54
,
30
arccos
arccos
=
=
=
d
d
b
a
α
0
2
2
2
18
,
25
05
,
96
92
,
86
arccos
arccos
=
=
=
d
d
b
a
α
(
)
(
)
[
]
(
)
(
)
[
]
51
,
1
20
18
,
25
37
20
36
,
38
13
2
1
2
1
2
2
1
1
=
−
⋅
+
−
⋅
⋅
=
−
⋅
+
−
⋅
⋅
=
o
o
o
o
a
a
tg
tg
tg
tg
tg
tg
z
tg
tg
z
π
α
α
α
α
π
ε
Zazębienie P
W tym przypadku następuje przesunięcie osi:
a
a
w
≠
Spowodowane jest tym, że oba koła mają różne korekcję:
0
2
1
≠
+
x
x
Zatem po nacięciu kół powinny być one umieszczone w odległości:
(
)
m
x
x
a
a
p
⋅
+
+
=
2
1
Jest to tzw.
pozorna odległość osi
Takie umieszczenie spowoduje duży luz boczny zębów (w wyniku
innej krzywizny ewolwenty)
20
Zazębienie P
Dlatego też koniecznej jest zbliżenie kół o pewną wielkość:
m
k
⋅
Zatem odległość rzeczywista wyniesie:
m
k
a
a
p
w
⋅
−
=
Zbliżenie to powoduje spadek luzu wierzchołkowego:
k
c
c
−
=
*
'
Aby pozostawić luz na niezmienionym poziomie należy zatem skrócić
wierzchołek zęba o wartość
współczynnika zeszlifowania głowy zęba
pomnożony przez moduł
m
k
⋅
Zazębienie P
Współczynnik ten nie musi być brany pod uwagę zawsze.
Nie wprowadzenie go do obliczeń będzie prowadziło do
zmniejszenia luzy wierzchołkowego do wartości:
k
c
c
−
=
*
'
Zatem jeżeli tak zmniejszony luz pozostanie w granicach
dopuszczalnych:
25
,
0
15
,
0
'
÷
=
c
Można pominąć współczynnik zeszlifowania zęba w dalszych
obliczeniach.
21
Zazębienie P
Przy odpowiednim przesunięciu środków kół otrzymujemy
zerowy luz międzyzębny
Zatem grubości zębów na okręgu tocznym są równe podziałce:
w
s
w
p
s
s
=
+
2
1
Po przekształceniach otrzymujemy podstawowy wzór w korekcji P
α
α
α
tg
z
z
x
x
inv
inv
w
⋅
+
+
⋅
=
−
2
1
2
1
2
Zazębienie P – przypadki
zastosowania
Korekcję P stosuje się gdy:
Konieczna jest korekcja dla
uniknięcia podcięcia zębów a nie
można zastosować korekcji P-0
Chcemy wymusić przesunięcie
odległości osi kół
P-technologiczna
P-konstrukcyjna
22
Korekcja P – technologiczna
Korekcję P-technologiczną stosuje się gdy:
gr
z
z
<
1
gr
z
z
z
⋅
<
+
2
2
1
Pierwszym krokiem jest określenie współczynników korekcji
dla obu kół (wartości granicznych)
gr
gr
gr
z
z
z
y
x
1
1
−
⋅
=
gr
gr
gr
z
z
z
y
x
2
2
−
⋅
=
A następnie przyjęcie ich wartości:
1
1
gr
x
x
≥
2
2
gr
x
x
≥
Korekcja P – technologiczna
Na podstawie tych wartości określa się
rzeczywisty toczny kąt przyporu:
Na jego podstawie określa się rzeczywistą odległość osi jako:
α
α
cos
cos
⋅
=
⋅
a
a
w
w
Następnie oblicza się współczynnik zeszlifowania głowy zęba:
m
a
a
k
w
p
−
=
(
)
m
x
x
a
a
p
⋅
+
+
=
2
1
α
α
α
tg
z
z
x
x
inv
inv
w
⋅
+
+
⋅
=
−
2
1
2
1
2
Obliczenie wymiarów kół.
23
Przykład 9.3
– korekcja P-technologiczna
z
1
=15
z
2
=18
m
= 2,5
y
= 1
α
= 20
°°°°
c* = 0,25
Obliczyć wymiary kół zębatych przekładni:
Przykład 9.3
– korekcja P-technologiczna
Sprawdzamy konieczność i rodzaj korekcji:
gr
z
z
<
1
34
17
2
2
33
18
15
2
1
=
⋅
=
⋅
<
=
+
=
+
gr
z
z
z
17
097
,
17
20
sin
1
2
sin
2
2
2
≈
=
⋅
=
⋅
=
o
gr
y
z
α
Zatem korekcja P-technologiczna
24
Przykład 9.3
– korekcja P-technologiczna
Określamy wartości graniczne współczynników korekcji dla obu kół
1176
,
0
17
15
17
1
1
1
=
−
⋅
=
−
⋅
=
gr
gr
gr
z
z
z
y
x
059
,
0
17
18
17
1
2
2
−
=
−
⋅
=
−
⋅
=
gr
gr
gr
z
z
z
y
x
Przyjmujemy wartości współczynników większe od granicznych
12
,
0
1
=
x
05
,
0
2
−
=
x
Przykład 9.3
– korekcja P-technologiczna
Obliczamy lub odczytujemy z tablicy wartość inwoluty kąta zarysu
narzędzia (zerowego kąta przyporu)
014904
,
0
180
20
20
=
⋅
−
=
−
=
o
o
o
tg
tg
inv
π
α
α
α
Obliczamy wartość inwoluty rzeczywistego tocznego kąta przyporu:
016449
,
0
014904
,
0
20
18
15
05
,
0
12
,
0
2
2
2
1
2
1
=
+
⋅
+
−
⋅
=
+
⋅
+
+
⋅
=
o
w
w
tg
inv
inv
tg
z
z
x
x
inv
α
α
α
α
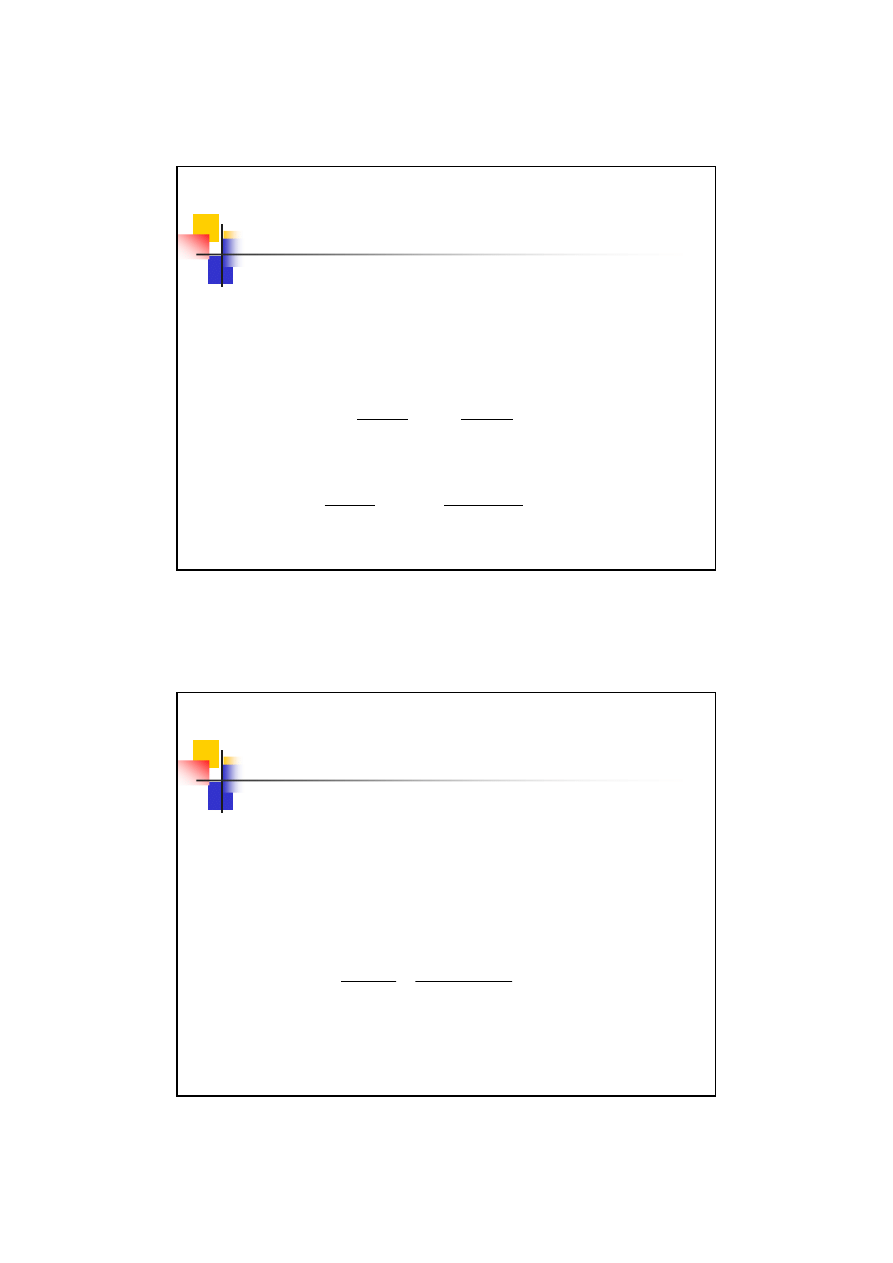
25
Przykład 9.3
– korekcja P-technologiczna
Z tabeli odczytujemy kąt:
o
o
w
65
,
20
'
39
20
=
=
α
Obliczamy zerową odległość osi:
25
,
41
2
18
15
5
,
2
2
2
1
=
+
⋅
=
+
⋅
=
z
z
m
a
Obliczamy rzeczywistą odległość osi:
mm
42
,
41
65
,
20
cos
20
cos
25
,
41
cos
cos
=
⋅
=
⋅
=
o
o
w
w
a
a
α
α
Przykład 9.3
– korekcja P-technologiczna
Oraz obliczamy współczynnik zeszlifowania głowy zęba:
004
,
0
5
,
2
42
,
41
43
,
41
=
−
=
−
=
m
a
a
k
w
p
(
)
(
)
mm
43
,
41
5
,
2
05
,
0
12
,
0
25
,
41
2
1
=
⋅
−
+
=
⋅
+
+
=
m
x
x
a
a
p
Następnie obliczamy pozorną odległość osi:
Przy założonym luzie wierzchołkowym
c*
= 0,25 obniżenie
go o 0,004 nie spowoduje wyjścia poza zakres dopuszczalny
to przyjmujemy:
0
=
k
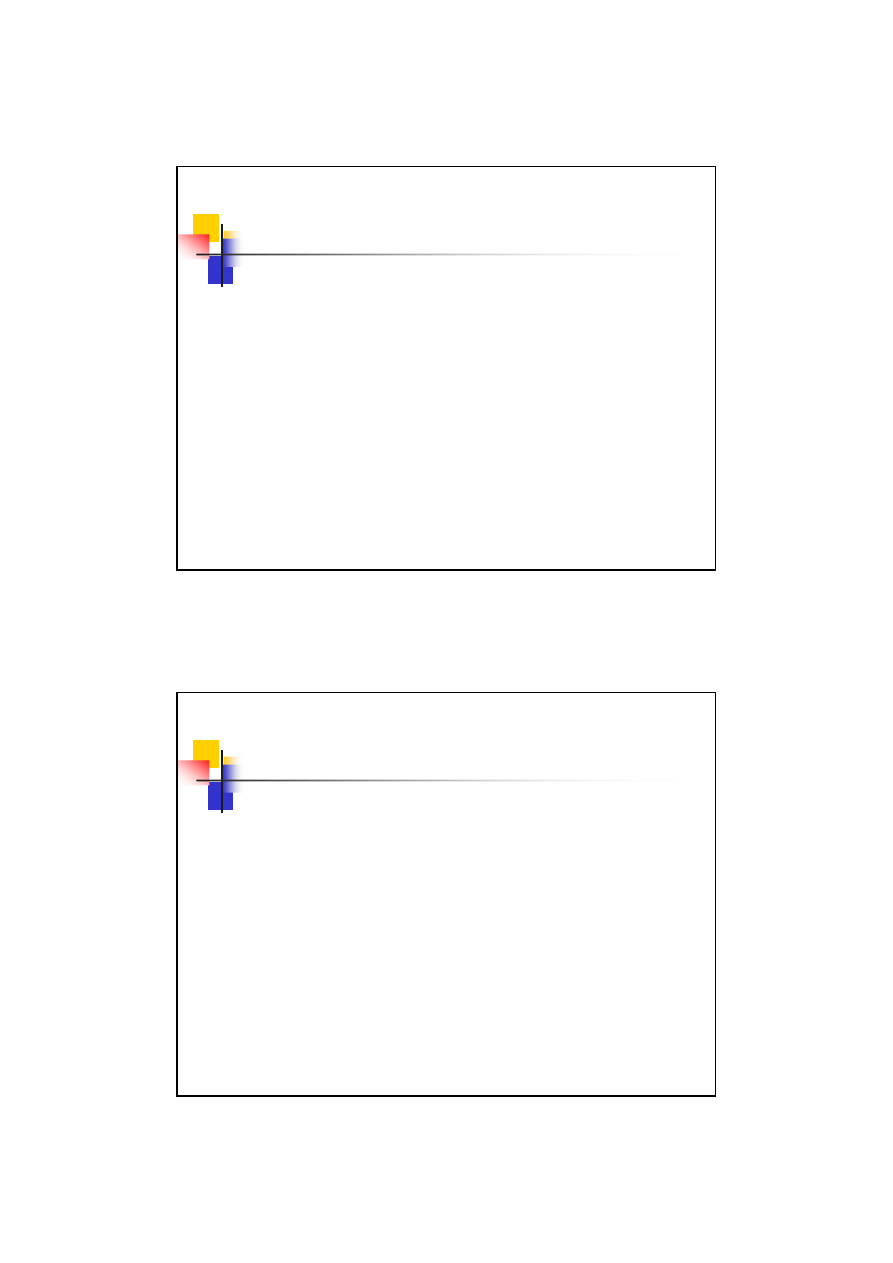
26
Przykład 9.3
– korekcja P-technologiczna
Zatem wymiary koła wynoszą
mm
50
,
37
15
5
,
2
1
1
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
10
,
43
0
2
12
,
0
2
1
2
15
5
,
2
2
2
2
1
1
1
=
⋅
+
⋅
+
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
85
,
31
25
,
0
2
12
,
0
2
1
2
15
5
,
2
*
2
2
2
1
1
1
=
⋅
−
⋅
+
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
mm
00
,
45
18
5
,
2
2
2
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
75
,
49
0
2
05
,
0
2
1
2
18
5
,
2
2
2
2
2
2
2
=
⋅
+
⋅
−
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
50
,
38
25
,
0
2
05
,
0
2
1
2
18
5
,
2
*
2
2
2
2
2
2
=
⋅
−
⋅
−
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
Korekcja P – konstrukcyjna
Korekcję P-konstrukcyjną stosuje się gdy mamy narzuconą
odległość osi
a
a
w
≠
Zatem korekcja P-konstrukcyjna jest odwrotna
do korekcji P-technologicznej
Pierwszym krokiem jest obliczenie rzeczywistego tocznego
kąta przyporu:
α
α
cos
cos
⋅
=
⋅
a
a
w
w
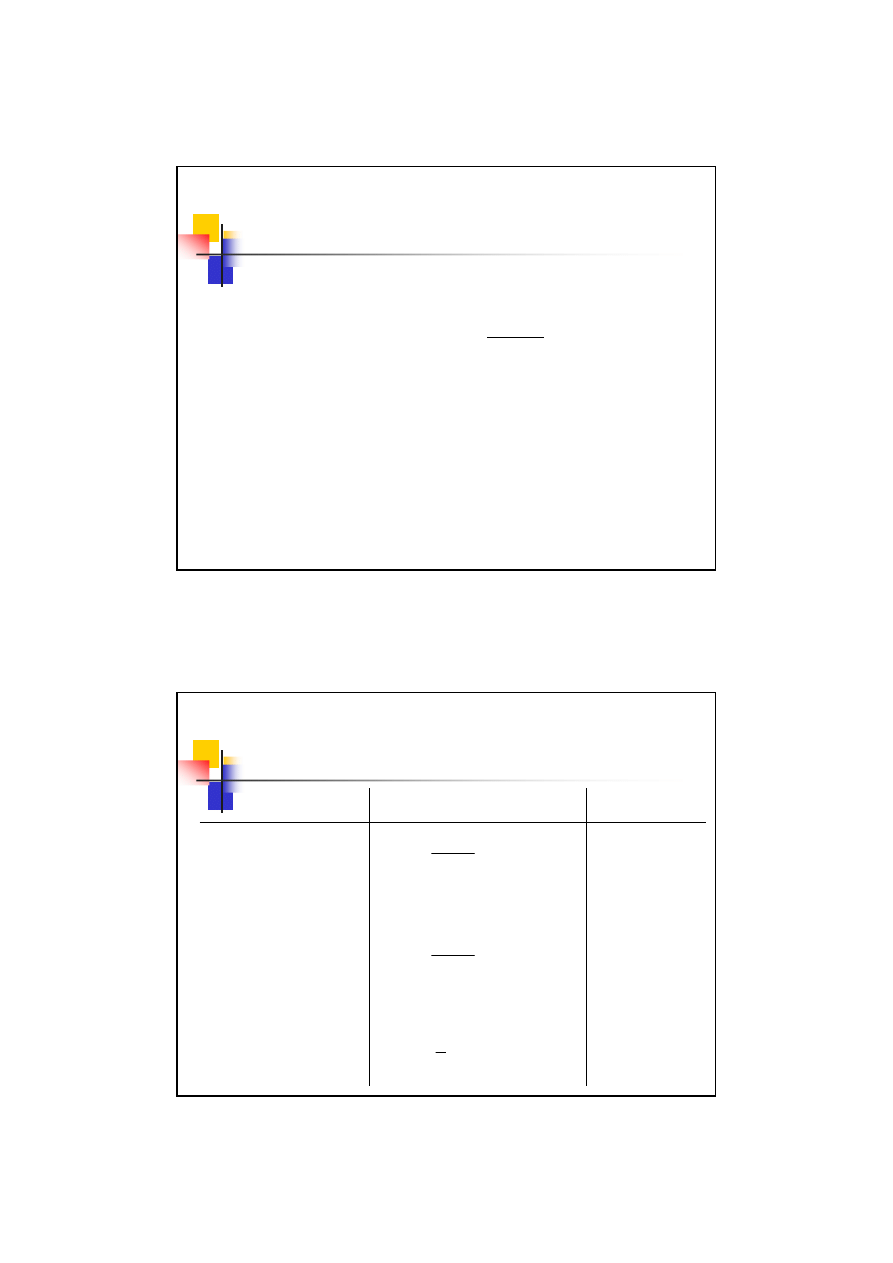
27
Korekcja P – konstrukcyjna
Następnie ze wzoru:
Wyznacza się sumę współczynników korekcji
x
1
+x
2
Następnym krokiem jest rozdział tej sumy
na poszczególne koła.
α
α
α
tg
z
z
x
x
inv
inv
w
⋅
+
+
⋅
=
−
2
1
2
1
2
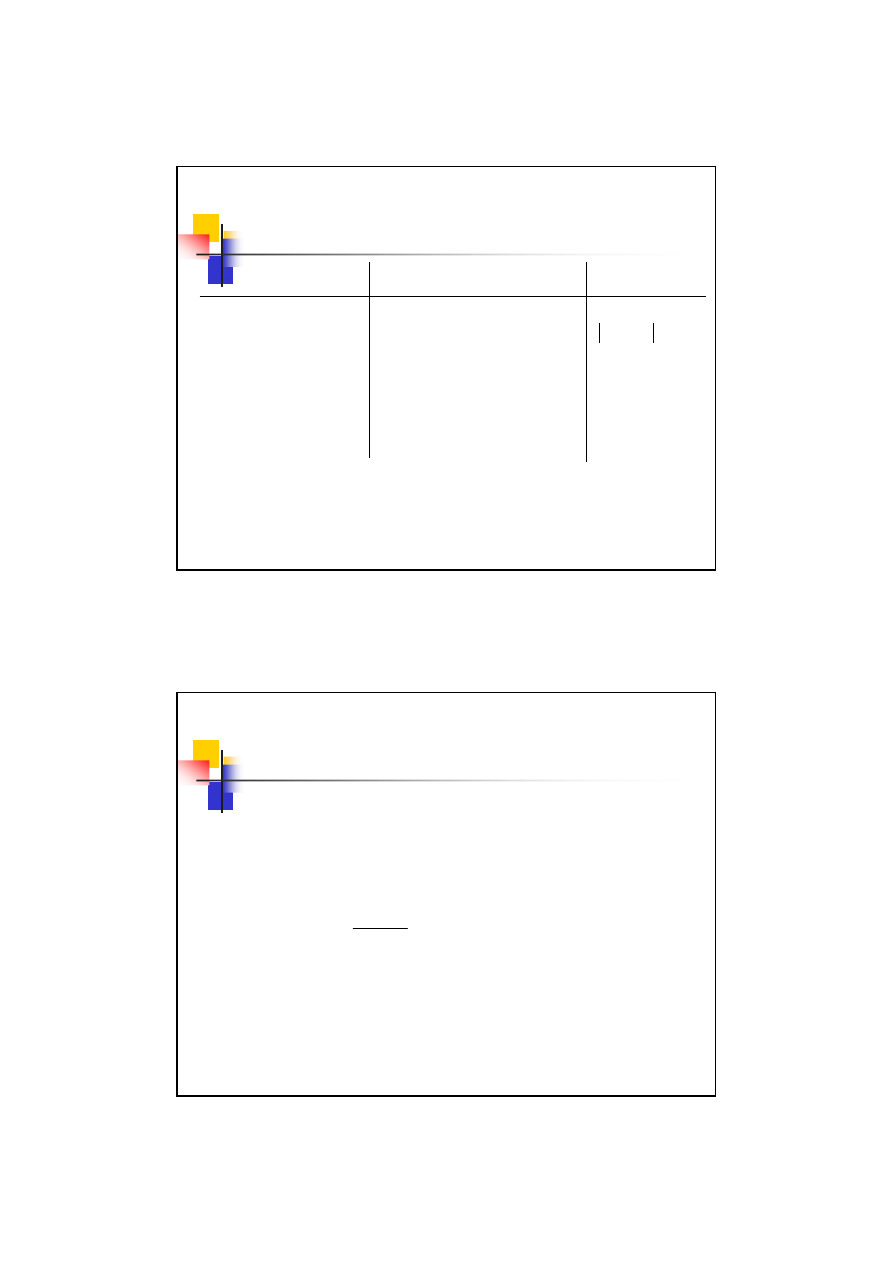
Korekcja P – konstrukcyjna
Kryteria podziału sumy współczynników x
Nazwa kryterium
Sposób przeprowadzania Zastosowanie
Odwrotnie
proporcjonalnie
(
)
(
)
1
2
1
2
2
1
2
1
2
1
x
x
x
x
x
x
z
z
z
x
−
+
=
+
⋅
+
=
Korekcja
dodatnia
(
)
0
2
1
>
+
x
x
Wprost
proporcjonalnie
(
)
(
)
1
2
1
2
2
1
2
1
1
1
x
x
x
x
x
x
z
z
z
x
−
+
=
+
⋅
+
=
Korekcja
ujemna
(
)
0
2
1
<
+
x
x
Po równo
(
)
1
2
2
1
1
2
1
x
x
x
x
x
=
+
⋅
=
2
1
z
z
≈
28
Korekcja P – konstrukcyjna
Kryteria podziału sumy współczynników x
Nazwa kryterium
Sposób przeprowadzania Zastosowanie
Wszystko na jedno
koło
(
)
0
2
2
1
1
=
+
=
x
x
x
x
(
)
3
,
0
2
1
<
+
x
x
Niestandardowy
2
2
1
1
gr
gr
x
x
x
x
≥
≥
Zagrożenie
podcięciem
jednego lub
obu kół
Przy obliczeniach często sprawdza się kilka metod do
danego zadania.
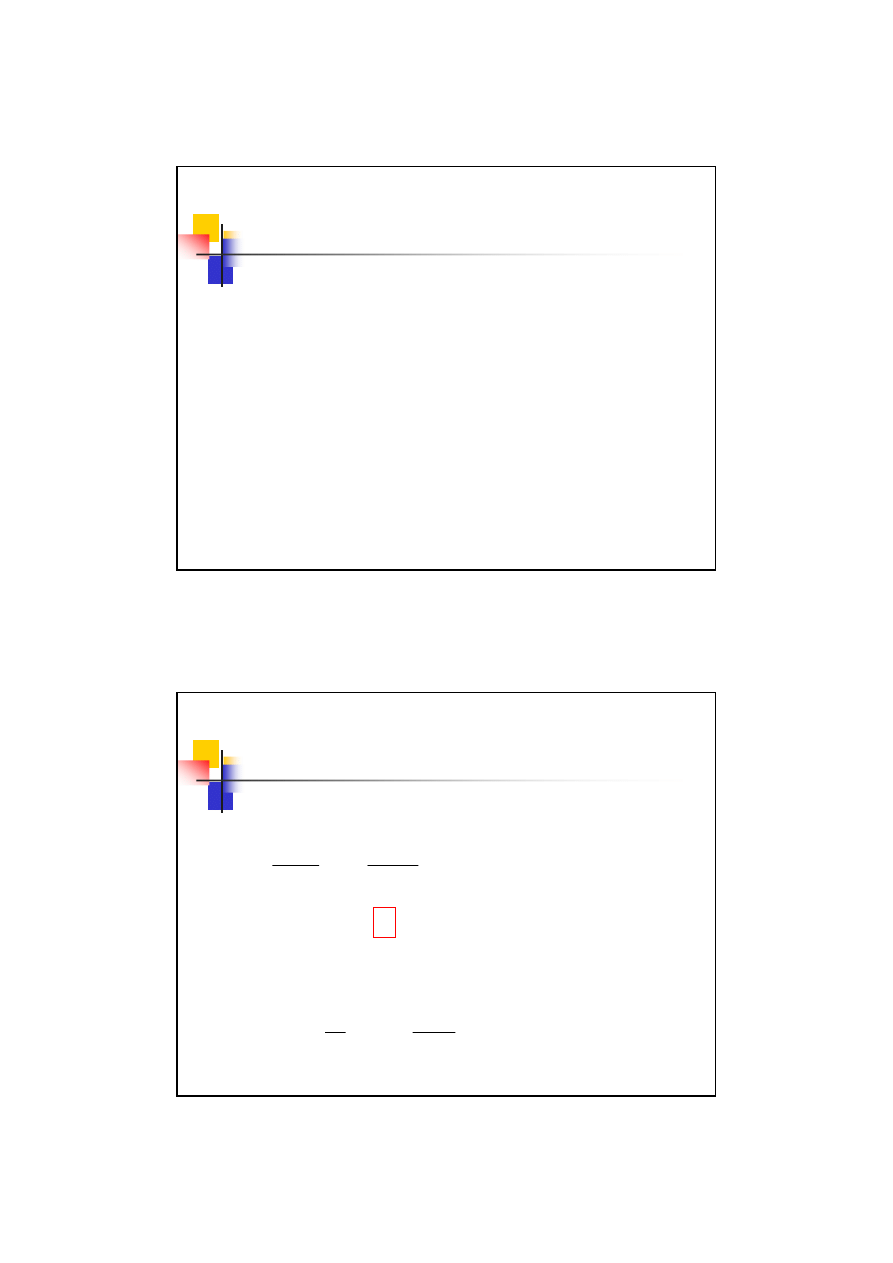
Korekcja P – konstrukcyjna
Mając wartości współczynników korekcji dla obu kół oblicza się
jeszcze współczynnik zeszlifowania głowy zęba:
m
a
a
k
w
p
−
=
(
)
m
x
x
a
a
p
⋅
+
+
=
2
1
Obliczenie wymiarów kół.
29
Przykład 9.4
– korekcja P-konstrukcyjna
z
1
=18
z
2
=29
m
= 2,5
y
= 1
α
= 20
°°°°
c* = 0,25
Obliczyć wymiary kół zębatych przekładni tak aby rzeczywista odległosć
osi wynosiła
a
w
= 60,00 mm
Przykład 9.4
– korekcja P-konstrukcyjna
Sprawdzamy konieczność i rodzaj korekcji:
mm
00
,
60
mm
78
,
58
=
≠
=
w
a
a
mm
75
,
58
2
29
18
5
,
2
2
2
1
=
+
⋅
=
+
⋅
=
z
z
m
a
Zatem korekcja P-konstrukcyjna
Obliczamy rzeczywisty toczny kąt przyporu:
'
3
23
9201
,
0
20
cos
00
,
60
75
,
58
cos
cos
o
w
o
w
w
a
a
=
=
⋅
=
⋅
=
α
α
α
30
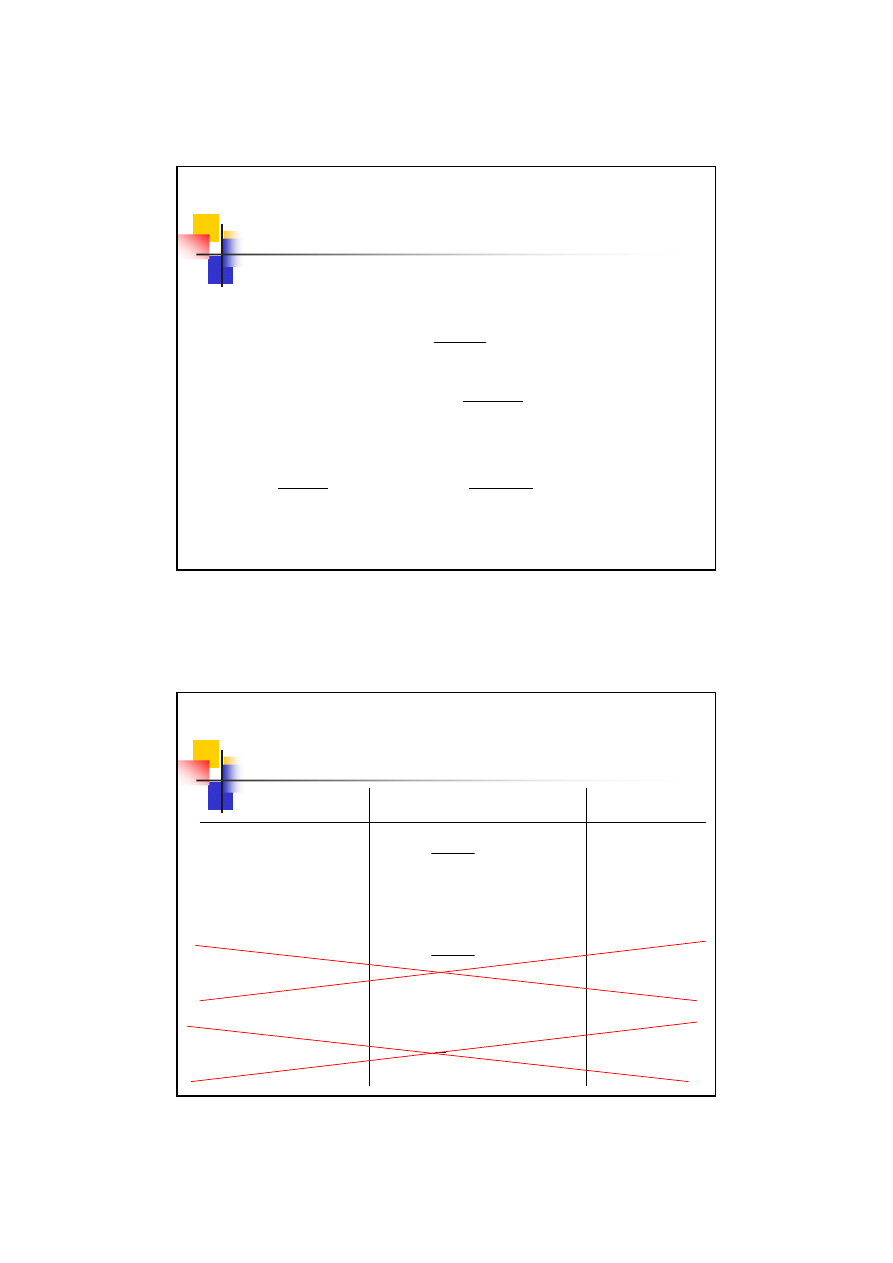
Przykład 9.4
– korekcja P-konstrukcyjna
014904
,
0
180
20
20
=
⋅
−
=
−
=
o
o
o
tg
tg
inv
π
α
α
α
Inwoluty kątów:
023228
,
0
180
'
3
23
'
3
23
=
⋅
−
=
−
=
o
o
o
w
w
w
tg
tg
inv
π
α
α
α
Zatem suma współczynników korekcji wyniesie:
(
)
(
)
(
)
(
)
537
,
0
014904
,
0
023228
,
0
20
2
29
18
2
2
1
2
1
2
1
=
+
−
⋅
⋅
+
=
−
⋅
⋅
+
=
+
x
x
tg
inv
inv
tg
z
z
x
x
o
w
α
α
α
Przykład 9.4
– korekcja P-konstrukcyjna
Nazwa kryterium
Sposób przeprowadzania Zastosowanie
Odwrotnie
proporcjonalnie
(
)
(
)
1
2
1
2
2
1
2
1
2
1
x
x
x
x
x
x
z
z
z
x
−
+
=
+
⋅
+
=
Korekcja
dodatnia
(
)
0
2
1
>
+
x
x
Wprost
proporcjonalnie
(
)
(
)
1
2
1
2
2
1
2
1
1
1
x
x
x
x
x
x
z
z
z
x
−
+
=
+
⋅
+
=
Korekcja
ujemna
(
)
0
2
1
<
+
x
x
Po równo
(
)
1
2
2
1
1
2
1
x
x
x
x
x
=
+
⋅
=
2
1
z
z
≈
√√√√
31
Przykład 9.4
– korekcja P-konstrukcyjna
(
)
0
2
2
1
1
=
+
=
x
x
x
x
17
097
,
17
20
sin
1
2
sin
2
2
2
≈
=
⋅
=
⋅
=
o
gr
y
z
α
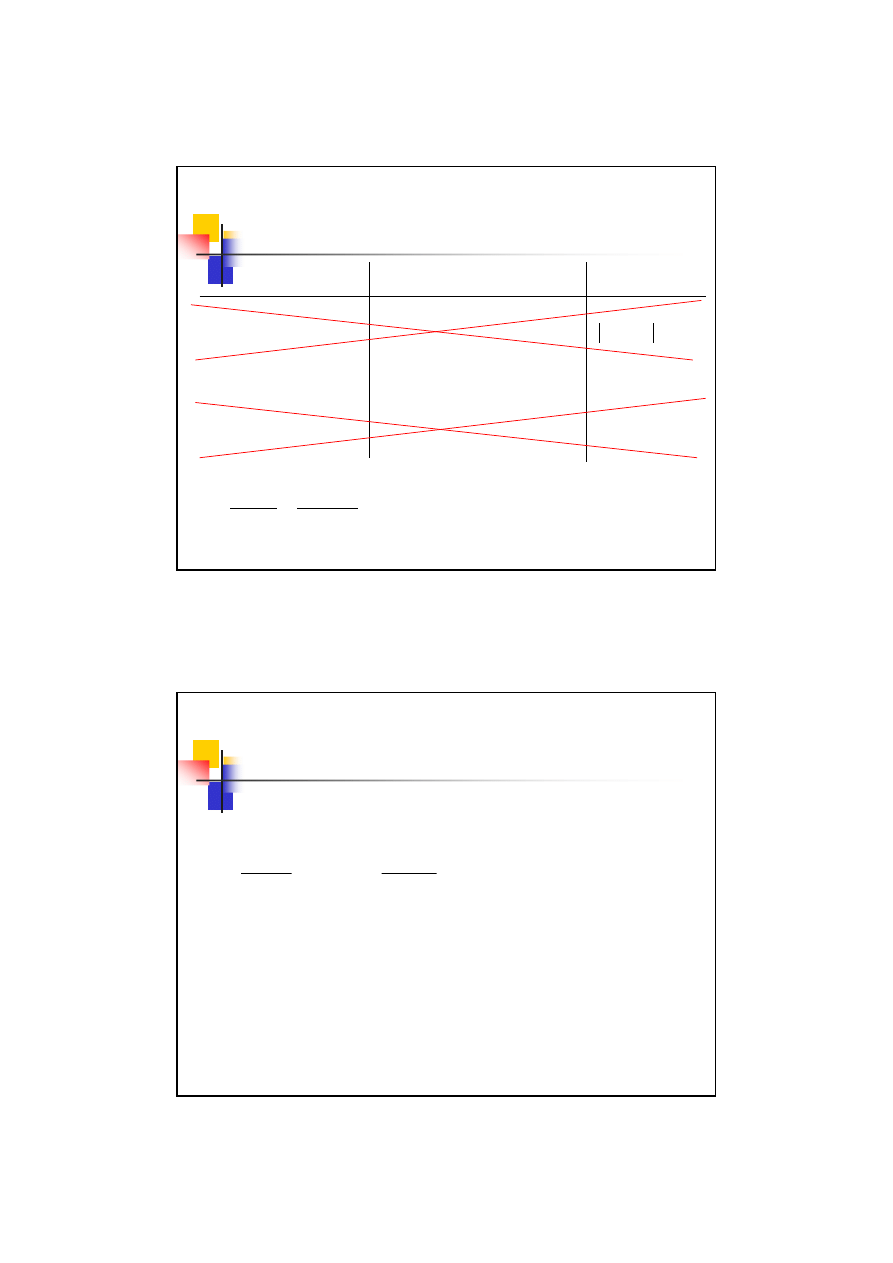
Nazwa kryterium
Sposób przeprowadzania Zastosowanie
Wszystko na jedno
koło
(
)
3
,
0
2
1
<
+
x
x
Niestandardowy
2
2
1
1
gr
gr
x
x
x
x
≥
≥
Zagrożenie
podcięciem
jednego lub
obu kół
?
gr
gr
z
z
z
z
>
>
2
1
(
)
0
537
,
0
2
1
>
=
+
x
x
Przykład 9.4
– korekcja P-konstrukcyjna
Zatem podział odwrotnie proporcjonalny:
(
)
331
,
0
537
,
0
29
18
29
2
1
2
1
2
1
=
⋅
+
=
+
⋅
+
=
x
x
z
z
z
x
33
,
0
1
=
x
Przyjmujemy:
(
)
207
,
0
33
,
0
537
,
0
1
2
1
2
=
−
=
−
+
=
x
x
x
x
21
,
0
2
=
x
Przyjmujemy:
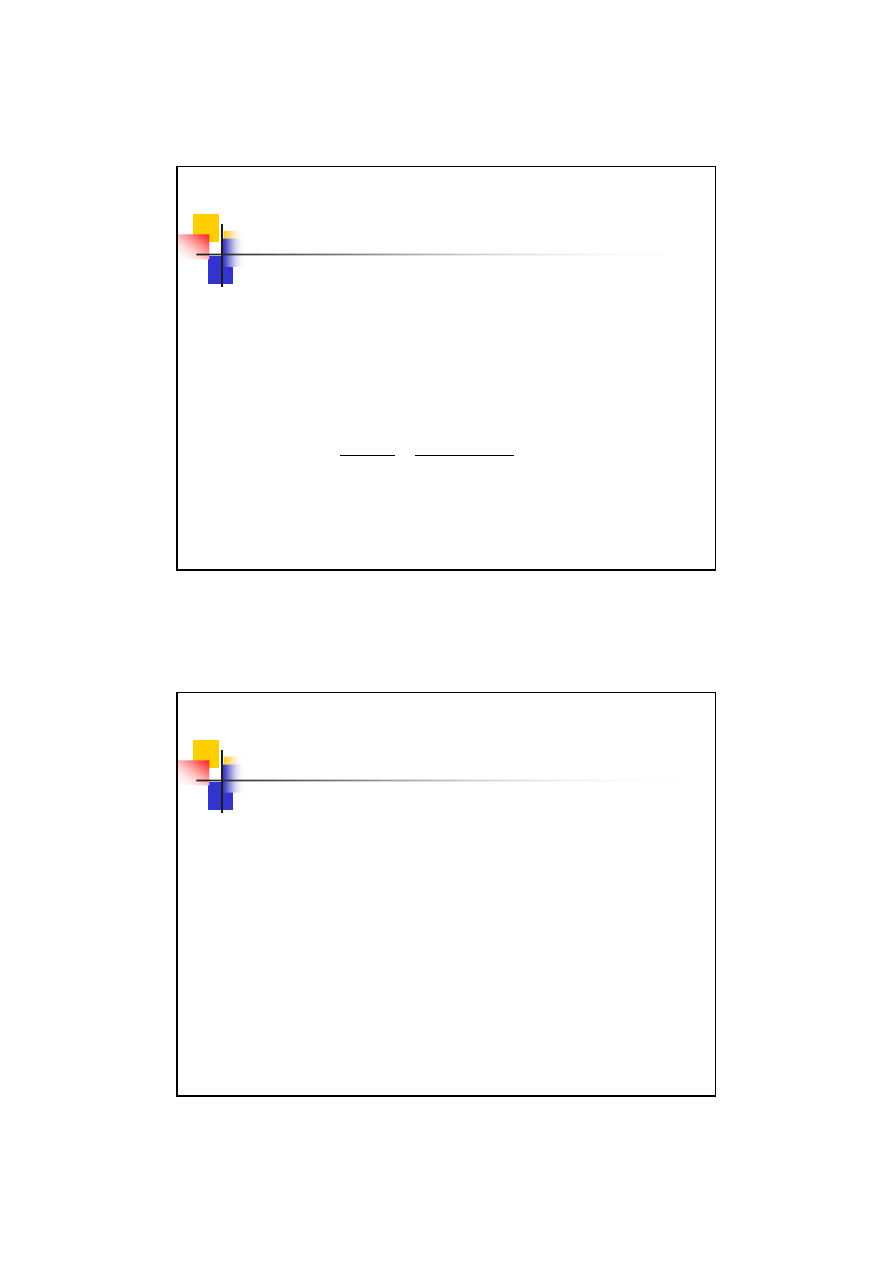
32
Przykład 9.4
– korekcja P-konstrukcyjna
Oraz obliczamy współczynnik zeszlifowania głowy zęba:
036
,
0
5
,
2
00
,
60
09
,
60
=
−
=
−
=
m
a
a
k
w
p
(
)
(
)
mm
09
,
60
5
,
2
21
,
0
33
,
0
74
,
58
2
1
=
⋅
+
+
=
⋅
+
+
=
m
x
x
a
a
p
Następnie obliczamy pozorną odległość osi:
Przy założonym luzie wierzchołkowym
c*
= 0,25 obniżenie
go o 0,036 nie spowoduje wyjścia poza zakres dopuszczalny
to przyjmujemy:
0
=
k
Przykład 9.4
– korekcja P-konstrukcyjna
Zatem wymiary koła wynoszą
mm
00
,
45
18
5
,
2
1
1
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
65
,
51
0
2
33
,
0
2
1
2
18
5
,
2
2
2
2
1
1
1
=
⋅
+
⋅
+
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
40
,
40
25
,
0
2
33
,
0
2
1
2
18
5
,
2
*
2
2
2
1
1
1
=
⋅
−
⋅
+
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
mm
50
,
72
29
5
,
2
2
2
=
⋅
=
⋅
=
z
m
d
(
)
(
)
mm
55
,
78
0
2
21
,
0
2
1
2
29
5
,
2
2
2
2
2
2
2
=
⋅
+
⋅
+
⋅
+
⋅
=
⋅
−
⋅
+
⋅
+
⋅
=
k
x
y
z
m
d
a
(
)
(
)
mm
30
,
67
25
,
0
2
21
,
0
2
1
2
29
5
,
2
*
2
2
2
2
2
2
=
⋅
−
⋅
−
⋅
−
⋅
=
⋅
−
⋅
+
⋅
−
⋅
=
c
x
y
z
m
d
f
Wyszukiwarka
Podobne podstrony:
projekt przekładnie zębate3
Przekładnie zębate
Przekładnie zębate
Obliczenia geometryczno wytrzymałościowe walcowej przekładni zębatej
Przekładnie zębate korekcja zazębienia
Koła i przekładnie zębate
PROJEKTY Z PKM, AGH, Semestr 5, PKM całość, PKM akademiki I, PKM-projekty, Projekt przekładni zębate
Przekladnie zebate
Przekładnie zębate
Strona tytułowa do przekładni zębatej, Projekt przekładni zębatej
pkm obliczenia przekładni zębatej(1), SiMR, PKM III, Projekt 3, PKM 3 - WZORY
Przekładnie zębate Dziama
Projekt wału, energetyka pwr, PKM I, przykładowe wały do jednostopniowych przekładni zębatych, Proje
przekladnie zebate id 404821 Nieznany
Przekładnie zębate 1
Przekładnie zebate Przykłady graficzne
Przekładnie zębate AB
przekladnie zebate parametry
więcej podobnych podstron