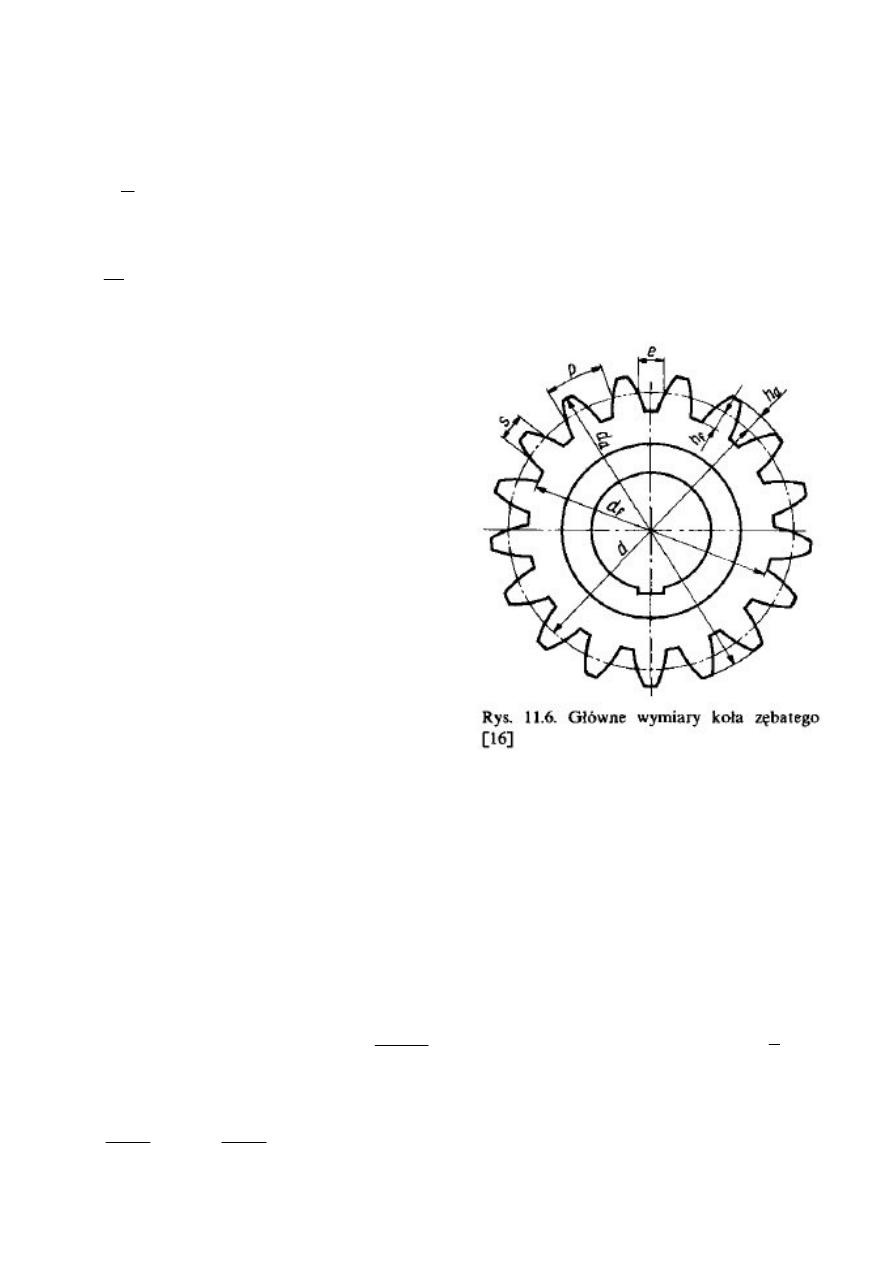
Temat: Parametry przekładni zębatych.
1. Przekładnia walcowa o zębach prostych.
Zęby – elementy okalające koło zębate, ograniczone kołami podstaw d
f
i wierzchołków d
a
,
Wręby międzyrębne – wolne przestrzenie między zębami, ograniczone kołami podstaw i wierzchołków,
Podziałka – odległość między sąsiednimi zarysami zębów na jednym kole, mierzona na kole podziałowym,
z
d
p
t
π
=
gdzie: d – średnica podziałowa koła, z – liczba zębów
Moduł – to odcinek, który w średnicy podziałowej mieści się tyle razy ile zębów ma koło,
(znormalizowany, mierzony w mm)
π
t
p
m
=
szereg 1 modułu: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; …
Średnica podziałowa
z
m
d
*
=
średnica wierzchołków
)
2
(
+
=
z
m
d
a
średnica podstaw
)
5
,
2
(
−
=
z
m
d
f
wysokość głowy zęba
m
h
a
=
wysokość stopy zęba
m
h
f
25
,
1
=
wysokość zęba
m
h
h
h
f
a
25
,
2
=
+
=
luz wierzchołkowy
m
h
h
c
f
a
25
,
0
=
−
=
luz boczny normalny (międzyrębny)
m
j
04
,
0
=
odległość osi kół współpracujących
)
(
5
,
0
)
(
5
,
0
2
1
2
1
z
z
m
d
d
a
+
=
+
=
2. Podstawowe pojęcia:
1) koła toczne – teoretyczne wyobrażalne koła toczące się po sobie bez poślizgu podczas obrotu
współpracujących kół zębatych,
2) punkt przyporu – miejsce chwilowego styku zębów,
3) linia przyporu – linia utworzona przez połączenie kolejnych punktów przyporu podczas obrotu kół
zębatych,
4) kąt przyporu – kąt zawarty między linią przyporu i styczną do obu kół tocznych,
5) liczba przyporu (stopień pokrycia) – stosunek długości łuku przyporu do podziałki na kole tocznym.
3. Korekcja zębów – występuje przy granicznej liczbie zebów kiedy może dojść do podcięcia zębów:
a) dla
;
oraz
o
o
20
=
α
17
=
g
z
14
'
=
g
z
b) dla
;
oraz
o
o
15
=
α
30
=
g
z
25
'
=
g
z
c) dla najczęściej stosowanych kątów przyporu
o
α
, przy której nie występuje podcięcie zęba podaje się:
-teoretyczna graniczna liczba zębów
o
g
z
α
2
sin
2
=
-praktyczna graniczna liczba zębów
g
g
z
z
6
5
'
=
4. Przesunięcie zarysu (stosowane w celu uniknięcia podcięcia zęba dla z < 14)
- odsunięcie narzędzia od materiału o wartość X:
g
g
z
z
z
X
−
=
lub
'
'
g
g
z
z
z
X
−
=
[mm]
gdzie: z – liczba zębów, z
g
– teoretyczna graniczna liczba zębów, z
’
g
– praktyczna graniczna liczba zębów
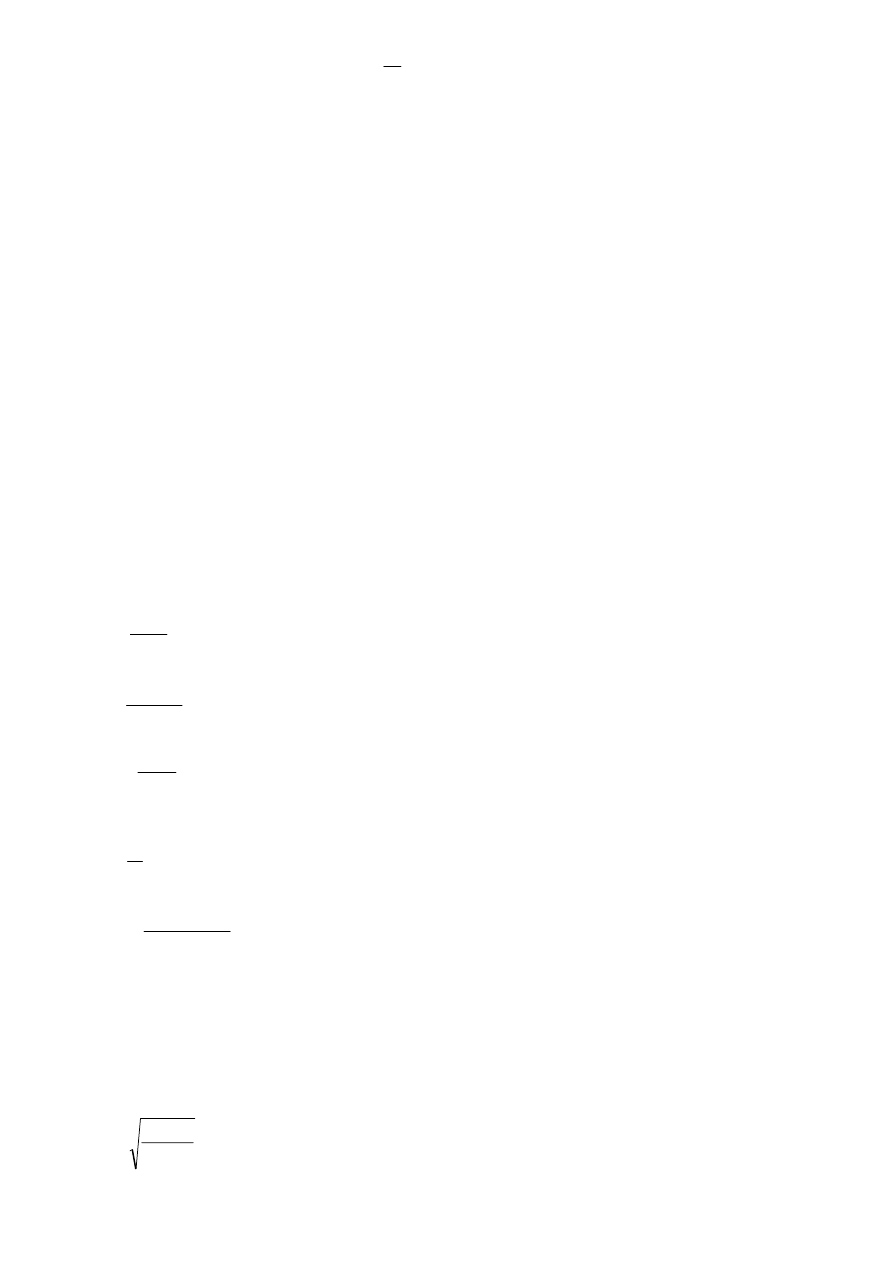
- współczynnik przesunięcia zarysu x:
m
X
x
=
gdzie m - moduł
Parametry koła zębatego po korekcji:
1) średnica wierzchołków
X
z
m
d
a
2
)
2
(
±
+
=
2) średnica podstaw
X
z
m
d
f
5
,
2
)
5
,
2
(
±
−
=
3) wysokość głowy zęba
X
m
h
a
±
=
4) wysokość stopy zęba
X
m
h
f
±
= 25
,
1
- dla (+) jeżeli narzędzie jest odsunięte na zewnątrz materiału
- dla (-) jeżeli narzędzie jest dosunięte do materiału
5. Korekcja X-X – bez zmiany odległości osi kół w przekładni
- w kole o mniejszej liczbie zębów (przesunięcie dodatnie – na zewnątrz)
- w kole o większej liczbie zębów (przesunięcie ujemne – do środka koła)
X
1
= –X
2
- przy spełnieniu warunku:
dla praktycznej granicznej liczby zębów
'
2
1
2
g
z
z
z
≥
+
dla teoretycznej granicznej liczby zębów
g
z
z
z
2
2
1
≥
+
6. Korekcja X+X – ze zmianą odległości osi kół w przekładni
a) pozorna odległość osi – odległość na którą należy rozsunąć osie obrotu kół zębatych, wynikających z
korekcji obu kół
a
p
= a + X
1
+X
2
b) rzeczywista odległość osi – odległość, którą uzyskuje się po usunięciu nadmiernego luzu obwodowego
a
r
= a + X
1
+X
2
– K = a
p
– k * m gdzie: K = k * m z tego wynika że K = a
p
– a
r
7. Obliczenia wytrzymałościowe
a) wytrzymałość zęba na zginanie u podstawy
d
M
F
o
2
=
gdzie M
o
– moment obrotowy, d – średnica podziałowa koła zębatego
b) współczynnik kształtu zęba
2
*
6
s
h
m
q
f
=
gdzie: s – grubość zęba przy średnicy podziałowej, h
f
– wysokość stopy zęba, m - moduł
c) naprężenie zginające
gj
g
k
m
b
q
F
≤
=
*
*
σ
gdzie: F – siła obwodowa, q – współczynnik kształtu zęba, m – moduł koła,
b – szerokość uzębienia [mm]
d) zależność między szerokością uzębienia a modułem
m
b
=
λ
gdzie
20
5do
=
λ
e) obciążenie obliczeniowe
ε
K
K
K
F
F
v
p
obl
*
*
=
gdzie:
- współczynnik przeciążenia (K
p
K
p
= 1 …2)
K
v
– współczynnik nadwyżek dynamicznych (K
v
=1,25 … 2,3)
K
ε
– współczynnik zależny od liczby przyporu
dla
o
o
20
=
α
- gdy liczba przyporu ε<2, przyjmuje się K
ε
= 1,
- gdy liczba przyporu ε 2, przyjmuje się K
≥
ε
= 2,
f) moduł z warunku na zginanie
gj
obl
k
q
F
m
*
*
λ
≥
g) moment obrotowy
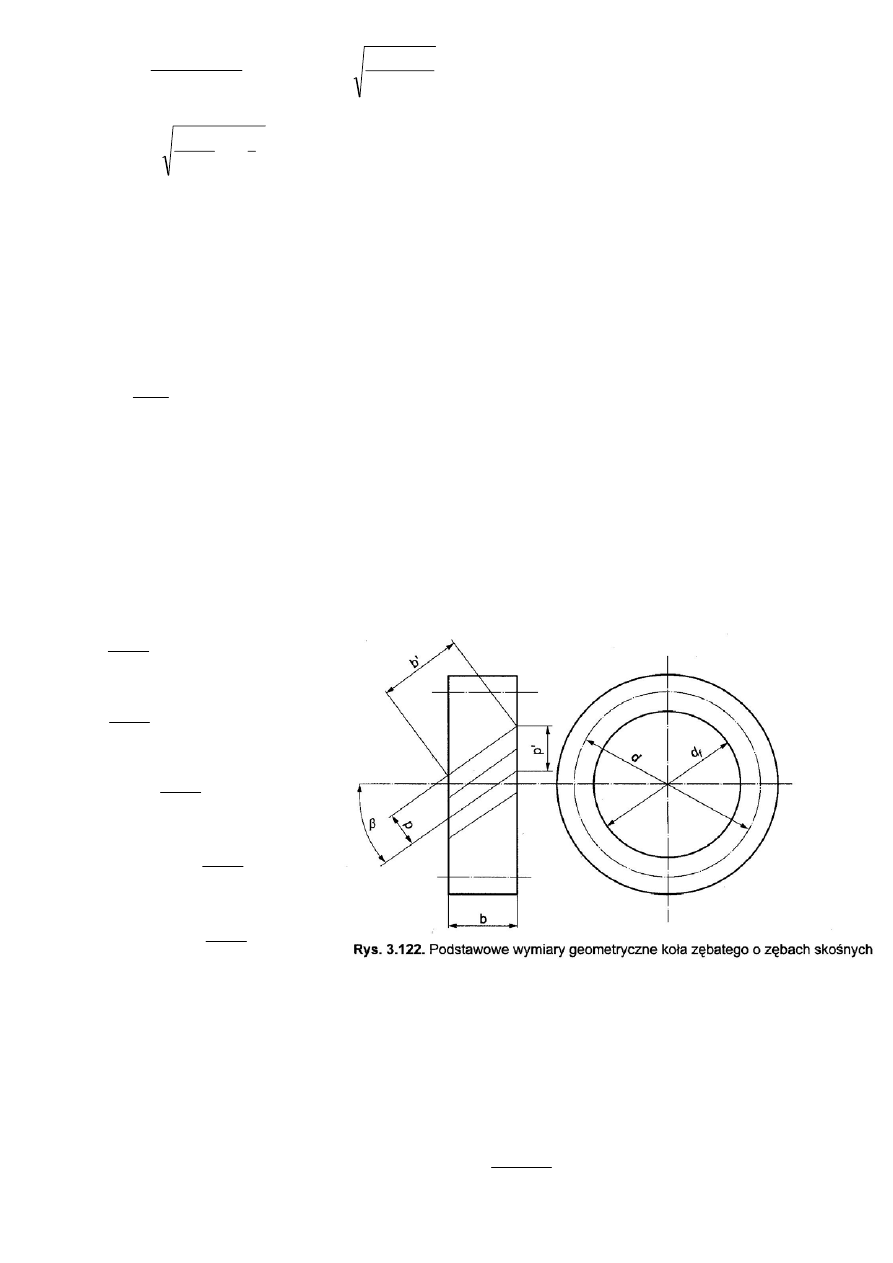
ε
K
K
K
M
M
v
p
obl
*
*
=
a zatem
3
*
*
*
2
gj
obl
k
z
q
M
m
λ
≥
h) sprawdzenie nacisków powierzchniowych bocznych powierzchni zęba
o
obl
k
i
d
b
F
C
p
≤
⎟
⎠
⎞
⎜
⎝
⎛ ±
=
1
1
*
1
max
gdzie:
k
o
– dopuszczalne naciski powierzchniowe [MPa],
F
obl
– siła obliczeniowa [N],
b – czynna szerokość uzębienia [mm],
d
1
– średnica podziałowa koła zębatego [mm]
i – przełożenie,
C – współczynnik zależny od rodzaju materiału kół i kąta przyporu, przy kącie przyporu
o
o
20
=
α
C = 478,2 dla kół stalowych (E=210 000 MPa, v=0,35)
C = 308,4 dla kół żeliwnych (E=90 000 MPa, v=0,25)
i) naciski jednostkowe
W
HB
k
o
5
=
gdzie: HB = twardość dla materiału w skali Brinella, W – współczynnik zależny od prędkości obrotowej
n i czasu pracy T przekładni (1,3 – 5)
8. Przekładnie walcowe o zębach skośnych i daszkowych
Zalety:
płynna współpraca zębów,
cichobieżność,
zdolność przenoszenia dużych obciążeń,
możliwość regulacji rozstawu osi przez zmianę kąta pochylenia linii zęba,
- podziałka czołowa
β
cos
p
p
t
=
- moduł czołowy
β
cos
m
m
t
=
- średnica podziałowa
z
m
z
m
d
t
*
cos
*
β
=
=
- średnica wierzchołków
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
=
+
=
2
cos
2
β
z
m
h
d
d
a
a
- średnica podstaw
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
−
=
5
,
2
cos
2
β
z
m
h
d
d
f
f
- korekcja zębów
β
β
3
cos
*
g
g
z
z
=
gdzie:
β
g
z
- graniczna liczba zębów koła o zebach skośnych,
z
g
– graniczna liczba zębów koła o zębach prostych
- całkowita liczba przyporu
s
c
ε
ε
ε
+
=
gdzie:
ε
- liczba przyporu dla koła o zębach prostych,
s
ε
- skokowa liczba przyporu obliczana z zależności
π
β
ε
*
sin
*
m
b
s
=
- odległość osi
(
)
(
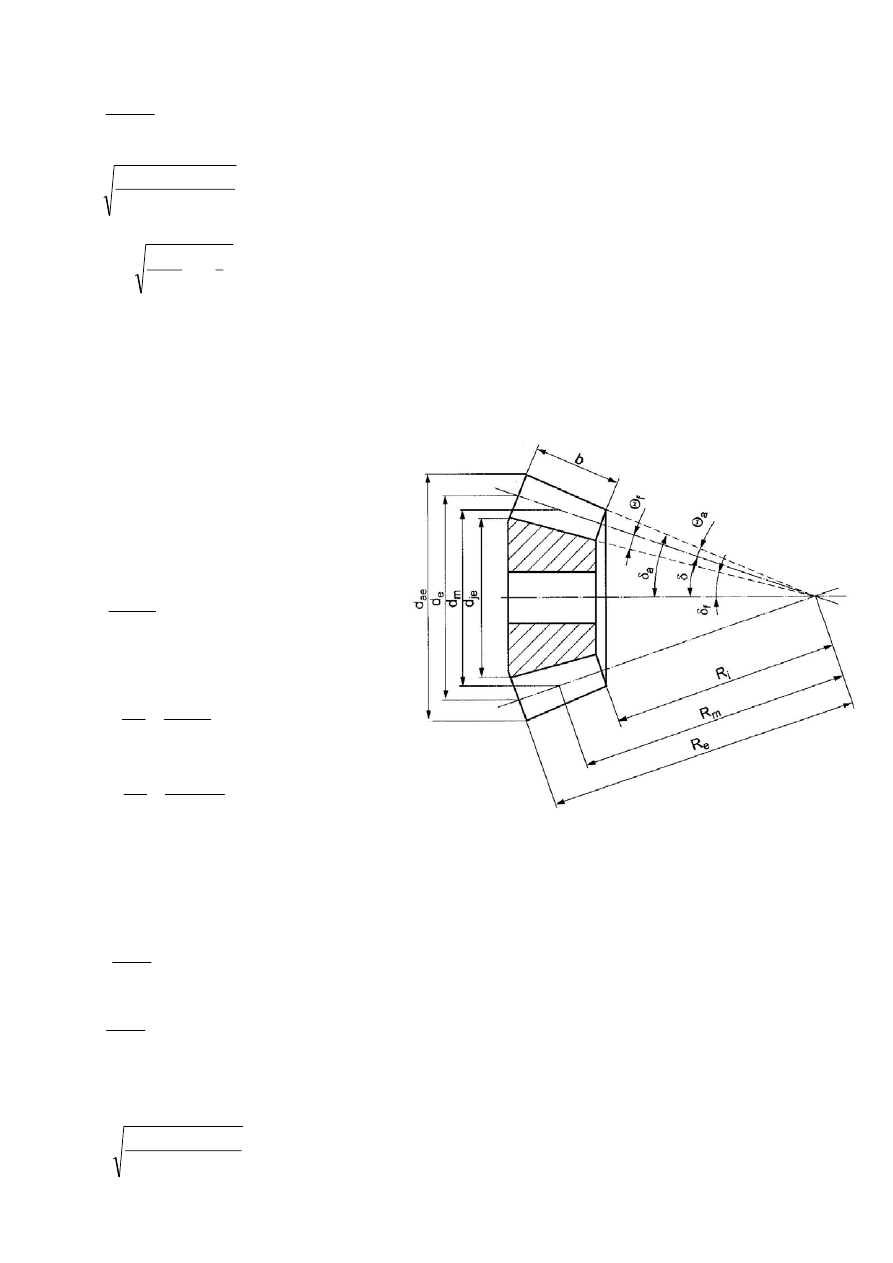
2
1
2
1
5
,
0
5
,
0
z
z
m
d
d
a
t
+
=
+
=
)
- obliczenia wytrzymałościowe, koło zastępcze z zastępczą liczbą zębów
β
2
cos
z
z
z
=
- moduł
3
*
*
cos
*
*
2
gj
obl
k
z
q
M
m
λ
β
≥
- naciski powierzchniowe
o
obl
k
i
d
b
F
C
p
≤
⎟
⎠
⎞
⎜
⎝
⎛ ±
=
1
1
*
max
9. Przekładnie stożkowe
Opis:
o
zęby w przekładni mogą być: proste, skośne, łukowe,
o
zarys zębów jest ewolwentowy lecz zmieniający się wzdłuż stożka,
- średnica podziałowa
z
m
d
e
*
=
- średnica wierzchołków
(
)
δ
cos
2
+
=
z
m
d
ae
- średnica podstaw
(
)
δ
cos
5
,
2
−
=
z
m
d
fe
- długość tworzącej stożka podziałowego
δ
sin
2
e
c
d
R
=
- szerokość wieńca b uzębienia
b = (0,25 …0,33)R
e
- tangens kąta głowy zęba
z
R
h
tg
e
ae
a
δ
θ
sin
2
=
=
- tangens kąta stopy zęba
z
R
h
tg
e
fe
f
δ
θ
sin
5
,
2
=
=
- kąt stożka wierzchołków zębów
a
a
θ
δ
δ
+
=
- kąt stożka podstaw zębów
t
t
θ
δ
δ
−
=
- obliczenia wytrzymałościowe, średnica podziałowa koła zastępczego
δ
cos
e
az
d
d
=
- zastępcza liczba zębów dla koła stożkowego
δ
cos
z
z
z
=
- graniczna liczba zębów dla koła walcowego o takim samym kącie przyporu
δ
cos
*
g
gs
z
z
=
- średni moduł (z warunku na zginanie)
3
*
*
cos
*
*
2
gj
obl
m
k
z
q
M
m
λ
δ
≥
- naciski powierzchniowe
o
m
obl
k
i
d
b
F
C
p
≤
⎟
⎠
⎞
⎜
⎝
⎛ +
=
2
max
1
1
*
cos
*
δ
- moduł normalny
z
z
m
m
m
δ
λ
sin
*
+
=
10. Przekładnie ślimakowe
Składa się z ślimaka i ślimacznicy (koła ślimakowego) o kącie osi
90
o
.
Rozróżniamy przekładnie ślimakowe:
a) walcowe
b) globoidalne
Zalety przekładni:
• płynność zazębienia
• duże przełożenie
• cichobieżność
• zwartość budowy
• możliwość uzyskania przekładni samohamownej
• możliwość przenoszenia znacznych obciążeń
• liniowy styk współpracujących zębów zmniejszający ich
zużycie
Wady przekładni:
o
mała sprawność,
o
konieczność stosowania drogich materiałów np. brązu,
o
utrudnione wykonanie i pomiary (zwłaszcza ślimacznicy),
o
konieczna duża dokładność wykonania oraz montażu.
- przełożenie przekładni
1
2
2
1
z
z
n
n
i
=
=
- sprawność przekładni ślimakowej
)
(
ρ
γ
γ
η
+
=
tg
tg
gdzie:
ρ
- kąt tarcia zależny od materiałów, z których wykonano ślimak i ślimacznicę (
µ
ρ
=
tg
)
γ
- kąt wzniosu linii zwoju (pochylenie linii zębów) ślimaka,
µ
- współczynnik tarcia ślizgowego
- wskaźnik średnicowy
x
m
d
q
1
=
gdzie m
x
– moduł osiowy
Wymiary ślimaka:
- kąt wzniosu linii zwoju ślimaka
q
z
d
z
p
d
p
tg
z
1
1
1
1
*
*
*
=
=
=
π
π
γ
gdzie p
z
– skok zwoju, p – podziałka osiowa
ślimaka, z
1
– liczba zębów ślimaka
- skok zwoju
p
z
= p*z
1
=
1
*
*
z
m
x
π
- podziałka osiowa
x
m
p
*
π
=
- wysokość głowy zęba
x
a
m
h
=
1
- wysokość stopy zęba
x
f
m
h
25
,
1
1
=
- wysokość zęba
x
f
a
m
h
h
h
25
,
2
1
1
1
=
+
=
- średnica podziałowa
x
m
q
d
*
1
=
- średnica wierzchołków
(
)
2
2
1
1
1
+
=
+
=
q
m
h
d
d
x
a
a
- średnica podstaw
(
)
5
,
2
2
1
1
1
−
=
−
=
q
m
h
d
d
x
f
f
- długość ślimaka L = 4p
Wymiary ślimacznicy:
- średnica podziałowa
2
2
* z
m
d
x
=
- średnica wierzchołków
(
)
2
2
2
+
=
z
m
d
x
a
- średnica podstaw
(
)
5
,
2
2
2
−
=
z
m
d
x
f
- szerokość zębów ślimacznicy
1
2
+
=
q
m
b
x
- odległość osi przekładni
(
)
(
2
2
1
5
,
0
5
,
0
z
q
m
d
d
a
x
+
=
+
=
)
- obliczenia wytrzymałościowe
przeprowadzamy dla ślimacznicy, która ma mniejszą wytrzymałość oraz jeżeli przekładnia pracuje z
prędkością mniejszą niż 2 m/s obliczamy z warunków na zginanie i naciski powierzchniowe a powyżej 2
m/s obliczamy z warunku na nagrzewanie.
11. Przekładnie obiegowe.
a) Przekładnia planetarna
Przekładnia składa się z:
- z koła centralnego (słonecznego) o uzębieniu zewnętrznym
- z koła pierścieniowego (wieńcowego) o uzębieniu
wewnętrznym
- z jednego lub kilku satelitów o uzębieniu zewnętrznym,
połączonych jarzmem
Zalety:
- każdy z tych trzech elementów może być napędzający, napędzany
lub unieruchomiony,
- istnieje możliwość wykorzystania trzech przełożeń,
- cichobieżność,
- duża wytrzymałość
Wady:
- produkcja skrzynek jest trudna i kosztowna
Parametry:
- przełożenie przy nieruchomym kole pierścieniowym
c
w
z
z
i
+
= 1
- przy nieruchomym kole słonecznym
w
c
z
z
i
+
=1
- przy nieruchomym jarzmie satelitów
c
w
z
z
i
=
gdzie:
z
w
– liczba zębów koła pierścieniowego,
z
c
– liczba zębów koła słonecznego
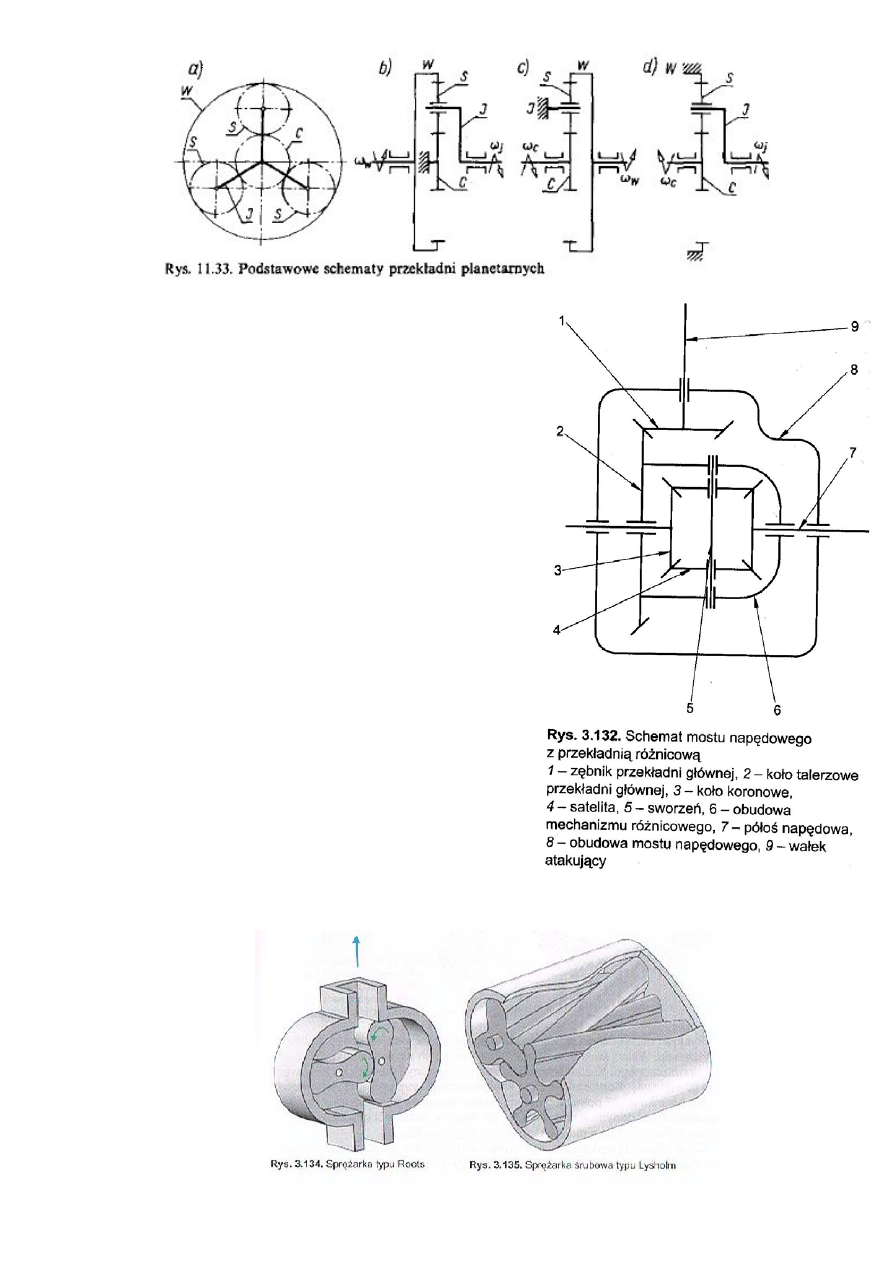
b) Przekładnia obiegowa
Zasada działania:
- napęd jest przenoszony na obudowę mechanizmu
różnicowego przez zespół zębatej przekładni stożkowej,
- napęd na półosie napędowe rozdziela przekładnia
różnicowa
1) przy jeździe prosto – koła napędowe mają jednakową
prędkość obrotową,
2) przy jeździe po łuku – koła napędowe obracają się z
różną prędkością, bo różne prędkości mają koła koronowe
(3) połączone z kołami jezdnymi.
- uzyskuje się to dzięki obrotowi satelitów (4) wokół
własnej osi,
- średnia prędkość ruchu obrotowego kół koronowych (3)
jest równa wartości prędkości obrotowej koła talerzowego
(2) połączonego trwale z obudową mechanizmu
różnicowego (6).
12. Przekładnie specjalne.
1) Sprężarka typu Roots
- ma dwa lub trzy wirniki
- łopatki przepompowują powietrze w przestrzeniach
międzyłopatkowych z komory ssawnej do komory
tłocznej,
- prędkość obrotowa dochodzi do 14 000 obr/min
- w pracy towarzyszą wahania ciśnienia tłoczenia.
2) Sprężarka śrubowa typu Lysholm
- posiada dwa ślimaki walcowe, jeden prawoskrętny,
drugi lewoskrętny,
- w wyniku zazębiania następuje zasysanie, a następnie sprężanie i przepychanie,
- duża sprawność około 90%
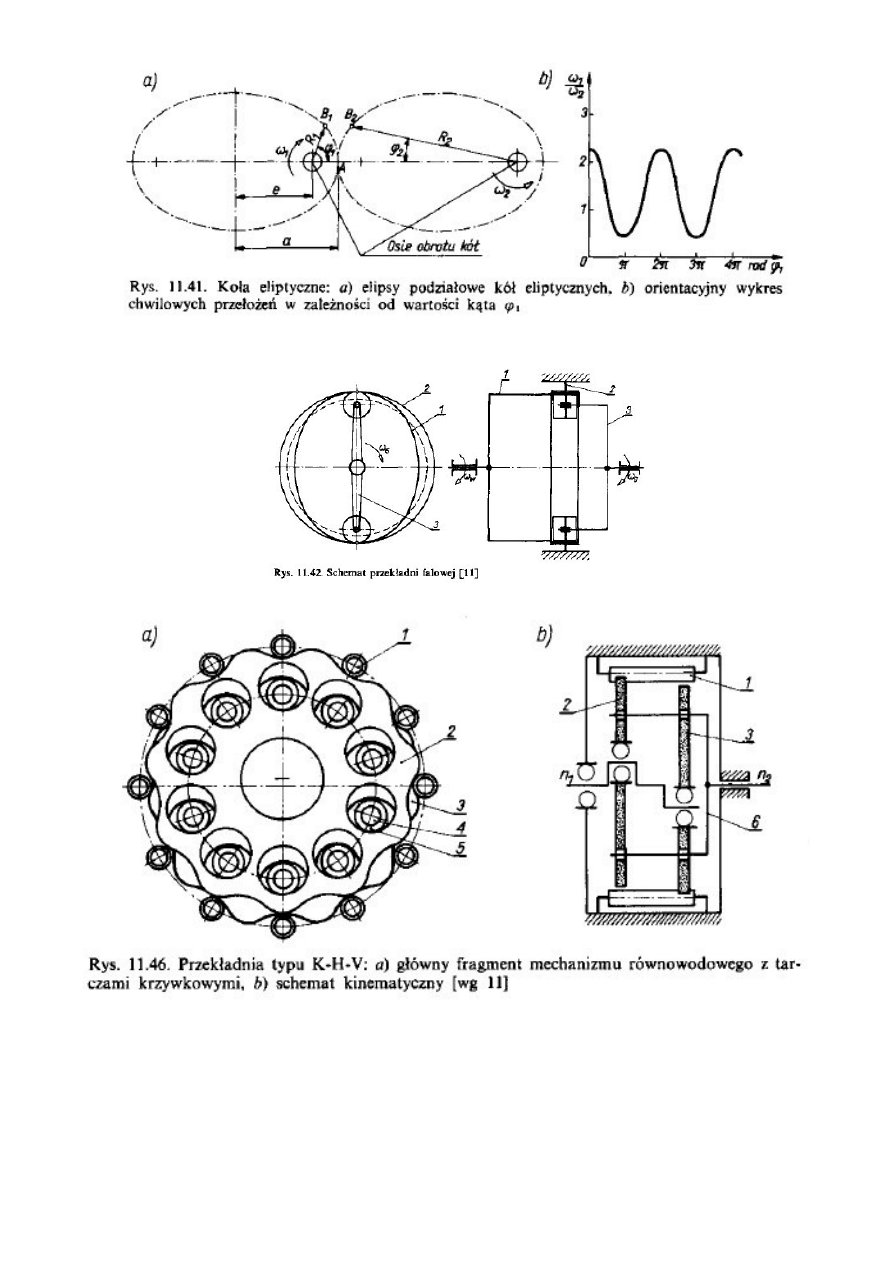
3) Przekładnia z kołami eliptycznymi
4) Przekładnia falowa
5) Przekładnia K-H-V