1

Podstawy Konstrukcji Maszyn

Wykład 8

Przekładnie zębate część 1

Dr inż. Jacek Czarnigowski

Klasyfikacja przekładni zębatych

1. Ze względu na miejsce zazębienia

O zazębieniu

zewnętrznym

O zazębieniu

wewnętrznym

2

Klasyfikacja przekładni zębatych

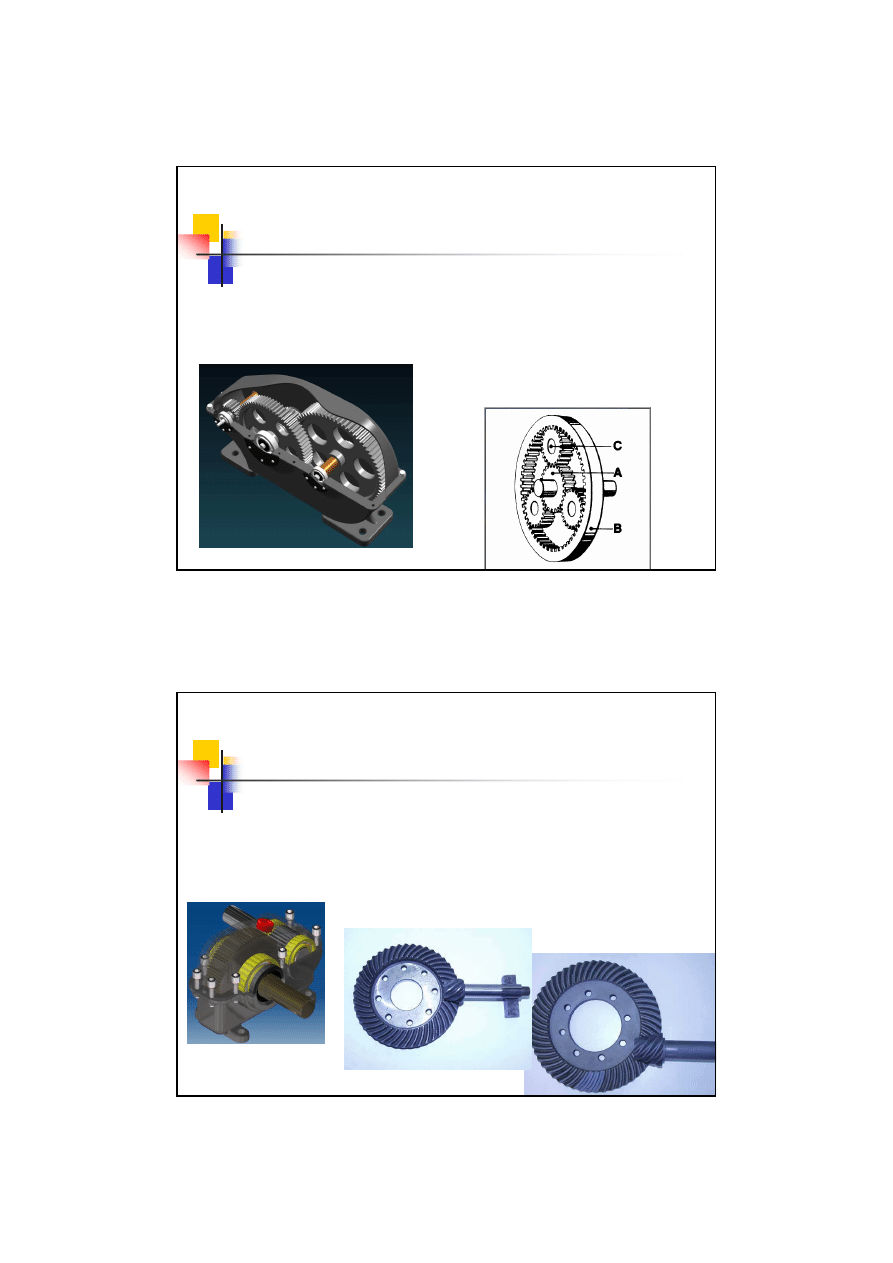
2. Ze względu na ruchomość osi

O osiach stałych

Planetarne –

przynajmniej jedna oś

przemieszcza się względem korpusu

wykonując ruch okrężny względem

osi centralnej

Klasyfikacja przekładni zębatych

3. Ze względu na wzajemne położenie osi

Równoległe

Kątowe

Osie obu kół

przecinają się

Wichrowate

(przekładnie

hipoidalne)

Osie obu kół nie

przecinają się

3

Klasyfikacja przekładni zębatych

4. Ze względu na kształt kół

Walcowe

Stożkowe

Ślimakowe

Klasyfikacja przekładni zębatych

4. Ze względu na kształt linii zęba

O zębach

prostych

O zębach

śrubowych

O zębach

daszkowych

O zębach

łukowych

4

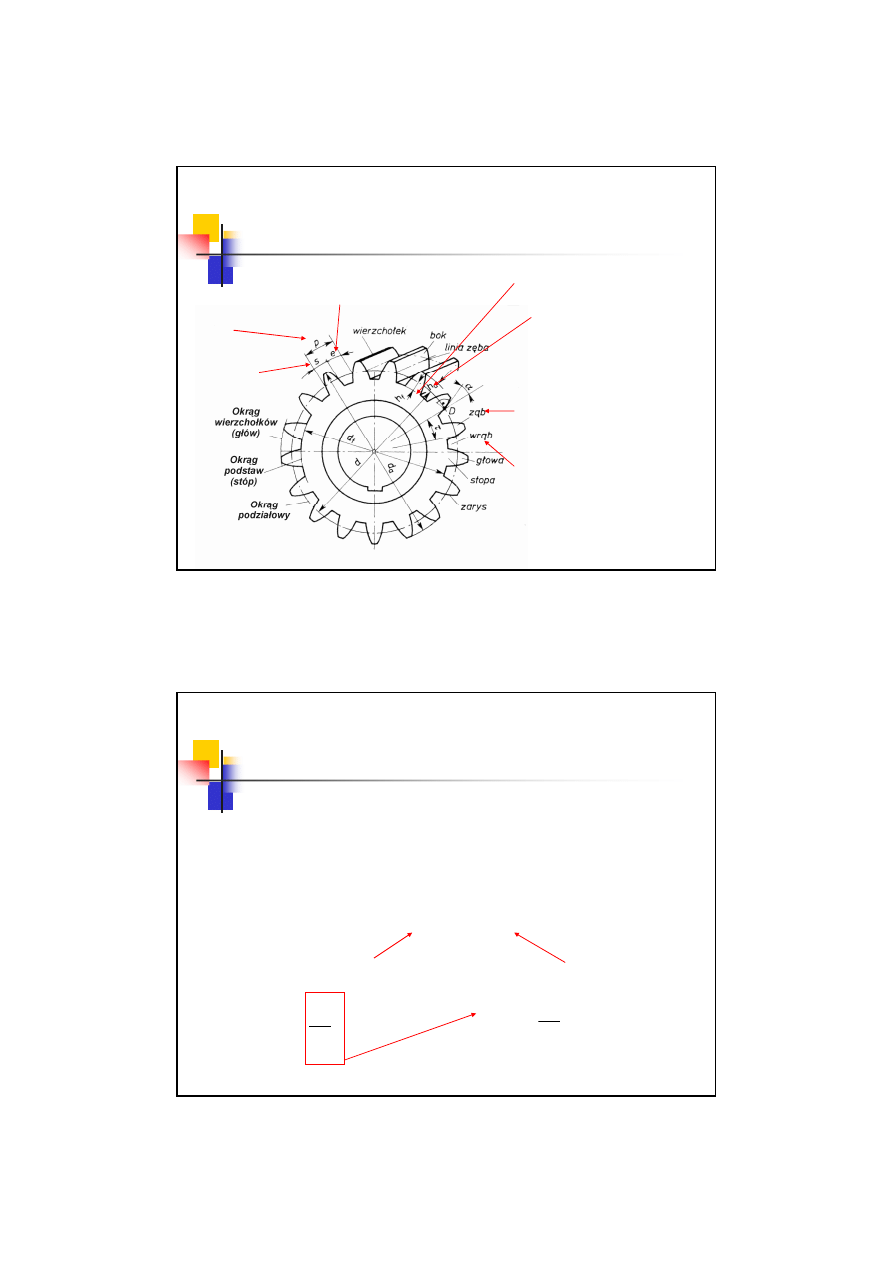
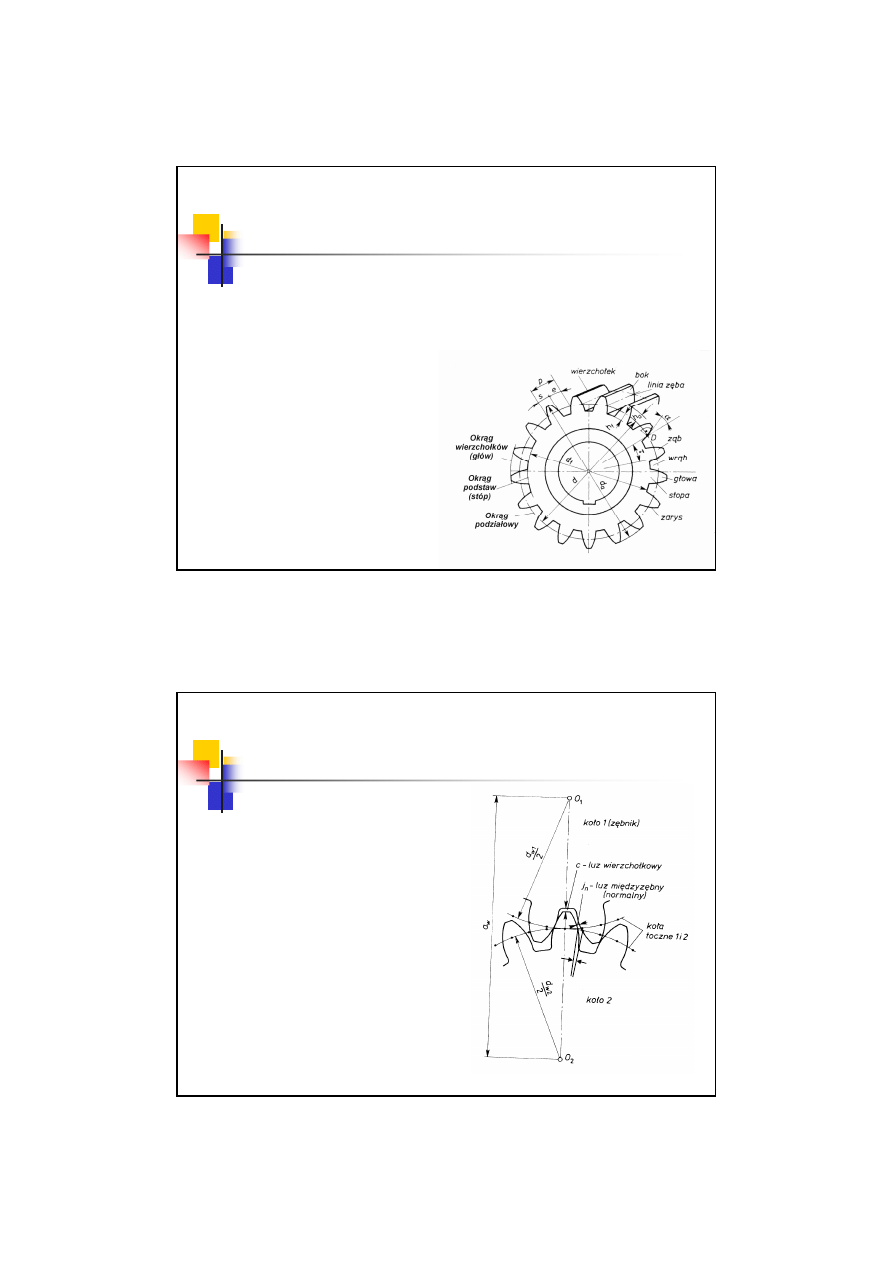
Pojęcia podstawowe – geometria
koła walcowego o zębach prostych

Występ w kole zębatym, poprzez
który w czasie pracy przekładni
przekazywany jest napęd

Przestrzeń między dwoma
sąsiednimi zębami

Wysokość głowy zęba

Wysokość stopy zęba

Grubość zęba

Szerokość wrębu

Podziałka

Pojęcia podstawowe – geometria
koła walcowego o zębach prostych

z

p

d

⋅

=

⋅

π

Podziałka obwodowa

p

– długość łuku koła podziałowego zawarta między

jednoimiennymi sąsiednimi bokami zębów.

Średnica podziałowa

Liczba zębów

z

p

d

⋅

=

π

π

p

m

=

Moduł nominalny

5

Pojęcia podstawowe – geometria
koła walcowego o zębach prostych

Moduł nominalny – miara wielkości zęba wyrażana w [mm].

π

p

m

=

Moduł jest znormalizowany:

Szereg 1 (zalecany): 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10 …

Szereg 2 (dopuszczalny): 1,125; 1,375; 1,75; 2,25; 2;75; 3,5; 4,5; 5,5; 7 …

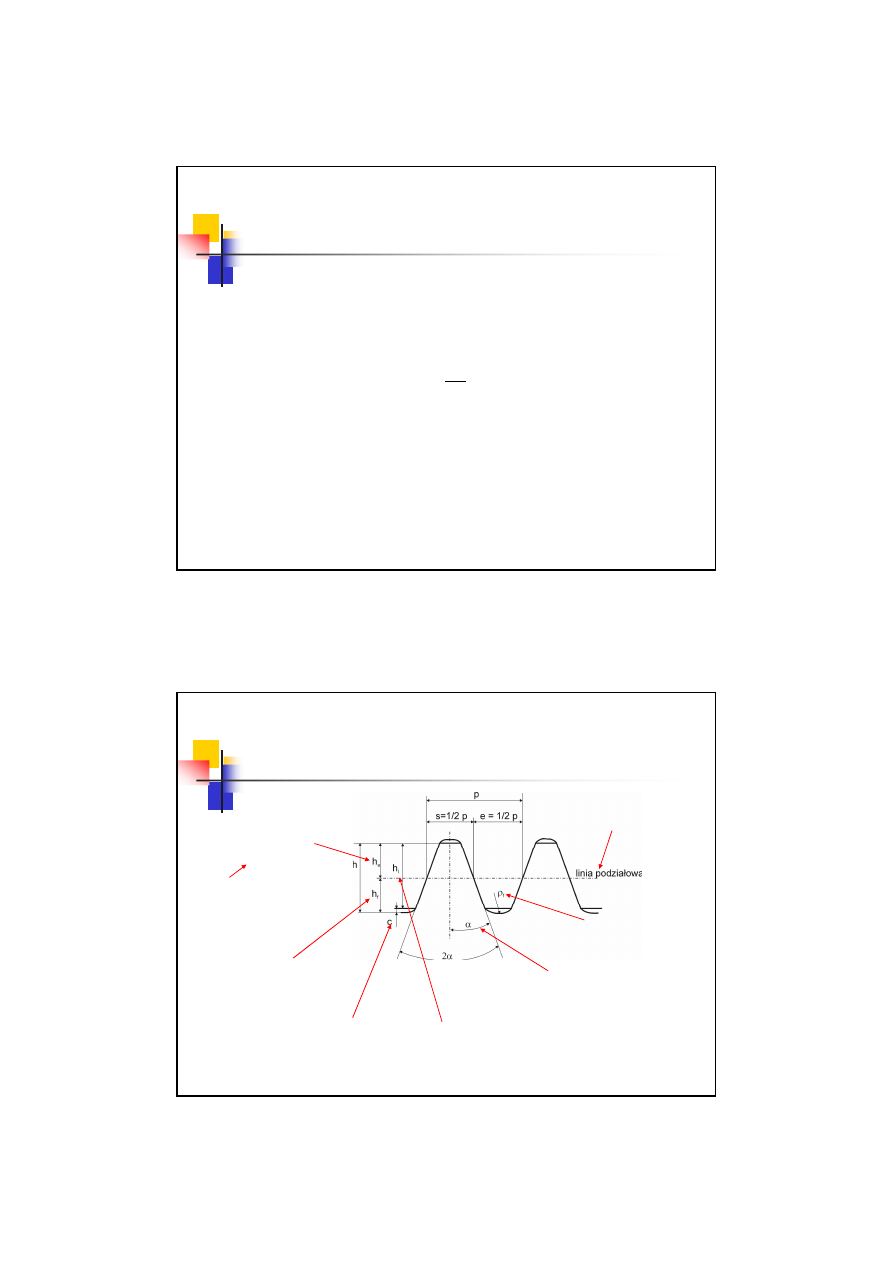
Pojęcia podstawowe – zarys
odniesienia

Dzieli koło tak, że

szerokość wrębu jest

równa grubości zęba

Kąt zarysu

α

αα

α

= 15

°°°°

; 17,5

°°°°

;

20

°°°°

;

22,5

°°°°

; 25

°°°°

;

Wysokość głowy zęba

h

a

m

y

h

a

⋅

=

y

– współczynnik

wysokości zęba

(najczęściej =1)

Wysokość stopy zęba

h

f

(

)

m

c

y

h

f

⋅

+

=

*

Luz wierzchołkowy

c

m

c

c

⋅

=

*

25

,

0

2

,

0

*

÷

=

c

Wysokość prostoliniowego

zarysu zęba

h

t

m

y

h

t

⋅

⋅

=

2

Promień krzywizny krzywej

przejściowej

ρρρρ

t

m

f

⋅

=

38

,

0

ρ

6

Pojęcia podstawowe – zarys
odniesienia

Podstawowe średnice

Średnica podziałowa

z

m

d

⋅

=

Średnica głów

(

)

y

z

m

h

d

d

a

a

⋅

+

⋅

=

⋅

+

=

2

2

Średnica stóp

(

)

*

2

2

2

c

y

z

m

h

d

d

f

f

⋅

−

⋅

−

⋅

=

⋅

−

=

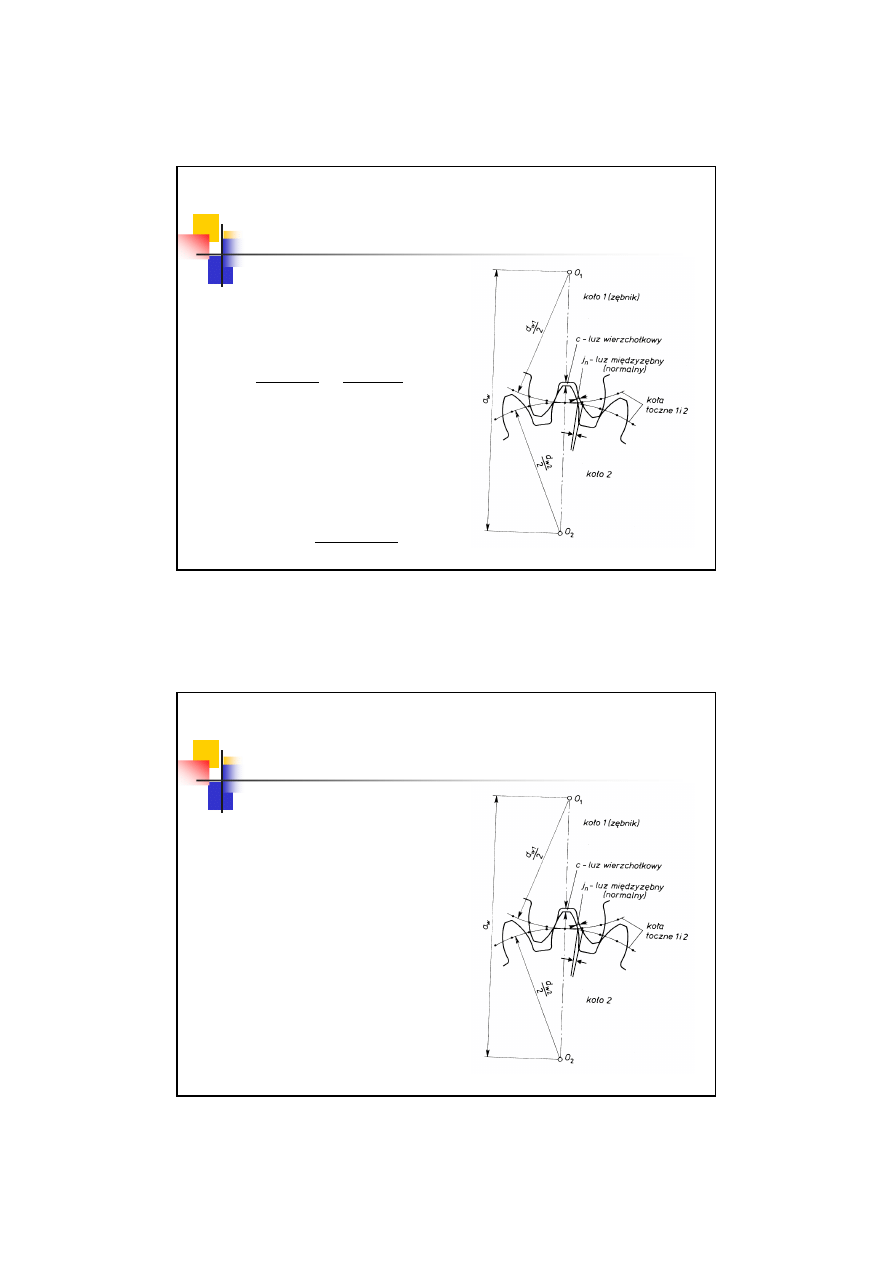
Pojęcia podstawowe – luzy

Luz wierzchołkowy

c

– najmniejsza odległość w

osi O

1

O

2

między walcem stóp jednego koła a

walcem wierzchołków koła współpracującego

Luz międzyzębny

j

n

– najkrótsza odległość

między niepracującymi bokami zęba przy istnieniu

kontaktu boków pracujących

Luz obwodowy

j

t

– długość łuku tocznego o który

można obrócić koło, aby doprowadzić boki

niepracujące do styku

j

t

– luz obwodowy

7

Pojęcia podstawowe – odległość osi

j

t

– luz obwodowy

Zerowa odległość osi – taka w
której stykają się okręgi podziałowe

m

z

z

d

d

a

⋅

+

=

+

=

2

2

2

1

2

1

Rzeczywista odległość osi – taka
w której stykają się okręgi toczne
(walce zastępujące koła pracujące
jak przekładnia cierna o stałym
przełożeniu bez poślizgu)

2

2

1

w

w

w

d

d

a

+

=

Pojęcia podstawowe – odległość osi

j

t

– luz obwodowy

Odległość osi jest znormalizowana
PN-76/M-88525

Szereg 1 (zalecany): 40; 50; 63; 80;
100; 125; 160; 200; 250 …

Szereg 2 (dopuszczalny): 71; 90;
112; 140; 180; 224 …

8

Podstawowe prawo zazębienia

Określa ono warunki jakie muszą spełniać zarysy zębów,
aby zapewnić stałość przełożenia kinematycznego kół
współpracujących

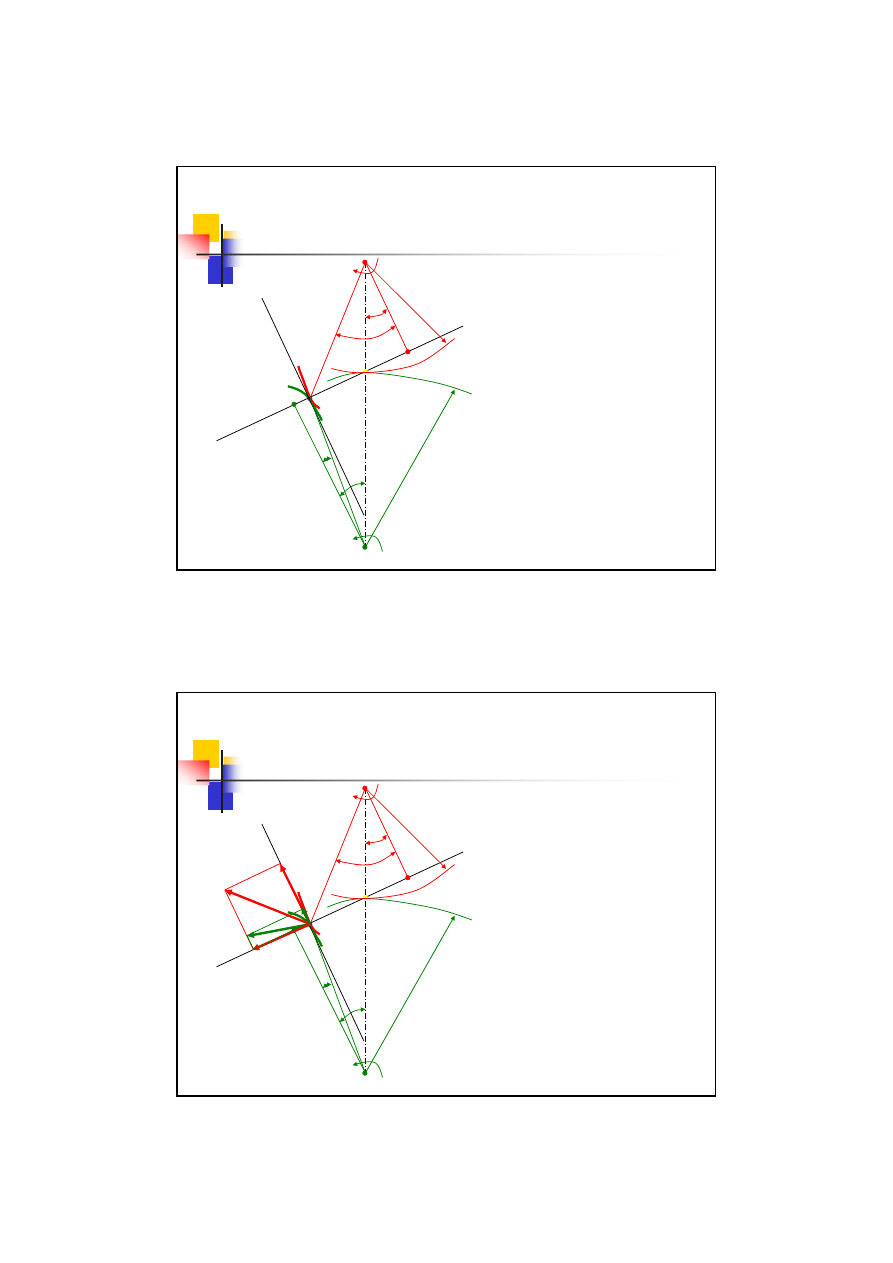
Podstawowe prawo zazębienia

O

1

O

2

B

Dwa koła obracają się z

prędkościami odpowiednio:

ω

ωω

ω

1

i

ω

ωω

ω

2

ω

ωω

ω

1

ω

ωω

ω

2

Zarys zębów styka się w punkcie B

–

punkt przyporu

N

N

T

T

Przez punkt B prowadzimy proste:

NN - normalną do styku zębów

TT – styczną do styku zębów

C

Określamy punkt C na przecięciu

prostych NN i O

1

O

2

Punkt C jest

biegunem zazębienia

a

więc punktem podziału linii O

1

O

2

na

koła toczne o promieniach r

w1

i r

w2

r

w2

r

w1

9

Podstawowe prawo zazębienia

O

1

O

2

B

Wyznaczamy proste prostopadłe do

prostej NN wychodzące odpowiednio

z punktów O

1

i O

2

Tworząc na przecięciu punkty G

1

i G

2

ω

ωω

ω

1

ω

ωω

ω

2

Odległości OG stanowią promień

koła zasadniczego r

b

N

N

T

T

Są one odchylone od osi O

1

O

2

o kąt

przyporu

α

αα

α

C

Punkt B oddalony jest od środków

obrotu kół o promień odpowiednio

r

1

i r

2

Promienie te są odchylone od

prostych OG o kąty odpowiednio

γγγγ

1

i

γγγγ

2

r

w2

r

w1

G

1

G

2

r

b1

r

b2

α

αα

α

α

αα

α

r

1

r

2

γγγγ

2

γγγγ

1

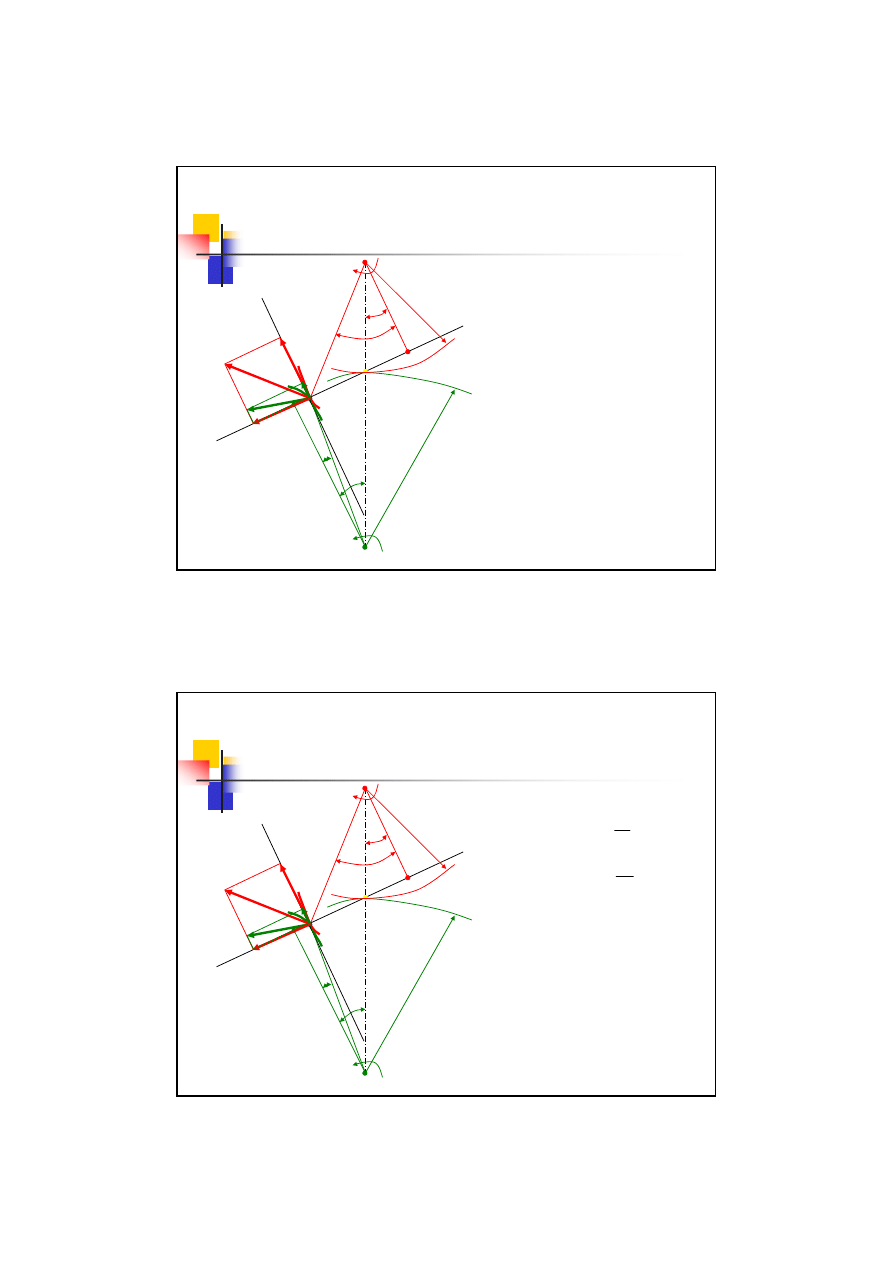
Podstawowe prawo zazębienia

O

1

O

2

B

Zakładając, że zęby są w stałym

kontakcie oraz, że są

nieodkształcalne to prędkości

punktów styku wynoszą:

ω

ωω

ω

1

ω

ωω

ω

2

Dla koła 1:

N

N

T

T

Prędkości są prostopadłe do

promieni r

C

Rozkładając te prędkości na proste

NN i TT otrzymujemy odpowiednio

prędkość normalną V

n

i prędkość

styczną W

r

w2

r

w1

G

1

G

2

r

b1

r

b2

α

αα

α

α

αα

α

r

1

r

2

γγγγ

1

1

1

1

r

V

⋅

=

ω

V

1

Dla koła 2:

2

2

2

r

V

⋅

=

ω

V

2

V

n1

=V

n2

W

1

W

2

γγγγ

2

10

Podstawowe prawo zazębienia

O

1

O

2

B

Założenie mówiące, że zęby są w

stałym kontakcie oraz, że są

nieodkształcalne to prędkości

punktów powoduje, że:

ω

ωω

ω

1

ω

ωω

ω

2

N

N

T

T

C

Stąd:

r

w2

r

w1

G

1

G

2

r

b1

r

b2

α

αα

α

α

αα

α

r

1

r

2

γγγγ

1

2

1

n

n

V

V

=

V

1

Zatem:

2

2

2

1

1

1

cos

cos

γ

γ

⋅

=

⋅

=

V

V

V

V

n

n

V

2

V

n1

=V

n2

W

1

W

2

2

2

2

1

1

1

cos

cos

γ

ω

γ

ω

⋅

⋅

=

⋅

⋅

r

r

γγγγ

2

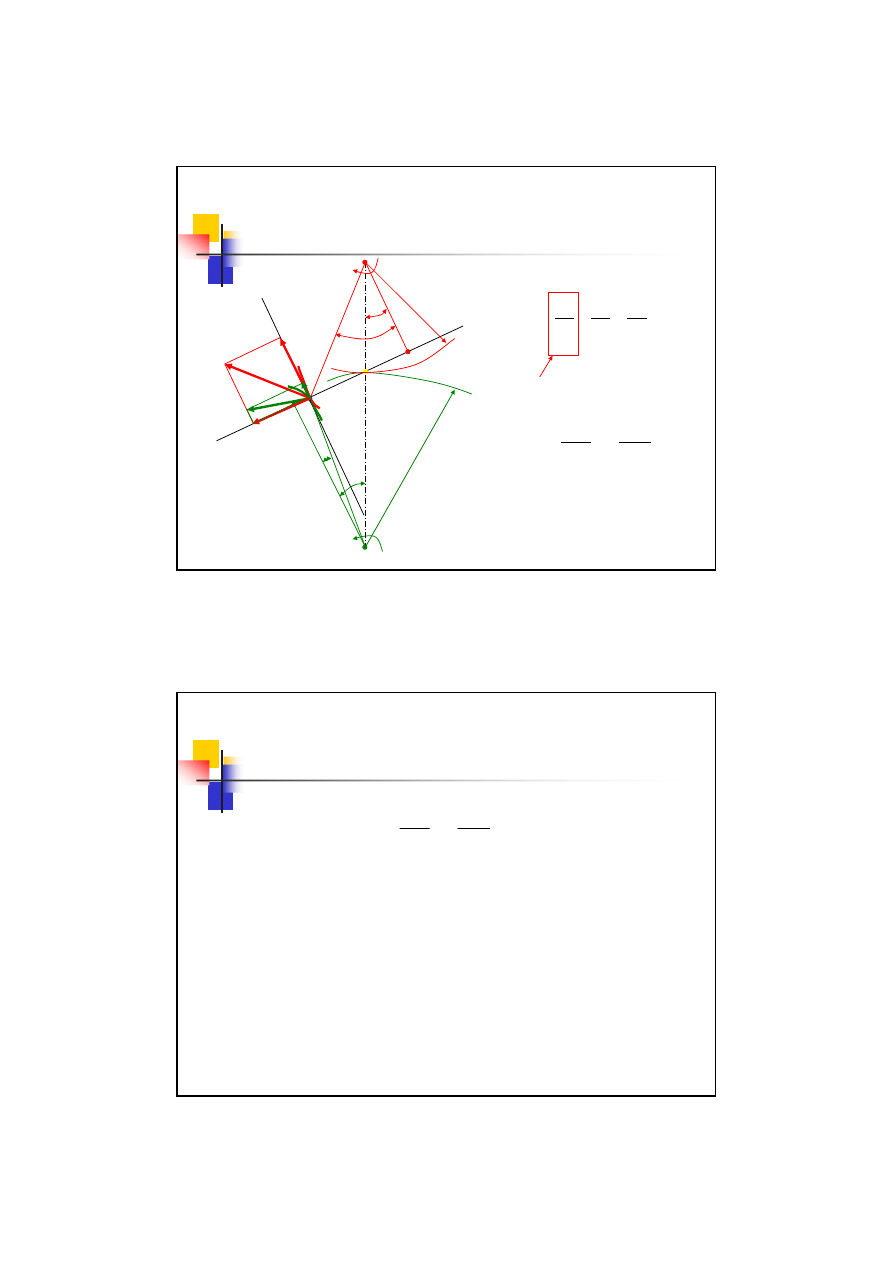
Podstawowe prawo zazębienia

O

1

O

2

B

Z rysunku wynika:

ω

ωω

ω

1

ω

ωω

ω

2

N

N

T

T

C

Ponieważ:

r

w2

r

w1

G

1

G

2

r

b1

r

b2

α

αα

α

α

αα

α

r

1

r

2

γγγγ

1

2

2

2

1

1

1

cos

cos

r

r

r

r

b

b

=

=

γ

γ

V

1

Zatem:

2

2

1

1

b

b

r

r

⋅

=

⋅

ω

ω

V

2

V

n1

=V

n2

W

1

W

2

α

α

cos

cos

2

2

1

1

⋅

=

⋅

=

w

b

w

b

r

r

r

r

γγγγ

2

11

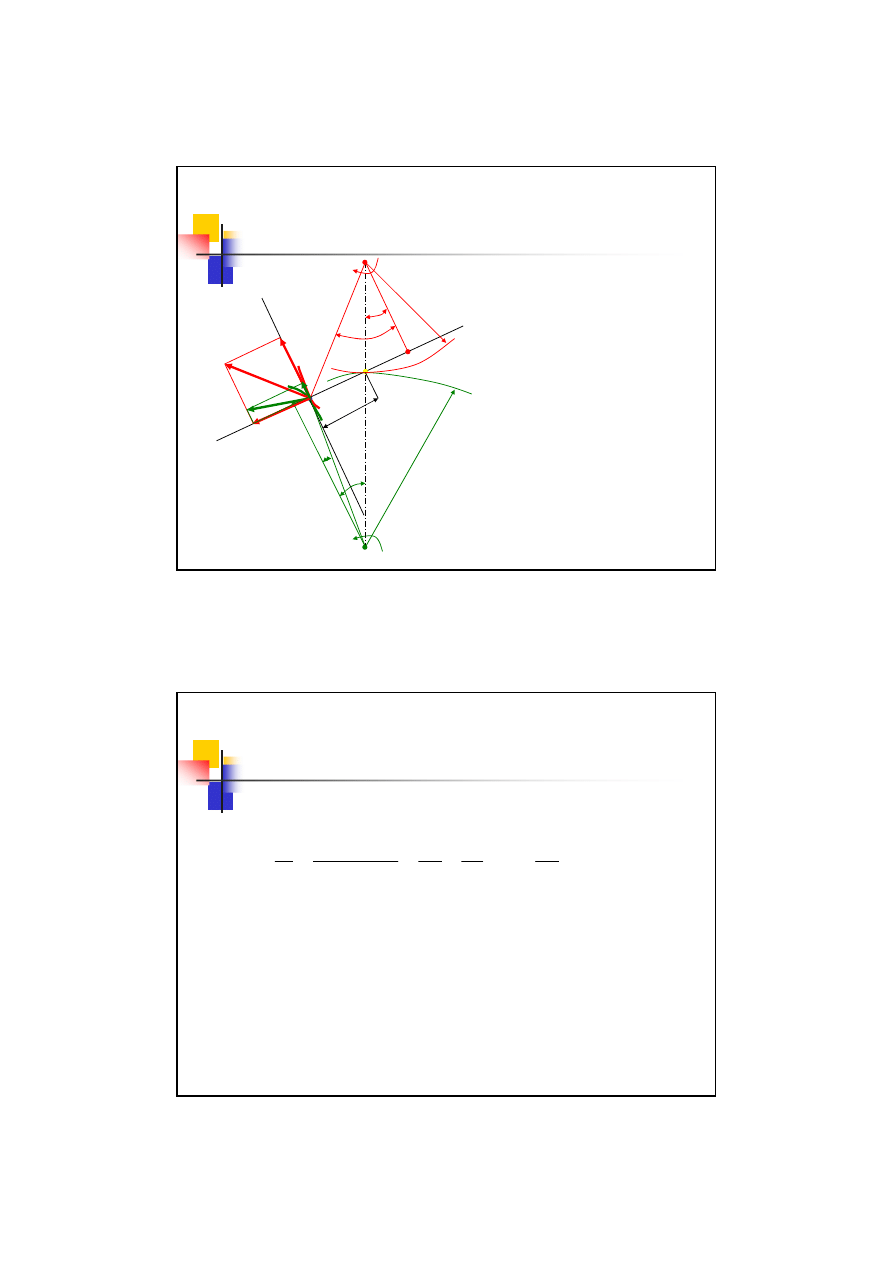
Podstawowe prawo zazębienia

O

1

O

2

B

Otrzymujemy:

ω

ωω

ω

1

ω

ωω

ω

2

N

N

T

T

C

r

w2

r

w1

G

1

G

2

r

b1

r

b2

α

αα

α

α

αα

α

r

1

r

2

γγγγ

1

1

2

1

2

2

1

w

w

b

b

r

r

r

r

=

=

ω

ω

V

1

Przełożenie kinematyczne

V

2

V

n1

=V

n2

W

1

W

2

1

2

2

1

w

w

r

r

i

=

=

ω

ω

γγγγ

2

Podstawowe prawo zazębienia

1

2

2

1

w

w

r

r

i

=

=

ω

ω

Podstawowe prawo zazębienie – prawo Willisa

W celu zapewnienia stałego przełożenia kinematycznego (

i=const

)

zarysy zębów powinny być takie, aby prosta normalna NN w
dowolnym punkcie styku B dzieliła odcinek O

1

O

2

w stałym

stosunku (aby punkt C był zawsze w tym samym miejscu)

Zarysy zębów spełniające ten warunek nazywamy

zarysami sprzężonymi

12

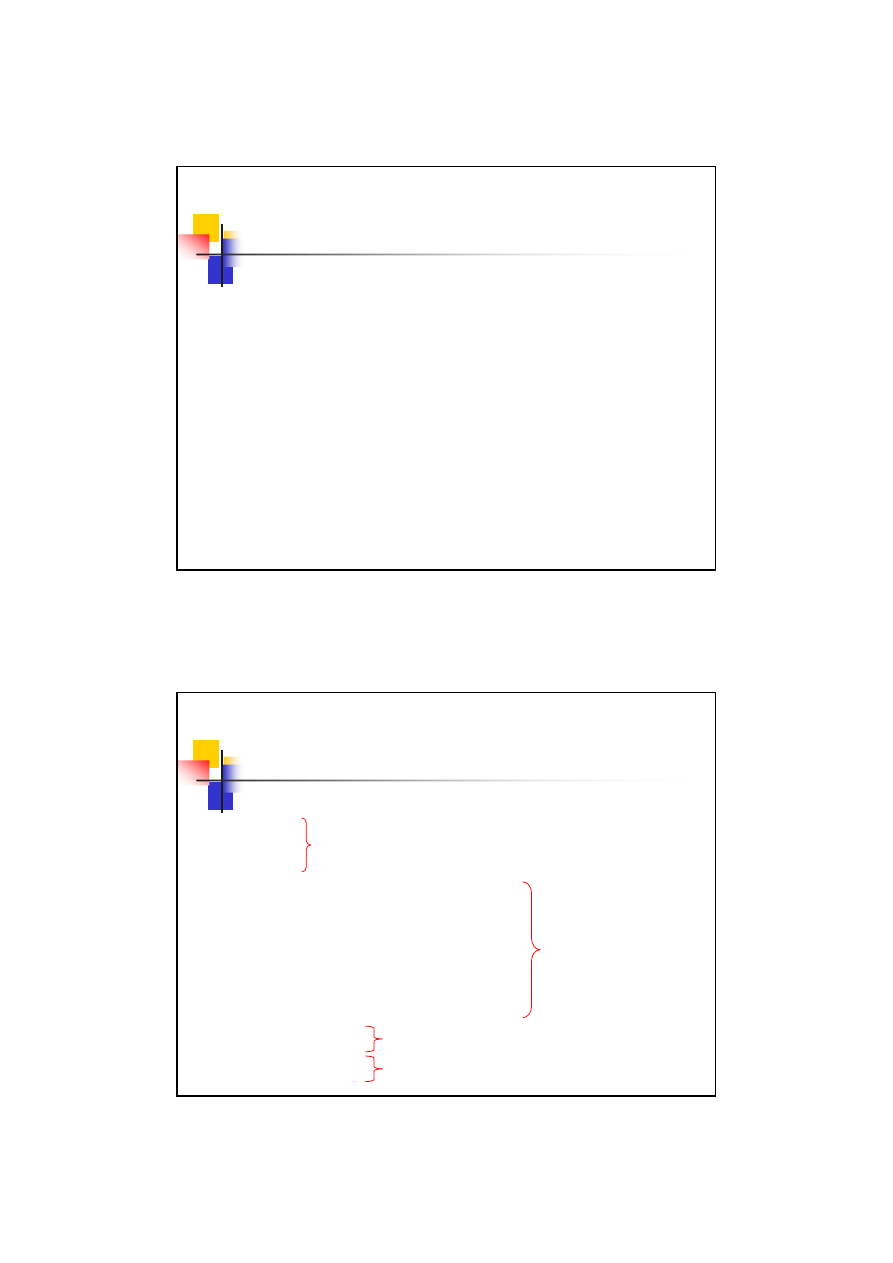
Poślizg względny

O

1

O

2

B

W odróżnieniu od prędkości

normalnych gdzie:

ω

ωω

ω

1

ω

ωω

ω

2

N

N

T

T

C

r

w2

r

w1

G

1

G

2

r

b1

r

b2

α

αα

α

α

αα

α

r

1

r

2

γγγγ

1

2

1

n

n

V

V

=

V

1

1

2

W

W

V

s

−

=

V

2

V

n1

=V

n2

W

1

W

2

Prędkości styczne dwóch zębów są

różne, a różnica ich jest prędkością

poślizgu:

Wprowadzając odległość punktu B od

punktu C możemy określić:

e

(

)

2

1

ω

ω

+

⋅

=

e

V

s

γγγγ

2

Poślizg względny

Zatem względny poślizg wynosi:

(

)

( )

1

1

2

2

1

2

2

2

2

1

+

⋅

=













+

⋅

=

⋅

+

⋅

=

i

r

e

r

e

r

e

V

V

w

w

w

s

ω

ω

ω

ω

ω

Wnioski:

Prędkość poślizgu wzrasta wraz z odległością punktu przyporu B od punktu zazębienia C

Prędkość poślizgu wzrasta wraz z przełożeniem

Zęby zużywać się będą u wierzchołka i w dolnej części podstawy zęba gdzie
prędkość poślizgu przy zazębieniu jest największa

13

Zarysy zębów

Zarys zębów powinien być sprzężony

(spełniać prawo Willisa)

Dodatkowe cechy:

- wytrzymałość

- technologiczność

- niewrażliwość na błędy odległości osi

- odporność na zużycie

- stałość kierunku sił międzyzębnych

Zarysy zębów

Stosowane zarysy zębów

Liniowe

Kołowe

Ortocylkoidy

( krzywa kreślona przez punkt

koła toczącego się po prostej)

Epicykloidy

(krzywa kreślona przez punkt

koła toczącego się na zewnątrz innego
koła)

Hipocykloidy

(krzywa kreślona przez

punkt koła toczącego się na wewnątrz
innego koła)

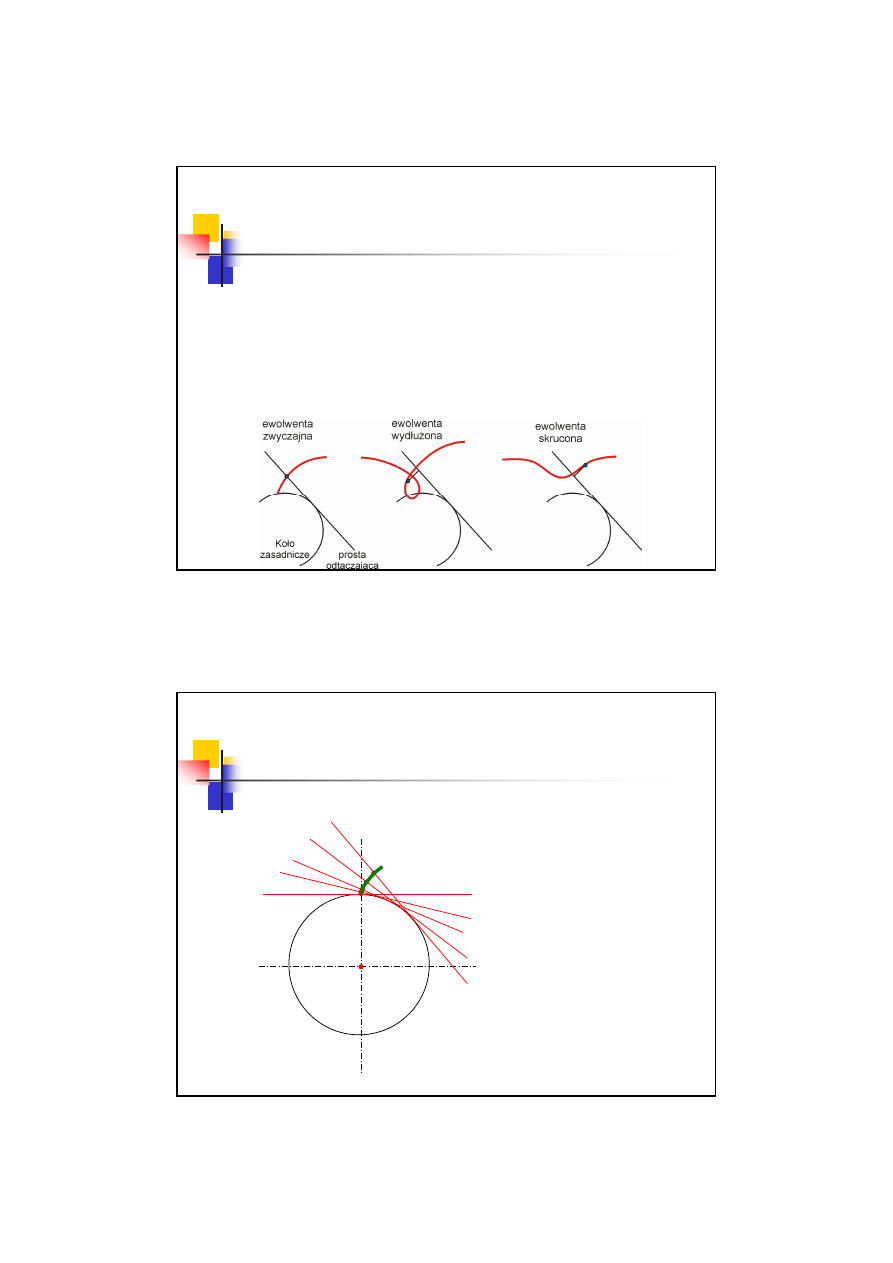
Ewolwenta

Kołowo-łukowe

Pierwsze zarysy stosowane na
koła zębate – obecnie
całkowicie wycofane

Wyparły zarysy liniowe i
kołowe a następnie zostały
wyparte przez zarys
ewolwentowy. Obecnie
stosowane w mechanizmach
zegarkowych. Zaleta:
możliwość stosowania dużych
przełożeń

Podstawowy obecnie
stosowany zarys koła

Najnowszy zarys. Charakteryzuje się małymi naciskami
między zębami. Wadę stanowi konieczność produkcji kół
jako par (brak uniwersalności i trudności obróbkowe)

14

Zarys ewolwentowy

Ewolwenta – linia będąca torem dowolnego punktu związanego z
prostą toczącą się po okręgu bez poślizgu.

Okrąg po którym toczy się prosta nazywany jest okręgiem
zasadniczym.

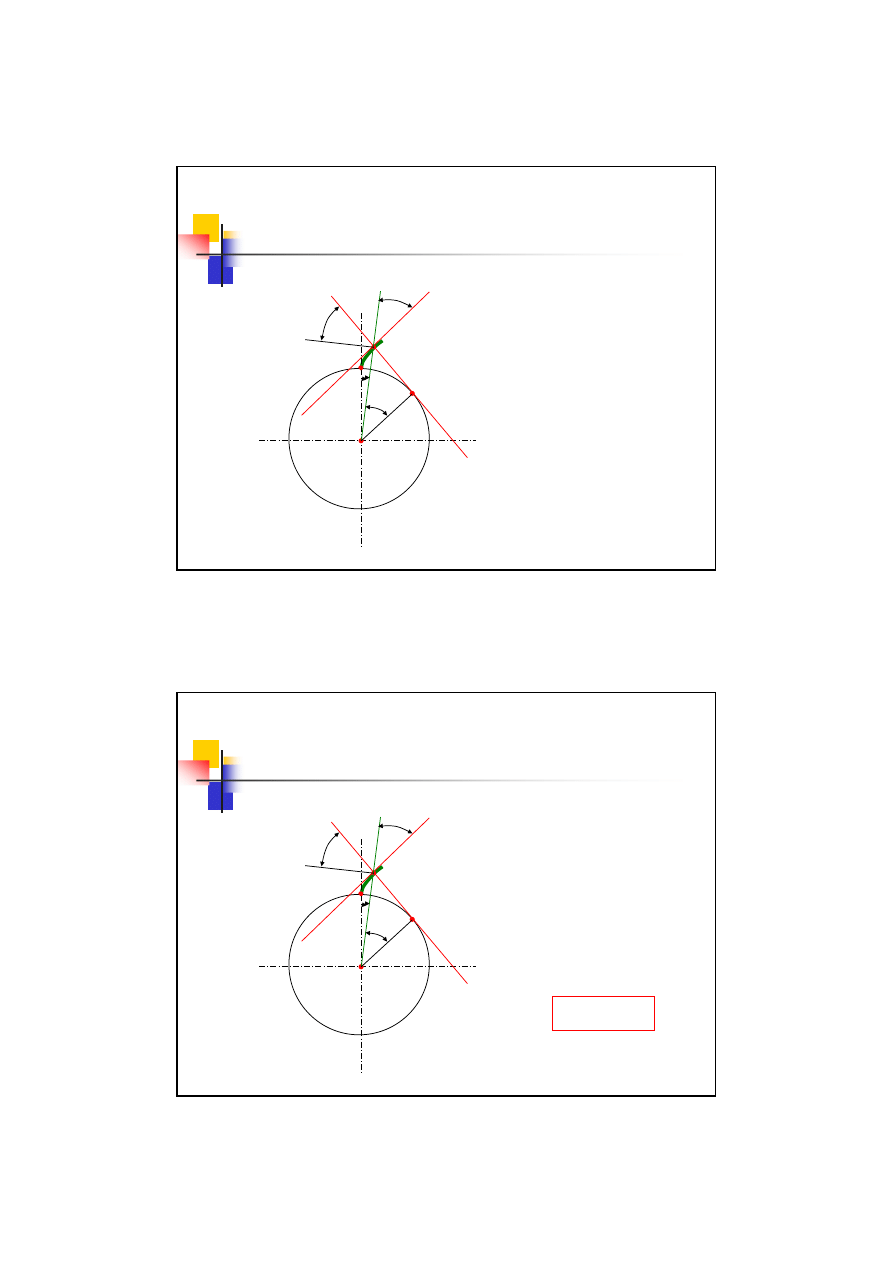
Zarys ewolwentowy

Geometria ewolwenty

Okrąg zasadniczy

O

P

Prosta toczy się po okręgu

zasadniczym a punkt na niej się

znajdujący wykreśla ewolwentę

15

Zarys ewolwentowy

Geometria ewolwenty

Okrąg zasadniczy

O

P

Dla wybranego położenia prostej

tworzącej mamy:

M

Prosta tworząca jest normalna do zarysu

w punkcie M –

punkt przyporu

N

N

Prosta TT styczna do ewolwenty w

punkcie M

T

T

γγγγ

Promień r – łączący punkt O z M

jest odchylony od osi OP o kąt

γγγγ

r

Prosta tworząca styka się z okręgiem

zasadniczym w punkcie N

1

N

1

r

b

Kąt pomiędzy prostą NN a normalną do

promienia r (OM) jest

Kątem zarysu

ewolwenty

α

αα

α

α

αα

α

α

αα

α

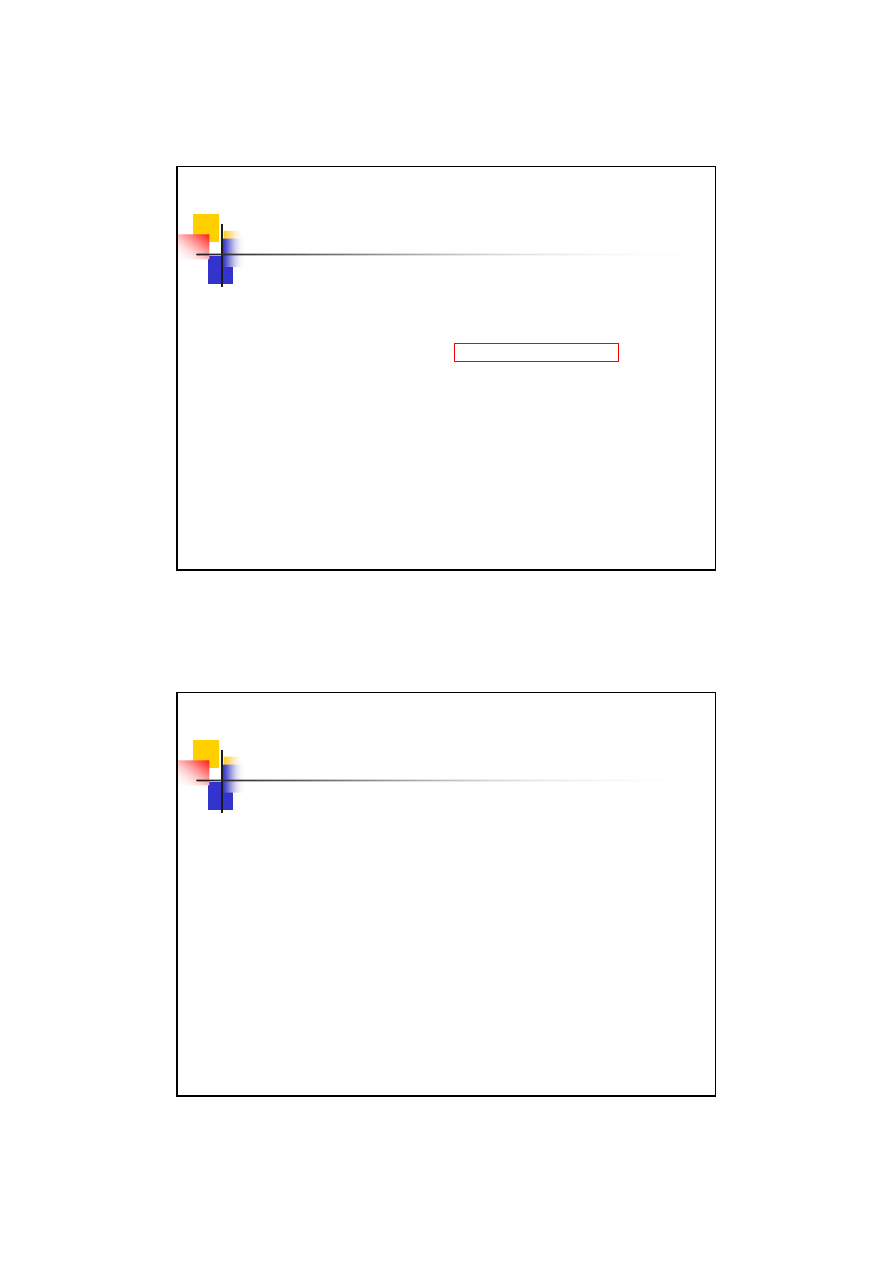
Zarys ewolwentowy

Geometria ewolwenty

Okrąg zasadniczy

O

P

Ze sposobu powstawania ewolwenty

wynika, że długość łuku PN

1

jest równa

odległości punków MN

1

M

N

N

T

T

γγγγ

r

N

1

r

b

α

αα

α

α

αα

α

α

αα

α

Ponieważ:

(

)

α

α

γ

tg

r

MN

r

PN

b

b

⋅

=

+

⋅

=

1

1

Zatem:

(

)

α

α

γ

tg

r

r

b

b

⋅

=

+

⋅

α

α

γ

−

=

tg

Kąt

γγγγ

jest

funkcją ewolwentową

zwaną

także

involutą

α

α

α

−

=

tg

inv

16

Inwoluta

Inwoluta = funkcja ewolwentowa

α

α

α

−

=

tg

inv

Kąt podawany w [radianach]

Wartość inwoluty jest także podawana w tabelach.

UWAGA!

Wartość inwoluty należy podawać

minimum do 5 miejsca po przecinku np. 0,02389.

Zarys ewolwentowy – zalety i wady

Zalety:

Jest zarysem sprzężonym. Zachowuje tę cechę także przy zmianie
odległości osi

Jest łatwy do wykonania. Uniwersalność narzędzi obróbkowych do
wielu kół. Możliwość uzyskania dużych dokładności i małej
chropowatości powierzchni styku.

Siła międzyzębna zachowuje stały kierunek w czasie współpracy
zębów

Uniwersalność kół. Praca kół o różnych ilościach zębów i tych
samych cechach geometrycznych.

17

Zarys ewolwentowy – zalety i wady

Wady:

Mała powierzchnia styku (stykają się dwie powierzchnie wypukłe)
Duże naciski są przyczyną zmniejszenia trwałości

Duże prędkości poślizgów przy zazębianiu i wyzębianiu się kół.
Zwiększone zużycie głów i podstaw zębów.

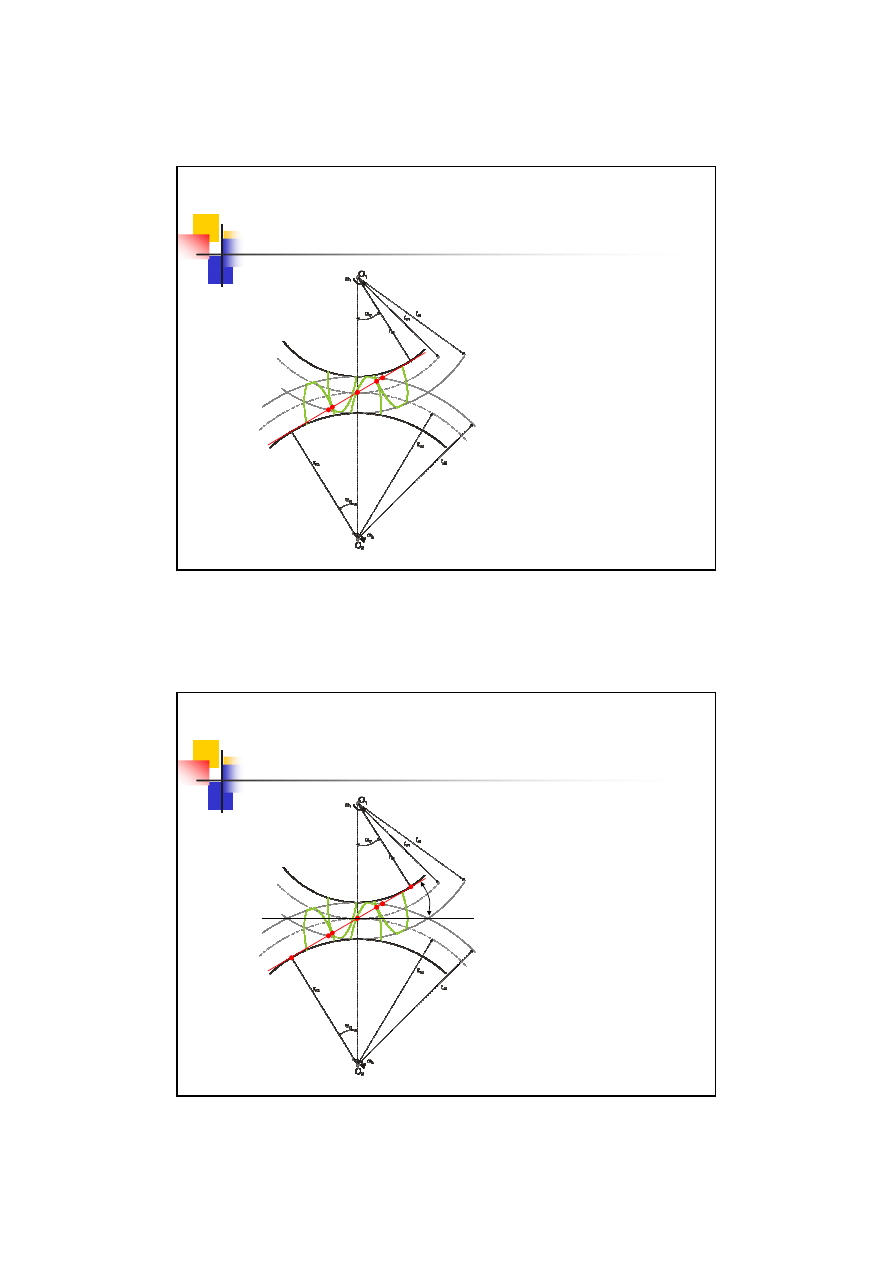
Zazębienie ewolwentowe

Dwa koła współpracujące mają

wspólną linię normalną do

punktów przyporu przecinającą

linię O

1

O

2

w punkcie C. Linia ta

jest styczna do kół

zasadniczych.

C

Na linii tej występuje styk par

zębów odpowiednio w

punktach P’ i P”

P’

P”

Linia ta zawiera wszystkie

punkty przyporu zachodzące
podczas współpracy obu kół.

Nosi ona nazwę

Linii Przyporu

18

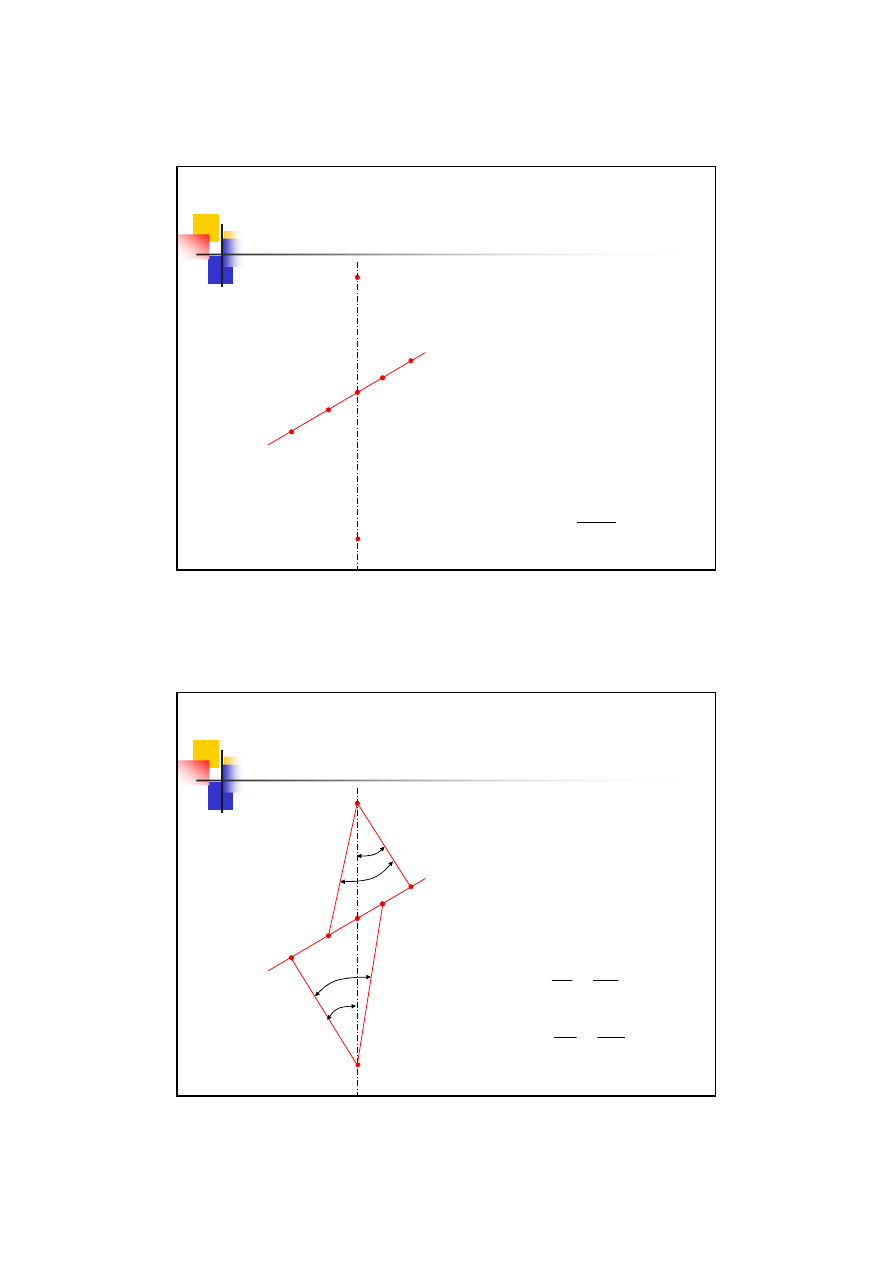
Zazębienie ewolwentowe

Ponieważ zarysy zębów są od

góry ograniczone okręgiem

wierzchołków zatem styk

między kołami może zachodzić

tylko na pewnym odcinku linii

przyporu.

C

P’

P”

E

1

E

2

Są to odpowiednio punkty

E

1

i E

2

Część linii przyporu

ograniczona tymi

punktami nosi nazwę

odcinka przyporu

Zazębienie ewolwentowe

Kąt zawarty między linią

przyporu a linią normalną do

osi O

1

O

2

w punkcie C nazywany

jest

tocznym kątem przyporu

C

P’

P”

E

1

E

2

α

αα

α

w

Linia przyporu styka się z

okręgami zasadniczymi w

punktach N

1

i N

2

N

1

N

2

19

Liczba przyporu

Liczba przyporu

jest

wskaźnikiem zazębienia,
mówiącym ile par zębów

jest jednocześnie we

współpracy (średnio dla

całego obrotu kół)

C

E

1

E

2

N

1

N

2

O

1

O

2

Można ją obliczyć jako

stosunek długości odcinka

przyporu do podziałki p

p

E

E

2

1

=

ε

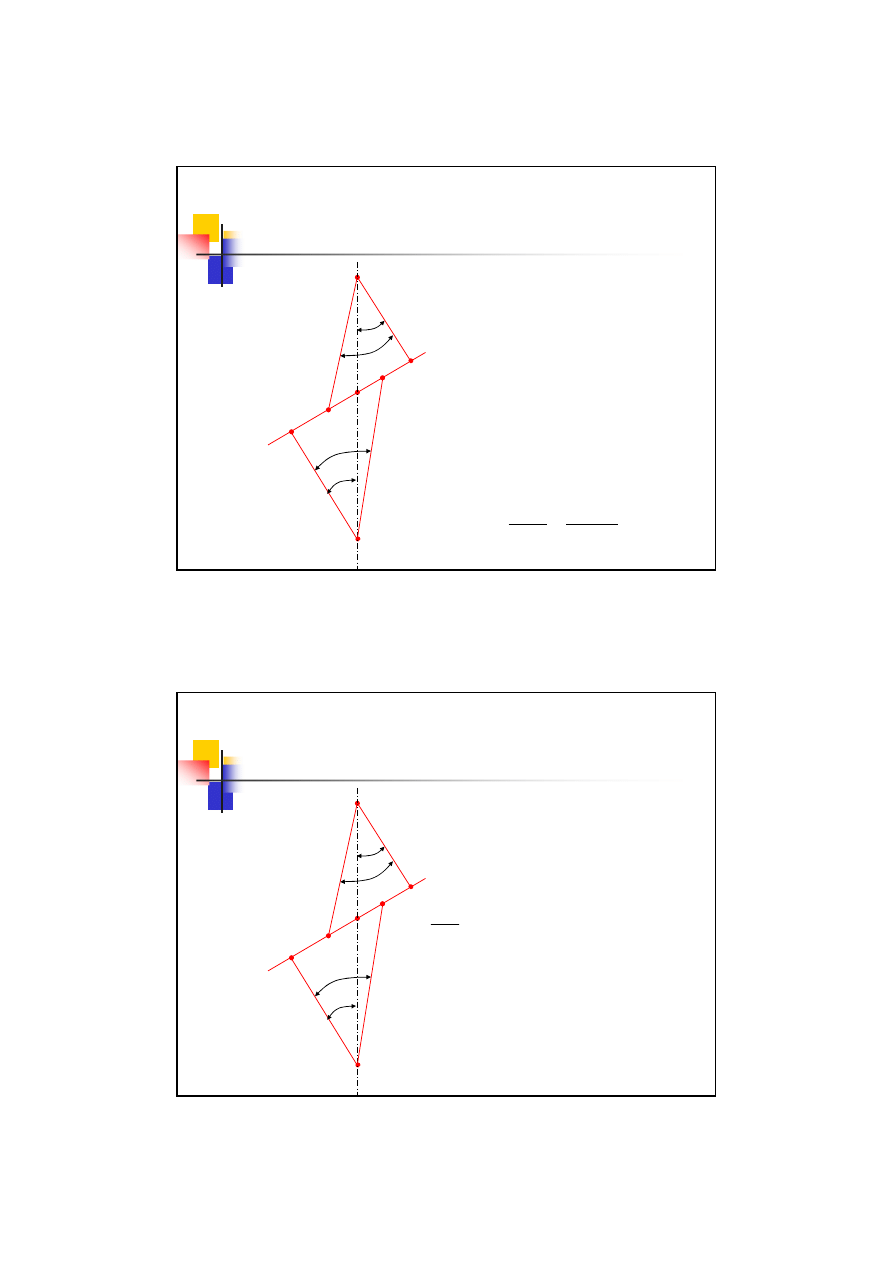
Liczba przyporu

Analizując rysunek można

zauważyć, że:

C

E

1

E

2

N

1

N

2

O

1

O

2

Wprowadzając odpowiednie kąty

i promienie

2

1

2

2

1

1

2

1

N

N

E

N

E

N

E

E

−

+

=

r

b1

r

a1

r

b2

r

a2

α

αα

α

w

α

αα

α

w

α

αα

α

a1

α

αα

α

a2

Gdzie

α

αα

α

a

–

kąt głów

w

a

a

b

a

w

a

a

b

a

d

d

r

r

d

d

r

r

α

α

α

α

cos

cos

cos

cos

2

2

2

2

2

1

1

1

1

1

⋅

=

=

⋅

=

=

20

Liczba przyporu

Otrzymujemy:

C

E

1

E

2

N

1

N

2

O

1

O

2

1

1

1

1

a

b

tg

r

E

N

α

⋅

=

r

b1

r

a1

r

b2

r

a2

α

αα

α

w

α

αα

α

w

α

αα

α

a1

α

αα

α

a2

2

2

2

2

a

b

tg

r

E

N

α

⋅

=

(

)

w

b

b

tg

r

r

N

N

α

⋅

+

=

2

1

2

1

Stąd:

(

)

w

b

b

a

b

a

b

tg

r

r

tg

r

tg

r

E

E

α

α

α

⋅

+

−

⋅

+

⋅

=

2

1

2

2

1

1

2

1

(

)

(

)

w

a

b

w

a

b

tg

tg

r

tg

tg

r

E

E

α

α

α

α

−

+

−

⋅

=

2

2

1

1

2

1

Podziałka wynosi:

z

r

z

d

p

b

b

⋅

⋅

=

⋅

=

π

π

2

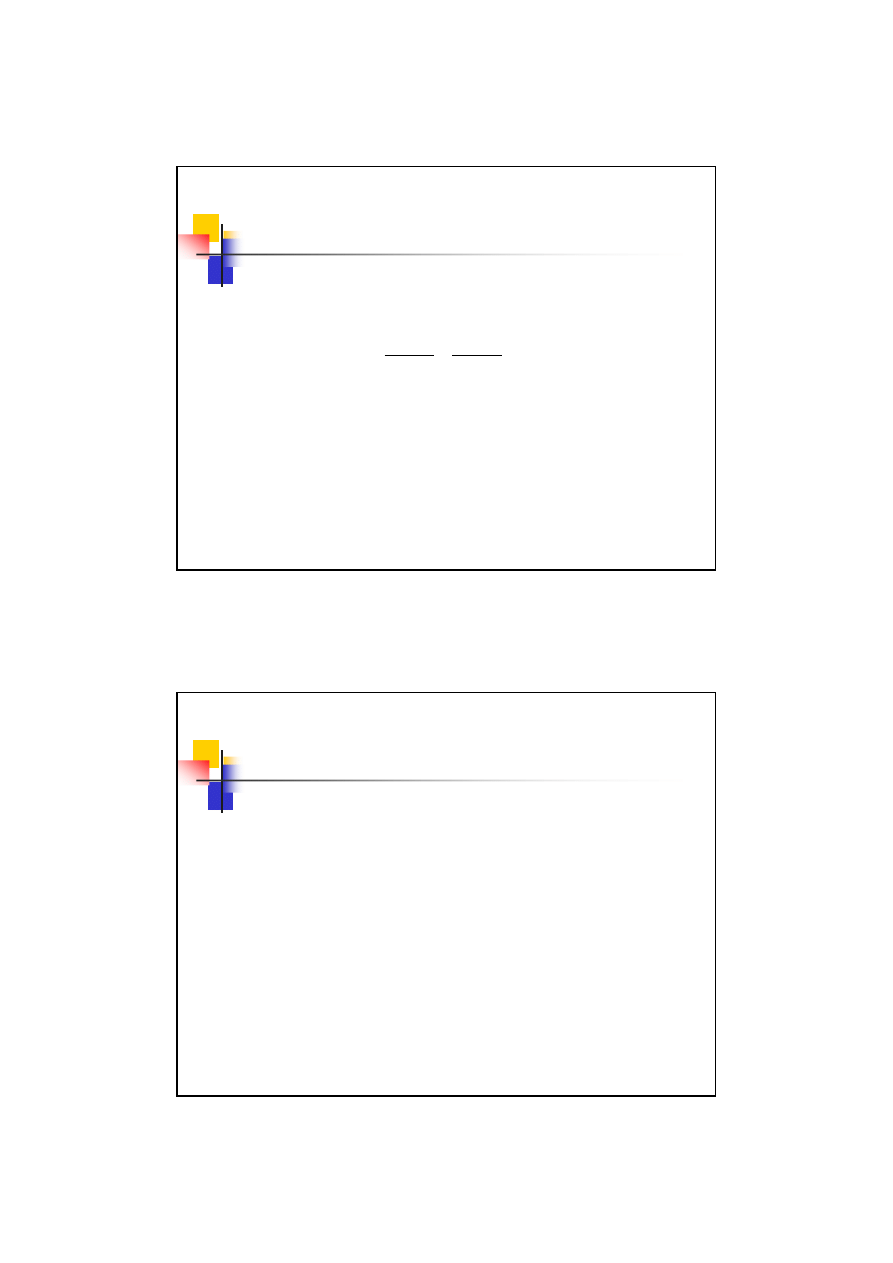
Liczba przyporu

Po przekształceniach

otrzymujemy liczbę przyporu:

C

E

1

E

2

N

1

N

2

O

1

O

2

(

)

(

)

[

]

w

a

w

a

tg

tg

z

tg

tg

z

α

α

α

α

π

ε

−

⋅

+

−

⋅

⋅

=

2

2

1

1

2

1

r

b1

r

a1

r

b2

r

a2

α

αα

α

w

α

αα

α

w

α

αα

α

a1

α

αα

α

a2

Dla zapewnienia ciągłości zazębienia

liczba przyporu powinna być większa od 1.

Ze względu na niedokładności

wykonania przyjmuje się:

25

,

1

15

,

1

÷

≥

ε

21

Zazębienie ewolwentowe

Analizując zazębienie można określić, że rzeczywista odległość osi wynosi:

w

b

w

b

w

r

r

a

α

α

cos

cos

2

1

+

=

Zatem:

2

1

cos

b

b

w

w

r

r

a

+

=

⋅

α

Jednocześnie z własności ewolwenty wynika:

α

cos

1

1

⋅

=

r

r

b

α

cos

2

2

⋅

=

r

r

b

Zazębienie ewolwentowe

Jednocześnie wiemy, że zerowa odległość osi to:

2

1

r

r

a

+

=

Zatem:

α

α

cos

cos

⋅

=

⋅

a

a

w

w

22

Metody obróbki kół zębatych

Stosowane są dwie podstawowe metody

obróbki kół zębatych:

Metoda kształtowa

Metoda obwiedniowa

Metody obróbki kół zębatych

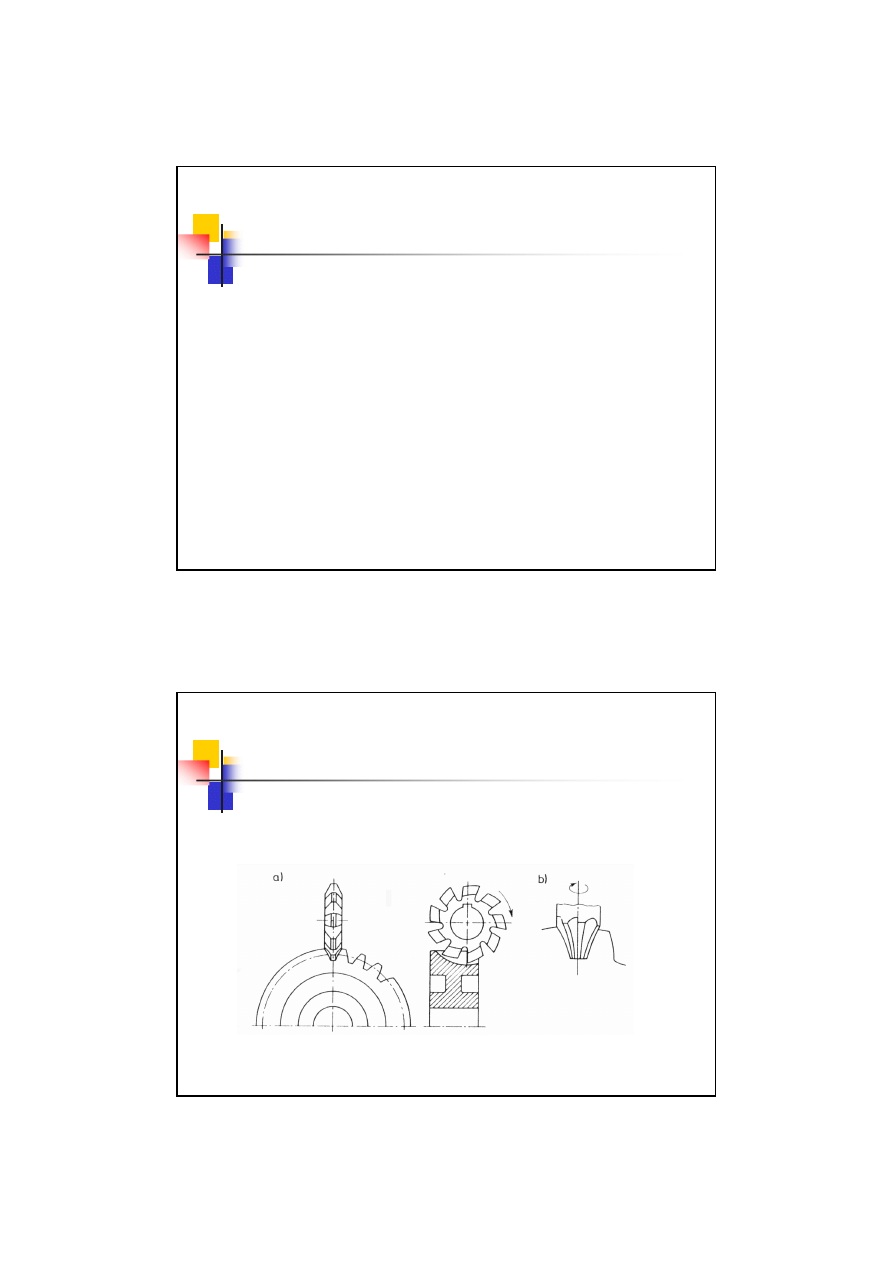
Metoda kształtowa

Polega na zastosowaniu narzędzia, którego część skrawająca na kształt wrębu
obrabianego koła.

Można zastosować:
Frezowanie krążkowe, palcowe, dłutowanie, przeciąganie

23

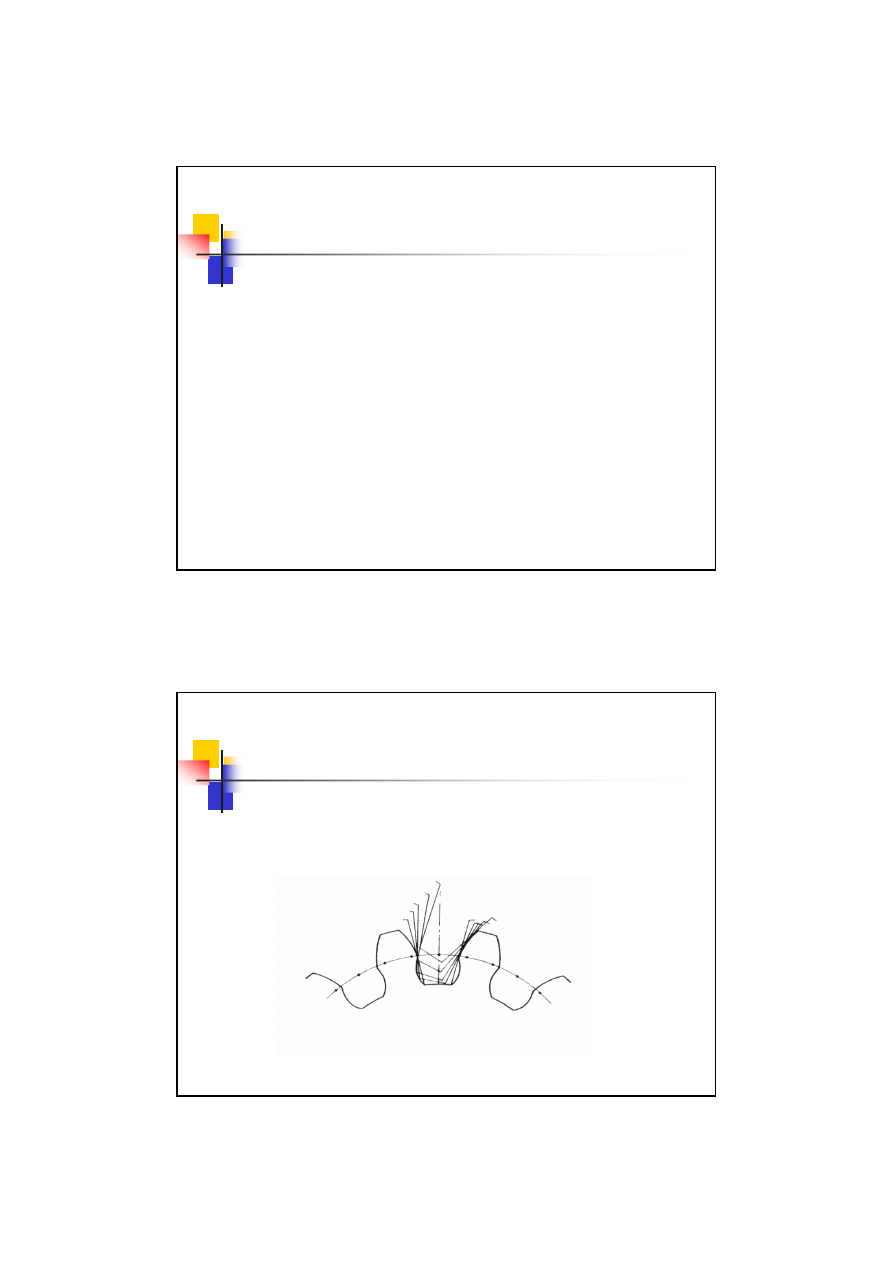
Metody obróbki kół zębatych

Metoda kształtowa

Ze względu na to, że wymiary wrębu koła zależą od modułu

oraz

ilości zębów,

narzędzia są specjalizowane do danego koła.

Dopuszczalne jest zastosowanie jednego narzędzia do kilku kół ale w ten sposób
wprowadza się błędy w zarys kół.

Metoda stosowana rzadko. Głównie do kół o małym znaczeniu lub bardzo dużych.

Metody obróbki kół zębatych

Metoda obwiedniowa

Polega na wykorzystaniu prostego narzędzia współpracującego z nacinanym
kołem. Zarys powstaje poprzez zazębienie się koła z narzędziem.

Narzędzie może mieć postać:
- listwy zębatej,
- koła zębatego
- ślimaka

24

Metody obróbki kół zębatych

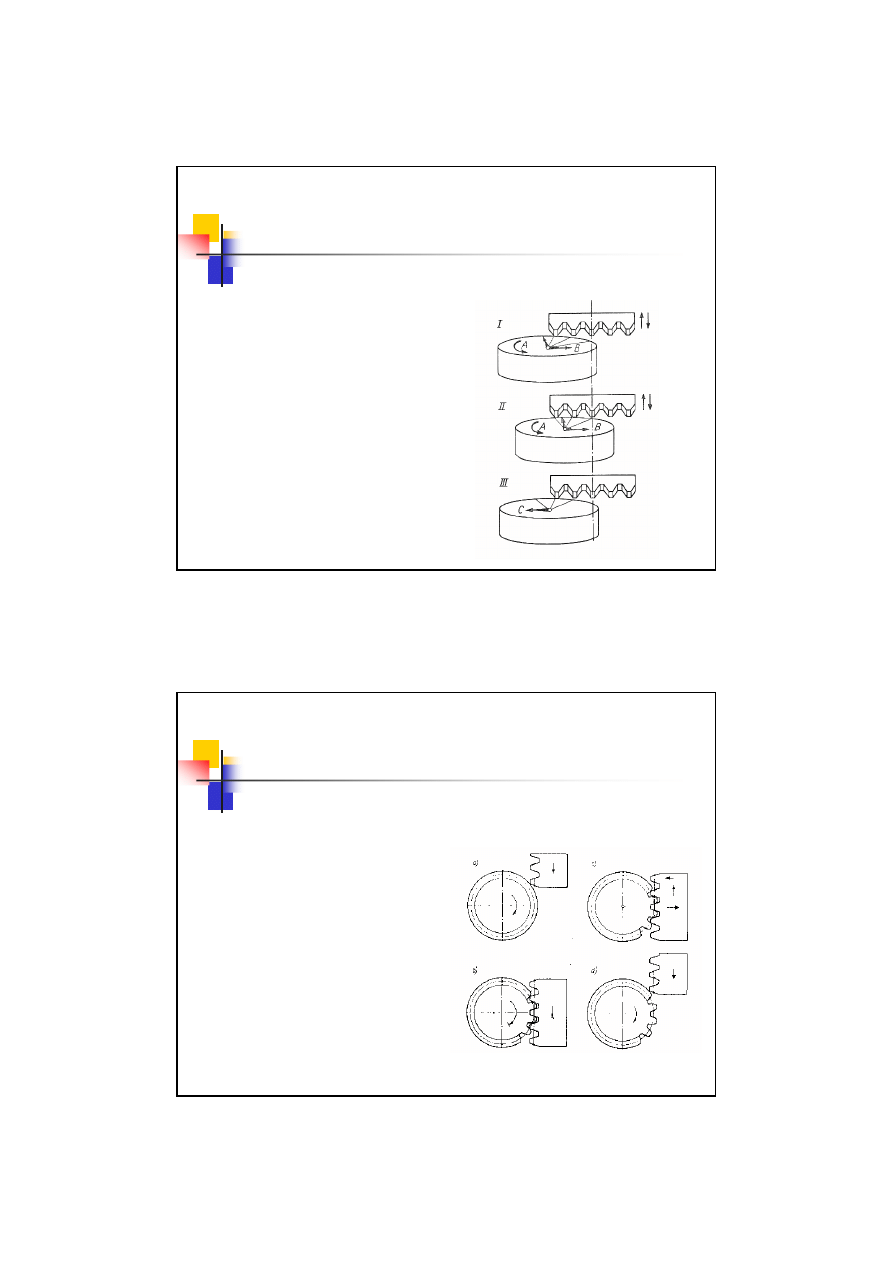
Metoda obwiedniowa Maaga

Narzędzie ma postać listwy zębatej.

Narzędzie wykonuje ruch roboczy
(postępowo-zwrotny).

Koło wykonuje ruch obrotowy i
postępowy.

Metody obróbki kół zębatych

Metoda obwiedniowa Sunderlanda

Narzędzie ma postać listwy zębatej.

Narzędzie wykonuje ruch roboczy
(postępowo-zwrotny) oraz
pomocniczy (postępowy).

Koło wykonuje ruch obrotowy.

25

Metody obróbki kół zębatych

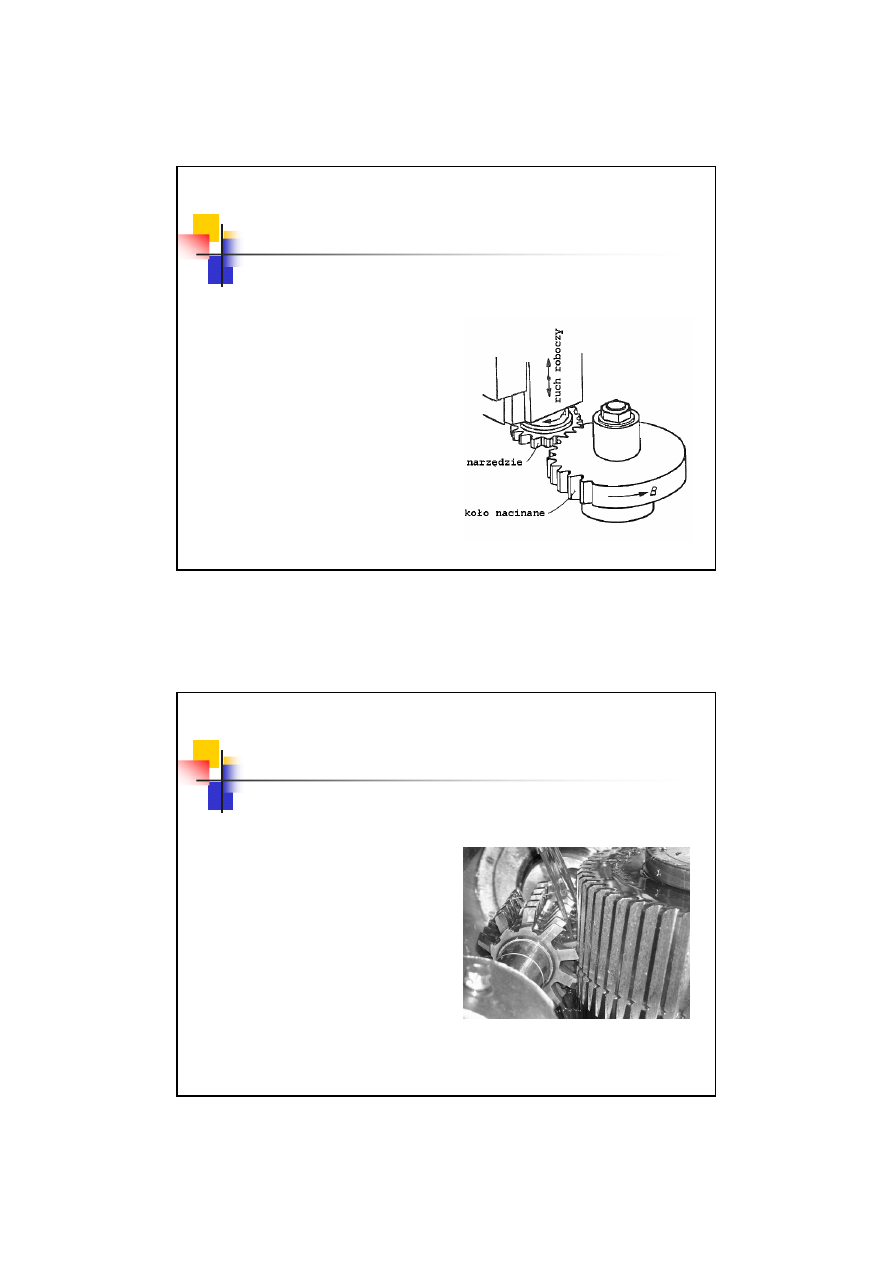
Metoda obwiedniowa Fellowsa

Narzędzie ma postać koła zębatego.

Narzędzie wykonuje ruch roboczy
(postępowo-zwrotny) oraz
pomocniczy (obrotowy).

Koło wykonuje ruch obrotowy.
Narzędzie i koło współpracują ze
sobą.

Metody obróbki kół zębatych

Metoda obwiedniowa Gleasona

Narzędzie ma postać ślimaka z wyciętymi
rowkami wzdłuż osi narzędzia. Ślimak ma
w przekroju kształt zębatki.

Narzędzie wykonuje ruch roboczy
(obrotowy).

Koło wykonuje ruch obrotowy oraz
postępowy (zbliża się do ślimaka).
Narzędzie i koło współpracują ze
sobą.