L

L

E

E

C

C

T

T

U

U

R

R

E

E

6

6

K

K

I

I

N

N

E

E

M

M

A

A

T

T

I

I

C

C

S

S

O

O

F

F

F

F

L

L

U

U

I

I

D

D

S

S

–

–

P

P

A

A

R

R

T

T

2

2

R

R

E

E

L

L

A

A

T

T

I

I

V

V

E

E

M

M

O

O

T

T

I

I

O

O

N

N

O

O

F

F

F

F

L

L

U

U

I

I

D

D

E

E

L

L

E

E

M

M

E

E

N

N

T

T

S

S

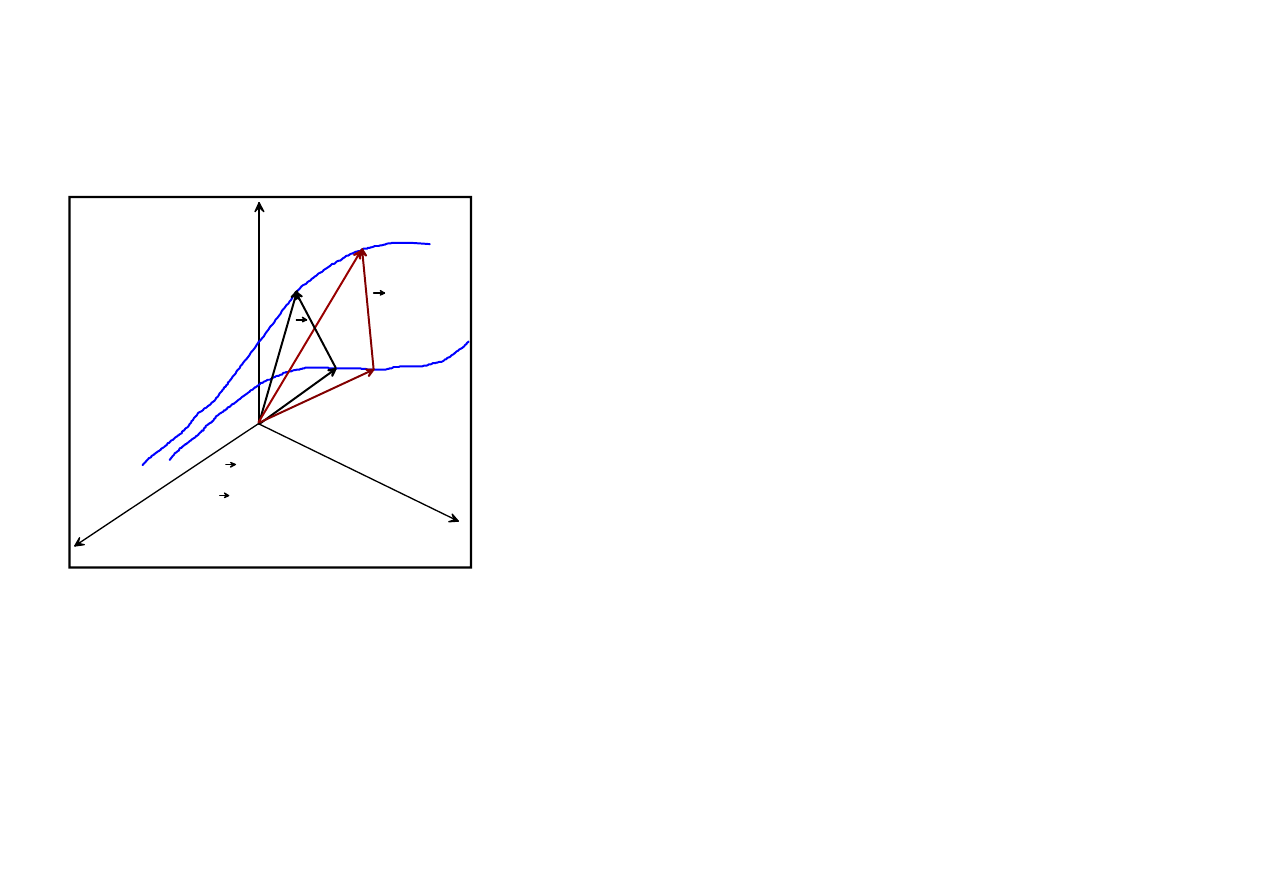
Consider two fluid elements located instantaneously at the close points A and B. We ask what
happens to the relative position of these fluid elements after a short time interval

t



.

The location of the first fluid element after the time

t



can

be expressed as follows

2

A

A

A

(t,

)Δt O(Δt )









x

x

v

x

Since

B

A





x

x

ρ

then analogously we have

2

B

A

A

(t,

)Δt O(Δt )





 





x

x

ρ v

x

ρ

,

where the vector

ρ

describes the relative position of the

fluid elements at the time

t

.

During a short time interval

t



this vector has changed and can be expressed as

2

2

B

A

A

A

2

(t

t)

(t) [ (t,

)

(t,

)] t O( t )

(t)

(t, )

t O( t , t | | )

































 



ρ

x

x

ρ

v

x

ρ

v

x

ρ

v

x ρ

ρ













In the above, we have dropped the lower index “A” at the location vector corresponding to the
first element.

t

t+t

x

1

x

3

x

2

0

A

A'

B

B'

=x

B

-x

A

'=x

B'

-x

A'



'

The rate of change of the vector describing the relative position of two close fluid elements
can be calculated

2

t

0

d

(t

t)

(t)

lim

(t, )

O(| | )

dt

t









 



ρ

ρ

ρ

v

x ρ

ρ







.

We have introduced the matrix (tensor) called the velocity gradient

j

x

i

ij

v

















v

.

The velocity gradient

v

can be written as a sum of two tensors

 



v

D R

, where

T

1

2

[

(

) ]



  

D

v

v

or

j

i

ij

j

i

v

v

1

d

2

x

x





























- symmetric tensor,

and

T

1

2

[

(

) ]



  

R

v

v

or

j

i

ij

j

i

v

v

1

r

2

x

x





























- skew-symmetric tensor

We will show that the change of the relative position of the fluid elements due to the
action of the antysymmetric tensor

R

corresponds to the local “rigid” rotation of the

fluid.

Next, we will show that the action of the symmetric part

D

corresponds to the “real”

deformation, i.e. it is responsible of the change in shape and volume.

To this end, we note that

1

2

ij

ijk

k

r



  

, where

k



are the Cartesian components of the

vorticity vector

k

k

ijk

i

j

v

rot

x







 



ω

v

e





.

Indeed, we have

j

j

i

i

1

1

2

2

ijk

k

i

j

i

j

ij

i

j

j

i

v

v

v

v

v

v

1

1

(

)

r

x

x

2

x

x

2

x

x



















 

 













































  

 



 





















Thus, we can write

1

1

1

2

2

2

ij

j

i

ijk

j

k

i

r



 



  

 







R ρ

e

e

ρ ω

ω ρ

.

Moreover, we get

2

d

d

d

dt

dt

dt

| |

( , )

2( ,

) 2( ,

)

(

)







 





ρ

ρ ρ

ρ

ρ

ρ Rρ

ρ ω ρ

0

i.e., the distance between two (arbitrary) fluid elements is fixed and there is no shape
deformation.

The skew-symmetric part of the velocity gradient describes

pure rigid rotation

of the

fluid and the

local angular velocity is equal

1

2

ω

.

D

D

E

E

F

F

O

O

R

R

M

M

A

A

T

T

I

I

O

O

N

N

O

O

F

F

F

F

L

L

U

U

I

I

D

D

E

E

L

L

E

E

M

M

E

E

N

N

T

T

S

S

The rate of change of the relative position vector (or – equivalently – the velocity of the
relative motion of two infinitely close fluid elements) can be expressed by the formula





deformation

rigid rotation

d

1

2

dt











ρ

Dρ

R ρ

Dρ

ω ρ

.

The first terms consists the symmetric tensor

D

, called the deformation rate tensor.

The tensor

D

can be expressed as the sum of the spherical part

D

SPH

and the deviatoric part

D

DEV

DEV

SPH





D

D

D

The spherical part

D

SPH

describes pure volumetric deformation (uniform expansion or

contraction without any shape changes) and it defined as



trace
of

k

SPH

SPH ij

ij

k

tr

v

1

1

1

(

)

(

)

3

3

3 x







 









D

D

D

I

v I

D

,

Note that

SPH

1

tr

(

) tr

(

)

div

3







 



D

v

I

v

v

.

The second part

D

DEV

describes shape changes which preserve the volume.

We have

j

i

k

DEV

DEV ij

ij

j

i

k

v

v

v

1

1

1

div

(

)

3

2

x

x

3 x











































D

D

v I

D



and

DEV

SPH

tr

tr

tr

0







D

D

D

To explain the geometric interpretation of both parts of the deformation rate tensor, consider
the deformation of a small, initially rectangular portion of a fluid in two dimensions. Assume
there is no rotation part and thus we can write

d

DEV

SPH

dt







ρ Dρ D

ρ D

ρ

.

For a short time interval

t



the above relation yields

2

1

2

DEV

SPH

(t

t)

(t)

t

t

O( t )











ρ

ρ

ρ

ρ

D

ρ

D

ρ

















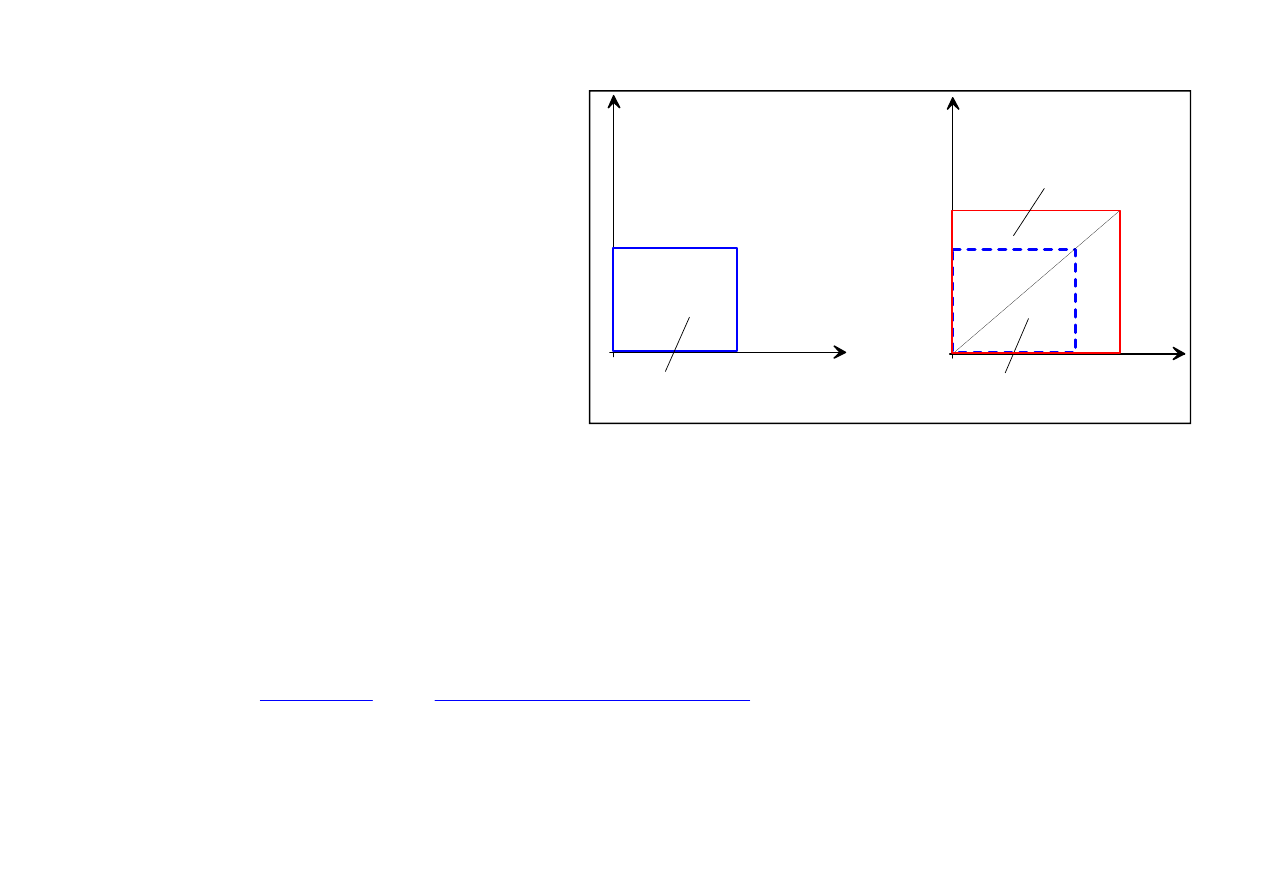
Consider the 2D case when only volumetric part of the deformation exists (see picture).

We have

SPH

d 0

0 d















D

,

tr

2d



D

The relative position vector at the time
instant

t

t





is expressed as

2

(t

t)

(1 d t) (t) O( t )















ρ

ρ

.

The shape of the volume is preserved because the above formula describes the isotropic
expansion/contraction. The volume of the region

1

2

Vol (t)

L L





has been changed to

2

2

1

2

Vol (t

t)

L L (1 d t)

Vol (t)(1 2d t) O( t )

























,

and

t

0

Vol (t

t) Vol (t)

1

lim

2d

tr

Vol (t)

t























  

D

v

O

x

1

x

2

A

B

C

(t)

B'

C'

A'

{

{

dt L

2

dt L

1

(t+t)

O

x

1

x

2

A

B

C

(t)

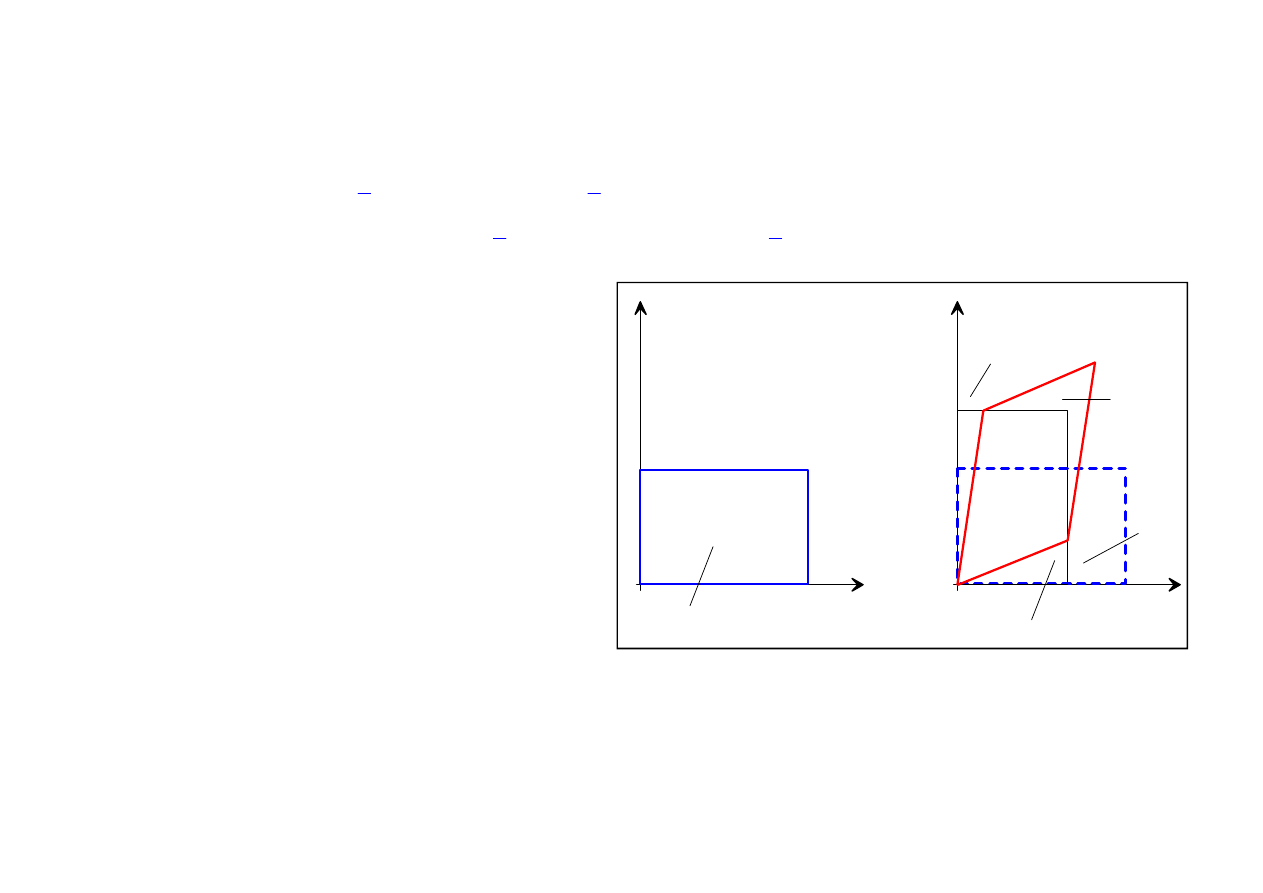
Assume now that the spherical part of the deformation rate tensor is absent. The deviatoric
part of this tensor in a 2D flow can be written as follows

1

1

2

2

11

12

11

22

12

DEV

1

1

2

2

12

22

12

22

11

d

d

d

(d

d )

d

d

d

d

d

(d

d )

 

























































D

.

The fluid deformation during the short time
interval can be now expressed as

2

DEV

O( t )

(t

t)

(

t

) (t)















ρ

I

D

ρ

or in the explicit form as

1

1

2

2

1

2

x (t

t)

(1

t) x (t)

t x (t)

x (t

t)

t x (t) (1

t) x (t)





























 

 



 

 

Note the presence of shear, which manifests in the change of the angles between the position
vectors corresponding to different fluid elements in the deforming region.

O

x

1

x

2

A

B

C

(t)

B'

C'

A'

{

{

t L

2

t L

1

(t+t)

{

{

t L

2

t L

1

O

x

1

x

2

A

B

C

(t)

Let’s compute again the change of the volume of the fluid region during such deformation.

We get

2

2

2

2

1

2

1

2

2

1

t

t

Vol (t

t)

L L

L L (1

t

t )

t

1

t

Vol (t) O( t )





 

 



 

 

 

 























,

so

t

0

Vol (t

t) Vol (t)

1

lim

0

Vol (t)

t





















.

We conclude that this time the instantaneous rate of the volume change is zero.

Thus, instantaneously, the deviatoric part of the deformation describes pure shear (no
expansion/contraction).