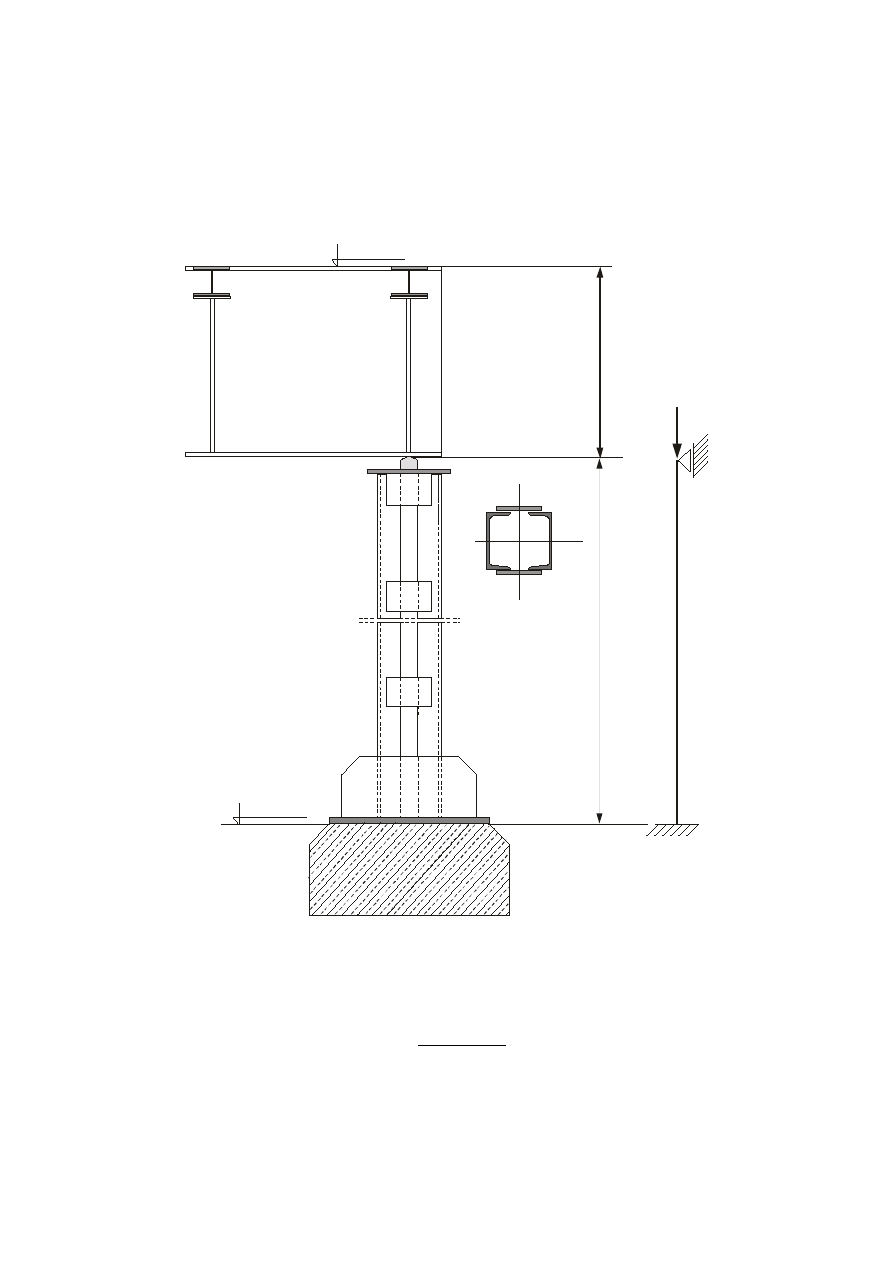
11. Słup stalowy.

11.1. Wstępna specyfikacja wymiarów słupa.

+7,40 m

+0,22 m

18

30

53

50

N

x

y

y

x

Zadane są poziomy posadzek na piętrze i na kondygnacji zerowej: +7,40 m i +0,22 m.
Reakcja podporowa od blachownicy: N = R

b

= 817,81 kN (poz. 5.3.1)

Długość wyboczeniowa: l

e

= 0,7

⋅

5,35 = 3,745 m

Warunek normowy:

1

≤

⋅

⋅

⋅

d

f

A

N

ψ

ϕ

Załóżmy wstępnie, że

ϕ

⋅ψ

= 0,6

1

wtedy

d

f

N

A

⋅

≥

6

,

0

2

2

67

,

44

004467

,

0

000

305

6

,

0

81

,

817

cm

m

A

=

=

⋅

=

Na jedną gałąź przekroju dwugałęziowego przypadnie A = 22,34 cm

2

Przyjmujemy ceownik normalny C 160
A = 24,0 cm

2

, I

x

= 925 cm

4

, I

y

= 85,3 cm

4

, W

x

= 116 cm

3

, i

x

= 6,21 cm, i

y

= 1,89 cm,

e = 1,84 cm, t

f

= 10,5 mm, t

w

= 7,5 mm, b

f

= 65 mm, R = 10,5 mm, R

1

= 5,5mm.

Ustalenie klasy przekroju

84

,

0

305

215

=

=

ε

półka:

55

,

7

9

48

,

4

5

,

10

5

,

10

5

,

7

65

=

<

=

−

−

=

−

−

ε

f

w

f

t

R

t

b

środnik:

72

,

27

33

73

,

15

5

,

7

)

5

,

10

5

,

10

(

2

160

)

(

2

=

<

=

+

⋅

−

=

+

⋅

−

ε

w

f

t

t

R

h

klasa pierwsza

11.2 Sprawdzenie słupa na wyboczenie względem osi materiałowej.

Smukłość względem osi x:

31

,

60

10

21

,

6

745

,

3

2

=

⋅

=

=

−

x

e

x

i

l

λ

526

,

70

305

215

84

215

84

=

=

=

d

p

f

λ

855

,

0

526

,

70

31

,

60

=

=

=

p

x

λ

λ

λ

Współczynnik wyboczeniowy odczytujemy z Tablicy 11 dla krzywej c (Tablica 10)

n

n

1

2

)

1

(

)

(

−

+

=

λ

λ

ϕ

n = 1,2

647

,

0

)

855

,

0

1

(

)

(

2

,

1

1

4

,

2

=

+

=

−

λ

ϕ

warunek nośności

1

≤

⋅

Rc

N

N

ϕ

N

Rc

= A

⋅

f

d

N = 817,81 kN

1

864

,

0

000

305

)

10

0

,

24

(

2

647

,

0

81

,

817

4

<

=

⋅

⋅

⋅

⋅

−

2

x

x

y

10

65

5,5

C160

1

60

x

y

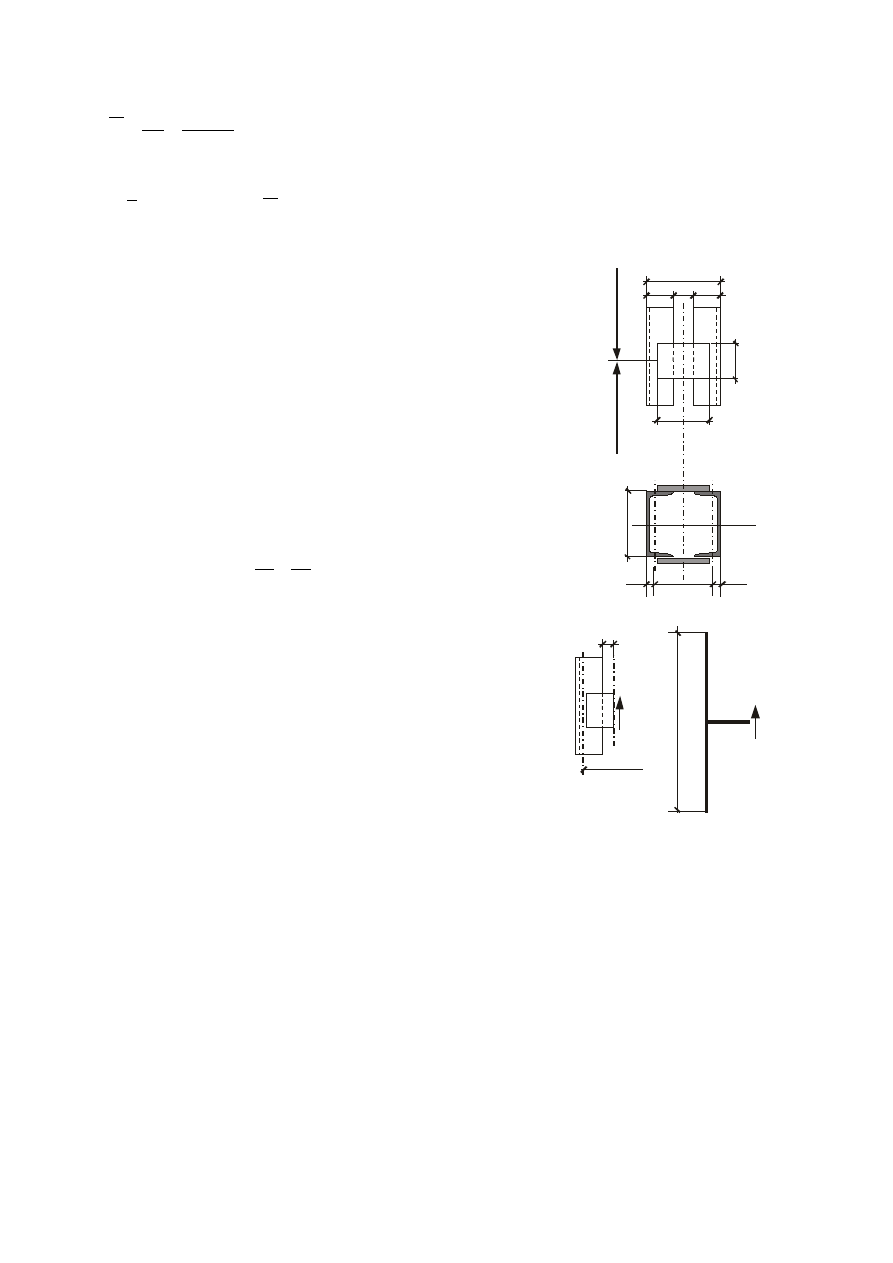
11.3 Ustalenie rozstawu gałęzi.

Smukłość względem osi x

31

,

60

10

21

,

6

745

,

3

i

l

2

x

e

x

=

⋅

=

=

λ

−

Postulujemy by smukłość zastępcza względem osi y (niemateriałowej)

2

v

2

y

m

λ

+

λ

=

λ

była nie większa niż

λ

x

, tzn.

λ

x

≥

λ

m

.

Z tego warunku dostaniemy wymagane

λ

y

dla przekroju całkowitego

2

v

2

x

wym

y

λ

−

λ

=

λ

Aby określić smukłość postaciową musimy przyjąć rozstaw przewiązek. Załóżmy 10
przewiązek (9 przedziałów). Odległość między przewiązkami musi spełniać warunek:

cm

4

,

113

89

,

1

60

i

60

cm

44

,

59

9

535

l

1

1

=

⋅

=

⋅

<

=

=

.

Smukłość postaciowa:

45

,

31

89

,

1

44

,

59

i

l

1

1

v

=

=

=

λ

obliczamy

46

,

51

45

,

31

31

,

60

2

2

wym

y

=

−

=

λ

Wymagany promień bezwładności względem osi y

cm

28

,

7

m

0728

,

0

46

,

51

745

,

3

l

i

i

l

wym

y

e

y

y

e

wym

y

=

=

=

λ

=

→

=

λ

Z tablic Żyburtowicza str. 85 przyjęto a’ = 180 mm dla którego i

y

= 7,40 cm,

I

y

= 2630 cm

4

, W

y

= 292 cm

3

.

11.4. Sprawdzenie słupa na wyboczenie względem osi y (nie
materiałowej).

Dla przyjętego rozstawu gałęzi słupa i

y

= 7,40 cm.

Smukłość

61

,

50

10

40

,

7

745

,

3

2

=

⋅

=

=

−

y

e

y

i

l

λ

Smukłość zastępcza

58

,

59

45

,

31

61

,

50

2

2

2

v

2

y

m

=

+

=

λ

+

λ

=

λ

λ

m

= 59,58 <

λ

x

= 60,31

Zgodnie z PN 4.7.1.a, str.18, współczynnik wyboczeniowy

ϕ

określamy dla smukłości

względnej

845

,

0

526

,

70

58

,

59

p

m

=

=

λ

λ

=

λ

)

(

λ

ϕ

=

ϕ

dla krzywej b

n

1

n

2

)

1

(

)

(

−

λ

+

=

λ

ϕ

n = 1,6

750

,

0

)

845

,

0

1

(

)

(

6

,

1

1

2

,

3

=

+

=

λ

ϕ

−

Smukłość względna pojedynczej gałęzi na odcinku l

1

3

a = 180

x

y

446

,

0

526

,

70

45

,

31

1

=

=

=

p

v

λ

λ

λ

Dla krzywej c (ceownik) n = 1,2

894

,

0

)

446

,

0

1

(

)

(

2

,

1

1

4

,

2

=

+

=

−

λ

ϕ

O nośności zadecydowało wyboczenie względem osi materiałowej (p. 11.2):

ϕ

= 0,647 < {0,75; 0,89}

Nośność słupa na ściskanie będzie zapewniona.

11.5. Obliczenie przewiązek słupa.

11.5.1. Dobór przewiązek słupa.

Z PN 4.7.3 p.19

b

≥

100 mm przyjęto

b

= 100 mm
zalecana długość przewiązki: 0,5

÷

0,75 szerokości słupa

(0,5

÷

0,75)

⋅

180 = 90

÷

135 mm przyjęto l = 130 mm

Grubość przewiązki:

g = 6

÷

12 mm,

2

,

5

13

25

1

10

1

÷

=

⋅













÷

l

przyjęto g = 10 mm

11.5.2. Obliczenie siły działającej na przewiązkę

Zastępcza siła poprzeczna

Q = 0,012

⋅

A

⋅

f

d

(PN (62) p.

19)
Q = 0,012

⋅

2

⋅

24,0

⋅

10

-4

⋅

305 000 = 17,57 kN

Siła działająca na pojedynczą przewiązkę

4

180

65 50 65

130

143,2

18,4

18,4

59

4

5

94

1

60

10

0

25

143,2

l

1

V

Q

V

Q

a

)

1

m

(

n

l

Q

V

1

Q

⋅

−

⋅

⋅

=

(PN (63) p. 19)

n - liczba płaszczyzn z przewiązkami
m - liczba gałęzi słupa

kN

V

Q

44

,

36

1432

,

0

1

2

594

,

0

57

,

17

=

⋅

⋅

⋅

=

Moment zginający działający na przewiązkę
M

Q

= V

Q

⋅

0,025 = 36,44

⋅

0,025 = 0,911 kNm

Naprężenia w przewiązce

MPa

m

kN

W

M

Q

66

,

54

/

54660

6

1

,

0

01

,

0

911

,

0

2

2

=

=

⋅

=

=

σ

MPa

44

,

36

kN/m

36440

1

,

0

01

,

0

44

,

36

2

=

=

⋅

=

=

p

Q

A

V

τ

Naprężenia zastępcze w przewiązce

MPa

305

f

MPa

49

,

83

44

,

36

3

66

,

54

3

d

2

2

2

2

=

<

=

⋅

+

=

+ τ

σ

11.5.3. Połączenie spawane przewiązki ze słupem.

Grubość spoin pachwinowych

0,2

⋅

10,5

≤

a

≤

0,7

⋅

10

2,1

≤

a

≤

7

Przyjmujemy a = 4 mm.
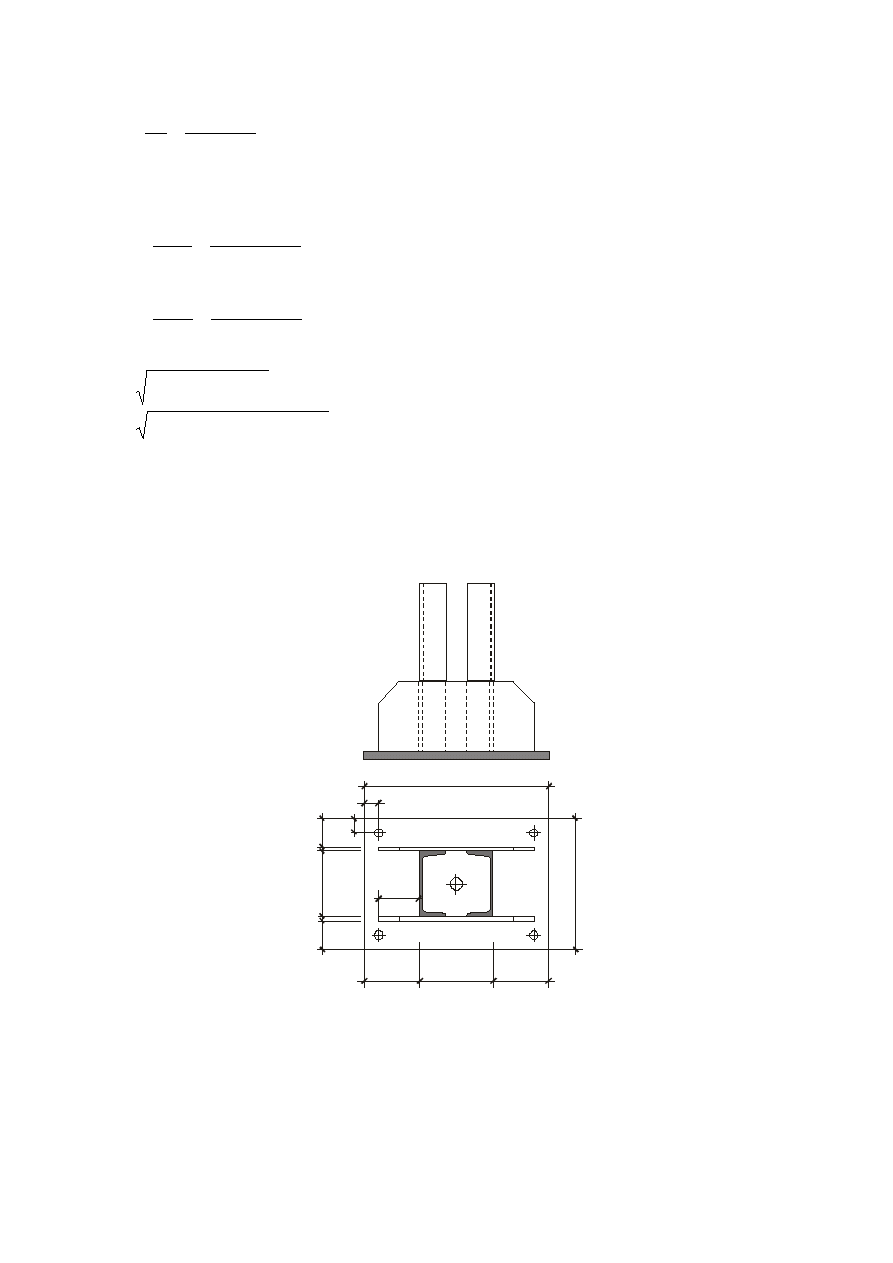
Charakterystyki geometryczne grupy spoin:

A = 108

⋅

4 + 2

⋅

36

⋅

4 = 720 mm

2

S

y1

= 108

⋅

4

⋅

2 + 2

⋅

36

⋅

4

⋅

22 = 7200 mm

3

mm

10

720

7200

A

S

e

1

y

x

=

=

=

4

4

3

2

3

90

,

119

040

199

1

12

4

36

52

4

36

2

12

108

4

cm

mm

I

x

=

=









⋅

+

⋅

⋅

⋅

+

⋅

=

4

4

2

3

2

3

08

,

10

800

100

12

36

4

12

36

4

2

8

4

108

12

4

108

cm

mm

I

y

=

=









⋅

⋅

+

⋅

⋅

+

⋅

⋅

+

⋅

=

I

0

= I

x

+ I

y

= 119,9 + 10,08 = 129,98 cm

4

Moment i siła w środku grupy spoin:
V = V

Q

= 36,44 kN

M = V

Q

⋅

0,059 = 36,44

⋅

0,059 = 2,15 kNm

Naprężenia styczne w punkcie najbardziej odległym od środka grupy spoin:

•

od siły poprzecznej:

5

40

40

59

4

4

4

e

x

x

x

1

y

1

y

25

10

8

4

4

MPa

61

,

50

kN/m

50611

10

720

44

,

36

2

6

=

=

⋅

=

=

−

A

V

Q

V

τ

•

od momentu:

- składowa pionowa

MPa

62

,

49

kN/m

49623

10

98

,

129

03

,

0

15

,

2

2

8

0

=

=

⋅

⋅

=

⋅

=

−

I

x

M

My

τ

- składowa pozioma

MPa

32

,

89

kN/m

89321

10

98

,

129

054

,

0

15

,

2

2

8

0

=

=

⋅

⋅

=

⋅

=

−

I

y

M

Mx

τ

Naprężenia styczne całkowite

(

)

d

V

My

Mx

f

⊥

≤

+

+

=

α

τ

τ

τ

τ

2

2

(

)

MPa

25

,

134

61

,

50

62

,

49

32

,

89

2

2

=

+

+

=

τ

dla stali o 255

≤

R

e

≤

355 MPa

⊥

α

= 0,8 ( tabl.18 p.31)

⊥

α ⋅

f

d

= 0,8

⋅

305 = 244 MPa

τ

max

= 134,25 MPa < 244 MPa

warunek spełniony

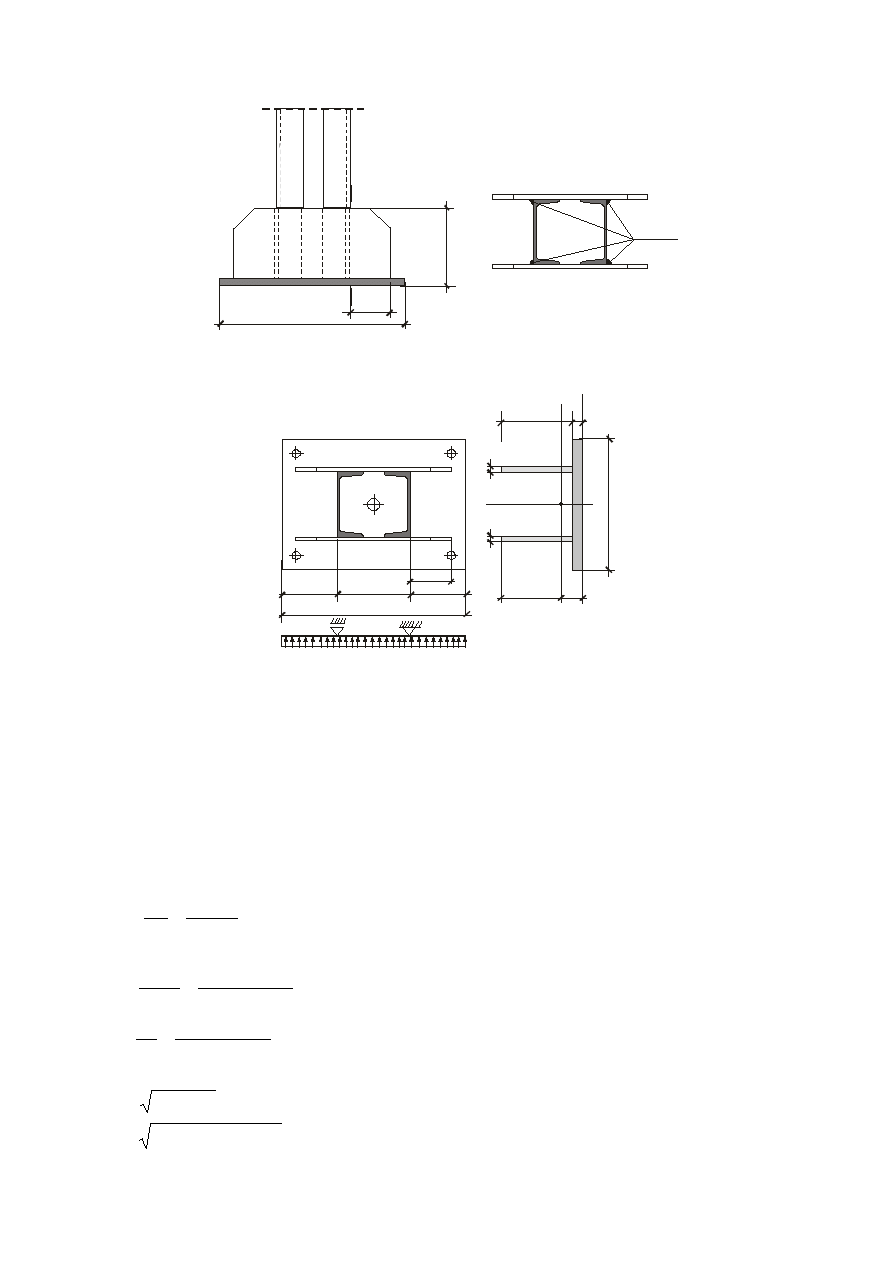
11.6. Obliczenia elementów stopy słupa.

35

450

135

180

135

100

3

5

70

32

0

1

0

10

7

0

1

60

11.6.1. Oparcie słupa na stopie fundamentowej.

Przyjęto beton B 15 o R

bb

= 7,1 MPa

Siła przekazywana na fundament (reakcja od blachownicy)
V

B

= 817,81 kN

(poz. 11.1)

Ciężar słupa długości 5,35 m
2 C 160 = 2

⋅

188 N/m = 376 N/m = 0,376 kN/m;

γ

= 1,1

6

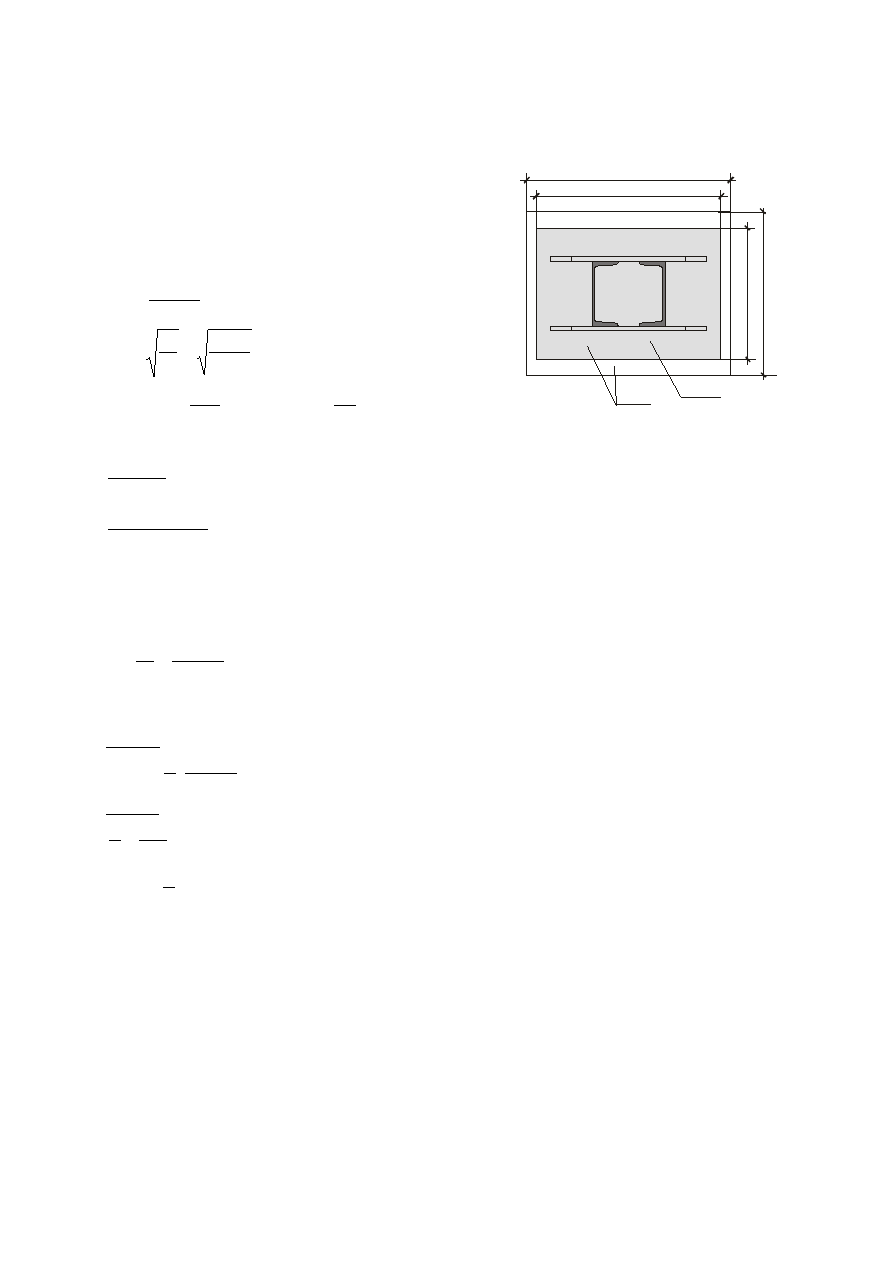
Q = 1,1

⋅

0,376

⋅

5,35 = 2,21 kN

siła przekazywana na fundament
N = 817,81 + 2,21 = 820,02 kN

Blacha podstawy: 450 x 320 mm
Stopa: 500 x 400 mm
F

d

= 0,45

⋅

0,32 = 0,144 m

2

F

r

= 0,5

⋅

0,4 = 0,20 m

2

MPa

1

,

4

m

/

kN

1

,

100

4

2

,

0

02

,

820

2

br

=

=

=

σ

8

,

1

18

,

1

144

,

0

20

,

0

F

F

max

d

r

d

=

ω

<

=

=

=

ω

(

)

(

)

07

,

1

1

18

,

1

1

,

7

1

,

4

18

,

1

1

R

m

d

bb

br

d

4

b

=

−

−

=

−

ω

σ

−

ω

=

R

d

= m

b4

⋅

R

bb

= 1,07

⋅

7,1 = 7,64 MPa

1

F

R

N

d

d

d

<

α

α

d

= 1,0 dla rozkładu równomiernego

1

745

,

0

144

,

0

7640

1

02

,

820

<

=

⋅

⋅

warunek spełniony

11.6.2. Wymiarowanie blachy podstawy słupa.

Odpór podłoża

2

d

m

/

kN

695

5

144

,

0

02

,

820

F

N

p

=

=

=

Maksymalne momenty zginające w poszczególnych fragmentach płyty.

Płyta A:

wspornik o szerokości jednostkowej

m

/

kNm

95

,

13

07

,

0

1

1

5695

2

1

M

2

max

=

⋅

⋅

⋅

=

Płyta B:

płyta oparta na trzech krawędziach

185

,

1

135

160

b

l

=

=

dla

18

,

1

b

l

=

k

3

= 0,120

M

max

= k

3

⋅

p

⋅

b

2

= 0,12

⋅

5695

⋅

0,135

2

= 11,21 kNm/m

7

450

500

32

0

40

0

F

F

r

d

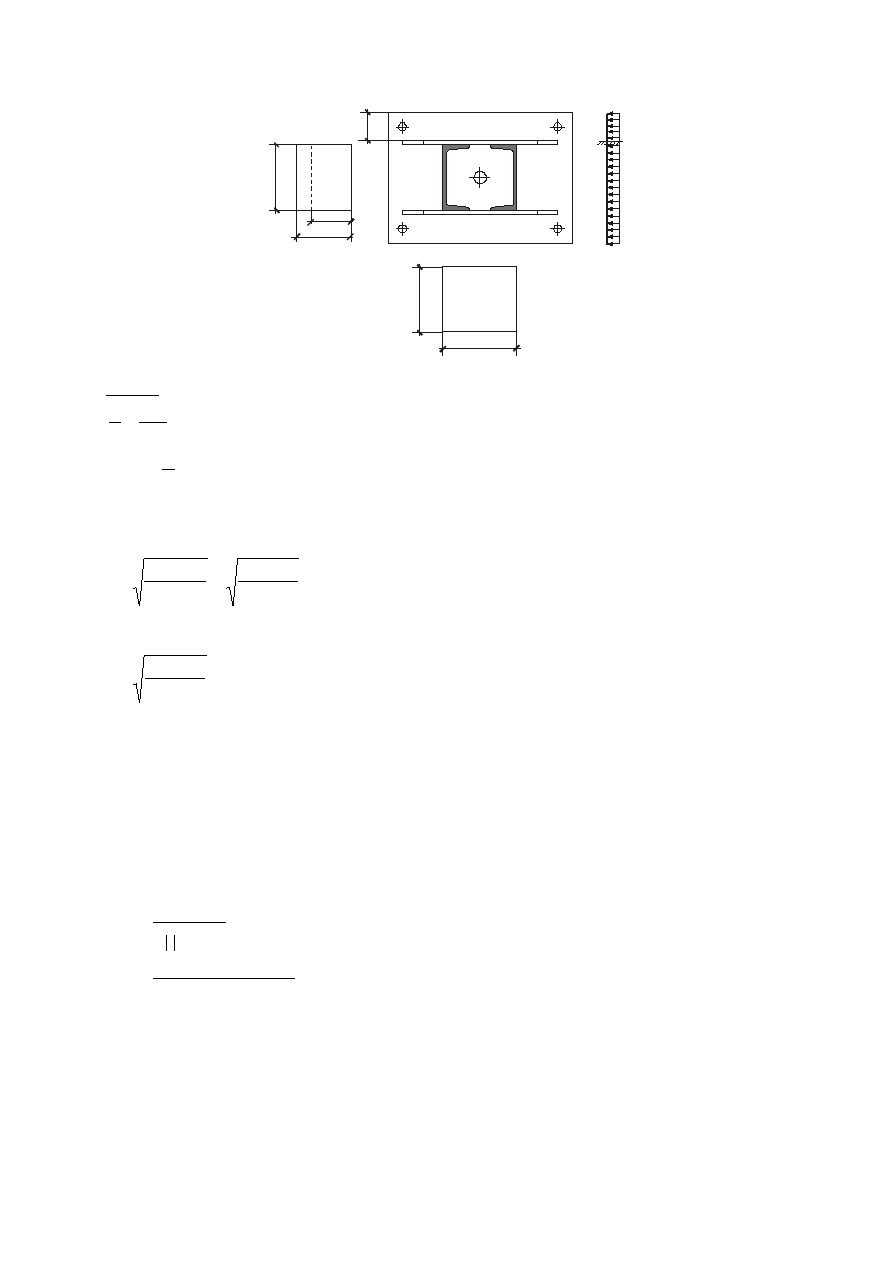
A

A

A

B

B

C

C

70

1

60

1

60

p

100

180

135

Płyta C:

płyta oparta na czterech krawędziach

125

,

1

160

180

a

b

=

=

dla

1

,

1

a

b

=

k

1

= 0,0554

M

max

= k

1

⋅

p

⋅

a

2

= 0,0554

⋅

5695

⋅

0,16

2

= 8,08 kNm/m

Niezbędna grubość blachy

m

f

M

t

d

0165

,

0

000

305

95

,

13

6

6

max

=

⋅

=

⋅

≥

,

a po korekcie f

d

mm

m

t

8

,

16

0168

,

0

000

295

95

,

13

6

=

=

⋅

≥

Przyjęto blachę podstawy słupa o wymiarach 450 x 320 x 18 mm

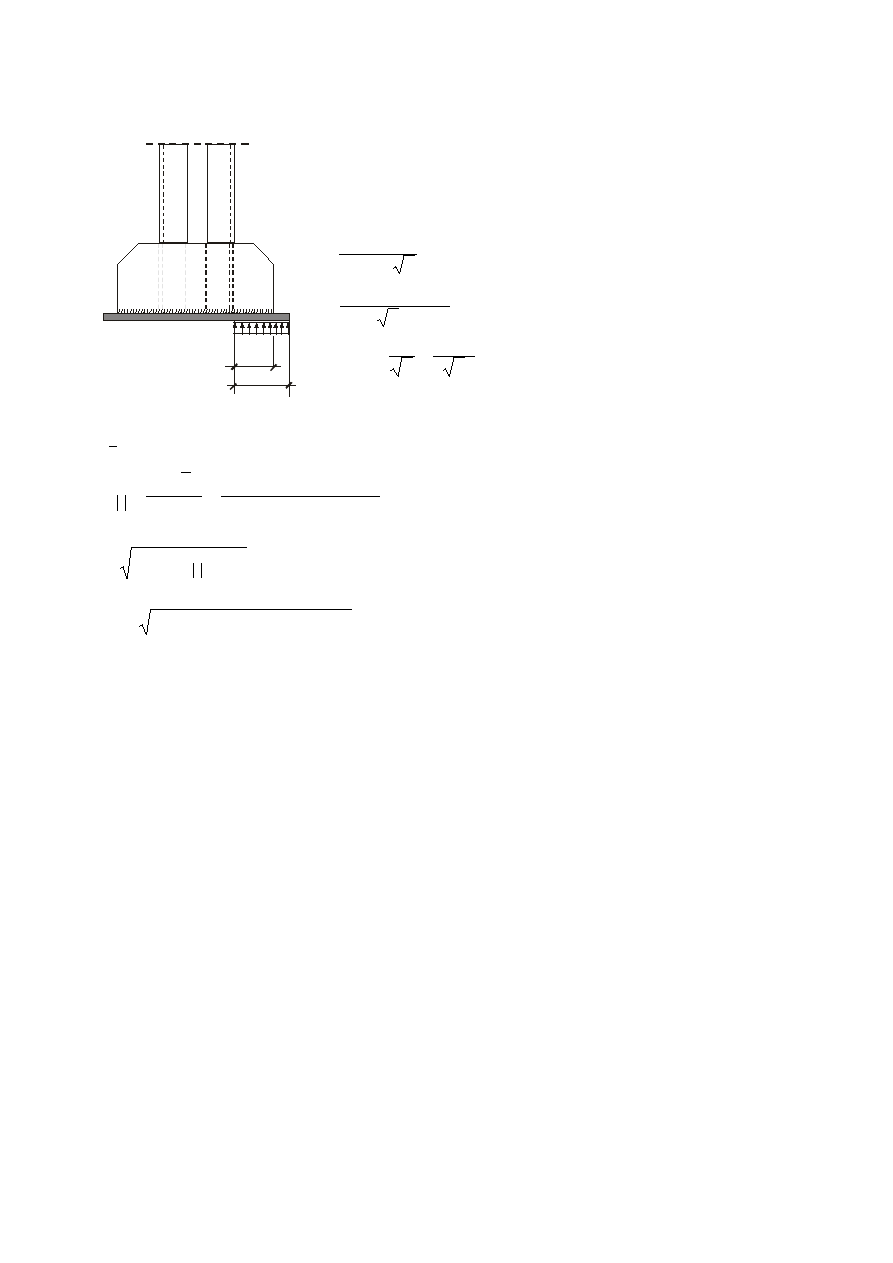
11.6.3. Wymiarowanie blach trapezowych.

Wysokość blachy trapezowej (przewiązki skrajnej) powinna być nie mniejsza niż 1,5 b (b –
szerokość pozostałych przewiązek). W poz. 11.5.1 przyjęto b = 100 mm
Wysokość blach trapezowych wyznaczamy z warunku na nośność połączenia spawanego.
Załóżmy, że słup był przycięty zgrubnie (bez frezowania). Całą siłę osiową muszą przenieść
spoiny pachwinowe. Załóżmy a = 6 mm. Warunek

min

max

7

,

0

2

,

0

t

a

t

≤

≤

spełniony.

a

f

N

l

d

⋅

⋅

≥

∑

α

m

l

64

,

0

006

,

0

000

305

7

,

0

02

,

820

=

⋅

⋅

≥

∑

cm

l 64

≥

∑

Przyjęto 4 spoiny o długości 160 mm

Stąd wynika niezbędna wysokość blach trapezowych. Przyjęto h = 170 mm > 1,5 b =150 mm

8

450

1

1

h

100

te spoiny

Sprawdzenie naprężeń w zginanym i ścinanym przekroju blachy trapezowej.

Schemat obliczeniowy dla zastępczej „belki” podstawy słupa

A

p

170

100

135

135

180
450

18

3

20

1

0

10

y

y

x

x

x

x

14,41 4,39

1

1

C

A

B

C

V

A

= V

B

= 5695

⋅

0,32

⋅

0,45/2 = 410,04 kN

M

C

= 5695

⋅

0,32

⋅

0,225

⋅

0,225/2 – 410,04

⋅

0,09 = 9,23 kNm

M

B

= 5695

⋅

0,135

2

/2

⋅

0,32 = 16,61 kNm

V

Bp

=5695

⋅

0,135

⋅

0,32 = 246,02 kN

A = 32

⋅

1,8 + 2

⋅

17

⋅

1,0 = 91,6 cm

2

S

x1

= 32

⋅

1,8

⋅

0,9 + 2

⋅

17

⋅

1,0

⋅

(1,8 + 8,5) = 402,04 cm

3

cm

39

,

4

6

,

91

04

,

402

A

S

y

1

x

1

c

=

=

=

Naprężenia:

MPa

88

,

87

kN/m

87883

10

5

,

2723

1441

,

0

61

,

16

2

8

=

=

⋅

⋅

=

⋅

=

−

x

I

y

M

σ

MPa

m

kN

A

Q

v

36

,

72

/

359

72

10

1

17

2

02

,

246

2

4

=

=

⋅

⋅

⋅

=

=

−

τ

Założono, że ścinanie przeniosą ścianki pionowe

d

f

≤

+

=

2

2

3

τ

σ

σ

MPa

305

MPa

07

,

153

36

,

72

3

88

,

87

2

2

=

<

=

⋅

+

=

d

f

σ

9

Sprawdzenie naprężeń w spoinach pachwinowych łączących blachę trapezową z blachą

podstawy.

Zakładamy, że 75% siły działającej w słupie przenoszą spoiny
łączące blachy trapezowe z blachą podstawy.
Przyjmujemy spoinę a = 5 mm

2

a

l

N

75

,

0

⋅

⋅

⋅

=

τ

∑

Σ

l = 0,38 + 0,38 + 4

⋅

0,1 = 1,16 m

MPa

98

,

74

kN/m

74997

005

,

0

2

16

,

1

02

,

820

75

,

0

2

=

=

⋅

⋅

⋅

=

τ

MPa

02

,

53

2

98

,

74

2

=

=

=

=

⊥

⊥

τ

σ

τ

Ścinanie w kierunku równoległym będzie pochodziło od naprężeń

rozwarstwiających przy zginaniu ze ścinaniem.
Moment statyczny półki

3

cm

02

,

201

)

9

,

0

39

,

4

(

8

,

1

32

S

=

−

⋅

⋅

=

MPa

79

,

90

kN/m

90793

005

,

0

4

10

5

,

2723

10

02

,

201

02

,

246

4

2

8

6

=

=

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

=

−

−

a

I

S

Q

x

τ

Warunek wytrzymałościowy spoiny pachwinowej w złożonym stanie naprężenia

d

f

≤

+

+

⊥

⊥

)

(

3

2

2

2

τ

τ

σ

κ

dla stali 18G2

κ

= 0,85

(PN str. 31)

MPa

305

MPa

21

,

161

)

02

,

53

79

,

90

(

3

02

,

53

85

,

0

2

2

2

=

<

=

+

+

d

f

135

100

10

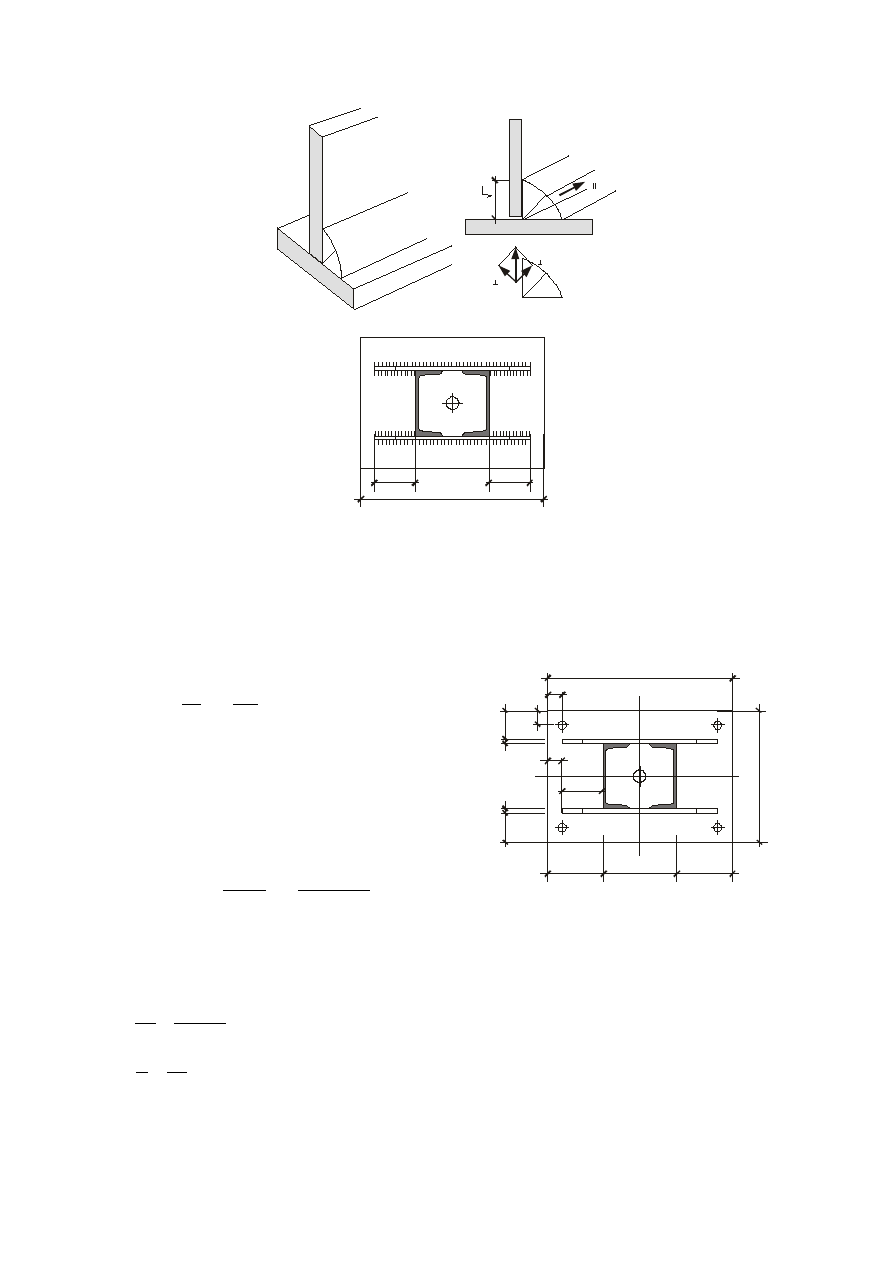
100

100

380

a

a

a

2

σ

τ

τ

τ

11.7. Dobór śrub fundamentowych

Śruby te są niezbędne ze względów montażowych oraz na okoliczność powstania
przypadkowych momentów. Norma zaleca (wz. (103) p.33) by projektując podstawy słupów
uwzględnić dodatkowo obciążenie momentem

A

W

1

1

N

M

i

i

i









−

ϕ

=

∆

ϕ

i

min otrzymaliśmy dla wyboczenia względem osi

x

ϕ

= 0,647 (poz. 11.3)

N = 820,02 kN
W

x

= 2

⋅

116 = 232 cm

3

A= 2

⋅

24 = 48 cm

2

kNm

M

63

,

21

10

48

10

232

1

647

,

0

1

02

,

820

4

6

=

⋅

⋅













−

⋅

=

∆

−

−

Przyjmujemy 4 śruby fajkowe F 20 ( wg PN-B-03215:1998 str. 19)
Nośność na zerwanie S

Rt

= 47 kN

Minimalna długość zakotwienia w betonie B 15 l

z

= 900 mm

Zgodnie z normą PB-B-03215:1998 ustalamy najpierw mimośród

cm

m

N

M

e

63

,

2

0263

,

0

02

,

820

63

,

21

=

=

=

=

cm

a

e

33

,

5

6

32

6

=

=

<

35

450

135

180

135

100

7

0

32

0

1

0

10

7

0

x

x

y

y

35

35

11

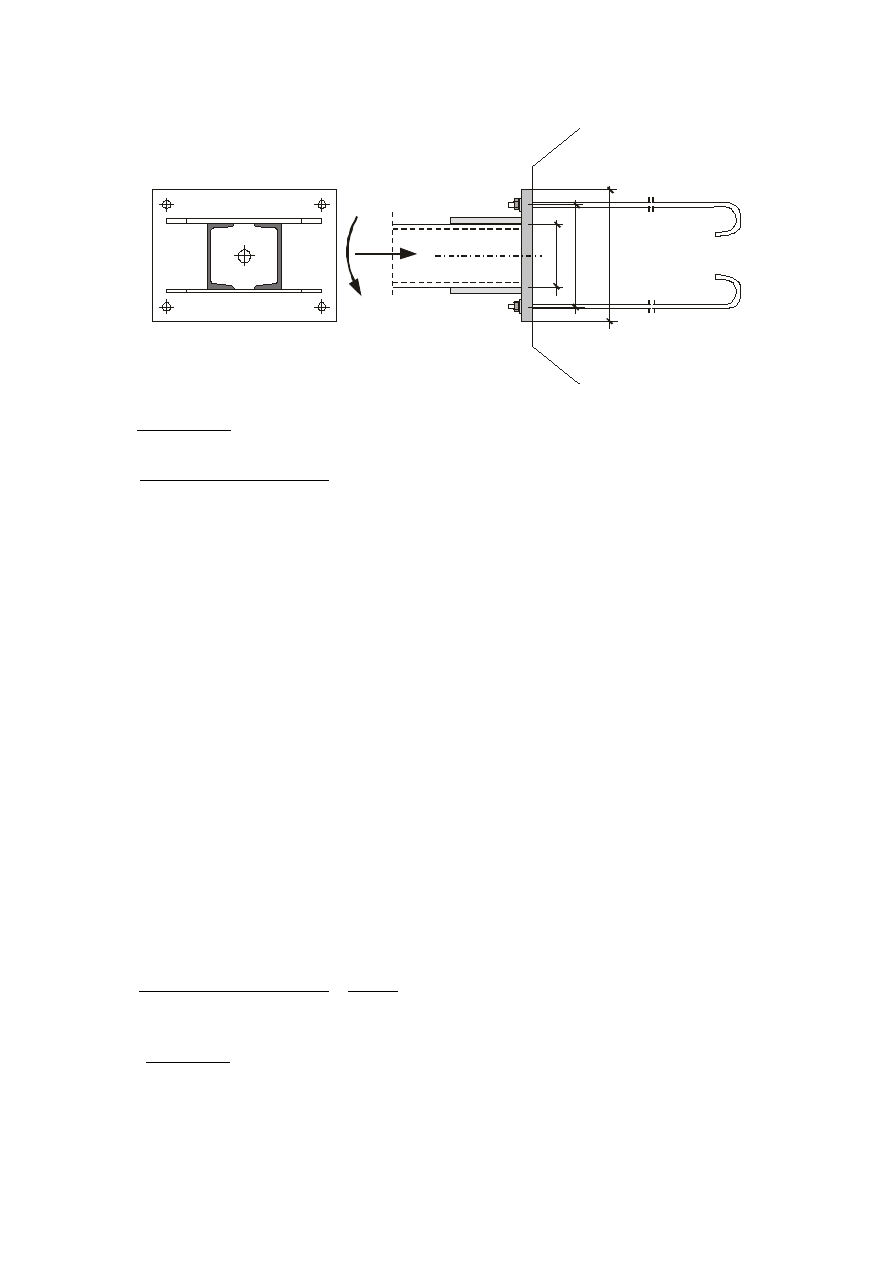
Wymiary podstawy: b = 450 mm, a = 320 mm

25

0

32

0

1

60

y

N

∆

M

Należy sprawdzić docisk do fundamentu wg wzoru

(

)

b

f

e

a

5

,

0

b

3

N

2

≤

−

⋅

=

σ

(

)

MPa

m

kN

09

,

9

/

3

,

086

9

0263

,

0

32

,

0

5

,

0

45

,

0

3

02

,

820

2

2

=

=

−

⋅

⋅

⋅

=

σ

R

d

= R

bb

gdyż F

r

= F

d

i f

b

=R

d

Przyjęto ostatecznie beton klasy B 20 R

d

= R

bb

= 9,4 MPa.

Warunek

b

f

≤

σ

spełniony.

Norma PN-B-03215 nie wymaga sprawdzania śrub w przypadku małego mimośrodu.

11.8. Głowica słupa.

11.8.1. Wstępne dobranie wymiarów

Przyjmujemy:

- blachę poziomą głowicy:

450 x 260 x 18 mm

- płytkę centrującą:

450 x 50 x 30 mm

- blachy prostokątne (przewiązki końcowe)

220x 180 x10 mm

- przeponę wewnętrzną

180 x 160 x 10 mm

- przepony zewnętrzne

180 x 135 x 10 mm

11.8.2. Sprawdzenie naprężeń dociskowych w płytce centrującej.

Nacisk liniowy na płytkę centrującą

m

kN

V

p

B

/

4

,

379

3

242

,

0

81

,

817

015

,

0

2

012

,

0

1

,

0

1

,

0

=

=

⋅

+

+

+

=

Naprężenia dociskowe na płytce centrującej

MPa

m

kN

b

59

,

67

/

6

,

587

67

05

,

0

242

,

0

81

,

817

2

=

=

⋅

=

σ

MPa

f

d

b

7

,

368

295

25

,

1

25

,

1

=

⋅

=

⋅

<

σ

12

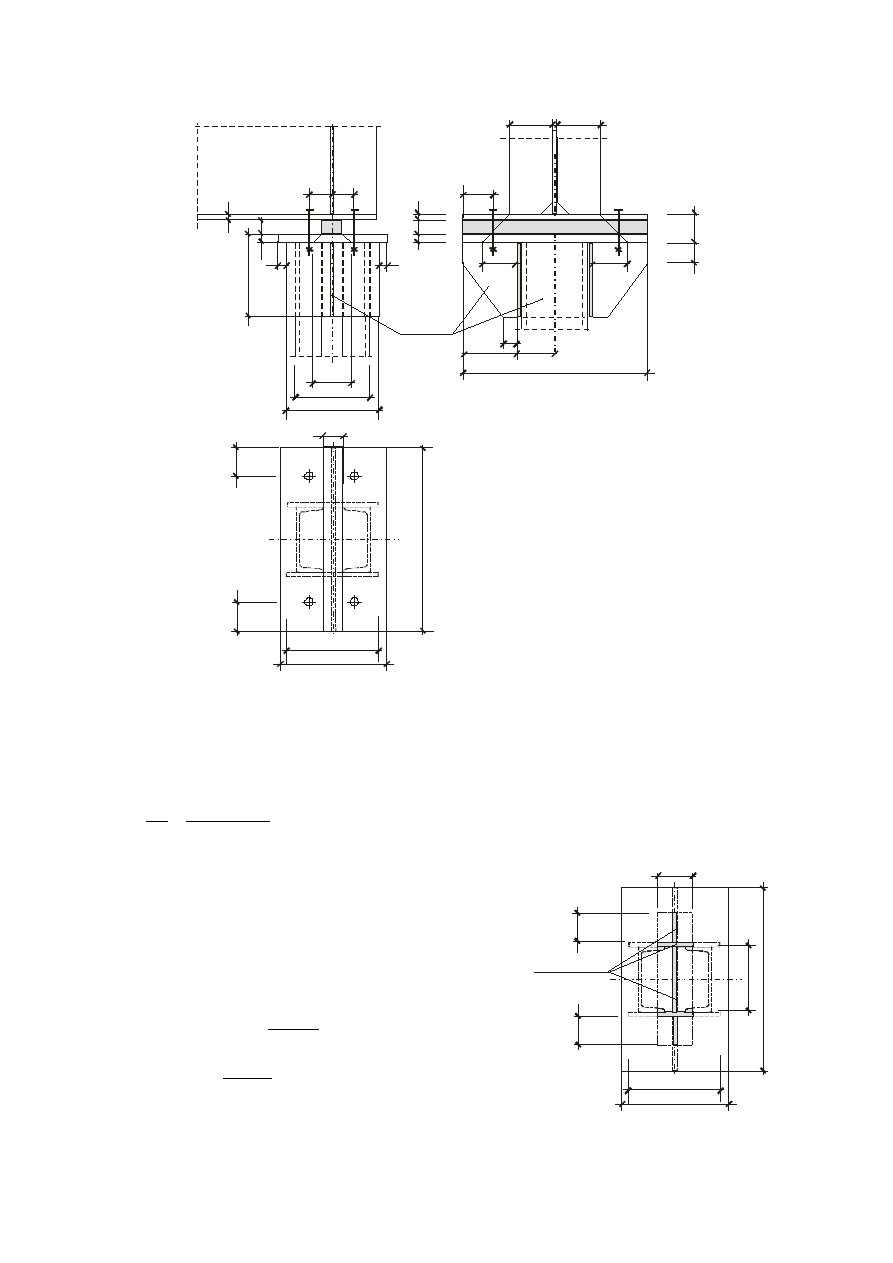
180

180

86

20

20

35 35

220

220

12

30

135

90

70

79

79

100

100

450

18

1

8

5

0

3

0

3

0

6

3

1515

1

5

1

80

przepona

50

260

220

70

4

50

7

0

11.8.3. Docisk między blachą poziomą a blachami trapezowymi, przeponą i trzonem
słupa.

t

f

= 10,5 mm

powierzchnia docisku
A

b

= 2

⋅

8,6

⋅

1 + 4

⋅

1,8

⋅

1,05 + 2

⋅

7,9

⋅

1,0 + 16

⋅

1 = 56,56 cm

2

MPa

6

,

144

kN/m

144591

10

56

,

56

81

,

817

2

4

=

=

⋅

=

=

−

b

b

A

N

σ

MPa

25

,

381

305

25

,

1

25

,

1

=

⋅

=

<

d

b

f

σ

11.8.4 Obliczenia sprawdzające przepony

Obciążenia przepony
p = 155595

⋅

0,01 = 1559,5 kN/m

V

A

= V

B

= 1559,5

⋅

0,338/2 = 263,56 kN

kNm

50

,

5

2

084

,

0

5

,

1559

2

−

=

⋅

−

=

=

B

A

M

M

kNm

132

,

0

085

,

0

56

,

263

2

169

,

0

5

,

1559

2

=

⋅

+

⋅

−

=

C

M

13

86

86

260

260

220

220

7

9

45

0
45

0

7

9

16

0

16

0

Powierzchnia
docisku

Powierzchnia
docisku

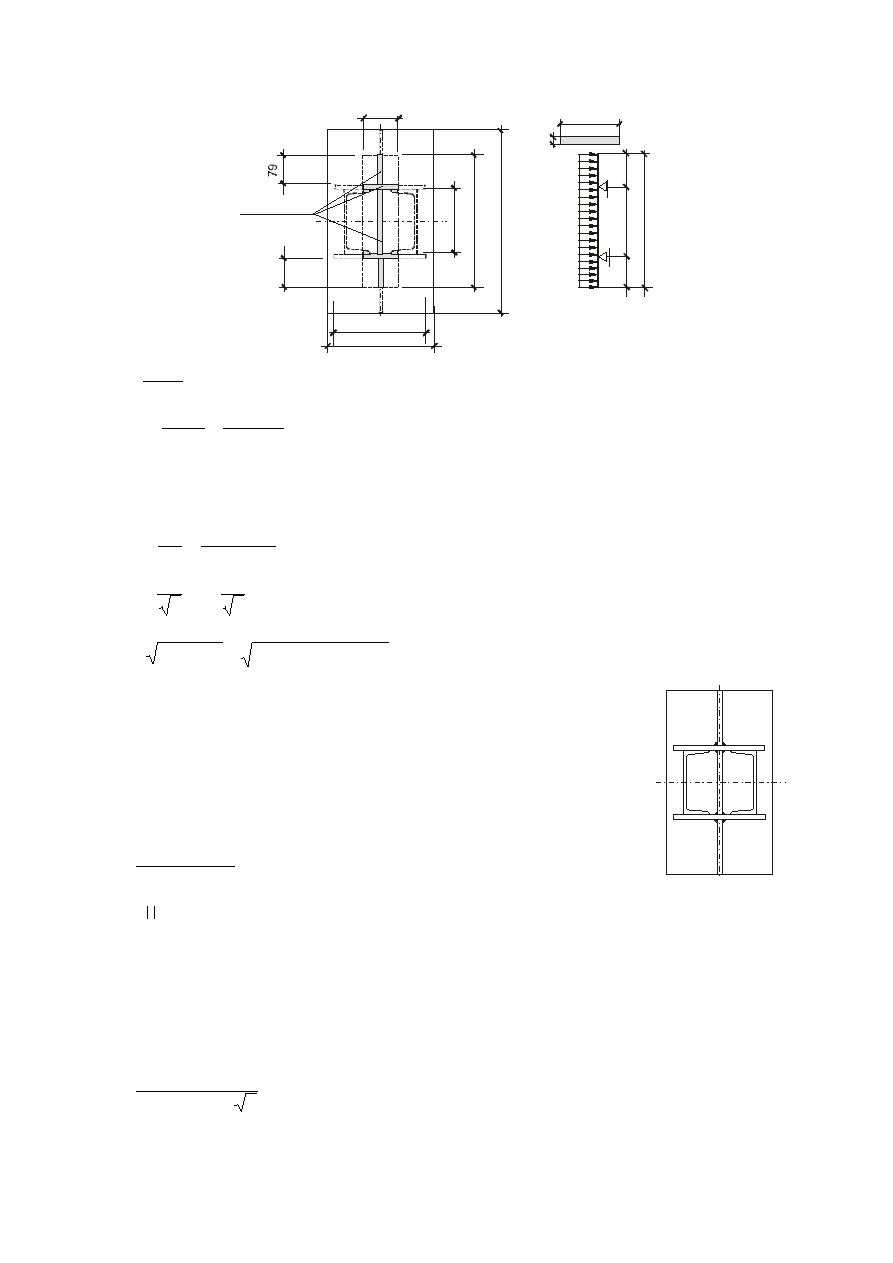
86

86

260

260

220

220

17

0

33

8

8

4

10

180

84

45

0
45

0

7

9

16

0

16

0

33

8

Powierzchnia
docisku

Powierzchnia
docisku

p

A

B

C

3

2

cm

54

6

18

1

=

=

W

MPa

85

,

101

kN/m

852

101

10

54

50

,

5

2

6

max

max

=

=

⋅

=

=

−

W

M

σ

MPa

305

max

=

<

d

f

σ

Q

Al.

= -1559,5

⋅

0,084 = -131,00 kN

Q

Ap

= Q

Al

+ V

A

= -131,00 + 263,56 = 132,56 kN

MPa

65

,

73

kN/m

73646

10

1

18

56

,

132

2

4

max

=

=

⋅

⋅

=

=

−

A

Q

A

τ

MPa

09

,

176

305

3

1

3

1

max

=

⋅

=

<

d

f

τ

Naprężenia zastępcze

MPa

24

,

163

65

,

73

3

85

,

101

3

2

2

2

2

=

⋅

+

=

+

=

τ

σ

σ

z

MPa

305

f

d

z

=

<

σ

11.8.5 Sprawdzenie naprężeń w spoinach pachwinowych.

Naprężenia w spoinach pachwinowych łączących przeponę z blachami
(przewiązkami końcowymi).
Przyjęto spoinę a = 5,0 mm
Maksymalna siła poprzeczna Q

max

= 132,56 kN

MPa

64

,

73

kN/m

664

73

18

,

0

005

,

0

2

56

,

132

2

=

=

⋅

⋅

=

τ

MPa

5

,

213

305

7

,

0

f

d

=

⋅

=

⋅

α

<

τ

Naprężenia w spoinach łączących blachę poziomą głowicy z trzonem słupa i przeponą.
Zgodnie z rys. z poz. 11.8.3, całkowita długość spoin pachwinowych w obszarze
przekazywania obciążenia :

Σ

l

i

= 0,16

⋅

2 + 0,086

⋅

2 + 0,079

⋅

4 = 0,808 m

Przyjmujemy spoinę pachwinową a = 5 mm
Zakładamy, że 25% siły przekazuje się przez docisk bezpośredni (przycięcie zgrubne)
Naprężenia styczne w spoinie

MPa

4

,

107

kN/m

354

107

2

005

,

0

808

,

0

81

,

817

75

,

0

2

=

=

⋅

⋅

⋅

=

τ

14

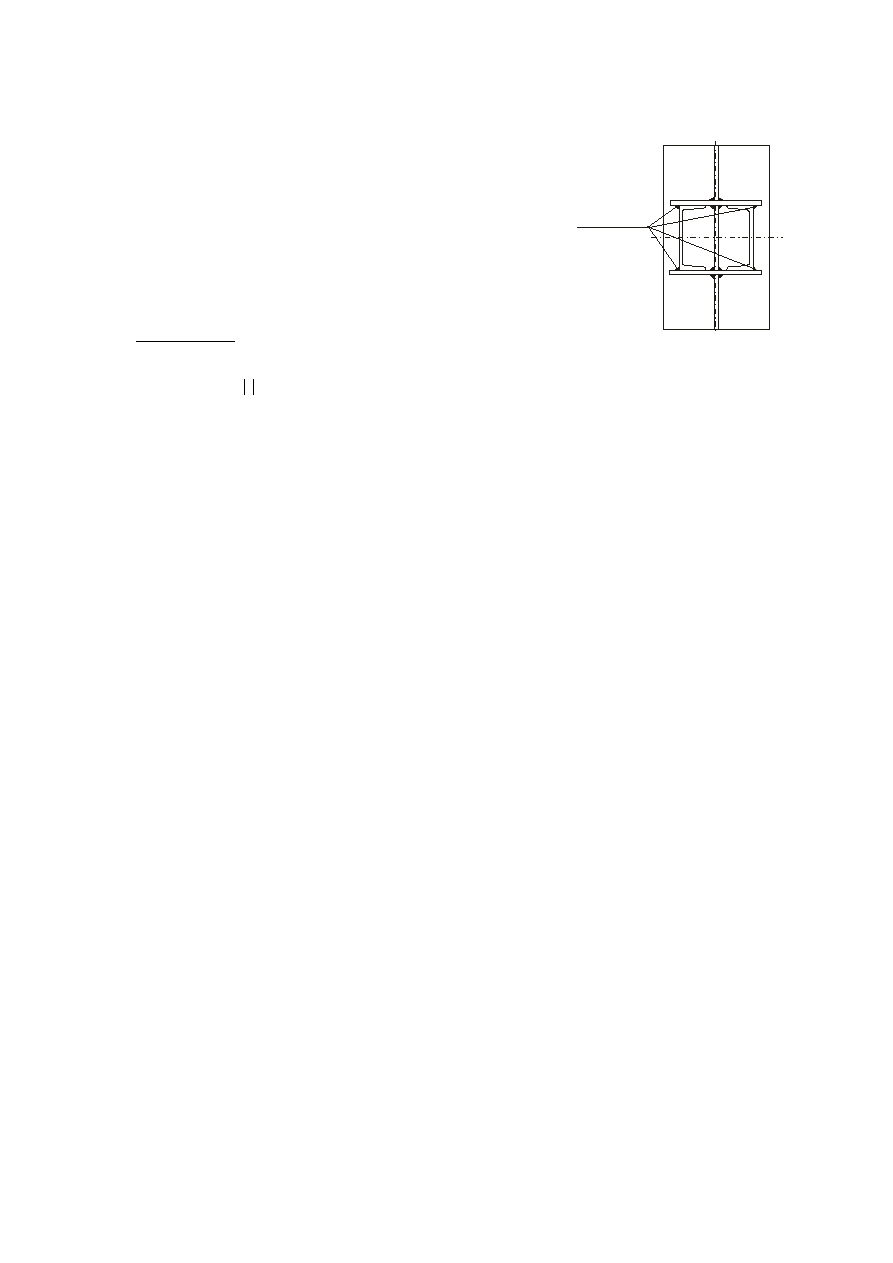
Sprawdzamy warunek:

τ

≤

α

⊥

⋅

f

d

α

⊥

= 0,8;

f

d

= 305 MPa

τ

= 107,4 MPa < 0,8

⋅

305 = 244 MPa

Naprężenia w spoinach pachwinowych łączących blachę
trapezową ze słupem. Spoiny te muszą przejąć reakcję V

A

=

V

B

= 253,31 kN wyznaczoną w p. 11.8.4. Przyjmujemy spoiny

grubości a = 5 mm.
Naprężenia w spoinach

MPa

4

,

146

kN/m

422

146

005

,

0

18

,

0

2

56

,

263

2

=

=

⋅

⋅

=

τ

MPa

f

d

5

,

213

305

7

,

0

MPa

4

,

146

=

⋅

=

⋅

<

=

α

τ

11.8.6 Śruby łączące głowicę słupa z pasem dolnym blachownicy.

Śruby mają spełniać funkcję mocującą w fazie montażu.
Przyjęto 4 śruby M20 klasy 4.8 o długości l = 120 mm

15

To są te spoiny