ŁUKI PIONOWE WYPUKŁE

zdjęcie ze strony www.webshots.com

zdjęcie ze strony

www.tibridge.com

zdjęcie ze strony www.dramainnature.com

zdjęcie ze strony www.webshots.com

Na krzywych pionowych wypukłych powinno się sprawdzać odległość widoczności

na zatrzymanie L

z

w dzień.

Ważne jest uwzględnienie długości łuku pionowego Ł, gdyż ma ona zasadnicze

znaczenie. Ponieważ pochylenia podłużne drogi mają małe wartości kątów, to wykorzystuje
się znane z geometrii uproszczenia wzorów. Dla małych kątów jakie tworzą pochylenia
podłużne zachodzi następująca zależność:

i

t

h

=

=

=

α

α

tan

sin

oraz

1

cos

=

α

L

z

R

R

Długość stycznej można określić wtedy z klasycznych wzorów geometrycznych:

2

2

tan

2

tan

2

1

2

1

i

i

R

t

+

=

+

=

=

α

α

α

→

2

2

1

i

i

R

t

+

=

[m]

(1)

gdzie:

i

1

i i

2

– pochylenia podłużne, podawane w ułamku dziesiętnym, znak „+” – stosuje się dla

pochyleń odwrotnych, a znak „–” – dla pochyleń jednakowego kierunku, tj. obydwa
pochylenia są wzniesieniami lub obydwa pochylenia są spadkami.

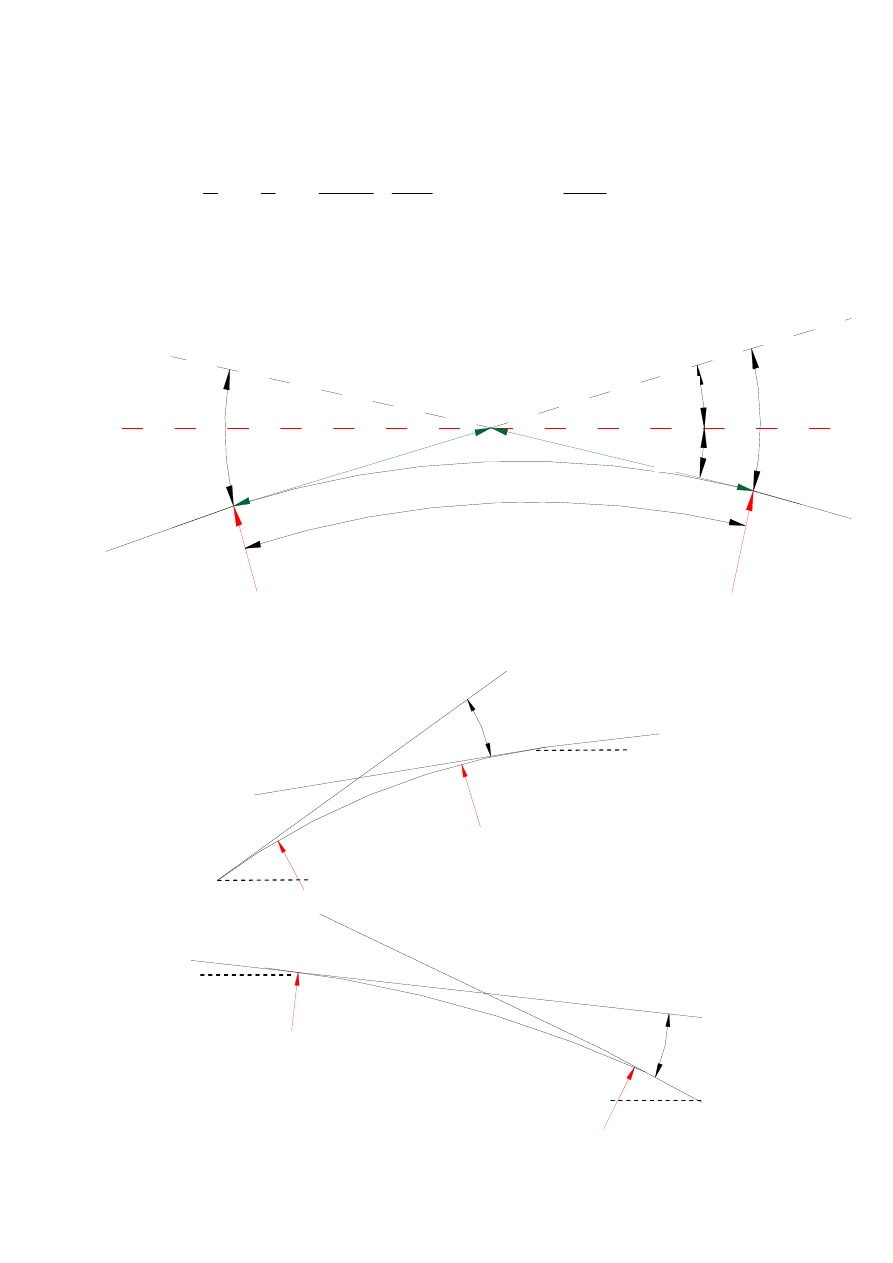
Rys. 1. Załom profilu podłużnego i łuk pionowy wypukły (pochylenia odwrotne)

a) przypadek wzniesienie – wzniesienie

b) przypadek spadek – spadek

Rys. 2. Załomy profilu podłużnego i łuki pionowe wypukłe (pochylenia jednakowego kierunku)

α

α

1

α

2

α

i

1

i

2

t

Ł

R

R

t

i

1

i

2

R

R

α

= α

1

– α

2

α

2

α

1

α

= α

1

– α

2

α

1

i

1

R

R

α

2

i

2

Długość łuku pionowego oblicza się z klasycznego wzoru, uwzględniając małe

wartości kątów:

(

)

2

1

i

i

R

Ł

+

=

[m]

(2)

gdzie:

i

1

i i

2

– pochylenia podłużne, podawane w ułamku dziesiętnym, znak „+” – stosuje się dla

pochyleń odwrotnych, a znak „–” – dla pochyleń jednakowego kierunku, tj. obydwa
pochylenia są wzniesieniami lub obydwa pochylenia są spadkami,

R – promień łuku pionowego, [m].

Dla wypukłych łuków pionowych rozróżnić należy dwa przypadki:

1.

odległość widoczności na zatrzymanie L

z

jest mniejsza od długości łuku

pionowego Ł, czyli L

z

< Ł,

2.

odległość widoczności na zatrzymanie L

z

jest większa od długości łuku

pionowego Ł, czyli L

z

> Ł,

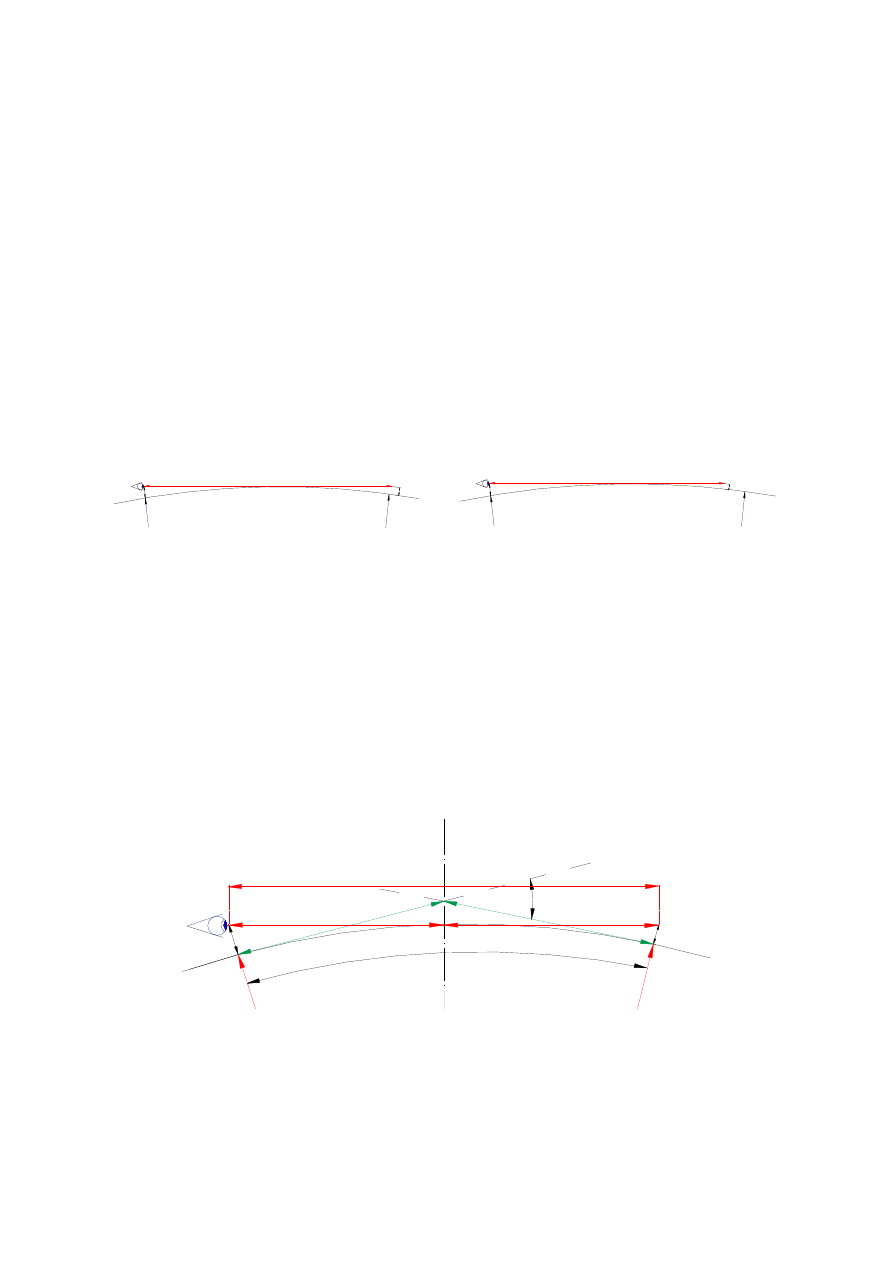
Rys. 3. Dwa przypadki analizy

W przypadku pierwszym, tj. L

z

< Ł wielkość potrzebnego promienia łuku pionowego

R

min

można wyznaczyć wykorzystując podstawowe zależności geometryczne (rys. 4).

(

)

2

1

1

2

2

1

2

2

1

2

h

Rh

R

h

R

R

L

z

+

+

=

+

=

+

gdzie:

R – promień łuku pionowego, [m],

L

z1

– część składowa wymaganej odległości widoczności na zatrzymanie L

z

, [m],

h

1

– wysokość oczu kierowcy nad jezdnią, wg Rozporządzenia MTiGM Dz.U. nr 43 § 168 –

wynosi 1 [m].

Rys. 4. Załom profilu podłużnego i łuk pionowy wypukły (pochylenia odwrotne)

Podobne zależności zachodzą dla pochyleń jednakowego kierunku.

L

z

R

R

h

2

i

1

i

2

L

z1

L

z2

α

Ł

R

R

h

1

h

2

L

z

L

z

R

R

h

2

Rys. 5. Załomy profilu podłużnego i łuki pionowe wypukłe (pochylenia jednakowego kierunku)

Odrzucając wielkość h

1

2

jako małą w stosunku do wielkości R

2

, otrzyma się

następującą zależność:

1

1

2Rh

L

z

=

(3)

Analogicznie postępując i wyprowadzając wzór na druga składową wymaganej

odległości widoczności na zatrzymanie L

z

otrzyma się zależność:

2

2

2Rh

L

z

=

(4)

gdzie:

R – promień łuku pionowego, [m],

L

z2

– część składowa wymaganej odległości widoczności na zatrzymanie L

z

, [m],

h

2

– wysokość celu obserwacji, znajdującego się nad osią ruchu tego samego pasa ruchu co

poruszający się pojazd, zależy od prędkości i jest określona w Rozporządzeniu MTiGM
Dz.U. Dz.U. nr 43 § 168 ustęp 2b.

Celem obserwacji może być w przypadku obliczania odległości widoczności na

zatrzymanie L

z

przede wszystkim uszkodzenie nawierzchni, przeszkoda na jezdni (zwalone

drzewo, rozlane paliwo i olej po wypadku, potrącony człowiek, zwierzę itd.).

fot. R. Strzałkowski

zdjęcie ze strony

www.drogowiec.pb.bialystok.pl

droga nr 10 kilometr 74

zdjęcie ze strony

www.ogrodnik.pl

- zielone mosty

zdjęcie ze strony

www.krbrd.gov.pl

zdjęcie ze strony

www.krbrd.gov.pl

i

1

i

2

L

z1

L

z2

α

Ł

R

R

h

1

h

2

L

z

i

1

i

2

L

z1

L

z2

α

Ł

R

R

h

1

h

2

L

z

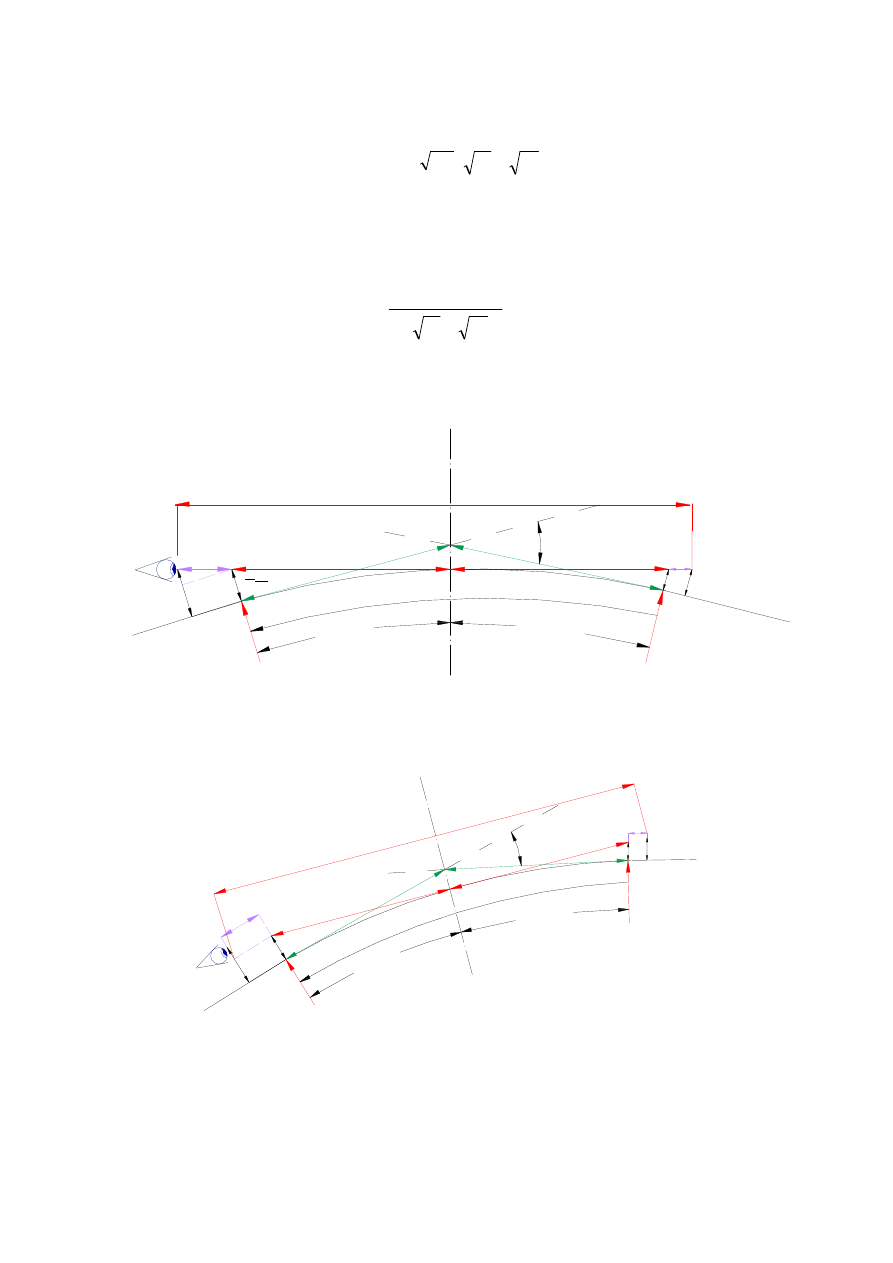
Odległość widoczności na zatrzymanie L

z

jest sumą dwóch składowych

(

)

2

1

2

1

2

h

h

R

L

L

L

z

z

z

+

=

+

=

(5)

Przekształcając wzór (5) względem promienia łuku R, który zapewnia wymaganą

odległość widoczności na zatrzymanie L

z

, otrzyma się klasyczny wzór podany w książce

„Inżynieria ruchu” autorstwa prof.: St. Datki, W. Suchorzewskiego i M. Tracza.

(

)

2

1

2

min

2

h

h

L

R

z

+

=

(6)

Podobnie należy postąpić, gdy zachodzi drugi przypadek tzn. L

z

> Ł.

Charakterystyczne zależności geometryczne przedstawia rys. 5.

Rys. 6. Załom profilu podłużnego i łuk pionowy wypukły (pochylenia odwrotne)

Podobne zależności zachodzą dla pochyleń jednakowego kierunku.

i

1

i

2

R

R

h

1

x

1

x

2

Ł

L

Z1

L

Z2

L

Z

α

h

2

i

2

R

i

1

R

α

α

2

L

Z1

L

Z2

α

1

x

2

h

1

x

1

h

2

L

Z

L

Z1

2R

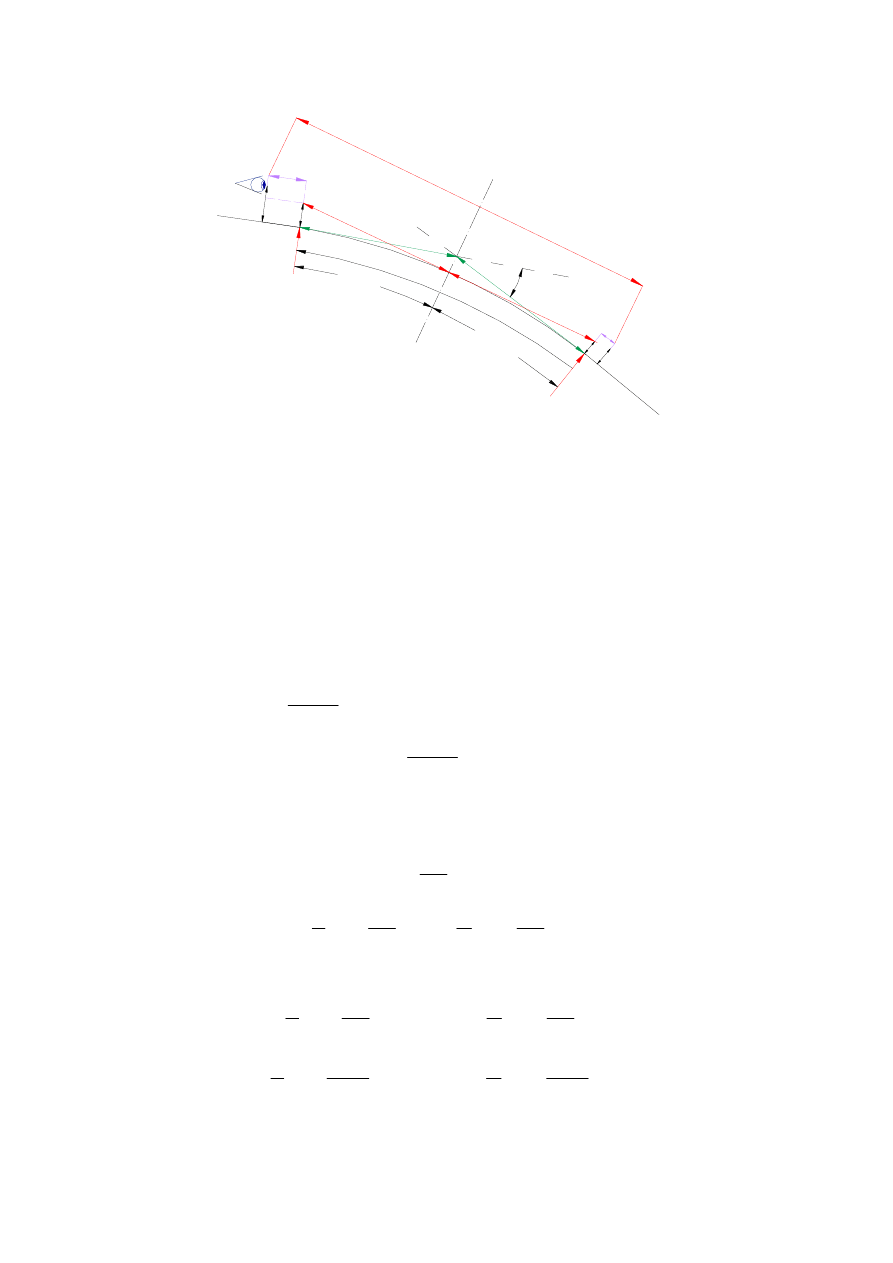
Rys. 7. Załomy profilu podłużnego i łuki pionowe wypukłe (pochylenia jednakowego kierunku)

Wielkość potrzebnego promienia łuku pionowego R

min

można wyznaczyć

wykorzystując podstawowe zależności geometryczne (rys. 6).

2

2

1

1

x

L

L

x

L

z

z

z

+

+

+

=

gdzie:

x

1

i x

2

, L

z1

oraz L

z2

– poszczególne części składowe wymaganej odległości widoczności na

zatrzymanie L

z

wynikające z rys. 6, [m].

Z zależności geometrycznych otrzymuje się, że:

1

1

1

1

sin

α

=

−

x

y

h

,

1

1

1

sin

tan

i

=

=

α

α

1

1

1

1

i

y

h

x

−

=

(

)

2

1

2

2

2

1

y

R

R

L

z

+

=

+

2

1

1

2

2

2

1

2

y

Ry

R

R

L

z

+

+

=

+

→

1

2

1

2Ry

L

z

=

R

L

y

z

2

2

1

1

=















−

=

R

L

h

i

x

z

2

1

2

1

1

1

1

,















−

=

R

L

h

i

x

z

2

1

2

2

2

2

2

1

1

i

R

L

z

=

i

2

2

i

R

L

z

=















−

+

+

+















−

=

R

L

h

i

i

R

i

R

R

L

h

i

L

z

z

z

2

1

2

1

2

2

2

2

2

1

2

1

1

1













−

+

+

+













−

=

R

i

R

h

i

i

R

i

R

R

i

R

h

i

L

z

2

1

2

1

2

2

2

2

2

2

1

2

1

2

1

1

x

1

R

R

α

α

1

α

2

L

Z1

h

1

i

1

i

2

h

2

X

2

L

Z2

L

Z

(

)

(

)

2

1

2

2

1

2

1

2

i

i

h

h

i

i

R

L

z

+

+

+

+

=

(7)

Przekształcając wzór (7) względem promienia łuku R, który zapewnia wymaganą

odległość widoczności na zatrzymanie L

z

, otrzyma się klasyczny wzór podany w książce

„Inżynieria ruchu” autorstwa prof.: St. Datki, W. Suchorzewskiego i M. Tracza.

przy załomach odwrotnego kierunku

(

)

(

)

2

2

1

2

2

1

2

1

2

2

i

i

h

h

i

i

L

R

z

+

+

−

+

=

,

przy załomach jednakowego kierunku:

(

)

(

)

2

2

1

2

2

1

2

1

2

2

i

i

h

h

i

i

L

R

z

−

+

−

−

=

(8)