Opis kształtu w 

przestrzeni 2D 

Mirosław Głowacki 
Wydział Inżynierii Metali i 
Informatyki Przemysłowej AGH 

Krzywe Beziera 



Pochodna z krzywej Hermite’a 

 



 





 



4

2

1

2

4

2

1

2

2

3

1

4

3

6

6

6

6

'

R

t

t

R

t

t

P

t

t

P

t

t

t

Q























 



 





 



3

2

2

2

4

2

1

2

2

3

1

4

3

4

3

1

2

3

'

P

t

t

P

t

t

P

t

t

P

t

t

t

Q



























Krzywe Beziera 



Prędkość wzdłuż krzywej 
Beziera ma być stała. Stąd 
druga pochodna z funkcji 
Hermite’a powinna się 
zerować (zerowe 
przyspieszenie) 

  

 







 





0

2

6

4

6

6

12

6

12

'

'

3

4

1

2

4

1



























P

P

t

P

P

t

P

t

P

t

t

Q

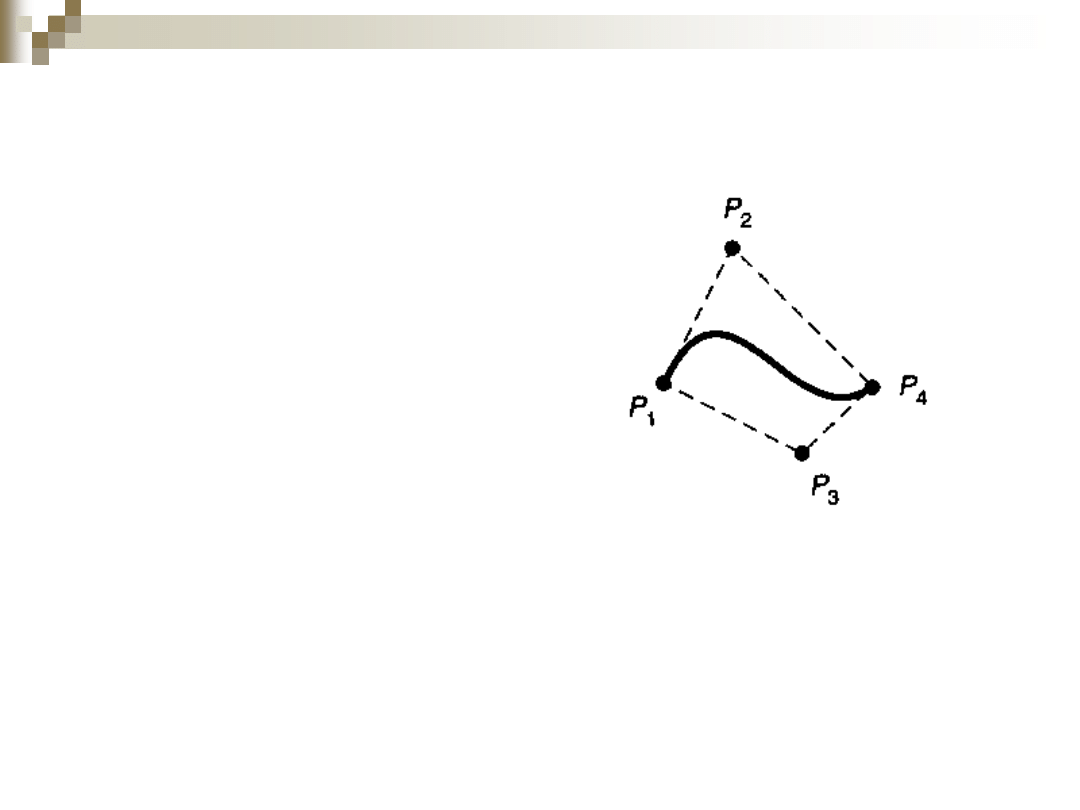
Krzywe Beziera 



W przypadku tych krzywych wektory styczne w punkach 

końcowych są określane bezpośrednio przez dwa punkt 

pośrednie, które nie leżą na krzywej. 



Wektory styczne początkowy i końcowy są określane przez 

wektory 𝑃

1

𝑃

2

 i 𝑃

3

𝑃

4

 i są związane z 𝑅

1

 i 𝑅

2

 zależnościami: 

𝑅

1

= 3𝑄

′

0 = 3 𝑃

2

− 𝑃

1

 

𝑅

4

= 3𝑄

′

1 = 3 𝑃

4

− 𝑃

3

 

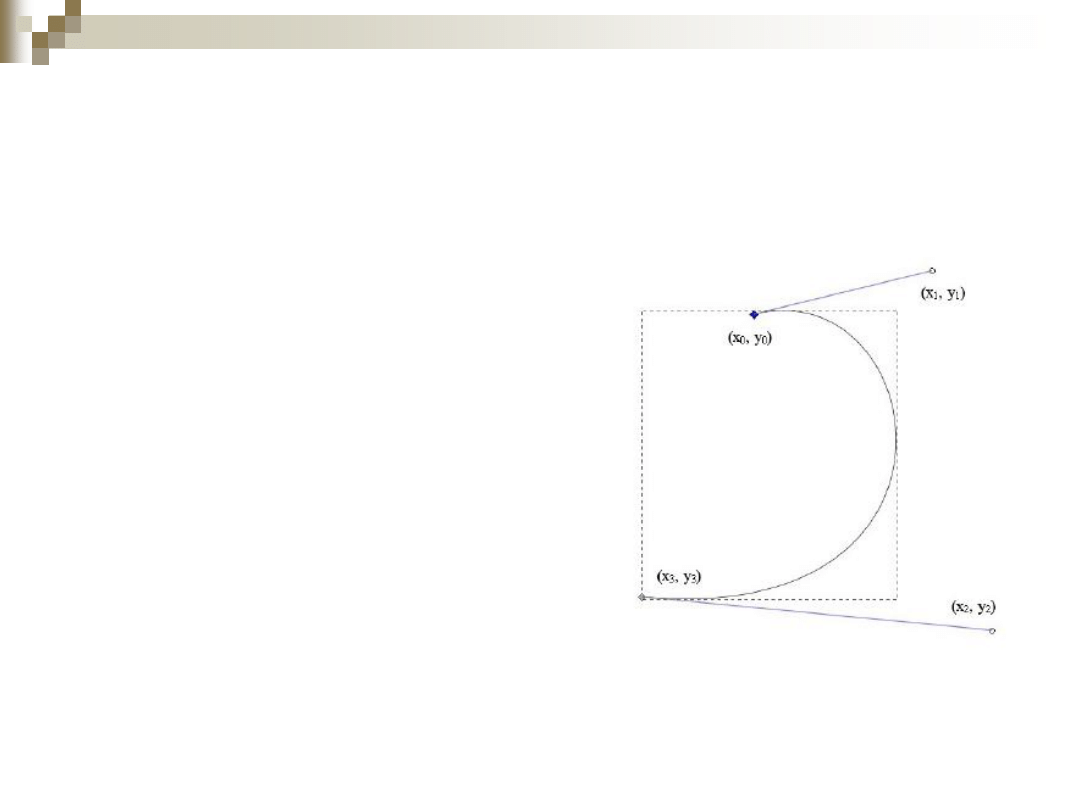
Krzywe Beziera 



W krzywych Bezier’a 

wykorzystujących wielomiany 

trzeciego stopnia 

często korzysta sie 

z faktu

, ze proste przechodzące przez 

punkty: 



 początkowy i następujący po nim 



końcowy i  poprzedzający go 

       są prostymi stycznymi do krzywej. 



Odcinki łączące punkt początkowy i 

następujący po nim oraz punkt 

końcowy i poprzedzający go często 

nazywa sie kierownicami 

 

Relacja pomiędzy macierzami 
geometrii Hermite’a i Beziera 



Krzywa Beziera 

interpoluje

 więc dwa końcowe 

punkty kontrolne i 

aproksymuje

 dwa pozostałe. 



Macierz geometrii Beziera wygląda następująco:  
𝐆

𝐵

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

 



Macierzą łączącą reprezentacje Hermite’a i 
Beziera jest macierz 𝐌

𝐻𝐵

. 



 Aby krzywe były identyczne bez względu na 
reprezentację musi zachodzić warunek: 
𝐆

𝐻

= 𝑃

1

, 𝑃

2

, 𝑅

1

, 𝑅

4

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

𝐌

𝐻𝐵

 

 

Relacja pomiędzy macierzami 
geometrii Hermite’a i Beziera 



Stąd: 

𝑃

1

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

1, 0, 0, 0

𝑇

𝑃

4

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

0 0, 0, 1

𝑇

𝑅

1

= 3 𝑃

2

− 𝑃

1

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

−3, 3, 0, 0

𝑇

𝑅

4

= 3 𝑃

4

− 𝑃

3

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

0, 0, −3, 3,

𝑇

 



Równania te można zastąpić jednym macierzowym z 
macierzą 𝐌

𝐻𝐵

 o rozmiarze 4 × 4: 

𝐆

𝐻

= 𝐆

𝐵

𝐌

𝐻𝐵

= 𝑃

1

, 𝑃

2

, 𝑃

3

, 𝑃

4

1 0 −3

0

0 0

3

0

0 0

0

−3

0 1

0

3

 

Relacja pomiędzy macierzami 
geometrii Hermite’a i Beziera 



W celu znalezienia macierzy bazowej Beziera M

B

 

korzystamy z równania: 𝐐 𝑡 = 𝑥 𝑡 , 𝑦 𝑡 , 𝑧 𝑡

𝑇

= 

𝐆

𝐻

𝐌

𝐻

𝐓 dla postaci Hermite’a i podstawiamy 

𝐆

𝐻

= 𝐆

𝐵

𝐌

𝐻𝐵

 



Stąd 
 

   
      
przy czym: 𝐌

𝐵

= 𝐌

𝐻𝐵

𝐌

𝐻 

𝐐 𝑡 = 𝐆

𝐻

𝐌

𝐻

𝐓 = 𝐆

𝐵

𝐌

𝐻𝐵

𝐌

𝐻

𝐓 =

𝐆

𝐵

𝐌

𝐻𝐵

𝐌

𝐻

𝐓 = 𝐆

𝐵

𝐌

𝐵

𝐓 

Relacja pomiędzy macierzami 
geometrii Hermite’a i Beziera 



Wykonując mnożenie: 

𝐌

𝐵

= 𝐌

𝐻𝐵

𝐌

𝐻

=

−1

3

−3

−1

3

−6

3

0

−3

3

0

0

1

0

0

0

 



Zatem krzywa Beziera jest opisana równaniem: 
 
 
 



Cztery wielomiany  1 − 𝑡

3

, 3𝑡 1 − 𝑡

2

, 3𝑡

2

1 − 𝑡  oraz 

𝑡

3

, które są wagami powyższego równania są nazywane 

wielomianami Bersteina. 
 

𝐐 𝑡 = 𝐆

𝐵

𝐌

𝐵

𝐓 = 

= 1 − 𝑡

3

𝑃

1

+ 3𝑡 1 − 𝑡

2

𝑃

2

+ 3𝑡

2

1 − 𝑡 𝑃

3

+ 𝑡

3

𝑃

4

 

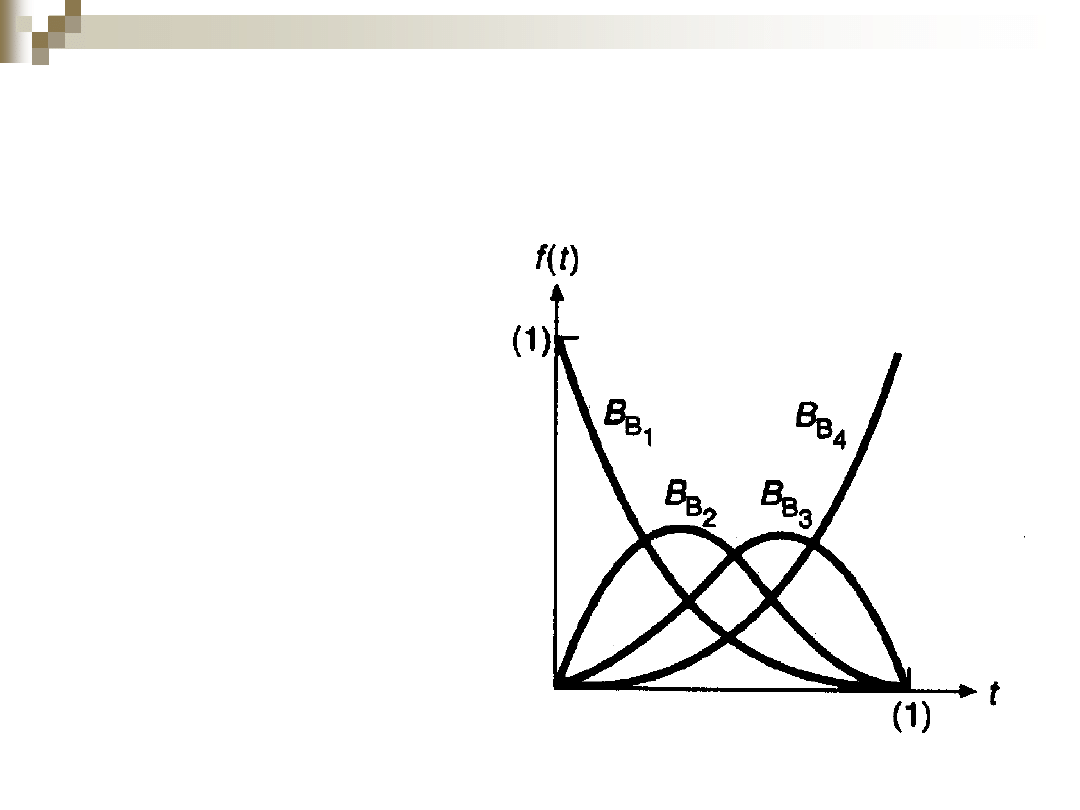
Wielomiany Bernsteina 



Wielomiany 
Bernsteina są 

funkcjami 
wagowymi

 

krzywych Beziera 

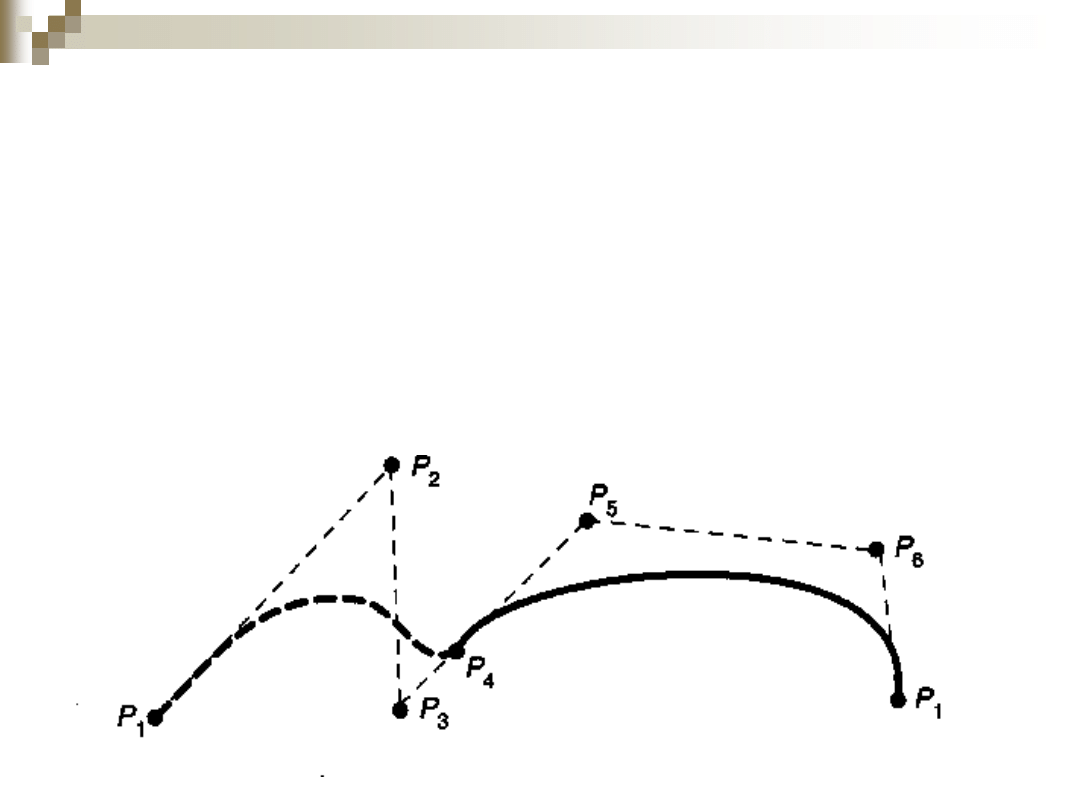
Łączenie krzywych Beziera 



Dwie krzywe Beziera łączące się w punkcie P4. 
Punkty P3, P4, P5 są współliniowe 

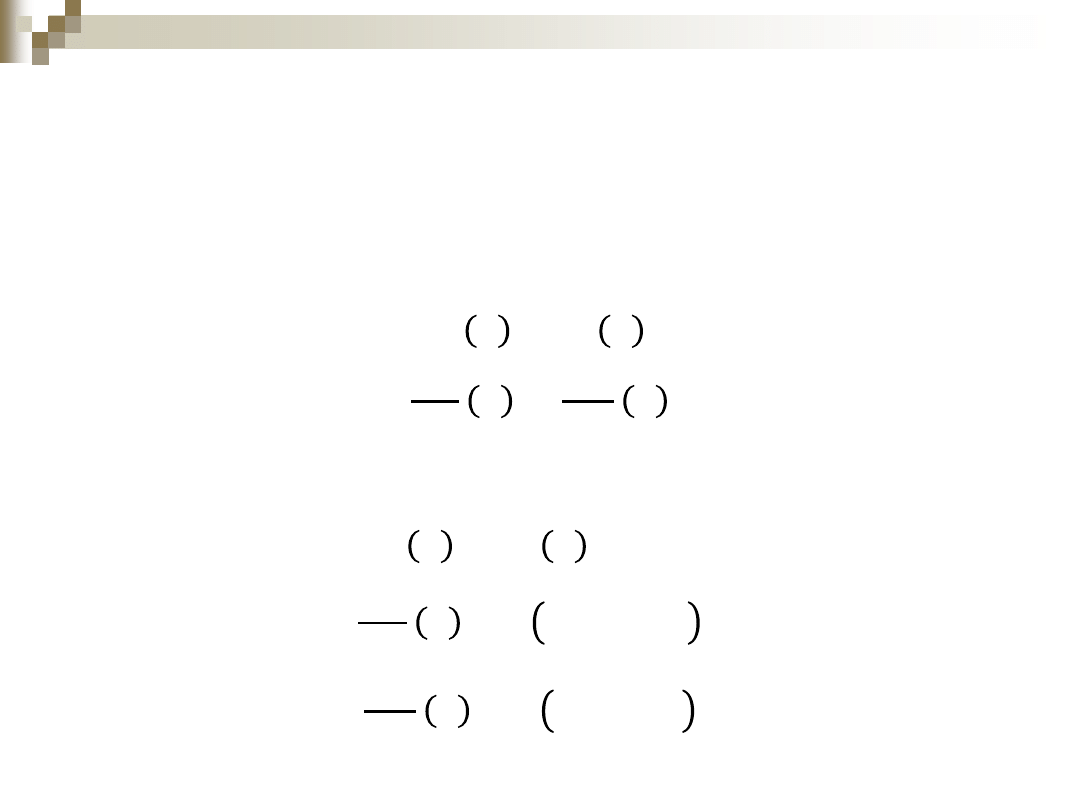
Łączenie krzywych Beziera 



Jeżeli segment lewy oznaczymy przez 𝑥

𝑙

 a prawy przez 𝑥

𝑟

 to 

warunki dla ciągłości C

0

 i C

1

 w punkcie połączenia są 

następujące: 
 
 



Stąd dla współrzędnej 𝑥 otrzymamy 

𝑥

𝑙

1 = 𝑥

𝑟

0

𝑑𝑥

𝑙

𝑑𝑡

1 =

𝑑𝑥

𝑟

𝑑𝑡

0

 

𝑥

𝑙

1 = 𝑥

𝑟

0 = 𝑃

4

𝑥

𝑑𝑥

𝑙

𝑑𝑡

1 = 3 𝑃

4

𝑥

− 𝑃

3

𝑥

𝑑𝑥

𝑟

𝑑𝑡

0 = 3 𝑃

5

− 𝑃

4

𝑥

 

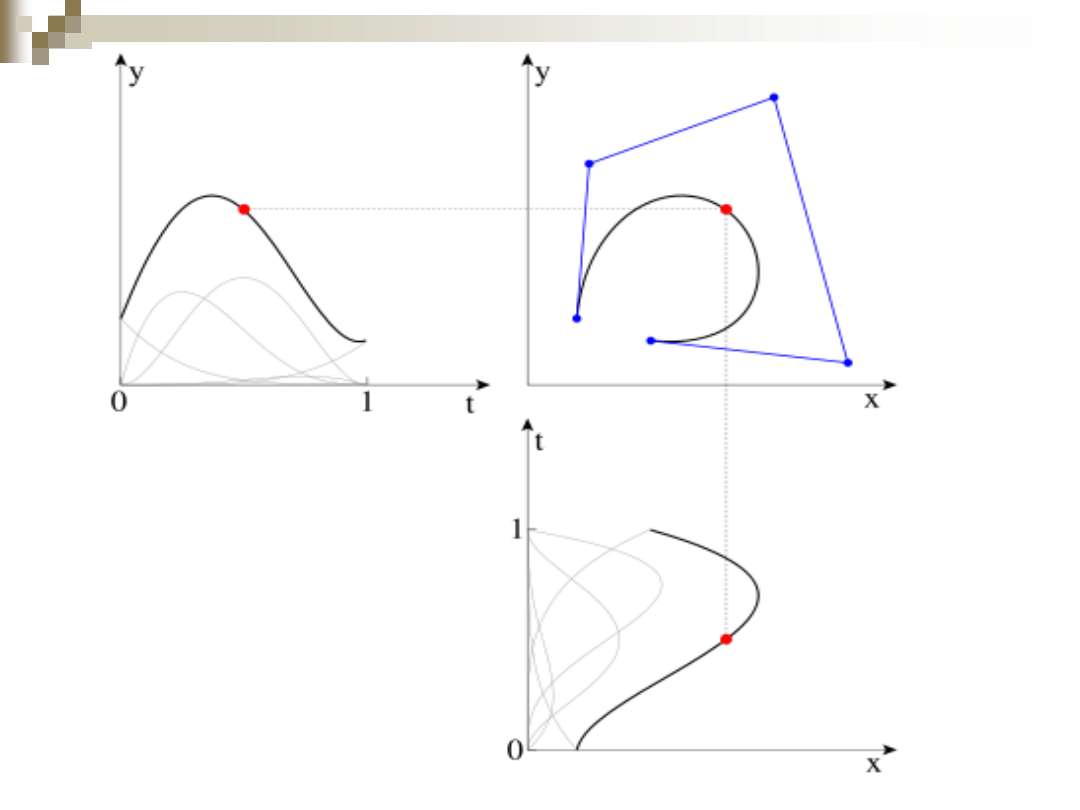
Krzywe Beziera 



Typowy wynik 
działania 
programu 
rysowania 
krzywych 
Beziera 

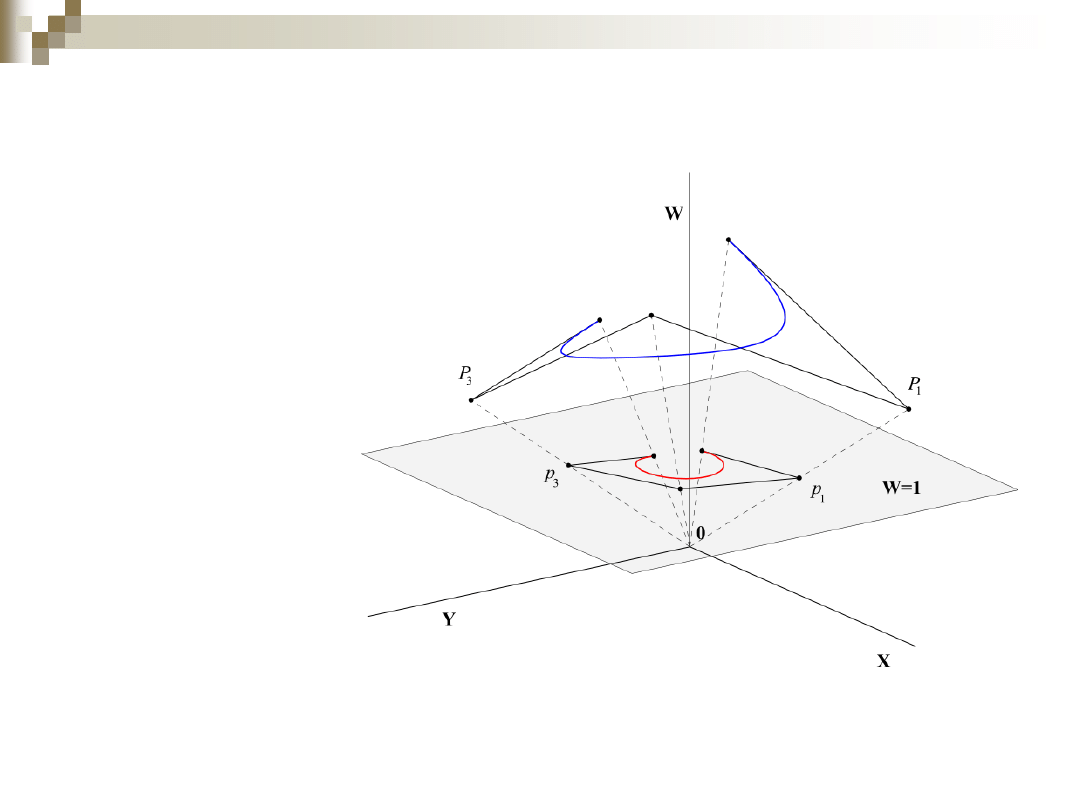
Wymierne krzywe  Beziera 



Wymierna 

krzywa Beziera to 

rzut środkowy

 

wielomianowej 

krzywej Béziera 

zdefiniowanej we 

współrzędnych 

jednorodnych 

na 

płaszczyznę: 

𝑊  =  1 

Krzywe Beziera 



Dowolny punkt krzywej wielomianowej jest dany jako 

     𝑃(𝑡) = 𝑥 𝑡 , 𝑦 𝑡 , 𝑧 𝑡 , … 𝑤 𝑡  



Po przejściu na współrzędne kartezjańskie (rzucie środkowym 
𝑃(𝑡) na płaszczyznę 𝑊  =  1 otrzymuje się 𝑘 

wyrażeń

 

wymiernych

, a punkt na tej płaszczyźnie dany jest wzorem 

 
 



Jeśli 𝑊(𝑡)   =  const to krzywa jest 

wielomianowa

 - mówiąc 

nieformalnie krzywe wielomianowe, to specjalny przypadek 
krzywych wymiernych 

 

𝑃 𝑡 = 𝑥 𝑡 , 𝑦 𝑡 , 𝑧 𝑡 , … =

𝑥 𝑡

𝑤 𝑡

,

𝑥 𝑡

𝑤 𝑡

,

𝑥 𝑡

𝑤 𝑡

, …  

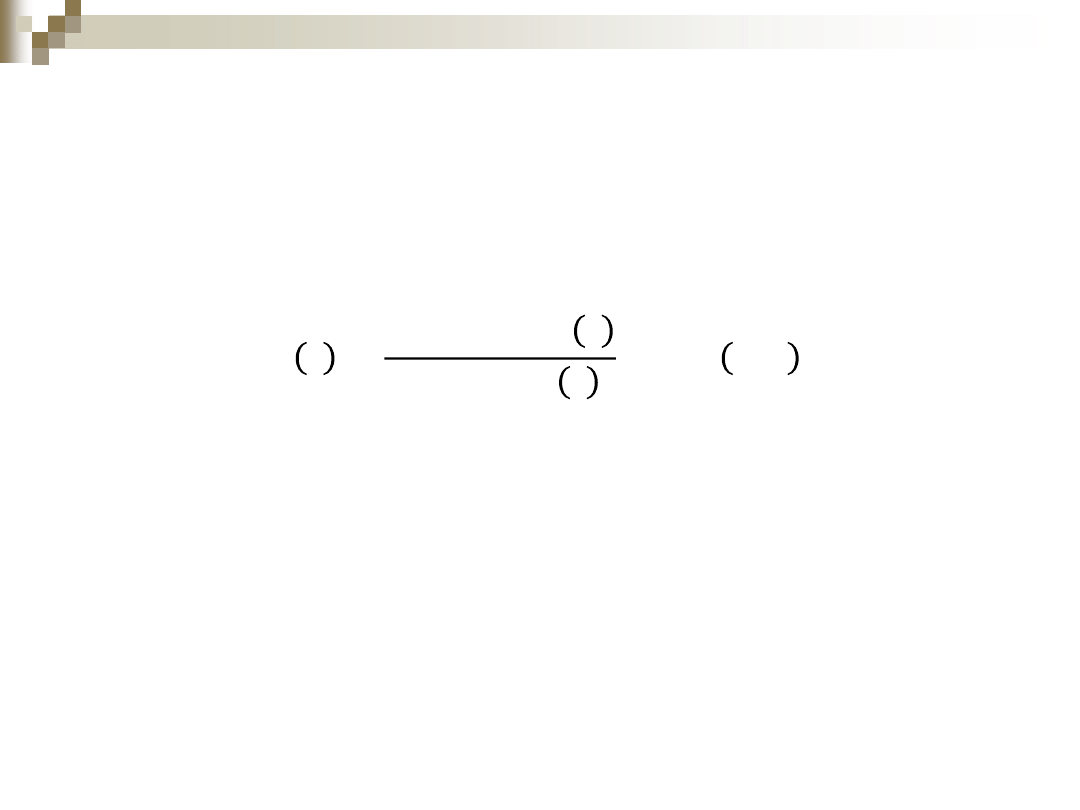
Krzywe Beziera 



Dowolny punkt krzywej wielomianowej we 

wpółrzędnych

 

rzeczywistych

 jest dany jako 

 

 

 



𝑛 — liczba punktów kontrolnych minus 1 (punkty kontrolne 
liczone są od zera)  



𝑝

𝑖

 — 𝑖 − ty punkt kontrolny  



𝑤

𝑖

 — 

waga

 𝑖 − tego punktu kontrolnego (dowolna 

liczba 

rzeczywista

) – jeśli 𝑤  =  0 punkt kontrolny nie jest brany pod 

uwagę  



𝐵

𝑖

𝑛

— 

wielomiany bazowe Bernsteina  

 

𝑃 𝑡 =

 

𝑤

𝑖

𝑃

𝑖

𝐵

𝑖

𝑛

𝑡

𝑛

𝑖=0

 

𝑤

𝑖

𝐵

𝑖

𝑛

𝑡

𝑛

𝑖=0

;    𝑡 ∈ 0, 1  

Cechy krzywej Beziera 



Krzywa ma nieskończenie wiele reprezentacji we współrzędnych 

jednorodnych.  



Konstrukcja krzywej jest 

niezmiennicza 

względem 

przekształceń 

afinicznych

, tzn. krzywa wyznaczona z przekształconych punktów 

kontrolnych jest taka sama jak krzywa po tym przekształceniu.  



Jeśli wszystkie wagi są 

równe i niezerowe

, to krzywa jest 

wielomianowa

.  



Jeśli wszystkie 

wagi są niezerowe 

i tego samego znaku, to krzywa 

spełnia własność 

otoczki wypukłej

, tzn. punkt 𝑝(𝑡) leży w 

otoczce

 

wypukłej

 punktów kontrolnych .  



Przemnożenie wszystkich wag przez tę samą liczbę różną od zera 

nie zmienia krzywej.  

Cechy krzywej Beziera 



Ponadto w stosunku do krzywych wielomianowych, 

wymierne krzywe Béziera mają następujące zalety: 



mogą reprezentować wszystkie 

krzywe

 

stożkowe

 (co 

ma znaczenie w zastosowaniach 

CAD

);  



rzut perspektywiczny 

krzywej 

wymiernej

 jest zawsze 

krzywą 

wymierną

, podczas gdy rzut perspektywiczny 

krzywej 

wielomianowej

 

nie

 musi być krzywą 

wielomianową (co ma znaczenie w grafice 

komputerowej);  



wagi 𝑤

𝑖

 pozwalają na lepszą kontrolę nad kształtem 

krzywej. 

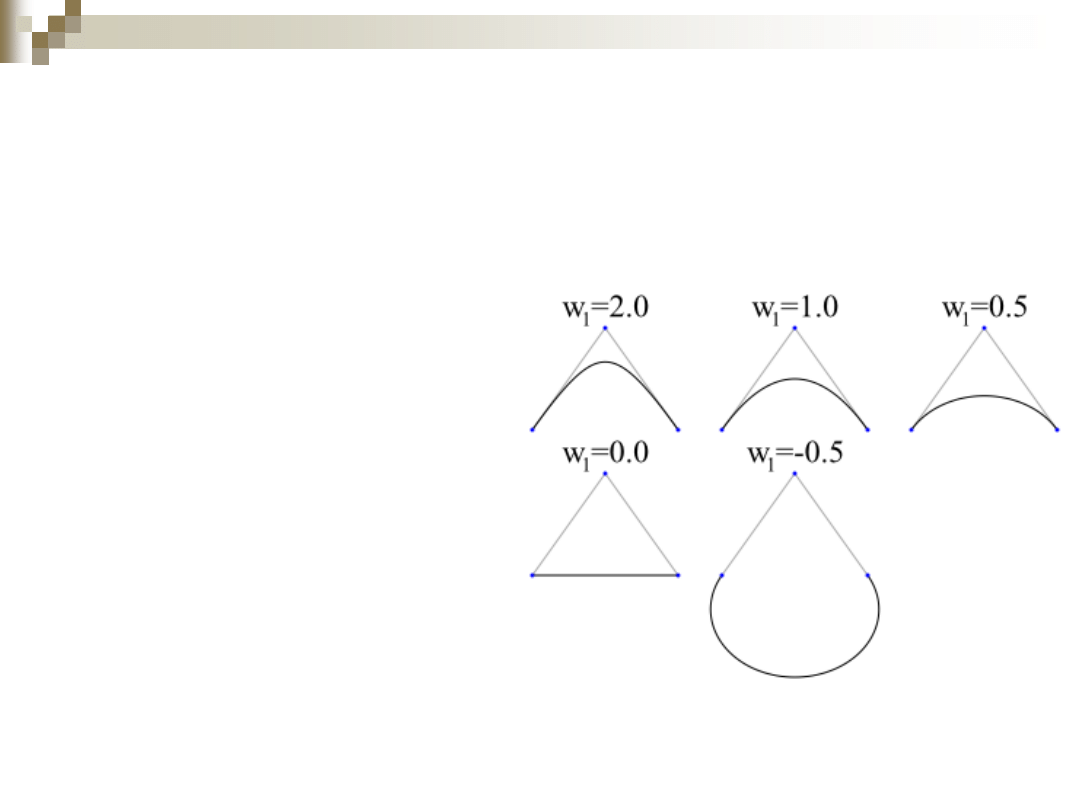
Krzywe stożkowe 



Jeśli dane są trzy 

niewspółliniowe

 

punkty kontrolne krzywej 𝑝

0

, 𝑝

1

, 𝑝

2

 i 

wagi 

𝑤

0

  =  𝑤

2

  =  1

, to waga w

1

 

określa rodzaj krzywej: 



𝑤

1

  >  1 — łuk 

hiperboli

  



𝑤

1

  =  1 — łuk 

paraboli

  



0  <  𝑤

1

  <  1 — krótszy łuk 

elipsy

 

lub 

okręgu 



 𝑤

1

  =  0 — sparametryzowany 

odcinek pomiędzy 𝑝

0 

i 𝑝

2

 



− 1  <  𝑤

1

  <  0 — dłuższy łuk 

elipsy

 lub 

okręgu 



𝑤

1

  =    − 1 — 

dwa

 łuki 

paraboli 



 𝑤

1

  <   − 1 — 

dwa

 łuki 

hiperboli 

Krzywe stożkowe 

Okrąg zbudowany z 

dwóch

 

krzywych tworzących 

dłuższy

 i 

krótszy

 

łuk 

okręgu (po lewej); czterech krzywych tworzących 

cztery krótsze 

łuki okręgu 

(po prawej) 

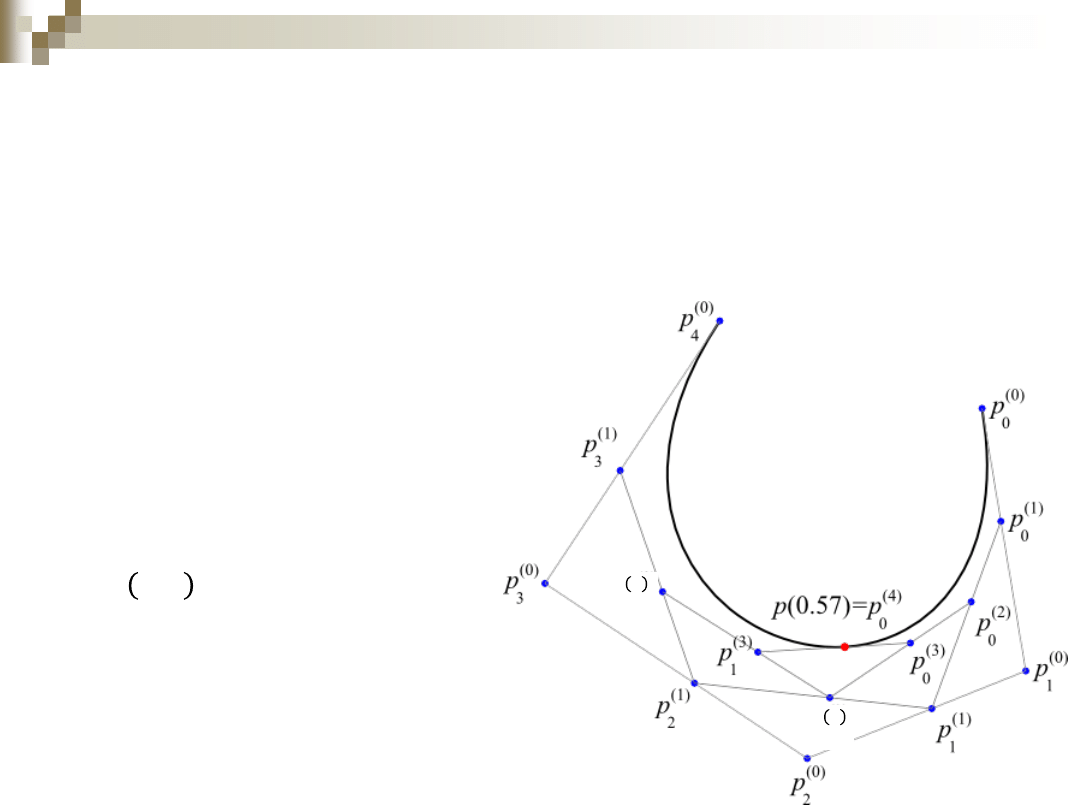
Algorytm de 
Casteljau 



Algorytm de Casteljau 

opracowany przez Paula de 

Casteljau pozwala na 

wyznaczenie punktów na 

wielomianowej krzywej 

Béziera, 

czyli obliczanie wartości 

wielomianów w 

bazie 

wielomianów Bernstaina

. 



Dana jest dowolna 

łamana

 

zdefiniowana przez 𝑛 + 1 

wierzchołków oraz liczba 

𝑡 ∈ 0, 1 .  



Każdy odcinek łamanej jest 

dzielony w stosunku 𝑡/(1  −  𝑡), 

czego wynikiem jest 𝑛 

wierzchołków, które wyznaczają 

nową łamaną.  

 

 

 

 

 

 

 

 

 









 

)

(

,

,

,

,

0

1

1

1

0

1

1

1

2

1

1

1

0

0

0

3

0

2

0

1

0

0

t

p

p

p

p

p

p

p

p

p

p

p

p

p

n

n

n

n

n















𝑝

1

2

 

𝑝

2

2

 

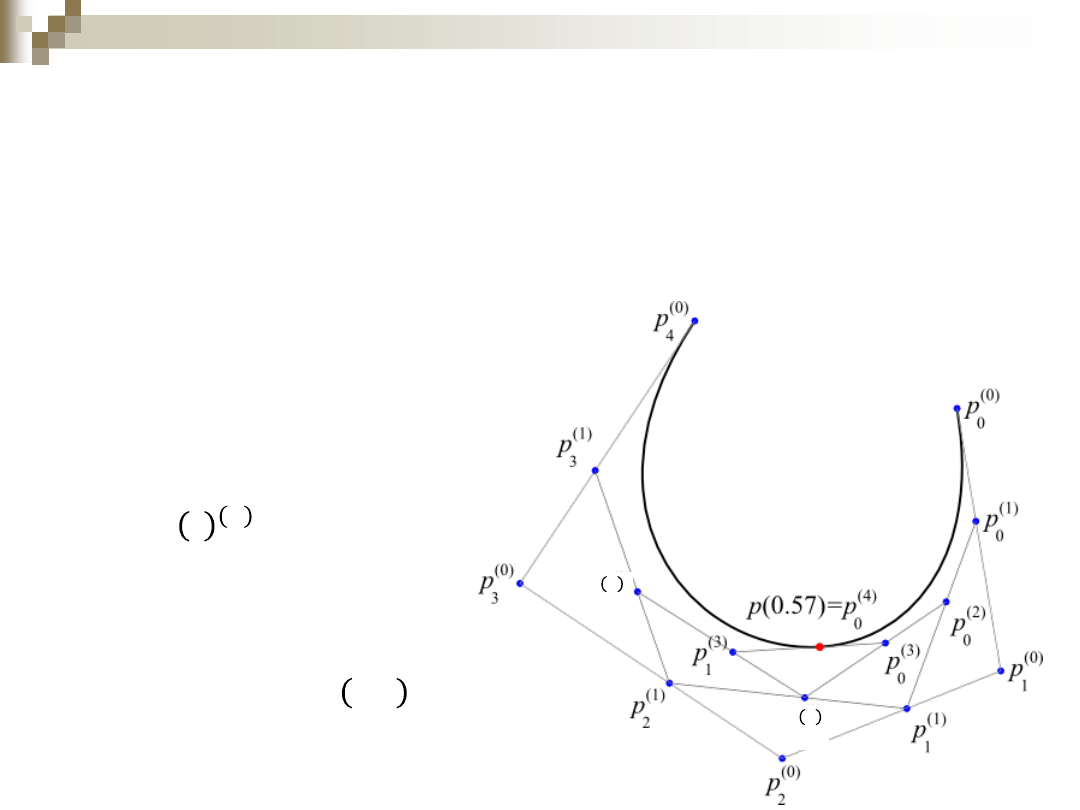
Algorytm de 
Casteljau 



Proces 

powtarzany

 jest do 

chwili, aż zostanie jeden 

punkt 𝑝(𝑡), co wymaga 

wykonania n kroków.  



Ostatecznie otrzymuje się 

𝑛  +  1 ciągów punktów 

(indeks górny oznacza krok 

algorytmu): 



Punkt 𝑝 𝑡

𝑛

 leży na 

krzywej Béziera, której 

łamaną kontrolną 

tworzą 

wyjściowe punkty.  



Wykonując algorytm dla 

wielu 𝑡 z przedziału  0,1  

otrzymywane są punkty 

krzywej Béziera. 
 

 

 

 

 

 

 

 

 

 









 

)

(

,

,

,

,

0

1

1

1

0

1

1

1

2

1

1

1

0

0

0

3

0

2

0

1

0

0

t

p

p

p

p

p

p

p

p

p

p

p

p

p

n

n

n

n

n















𝑝

1

2

 

𝑝

2

2

 

Algorytm de Casteljau 

𝑝

1

2

 

𝑝

2

2

 

Algorytm de Casteljau 



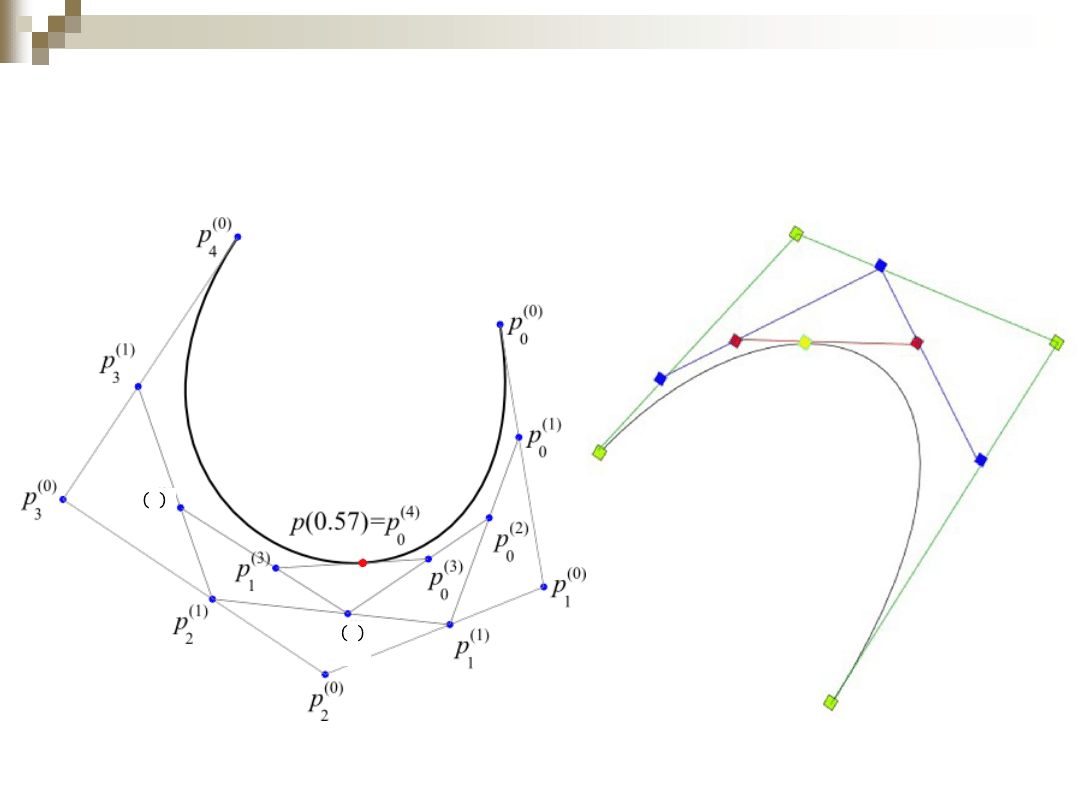
Za pomocą algorytmu de Casteljau można również: 



Wyznaczyć punkty kontrolne dwóch krzywych, tak aby 

połączyć je z zadaną ciągłością geometryczną – 

krz

ywa B-

sklejana

.  



Podzielić krzywą na dwie krzywe w punkcie 𝑝(𝑡).  



Łamane kontrolne są wyznaczane przez punkty leżące na 

brzegach przedstawionego wyżej 

trójkąta

 

punktów

 - 

łamaną kontrolną pierwszej krzywej opisują punkty: 
 
 



a drugą:  
 
 



Obie krzywe są tego samego stopnia co dzielona krzywa.  

 

𝑝

𝑛

0

, 𝑝

𝑛−1

1

,  𝑝

𝑛−2

2

, … , 𝑝

1

𝑛−1

, 

𝑝

0

𝑛

   

𝑝

0

0

, 𝑝

0

1

,  𝑝

0

2

, … , 𝑝

0

𝑛−1

, 

𝑝

0

𝑛

 

 

 

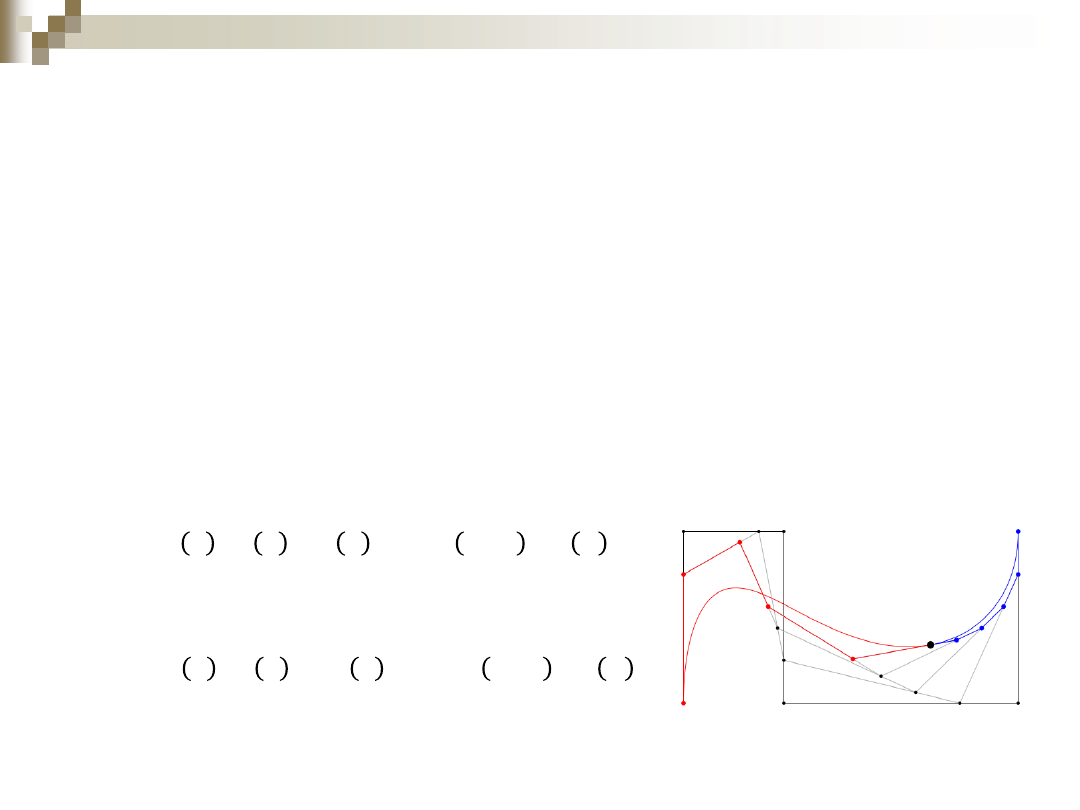
Dopasowanie krzywych do zbioru 
punktów 



Znak przedstawiony w postaci cyfrowej 



Oryginalny kształt, dopasowana krzywa i punkty 
kontrolne Beziera