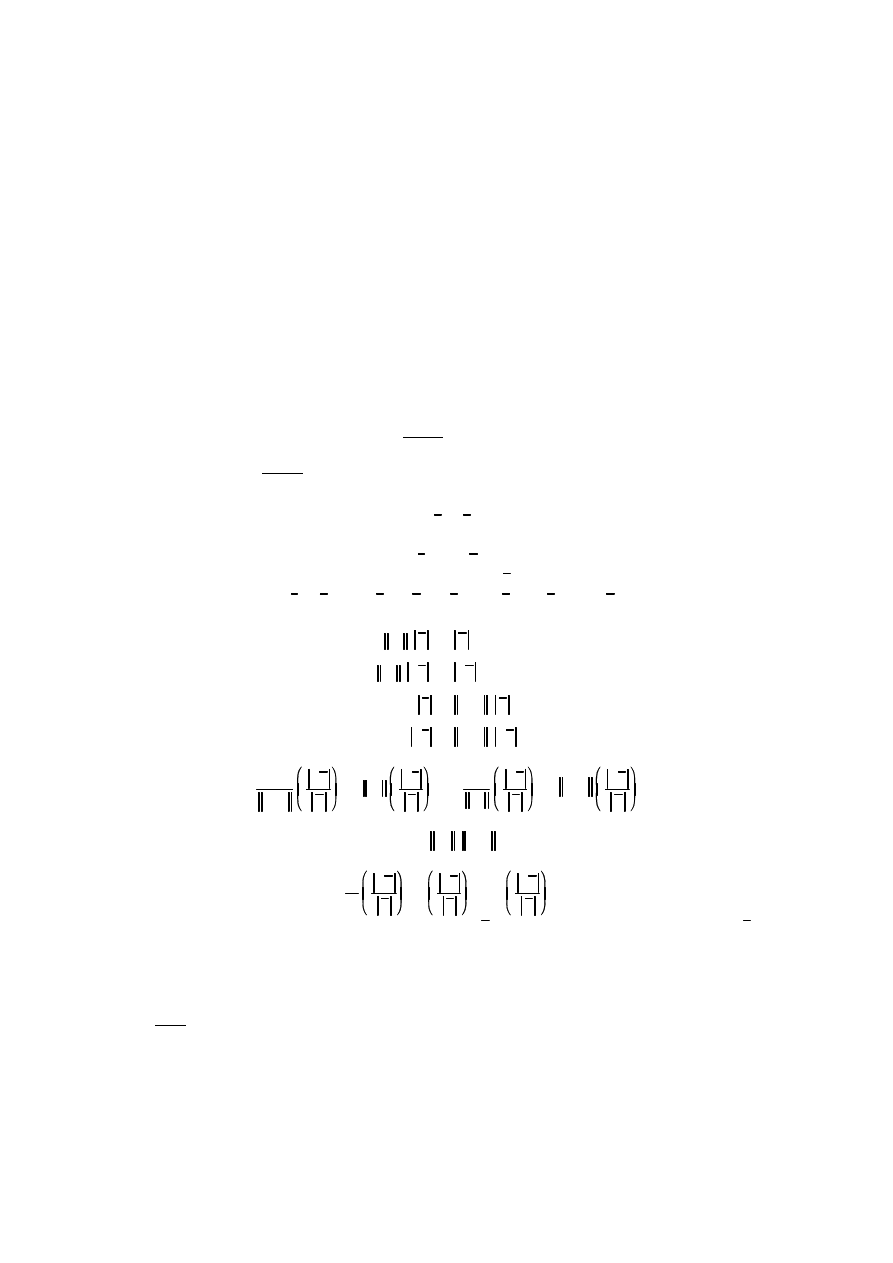
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
1
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
Rozwi zywanie układów równa
Metody dokładne
Metody, w których rozwi zanie otrzymuje si po sko czonej liczbie kroków. Gdyby wszystkie działania
arytmetyczne były przeprowadzane dokładnie otrzymane rozwi zanie równie byłoby dokładne — oczywi cie z
powodu bł dów obci cia dokładne nie b dzie (nale y jednak pami ta , e w przypadku wi kszo ci zastosowa bł dy
rozwi za wynikaj ce z bł dów obci cia s niezauwa alnie małe).
Przykłady i wzory b d zapisywane dla układu czterech równa z czterema niewiadomymi, ale oczywi cie równa i
niewiadomych mo e by n.
Warunki istnienia rozwi za
Aby rozwi zanie układu równa było mo liwe macierz współczynników musi by nieosobliwa, ale w przypadku
oblicze numerycznych je li które z równa b dzie bliskie liniowej kombinacji pozostałych to ju mo e to
uniemo liwi rozwi zanie. Poza tym w trakcie oblicze kumulowa si b d bł dy obci cia (zwłaszcza gdy macierz
jest bliska osobliwej) i mog bardzo zniekształci wyniki.
Sposób w jaki bł dy (czy niedokładno ci) wyst puj ce w wektorze prawych stron wpływaj na wynik mo na
okre li nast puj co. Zakładamy, e dane jest równanie postaci:
Ax
b
którego rozwi zaniem b dzie oczywi cie:
x
A
1
b
Je li bł dy wyst puj ce w wektorze prawych stron oznaczymy jako b dziemy mogli zapisa :
b
Ax
b ;
A x
b ; x
A
1
b ;
x
A
1
b
Wynika st d (zakładaj c, e norm liczymy jako pierwiastek z sumy kwardatów):
A x
b
A
x
b
x
A
1
b
x
A
1
b
Mo na wi c zapisa nast puj ce nierówno ci:
1
A
1
b
b
A
x
x
;
1
A
x
x
A
1
b
b
Wprowadzimy teraz oznaczenie:
K
A
A
1
które umo liwi nam poł czenie zapisanych powy ej nierówno ci:
1
K
b
b
x
x
K
b
b
Nierówno ta okre la „granice” bł du (wynikaj cego z bł dów ) jakim obarczone mo e by rozwi zanie . Wida ,
b
x
e „im wi ksze K tym gorzej”. Macierze, dla których K przybiera du e warto ci nazywane s „ le uwarunkowanymi”,
w szczególno ci dla macierzy osobliwej K ma warto niesko czon .
Warto tu jeszcze raz powtórzy , e o ile rozwi zanie „na karteczce” (analityczne) nie powiedzie si (tzn. nie uda si
przedstawi wzorów okre laj cych rozwi zanie, kwesti obliczenia warto ci liczbowych tego rozwi zania pozostawiam
„na boku”) tylko gdy macierz jest osobliwa, o tyle w przypadku rozwi za numerycznych do braku rozwi zania
wystarczy, e macierz b dzie „bliska osobliwej”.

Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
2
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
Wzory Cramera
Oczywi cie jeszcze ze szkoły wszyscy pami taj wzory Cramera (metod wyznaczników). Je li dany jest układ
równa postaci:
a
11
x
1
a
12
x
2
a
13
x
3
a
14
x
4
b
1
a
21
x
1
a
22
x
2
a
23
x
3
a
24
x
4
b
2
a
31
x
1
a
32
x
2
a
33
x
3
a
34
x
4
b
3
a
41
x
1
a
42
x
2
a
43
x
3
a
44
x
4
b
4
to nale y obliczy jego wyznacznik główny :
a
11
a
12
a
13
a
14
a
21
a
22
a
23
a
24
a
31
a
32
a
33
a
34
a
41
a
42
a
43
a
44
oraz wszystkie pozostałe wyznaczniki postaci (np.):
;
2
a
11
b
1
a
13
a
14
a
21
b
2
a
23
a
24
a
31
b
3
a
33
a
34
a
41
b
4
a
43
a
44
3
a
11
a
12
b
1
a
14
a
21
a
22
b
2
a
24
a
31
a
32
b
3
a
34
a
41
a
42
b
4
a
44
Po czym wyznaczy niewiadome z wzorów:
x
1
1
; x
2
2
; x
3
3
; x
4
4
Jak łatwo zauwa y metoda ta b dzie bardzo pracochłonna w przypadku du ych układów równa (dla układu n
równa wymaga obliczenia n+1 wyznaczników stopnia n).
Metoda eliminacji Gaussa
Załó my, e mamy układ równa (w przykładowych zapisach poni ej wektor wolnych wyrazów b d oznacza
przez a z indeksami odpowiadaj cymi n+1 kolumnie (ma to podkre la fakt, e podczas rozwi zywania układu równa
b dziemy operowa na całej tablicy, wł cznie z wektorem wyrazów wolnych):
a
11
x
1
a
12
x
2
a
13
x
3
a
14
x
4
a
15
a
21
x
1
a
22
x
2
a
23
x
3
a
24
x
4
a
25
a
31
x
1
a
32
x
2
a
33
x
3
a
34
x
4
a
35
a
41
x
1
a
42
x
2
a
43
x
3
a
44
x
4
a
45
załó my, e element a
11
0, je li podzielimy pierwsze równanie układu przez a
11
otrzymamy:
x
1
b
12
x
2
b
13
x
3
b
14
x
4
b
15
gdzie:
b
1j
a
1j
a
11
j 2,3,4,5
Wykorzystuj c powy sze równanie mo na łatwo wyeliminowa zmienn x
1
z pozostałych równa . W tym celu
mno ymy je odpowiednio przez a
21
, a
31
i a
41
i odejmujemy od odpowiednich równa . Otrzymujemy układ trzech
równa :
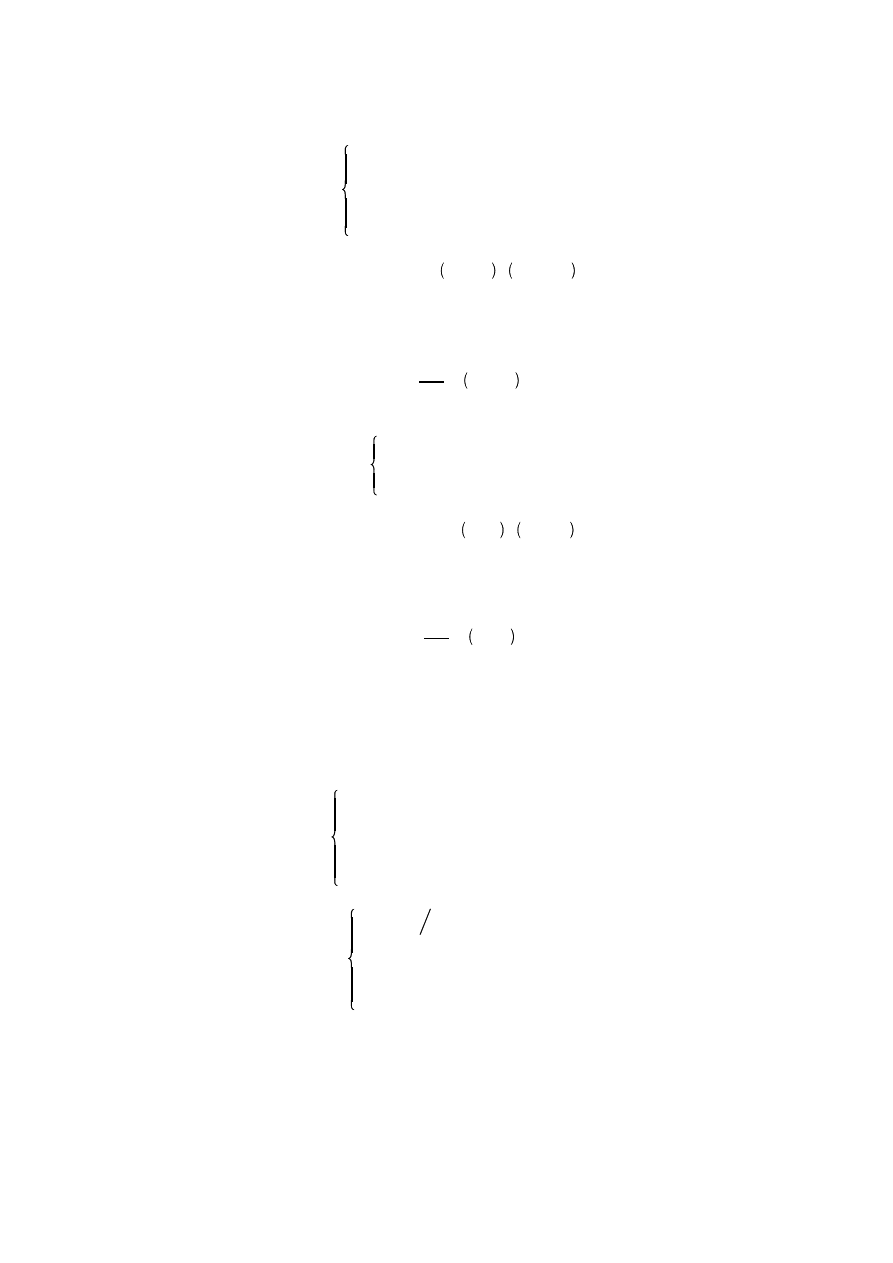
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
3
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
a
(1)
22
x
2
a
(1)
23
x
3
a
(1)
24
x
4
a
(1)
25
a
(1)
32
x
2
a
(1)
33
x
3
a
(1)
34
x
4
a
(1)
35
a
(1)
42
x
2
a
(1)
43
x
3
a
(1)
44
x
4
a
(1)
45
gdzie współczynniki:
a
(1)
ij
a
ij
a
i1
b
1i
i 2,3,4
j 2,3,4,5
Znowu pierwsze równanie układu dzielimy przez jego pierwszy współczynnik (a
22
(1)
) i otrzymujemy:
x
2
b
(1)
23
x
3
b
(1)
24
x
4
b
(1)
25
gdzie:
b
(1)
2j
a
(1)
2j
a
(1)
22
j 3,4,5
W taki sam jak poprzednio sposób eliminujemy zmienn x
2
i otrzymujemy układ:
a
(2)
33
x
3
a
(2)
34
x
4
a
(2)
35
a
(2)
43
x
3
a
(2)
44
x
4
a
(2)
45
gdzie współczynniki:
a
(2)
ij
a
(1)
ij
a
(1)
i2
b
(1)
2j
i 3,4
j 3,4,5
Pierwsze z równa znowu dzielimy przez pierwszy współczynnik:
x
3
b
(2)
34
x
4
b
(2)
35
gdzie:
b
(2)
3j
a
(2)
3j
a
(2)
33
j 4,5
i za pomoc tego równania eliminujemy zmienn x
3
:
a
(3)
44
x
4
a
(3)
45
gdzie:
a
(3)
4j
a
(2)
4j
a
(2)
43
b
(2)
3j
W ten sposób przekształcili my wyj ciowy układ równa do postaci:
x
1
b
12
x
2
b
13
x
3
b
14
x
4
b
15
x
2
b
(1)
23
x
3
b
(1)
24
x
4
b
(1)
25
x
3
b
(2)
34
x
4
b
(2)
35
a
(3)
44
x
4
a
(3)
45
który mo emy ju łatwo rozwi za obliczaj c kolejno:
x
4
a
(3)
45
a
(3)
44
x
3
b
(2)
35
b
(2)
34
x
4
x
2
b
(1)
25
b
(1)
24
x
4
b
(1)
23
x
3
x
1
b
15
b
14
x
4
b
13
x
3
b
12
x
2
Jak wida metoda Gaussa składa si z dwóch cz ci: w pierwszej z nich nast puje eliminacja kolejnych
niewiadomych — w efekcie nast puje przekształcenie macierzy współczynników w macierz trójk tn ; w drugiej cz ci
nast puje obliczenie kolejnych niewiadomych.
Wszystkie układy, które drog zamiany kolejno ci równa mog zosta sprowadzone do przypadku macierzy
trójk tnej mo na rozwi za bardzo łatwo — stosuj c tylko drug cz
metody Gaussa.
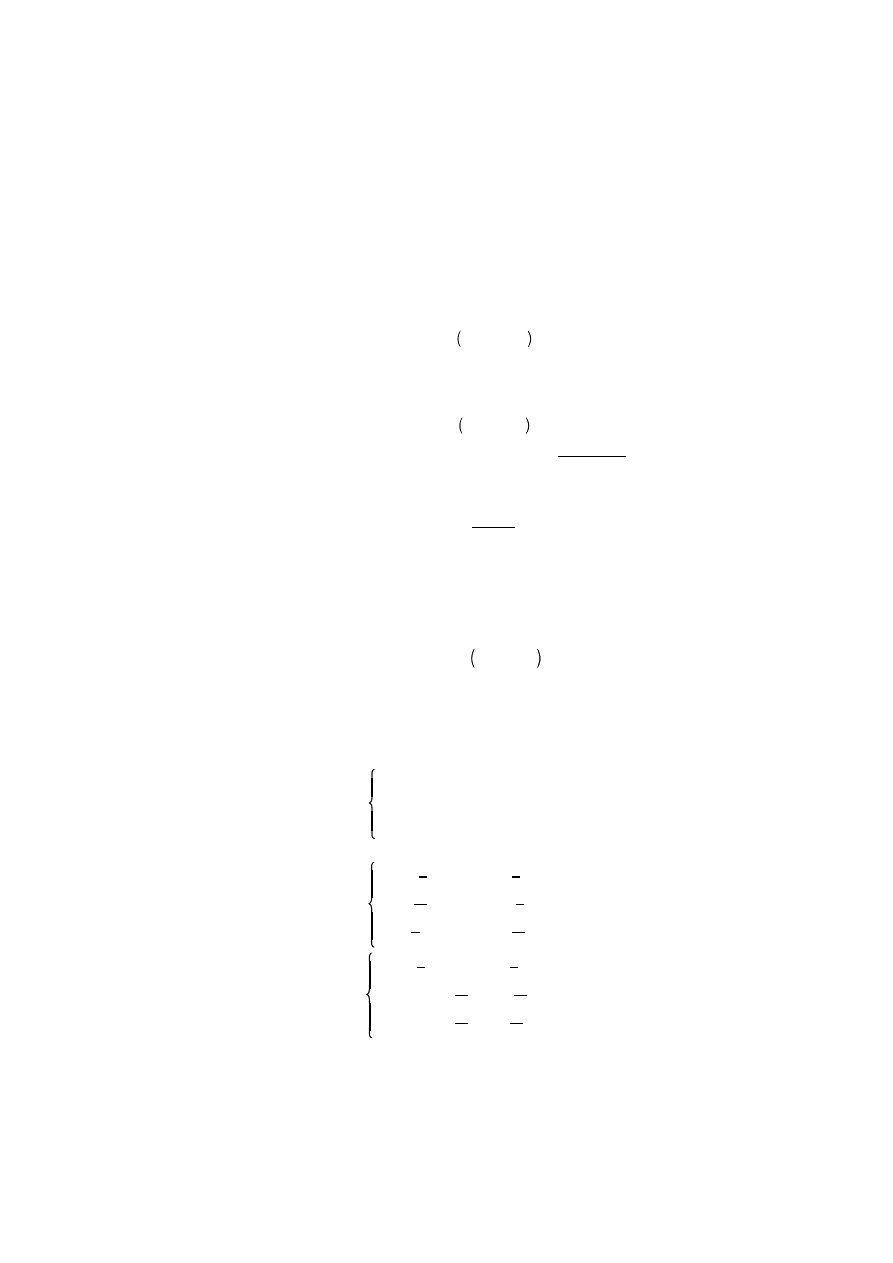
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
4
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
Jak łatwo zauwa y opisana powy ej metoda ma pewne mankamenty:
— je li który z kolejnych elementów macierzy wykorzystywanych do normalizowania wierszy (a
ii
(i)
) b dzie
wynosi zero to nie uda si przeprowadzi oblicze ,
— je li który z powy szych elementów b dzie wystarczaj co mały to spowoduje to wyst pienie du ych
bł dów, — dowiedziono, e przedstawiona powy ej metoda jest numerycznie niestabilna — zawsze nale y
stosowa przedstawion poni ej modyfikacj — wybór elementu głównego.
Z powy szych powodów stosuje si raczej pewn modyfikacj metody Gaussa, polegaj c na zmianie kolejno ci
równa i zmiennych w taki sposób, aby za ka dym razem do normalizacji kolejnych wierszy wykorzystywa
najwi kszy co do warto ci element przekształcanej macierzy.
Najpierw zamieniaj c kolejno kolumn macierzy wyj ciowej doprowadzamy do spełnienia warunku:
a
(0)
11
a
(0)
ij
i,j 1,2, ,n
w rezultacie element a
11
(0)
ma najwi ksz warto bezwzgl dn .
Nast pnie, tak samo jak poprzednio, dzielimy pierwsze równanie przez a
11
(0)
i eliminujemy x
1
z pozostałych równa .
W nowootrzymanym układzie równa znowu wyszukujemy najwi kszy element:
a
(1)
22
a
(1)
ij
i,j 2,3, n
i tak przestawiamy wiersze i kolumny aby znalazł si on na pierwszej pozycji. Koniecznie nale y przy tym pami ta o
odpowiednim przestawieniu równa otrzymanych wcze niej (oczywi cie dotyczy to przypadku gdy przestawiamy
kolumny macierzy) oraz (w przypadku przestawiania wierszy) o odpowiednim przestawieniu wierszy wektora
niewiadomych x.
Dalsze obliczenia s analogiczne jak poprzednio, przy czym zawsze przy okazji wyboru kolejnego maksymalnego
elementu pami ta nale y o odpowiednim przestawieniu poprzednich (ju gotowych) równa (je li dokonywano
zamiany kolumn) i wierszy (równie wektora x).
W praktyce najcz ciej stosuje si tzw. cz ciowy wybór elementu głównego — tzn. bada si tylko aktualn
pierwsz kolumn i dokonuje ewentualnej zamiany tylko dla wierszy. Jest to znacznie prostsze od wyboru pełnego, a
najcz ciej wystarcza.
Dokonywanie wyboru jest zb dne w przypadku macierzy z dominuj c przek tn :
a
ii
n
j 1
j i
a
ij
i 1,2, ,n
Szacuje si , e w metodzie Gaussa ilo ci koniecznych do wykonania mno e i dziele oraz dodawa i odejmowa
s rz du n
3
.
Przykład: Rozwa my układ równa :
2x
1
7x
2
4x
3
9
x
1
9x
2
6x
3
1
3x
1
8x
2
5x
3
6
kolejne przekształcenia daj nast puj ce układy:
x
1
7
2
x
2
2x
3
9
2
25
2
x
2
8x
3
7
2
5
2
x
2
11x
3
39
2
x
1
7
2
x
2
2x
3
9
2
x
2
16
25
x
3
7
25
47
5
x
3
94
5
Rozwi zaniem s : x
1
= 4, x
2
= 1, x
3
= 2.

Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
5
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
Metoda eliminacji Jordana (Gaussa-Jordana, eliminacji zupełnej)
W metodzie tej, b d cej modyfikacj zwykłej metody Gaussa, ł czy si przekształcenie macierzy opisuj cej układ
równa z obliczaniem wyników.
Algorytm jest nast puj cy:
a
kj
a
kj
a
kk
j n m, n m 1, ,k
a
ij
a
ij
a
ik
a
kj
j n m,n m , ,k
i 1,2, ,n i !n
k 1,2, ,n
Przykład. Dla ilustracji rozpatrzymy ten sam układ równa :
2x
1
7x
2
4x
3
9
x
1
9x
2
6x
3
1
3x
1
8x
2
5x
3
6
Macierz współczynników równania, wraz z wyrazami wolnymi ma posta :
2
7 4 9
1
9
6 1
3 8
5 6
Tak jak poprzednio pierwszy wiersz macierzy normalizujemy za pomoc pierwszego jej elementu, a nast pnie
od wszystkich nast pnych wierszy odejmujemy otrzymany wła nie pierwszy rz d pomno ony przez pierwszy
współczynnik w danym wierszu — w rezultacie w pozostałych wierszach współczynniki a
i1
wynosz zero.
1
7
2
2
9
2
0
25
2
8
7
2
0
5
2
11
39
2
Nast pnie normalizujemy wiersz drugi, dziel c wszystkie jego elementy przez 25/2 i redukujemy pozostałe
równania (tak e ju przekształcone równanie pierwsze) odejmuj c od nich wiersz drugi pomno ony przez
odpowiedni współczynnik a
i2
:
1
0
6
25
88
25
0 1
16
25
7
25
0 0
47
5
94
5
Na koniec (w tym przykładzie) normalizujemy wiersz trzeci dziel c jego współczynniki (teraz ju tylko wyraz
wolny) przez 47/5 i redukujemy pozostałe równania tak jak poprzednio. Otrzymujemy:
1
0
0
4
0
1
0
1
0
0
1
2
Ostatnia kolumna (w której na pocz tku umie cili my wyrazy wolne) zawiera rozwi zanie.
Szacuje si , e w metodzie Jordana ilo mno e i dziele oraz dodawa i odejmowa s rz du ½n
3
, a wi c nieco
wi cej ni w metodzie Gaussa, przewaga metody Jordana polega na nieco mniejszej zaj to ci pami ci.
Obie powy ej opisane metody mo na zastosowa do rozwi zywania układów równa o wi kszej liczbie „prawych
stron”. W wielu przypadkach mamy do czynienia z zagadnieniami, w których macierz współczynników wynika z
charakteru równa opisuj cych modelowane zjawisko, natomiast posta prawej strony układu równa wynika np. z
warunków brzegowych. Cz sto mo emy spotka si z sytuacj gdy b dziemy chcieli rozwi za kilka (lub nawet wiele)
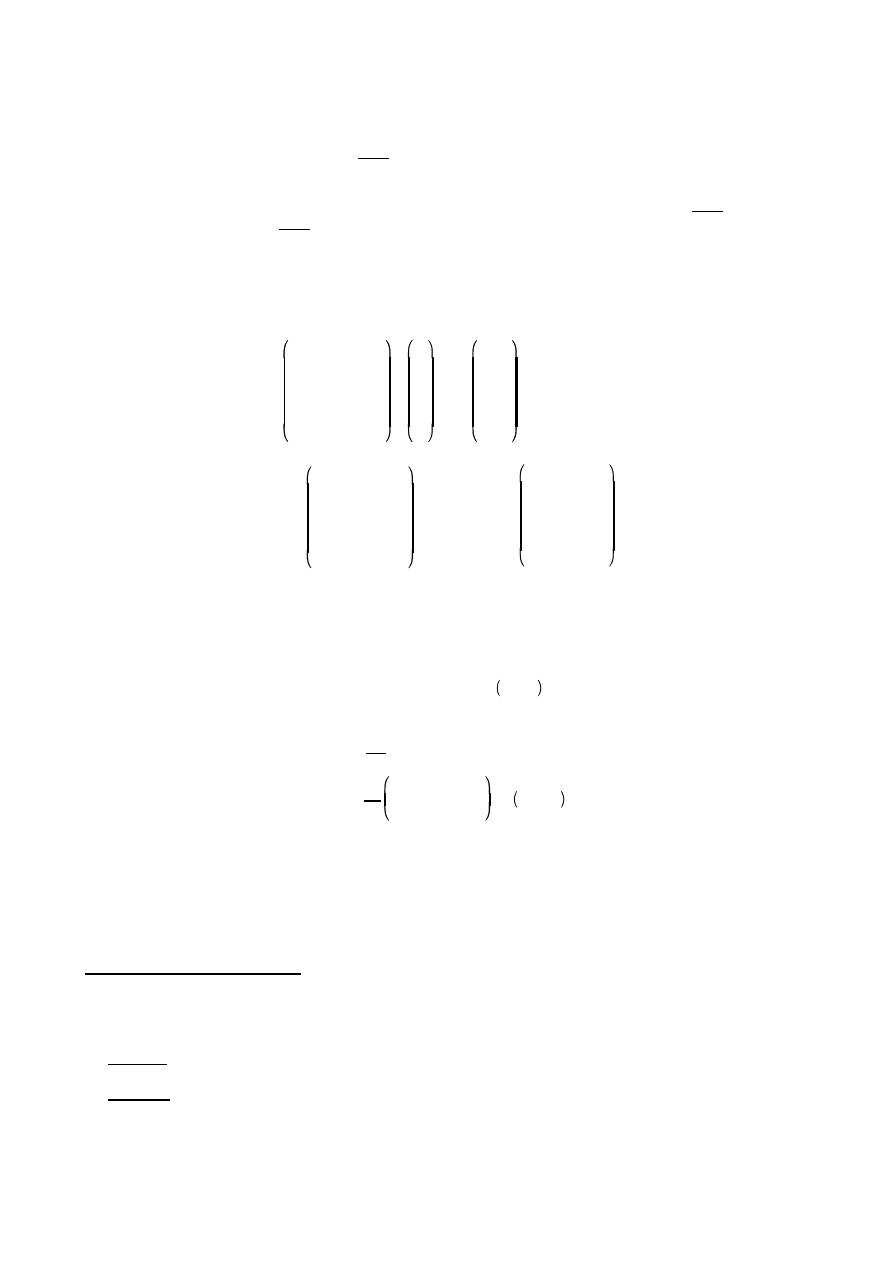
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
6
1
Rzeczywista symetryczna macierz A (n×n) jest dodatnio okre lona je li istnieje rzeczywista,
nieosobliwa macierz M taka, e
. Albo: je li dla ka dego wektora x zachodzi
. Albo:
A
MM
T
x
T
Ax
0
wszystkie wyznaczniki postaci
, dla i od 1 do n, s dodatnie (jest to tzw. kryterium Sylwestra).
a
11
a
ii
Wszystkie warto ci własne macierzy dodatnio okre lonej s dodatnie.
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
układów równa ró ni cych si mi dzy sob tylko prawymi stronami. W takim przypadku nasza macierz b dzie mie
odpowiednio wi ksz liczb kolumn (po prawej stronie dopiszemy wszystkie „dodatkowe” prawe strony) — natomiast
sam algorytm nie zmieni si . Oczywi cie równoczesne rozwi zywanie kilku układów równa daje wyra n
oszcz dno czasu w stosunku do rozwi zywania ka dego zagadnienia osobno (jest jednak mo liwe tylko w przypadku
układów równa ró ni cych si tylko prawymi stronami).
Metoda Cholesky'ego (Banachiewicza)
Rozwa my znowu układ równa (zakładamy, e macierz współczynników jest symetryczna i dodatnio okre lona
1
).
Je li metod t mo na zastosowa to jest około 2 razy szybsza od opisanych wcze niej.
a
11
a
12
a
1n
a
21
a
22
a
2n
a
n1
a
n2
a
nn
x
1
x
2
x
n
a
1,n 1
a
2,n 1
a
n,n 1
Ax
w
i przekształcimy macierz
A do postaci BC, gdzie:
B
b
11
0
0
b
21
b
22
0
b
n1
b
n2
b
nn
i
C
1 c
12
c
1n
0 1
c
2n
0 0
1
Dzi ki czemu mamy:
Ax
w
A
BC
BCx
w
Cx
y
By
w
Elementy macierzy
B i C obliczane s nast puj co:
b
i1
a
i1
b
ji
a
ji
i 1
k 1
b
jk
c
ki
i j>1
oraz:
c
1j
a
1j
b
11
c
ij
1
b
ii
a
ij
i 1
k 1
b
ik
c
kj
1<i<j
Obliczenia prowadzimy naprzemiennie wierszami i kolumnami: najpierw kolumna 1-sza macierzy
B, po niej 1-szy
wiersz macierzy
C; nast pnie 2-ga kolumna macierzy B i po niej 2-gi wiersz macierzy C itd.
Maj c dane macierze
B i C mo emy znale poszukiwany wektor rozwi za x — rozwi zuj c kolejno dwa
równania:
B y = w i C x = y
Poniewa obie macierze (
B i C ) s trójk tne rozwi zanie znajduje si nast puj co:
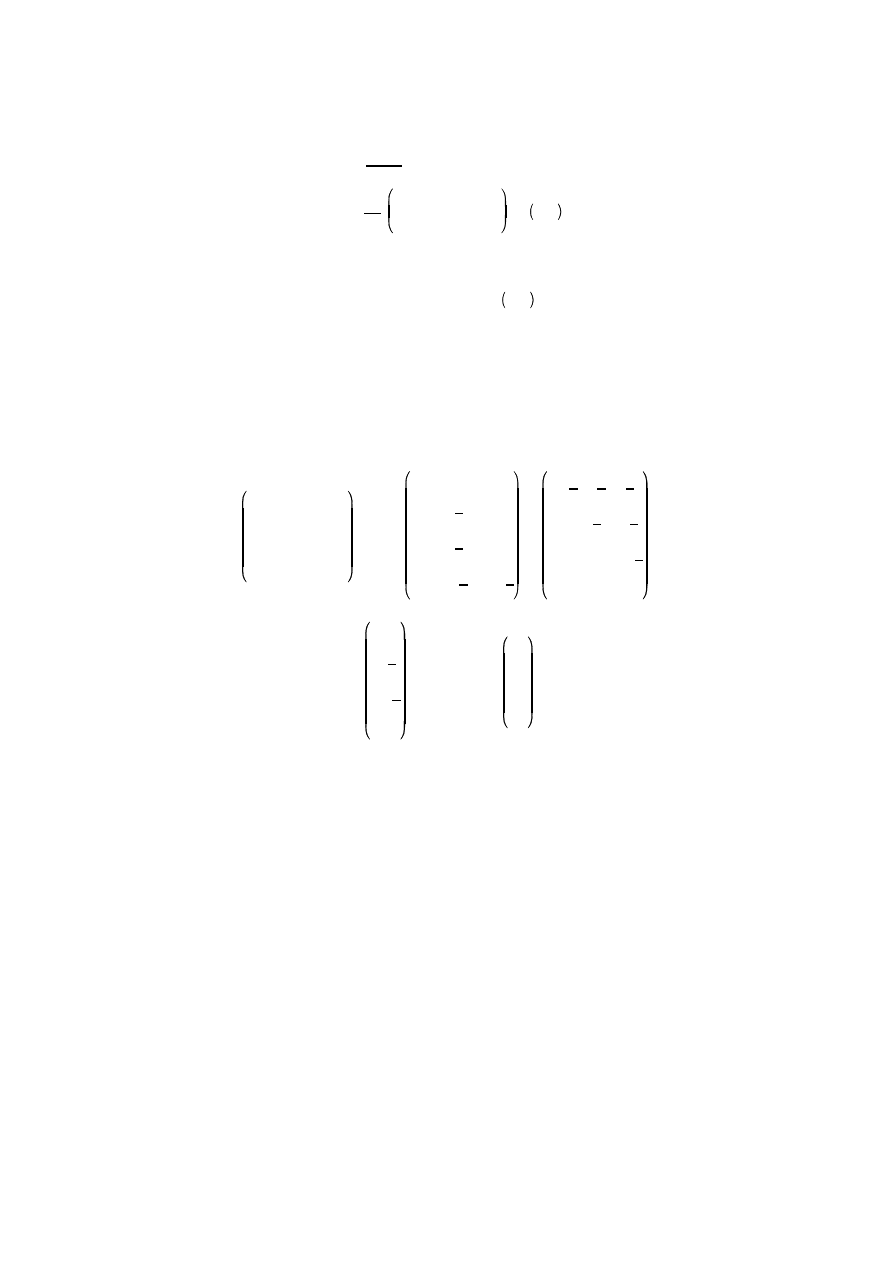
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
7
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
y
1
a
1,n 1
b
11
y
i
1
b
ii
a
i,n 1
i 1
k 1
b
ik
y
k
i >j
a potem:
x
n
y
n
x
i
y
i
n
k i 1
c
ik
x
k
i<n
Dla przykładu metod t zastosujemy do nast puj cego układu równa :
3x
1
x
2
x
3
2x
4
6
5x
1
x
2
3x
3
4x
4
12
2x
1
x
3
x
4
1
x
1
5x
2
3x
3
3x
4
3
macierze
B i C s postaci:
3
1
1 2
5 1
3
4
2
0
1
1
1
5 3
3
3
0
0 0
5 2
2
3
0 0
2
2
3
2 0
1
5
1
3
6 2
1
2
1
1
3
1
3
2
3
0 1
1
2
1
4
0 0 1
1
1
4
0 0 0
1
ostatecznie obliczamy wektory
y i x (strzałki odpowiadaj kolejno ci oblicze ):
y
2
3
4
1
3
4
3
;
x
1
1
2
3
Metoda przemiatania
Metoda ta ma zastosowanie do rozwi zywania układów równa , których współczynniki tworz macierz
trójdiagonaln (tzn. maj c elementy niezerowe tylko na trzech rodkowych przek tnych). Znana jest równie pod
nazw the sweep method albo
.
b
1
x
1
c
1
x
2
d
1
a
2
x
1
b
2
x
2
c
2
x
3
d
2
a
3
x
2
b
3
x
3
c
3
x
4
d
3
a
i
x
i 1
b
i
x
i
c
i
x
i 1
d
i
a
n 1
x
n 2
b
n 1
x
n 1
c
n 1
x
n
d
n 1
a
n
x
n 1
b
n
x
n
d
n
Rozwi zanie takiego układu równa przeprowadza si w dwóch etapach. W etapie pierwszym oblicza si kolejno
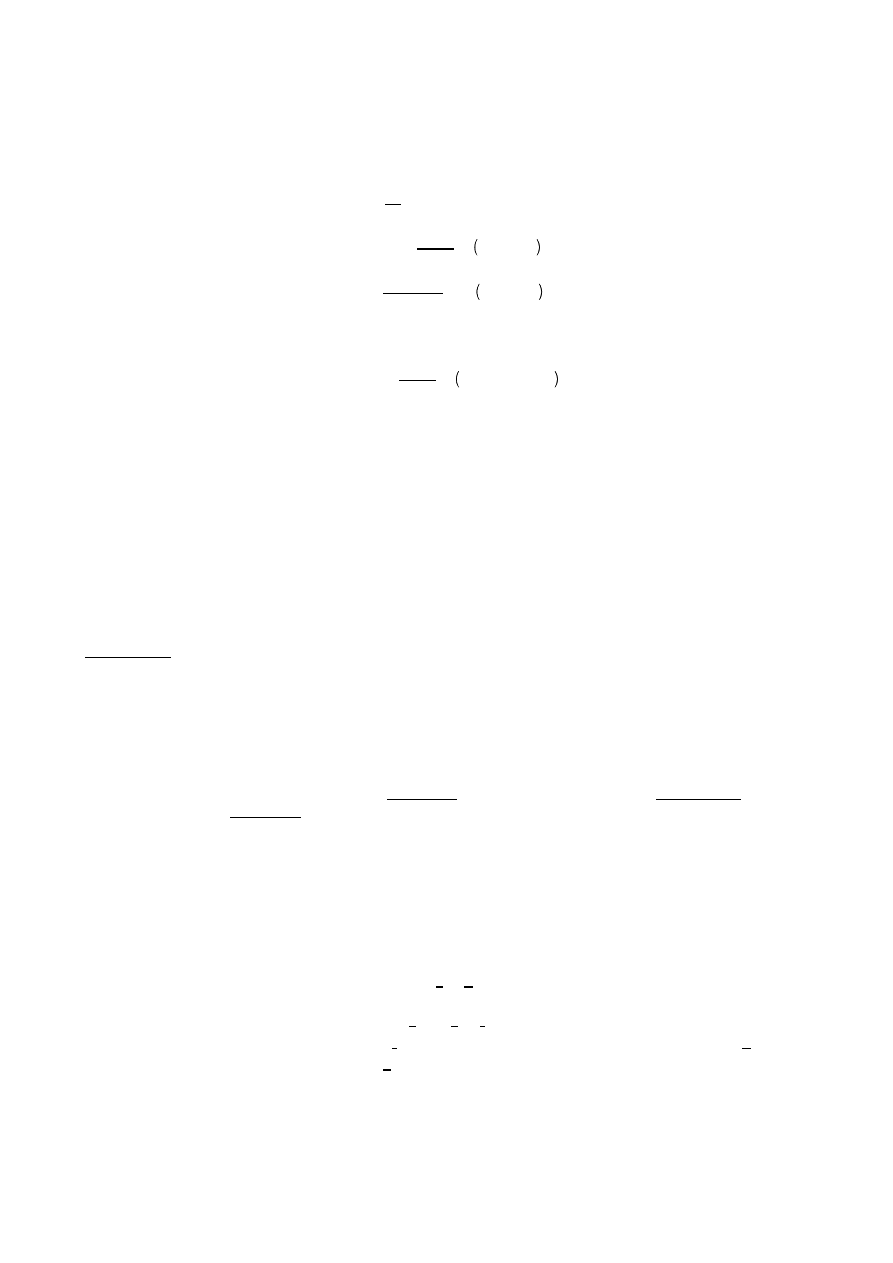
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
8
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
współczynniki i :
1
b
1
1
d
1
1
i
b
i
a
i
c
i 1
i 1
i 2,3, ,n
i
d
i
a
i i 1
i
i 2,3, ,n
a w drugim na ich podstawie znajduje si rozwi zania:
x
n
n
x
i
i
c
i
x
i 1
i
i n 1,n 2, ,1
Jest to metoda bardzo szybka, za macierze trójdiagonalne na szcz cie do cz sto wyst puj w zagadnieniach
oblicze numerycznych (zwłaszcza podczas rozwi zywania układów równa ró niczkowych cz stkowych metod
ró nic sko czonych).
Poniewa współczynniki
i
s obliczane jako sumy (ró nice), a nast pnie pojawiaj si w mianowniku wzoru na
kolejny współczynnik
i
nale y liczy si z mo liwo ci wyst pienia dzielenia przez warto blisk zeru (albo nawet
przez zero) — mogłoby to uniemo liwi obliczenia. Sytuacja taka na pewno nie wyst pi je li macierz współczynników
równania jest diagonalnie dominuj ca (tzn. moduł warto ci diagonalnej jest wi kszy lub równy od sumy modułów obu
pozostałych współczynników).
Metody przybli one — iteracyjne
Metody iteracyjne okre lane s jako przybli one z tego wzgl du, e daj rozwi zanie dokładne dopiero po
niesko czonej liczbie kroków — kolejne wyniki s coraz dokładniejszymi przybli eniami „prawdziwego” rozwi zania.
S one wła ciwie jedynymi metodami skutecznymi w przypadku układów równa nieliniowych (podobnie jak w
przypadku nieliniowych funkcji jednej zmiennej). Mo na jednak stosowa je tak e do układów równa liniowych.
Metody iteracyjne maj pewn przewag nad metodami dokładnymi — polega ona na tym, e nie trzeba
przejmowa si przenoszeniem bł dów pomi dzy kolejnymi iteracjami. W przypadku metod dokładnych bł dy obci cia
popełnione w dowolnym momencie kumuluj si i mog nawet bardzo znacznie zniekształci ostateczne rozwi zanie.
Tymczasem w metodach iteracyjnych, nawet gdy kolejne przybli enia s obarczone dodatkowo bł dami wynikaj cym z
bł dów obci cia itp., to s one traktowane jako kolejne podstawy do wyznaczenia nast pnego, dokładniejszego
przybli enia. Z tego powodu mówimy, e metody przybli one (iteracyjne) mo na stosowa do udokładniania wyników
otrzymanych metodami dokładnymi.
Układy równa liniowych
Metoda iteracyjna (prosta)
Mo na powiedzie , e metoda ta jest adaptacj metody iteracyjnej przedstawionej ju wcze niej dla równa jednej
zmiennej. Załó my, e układ równa :
A x
b
mo e zosta przekształcony do postaci:
x
C x
f
gdzie
C jest pewn , nieznan jeszcze, macierz , a jest przekształconym wektorem prawych stron prawych (w
f
b
szczególno ci mo e to by niezmieniony wektor — zale nie od przekształce które zastosowano aby przej od
A do
b
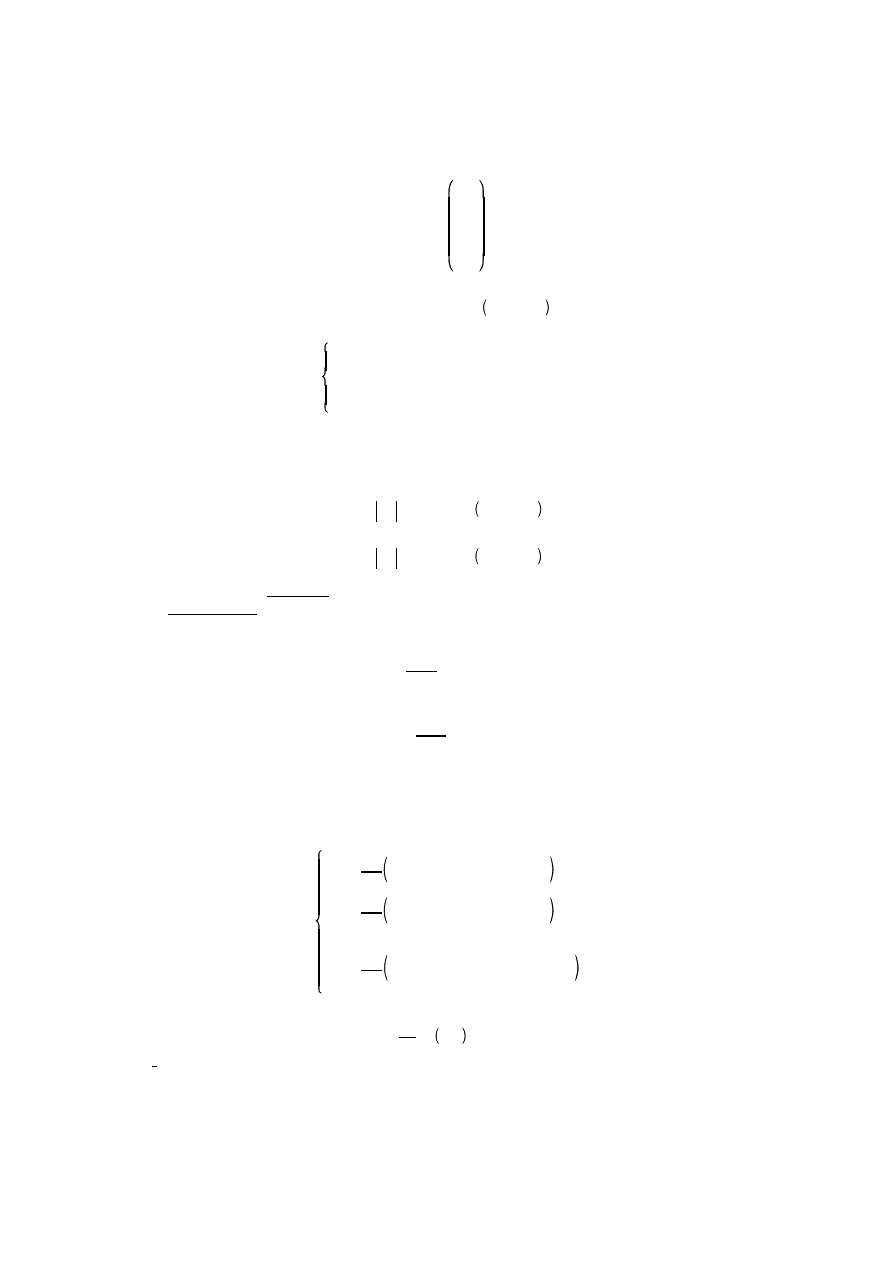
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
9
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
C).
Wychodz c od dowolnie wybranego wektora:
x
(0)
x
(0)
1
x
(0)
2
x
(0)
n
mo na okre li proces iteracyjny:
x
(i 1)
Cx
(i )
f
i 0,1,2,
czyli:
x
(i 1)
1
c
11
x
(i )
1
c
12
x
(i )
2
c
1n
x
(i )
n
f
1
x
(i 1)
n
c
n1
x
(i )
1
c
n2
x
(i )
2
c
nn
x
(i )
n
f
n
Przeprowadzaj c kolejne iteracje otrzymamy ci g wektorów x
(i)
, który powinien by zbie ny do rozwi zania
dokładnego.
Warunkiem zbie no ci tego ci gu jest spełnienie jednego z nast puj cych warunków:
n
j 1
c
ij
< 1
i 1,2, ,n
lub:
n
i 1
c
ij
< 1
j 1,2, ,n
Nale y zwróci uwag , e spełnienie którego z wymienionych warunków gwarantuje zbie no , natomiast jego
niespełnienie nie gwarantuje braku zbie no ci.
W przypadku spełnienia którego z tych warunków mo liwe jest te wyznaczenie bł du jakim obarczone jest k-te
przybli enie rozwi zania:
x
i
x
(k)
i
1
max
j 1,2, ,n
x
(k)
j
x
(k 1)
j
lub:
x
i
x
(k)
i
1
n
j 1
x
(k)
j
x
(k 1)
j
Problem mo e stanowi znalezienie odpowiedniej macierzy
C (spełniaj cej warunki zbie no ci metody).
Najcz ciej stosuje si jeden z dwóch sposobów:
1) Je li diagonalne elementy macierzy s niezerowe to układ równa mo na przepisa w postaci:
x
1
1
a
11
b
1
a
12
x
2
a
13
x
3
a
1n
x
n
x
2
1
a
22
b
2
a
21
x
1
a
23
x
3
a
2n
x
n
x
n
1
a
nn
b
n
a
n1
x
1
a
n2
x
2
a
n,n 1
x
n 1
w tym przypadku elementy macierzy
C okre la si nast puj co:
c
ij
a
ij
a
ii
i j
c
ii
0
a wektora :
f
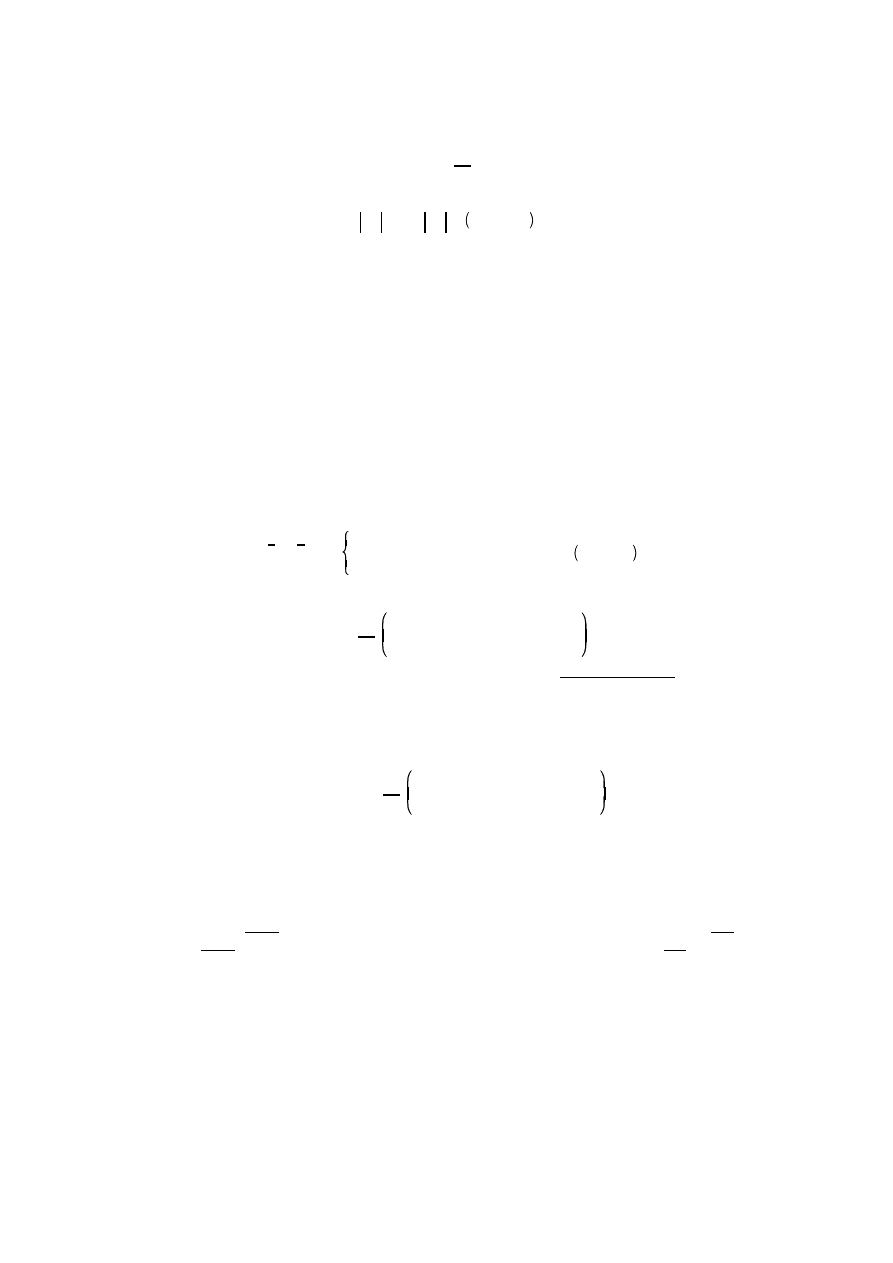
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
10
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
f
i
b
i
a
ii
Warunki zbie no ci b d wówczas spełnione je li zachodzi:
a
ii
>
i j
a
ij
i 1,2, ,n
Jest to tzw. macierz z dominuj c przek tn .
2) Druga metoda ma zastosowanie gdy elementy na przek tnej macierzy współczynników równania s bliskie jedno ci,
a wszystkie pozostałe s znacznie od jedno ci mniejsze. Wówczas równania przekształcamy przenosz c x
i
na lew
stron , a po prawej pozostawiaj c wszystkie (wł cznie z wyci gni t na lewo zmienn x
i
ze współczynnikiem
zmniejszonym o 1) zmienne i wyrazy wolne. Taki układ ju bez dalszych przekształce jest wykorzystywany do
iteracji. Warunki zbie no ci s w takim przypadku z reguły spełnione.
Metoda Seidel'a (Gaussa-Seidel'a)
Jest to pewna modyfikacja prostej metody iteracyjnej. Polega ona na tym, e do obliczania kolejnego przybli enia
wykorzystuje si „najnowsze” dost pne warto ci zmiennych. Np. do obliczenia (k+1)-go przybli enia zmiennej x
i
wykorzystuje si wszystkie nowoobliczone warto ci zmiennych: x
1
(k+1)
, x
2
(k+1)
, ..., x
i–1
(k+1)
oraz „starsze” warto ci
nast pnych zmiennych: x
i
(k)
, ..., x
n
(k)
. Inaczej mówi c zakłada si , e układ równa jest spełniony przez taki wła nie
wektor zawieraj cy„mieszanin ” dwóch kolejnych przybli e rozwi zania:
A x
b
i
j i
a
ij
x
(k 1)
j
N
j i 1
a
ij
x
(k)
j
b
i
i 1, ,N
Oczywi cie dopóki nie osi gniemy „docelowego” wektora b d cego rozwi zaniem dokładnym równo po prawej
stronie zapisanego powy ej równania nie jest spełniona. Powy sze równanie mo na przekształci do postaci:
x
(k 1)
i
1
a
ii
b
i
i 1
j 1
a
ij
x
(k 1)
j
N
j i 1
a
ij
x
(k)
j
Stosuj c t metod uzyskuje si szybsz zbie no ni w metodzie prostej (chocia nie zawsze), a dodatkow
korzy ci jest mo liwo posługiwania si tylko jedn macierz , w której nowoobliczone elementy natychmiast
zast puj stare — daje to oszcz dno pami ci.
Zapisany powy ej wzór mo na przepisa nieco inaczej — w nawiasie mo emy doda i odj składnik
—
a
ii
x
(k)
i
dostaniemy wówczas nieco inny wzór iteracyjny na
:
x
(k 1)
i
x
(k 1)
i
x
(k)
i
1
a
ii
b
i
i 1
j 1
a
ij
x
(k 1)
j
N
j i
a
ij
x
(k)
j
którego drugi składnik mo na traktowa jak poprawk dla kolejnej obliczanej warto ci.
Metod t mo na znacznie krócej zapisa w notacji macierzowej. Zakładamy, e macierz
A mo na zapisa w
postaci sumy trzech macierzy:
A = L + D + U
gdzie
D jest macierz diagonaln , której jedynymi elementami niezerowymi s elementy macierzy A le ce na jej
głównej przek tnej,
L jest doln macierz trójk tn zawieraj c elementy macierzy A le ce wył cznie pod jej główn
przek tn , a
U jest górn macierz trójk tn zawieraj c elementy macierzy A le ce wył cznie nad jej główn
przek tn . Je eli teraz nast puj co zdefiniujemy macierz
B oraz wektor c :
B = –(L+D)
–1
U oraz c = (L+D)
–1
b
to przedstawiony algorytm mo na zapisa w takiej postaci:
x
(i+1)
=
Bx
(i)
+
c
Metoda „nadrelaskacji”
Z przedstawionym powy ej przekształceniem wi e si kolejna metoda, zwana „nadrelaksacj ” (over-relaxation) —
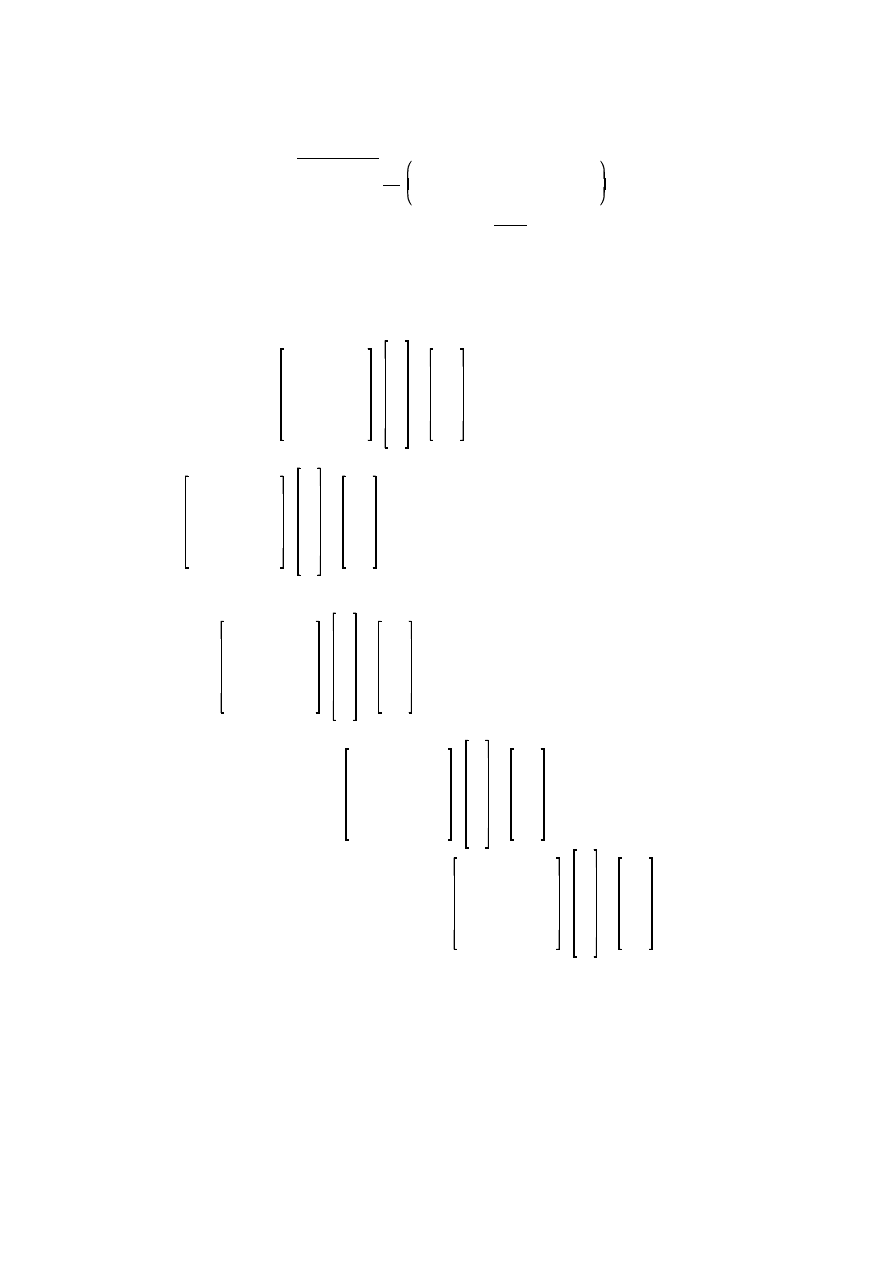
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
11
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
wyznaczon poprzednio poprawk powi kszamy o jaki czynnik :
x
(k 1)
i
x
(k)
i
a
ii
b
i
i 1
j 1
a
ij
x
(k 1)
j
N
j i
a
ij
x
(k)
j
Zmiana ta, wydawałoby si niczym nie uzasadniona, powoduje (mo e powodowa ) kolejne przyspieszenie
zbie no ci oraz wi ksz „odporno ” na złe uwarunkowanie macierzy współczynników układu równa .
Przykłady
Dla przykładu rozwi emy kilka prostych układów równa . Wszystkie one maj rozwi zania dokładne postaci:
, które mo na oczywi cie bez problemu znale innymi metodami, ale tu posłu y nam
x
1
1 ; x
2
2 ; x
3
3 ; x
4
4
jako dobra ilustracja.
Pierwszy układ ma posta :
— jak wida jest to układ z dominuj c główn
9 1
1 2
1 8 3 2
2 1
8 3
3 2
1 7
x
1
x
2
x
3
x
4
16
32
12
26
przek tn .
W drugim:
— zmieniony został ostatni wiersz — nie mamy ju dominacji
9 1
1 2
1 8
3
2
1 1
8 3
3 2
11 7
x
1
x
2
x
3
x
4
16
32
11
4
głównej przek tnej.
Układ trzeci jest analogiczny jak drugi, z t tylko ró nic , e brak dominacji głównej przek tnej wynika z postaci
pierwszego wiersza:
.
9 1
1 12
1 8 3
2
2 1
8 3
3 2
1 7
x
1
x
2
x
3
x
4
56
32
12
26
Układ czwarty stanowi poł czenie zmian wprowadzonych w układach drugim i trzecim:
.
9 1
1 12
1 8
3
2
2 1
8 3
3 2
11 7
x
1
x
2
x
3
x
4
56
32
12
4
W układzie pi tym dodatkowo zmieniono wiersz drugi:
.
9 1
1 12
1 8 13
2
2 1
8 3
3 2
11 7
x
1
x
2
x
3
x
4
56
62
12
4
I w ko cu w układzie szóstym adna z warto ci z głównej przek tnej nie jest dominuj ca w swoim wierszu (jest to
wi c układ najgorszy z punktu widzenia mo liwo ci rozwi zania iteracyjnego):
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
12
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
.
9
1
1 12
1 8
13
2
2 11
8 3
3 2
11 7
x
1
x
2
x
3
x
4
56
62
8
4
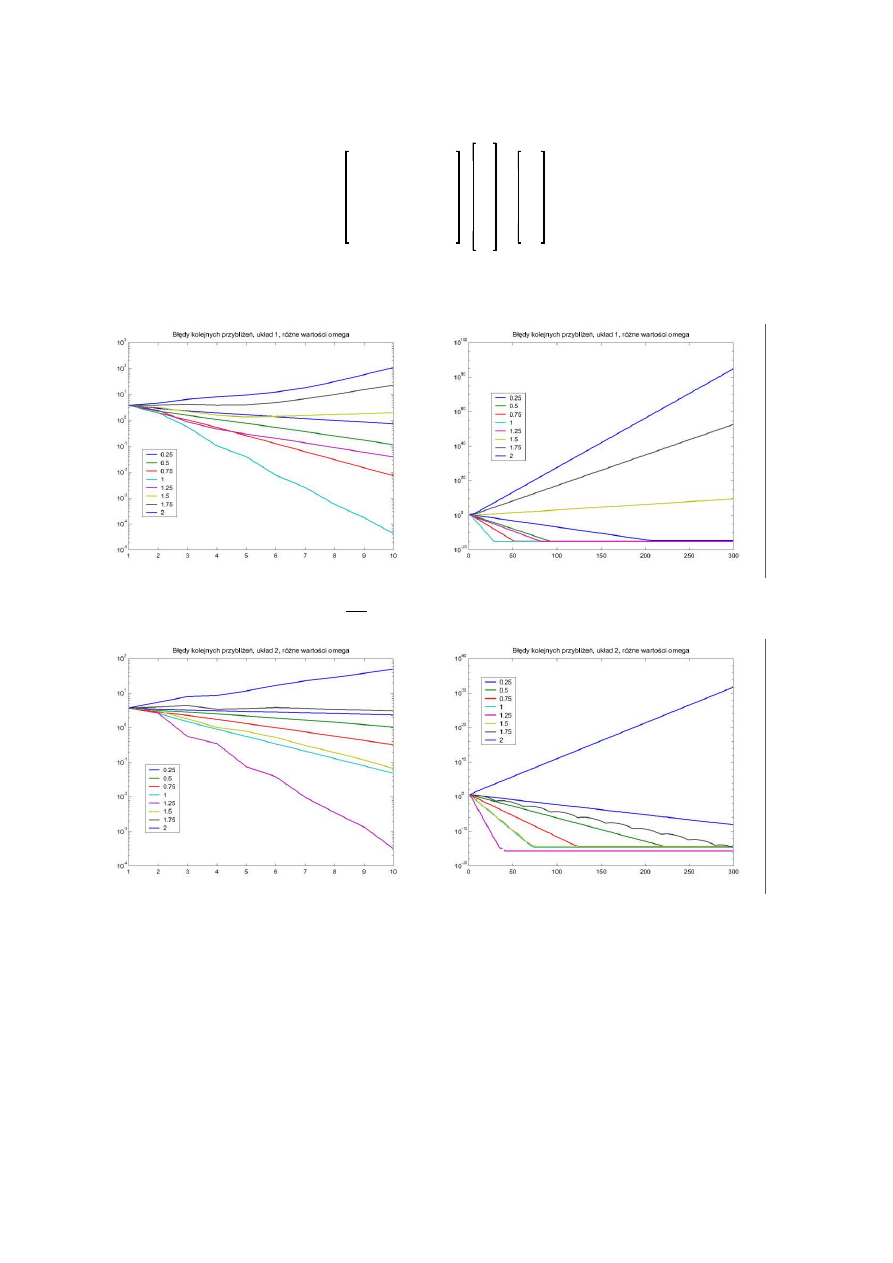
Bł dy rozwi zania (wektor czteroelementowy) obliczone jako norm ró nicy wektorów — aktualnego przybli enia i
rozwi zania dokładnego. Dla ka dego układu przedstawione b d dwa wykresy — pocz tkowe 10 oraz 300 ietracji.
Układ pierwszy:
Wida , e poczynaj c od warto ci ok. 1.5 metoda nadrelaksacji nie działa (wyniki „rozbiegaj si ”), najszybsza
zbie no wsyt puje jednak dla =1 (czyli bez nadrelaksacji).
Układ drugi:
Tym razem widzimy, e najszybsz zbie no otrzymujemy dla =1.25 (chocia warto 1 jest niewiele gorsza).
Metoda jest rozbie na tylko dla jednej (spo ród badanych) warto ci .
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
13
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
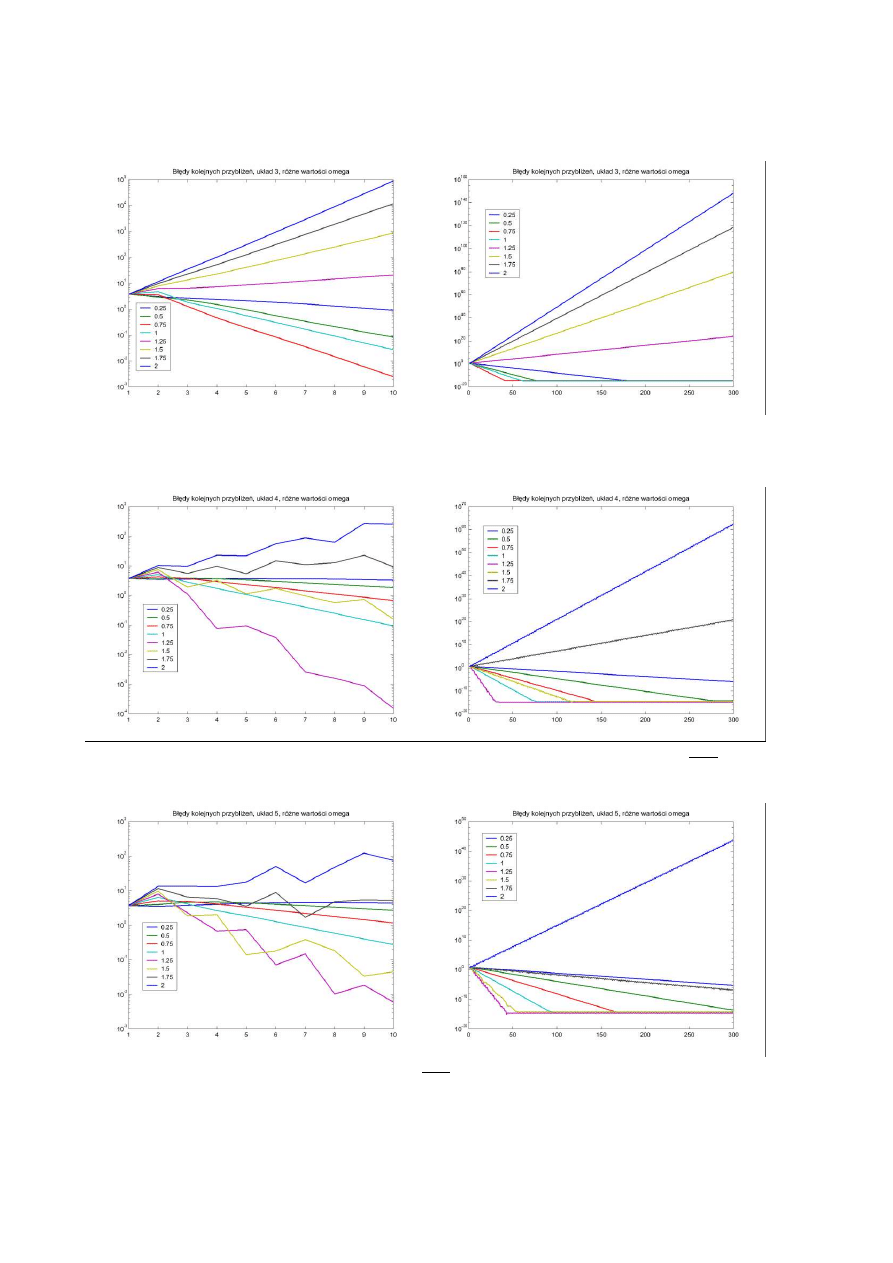
Układ trzeci:
W przypadku układu trzeciego =1 nadal jest „na drugim miejscu”, jednak najlepsz zbie no uzyskujemy
dla warto ci mniejszej od 1 — =0.75. Metoda jest zbie na tylko dla
1 (spo ród badanych warto ci).
Układ czwarty:
W układzie czwartym ju w dwóch wierszach maksymalne warto ci współczynników wyst puj poza główn
przek tn , jednak metoda nadal działa (jest rozbie na tylko dla dwóch maksymalnych badanych warto ci ).
Układ pi ty:
W układzie pi tym maksymalne warto ci wyst puj poza główn przek tn w trzech wierszach, nadal jednak
uzyskujemy zbie no dla wszystkich (poza jedn ) badanych warto ci .
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
14
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
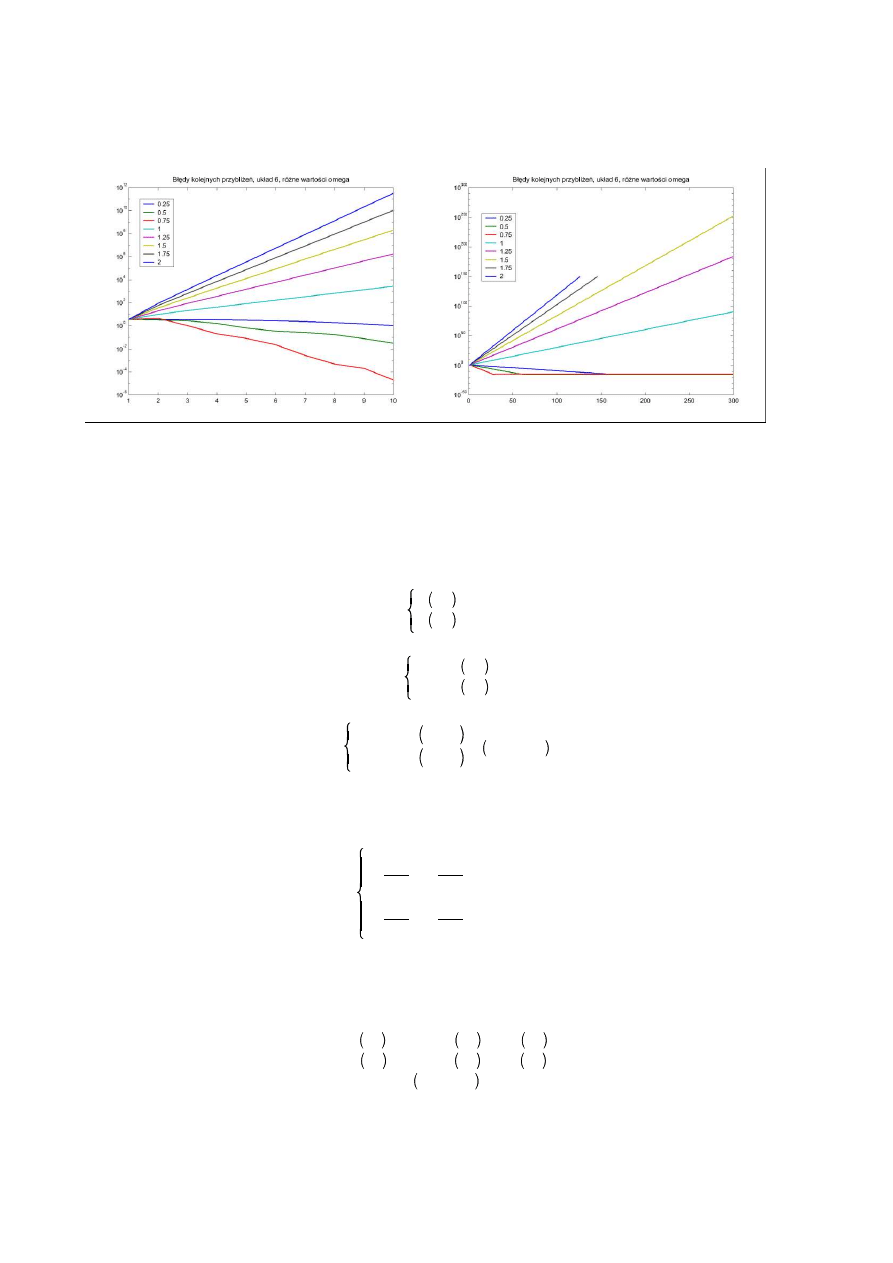
Układ szósty:
W układzie szóstym w ogóle nie mo na ju mówi o dominacji głównej przek tnej. Metoda jest rozbie na dla
wi kszo ci badanych warto ci , ale dla warto ci mniejszych od 1 nadal jest zbie na.
Układy równa nieliniowych
Metoda iteracyjna
Załó my, e mamy układ dwóch równa nieliniowych:
f
1
x,y
0
f
2
x,y
0
musimy przekształci go do postaci:
x
F
1
x,y
y
F
2
x,y
wybrawszy jakie warto ci x
0
i y
0
mo na posłu y si wzorami iteracyjnymi:
x
i 1
F
1
x
i
,y
i
y
i 1
F
2
x
i
,y
i
i 1,2,3,
Je li spełnione s warunki:
a) funkcje F
1
i F
2
maj ci głe pochodne w pewnym obszarze R,
b) przybli enia pocz tkowe (x
0
i y
0
) oraz wszystkie kolejne le w tym e obszarze R,
c) w całym obszarze R spełnione s nierówno ci:
F
1
x
F
2
x
q
1
< 1
F
1
y
F
2
y
q
2
< 1
to kolejne przybli enia zbiegaj si do rozwi za układu.
Osobnym problemem jest sposób znalezienia funkcji F
1
i F
2
. Jeden z mo liwych sposobów jest nast puj cy
(niestety — dla układu dwóch równa ):
Funkcje F
1
i F
2
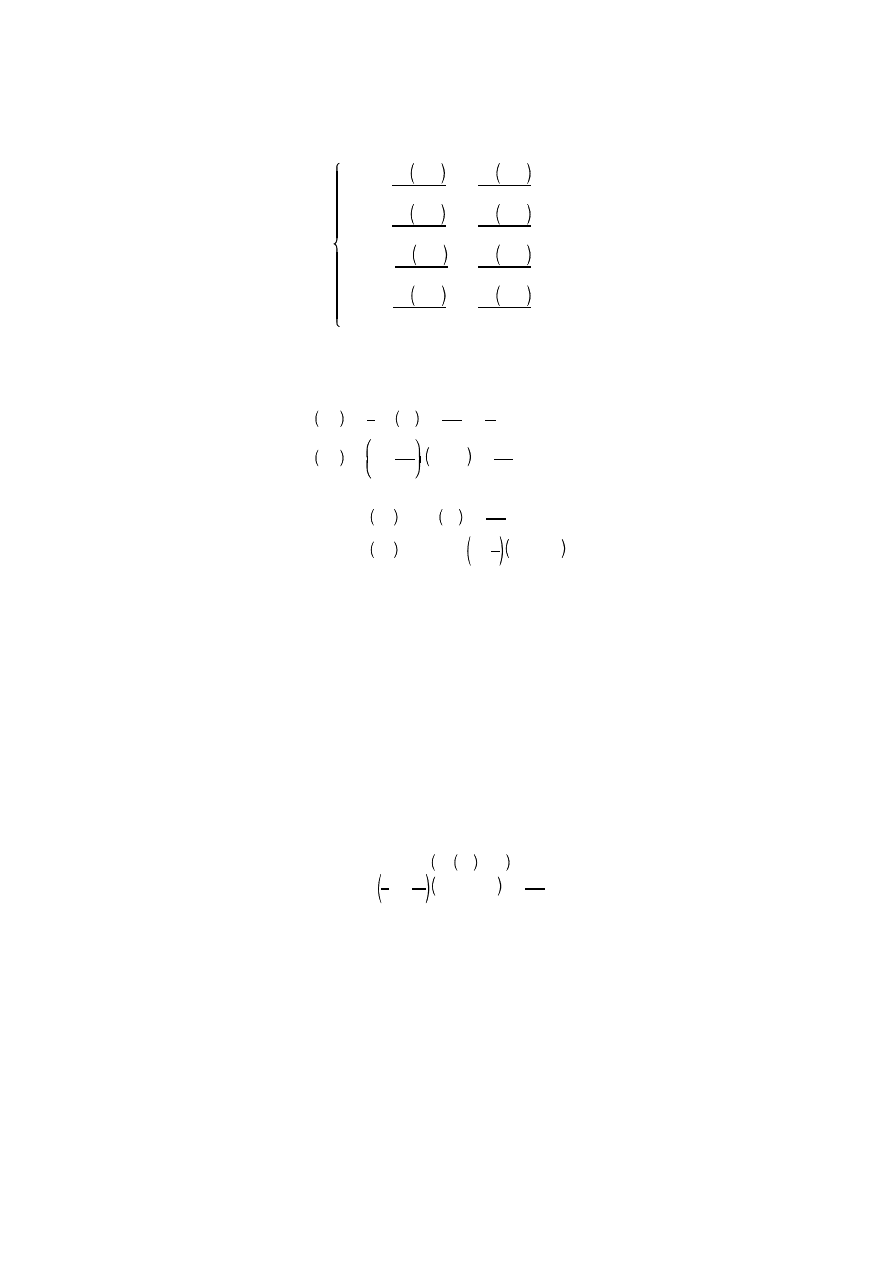
maj posta :
F
1
x,y
x
f
1
x,y
f
2
x,y
F
2
x,y
y
f
1
x,y
f
2
x,y
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
15
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
gdzie współczynniki , , i stanowi przybli one rozwi zania nast puj cego układu równa :
1
f
1
x
0
,y
0
x
f
2
x
0
,y
0
x
0
f
1
x
0
,y
0
y
f
2
x
0
,y
0
y
0
f
1
x
0
,y
0
x
f
2
x
0
,y
0
x
0
1
f
1
x
0
,y
0
y
f
2
x
0
,y
0
y
0
Je li tylko pochodne cz stkowe f
1
i f
2
nie zmieniaj si zbyt szybko w otoczeniu punktu (x
0
,y
0
) to warunki zbie no ci
b d spełnione.
Przykład. Rozwa my układ równa :
f
1
x,y
1
2
sin xy
y
4
x
2
0
f
2
x,y
1
1
4
e
2x
e
ey
2ex
0
Przepiszmy je w postaci wła ciwej dla oblicze iteracyjnych:
x
F
1
x,y
sin xy
y
2
y
F
2
x,y
2 x
1
4
e
2x 1
1
Je li wybierzemy nast puj ce warto ci pocz tkowe: x
0
= 0.4 i y
0
= 3.0 to otrzymamy nast puj cy ci g rozwi za :
x
i
:
0.455 0.498 0.505 0.499 0.499 0.500
y
i
:
3.037 3.107 3.141 3.144 3.142 3.142
Je li posłu ymy si metod Gaussa-Seidel'a (tzn. w ka dym obliczeniu b dziemy wykorzystywa najnowsze
dost pne warto ci) to przy tych samych warto ciach wyj ciowych otrzymamy taki ci g rozwi za (gdy najpierw
obliczamy x, a potem obliczaj c y wykorzystujemy wła nie obliczon warto x):
x
i
:
0.455 0.493 0.500 0.500
y
i
:
3.107 3.138 3.142 3.142
Jak wida zbie no b dzie nieco szybsza. Mo emy te najpierw oblicza y i wykorzystywa jego warto do
obliczenia x:
x
i
:
0.454 0.493 0.500 0.500 0.500
y
i
:
3.037 3.107 3.138 3.142 3.142
Mo liwy jest te odwrotny wybór równa — tzn. z pierwszego z nich obliczamy y, a z drugiego x:
y
2 sin xy
x
x
1
2
1
8
e
2x 1
1
y
2
x
i
:
0.394 0.444 0.525 0.579 0.519 0.438 0.407 0.439 0.509
y
i
:
3.343 3.607 3.489 2.767 2.640 2.895 3.244 3.530 3.526
x
i
:
0.187 0.241 0.107 0.034 –0.181 –0.302 –0.097 –0.348 –0.159
y
i
:
3.343 2.497 2.044 0.688 –0.067 1.217 –0.359 0.831 0.396
x
i
:
0.394 –0.488 –0.790 0.062 –0.042 –0.827 –0.386 0.445
y
i
:
–2.513 –2.476 3.066 4.967 –3.280 0.262 5.193 2.428
Przebieg oblicze dla obu przypadków ilustruj poni sze wykresy (w przypadku dolnego zamieniono kolejno
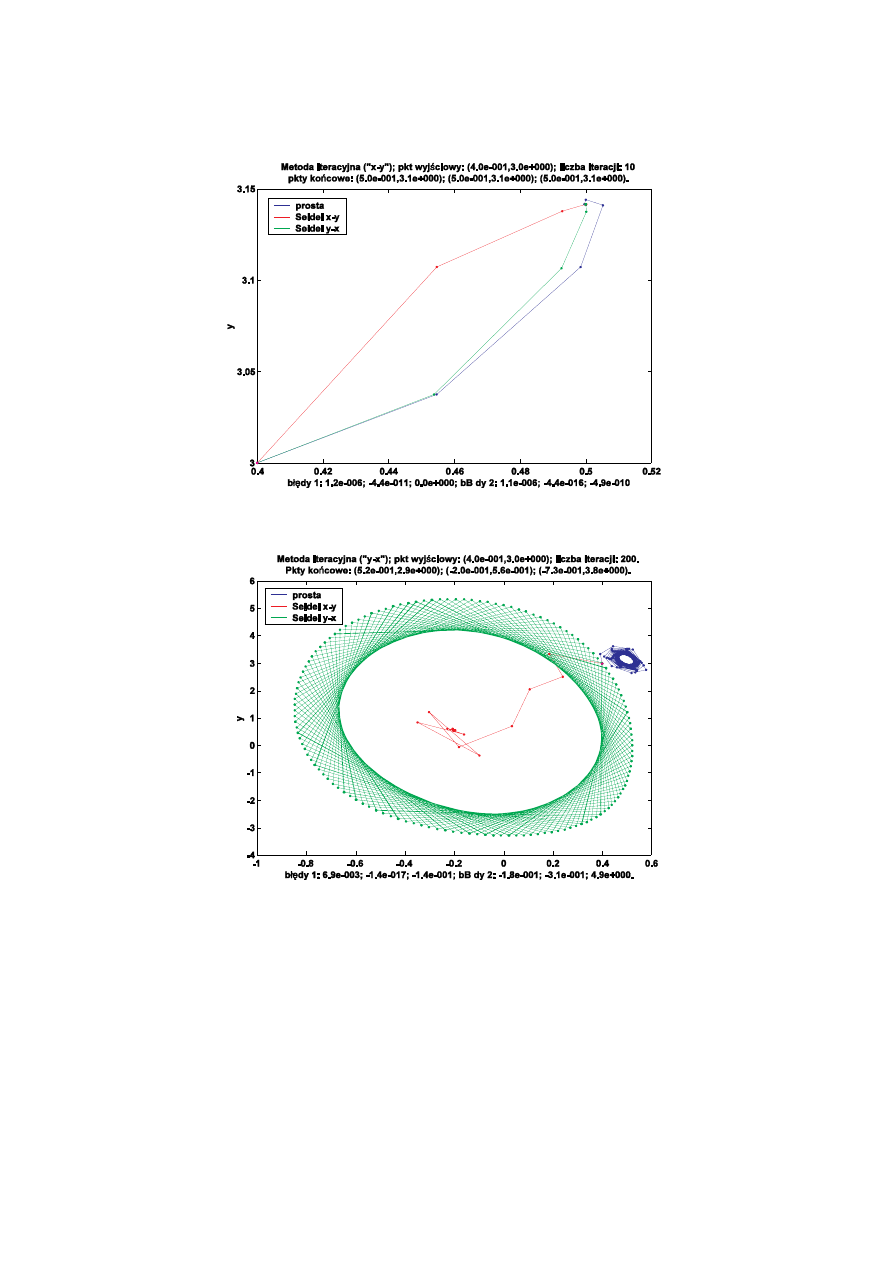
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
16
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
równa ):
Przebieg zbiegania si rozwi zania mo na równie analizowa obserwuj c zmiany normy kolejnych przybli e
rozwi zania:
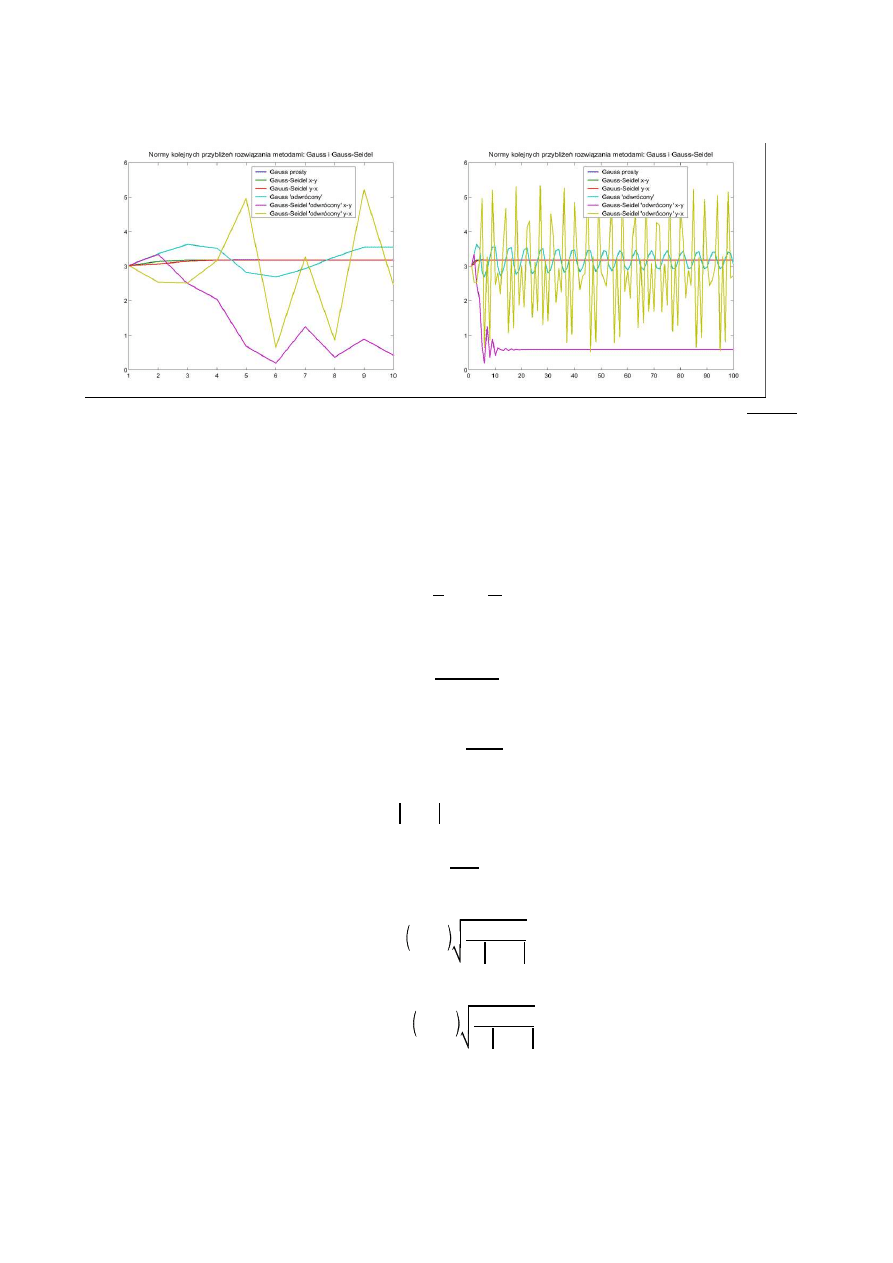
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
17
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
Linia pozioma na takim wykresie oznacza osi gni cie warto ci stabilnej — czyli znalezienie rozwi zania (jakiego
— niekoniecznie akurat tego, na którym na zale ało).
Przykład zastosowania prostej metody iteracyjnej
Dany jest układ poziomych rur, o znanych długo ciach i rednicach, poł czonych w n w złach. Dla niektórych
w złów znane jest ci nienie. Problem polega na znalezieniu ci nie we wszystkich nieznanych w złach oraz pr dko ci
przepływów (w m
3
/s) pomi dzy wszystkimi w złami (i ich kierunki).
Wiadomo, e spadek ci nienia w poziomej rurze jest dany wzorem:
p
1
2
f
M
u
2
L
D
gdzie f
M
jest tzw. współczynnikiem Moody'ego, jest g sto ci cieczy, u jest pr dko ci redni , a D i L s
odpowiednio rednic i długo ci rury. Wykorzystuj c obj to ciow pr dko przepływu Q mo na zapisa :
p
8f
M
Q
2
L
2
D
5
przy czym wszystkie stałe (niezale ne od konkretnej rury) mo na zebra razem (ozn. C ):
p
i
p
j
C
L
ij
Q
2
ij
D
5
ij
wówczas dla ka dej pary w złów otrzymamy równanie:
p
i
p
j
c
ij
Q
2
ij
gdzie:
c
ij
CL
ij
D
5
ij
ostatnie równanie mo na przekształci tak aby automatycznie miało prawidłowy znak:
Q
ij
p
i
p
j
1
c
ij
p
i
p
j
W ka dym w le, w którym nie okre lono ci nienia (np. o numerze j), suma przepływów pochodz cych z
wszystkich s siednich w złów musi wynosi zero:
i j
Q
ij
i j
p
i
p
j
1
c
ij
p
i
p
j
0
(j — w zeł badany, i — w zły s siednie) i te wła nie równania, zapisane dla wszystkich w złów o nieznanym ci nieniu
stanowi układ, który b dziemy rozwi zywa .
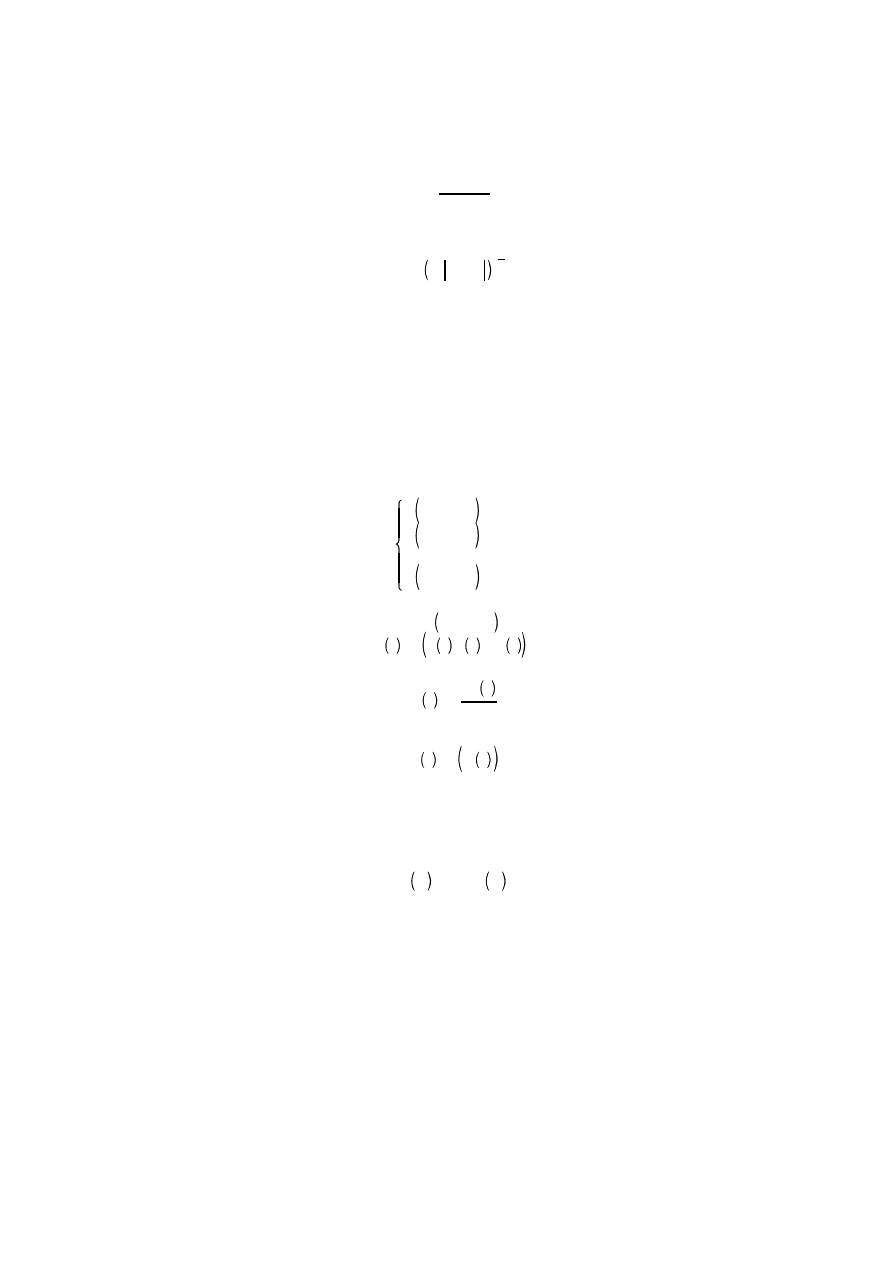
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
18
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
1
2
3
4
5
Wzór iteracyjny b dzie mie posta :
p
j
i j
a
ij
p
i
i j
a
ij
gdzie (dla skrócenia zapisu):
a
ij
c
ij
p
i
p
j
1
2
Dane do oblicze :
f
M
= 0.056
= 820 kg/m
3
p
1
= 3.8 atm
p
3
= 0
L
12
= L
23
= 45 m
L
14
= L
45
= L
25
= 30 m
D
12
= D
23
= 3"
D
14
= D
45
= D
25
= 4"
Metoda Newtona-Raphsona
Załó my, e dany jest nast puj cy układ równa nieliniowych:
f
1
x
1
,x
2
, ,x
n
0
f
2
x
1
,x
2
, ,x
n
0
f
n
x
1
,x
2
, ,x
n
0
Aby zapisa wzory w postaci macierzowej najpierw zdefiniujemy nast puj ce macierze:
x
1
,x
2
, ,x
n
f
f
1
,f
2
, ,f
n
Zdefiniujemy:
f
ij
f
i
x
j
i okre limy macierz pochodnych cz stkowych:
f
ij
dla: 1 i n, 1 j n.
Przy takim zapisie, zakładaj c e wybrali my wektor zawieraj cy pocz tkowe przybli enia wszystkich
niewiadomych (
0
= (x
1
0
,x
2
0
,...,x
n
0
)) mo emy zapisa wzór iteracyjny:
k 1
k
k
gdzie
k
jest rozwi zaniem nast puj cego układu równa algebraicznych:
k
k
f
k
gdzie k jest oczywi cie numerem iteracji.
Metoda ta ma pewn przewag nad poprzedni — warunek zbie no ci wymaga tylko aby składowe wektora
pochodnych były ci głe w otoczeniu pierwiastka ( jest oczywi cie wektorem), wyznacznik det( ( )) 0 oraz by
przybli enie pocz tkowe
0
było „dostatecznie” blisko pierwiastka .
Przykład. Rozpatrzymy znowu ten sam układ równa :
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
19
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
f
1
x,y
1
2
sin xy
y
4
x
2
0
f
2
x,y
1
1
4
e
2x
e
ey
2ex
0
Obliczymy odpowiednie pochodne:
f
1
x
1
2
y cos xy
2
f
1
y
1
4
x cos xy
2
f
2
x
2e
2
1
2
e
2x
f
2
y
e
Kolejne poprawki zmiennych x i y b dziemy oblicza rozwi zuj c układ równa :
f
1
x
x
k
,y
k
x
f
1
y
x
k
,y
k
y
f
1
x
k
,y
k
f
2
x
x
k
,y
k
x
f
2
y
x
k
,y
k
y
f
2
x
k
,y
k
(oczywi cie w ka dym przypadku chodzi o warto funkcji lub warto jej odpowiedniej pochodnej w punkcie
b d cym aktualnym przybli eniem rozwi zania).
Przy takich samych jak poprzednio (w metodzie iteracyjnej) danych pocz tkowych (tzn. 0.4 i 3) otrzymamy
nast puj cy ci g rozwi za :
x
i
:
–0.431 –0.243 –0.258 –0.261 –0.261
y
i
:
1.693 1.181 0.538 0.623 0.623
czyli inn par rozwi za . Jednak przyj cie warto ci pocz tkowych x
0
= 0.6 i y
0
= 3.0 prowadzi do rozwi za
uzyskanych poprzednio:
x
i
:
0.502 0.500 0.500 0.500 0.500 0.500 0.500 0.500
y
i
:
3.082 3.094 3.105 3.113 3.124 3.128 3.131 3.133
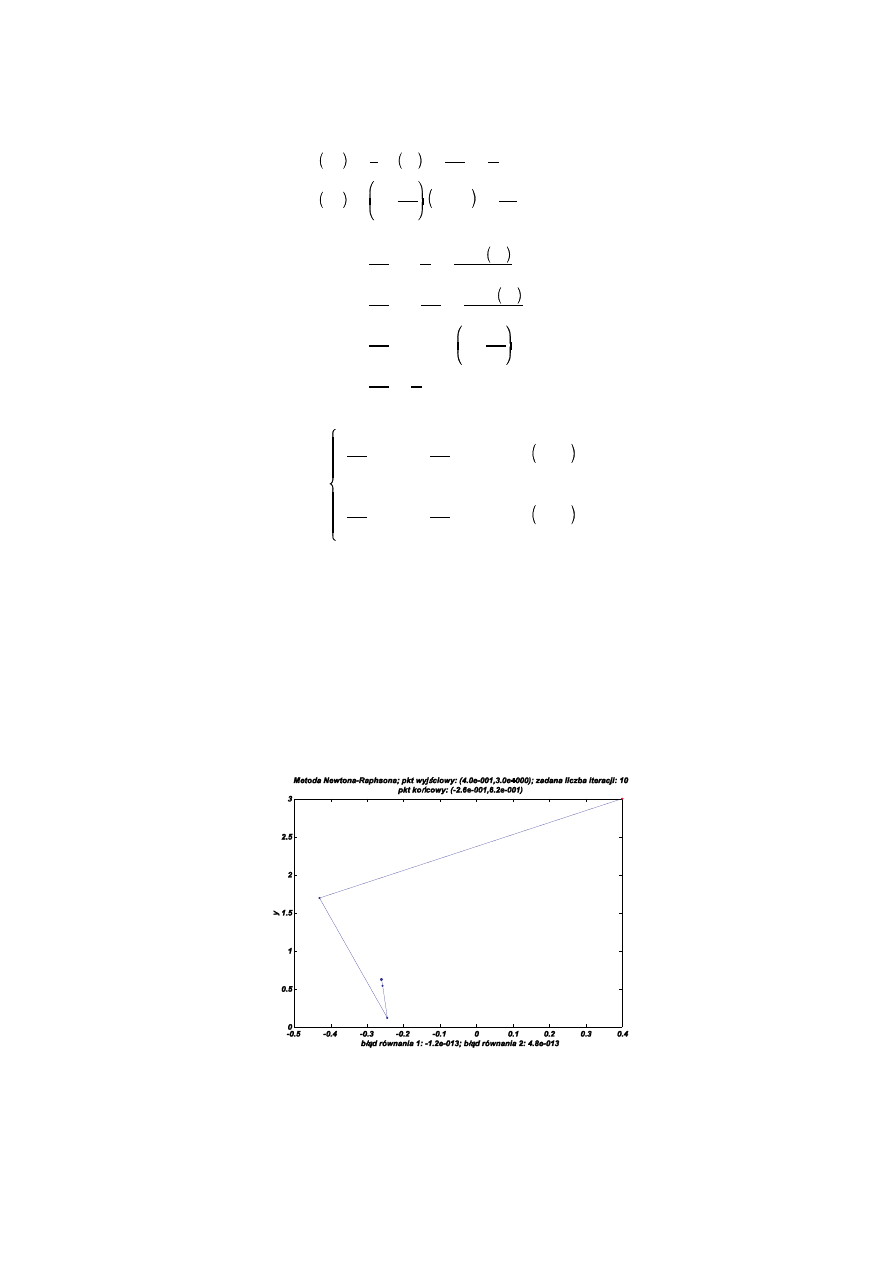
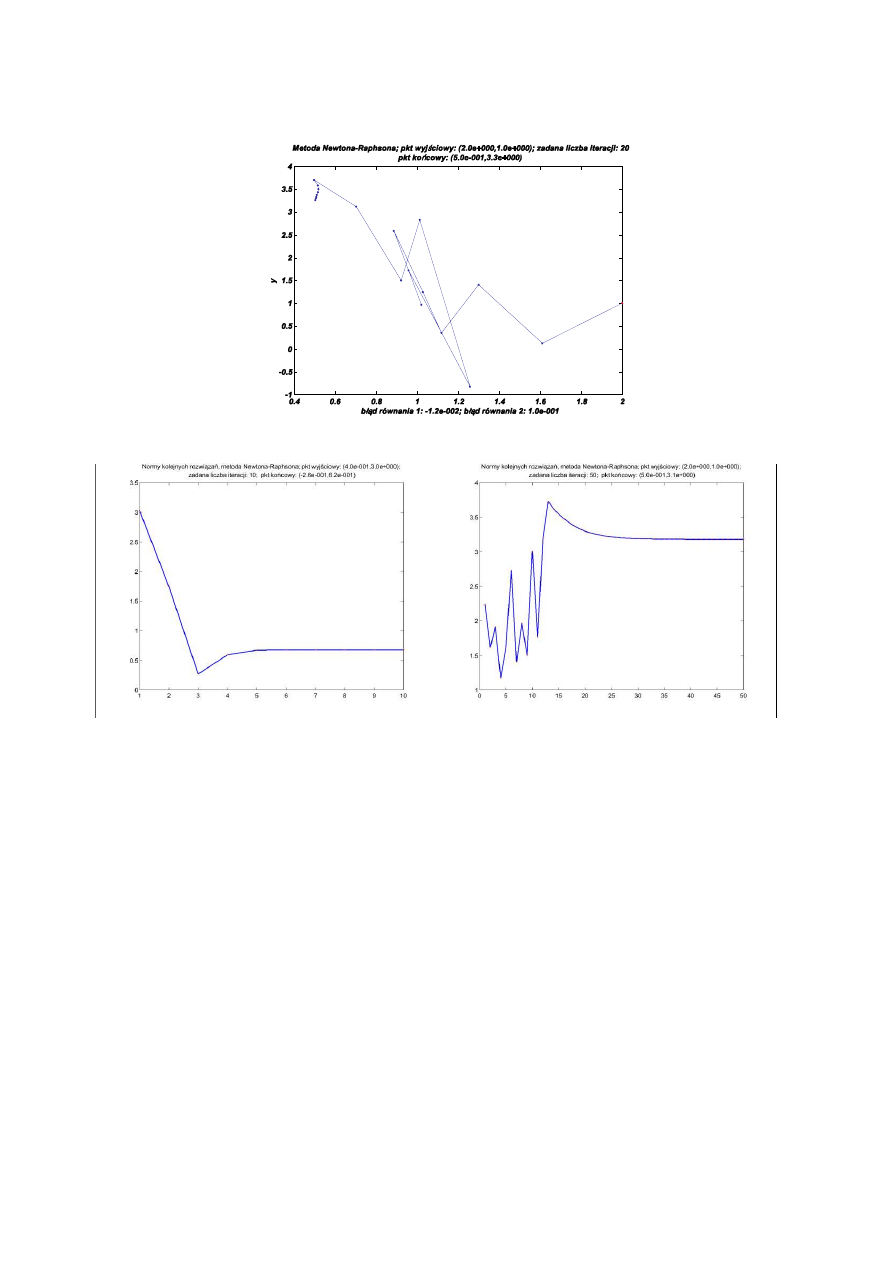
Poni ej znajduj si dwie ilustracje metody Newtona-Raphsona dla punktów pocz tkowych (0.4,3.0) i (2.0,1.0):
Metody Numeryczne w Fizyce 1
Rozwi zywanie układów równa
20
© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej
Tak e i w tym przypadku spojrzymy jeszcze na przebieg zmian norm wektorów b d cych kolejnymi
przybli eniami rozwi zania:
Dla drugiego punktu pocz tkowego na wykresie norm pokazałem 50 iteracji (podczas gdy na wykresie rozwi za
było ich 20) — dzi ki temu wyra niej wida , e osi gamy zbie no .
Wyszukiwarka
Podobne podstrony:
podrecznik 2 18 03 05
regul praw stan wyjątk 05
05 Badanie diagnostyczneid 5649 ppt
Podstawy zarządzania wykład rozdział 05
05 Odwzorowanie podstawowych obiektów rysunkowych
05 Instrukcje warunkoweid 5533 ppt
05 K5Z7
05 GEOLOGIA jezior iatr morza
05 IG 4id 5703 ppt
05 xml domid 5979 ppt
Świecie 14 05 2005
Wykł 05 Ruch drgający
TD 05
więcej podobnych podstron