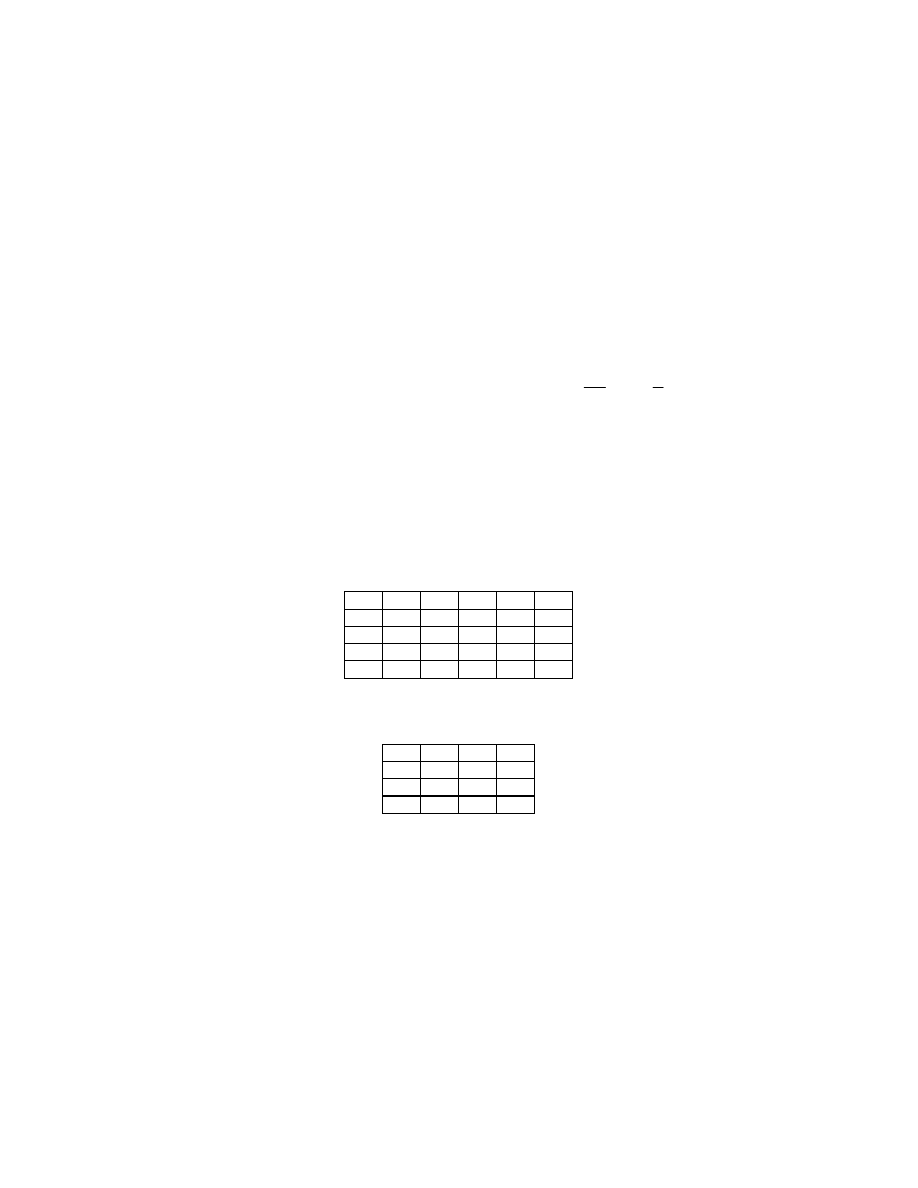
Regresja, kowariancja, korelacja

Zakres teorii:

•

regresja I i II rodzaju

•

współczynnik kowariancji

•

współczynnik korelacji

Zadania:

Zad 1. Zmienne X i Y związane są zależnością funkcyjną Y=X

2

. Zmienna losowa X przyjmuje wartości –1, 0 , 1 każdą z

jednakowym prawdopodobieństwem równym 1/3. Sprawdzić czy zmienne są skorelowane.

Zad 2. Niech dwuwymiarowa zmienna losowa (X,Y) ma gęstość







≤

≤

∧

≤

≤

+

=

.

.

0

2

0

1

0

)

2

(

2

,

0

)

,

(

p

p

w

y

x

y

x

y

x

f

Znaleźć proste regresji drugiego rodzaju oraz kąt jaki tworzą nożyce korelacyjne.

Zad 3. Czy zmienne X i Y są skorelowane, jeśli funkcja gęstości jest postaci

(

)









+

−

=

2

2

2

1

exp

2

1

)

,

(

y

x

y

x

f

π

?

Zad 4. Dwuwymiarowa zmienna losowa (X,Y) ma rozkład o gęstości







≤

≤

∧

≤

≤

+

=

.

.

0

2

0

1

0

)

2

(

2

,

0

)

,

(

p

p

w

y

x

y

x

y

x

f

Wyznaczyć równanie linii regresji I rodzaju zmiennej Y względem X oraz zmiennej X względem Y.

Zad 5. Obliczyć

a)

kowariancję

b)

współczynnik korelacji

dwuwymiarowej zmiennej losowej, której rozkład podany jest w tabeli.

Y\X

-2

-4

2

3

5

-1

0,06

0,1

0,04 0,08 0,02

-2

0,04 0,01

0

0,15

0

4

0,1

0,06 0,06 0,08

0

6

0

0

0,02

0,1

0,08

Zad 6. Jaki warunek muszą spełniać zmienne losowe X i Y, aby D

2

(X,Y)=D

2

(X)+D

2

(Y)?

Zad 7. Niech dwuwymiarowa zmienna losowa ma rozkład podany w tabeli.

Y\X

5

6

7

0

0

0

0,1

1

0,1

0,2

0,1

2

0,3

0,1

0,1

Wyznaczyć i naszkicować wykresy prostych regresji II rodzaju.

Zad 8. Niech dwuwymiarowa zmienna losowa (X,Y) ma gęstość







≤

≤

≤

≤

−

=

.

.

0

1

0

,

2

0

)

,

(

p

p

w

y

x

dla

xy

x

y

x

f

Znaleźć proste regresji drugiego rodzaju oraz kąt jaki tworzą nożyce korelacyjne.

Zad 9. Napisać gęstość rozkładu normalnego, dla którego wektor wartości oczekiwanych jest wektorem zerowym, a macierz
momentów centralnych rzędu drugiego jest postaci:













4

2

2

7