1.  Narysuj filtr adaptacyjny i podaj algorytm filtracji LMS 

Ogólny  schemat  filtra  adaptacyjnego  przedstawiony  jest  na  rys.10.10.  Filtr  adaptacyjny 
jest  to  filtr,  przeważnie  typu  FIR,  którego  współczynniki  h[n]  są  przestrajane  w  trakcie 
filtracji  w  taki  sposób,  aby  sygnał  wyjściowy  filtra  y[n]  był  dopasowany  do  sygnału 
pożądanego  (desired)  d[n]  (nazywanego  również  sygnałem  odniesienia),  tzn.,  aby  błąd 
zdefiniowany  jako:    e[n]=d[n]-y[n]  i  był  jak  najmniejszy.  Przykładami  filtrów 
adaptacyjnych są filtry RLS i LMS. 

 

 

2.  Narysuj schemat obliczeo LWT w wersji całkowitoliczbowej 

 

 

 

 

 
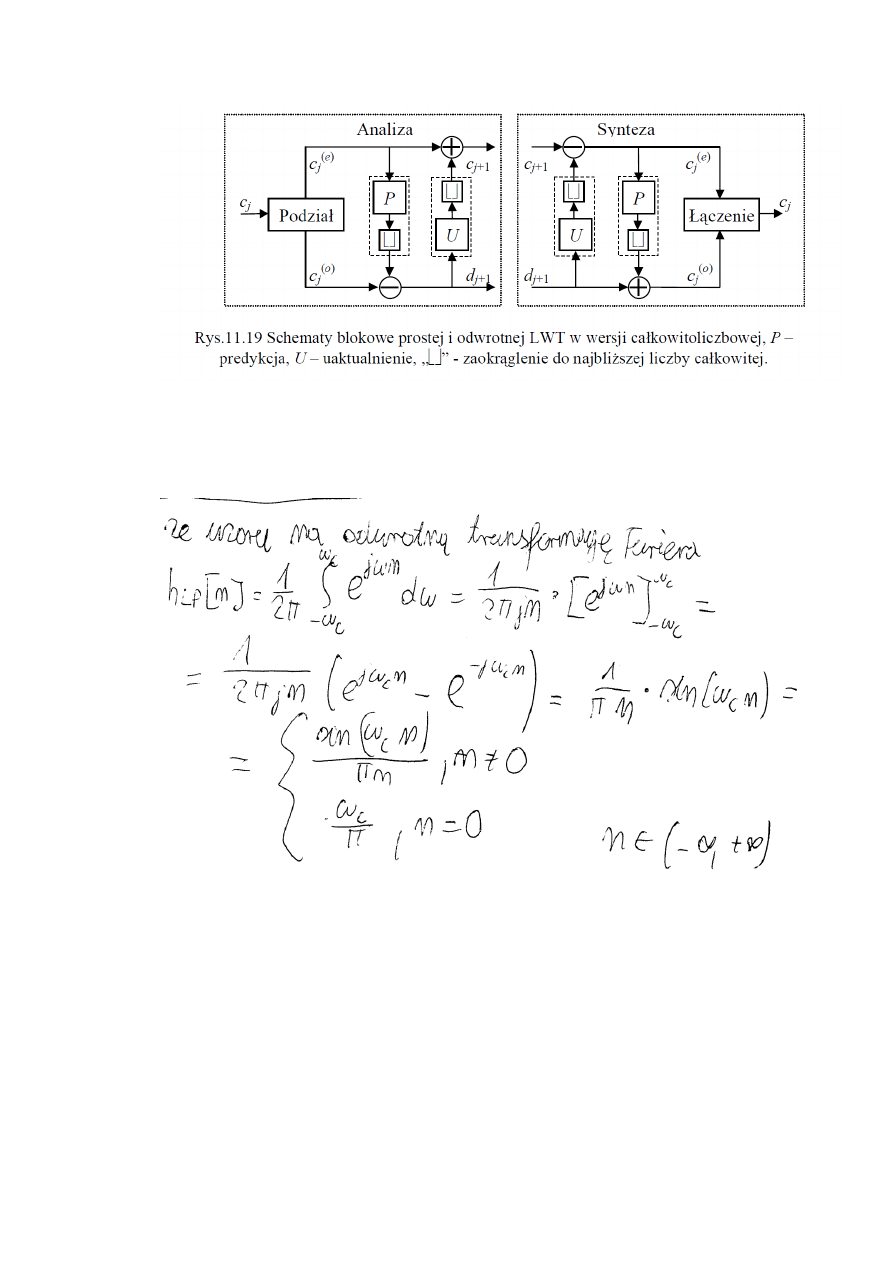
d – współczynniki detali 
c – współczynniki aproksymacji 
 

3.  Wyprowadź wzór na odpowiedź impulsową idealnego filtra dolnoprzepustowego. 

 

 

4. Podaj twierdzenie o próbkowaniu dla sygnałów dolno i pasmowoprzepustowych 

 

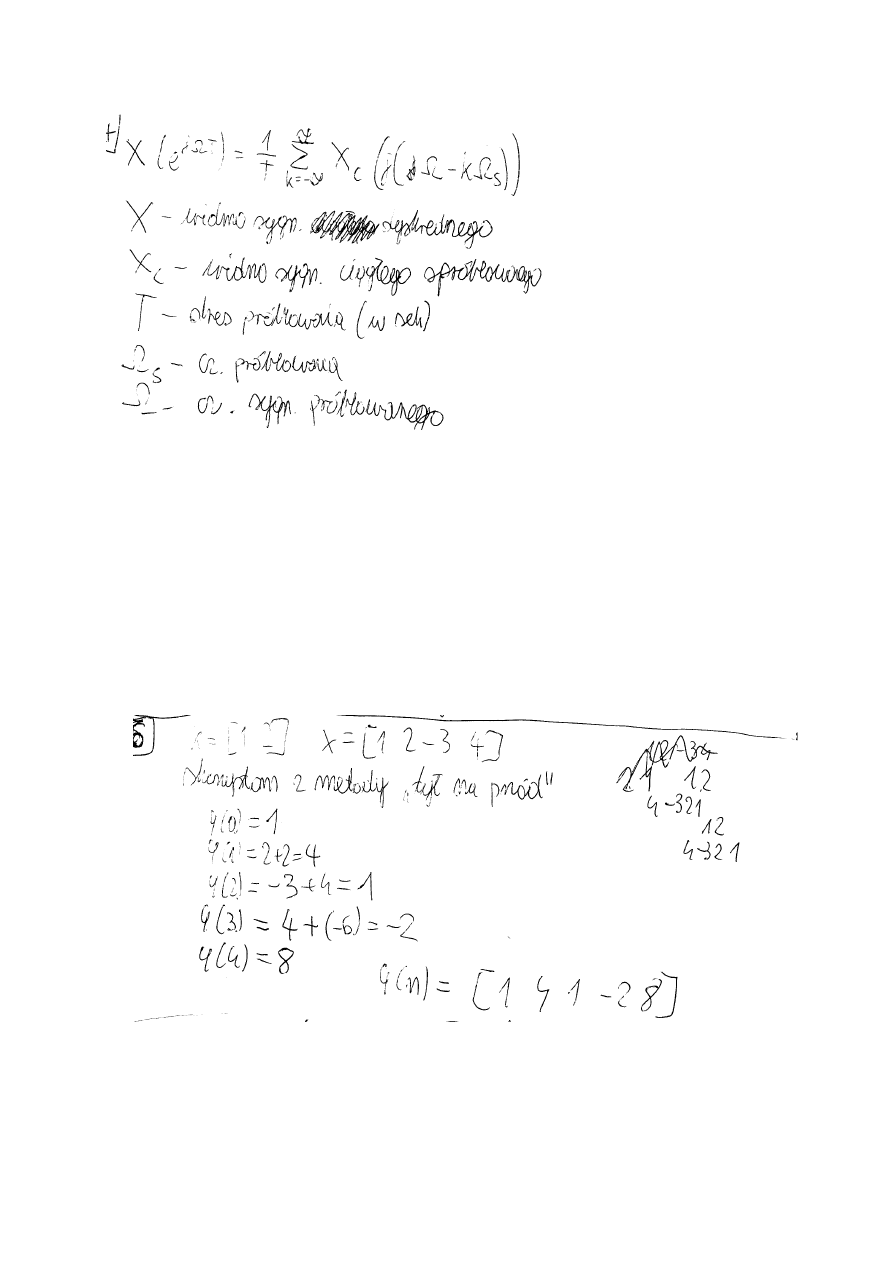
5.  Podaj algorytm liczenia splotu liniowego sygnałów dyskretnych 
 
Algorytm  liczenia  splotu  liniowego  sygnałów  o  skończonej  długości  poprzez  DFT  jest 
następujący:  
1. Określić długości N

1 

i N

2 

sygnałów x

1

[n] i x

2

[n],  

2. Uzupełnić zerami sygnały x

1

[n] i x

2

[n] do długości N

1

+N

2

-1,  

3. Obliczyć DFT obu sygnałów,  
4. Obliczyć odwrotne DFT iloczynu widm. 

 

6.  Oblicz splot wektorów k=[1 2] i x=[1 2 -3 4] 

 

 

 

 

7.  Oblicz DFT wektora x=[1 2 -3 4] 

 

 

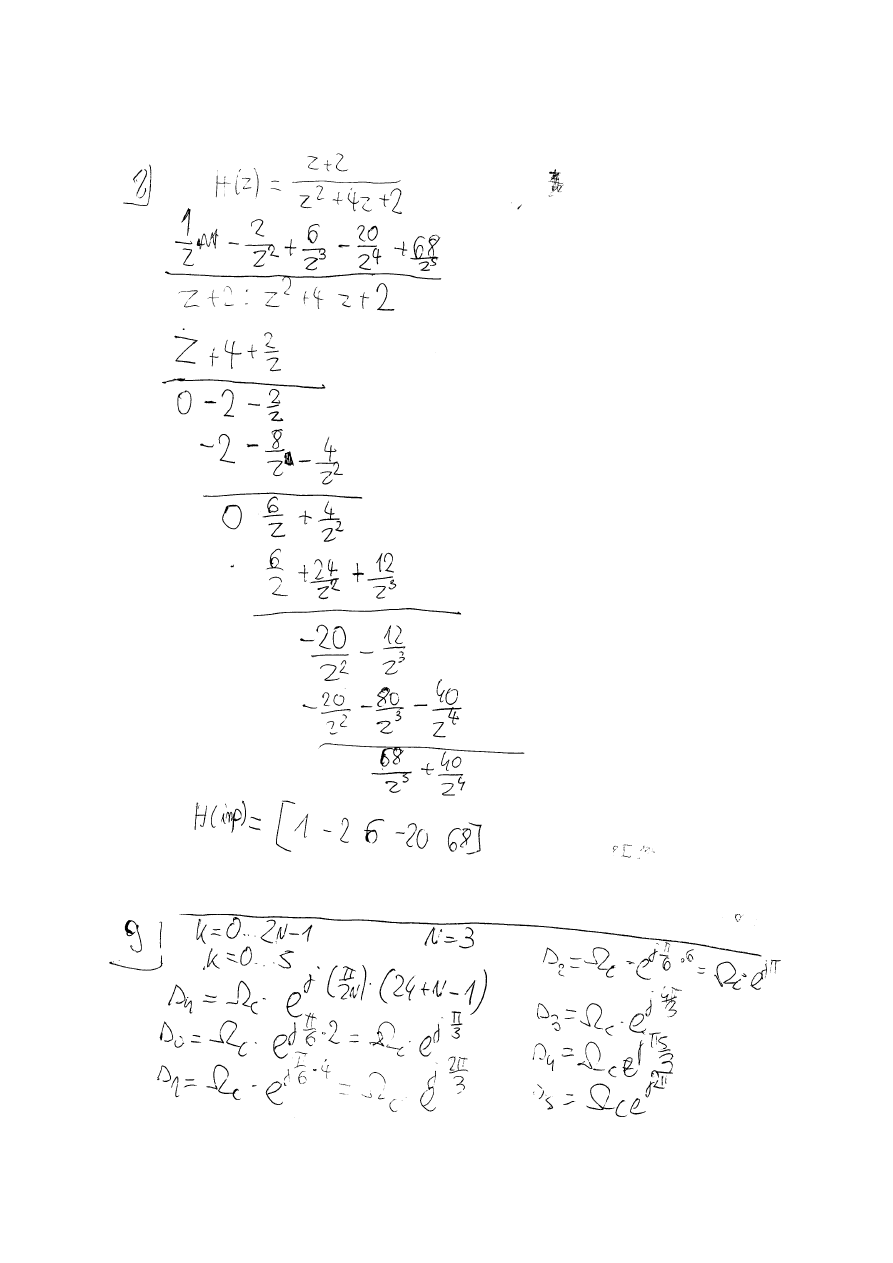
8 . Oblicz 5 pierwszych wyrazów odpowiedzi impulsowej układu dyskretnego o 
transmitancji H(z)=(z+1)/(z^2+4z+2)

 

9. Podaj bieguny transmitancji analogowego prototypu filtra Butterwortha rzędu N=3 

 

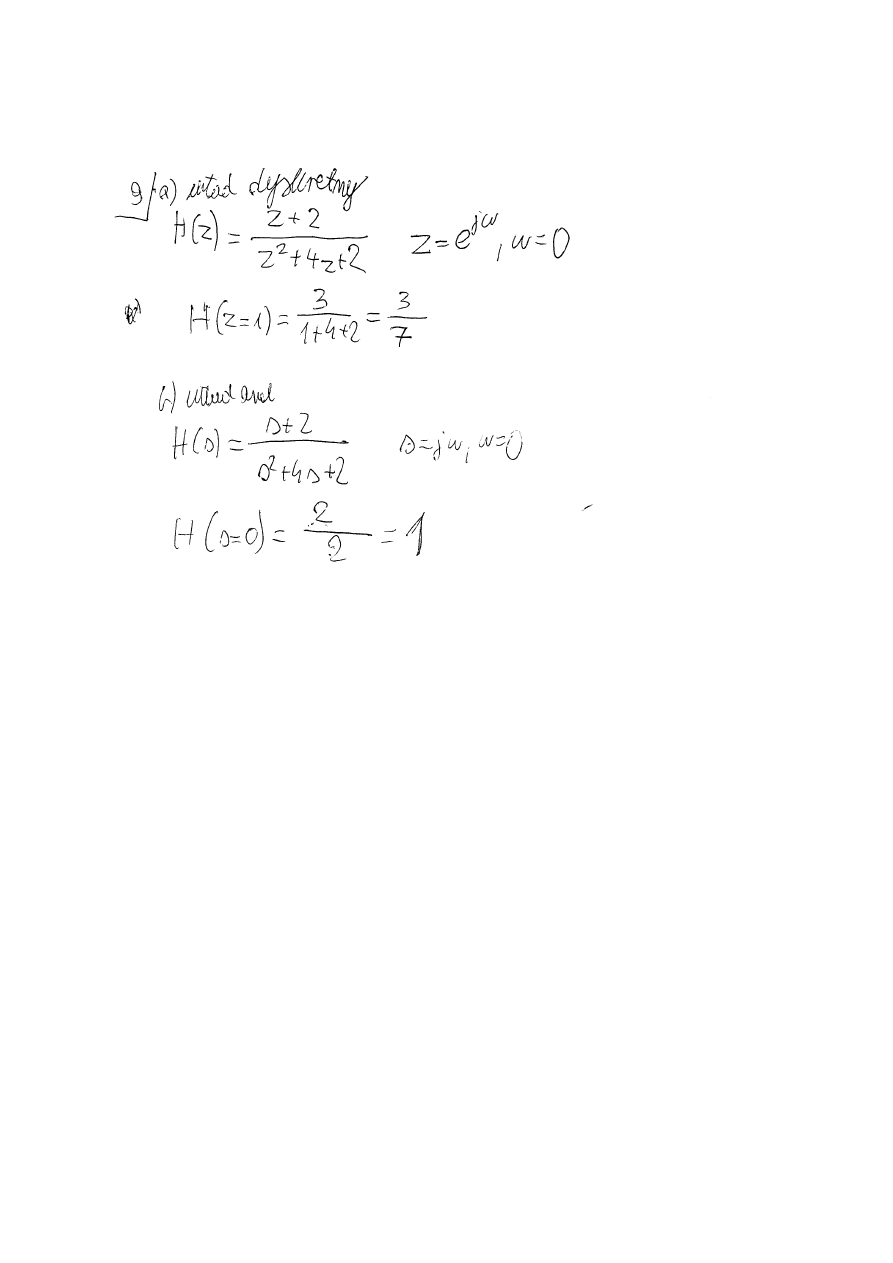
10. Oblicz wzmocnienie składowej stałej układu dyskretnego oraz układu analogowego dla 
transmitancji 

H(z)=(z+1)/(z^2+4z+2)