Ocena dokładności pomiarów. Ocena dokładności wielkości

obliczanych.

Podział błędów:

1. Błędy absolutne l

∆ przypadające na całą mierzoną wielkość.

2. Błędy względne

l

l

∆

wyrażają stosunek błędu absolutnego do wielkości mierzonej, a

więc są to błędy przypadające na jednostkę wielkości mierzonej. Błędy względne
służą do oceny dokładności pomierzonych wielkości. Przedstawiamy je zazwyczaj

w postaci ułamka

c

1

lub w procentach.

Błędy pomiarów ponadto możemy podzielić na trzy grupy: grube, czyli omyłki,

systematyczne i przypadkowe.

Błędy grube są spowodowane zazwyczaj omyłkami popełnionymi przy wykonywaniu

obserwacji lub błędnymi zapisami. Na przykład przy pomiarze długości taśmą przez nieuwagę
policzono o jedno odłożenie taśmy za mało lub za dużo, przy pomiarze kąta zamiast odczytu
46g odczytano 64g itp. Błędy grube powinny zostać ujawnione podczas opracowywania
wyników pomiarów. W większości wypadków są one wykrywane przy powtórzeniu pomiarów.
Pomiary obarczone błędami grubymi nie mogą być wykorzystywane do dalszych opracowań.

Do błędów grubych zaliczamy nie tylko duże błędy w pomiarze, ale również zdarzające się

pomyłki przy wykonywaniu obliczeń. W trakcie wykonywania obliczeń istnieje możliwość
kontroli i sprawdzania poprawności wykonywanych prac. W wypadku wykrycia błędu grubego
najpierw powtarzamy obliczenia, a jeżeli stwierdzimy, że zostały wykonane prawidłowo,
powtarzamy pomiary w terenie. Istnieją pewne możliwości określenia, która z wielkości
mierzonych jest obarczona błędem grubym. Sprawdzenie należy wówczas rozpocząć od
powtórnego pomiaru tej wielkości.

Błędy systematyczne zniekształcają wyniki pomiarów według określonego prawa.

Znajomość tego prawa umożliwia wyeliminowanie błędów systematycznych. Do błędów
systematycznych należy np. wpływ temperatury na pomiar długości przy użyciu taśmy
stalowej. W wyższej temperaturze taśma wydłuża się i przy pomiarze odcinka otrzymamy
mniejszą wartość, niż gdy mierzymy taśmą o prawidłowej długości. Wpływ temperatury na
długość taśmy możemy obliczyć i jako poprawkę uwzględnić przy obliczaniu długości całego
odcinka. A więc jesteśmy w stanie uwolnić się od wpływu błędu systematycznego,
wywołanego zmianą temperatury taśmy w trakcie wykonywania pomiarów.

Eliminowanie błędów systematycznych z pomiarów dokonuje się czasami przez

odpowiednie zaprogramowanie pomiaru. Na przykład eliminowanie błędów systematycznych z
pomiarów kątów poziomych, wynikłych z niedopełnienia warunków konstrukcyjnych
teodolitu, tzw. kolimacji i inklinacji, odbywa się przez wykonanie podwójnych pomiarów. Przy
czym drugi pomiar wykonuje się po tzw. przerzuceniu lunety przez zenit.

Źródłem błędów systematycznych może być obserwator, jeżeli wykonuje odczyty zawsze

nieco większe lub nieco mniejsze od prawdziwych. Może to być spowodowane
właściwościami jego wzroku. Systematyczny błąd obserwatora nazywany bywa błędem
osobowym. Błąd ten powinien być określony i usuwany z obserwacji pomiarowych.

Błędy systematyczne mogą być stałe lub zmienne. Błędy systematyczne stałe

zniekształcają w określonych warunkach wyniki pomiaru zawsze z tym samym znakiem, np.
długość taśmy użytej do pomiaru nie odpowiada jej długości nominalnej, lecz jest większa lub
mniejsza o określoną wartość. Każde odłożenie taśmy będzie wówczas obarczone błędem tej
wartości, zawsze z tym samym znakiem.

Błędy systematyczne zmienne wynikają ze zmiennych warunków pomiaru, np. pod

wpływem wahań temperatury ulega zmianie długość użytej do pomiaru taśmy i poszczególne
odłożenia obarczone są różnymi błędami systematycznymi. Wpływy błędów systematycznych
jesteśmy obowiązani usunąć z wyników pomiaru. Nie zawsze udaje się je usunąć całkowicie.
Drobne pozostałości błędów systematycznych stają się wówczas błędami przypadkowymi.

Błędy przypadkowe są drobne i nieuchwytne, o nieznanym znaku, uzależnione od stale

zmieniających się warunków pomiaru. Błędy te spowodowane są czynnikami, które pojawiają
się chwilowo, których nie można przewidzieć i których ścisłej wartości liczbowej nie można
obliczyć z żadnej zależności matematycznej. Ponieważ błędów przypadkowych nie można
uniknąć przy pomiarze, ani też usunąć przez obliczenia rachunkowe z wyników pomiarów,
należy dążyć do osłabienia ich wpływu na wyniki pomiarów oraz oszacować ich wielkość.
Oszacowanie wielkości tych błędów pozwoli określić dokładność pomiarów. Charakterystyką
błędów przypadkowych, analizą ich właściwości i wpływu na pomiary oraz sposobami
osłabienia ich wpływu na wyniki pomiarów zajmuje się teoria błędów, rachunek
prawdopodobieństwa oraz rachunek wyrównawczy.

Do głównych zadań rachunku wyrównania należy:

1) wyznaczenie najprawdopodobniejszych wartości wielkości mierzonych oraz,
2) określenie dokładności wielkości mierzonych oraz funkcji tych wielkości.

Aby te zadania mogły być wykonane w danym zestawie obserwacyjnym, musi być wykonana,
choć jedna obserwacja nadliczbowa. Im więcej jest obserwacji nadliczbowych, tym pewniejsze
jest rozwiązanie powyższych zadań rachunku wyrównawczego.
Rachunek wyrównawczy zajmuje się tylko błędami przypadkowymi.

Błędy przypadkowe dzielimy na:

1. Błędy prawdziwe (rzeczywiste).
2. Błędy pozorne.

W praktyce najczęściej do czynienia mamy z błędami pozornymi.

Błąd prawdziwy ε, jest to różnica między wartością prawdziwą X a obserwowaną l.

l

X

+

=

ε

Błąd pozorny υ, jest to różnica między wartością najprawdopodobniejszą x (średnią
arytmetyczną) a wartością obserwowaną (pomierzoną) l.

l

x

+

=

υ

Dla charakterystyki dokładności pomiarów przyjmuje się najczęściej następujące wielkości:

1. Błąd względny (ω).
2. Błąd średni (m).
3. Błąd graniczny (g).
4. Błąd przeciętny (t).
5. Błąd prawdopodobny (r).

Ad. 3) Błędem granicznym nazywamy trzykrotną wartość błędu średniego, czyli:

g = 3 m

Prawdopodobieństwo nie przekroczenia tego błędu wynosi 0,9973.

Ad. 4) Błędem przeciętnym t nazywamy średnią arytmetyczną z bezwzględnych wartości
błędów pozornych (lub prawdziwych, jeśli je znamy), czyli:

[ ]

n

t

υ

=

Związek między błędem przeciętnym a średnim jest następujący:

t = 0,79788 m albo m = 1,2533 t

Prawdopodobieństwo nie przekroczenia tego błędu wynosi 0,5753.

Ad.5) Błędem prawdopodobnym

r

nazywamy taki błąd, którego prawdopodobieństwo

przekroczenia równe jest prawdopodobieństwu nie przekroczenia i wynosi 0,5. To znaczy, że
w danym szeregu obserwacji możliwe jest wystąpienie zarówno błędu mniejszego,
jak i większego od błędu prawdopodobnego. Związek między błędem prawdopodobnym
a średnim jest następujący:

r = 0,67449 m albo m = 1,4826 r

Ocena dokładności spostrzeżeń i wartości wyrównanej:

I.

Spostrzeżenia jednakowo dokładne.

Błąd średni – wskaźnik dokładności – pozwala na ocenę dokładności spostrzeżeń
jak i wartości wyrównanych.

Błąd średni pojedynczego spostrzeżenia wyznaczony na podstawie błędów prawdziwych
wyraża się wzorem:

[ ]

n

m

εε

±

=

Błąd średni pojedynczego spostrzeżenia wyznaczony na podstawie błędów pozornych wyraża
się wzorem:

[ ]

( )

1

−

±

=

n

m

υυ

Błąd średni m pozwala ocenić dokładność wykonania poszczególnego pojedynczego pomiaru,
czyli przy kilku pomiarach tej samej wielkości charakteryzuje nam dokładność każdego z nich.

Jeśli mamy n obserwacji (spostrzeżeń) tej samej wielkości X, np. l

1

, l

2

,…l

n

to

najprawdopodobniejszą wartością tej mierzonej wielkości będzie średnia arytmetyczna:

[ ]

n

l

x

=

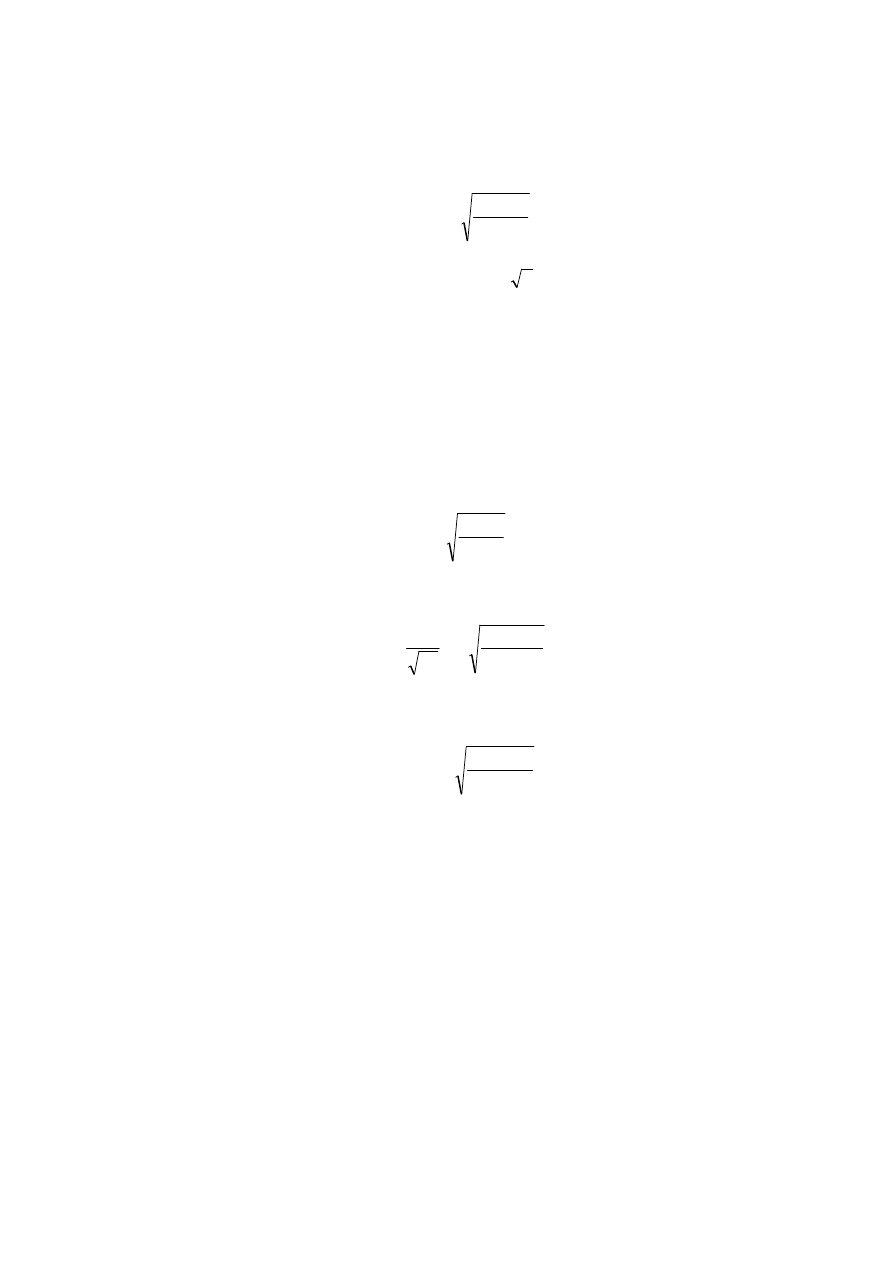
Oczywiście wyznaczona z tego wzoru średnia arytmetyczna jest również obarczona

pewnym błędem. Ten średni błąd średniej arytmetycznej (tzw. wartości wyrównanej)
wyznaczamy na podstawie wzoru:

[ ]

( )

1

−

±

=

=

n

n

M

m

L

υυ

Zatem błąd średni średniej arytmetycznej jest

n razy mniejszy od błędu średniego

pojedynczego spostrzeżenia. Błąd ten pozwala ocenić dokładność przyjętej przez nas
najprawdopodobniejszej wartości wyrównanej.

II.

Spostrzeżenia niejednakowo dokładne.

Oceną dokładności tych spostrzeżeń będą błędy średnie: typowego spostrzeżenia,

spostrzeżeń grupowych i błąd średni ogólnej średniej arytmetycznej:

[ ]

( )

1

−

±

=

n

p

m

o

υυ

•

jest to wzór na średni błąd typowego spostrzeżenia o wadze równej jedności;

[ ]

( )

1

−

±

=

±

=

n

p

p

p

m

m

i

i

o

i

υυ

•

jest to wzór na średni błąd i-tego (dowolnego) spostrzeżenia o wadze p

i

;

[ ]

[ ]

( )

1

−

±

=

=

n

p

p

M

m

L

υυ

•

jest to wzór na średni błąd wartości średniej ważonej (błąd średni ogólnej średniej
arytmetycznej o wadze [p]).

III.

Pary spostrzeżeń jednakowo dokładnych.

Ocena dokładności pomiarów parami opierać się będzie na różnicach d, obliczonych ze

spostrzeżeń każdej pary. Dla wielu par spostrzeżeń l

1

’

i l

1

’’

, l

2

’

i l

2

’’

,…, l

n

’

i l

n

’’

różnice są

następujące:

d

1

= l

1

’

- l

1

’’

d

2

= l

2

’

– l

2

’’

...…………

d

n

= l

n

’

– l

n

’’

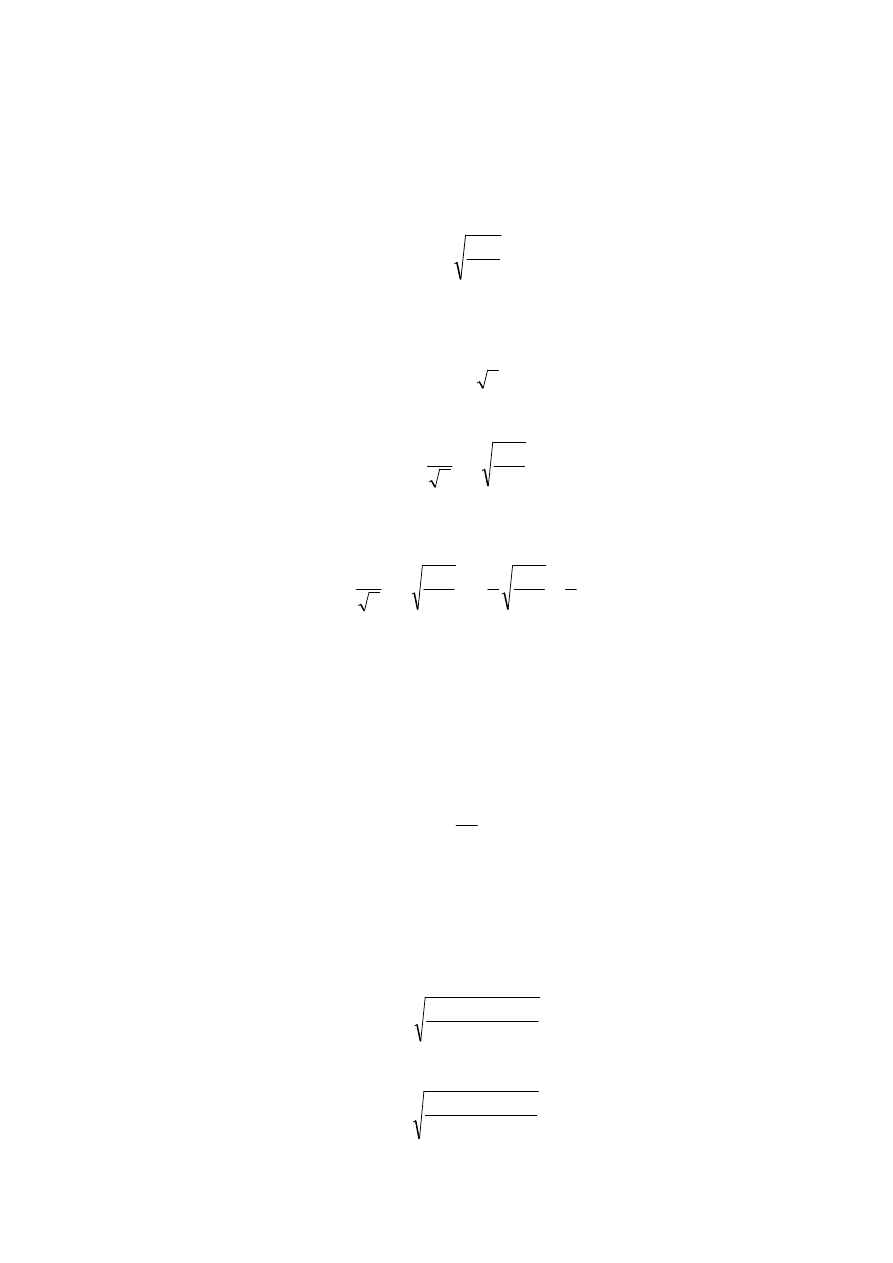
Przy bezbłędnym pomiarze każda różnica powinna równać się zero (dla każdej pary

l

’

= l

’’

) i stąd wyprowadzamy wniosek, że otrzymane różnice wynikające z błędów pomiarów

są prawdziwymi błędami różnic i jako takie mogą być zastosowane w wyprowadzonych
uprzednio wzorach rachunku wyrównania. Zatem błąd średni różnicy dwóch pomiarów pewnej
wielkości zostanie wyrażony wzorem:

[ ]

n

dd

m

d

±

=

Oznaczając błąd średni jednego pomiaru przez m

o

możemy błąd średni różnicy dwóch

jednakowo dokładnych pomiarów pewnej wielkości wyrazić wzorem:

2

o

d

m

m

±

=

stąd błąd średni jednego pomiaru:

[ ]

n

dd

m

m

d

o

2

2

±

=

±

=

Błąd średni wyniku z poszczególnych par - błąd średni średniej arytmetycznej wynosi:

[ ]

[ ]

d

o

L

m

n

dd

n

dd

m

m

2

1

2

1

4

2

=

±

=

±

=

±

=

Ocena dokładności pomiarów jest tym właściwsza, im większa liczba n różnic par

spostrzeżeń wchodzi do obliczeń.

Jeśli zauważymy, że większość obliczonych różnic ma ten sam znak (+ lub

-), to tym

samym stwierdzimy, że w poszczególnych różnicach znajdują się błędy systematyczne. Należy
wówczas usunąć wpływ tych błędów. Za najprawdopodobniejszą wartość tego błędu
przyjmujemy średnią arytmetyczną z otrzymanych różnic:

[ ]

n

d

=

σ

Wpływ błędu systematycznego eliminujemy odejmując otrzymaną wartość

σ od po-

szczególnych różnic. Uwolnione od błędu systematycznego różnice

d wyniosą d

’’

= d - σ.

Poprawione różnice

d

i

’

są już błędami przypadkowymi, gdyż straciły charakter błędów

prawdziwych. Stąd do oceny dokładności stosujemy wzory oparte na błędach pozornych υ,
wówczas błąd średni różnicy dwóch pomiarów wynosi:

(

)(

)

[

]

1

−

−

−

±

=

n

d

d

m

d

σ

σ

a błąd średni jednego pomiaru:

(

)(

)

[

]

( )

1

2

−

−

−

±

=

n

d

d

m

o

σ

σ

IV. Pary spostrzeżeń niejednakowo dokładnych

Jeśli pomiary parami są niejednakowo dokładne, wówczas błąd średni różnicy dwóch

pomiarów wyrazi się wzorem:

[ ]

n

pdd

m

d

±

=

Błąd średni typowego spostrzeżenia (o wadze równej jedności) określony z pomiarów

podwójnych wyraża się wzorem:

[ ]

n

pdd

m

o

2

±

=

Wyprowadzenia wzorów.

Postać wzoru na błąd średni w oparciu o błędy prawdziwe w praktyce jest niedogodna

do stosowania ze względu na nieznajomość błędów prawdziwych. W celu wyrażenia błędu
średniego za pomocą błędów pozornych przeprowadźmy następujące rozumowanie:

i

i

l

X

−

=

ε

i

i

l

x

−

=

υ

Odejmując pierwsze równanie od drugiego otrzymamy:

x

X

i

i

−

=

−υ

ε

Lub

(

)

i

i

x

X

υ

ε

+

−

=

Powyższe równanie rozpisane szczegółowo da nam taki oto zestaw równań:

(

)

1

1

υ

ε

+

−

=

x

X

(

)

2

2

υ

ε

+

−

=

x

X

…………………

(

)

n

n

x

X

υ

ε

+

−

=

Po podniesieniu do kwadratu każdego z równań i zsumowaniu ich otrzymamy:

(

) (

)

2

1

1

2

2

2

1

υ

υ

ε

+

−

+

−

=

x

X

x

X

(

) (

)

2

2

2

2

2

2

2

υ

υ

ε

+

−

+

−

=

x

X

x

X

…………………………………

(

) (

)

2

2

2

2

n

n

n

x

X

x

X

υ

υ

ε

+

−

+

−

=

[ ]

(

) (

)

[ ]

[ ]

2

2

2

2

υ

υ

ε

+

−

+

−

=

x

X

x

X

n

Można udowodnić, że

(

)

[ ]

2

2

2

n

x

X

ε

≈

−

Uwzględniając powyższą zależność oraz wiedząc, że

[ ]

0

=

υ

co wynika ze szczególnych cech

średniej arytmetycznej, równanie przedstawiające zsumowanie przyjmie postać:

[ ] [ ] [ ]

2

2

2

υ

ε

ε

+

=

n

Następnie otrzymamy:

( )

[ ] [ ]

2

2

1

υ

ε

n

n

=

−

I ostatecznie

[ ] [ ]

1

2

2

−

=

n

n

υ

ε

Otrzymany wzór jest niezwykle użyteczny, gdyż pozwala zastąpić wyrazy, w których
występują błędy prawdziwe (których wartości prawie nigdy nie znamy), przez wyrazy, w
których występują błędy pozorne (których wartość prawie zawsze da się obliczyć). Tym
sposobem podstawiając otrzymaną zależność do wzoru na błąd średni wyrażony za pomocą
błędów prawdziwych otrzymamy zależność na błąd średni wyrażony przy pomocy błędów
pozornych:

[ ]

( )

1

−

±

=

n

m

υυ

Dygresja:

1

1

l

X

−

=

ε

2

2

l

X

−

=

ε

……………

n

n

l

X

−

=

ε

Po zsumowaniu otrzymamy zależność:

[ ]

[ ]

l

nX

−

=

ε

Dzieląc obustronnie przez liczbę spostrzeżeń n, otrzymujemy:

[ ]

[ ]

n

l

X

n

−

=

ε

Wiedząc, że:

[ ]

x

n

l

=

Gdzie x oznacza średnią arytmetyczną ze wszystkich spostrzeżeń, zastępując wobec tego drugi
wyraz po prawej stronie równania przez x, otrzymamy:

[ ]

x

X

n

−

=

ε

A po podniesieniu obu stron do kwadratu:

[ ]

(

)

2

2

2

x

X

n

−

=

ε

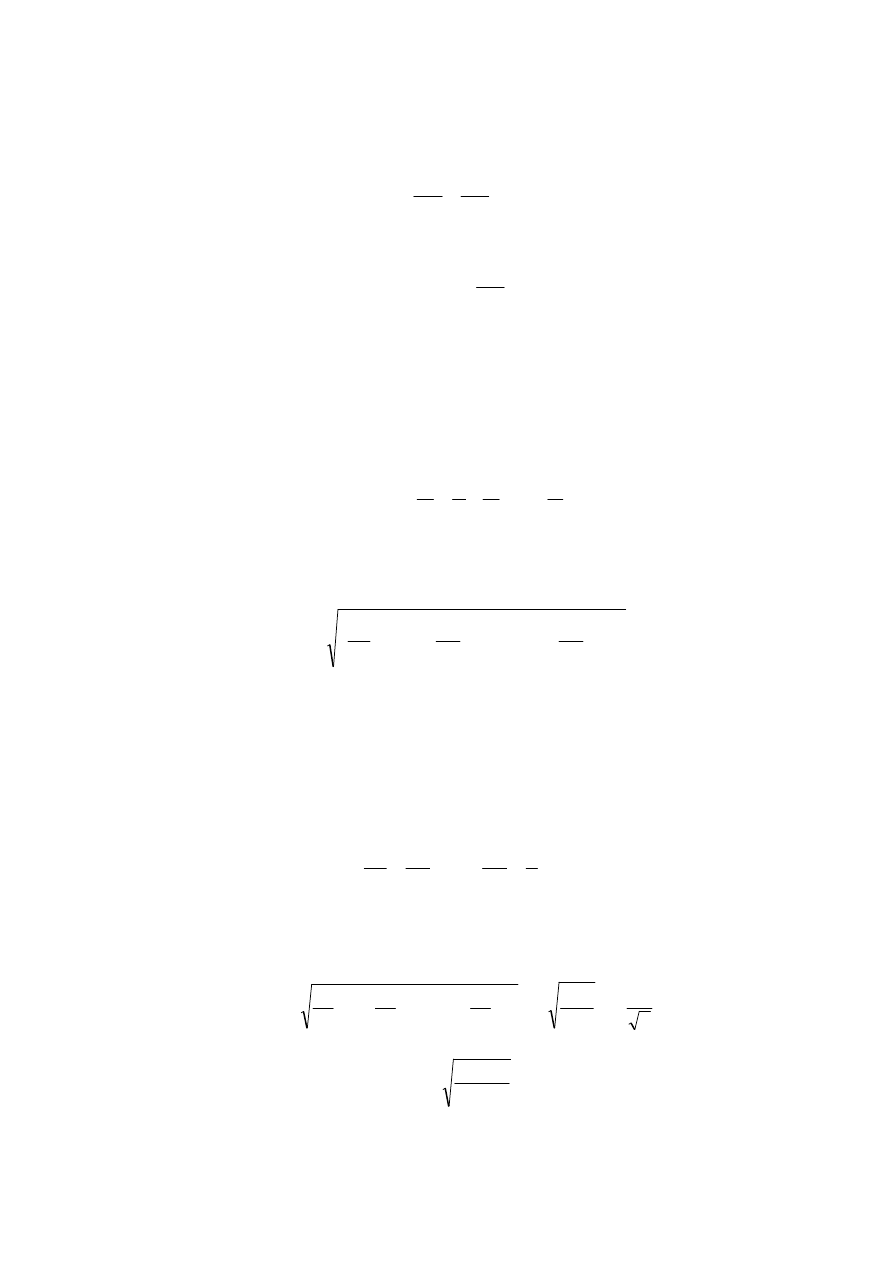
Zakładając, że kwadrat sumy błędów prawdziwych jest w przybliżeniu równy sumie
kwadratów błędów prawdziwych, czyli:

[ ]

[ ]

2

2

2

2

n

n

ε

ε

≈

Otrzymamy ostatecznie:

(

)

[ ]

2

2

2

n

x

X

ε

≈

−

c.b.d.u.



Błąd średni średniej arytmetycznej wyznaczamy, wykorzystując wiadomości o przenoszeniu
się błędów średnich i wyznaczaniu błędów średnich funkcji wielkości pomierzonych, czyli:

[ ]

n

l

n

l

n

l

n

l

l

f

L

n

+

+

+

=

=

=

L

2

1

)

(

Wzór ten określa średnią arytmetyczną.
Błąd średni średniej arytmetycznej możemy zapisać zatem w następującej postaci:

2

2

2

2

2

2

2

1

2

1

n

l

n

l

l

L

m

l

L

m

l

L

m

l

L

m













∂

∂

+

+













∂

∂

+













∂

∂

±

=

L

Rozpatrując obserwację jednakowo dokładne, czyli:

m

m

m

m

n

l

l

l

=

=

=

=

L

2

1

Błędy średnie poszczególnych pojedynczych spostrzeżeń są sobie równe. Również pochodne
cząstkowe są sobie równe, czyli:

n

l

L

l

L

l

L

n

1

2

1

=

∂

∂

=

=

∂

∂

=

∂

∂

L

Po podstawieniu do wzoru na

m

L

wartości pochodnych cząstkowych i pamiętając, że

obserwacje są jednakowo dokładne, otrzymamy:

n

m

n

nm

m

n

m

n

m

n

m

n

l

l

l

L

±

=

±

=

+

+

+

±

=

2

2

2

2

2

2

2

2

1

1

1

2

1

L

[ ]

( )

1

−

±

=

n

n

m

L

υυ

Przykłady i zadania:

1.

Błąd względny

Zadanie 1. Pomierzono następujące odcinki z określonymi dokładnościami:

•

Odcinek I o długości 322m, pomierzony z błędem absolutnym 0,30m

•

Odcinek II o długości 281m, pomierzony z błędem absolutnym 0,21m

•

Odcinek III o długości 167m, pomierzony z błędem absolutnym 0,14m

•

Odcinek IV o długości 110m, pomierzony z błędem absolutnym 0,11m

Błędy względne tych pomiarów wynoszą odpowiednio:

1073

1

322

30

,

0

1

1

=

=

∆

l

l

1338

1

281

21

,

0

2

2

=

=

∆

l

l

1193

1

167

14

,

0

3

3

=

=

∆

l

l

1000

1

110

11

,

0

4

4

=

=

∆

l

l

Zadanie 2. Zmierzono długości trzech różnych odcinków:

•

Odcinek I o długości 145 m z błędem absolutnym 7 cm

•

Odcinek II o długości 198 m z błędem absolutnym 9 cm

•

Odcinek III o długości 263 m z błędem absolutnym 13 cm

Który odcinek został pomierzony najdokładniej?

Odp.

2071

1

=

I

,

2200

1

=

II

,

2023

1

=

III

2.

Spostrzeżenia jednakowo dokładne

Zadanie 1.
Pewną długość pomierzono czterokrotnie i otrzymano wyniki:
1. 154,152 m
2. 154,147 m
3. 154,155 m
4. 154,150 m
Obliczyć najprawdopodobniejszą długość, błąd średni pojedynczego spostrzeżenia oraz błąd
średni wartości wyrównanej (średniej arytmetycznej).

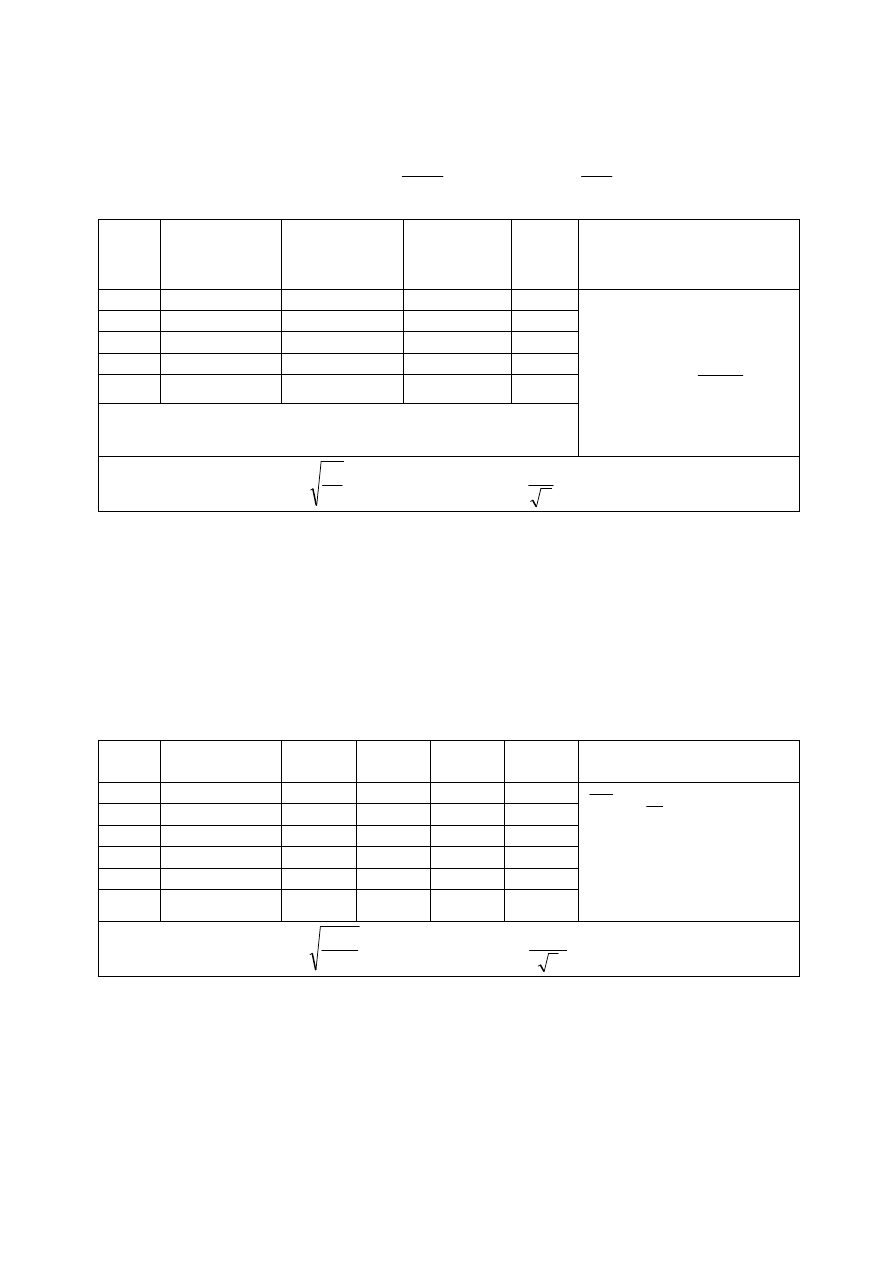
W celu przeprowadzenia kontroli obliczeń wykorzystuje się zależność:

[ ]

( )

[ ]

[ ]

n

L

L

2

2

∆

−

∆

=

υυ

lub

[ ] [ ] [ ][ ]

n

t

t

tt

−

=

υυ

Nr

Spostrzeżenia

i

L

[m]

Różnice

0

x

L

L

i

i

−

=

∆

[mm]

Poprawki

i

i

L

x

−

=

υ

[mm]

υυ

Obliczenia

1

154,152

+5

-1

1

2

154,147

0

+4

16

3

154,155

+8

-4

16

4

154,150

+3

+1

1

Suma

616,604

+16

0

34

Kontrola ogólna:

[

vv]=98-16

2

:4=34

n=4;

x=616,604:4=154,151m

x

0

=154,147m;

x=154,147m+

4

16

mm

x=154,147m+0,004m=
=154,151m

mm

m

4

,

3

3

34

±

=

±

=

mm

m

x

7

,

1

4

4

,

3

±

=

±

=

Odp. Najprawdopodobniejsza długość mierzonego odcinka wnosi 154,151 m; błąd średni
pojedynczego spostrzeżenia 3,4 mm, a błąd średni średniej arytmetycznej 1,7 mm.
Zatem pomierzony odcinek ma długość 154,151 m ±1,7 mm.

Zadanie 2.

Na pewnym punkcie pomierzono kąt 5 razy z tą samą dokładnością i otrzymano wyniki podane
poniżej w tabeli. Obliczyć najprawdopodobniejszą wartość kąta, błąd średni pojedynczego
pomiaru oraz błąd średni wartości wyrównanej (średniej arytmetycznej).

Nr

Wyniki

pomiarów

t

υ

υυ

tt

Obliczenia

1

82º41’15’’

15’’

+12’’

144

225

2

82º41’30’’

30’’

-3’’

9

900

3

82º42’00’’

60’’

-33’’

1089

3600

4

82º41’00’’

0

+27’’

729

0

5

82º41’30’’

30’’

-3’’

9

900

0

x

82º41’00’’

135

0

1980

5625

[ ]

''

27

'

41

82

0

°

=

+

=

n

t

x

x

Kontrola
[vv]=5625-3645=1980

x=82º41’27’’±10’’0

2

''

22

4

1980

±

=

±

=

m

0

''

10

5

2

''

22

±

=

±

=

M

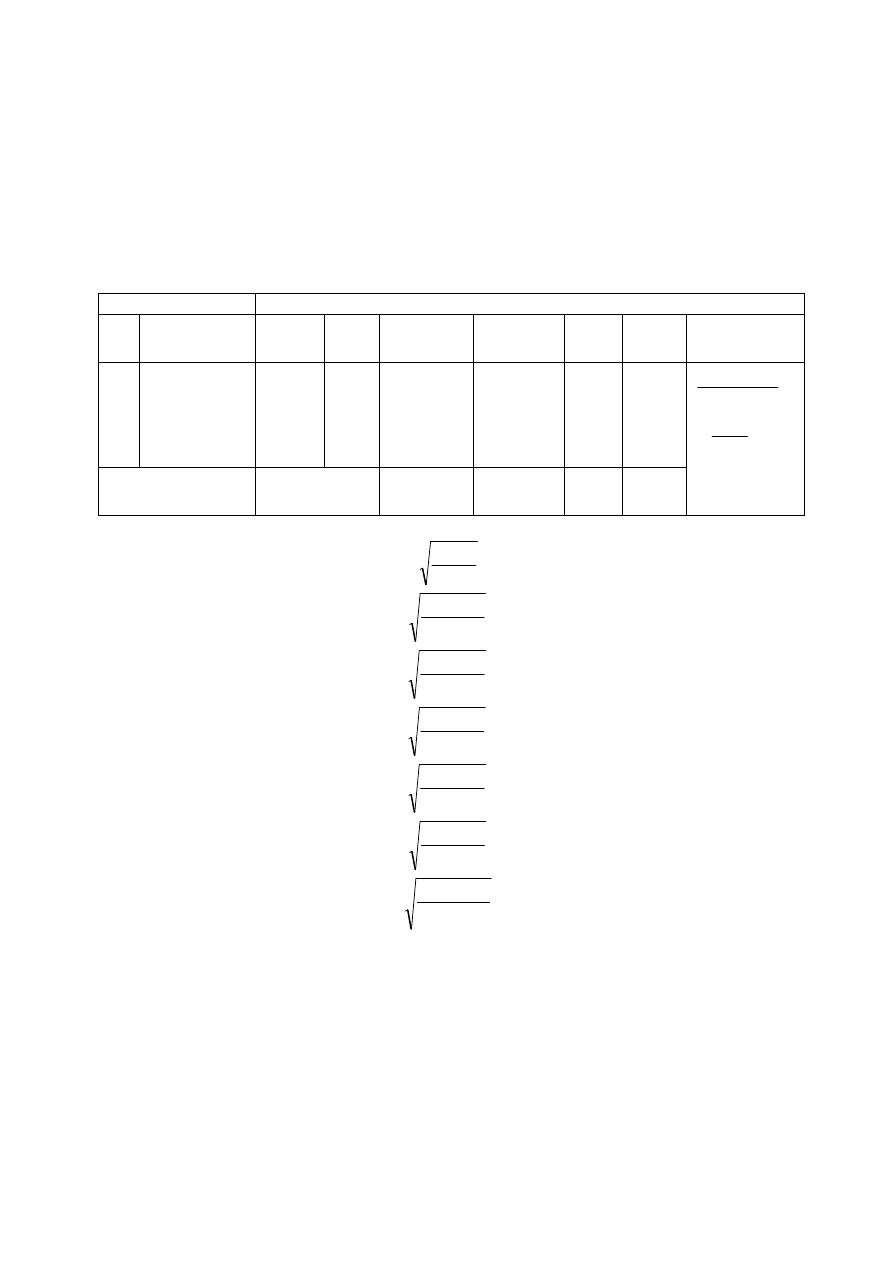
3.

Spostrzeżenia niejednakowo dokładne.

Dane są wartości pewnego kąta wraz z odpowiednimi wagami. Obliczyć:
- wagę ogólnej średniej arytmetycznej
- wartość ogólnej średniej arytmetycznej
- średni błąd spostrzeżenia typowego
- średnie błędy poszczególnych spostrzeżeń
- średni błąd ogólnej średniej arytmetycznej

Obserwacje

Obliczenia

Lp. Spostrzeżenie

i

α

0

α

α −

Wagi

p

)

(

0

α

α −

p

i

x

α

υ

−

=

υ

p

υυ

p

Uwagi

1.
2.
3.
4.
5.

105º11’31’’
105º11’24’’
105º11’19’’
105º11’27’’
105º11’26’’

+12’’

+5’’

0

+8’’
+7’’

3
6
2
5
4

+36
+30

0

+40
+28

-5’’3

+1’’7
+6’’7

-1’’3
-0’’3

-15,9

+10,2
+13,4

-6,5
-1,2

84,30

17,3
89,9

8,4
0,4

''

19

'

11

105

0

°

=

α

x=105º11’25’’7

20

134

0,0

200,3

(

)

[

]

[ ]

=

−

p

p

0

α

α

7

'

'

6

20

''

134

=

=

[ ]

1

''

7

1

0

±

=

−

±

=

n

p

m

υυ

[ ]

( )

1

''

4

1

1

1

±

=

−

±

=

n

p

p

m

υυ

[ ]

( )

9

''

2

1

2

2

±

=

−

±

=

n

p

p

m

υυ

[ ]

( )

0

''

5

1

3

3

±

=

−

±

=

n

p

p

m

υυ

[ ]

( )

2

''

3

1

4

4

±

=

−

±

=

n

p

p

m

υυ

[ ]

( )

5

''

3

1

5

5

±

=

−

±

=

n

p

p

m

υυ

[ ]

[ ]

( )

6

''

1

1

±

=

−

±

=

n

p

p

m

x

υυ

Zadanie 2.

Wyznaczyć najprawdopodobniejszą wartość kąta ABC, który pomierzono czterokrotnie
teodolitami teodolitami różnej dokładności, uzyskując wyniki:

1.

44º15’20’’ z błędem ±20’’

2.

44º14’58’’ z błędem ±10’’

3.

44º15’05’’ z błędem ±5’’

4.

44º15’10’’ z błędem ±15’’

Wartość średniego błędu jednostkowego wynosi:

''

10

0

±

=

m

Nr

Obserwacje

L

i

Błędy

średnie

m

i

Wagi

p

i

Różnice

0

x

L

L

i

i

−

=

∆

p ∆L

Poprawki

i

i

L

x

−

=

υ

υ

p

υυ

p

1.
2.
3.
4.

44º15’20’’
44º14’58’’
44º15’05’’
44º15’10’’

±20’’
±10’’

±5’’

±15’’

0,25
1,00
4,00
0,44

22’’

0

7’’

12’’

5,50

0

28,00

5,28

-15,2

+6,8

-0,2
-5,2

-3,8

+6,8

-0,8
-2,3

57,76
46,24

0,16

11,96

Suma

5,69

38,78

-0,1

116,12

Wagi obliczamy ze wzoru:

2

2

0

i

i

m

m

p

=

''

58

'

14

44

0

°

=

x

[ ]

[ ]

'

'

04

'

15

44

69

,

5

78

,

38

''

58

'

14

44

8

0

°

=

+

°

=

∆

+

=

p

L

p

x

x

2

''

6

3

12

,

116

0

±

=

±

=

m

[ ]

6

''

2

0

±

=

±

=

p

m

m

x

Kontrola ogólna:

[ ]

( )

[

]

[ ]

[ ]

06

,

116

69

,

5

:

78

,

38

36

,

380

2

2

2

=

−

=

∆

−

∆

=

p

L

p

L

p

p

υυ

Suma kontrolna różni się nieco od podanej w tabeli, ale wynika to z zaokrągleń czasie
obliczeń.

4.

Pary spostrzeżeń jednakowo dokładnych.

Zadanie 1.
Na podstawie wyników dwukrotnego pomiaru pięciu boków poligonu obliczyć błąd średni
różnicy pomiarów, błąd średni jednego pomiaru oraz błąd średni wyniku z poszczególnych par:

Spostrzeżenia

Nr

odcinka

l’

l’’

Średnia

arytmetyczna

L

d

dd

1.
2.
3.
4.
5.

155,64
150,83
152,39
153,28
154,47

155,68
150,80
152,46
153,22
154,52

155,66
150,82
152,42
153,25
154,50

-0,04

+0,03

-0,07

+0,06

-0,05

0,0016
0,0009
0,0049
0,0036
0,0025

[dd]=0,0135

Błąd średni różnicy pomiarów obliczamy następująco:

[ ]

052

,

0

5

0135

,

0

±

=

±

=

±

=

n

dd

m

d

Błąd średni jednego pomiaru obliczmy następująco:

[ ]

037

,

0

10

0135

,

0

2

0

±

=

±

=

±

=

n

dd

m

Błąd średni wyniku z poszczególnych par wynosi:

026

,

0

2

052

,

0

2

±

=

±

=

±

=

d

L

m

m

Zadanie 2.
Na podstawie wyników dwukrotnego pomiaru pięciu boków poligonu, obarczonych błędem
systematycznym, obliczyć błąd średni jednego pomiaru oraz błąd średni z poszczególnych par:

Spostrzeżenia

Nr

odcinka

l’

l’’

Średnia

arytmetyczna

L

d

d-σ

(d-σ)(d-σ)

1.
2.
3.
4.
5.

110,31
112,25
108,19
109,70
114,39

110,35
112,33
108,25
109,90
114,36

110,33
112,29
108,22
109,80

114,375

-0,04
-0,08
-0,06
-0,20

+0,03

+0,03

-0,01

+0,01

-0,13

+0,10

0,0009
0,0001
0,0001
0,0169
0,0100

[d]=-0,35

[(d-σ)

2

]=0,0280

[ ]

07

,

0

5

35

,

0

−

=

−

=

=

n

d

σ

błąd średni pojedynczego pomiaru obliczamy następująco:

(

)(

)

[

]

( )

059

,

0

8

0280

,

0

1

2

±

=

±

=

−

−

−

±

=

n

d

d

m

o

σ

σ

błąd średni wyniku z poszczególnych par wynosi:

042

,

0

2

±

=

±

=

o

L

m

m