Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

BADANIE MOLEDU PIECA ŁUKOWEGO

1. Cel i zakres ćwiczenia

Celem ćwiczenia jest zapoznanie się z działaniem urządzenia elektrotermicznego

łukowego oraz zbadanie najważniejszych parametrów i charakterystyk tego urządzenia.

Zakres ćwiczenia obejmuje wyznaczenie charakterystyk urządzenia elektrotermicznego

łukowego dwoma sposobami:

a)

na podstawie pomiarów wszystkich charakterystycznych wielkości w funkcji

prądu

b)

na podstawie próby zwarcia i wykresu kołowego

2. Wprowadzenie do ćwiczenia

Charakterystyki urządzenia elektrotermicznego łukowego

Charakterystyki urządzenia elektrotermicznego łukowego są to zależności wielkości

elektrycznych i energetycznych oraz wskaźników pracy urządzenia od natężenia prądu

roboczego. Najważniejsze znaczenie praktyczne mają następujące charakterystyki:

P

g

= f(I) – charakterystyka mocy grzejnej;

P

e

= f(I) – charakterystyka mocy elektrycznej (czynnej) urządzenia;

P

se

= f(I) – charakterystyka mocy strat elektrycznych urządzenia;

Q

e

= f(I) – charakterystyka mocy biernej urządzenia;

S

e

= f(I) – charakterystyka mocy pozornej urządzenia;

η

e

= f(I) - charakterystyka sprawności elektrycznej (czynnej) urządzenia;

cos

ϕ

e

= f(I) – charakterystyka współczynnika mocy;

U

a

= f(I) – charakterystyka napięcia łuku.

Charakterystyki nogą być wyznaczone bezpośrednio, -lub pośrednio na podstawie wielu

pomiarów charakterystycznych wielkości przy różnych. wartościach prądu pomiarowego.

Zazwyczaj pomiary takie "są bardzo uciążliwe i mało dokładne, gdyż ze względu na

niespokojną pracę łuku mierzone wielkości ulegają ciągłym, zmianom.

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

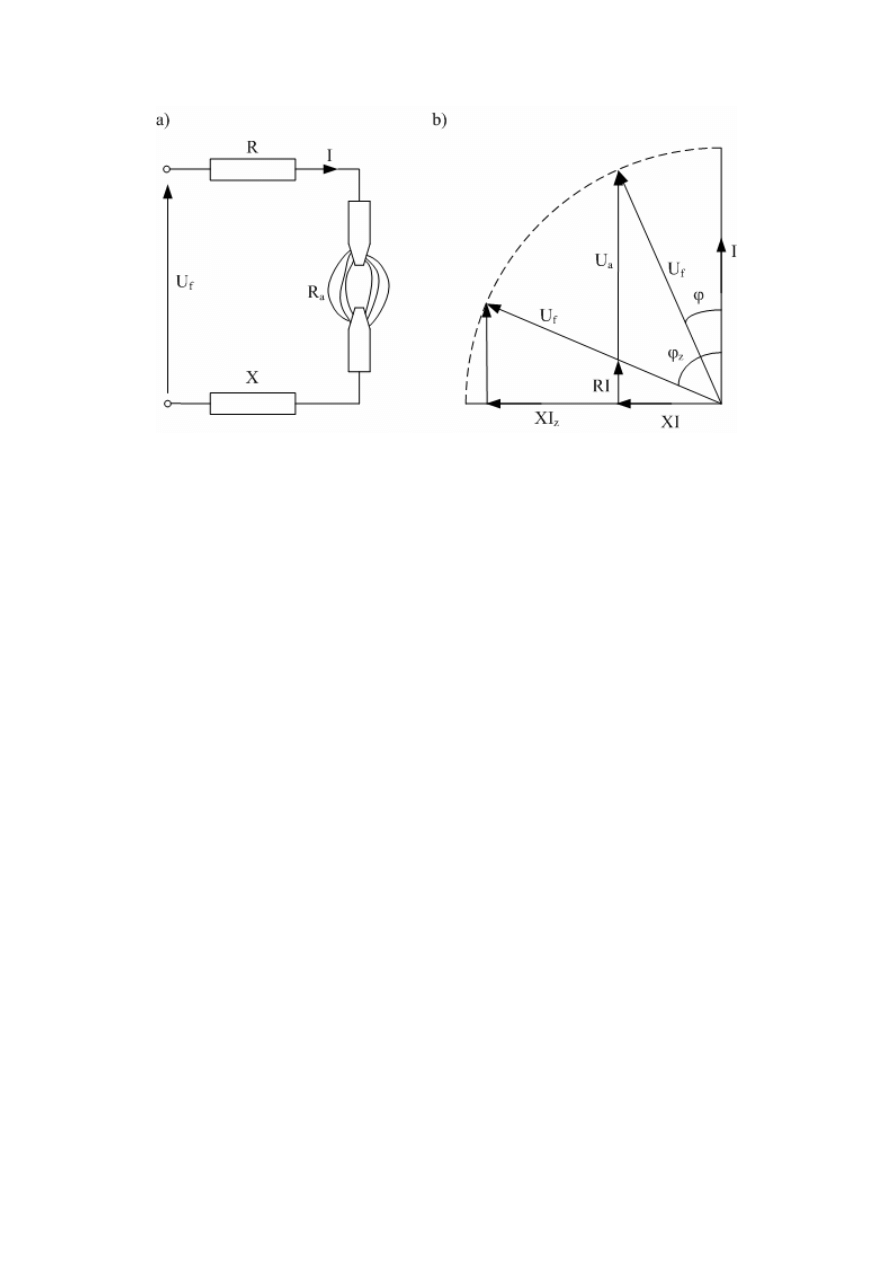
Rys. 1. zastępczy schemat elektryczny urządzenia elektrotermicznego łukowego: a) schemat,

b) wykres wektorowy

Przyjmując pewne założenia upraszczające można wyznaczyć charakterystyki

urządzenia elektrotermicznego łukowego w sposób analityczny. Zwykle przyjmuje się, że

schemat zastępczy trójfazowego urządzenia łukowego ma postać obwodu nierozgałęzianego

(rys.1 a), w którym: U

f

–napięcie fazowe, R, X – wypadkowa rezystancja i reaktancja układu

zasilania R

o

– zastępcza rezystancja łuku. Zależnie od tego czy U

f

oznacza napięcie po stronie

pierwotnej czy wtórnej transformatora piecowego, rezystancja i reaktancja obwodu powinny

być odpowiednio przeliczone, z uwzględnieniem przekładni transformatora. Charakterystyki

urządzenia wyznacza się przyjmując następujące założenia:

a)

napięcie zasilania U

f

i prąd I są sinusoidalnie zmienne w czasie a ponadto wartość

skuteczna U

f

= const,

b)

rezystancja R i reaktancja X obwodu zasilającego są stałe i niezależne od prądu I,

c)

łuki palą się stabilnie i bezprzerwowo, ponadto są jednakowe (symetryczne) we

wszystkich fazach,

d)

istnieje symetria napięć zasilających i trójfazowego układu zasilania pieca łukowego.

Rzeczywisty przebieg napięcia łuku w czasie U

a

= f(t) o wartości skutecznej U

a

zastępuje się

przebiegiem sinusoidalnym o tej samej wartości skutecznej. Zastępcza rezystancja łuku

R

a

=U

a

/I . Ponieważ rezystancja R

a

i napięcie U

a

są trudne do zmierzenia, w obliczeniach

wielkości te wyraża się za pomocą innych, znanych lub łatwo mierzalnych parametrów.

Natężenie prądu w urządzeniu elektrotermicznym łukowym zależy od zmiennej

rezystancji łuku R

a

i wyraża się zależnością:

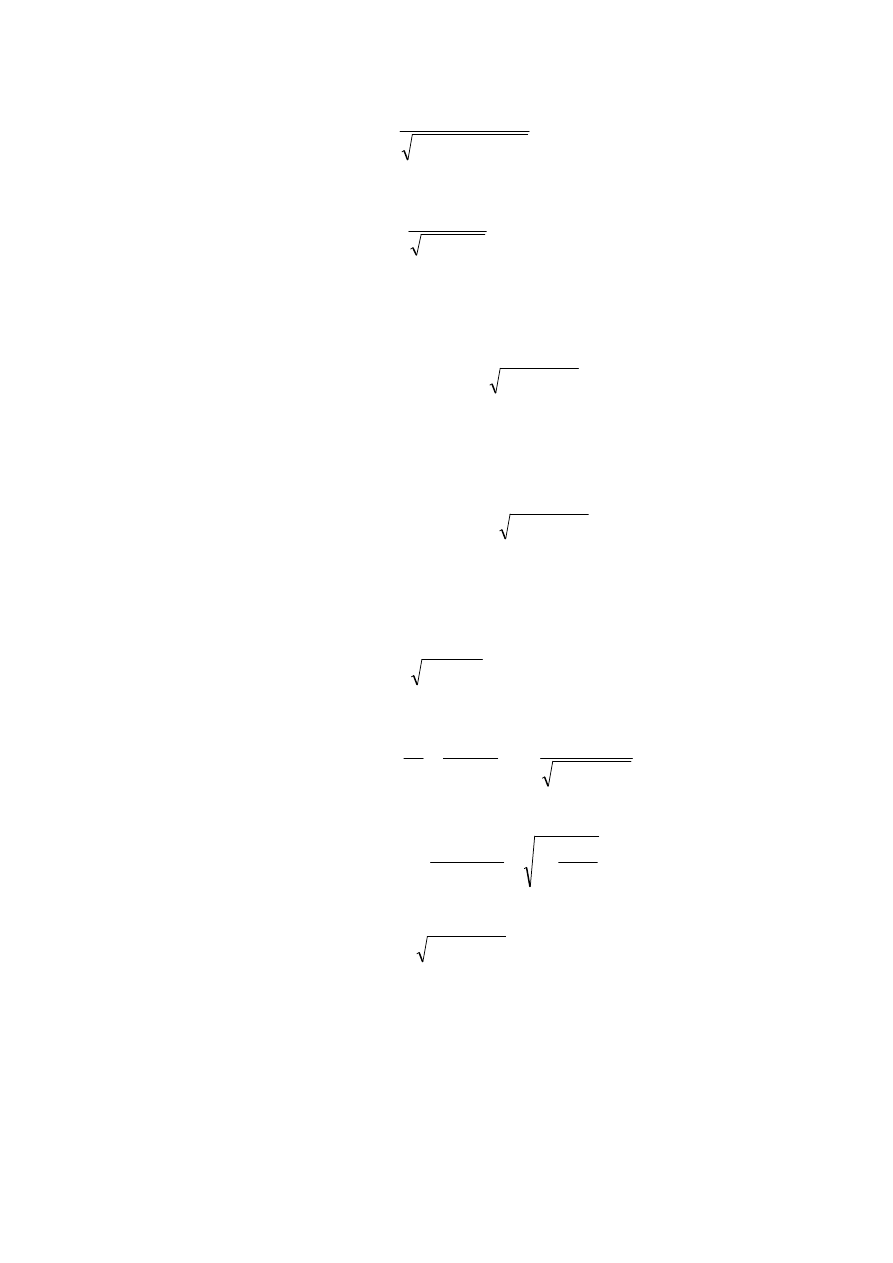
Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

(1)

2

2

a

f

X

)

R

R

(

U

I

+

+

=

Prąd zwarciowy w stanie zwarcia eksploatacyjnego (R

a

=0)

(2)

2

2

f

z

X

R

U

I

+

=

Charakterystyki trójfazowego urządzenia elektrotermicznego łukowego wyrażają się

następującymi zależnościami:

a)

moc grzejna

(3)

2

2

2

2
f

2

a

g

RI

3

I

X

U

I

3

I

R

3

P

−

−

=

=

b) moc strat elektrycznych

(4)

2

se

RI

3

P

=

c) moc elektryczna czynna urządzenia

(5)

2

2

2
f

se

g

e

I

X

U

I

3

P

P

P

−

=

+

=

d) moc bierna urządzenie

(6)

2

e

XI

3

Q

=

e) moc pozorna urządzenia

(7)

2
e

2

e

e

Q

P

S

+

=

f) sprawność elektryczna urządzenia

(8)

2

2

2
f

a

a

e

g

I

X

U

RI

1

R

R

R

P

P

−

−

=

+

=

=

η

g) współczynnik mocy urządzenia

(9)

2
f

2

2

f

a

U

I

X

1

U

I

)

R

R

(

cos

−

=

+

=

ϕ

h) napięcie łuku

(10)

RI

I

X

U

U

2

2

2
f

a

−

−

=

Z zależności (3) –(10) wynika , że charakterystyki urządzenia elektrotermicznego

łukowego można wykreślić wówczas, gdy są znane parametry R i X obwodu zasilającego.

Parametry te mogą być wyznaczone na podstawie pomiarów wykonanych w stanie zwarcia

eksploatacyjnego (zwarcia elektrod z wsadem).

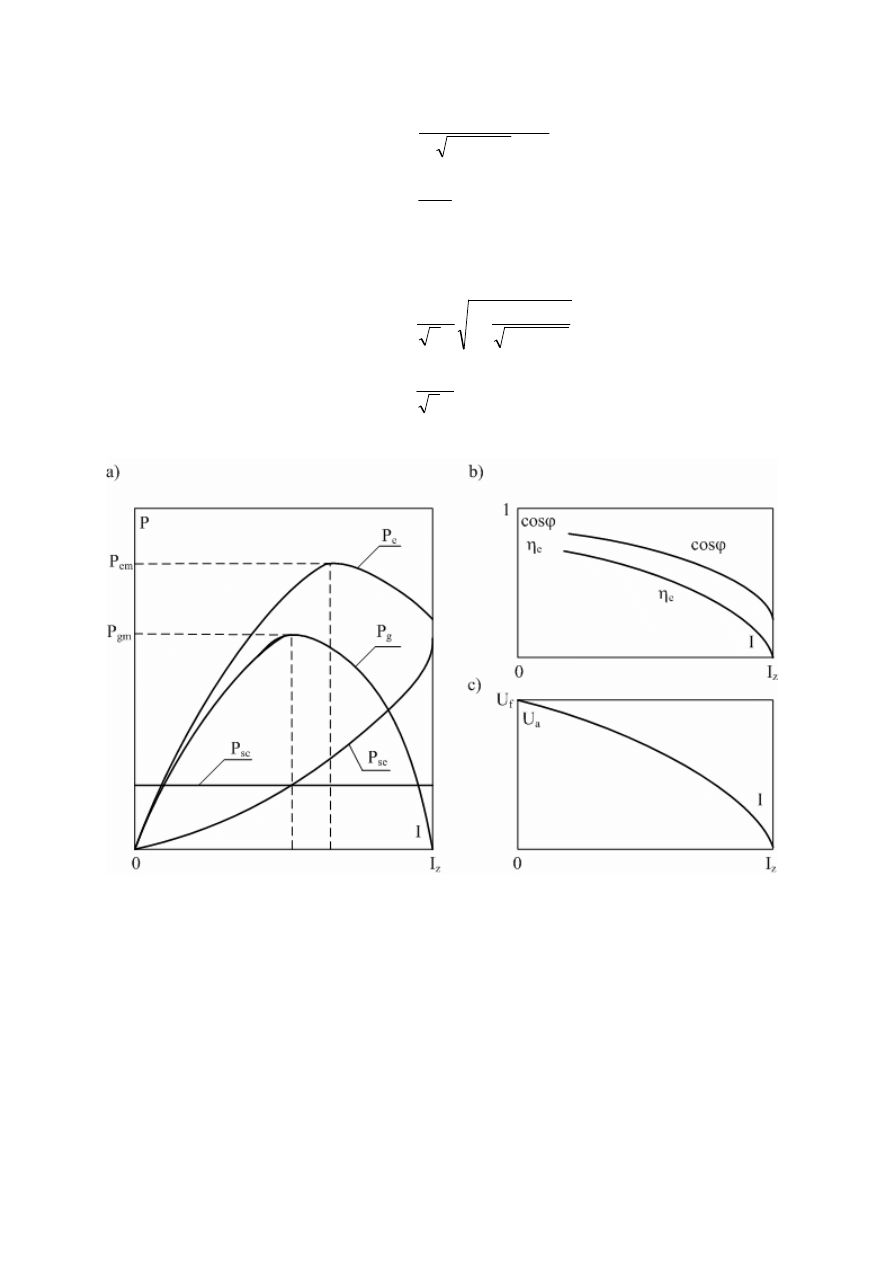
Niektóre typowe charakterystyki pieca łukowego bezpośrednio przedstawiono na rys.

2. Charakterystyki P

g

= f(I) i P

e

= f(I) mają maksima wynoszące odpowiednio

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

(11)

)

R

X

R

(

2

U

3

P

2

2

2
f

gm

+

+

=

(12)

X

2

U

3

P

2
f

em

=

Eksperymentalne wartości P

gm

i P

em

występują dla prądów o wartościach wynoszących

odpowiednio

(13)

2

2

f

gm

X

R

R

1

X

2

U

I

+

−

=

(14)

X

2

U

I

f

em

=

Rys. 2. Charakterystyki urządzenia elektrotermicznego łukowego

Wykres kołowy urządzenia elektrotermicznego łukowego

Stosując zasady inwersji elektrycznej można zbudować wykres kołowy urządzenia

elektrotermicznego łukowego. Wykres taki dostarcza wielu istotnych informacji o stanie

układu w warunkach, zmienności niektórych, parametrów elektrycznych. Na podstawie

wykresu kołowego można wyznaczy przebiegi charakterystyk urządzenia łukowego.

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

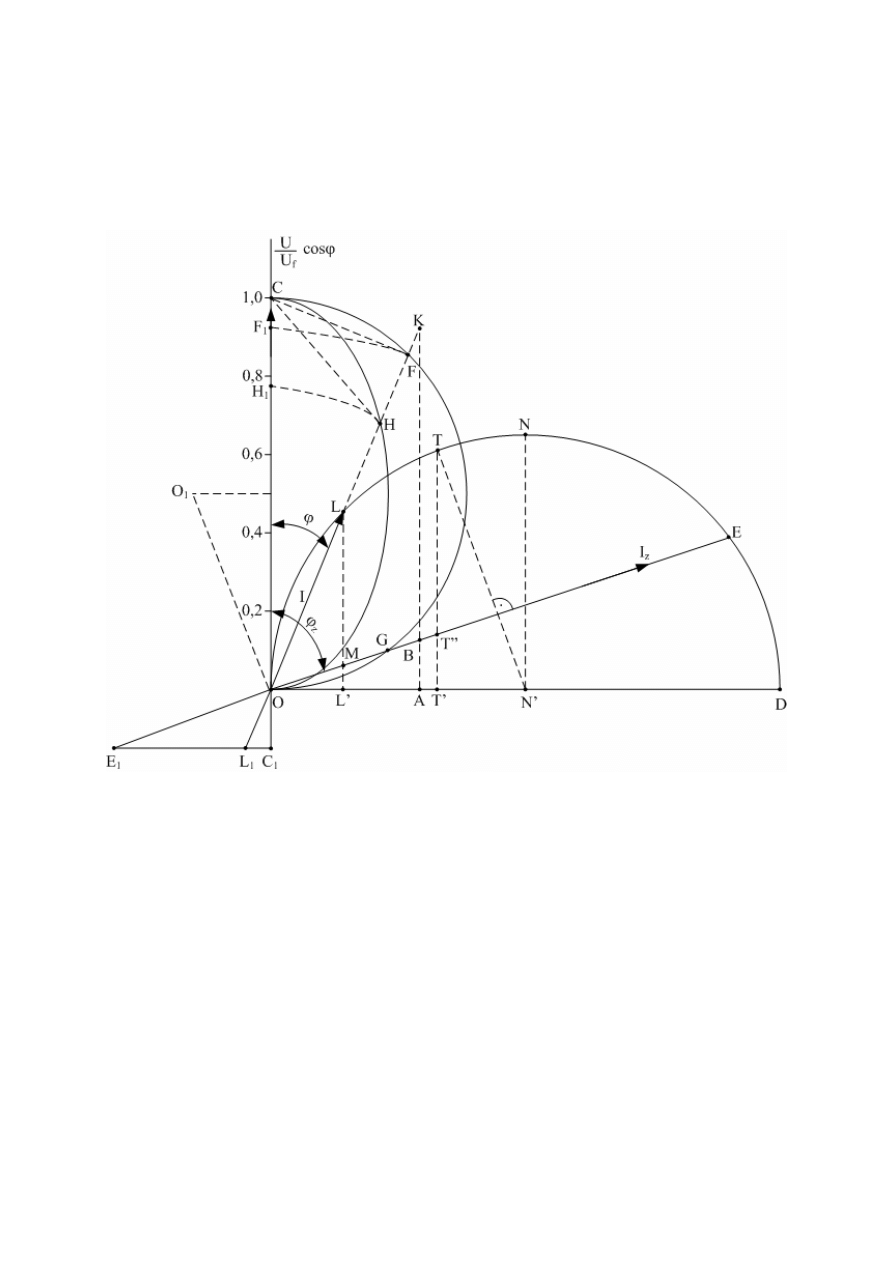
Na rysunku 3 przedstawiono wykres kołowy układu e elektrotermicznego łukowego,

którego, zastępczy schemat elektryczny ma postać obwodu nierozgałęzionego, złożonego z

elementów R, Ra, X (rys.1). Przyjęto że w obwodzie tym są spełnione założenia wymienione

w podpunkcie 2.

Rys.3 Wykres kołowy urządzenia elektrotermicznego kołowego

Wykres kołowy (rys. 3) wykonuje się w następujący sposób. Przyjmując odpowiednią

podziałkę impedancyjną m

z

(w mm/

Ω

) wykreśla się trójkąt impedancji OAB, w którym bok

OA = m

z

X, a prostopadły do niego bok AB = m

z

R. Bok AB reprezentuje impedancję

obwodu w stanie zwarcia eksploatacyjnego. Od punktu 0 odkłada się na osi rzędnych

wektor napięcia fazowego o długości OC = m

u

U

f

, przy czym m

u

jest oznacza przyjętą

podziałkę napięciową (w mm/V). Następnie wykonuje się półokrąg o średnicy OD =

m

i

I

zx

, leżącej na osi odciętych. Średnica OD, w podziałce prądowej m

i

(w mm/A),

odpowiada abstrakcyjnemu prądowi I

zx

= U

f

/X, który płynąłby w obwodzie zawierającym

tylko reaktancje X (tzn. w obwodzie o rezystancjach R=0 i R

a

=0). Półokrąg o średnicy OD

stanowi wykres kołowy prądu w obwodzie nierozgałęzionym (rys. 1). Wektor OE, otrzymany

w wyniku przedłużenia linii OB do przecięcia z półokręgiem, reprezentuje prąd I

z

zwarcia

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

eksploatacyjnego. Dla rezystancji łuku R

a

zmieniającej się od zera do nieskończoności

koniec wektora prądu I, zaczepionego w punkcie 0, przemieszcza się po łuku półokręgu od

punktu E do 0. Luk EO półokręgu jest miejscem geometrycznym końców wektorów prądu

w różnych stanach roboczych urządzenia łukowego. Kąt przesunięcia fazowego między

napięciem i prądem zmienia się od wartości

ϕ

z

=arctg X/R do

ϕ

= 0, zależnie od rezystancji

łuku R

a

.

W celu wyznaczenia składowych czynnej i biernej napięcia fazowego wykreśla się

półokrąg o średnicy OC, położony na prawo od osi rzędnych. Przedłużenie wektora prądu I

do przecięcia się z tym półokręgiem w punkcie F wyznacza odcinki OF i FC, reprezentujące

w podziałce m

u

odpowiednio składowe czynna i bierną napięcia U

f

. Punkt G przecięcia

półokręgu OFC z odcinkiem OE wyznacza minimalną wartość U

R min

= OG/m

u

składowej

czynnej i maksymalna wartość U

X max

= GC/m

u

składowej biernej napięcia fazowego,

występujących w czasie zwarcia eksploatacyjnego. Ze wzrostem rezystancji łuku R

a

od zera

do nieskończoności składowa czynna napięcia rośnie od U

R min

do U

f

, składowa bierna

natomiast maleje od wartości U

X max

do zera. Aby łatwiej odczytać wartości składowej

czynnej napięcia na odcinku OC nanosi się podziałkę wartości względnych napięcia w

zakresie od zera do (punkt 0) do 1 (punkt C).

Stosunek składowej czynnej U

R

napięcia do napięcia fazowego U

f

jest równy

współczynnikowi mocy, a więc cos

ϕ

= OF/OC. Wynika stąd że półokrąg OFC może służyć

do wyznaczania wartości współczynnika mocy. W celu ustalenia wartości współczynnika

mocy promieniem OF zaznacza się na odcinku OC punkt F

1

, który wyznacza wartość cos

ϕ

na

przyjętej uprzednio podziałce.

W analizie warunków pracy układu elektrotermicznego łukowego jest konieczna

znajomość napięcia łuku U

a

w różnych stanach roboczych urządzenia. W celu wyznaczenia

napięcia U

a

wykreśla się następny okrąg , którego łuk jest miejscem geometrycznym końców

wektorów U

a

za czepionych w punkcie O. Środkiem tego okręgu jest punkt O

1

przecięcia

półprostej prostopadłej do wektora I

z

poprowadzonej z punktu O i półprostej

poprowadzonej ze środka odcinka OC prostopadle do osi rzędnych. Okrąg ten jest

zatoczony promieniem OO

1

. Punkt H przecięcia tego okręgu przez linię określającą kierunek

wektora prądu Iz wyznacza odpowiadającą temu prądowi wartość napięcia łuku U

a

= OH/m

u

.

Odcinek HC reprezentuje natomiast spadek napięcia w układzie zasilającym ( na impedancji

R+jX) przy czym składowe tego spadku napięcia: RI = HF/ m

u

, XI = m

u

. zaznaczając

promieniem OE punkt H

1

na odcinku OC można bezpośrednio z podziałki na osi rzędnych

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

odczytać wartość względną napięcia łuku U

a

/U

f

. Ze wzrostem rezystancji łuku R

a

od zera do

nieskończoności, koniec wektora napięcia U

a

przemieszcza się po łuku OHC, przy czyn

wartość napięcia U

a

zmienia się od zera do U

f

.

Przedłużając odcinek AB do przecięcia się z kierunkiem wektora prądu I (punkt

przecięcia K) otrzymuje się trójkąt impedancji OAK, odpowiadający tej wartości prądu. W

trójkącie tym odcinek BK reprezentuje rezystancję łuku R

a

= BK/m

z

, a przeciwprostokątna

OK – impedancję

2

2

a

X

)

R

R

(

Z

+

+

=

obwodu z łukiem.

Rzutując prostopadle koniec L wektora prądu I na osi odciętych o trzymuje się trójkąt

OLL’, którego boki LL’ i OL’ przedstawiają w podziałce m

i

odpowiednio składowe czynną

(Icos

ϕ

) i bierną (Isin

ϕ

) prądu I.

Ponieważ moc pozorna obwodu

(15)

I

U

3

S

f

e

=

moc czynna

(16)

ϕ

=

cos

I

U

3

P

f

e

i moc bierna

(17)

ϕ

=

sin

I

U

3

Q

f

e

więc dla U

f

= const trójkąt OLL’ można traktować jako trójkąt mocy, w którym bok OL

reprezentuje moc pozorną S

e

, bok LL’ – moc czynną P

e

i bok OL’ – moc bierną Q

e

obwodu.

W tych warunkach podziałka mocy

(18)

f

i

p

U

3

m

m

=

A poszczególne moce można obliczyć korzystając z zależności

(19)





















=

=

=

p

e

p

e

p

e

m

'

OL

Q

m

'

LL

P

m

OL

S

Mocz czynna P

e

jest sumą mocy grzejnej P

g

i mocy strat elektrycznych P

se

(20)

)

R

R

(

I

3

P

P

P

a

2

se

g

e

+

=

+

=

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

Można wykazać, że w podziałce m

p

odcinek IM przedstawia moc grzejną P

g

a odcinek ML’ –

moc strat elektrycznych P

se

. W związku z tym

(21)













=

=

p

se

p

g

m

'

ML

P

m

IM

S

W warunkach zmiany rezystancji łuku od zera do nieskończoności, moc elektryczną P

e

w

podziałce m

p

przedstawiają rzędne punktu końcowego wektora prądu I, przemieszczającego

się od punktu E do punktu O po łuku okręgu ELO. Odcinek OE odpowiada mocy grzejnej, a

część leżąca pod odcinkiem OE – mocy strat elektrycznych.

Maksymalną moc elektryczną P

em

obwodu wyraża w podziałce m

p

odcinek NN’ równy

promieniowi półokręgu prądów. Maksymalnej mocy grzejnej odpowiada na wykresie odcinek

TT”, przy czym punkt T jest punktem przecięcia łuku OLN prostą prostopadłą do wektora

prądu zwarciowego I

z

przechodzącą przez środek półokręgu prądów.

Sprawność elektryczna urządzenia łukowego wyraża się stosunkiem długości

odcinków LM i LL’.

(22)

'

LL

LM

P

P

e

g

=

=

η

Sprawność elektryczną można także wyznaczyć graficznie. W tym celu odcinki OC i CE

przedłuża się poza punkt O w dół i przedłużenia te przecina się linią równoległą do osi

odciętych. Powstaje w ten sposób trójkąt OE

1

C

1

który wyznacza sprawność

η

e

dla

określonego prądu I przedłuża się kierunek wektora tego prądu do przecięcia z odcinkiem

E

1

C

1

(punkt L

1

). Uwzględniając podobieństwo trójkątów OL

1

C

1

i OLL oraz OE

1

C

1

i OML’

można wykazać równość stosunków

(23)

1

1

1

1

e

C

E

L

E

'

LL

LM

=

=

η

Jeżeli na odcinku E

1

C

1

naniesie się podziałkę sprawności, przyporządkowując punktowi E

1

wartość

η

e

= 0 i punktowi C

1

– wartość

η

e

= 1, to punkt L

1

wyznaczy na tej podziałce szukaną

wartość sprawności

η

e

dla określonego prądu I.

Jak wynika z przedstawionego toku postępowania podczas wykonywania wykresu

kołowego urządzenia łukowego, wykres ten można narysować pod warunkiem, że znane są

wartości U

f

, R i X.

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

3. Badania

Układ pomiarowy

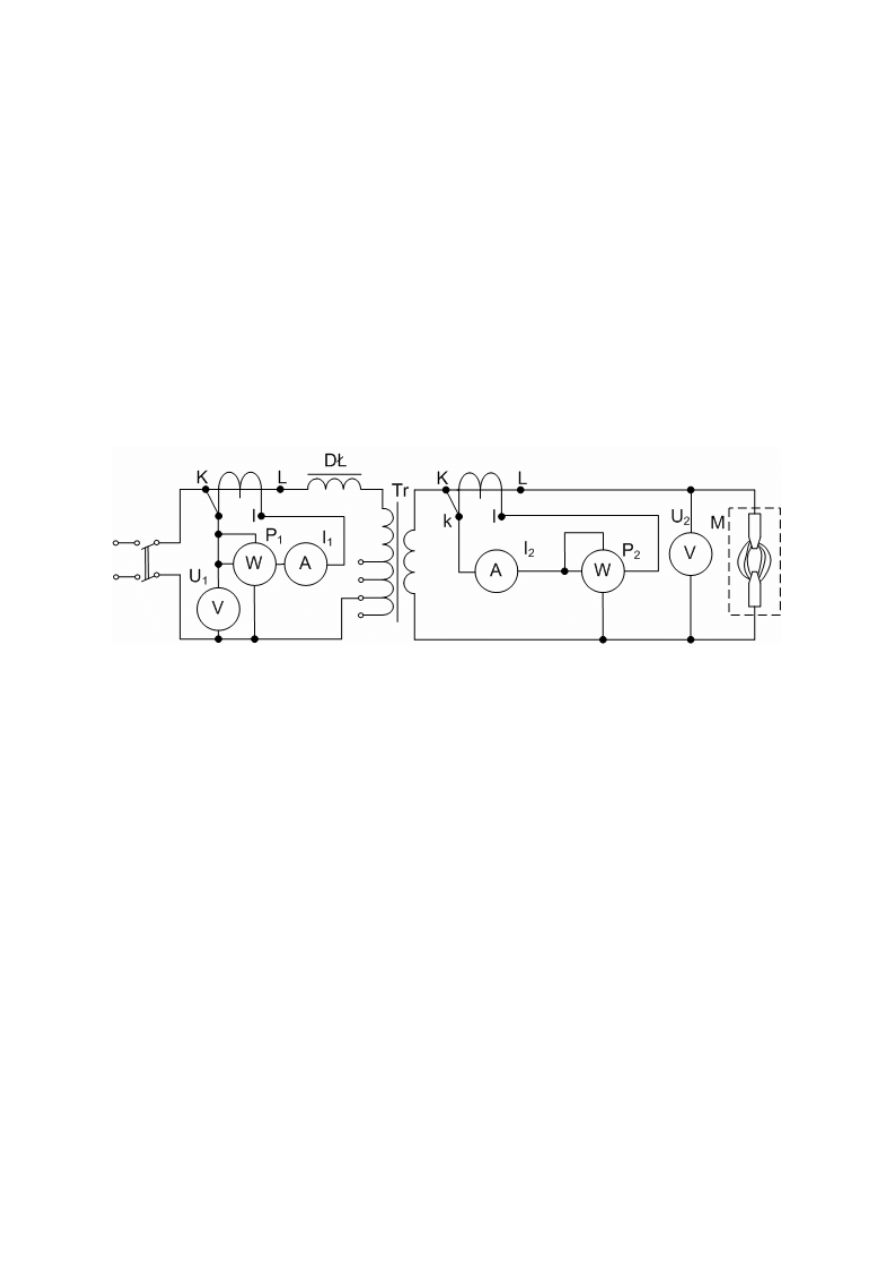
Pomiary wykonuje się w układzie, którego schemat elektryczny przedstawiono na

rysunku 4.

Obiektem badanym jest urządzenie łukowe jednofazowe, stanowiące model fizyczny

pieca łukowego pośredniego. Model jest wyposażony w elektrody węglowe o średnicy 10mm,

z których jedna jest umocowana w uchwycie stałym, a druga w uchwycie ruchomym. Długość

łuku reguluje się ręcznie za pomocą śruby pociągowej połączonej z ruchomym uchwytem

elektrodowym.

Rys. 4. Schemat układu do badania urządzenia elektrotermicznego łukowego

Urządzenie łukowe jest zasilane przez transformator jednofazowy o znamionowym napięciu

230V. Napięcie wtórne jest regulowane za pomocą zaczepów uzwojenia pierwotnego. W celu

ograniczenia prądu w stanie zwarcia elektrod i dla polepszenia warunków palenia się łuku,

szeregowo z uzwojeniem pierwotnym jest włączony dławik o indukcyjności regulowanej

skokowo.

Badanie urządzenia łukowego

Przed przystąpieniem do właściwych pomiarów należy nastawić wartość napięcia

wtórnego transformatora w stanie jałowym U

20

, zgodnie ze wskazówkami prowadzącego

ć

wiczenie. Ustalonej przekładni transformatora nie można zmieniać w trakcie dalszych

pomiarów.

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

W układzie jak na rysunku 4 należy wykonać pomiary napięć U

1

, U

2

prądów I

1

, I

2

i

mocy P

1

, P

2

. Pomiary te powinny być wykonane w zakresie zmian natężenia prądu,

poczynając od stanu zwarcia elektrod aż do stanu, w którym następuje zgaśnięcie łuku. Prąd

łuku reguluje się przez zmianę długości łuku. Odczyty wskazań wszystkich przyrządów

powinny być wykonane w miarę możliwości jednocześnie.

Bezpośrednie pomiary mocy grzejnej i napięcia łuku są niemożliwe gdyż wysoka

temperatura w obszarze wyładowania łukowego nie pozwala na przyłączenie przewodów do

końców elektrod. Mierzone napięcie U

2

jest sumą napięcia łuku U

a

i spadku napięcia R

e

I

2

na

elektrodach, a moc P

2

jest sumą mocy grzejnej i mocy strat R

e

I

2

w elektrodach. Aby móc

obliczyć napięcie łuku U

a

oraz i moc grzejną P

g

, należy wyznaczyć rezystancję elektrod R

e

przez pomiar. Rezystancję R

e

mierzy się metoda pośrednią (techniczną) mierząc napięcie U

2

i

prąd I

2

w stanie zwarcia elektrod. Ze względu na wypalanie się elektrod i związaną z tym

zmianę ich rezystancji, pomiary te należy wykonać dwukrotnie : na początku i na końcu serii

pomiarów. Do obliczeń napięcia U

a

i mocy P

g

bierze się średnią wartość rezystancji R

e

z tym

pomiarów.

Na podstawie pomiarów zwarcia można obliczyć następujące wielkości:

a) impedancję obwodu zasilającego

(24)

1

1

I

U

Z

=

b) rezystancję obwodu zasilającego

(25)

2

1

1

I

P

R

=

c) reaktancję obwodu zasilającego

(26)

2

2

R

Z

X

−

=

d) teoretyczny prąd zwarcia

(27)

X

U

I

1

zX

=

e) rezystancję elektrod

(28)

2

2

e

I

U

R

=

Obliczone w ten sposób R, X, I

zX

stanowią podstawę do sporządzenia wykresu kołowego

urządzenia łukowego.

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

Wielkości niezbędne do wykreślenia charakterystyk urzadzenia łukowego oblicza się

według następujących zależności:

(29)

2
2

e

2

g

I

R

P

P

−

=

(30)

g

e

se

P

P

P

−

=

(31)

1

1

e

I

U

S

=

(32)

e

g

e

P

P

=

η

(33)

e

e

S

P

cos

=

ϕ

(34)

2

e

2

a

I

R

U

U

−

=

4. Opracowanie wyników badań

W sprawozdaniu należy zamieścić:

1. Wyniki pomiarów i obliczeń zestawione w tabelach 1, 2, i 3

Tabela 1. Wyniki pomiarów bezpośrednich dla stanu roboczego urządzenia łukowego

U

1

I

1

P

1

= P

e

U

2

I

2

P

2

Lp.

V

A

W

V

A

W

Tabela 2. Wyniki pomiarów i obliczeń dla stanu zwarcia urządzenia łukowego

U

1

I

1

P

1

= P

e

U

2

I

2

Z

R

X

I

zX

R

1

Lp.

V

A

W

V

A

Ω

Ω

Ω

A

Ω

Wersję elektroniczną opracował:

mgr inż. Robert Fiuk

Tabela 3. Zestawienie wyników pomiarów i obliczeń charakterystyk urządzenia łukowego

I

1

I

2

P

1

= P

e

P

g

P

se

S

e

η

e

cos

ϕ

Lp.

A

A

W

W

W

VA

-

-

2. Wykresy charakterystyk P

e

, P

g

, P

se

,

η

e

, cos

ϕ

, U

a

w funkcji prądu I

1

wykonane na podstawie

wyników pomiarów i obliczeń zestawionych w tabeli 3.

3. Wykres kołowy urządzenia łukowego.

4. Wykresy charakterystyk wymienionych w punkcie 2, wykonane na podstawie wykresu

kołowego.

5. Wyjaśnienia i wnioski dotyczące różnic istniejących między charakterystykami

wyznaczonymi na podstawie pomiarów i charakterystyk wyznaczonych na podstawie

wykresu kołowego.

6. Wyjaśnienia i wnioski dotyczące różnic w kształcie przebiegów przedstawionych na rys. 2

i charakterystyk wyznaczonych na podstawie badań urządzenia łukowego.