
Statystyka w analizie i planowaniu eksperymentu
Wykład 6
Analiza regresji
Przemysław Biecek
Dla 1 roku studentów Biotechnologii

Wejściówka
Proszę na (niewielkiej) kartce napisać:
1
Imię, nazwisko,
2
Nr. indeksu,
3
Nazwisko osoby prowadzącej ćwiczenia
2/24

Wejściówka
Wybierz dwie ostatnie różne cyfry swojego numeru indeksu.
Na poziomie istotności α = 0.01 zweryfikuj hipotezę o równości
średnich liczb w kolumnach odpowiadających wybranym powyżej
cyfrom.
Przyjmij, że rzeczywista wariancja tych liczb wynosi 8.
cyfra indeksu
1
2
3
4
5
6
7
8
9
0
próba
1
5
8
2
7
8
6
8
8
0
4
7
4
9
8
8
9
3
7
3
7
8
4
2
0
3
4
1
6
8
9
8
5
6
1
4
5
5
4
6
4
7
2
8
8
1
4
5
3
3
Wyznacz p wartość dla tej hipotezy.
3/24
Kilka zdań o historii regresji
Charles Darwin
Friedrich Gauss
Francis Galton
Karl Pearson
4/24
Regresja prosta
Obserwujemy zależność pomiędzy czasem reakcji a logarytmem
stężenia produktu w roztworze.
●
●
●
●
●
●
●
●
●
●
●
●
●
0.0
0.2
0.4
0.6
0.8
1.0
1.2
−1.0
−0.5
0.0
0.5
1.0
1.5
2.0
x
y
5/24
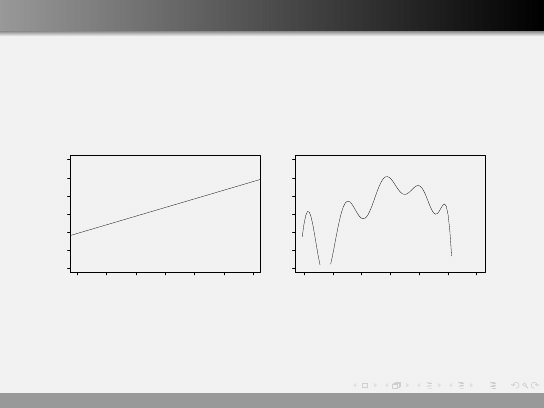
Regresja prosta
Na podstawie wyników eksperymentu możemy ocenić zależność
pomiędzy czasem a stężeniem produktu.
Możemy rozważać różne modele zależności pomiędzy tymi
zmiennymi.
●
●
●
●
●
●
●
●
●
●
●
●
●
0.0
0.2
0.4
0.6
0.8
1.0
1.2
−1.0
−0.5
0.0
0.5
1.0
1.5
2.0
x
y
0.0
0.2
0.4
0.6
0.8
1.0
1.2
−1.0
−0.5
0.0
0.5
1.0
1.5
2.0
x
y
●
●
●
●
●
●
●
●
●
●
●
●
●
y =
−0.05 + 1.2x
y =
0.2 + 24.5x − 375x
2
− 2452x
3
+ 38641x
4
− 58765x
5
− 720012x
6
+3441503x
7
− 3341678x
8
− 16322170x
9
+ 66451510x
10
− 120777700x
11
+132393300x
12
− 93195130x
13
+ 42084630x
14
− 11654990x
15
+ 1775557x
16
−111920x
17
6/24
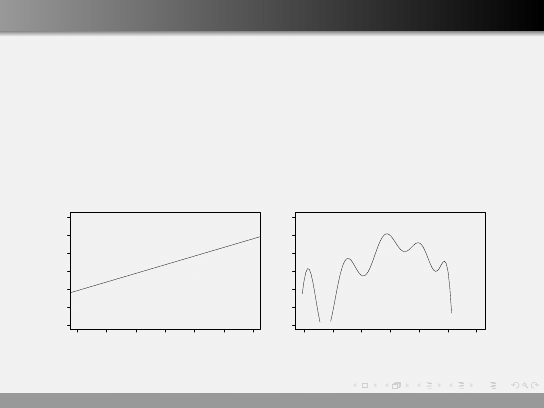
Regresja prosta
„As simple as possible, but not simpler” Albert Einstein.
Opisując zależności pomiędzy zmiennymi powinniśmy używać
najprostszych możliwych związków.
Zasada KISS („Keep It Simple, Stupid”).
Prostych modeli łatwiej używać, mają też najczęściej równie dobrą
lub lepszą zdolność predykcyjną.
●
●
●
●
●
●
●
●
●
●
●
●
●
0.0
0.2
0.4
0.6
0.8
1.0
1.2
−1.0
−0.5
0.0
0.5
1.0
1.5
2.0
x
y
●
0.0
0.2
0.4
0.6
0.8
1.0
1.2
−1.0
−0.5
0.0
0.5
1.0
1.5
2.0
x
y
●
●
●
●
●
●
●
●
●
●
●
●
●
●
7/24
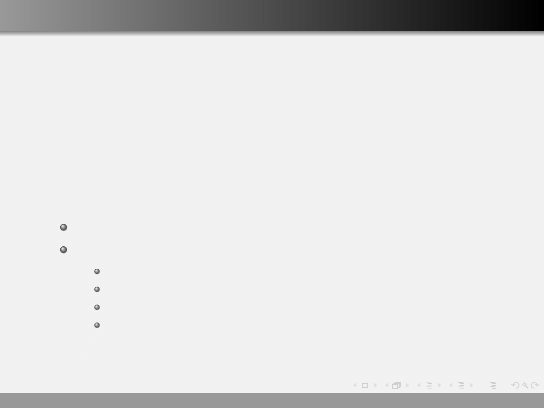
Regresja prosta
Dziś będziemy rozważać model regresji prostej, jest on postaci:
y = β
0
+ β
1
x + ε,
gdzie y to zmienna objaśniana, x zmienna objaśniająca a ε to
zakłócenie losowe.
Założenia:
Postać modelu jest liniowa,
Zakłócenia ε
mają rozkład normalny,
są niezależne,
mają średnie 0,
mają wariancje niezależną od wartości x .
8/24

Regresja prosta
Interesuje nas ocena współczynników β
0
, i β
1
.
Mając oceny współczynników możemy dokonywać predykcji
wartości y
ˆ
y = ˆ
β
0
+ ˆ
β
1
x ,
gdzie ˆ
β
0
to wyraz wolny a ˆ
β
1
to efekt zmiennej x .
Możemy określić błąd dopasowania
ˆ
ε
i
= y
i
− ˆ
y
i
.
9/24
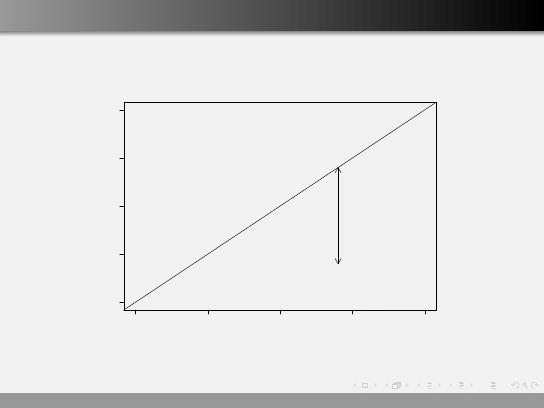
Regresja prosta
●
●
●
●
●
●
●
●
●
●
●
0.0
0.5
1.0
1.5
2.0
0.0
0.5
1.0
1.5
2.0
x
y
Y
^
== ββ
1
^ X
++ ββ
0
^
((
X
i
,,
Y
i
^
))
e
i
^
==
Y
i
−−
Y
i
^
((
X
i
,,
Y
i
))
10/24

Oceny współczynników
Ocen współczynników β
0
i β
1
szukamy tak, by zminimalizować
błąd kwadratowy
min
X
i
(y
i
− ˆ
y
i
)
2
= min
X
i
(y
i
− ˆ
β
0
− ˆ
β
1
x
i
)
2
.
Okazuje się, że takie oceny możemy wyznaczyć z następujących
wzorów
ˆ
β
1
=
P
i
(x
i
− ¯
x )(y
i
− ¯
y )
P
i
(x
i
− ¯
x )
2
=
cov (x , y )
var (x )
,
ˆ
β
0
= ¯
y − ˆ
β
1
¯
x .
11/24

Testy dla współczynników
Dla ocen tych współczynników możemy wyznaczyć rozkłady
prawdopodobieństwa
ˆ
σ
2
∼
χ
2
n−2
n−2
σ
2
ˆ
β
1
∼ β
1
+ t
n−2
q
ˆ
σ
2
P(x
i
−¯
x )
2
E [ ˆ
β
1
]
= β
1
Var [ ˆ
β
1
]
=
ˆ
σ
2
P
i
(x
i
−¯
x )
2
12/24

Testy dla współczynników
... dzięki czemu możemy wyznaczać przedziały ufności dla
współczynników modelu
β
1
= ˆ
β
1
± t
1−α/2
n−2
ˆ
σ
s
1
P(x
i
− ¯
x )
2
,
oraz dla prognozy wartości zmiennej objaśnianej dla wartości x
0
y
0
= ˆ
y ± t
1−α/2
n−2
ˆ
σ
s
1
n
+
(x
0
− ¯
x )
2
P
i
(x
i
− ¯
x )
2
.
13/24

Testy dla współczynników
... oraz testy na istotność dla tych współczynników
H
0
:
β
1
= 0,
H
A
:
β
1
6= 0.
Za statystykę testową wybiera się
T =
ˆ
β
1
ˆ
σ
s
X
i
(x
i
− ¯
x )
2
.
Ta statystyka testowa ma rozkład t-Studenta z n − 2 stopniami
swobody (nie będziemy z niej korzystać).
14/24

Testy dla współczynników
Tą samą hipotezę można też weryfikować korzystając ze statystyki
testowej
F =
(n − 2)
P
i
(y
i
− ¯
y
i
)
2
P
i
(y
i
− ˆ
y
i
)
2
Ta statystyka testowa ma rozkład F z 1, n − 2 stopniami swobody.
15/24

Dopasowanie modelu
Do oceny dopasowania często wykorzystywany jest współczynnik
R
2
, nazywany współczynnikiem determinacji.
Przedstawia on procent wariancji wyjaśnionej przez model
R
2
= 1 −
P
i
(y
i
− ˆ
y )
2
P
i
(y
i
− ¯
y )
2
.
Wysoka wartość tego współczynnika (bliska 1) oznacza, że użyty
model dobrze i wyczerpująco wyjaśnia zmienność w danych.
Niska wartość tego współczynnika (bliska 0) oznacza, że użyty
model wyjaśnia niewielki fragment całej zmienności.
16/24

Przykład w R
> summary(lm(wzrost ∼ waga))
Call:
lm(formula = wzrost ∼ waga)
Residuals:
Min
1Q
Median
3Q
Max
-73.1599 -21.6536
0.5492
17.6769
77.6339
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 869.37234
29.65927
29.31
<2e-16 ***
waga
1.26559
0.04636
27.30
<2e-16 ***
---
Signif. codes: 0 ‘***’ 01 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 27.96 on 98 degrees of freedom
Multiple R-Squared: 0.8838, Adjusted R-squared: 0.8826
F-statistic: 745.4 on 1 and 98 DF, p-value: < 2.2e-16
17/24
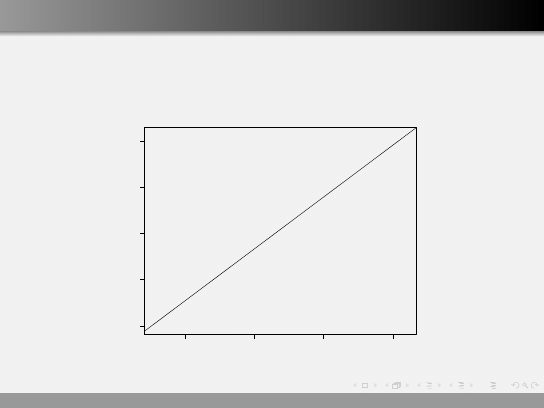
Badanie modelu
Po dopasowaniu modelu, powinniśmy zbadać reszty. Badając reszty
jesteśmy w stanie zweryfikować założenia modelu.
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
60
70
80
90
150
160
170
180
190
waga
wzrost
18/24
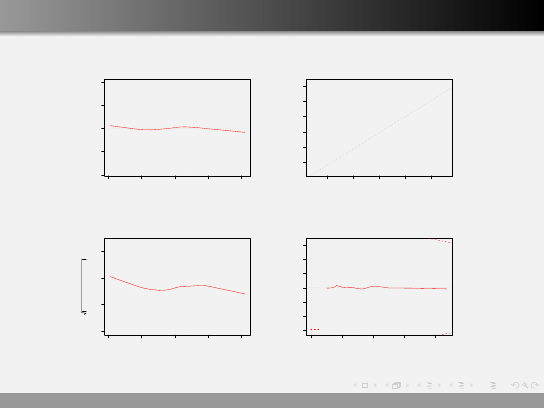
Przykład w R
150
160
170
180
190
−10
−5
0
5
10
Fitted values
Residuals
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Residuals vs Fitted
63
21
64
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
−2
−1
0
1
2
−2
−1
0
1
2
3
Theoretical Quantiles
Standardized residuals
lm(y ~ x)
Normal Q−Q
63
21
64
150
160
170
180
190
0.0
0.5
1.0
1.5
Fitted values
S
ta
n
d
a
rd
iz
e
d
r
e
s
id
u
a
ls
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Scale−Location
63
21
64
0.00
0.02
0.04
0.06
0.08
−3
−2
−1
0
1
2
3
Leverage
Standardized residuals
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Cook's distance
0.5
0.5
Residuals vs Leverage
11
95
40
19/24
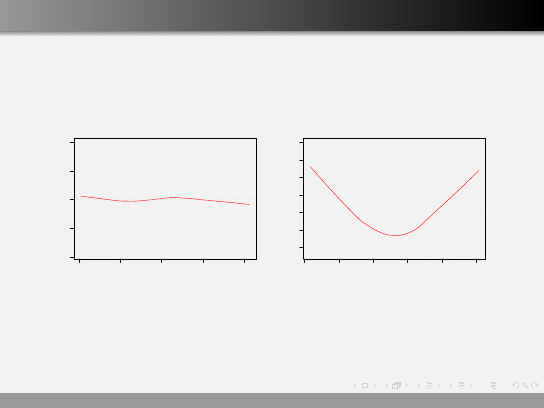
Wykresy diagnostyczne
Sprawdzian, czy średnia wartość ˆ
ε zależą od x lub od y .
150
160
170
180
190
−10
−5
0
5
10
Fitted values
Residuals
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Residuals vs Fitted
63
21
64
−20
0
20
40
60
80
−10
−5
0
5
10
15
20
Fitted values
Residuals
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Residuals vs Fitted
20
143
70
Oczekujemy, że lokalna średnia będzie bliska 0.
20/24
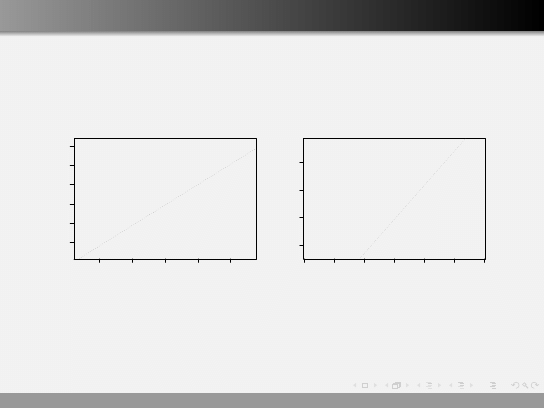
Wykresy diagnostyczne
Sprawdzian, czy rozkład wartości ˆ
ε jest zgodny z r. normalnym.
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
−2
−1
0
1
2
−2
−1
0
1
2
3
Theoretical Quantiles
Standardized residuals
lm(y ~ x)
Normal Q−Q
63
21
64
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
−3
−2
−1
0
1
2
3
−1
0
1
2
Theoretical Quantiles
Standardized residuals
lm(y ~ x)
Normal Q−Q
20
143
70
Oczekujemy, że punkty ułożą się wzdłuż linii prostej.
21/24
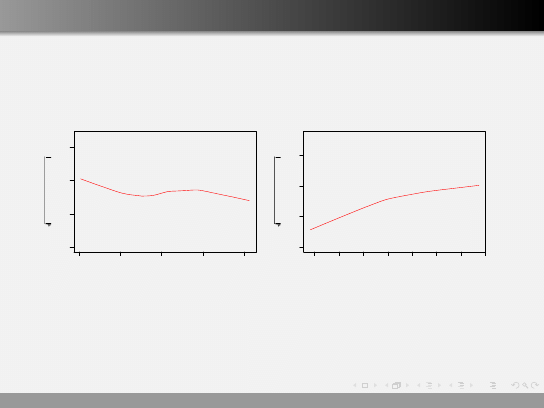
Wykresy diagnostyczne
Sprawdzian, czy wariancja wartości ˆ
ε zależy od x lub od y .
150
160
170
180
190
0.0
0.5
1.0
1.5
Fitted values
S
ta
n
d
a
rd
iz
e
d
r
e
s
id
u
a
ls
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Scale−Location
63
21
64
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
0.0
0.5
1.0
1.5
Fitted values
S
ta
n
d
a
rd
iz
e
d
r
e
s
id
u
a
ls
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Scale−Location
137
132
36
Oczekujemy, że średnie lokalne odchylenie standardowe będzie
stałe.
22/24
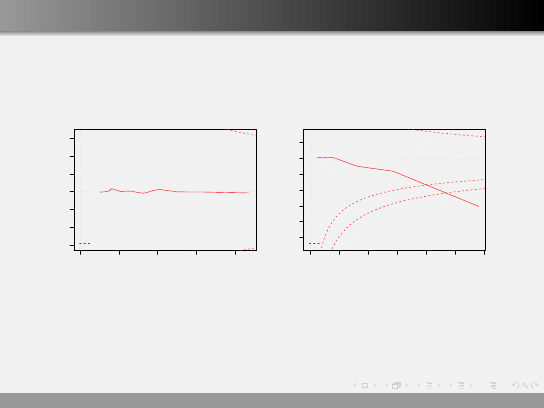
Wykresy diagnostyczne
Sprawdzian, czy obserwujemy wartości nietypowe lub odstające.
0.00
0.02
0.04
0.06
0.08
−3
−2
−1
0
1
2
3
Leverage
Standardized residuals
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
lm(y ~ x)
Cook's distance
0.5
0.5
Residuals vs Leverage
11
95
40
0.00
0.02
0.04
0.06
0.08
0.10
0.12
−10
−8
−6
−4
−2
0
2
Leverage
Standardized residuals
●
●
●
●
●
●
●●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●
●● ●
●
●
●
●
●
●
●●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
●
●●
●
●
●
●
● ●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
● ●
●
●
●
●
lm(y ~ x)
Cook's distance
1
0.5
0.5
Residuals vs Leverage
201
202
203
Oczekujemy, że nie zaobserwujemy punktów o dużych wartościach
Leverage oraz Cook.
23/24

Co trzeba zapamiętać?
Dlaczego regresja liniowa jest popularna pomimo tego, że jest
prosta.
Jak wyznaczać oceny współczynników modelu.
Jak weryfikować istotność współczynników modelu.
Jak wykonywać predykcje.
Jak weryfikować dokładność dopasowania modelu.
24/24
Wyszukiwarka
Podobne podstrony:
Analiza regresji ostatnie notaki z wykladu
06 Analizowanie ukladow elektry Nieznany (2)
06 Analiza ryzyka [tryb zgodnos Nieznany
analiza regresji
06 analizaw wrazliwosci
Analiza regresji, Statystyka - ćwiczenia - Rumiana Górska
ANALIZA REGRESJI WIELOKROTN, Zarządzanie projektami, Zarządzanie(1)
Statystyka matematyczna, 4-część, Analiza regresyjna
cw analiza regresji prostej, Badano właściwości soi — polskiej odmiany ALDANA
cw 06 analiza modeli predykcyjnych
Analiza regresji
Analiza regresji między dwiema zmiennymi, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Procedura związana z analizą regresji
06 Analizowanie psychospołecznych aspektów rozwoju
ANALIZA REGRESJI PROSTEJ
Analiza regresji ppt
3 Analiza regresji
więcej podobnych podstron