Zajęcia wyrównawcze z Podstaw Konstrukcji Maszyn

Materiały pomocnicze do zajęć

dr inż. Adam Cholewa
dr inż. Krzysztof Psiuk

Gliwice 2011

1 Ze

stawienie podstawowych wzorów wytrzymałościowych

Poniżej zestawiono podstawowe wzory wytrzymałościowe, które wykorzystywane są w obliczeniach
inżynierskich w budowie maszyn. Wzory zostały pogrupowane w zależności od występującego
stanu naprężeń.

1.1

Rozciąganie

Naprężenia rozciągające wyznaczamy z zależności:

r

nt

r

k

A

P







gdzie:

r



-

nominalne naprężenia rozciągające

P

-

siła rozciągająca

nt

A

- pole przekroju poprzecznego netto

r

k

-

naprężenia dopuszczalne na rozciąganie

1.2

Ścinanie

Naprężenia ścinające wyznaczamy z zależności:

t

sr

k

A

T







gdzie:

sr



-

nominalne naprężenia ścinające

T

-

siła tnąca

A

- pole przekroju poprzecznego

t

k

-

naprężenia dopuszczalne na ścinanie

1.3

Skręcanie

Naprężenia skręcające wyznaczamy z zależności:

s

s

k

W

M





0



gdzie:



-

nominalne naprężenia skręcające

s

M

-

moment skręcający

0

W

-

wskaźnik wytrzymałości przekroju na skręcanie

s

k

-

naprężenia dopuszczalne na skręcanie (dla materiałów plastycznych przyjmuje się

r

s

k

k

6

,

0



)

1.4 Zginanie

Naprężenia zginające wyznaczamy z zależności:

g

g

g

k

W

M







gdzie:

g



-

nominalne naprężenia zginające

g

M

-

moment gnący

W

-

wskaźnik wytrzymałości przekroju na zginanie

g

k

-

naprężenia dopuszczalne na zginanie

1.5

Inne zależności

Wydłużenie:

EA

Pl





gdzie:



-

wydłużenie

P

-

siła rozciągająca

E

-

moduł Young'a

A

- pole przekroju poprzecznego

Wydłużenie względne:

E

EA

P

l













gdzie:



-

wydłużenie względne

Wydłużenie spowodowane przyrostem temperatury:

l

t













gdzie:



-

wydłużenie

t



- przyrost temperatury



-

współczynnik rozszerzalności liniowej

2

Połączenia śrubowe

2.1

Stan naprężenia połączeń śrubowych

Obliczenia wytrzymałościowe połączeń śrubowych przeprowadza się w zależności od rodzaju i
charakteru obciążeń. Można rozróżnić następujące przypadki obciążeń:



połączenie śrubowe z śrubami bez napięcia wstępnego, obciążone tylko siłą osiową stałą
lub zmienną,



połączenie śrubowe z śrubami napiętymi wstępnie, obciążona siłą osiową,



połączenie śrubowe z śrubami bez napięcia wstępnego, obciążone siłą osiową oraz
momentem skręcającym,



połączenie śrubowe obciążone siłą poprzeczną.

Uwaga!!!
Podane poniżej zależności są ważne w granicach odkształceń sprężystych.

2.1.1 P

ołączenie śrubowe z śrubami bez napięcia wstępnego

W takim przypadku obliczenia przeprowadza się tylko ze względu na naprężenia rozciągające.

r

r

c

r

c

r

k

d

Q

A

Q











2

4





(1)

gdzie:



r

– naprężenia normalne w śrubie, [MPa]

A

r

– pole przekroju poprzecznego śruby, [mm

2

]

d

r

– średnica rdzenia śruby, [mm]

k

r

– naprężenia kryterialne w przypadku rozciągania, [MPa]

Q

c

– siła osiowa, [N]

Naprężenia dopuszczalne wyznacza się z zależności:

X

R

k

e

r



(1)

gdzie:

Re

– grania plastyczności, [MPa]

X

– liczba bezpieczeństwa,

Dla obciążeń stałych przyjmuje się liczbę bezpieczeństwa X = 1,3 ÷ 2,5.
Dla obciążeń zmiennych liczbę bezpieczeństwa przyjmuje się z przedziału X = 2,5 ÷ 5.

2.1.2 P

ołączenie śrubowe z śrubami napiętymi wstępnie i obciążonymi siłą

osiową

Całkowite obciążenie śruby zależy od odkształceń śruby oraz elementów łączonych.

s

k

p

w

c

c

c

Q

Q

Q









1

1

(2)

gdzie:
Q

w

– napięcie wstępne, [N]

Q

p

– obciążenie robocze, [N]

c

k

– sztywność elementów ściskanych, [N/m]

c

s

– sztywność śruby, [N/m]

a)

Wyznaczenie sztywności elementów ściskanych i śruby

Wyznaczenie sztywności elementów złącza jest jednym z etapów konstruowania połączenia.
Zależność (3) przedstawia ogólny wzór na sztywność.

L

EA

c



(3)

gdzie:
E

– moduł Young’a, [MPa]

A

– pole przekroju poprzecznego, [mm

2

]

L

– długość elementu (wymiar elementu wzdłuż działania siły), [mm]

W przypadku złącza śrubowego wyznacza się sztywności poszczególnych jego elementów
(bierzemy pod uwagę te elementu na które działa obciążenie robocze – tzn. rozciągana cześć śruby
i ściskana część blach). W przypadku śruby dzieli się ją na dwie części – gwintowaną i
niegwintowaną. Dla każdej części śruby wyznacza się oddzielnie sztywność. W kolejnym kroku
wyznacza się sztywności zastępcze. Sztywność zastępczą można wyznaczyć na podstawie
podatności zastępczej opisanej wzorem (4).















N

i

i

i

i

N

i

i

A

E

L

c

c

1

1

1

1

(4)

Stąd podatność zastępczą śruby można wyznaczyć (patrz rys.1a):

2

2

1

1

1

A

E

L

A

E

L

c

s

s

s









(5)

gdzie:

4

2

1

r

d

A







oraz

4

2

2

d

A







d

r

– średnica rdzenia śruby, [mm]

d

– średnica śruby w części niegwintowanej, [mm]

E

s

– moduł Younga tworzywa śruby, [MPa]

L

1

, L

2

– długości odpowiednio odcinka gwintowanego i niegwintowanego rozciąganej części śruby

(Rys.1a)

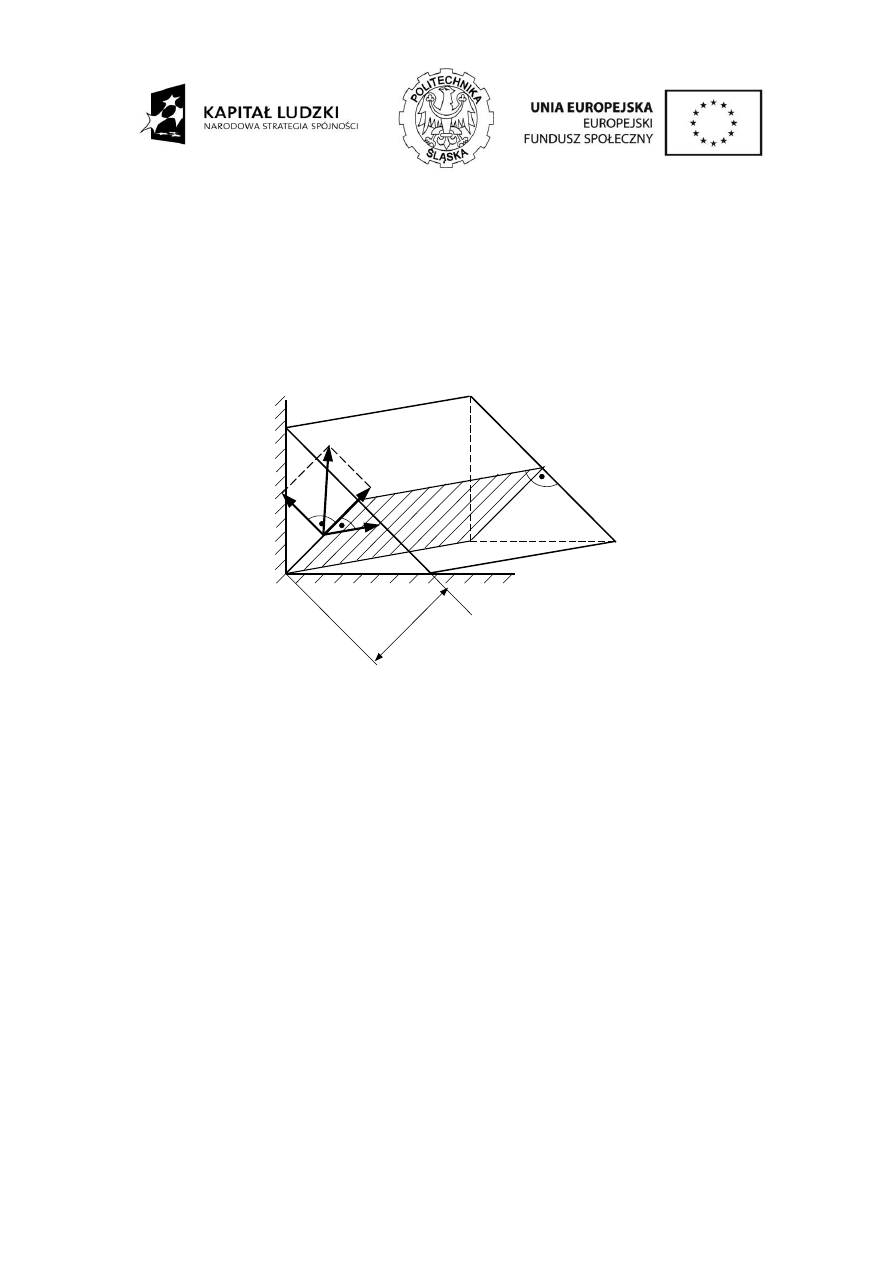
W przypadku elementów ściskanych sytuacja jest bardziej złożona. Wszystkie łączone elementy
rozpatruje się jako pakiet elementów ściskanych. Nie ma tu problemu na ile „części” należy
podzielić ten pakiet – jest to liczba blach (każda blacha ma inną sztywność w zależności od
grubości i tworzywa). Problem pojawia się przy określaniu niezbędnych do wyznaczenia sztywności
wymiarów geometrycznych blach. Z uwagi na to, że połączenie śrubowe ma charakter zbliżony do
punktowego, na stan odkształcenia/naprężenia złącza wpływ ma tylko część blachy w jego
najbliższym otoczeniu. Rzeczywisty wpływ siły ściskającej blachy na ich stan odkształcenia nie jest
znany. W związku z tym w obliczeniach inżynierski zakłada się przybliżony kształt strefy naprężeń
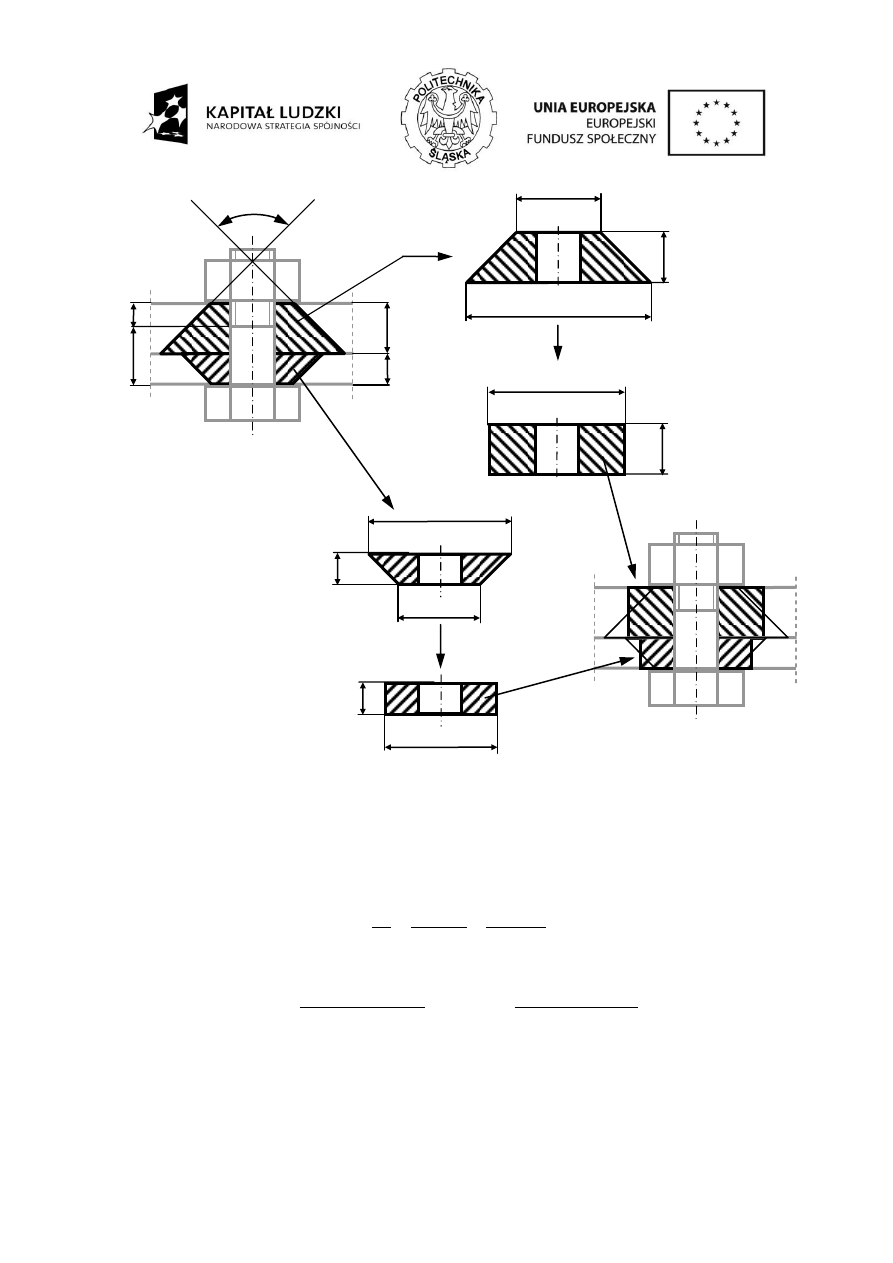
ściskających w elementach łączonych. Na rysunku 1a przedstawiono przybliżony kształt
przyjmowany w obliczeniach. Strefę naprężeń ściskających stanowią dwa ścięte stożki złączone
większymi podstawami. Kąt wierzchołkowy przyjmowany jest około 90º, wysokość każdego stożka
jest równa grubości blachy a mniejsza średnica jest równa średnicy oporowej łba śruby lub nakrętki
(średnica powierzchni oporowej jest jedną z wielkości podawanych w normach). Średnica otworu
osiowego w stożku jest równa średnicy otworu pod śruby d

0

. W celu ułatwienia dalszych obliczeń

stożki te są zamieniane na walce drążone, których średnica wewnętrzna pozostaje bez zmian, zaś
średnica zewnętrzna jest średnią średnic podstaw stożka (górna blacha – rys. 1 b, c , dolna blacha
rys. 1 d, e). Rysunek 1f

przedstawia model strefy ściskania blach w postaci otrzymanych dwóch

drążonych walców.

Sztywność elementów łączonych wyznaczamy przez wyznaczenie sztywności poszczególnych
walców drążony a następnie wyznaczenie sztywności zastępczej analogicznie jak dla śruby. Na
podstawie zależności (4) można wyrazić podatność zastępczą elementów łączonych:

2

2

4

1

1

3

1

w

w

k

A

E

L

A

E

L

c









(6)

gdzie:





4

2

0

3

1

d

L

D

A

w











oraz





4

2

0

4

1

d

L

D

A

w











E

1

, E

2

– moduły Younga tworzyw poszczególnych elementów ściskanych,

A

w1

, A

w2

– pole powierzchni walców drążonych

L

1

L

2

L

3

L

4

90



L

3

D

D

D+2L

4

D+2L

3

L

4

L

3

D+L

4

D+L

3

L

4

a)

b)

d)

c)

e)

f)

Rys. 1. Modelowanie wpływu połączenia śrubowego na łączone elementy.

2.1.3 P

ołączenie śrubowe z śrubami bez napięcia wstępnego, obciążone siłą

osiową oraz momentem skręcającym,

W takim przypadku wyznacza się obciążenie zastępcze:

r

s

s

c

r

r

z

k

k

k





















2

,

2







(7)

gdzie:



z

– naprężenia zredukowane, [MPa]



s

– naprężenia styczne, [MPa]

k

r,c

– naprężenie kryterialne w przypadku rozciągania lub ściskania (dla stali k

r

= k

c

), [MPa]

k

s

– naprężenia kryterialne w przypadku skręcania, [MPa]

2.1.4

Połączenie śrubowe obciążone siłą poprzeczną

W przypadku połączenia śrubowego obciążonego siłą poprzeczną rozpatruje się dwa przypadki:



połączenie z śrubami luźnymi,



połączenie z śrubami pasowanymi.

a) P

ołączenie z śrubami luźnymi

W przypadku połączenia śrubowego z śrubami luźnymi, siła poprzeczna jest przenoszona za
pośrednictwem sił tarcia, powstałych na powierzchniach styku łączonych elementów, w wyniku
naciągu wstępnego śruby. Siła tarcia powstała w ten sposób, powinna zrównoważyć siłę
poprzeczną obciążającą połączenie. Siła napinająca śrubę nie może wywołać w śrubie naprężeń
większych niż wynikałoby to z własności wytrzymałościowych tworzywa, z którego śruba jest
wykonana. Zazwyczaj w takim przypadku wyznacza się wymaganą średnicę śruby. Można ją
wyznaczyć z zależności:



















P

d

r

4

Q

T

Q

2

w

T

(8)

gdzie:
Q

T

– siła poprzeczna, [N]

T

– siła tarcia, [N]



– liczba tarcia

P

– naciski powierzchniowe, [MPa]

b) P

ołączenie z śrubami pasowanymi

W przypadku połączeń śrubowych z śrubami pasowanymi, obliczenia przeprowadza się jak dla
połączenia kształtowego. W takim przypadku obliczenia przeprowadza się sprawdzając dwa
warunki wytrzymałościowe:
-

warunek na naprężenia tnące

t

T

T

k

d

z

Q

A

z

Q













4

2

1





(1)

gdzie:



– naprężenia styczne w śrubie(ścinanie), [MPa]

T

Q

– siła tnąca, [N]

A

– pole powierzchni ścinanej, [mm

2

]

1

d

– średnica trzpienia pasowanego śruby, [mm]

z

– liczba powierzchni ścinanych

t

k

– naprężenia kryterialne na ścinanie:

Naprężenia dopuszczalne wyznaczamy z zależności:









2

1

,

0

1











r

s

e

t

n

R

k



(2)

gdzie:

R

e

– granica plastyczności tworzywa śruby, [MPa]

δ

s

– liczba bezpieczeństwa na ścinanie

n

r

– liczba rzędów śrub w połączeniu

- warunek na naciski powierzchniowe

dop

p

g

d

Q

p







1

(3)

gdzie:

p

–

naciski

powierzchniowe między powierzchnią boczną śruby a powierzchnią boczną otworu,

[MPa]

Q

–

siła tnąca, [N]

d

1

–

średnica trzpienia pasowanego śruby, [mm]

g

–

grubość blachy, [mm]

p

dop

–

naciski dopuszczalne, [MPa]









2

1

,

0

1

8

,

0













r

d

e

dop

n

R

p



(4)

gdzie:

δ

d

– liczba bezpieczeństwa na naciski

Sprawdzeniu podlegają również łączone elementy (w przekroju osłabionym otworami pod śruby).

2.1.5 Informacje dodatkowe

Własności wytrzymałościowe śrub

Własności wytrzymałościowe śrub są opisane przez klasę wytrzymałości takich łączników. Klasy
wytrzymałości śrub określone są przez normę i opisane w postaci zapisu dwóch liczb rozdzielonych
znakiem kropki. Wybrane klasy wytrzymałości śrub to: 4.8, 5.6, 6.8, 8.8, 10.9, 12.9.
Symbol ten należy odczytywać następująco. pierwsza liczba pomnożona przez 100, da nam
wartość wytrzymałości na rozciąganie Rm, natomiast pozostała część, podaje nam wartość ilorazu
Re/Rm. Np. dla śruby o klasie wytrzymałości 5.6, otrzymamy:









MPa

R

R

MPa

R

m

e

m

300

500

6

.

0

6

.

0

500

100

5

















Moment dokręcenia w połączeniu śrubowym

Siłę wzdłużną w śrubie wywołuje się przez wprowadzenie napięcia wstępnego. Powstaje ono w
czasie dokręcania nakrętki, w czasie montażu połączenia śrubowego. W wyniku tego na
powierzchniac

h styku pomiędzy nakrętką i elementem łączonym, oraz pomiędzy gwintem śruby i

gwintem nakrętki powstają siły tarcia, które należy pokonać w czasie dokręcania nakrętki. Całkowity
moment tarcia będzie równy:

o

T

c

M

M

M





gdzie:







w

s

o

w

s

T

Q

D

M

tg

Q

d

M

5

.

0

)

'

(

5

.

0







s

d

-

średnica robocza gwintu, [mm],



-

kąt wzniosu linii śrubowej

'



-

pozorny kąt tarcia,

s

D

-

średnica robocza powierzchni oporowej nakrętki.

2.2

Przykład rozwiązania zadania:

Dobrać śruby łączące dwa wały obciążone momentem skręcającym M

s

= 600 Nm

. Do połączenia

wałów zaproponowano sześć śrub pasowanych. Tarcze wałów wykonane są ze stali 45. Liczba
bezpieczeństwa na ścinanie δ

s

=1,5, a na naciski

δ

d

=2.

D

w

= 110 mm

D

0

= 115 mm

D

z

= 200 mm

n = 6
n

r

= 1

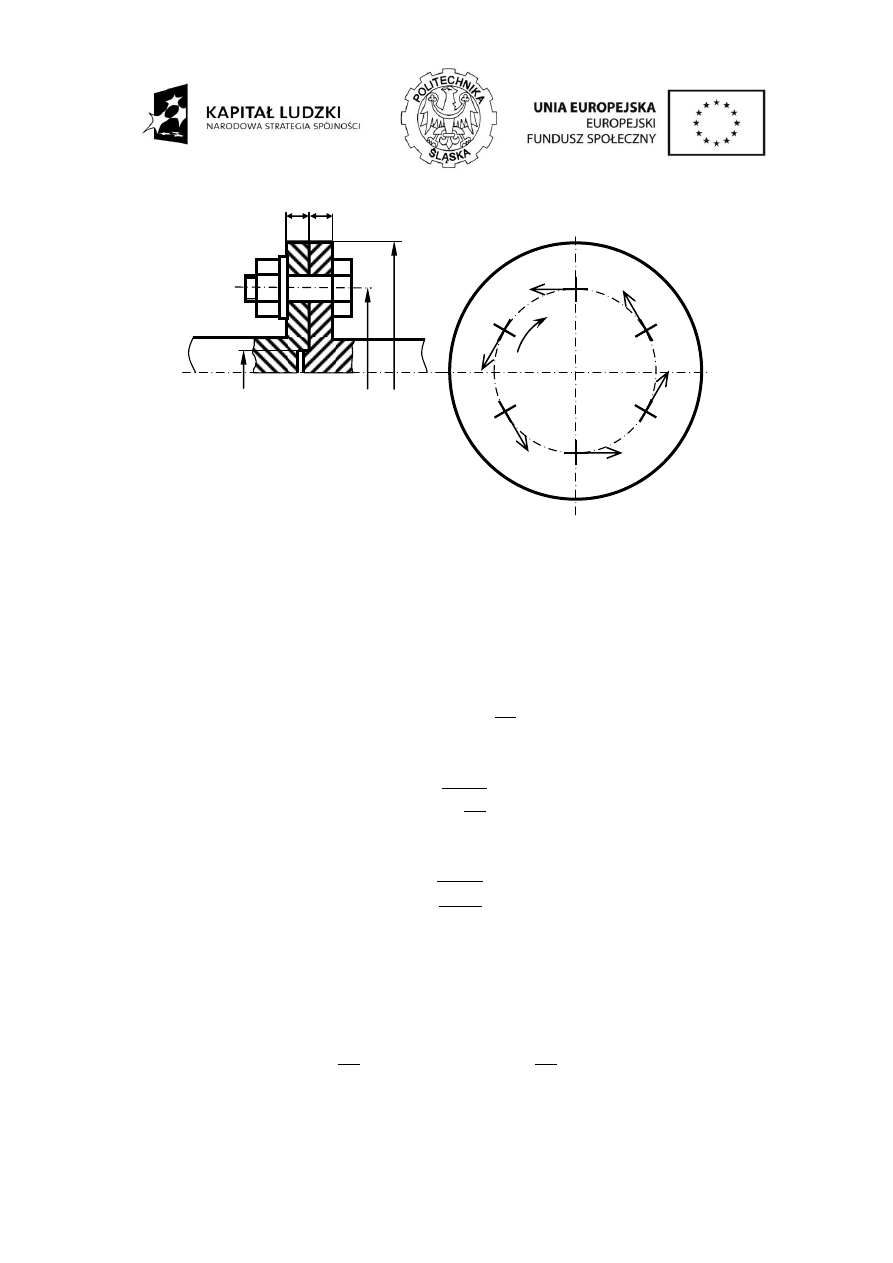
Rys. 2. Połączenie śrubowe

Momentowi skręcającemu M

s

odpowiada moment oporowy M

0,

równy mu co do wartości ale o

przeciwnym zwrocie. Moment oporowy M

0

można rozłożyć na sześć równych momentów

składowych (zakładamy równy rozkład obciążenia na każdą ze śrub). Każdy z tych momentów
można zastąpić iloczynem siły i ramienia (patrz rysunek), gdzie siła jest przyłożona w środku
ciężkości śruby, natomiast ramię jest promieniem koła, na którym rozmieszczone są śruby (D

0

/ 2).

Wówczas moment oporowy można wyrazić następująco:

2

0

0

D

P

n

M







(3.1)

stąd:

2

0

0

D

n

M

P





(3.2)

1. Naprężenia tnące w śrubie:

t

k

d

P







4

2

1





(3.3)

Zakładamy śruby klasy 5.6.

R

m

= 500 MPa

R

e

= 300 MPa

wówczas:









MPa

R

n

R

k

s

e

r

s

e

t

180

9

0

2

1

0

1





















,

,

(3.4)

stąd:

D

W

D

0

D

Z

M

0

1
0

1
0

P

P

P

P

P

P

mm

k

D

n

M

k

P

d

t

t

51

,

3

8

4

0

0

1























(3.4)

2. Naciski powierzchniowe:

dop

p

d

g

P

p







1

(3.5)

stal 45

– R

e

= 360 MPa

Granica plastyczności tworzywa śruby jest niższa, dlatego na naciski powierzchniowe weryfikujemy
śrubę.









MPa

R

n

R

p

d

e

r

d

e

dop

132

88

,

0

2

1

,

0

1

8

,

0























(3.6)

stąd:

mm

p

g

D

n

M

p

g

P

d

dop

dop

32

,

1

2

0

0

1

















(3.7)

Na podstawie zależności (3.4) oraz (3.7) dobrano śruby M8 o średnicy trzpienia pasowanego d

1

= 9

mm

2.3 Zadania do

samodzielnego rozwiązania:

2.4 Zadanie 1

Płaskownik o grubości g = 15 mm zamocowany przy pomocy trzech śrub pasowanych obciążony jest siłą
poprzeczną P=20 000N. Obliczyć średnicę śrub i dobrać śruby znormalizowane. Liczba bezpieczeństwa na
ścinanie δ

s

= 2,5, a na naciski wynosi

δ

d

= 2

. Płaskownik wykonano ze stali 45.

Dane:
a = 50 mm
l = 100 mm

Rys. 3. Rysunek połączenia do zadania 1

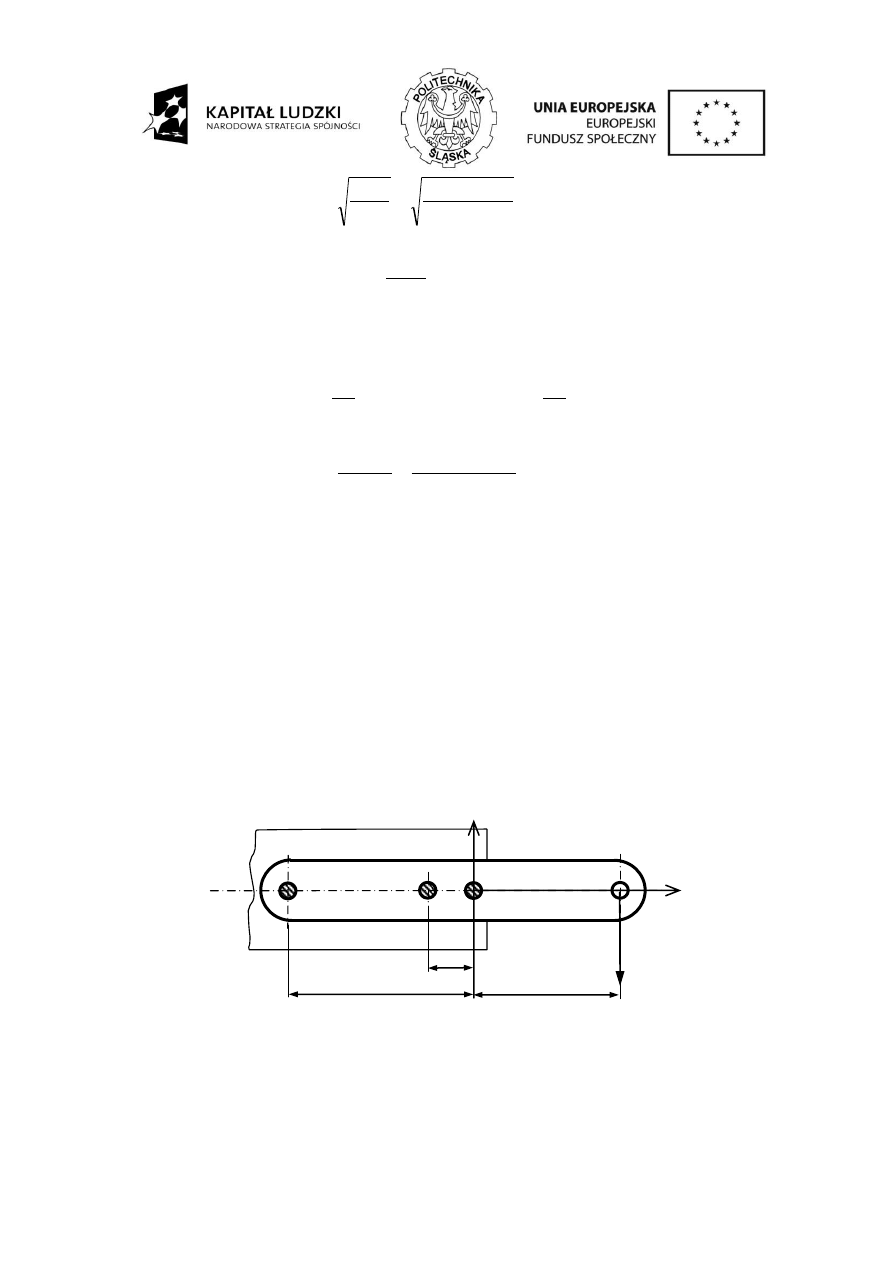
2.5 Zadanie 2

Trzy płaskowniki połączono 2 śrubami pasowanymi jak na rysunku i obciążono siłą P = 30 000 N.
Kierunek działania siły jest prostopadły do osi śrub. Skonstruować połączenie śrubowe. Wymiary i

l

5
a

a

y

1.1.1

P

x

tworzywo płaskowników są znane. Liczba bezpieczeństwa wynosi δ

s

=2

. Szerokość płaskowników b

= 50 mm.

Dane:
Płaskownik 1:

stal 25
g

1

= 15 mm

Płaskownik 2:

stal 45
g

2

= 10 mm

Płaskownik 3:

stal 35
g

3

= 20 mm

Rys. 4. Rysunek połączenia do zadania 2

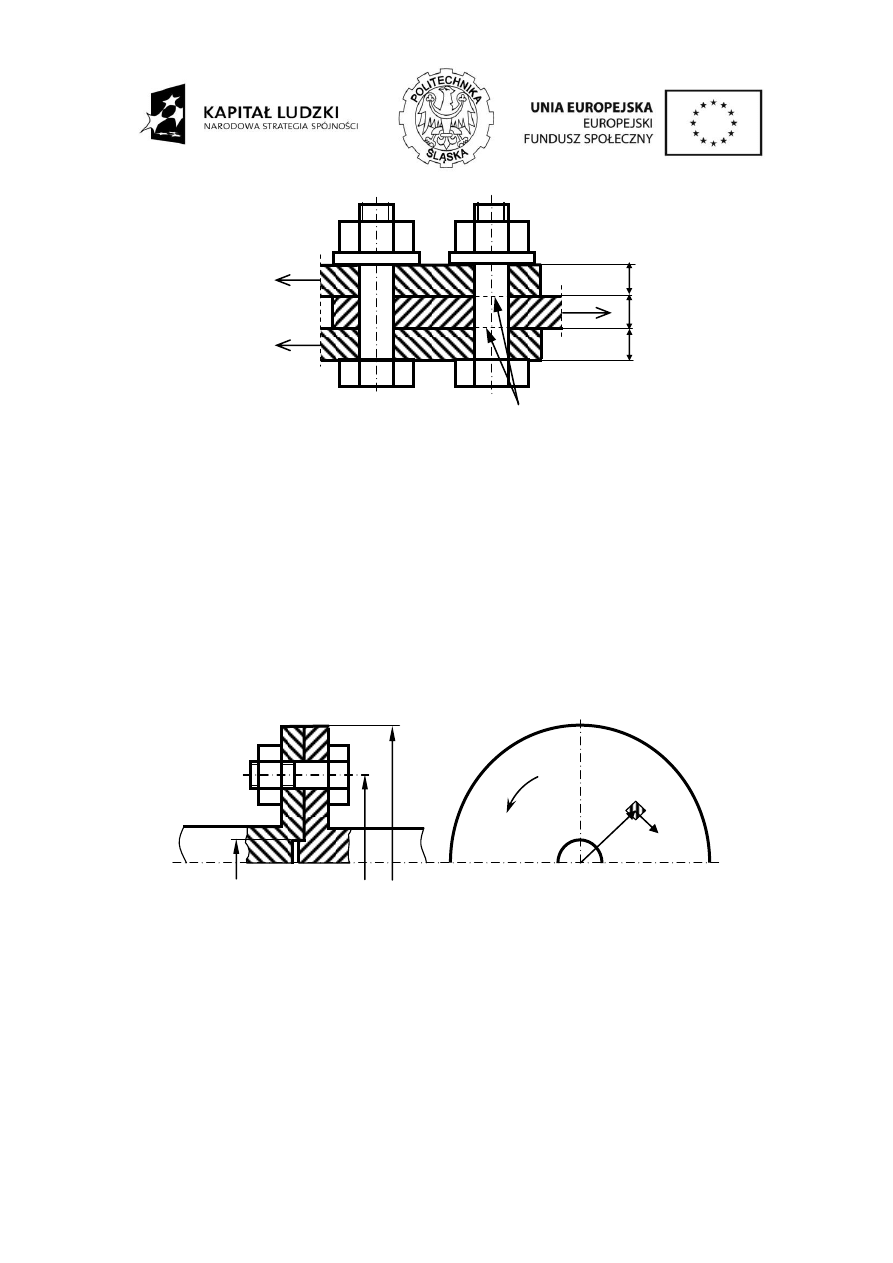
2.6 Zadanie 3

Obliczyć śruby łączące dwa wały obciążone momentem skręcającym M

s

=600 Nm. Sześć

śrub założonych z luzem założono tak, że moment M

s

przenoszony jest przez moment tarcia

miedzy powierzchniami tarcz ukształtowanych na wale. Liczba tarcia



= 0,15. Liczba

bezpieczeństwa wynosi δ = 2.6

D

w

= 110 mm

D

0

= 115 mm

D

z

= 200 mm

n = 6

Rys. 5. Rysunek połączenia do zadania 3

D

W

D

0

D

Z

r

d
A

1

τ

M

s

P

0,5
P

0,5
P

g

1

g

2

g

3

Powierzchnie
ścinania śrub

3

Połączenia spawane

3.1

Wymagania dotyczące spoin.

3.1.1

Wymagania dla spoin czołowych.

W obliczeniach połączeń spawanych ze spoinami czołowymi przyjmuje się, że grubość
obliczeniowa spoiny

jest równa grubości cieńszego z łączonych elementów. W przypadku

niepełnej spoiny czołowej grubość ta jest równa głębokości rowka do spawania
pomniejszonej o 2 mm.
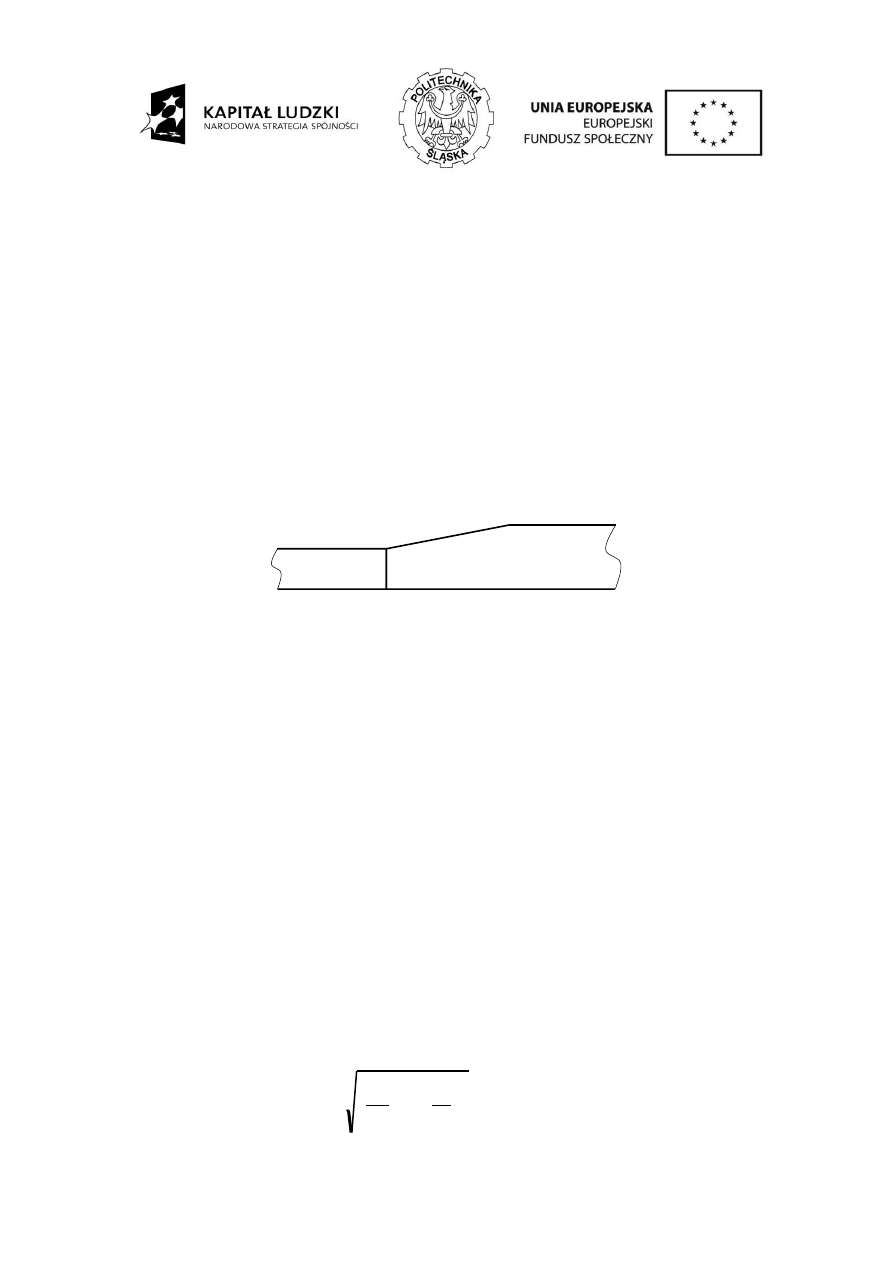
Jeżeli połączone mają być blachy o różnych grubościach, to należy tak skonstruować złącze
s

pawane, aby zapewnić ciągłą zmianę przekroju. W tym celu stosuje się pochylenie, które

powinno być nie większe niż:
1 : 1 -

w przypadku obciążeń statycznych,

1 : 4 -

w przypadku obciążeń dynamicznych.

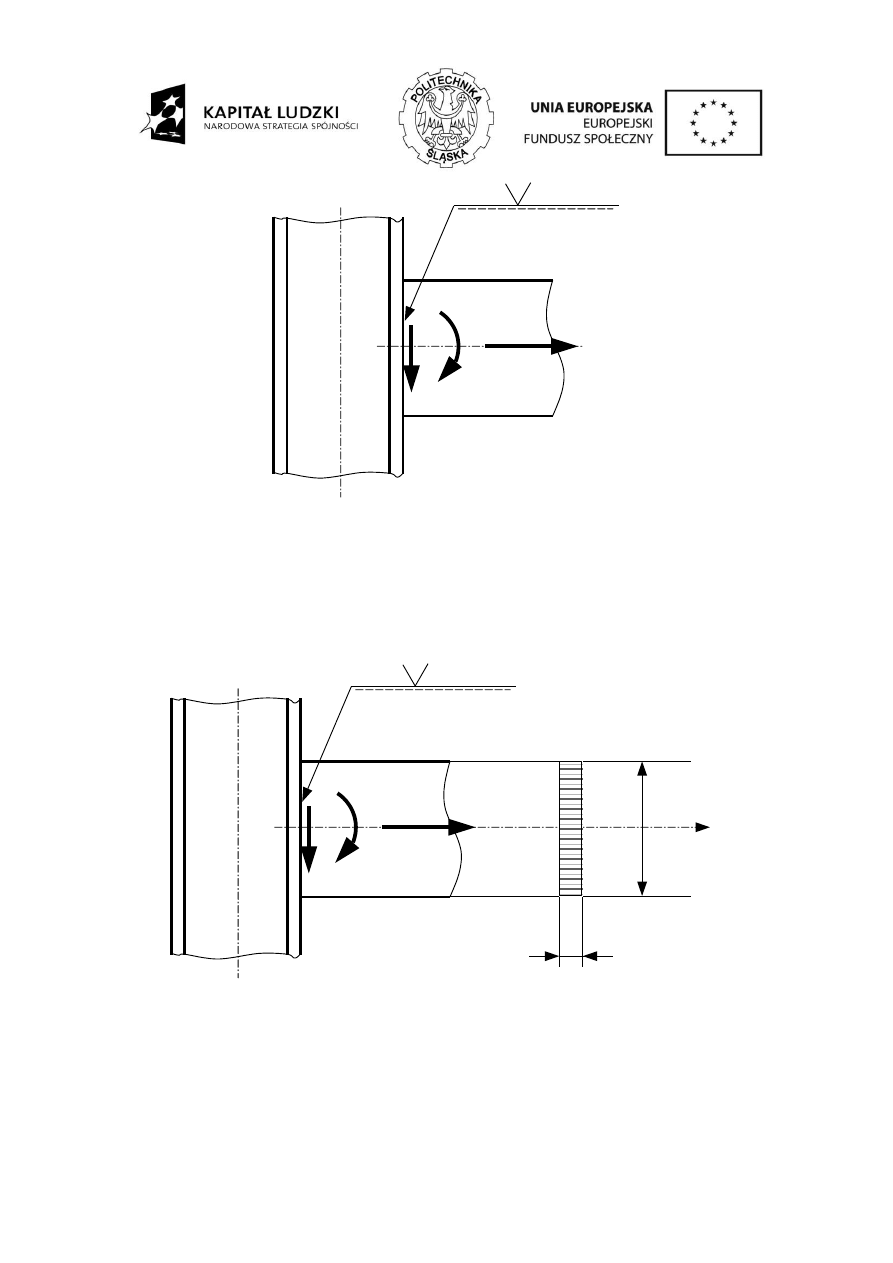
Rys. 6. Połączenie spawane czołowe

3.1.2 Wymagania dla spoin pachwinowych.

W przypadku spoin pachwinowych, zaleca się stosować spoiny nie większe niż wynika to z
przeprowadzonych obliczeń, a ponadto zaleca się aby:









mm

10

najwyzej

co

lecz

t

0,2

mm

2,5

wyjatkowo

mm

3

max

max

min

a









min

max

t

0,7

mm

16

min

a

gdzie:
t

min

, t

max

grubość cieńszej i grubszej blachy

3.2

Weryfikacja połączeń spawanych – spoiny czołowe.

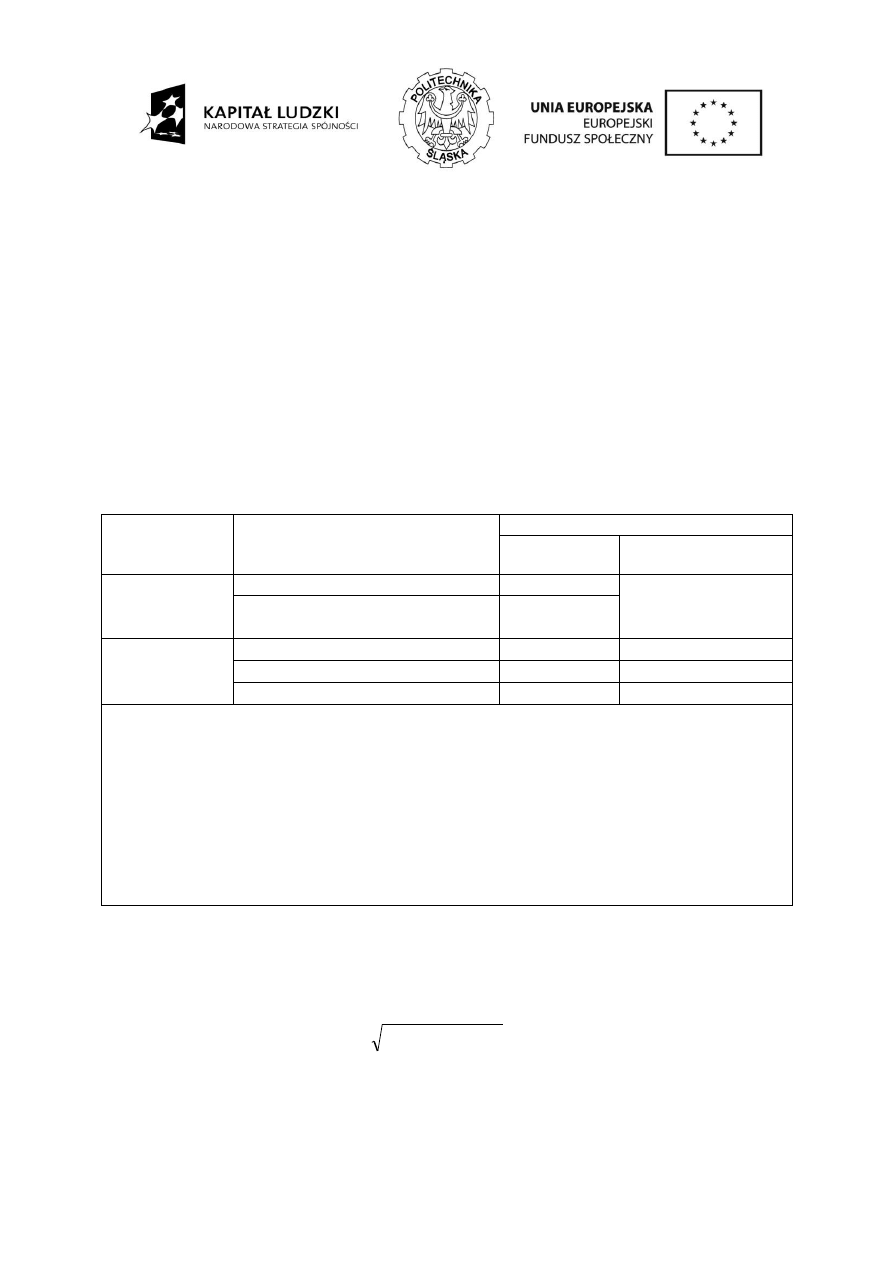
Nośność spoiny czołowej wyznacza się z zależności:

d

f

































2

||

2









i)













15

,

0

1

gdzie:



,



– naprężenia w przekroju obliczeniowym połączenia,





,



||

– współczynniki wytrzymałości spoin,

f

d

– wytrzymałość obliczeniowa stali (odczytywana z tablic dla danego tworzywa),



– współczynnik stosunku naprężeń średnich do maksymalnych

Sposób określania wartości współczynników



||

oraz





określa norma.

Poniżej przedstawiono wyciąg z normy PN-90/B-03200 dotyczący wyznaczania wartości
współczynników



:

Tablica 1

Rodzaj spoiny

Stan naprężeń w rozpatrywanej

części lub wytrzymałość stali

Re w MPa

Współczynniki wytrzymałości spoin

1)







||

Spoiny czołowe

ściskanie lub zginanie

1

0,6

(przy ścinaniu)

rozciąganie równomierne (



=1) lub

mimośrodowe ((



<1))

1 - 0,15



2)

Spoiny
pachwinowe

Re



225

0,9

0,8

255 < Re



355

0,8

0,7

355 < Re



460

0,7

0,6

1)

Podane wartości współczynników należy zmniejszyć:

a) o 10% -

w przypadku spoin montażowych,

b) o 20% -

w przypadku spoin pułapowych,

c) o 30% -

gdy zachodzą jednocześnie obydwa przypadki a) i b)

2)

Podana zależność dotyczy spoin normalnej jakości, kontrolowanych zgrubnie:



-

iloraz naprężeń

średnich do naprężeń maksymalnych. W przypadku przeprowadzenia kontroli defektoskopowej można
przyjmować wartości





= 1, przy czym klasa wadliwości złącza wg PN-87/M-69772 powinna wynosić

najwyżej R4 - przy grubości łączonych części do 20 mm, R3 - przy grubości większej niż 20 mm, R2 -
przy obciążeniach zmiennych.

3.3

Weryfikacja połączeń spawanych – spoiny pachwinowe

W przypadku złożonego stanu naprężeń warunek wytrzymałościowy ma postać:





























d

d

f

f











2

2

||

2

3

ii)

gdzie:



– współczynnik zależny od granicy plastyczności stali (określany wg normy w zależności od

Re),





,





– naprężenia w kierunku prostopadłym do osi spoiny (patrz rysunek poniżej),



||

– naprężenia w kierunku równoległym do osi spoiny (patrz rysunek poniżej),























]

[

460

355

1

]

[

355

255

85

,

0

]

[

255

7

,

0

MPa

R

MPa

R

gdy

MPa

R

e

e

e



iii)







||





a



Rys. 7

. Składowe naprężeń w spoinie pachwinowej

3.4

Przykład rozwiązania zadania:

Sprawdzić wytrzymałość spoiny czołowej łączącej blachę węzłową ze słupem, jak pokazano
na rysunku. Zakłada się, że spoina nie ma kraterów końcowych i jest kontrolowana zgrubnie.
Obciążenie połączenia jest złożone i obejmuje obciążenie siłą rozciągającą N, siłą tnącą V
oraz momen

tem zginającym M.

Dane:
Tworzywo elementów:

stal 18G2

Wytrzymałość obliczeniowa:

f

d

= 305 [MPa]

N

=

360

[kN]

V

=

270

[kN]

M

=

12

[kNm]

10

300

V

N

M

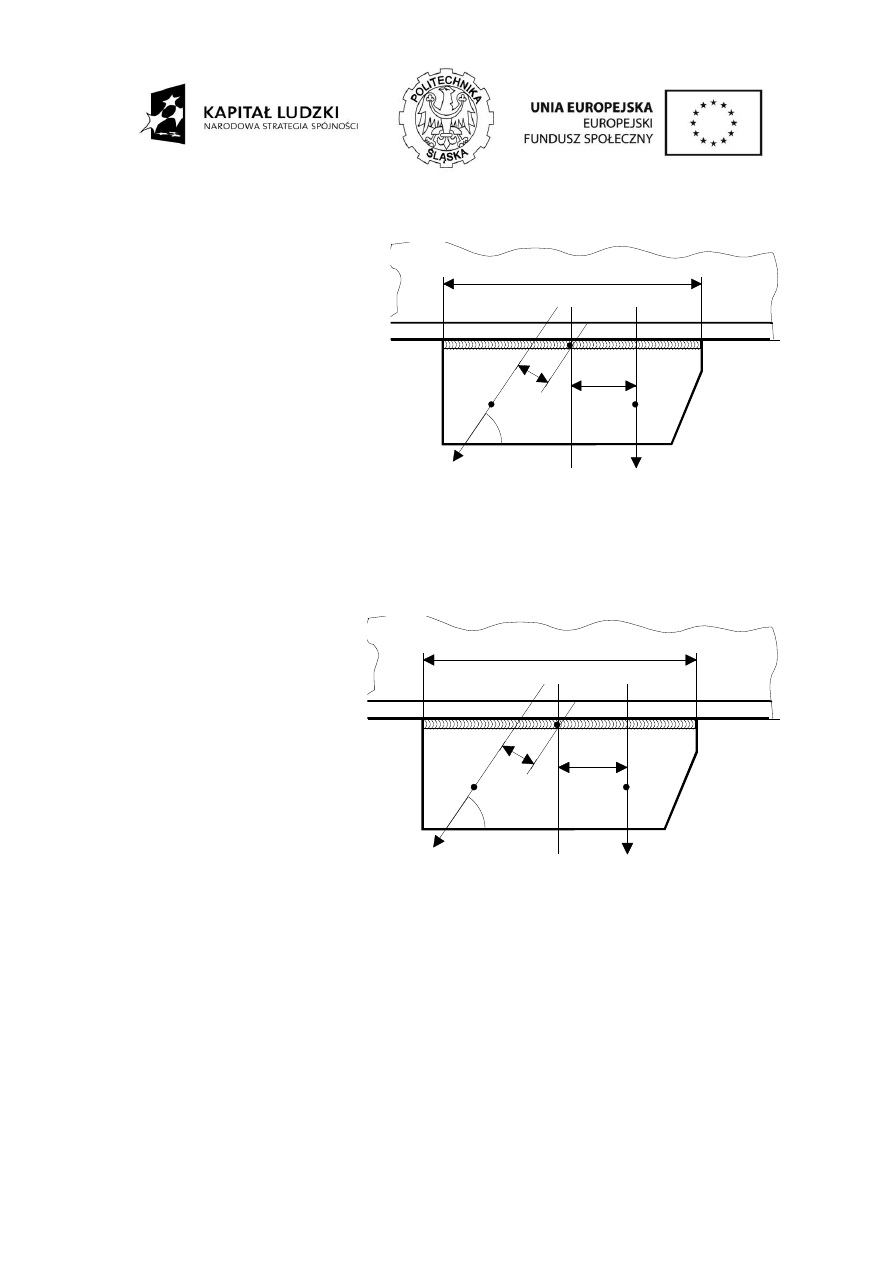
Rozwiązanie:
W rozpatrywanym przypadku połączenia spawanego mamy do czynienia ze złożonym
stanem naprężeń. Zgodnie z zależnością i), do weryfikacji połączenia konieczne jest
określenie naprężeń normalnych oraz stycznych, występujących w tym połączeniu.

1. Charakterystyki geometryczne spoiny
W pierwszym kroku wyznaczamy charakterystyki geometryczne spoiny.

10

300

V

N

M

10

300

x

Na rysunku przedstawiono

postać i wymiary pola przekroju poprzecznego spoiny czołowej.

Zgodnie z podanymi wymiarami spoiny, polem jest prostokąt o szerokości podstawy równej
10 mm oraz wysokości 300 mm.

Obliczenie pola przekroju poprzecznego spoiny:

]

cm

[

30

]

mm

[

3000

300

10

2

2









s

A

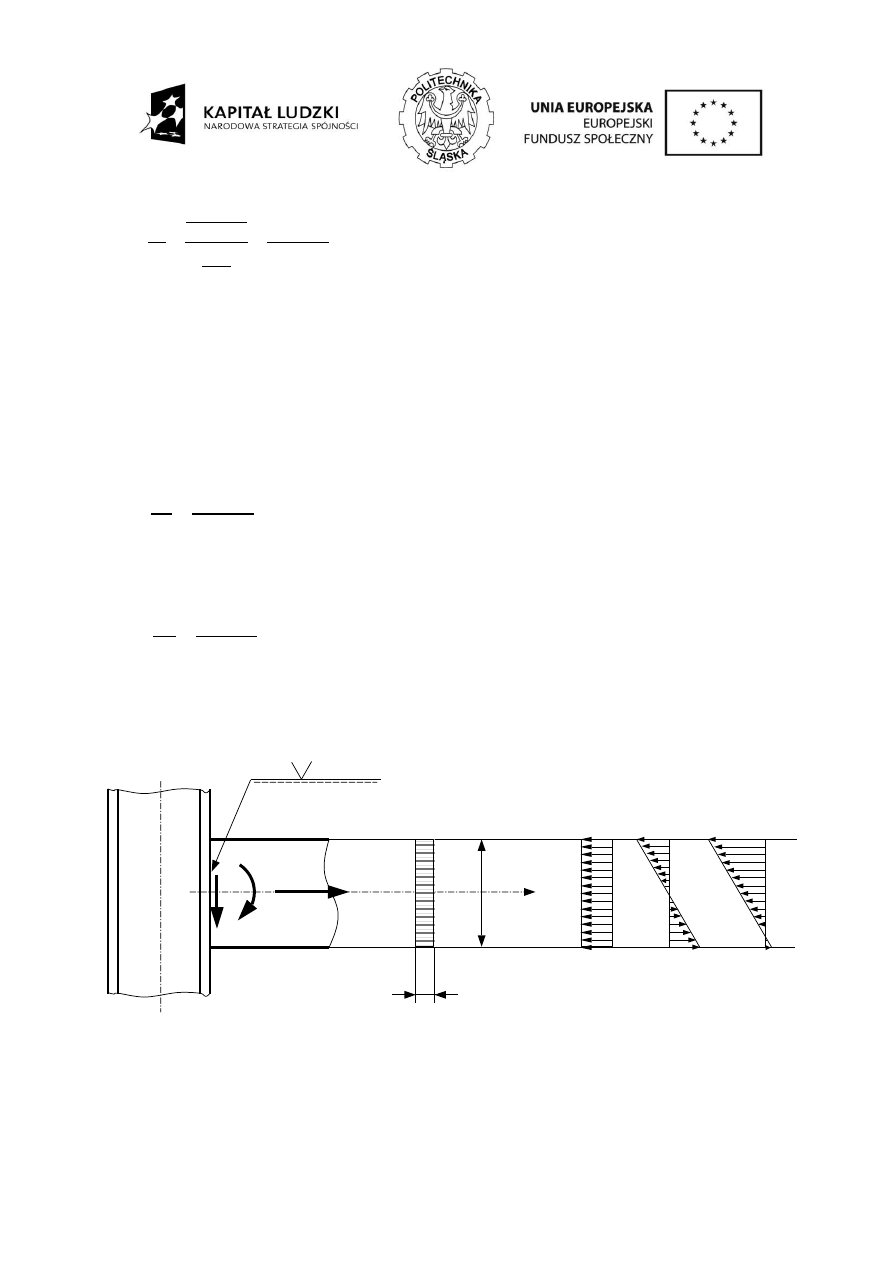
Oblicze

nie wskaźnika wytrzymałości przekroju poprzecznego na zginanie względem osi x:

]

cm

[

150

]

mm

[

150000

6

300

10

2

300

12

300

10

3

3

2

3















e

I

W

x

x

2. Składowe naprężeń
Z obciążenia spoiny wynika, że naprężenia normalne występujące w spoinie będą pochodziły
od siły normalnej oraz momentu zginającego, a naprężenia styczne będą pochodziły tylko od
siły tnącej. Konieczne jest więc wyznaczenie naprężeń cząstkowych pochodzących od
poszczególnych sił obciążających spoinę.

a) składowa naprężeń pochodząca od siły poosiowej N

]

M Pa

[

120

3000

10

360

3









s

N

A

N



b)

składowa naprężeń pochodząca od momentu zginającego M

]

M Pa

[

80

10

150

10

12

3

3











x

M

W

M



Na rysunku poniżej przedstawiono wykresy obliczonych naprężeń (można je dorysować do
istniejącego rysunku):

10

300

V

N

M

10

300

x



N



M



Całkowite naprężenia normalne będą złożeniem naprężeń pochodzących od siły
rozciągającej i momentu zginającego. Maksymalne naprężenia normalne są równe:

]

MPa

[

200

80

120











M

N







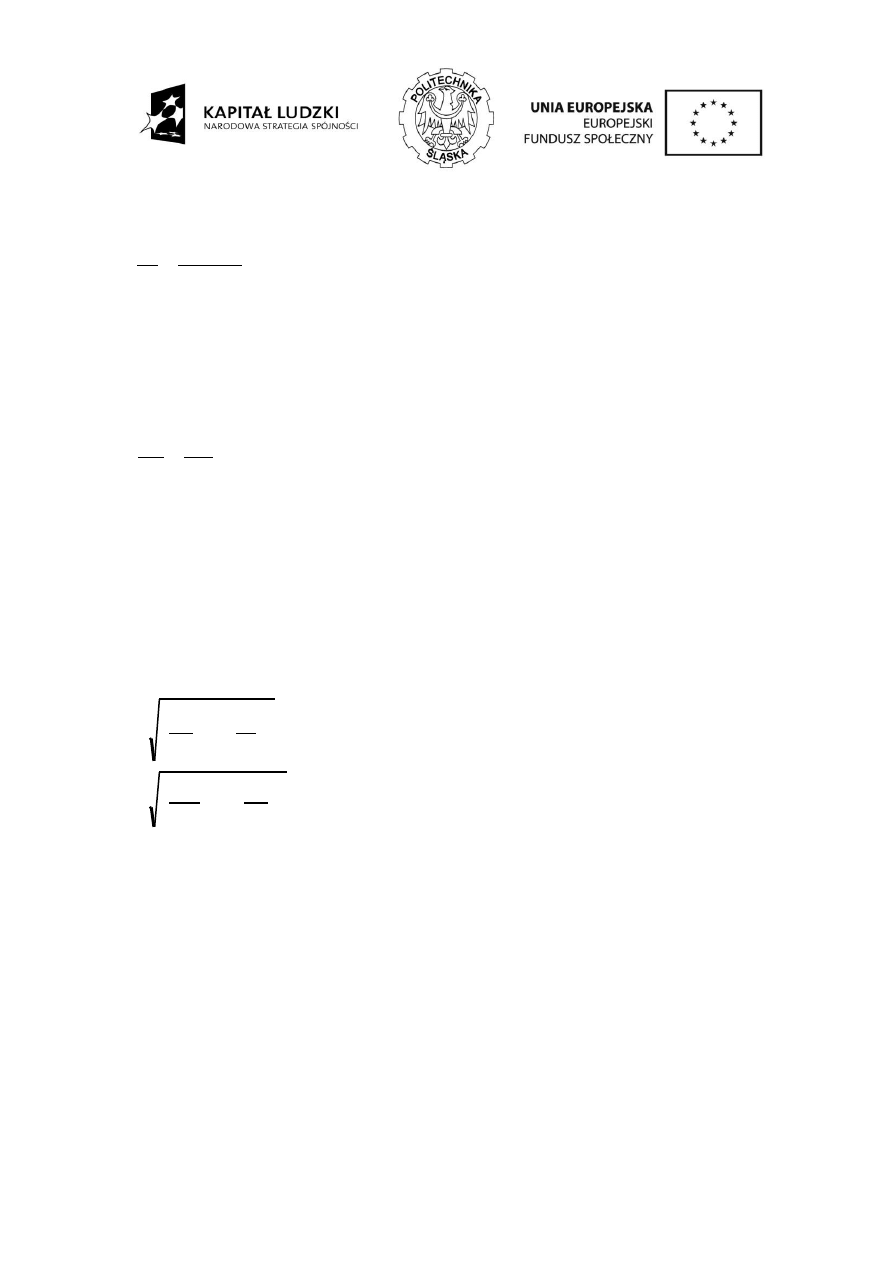
c) naprężenia styczne pochodzące od siły tnącej V

]

M Pa

[

90

3000

10

270

3









s

A

V



3. Określenie współczynnika





W celu określenia wartości współczynnika





konieczne jest wyznaczenia ilorazu wartości

naprężeń normalnych średnich do wartości naprężeń normalnych maksymalnych.
Maksymalne naprężenia normalne są równe



. Natomiast naprężenia normalne średnie są

równe



N

(bo w tym przypadku



M

są symetryczne i nie zmieniają wartości średniej). Stąd:

6

,

0

200

120













N

Współczynniki wytrzymałości spoiny wynoszą:

91

,

0

6

,

0

15

,

0

1

15

,

0

1



















6

,

0

||





4. Warunek nośności spoiny
Po wyznaczeniu wszystkich

koniecznych wartości należy sprawdzić warunek nośności

spoiny:

d

z

z

d

z

f

f

















































































]

M Pa

[

8

,

275

6

,

0

90

91

,

0

200

2

2

2

||

2

Warunek został spełniony.

3.5

Zadania do samodzielnego rozwiązania:

3.5.1 Zadanie 1

Blachę węzłową połączono z słupem
spoiną

czołową.

Sprawdzić

wy

trzymałość tego połączenia, jeżeli

obciążone jest ono jak na rysunku.
Blacha wykonana jest ze stali St3S.
Dane:
P

=

40

[kN]

R

=

10

[kN]



=

45

0

e

1

=

60

[mm]

e

2

=

90

[mm]

l

1

=

350

[mm]

Tworzywo stal St3S
R

e

=

235

[MPa]

f

d

=

215

[MPa]



||

=

0,6





=

1

3.5.2 Zadanie 2

Blachę węzłową połączono z słupem
spoiną

pachwinową.

Sprawdzić

wytrzymałość tego połączenia, jeżeli
obciążone jest ono jak na rysunku.
Blacha wykonana jest ze stali St3S.

Dane:
F

=

45

[kN]

Q

=

8

[kN]



=

60

0

e

1

=

50

[mm]

e

2

=

90

[mm]

l

1

=

360

[mm]

Wymiar charakterystyczny spoiny
a

=

5

[mm]

Tworzywo stal St3S
R

e

=

235

[MPa]

f

d

=

215

[MPa]



||

=

0,7





=

0,8

3.5.3 Zadanie 3

Wysięgnik promieniowy o postaci przedstawionej na rysunku poniżej, obciążono siłą P. Pręty
3 i 4

połączono z prętem 1 poprzez blachę węzłową przedstawioną na rys. 2. Blachę

węzłową połączono z prętem 1 spoiną czołową. Sprawdzić wytrzymałość tego połączenia.
Wszystkie elementy wykonane są ze stali St3S.

e

1

e2



P

R

x10

l

1

e

1

e2



F

Q

x10

l

1

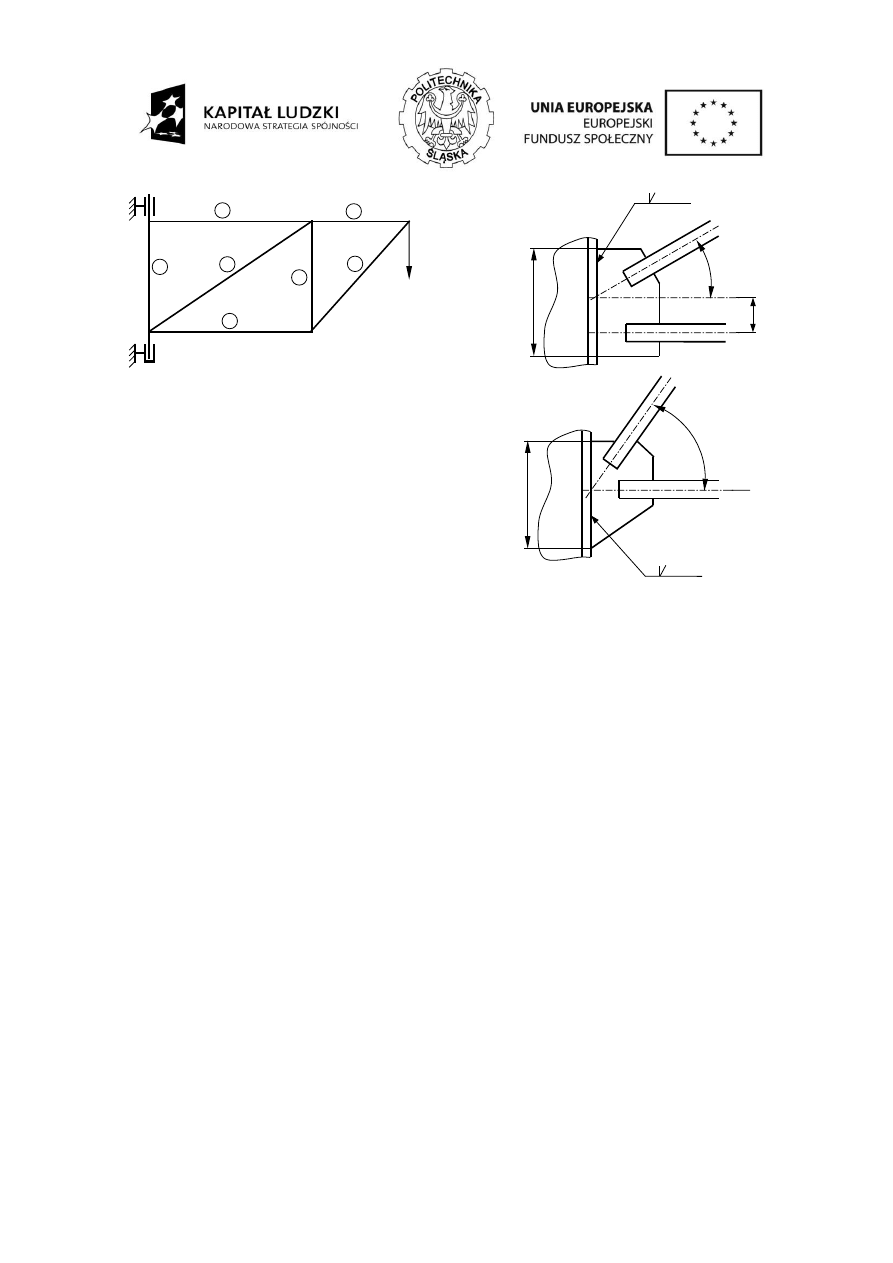
Rys. 1

Rys. 2

1

2

3

4

5

6

7

P

x10

L

350

10



e

2

x10

L

350

10



Dane:
P

=

40

[kN]



=

30

[

0

]

e

2

=

90

[mm]

L

= 350

[mm]

Tworzywo stal St3S
R

e

= 235

[MPa]

f

d

= 215

[MPa]



||

=

0,6





=

1

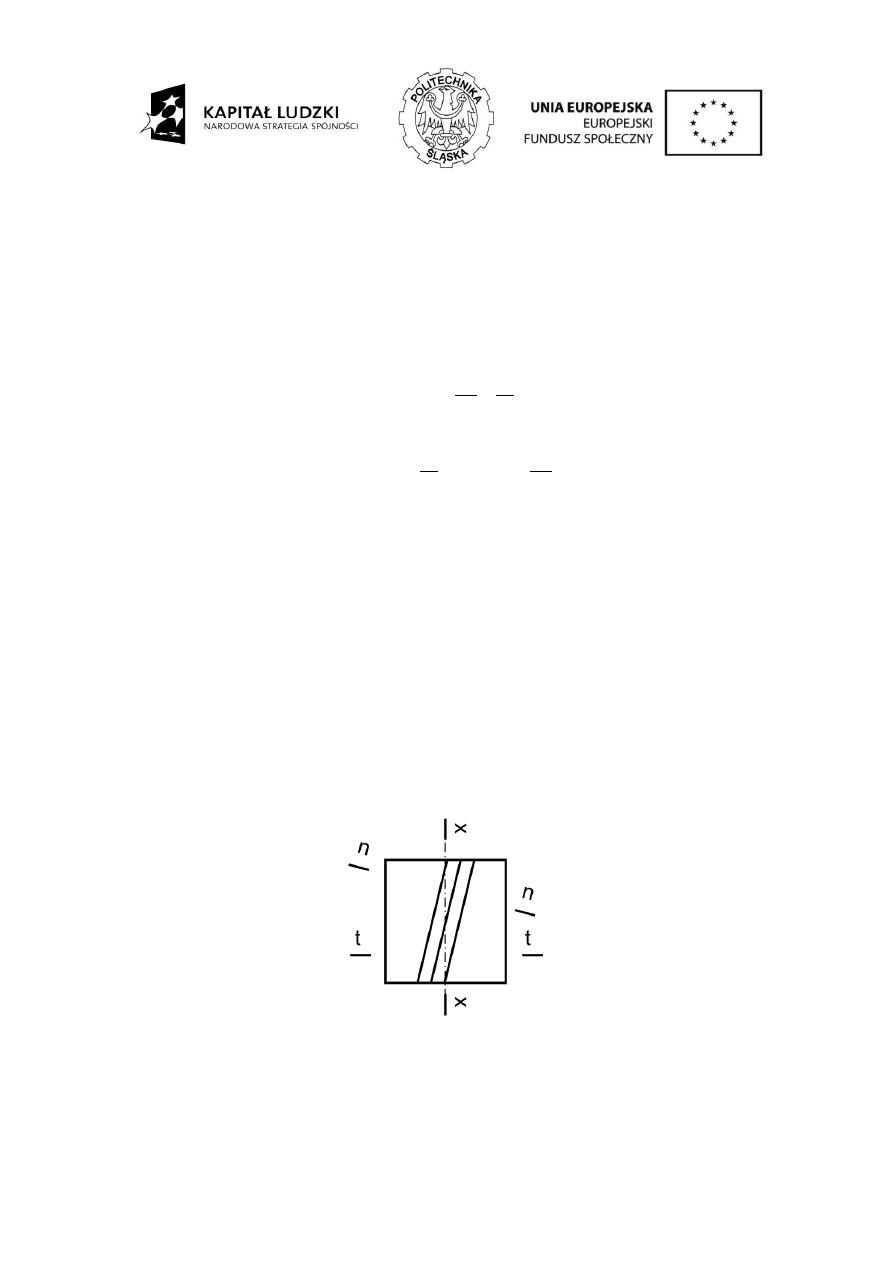
4

Projektowanie przekładni mechanicznych

4.1

Projektowanie przekładni zębatych

Zagadnienia dotyczące projektowania przekładni zębatych zostaną omówione na podstawie
przekładni zębatych walcowych o zębach śrubowych, z zazębieniem ewolwentowym.

Przełożenie przekładni:

• Przełożenie kinematyczne

b

a

b

a

n

n

i









• Przełożenie geometryczne

1

2

1

2

lub

D

D

u

z

z

u





• Dla przekładni o stałych osiach

i

u



4.1.1

Podstawowe wielkości geometryczne kół

Wielkości charakterystyczne uzębienia mierzone są w dwóch płaszczyznach:



płaszczyźnie normalnej,



płaszczyźnie czołowej.

Wielkości mierzone w płaszczyźnie normalnej oznaczane są indeksem n, a mierzone w
płaszczyźnie czołowej oznaczane są indeksem t.
Na rysunku poniżej przedstawiono położenie płaszczyzny normalnej i czołowej.

Rys. 4.1.

Położenie płaszczyzny normalnej i płaszczyzny czołowej

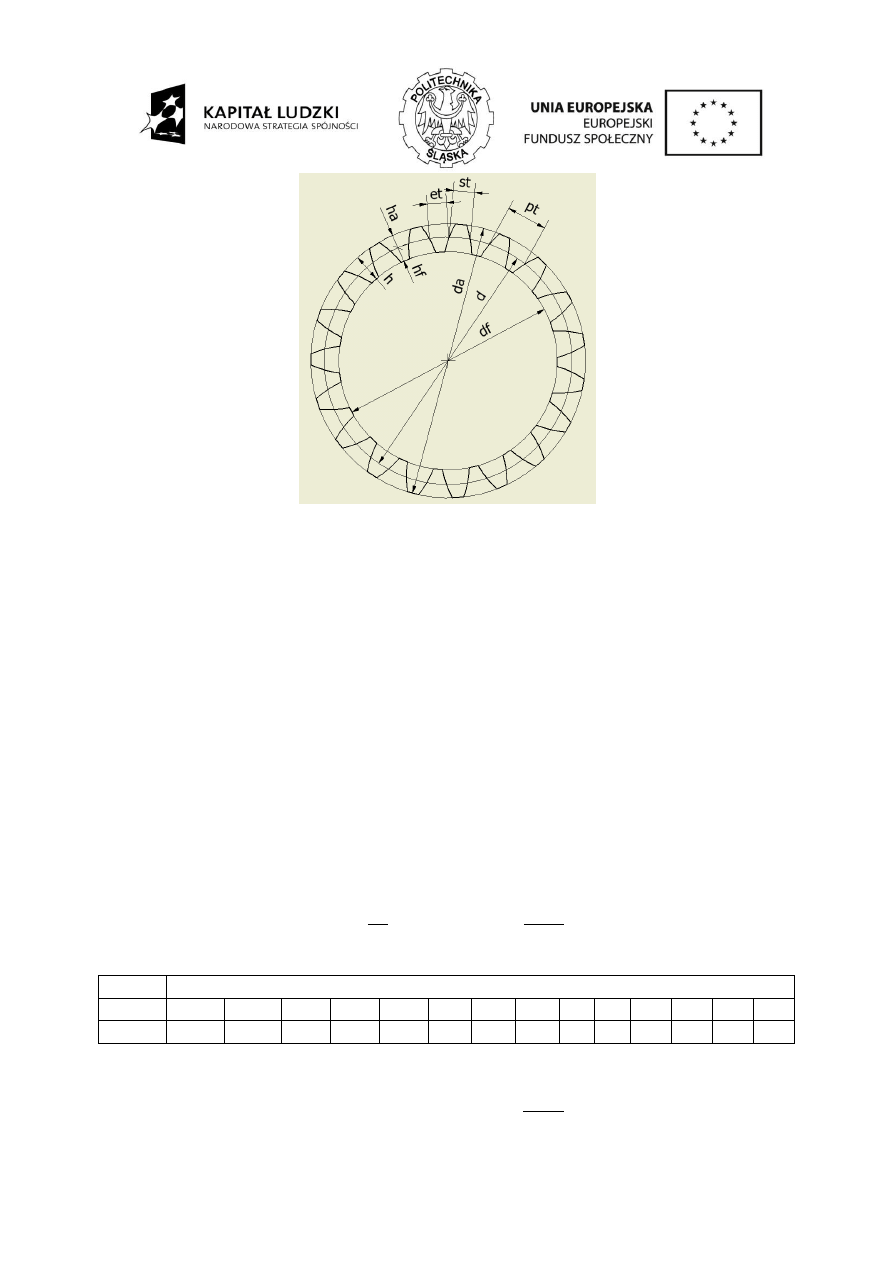
Rys. 4.2.

Podstawowe cechy geometryczne uzębienia

Podstawowe cechy geometryczne uzębienia przedstawiono na rys. 4.2 i opisano poniżej:

d -

średnica podziałowa,

d

a

-

średnica wierzchołków,

d

f

-

średnica stóp,

h -

wysokość zęba,

h

a

-

wysokość głowy zęba,

h

f

-

wysokość stopy zęba,

p

t

-

podziałka podziałowa,

s

t

-

grubość zęba,

et -

szerokość wrębu,

b -

szerokość zęba,



-

kąt pochylenia linii zęba.

Podstawowe zależności geometryczne pomiędzy tymi wielkościami:

Moduł normalny:



n

n

p

m





cos

n

t

m

m



Tabela modułów normalnych
Szereg

m [mm]

1

1

1,25

1,5

2

2,5

3

4

5

6

8

10

12

16

20

2

1,125 1,375 1,75 2,25 2,75 3,5

4,5

5,5

7

9

11

14

18

22

Podziałka:



n

n

m

p





cos

n

t

p

p



Szerokość zęba:

2

n

n

p

s





cos

n

t

s

s



Szerokość wrębu:

2

n

n

p

e





cos

n

t

e

e



Dla kąta zarysu





20

n



Koła o zębach prostych

Koła o zębach śrubowych

m

m

m

t

n







n

n

p

m



,



cos

n

t

m

m



mz

d





cos

z

m

d

n



n

a

m

h



n

f

m

h

25

,

1



)

2

(





z

m

d

a

)

2

cos

(







z

m

d

n

a

)

5

,

2

(





z

m

d

f

)

5

,

2

cos

(







z

m

d

n

f

2

)

(

2

1

z

z

m

a

w







cos

2

)

(

2

)

(

2

1

2

1

z

z

m

z

z

m

a

n

t

w









2

f

a

d

d

h





2

d

d

h

a

a





2

f

f

d

d

h





4.1.2

Weryfikacja wytrzymałościowa zębów

Istnieje wiele metod weryfikacji wytrzymałościowej uzębień kół zębatych. W celu ich
ujednolicenia organizacje normalizacyjne, ISO, DIN, wprowadziły zalecenia dotyczące
sposobu obliczeń wytrzymałościowych uzębień. Przedstawione poniżej zależności zostały
opracowane na podstawie norm DIN.
Weryfikacja wytrzy

małościowa uzębień prowadzona jest w oparciu o dwa kryteria. Kryteria te

dotyczą naprężeń gnących w przekroju stopy zęba oraz naprężeń stykowych na boku zęba.

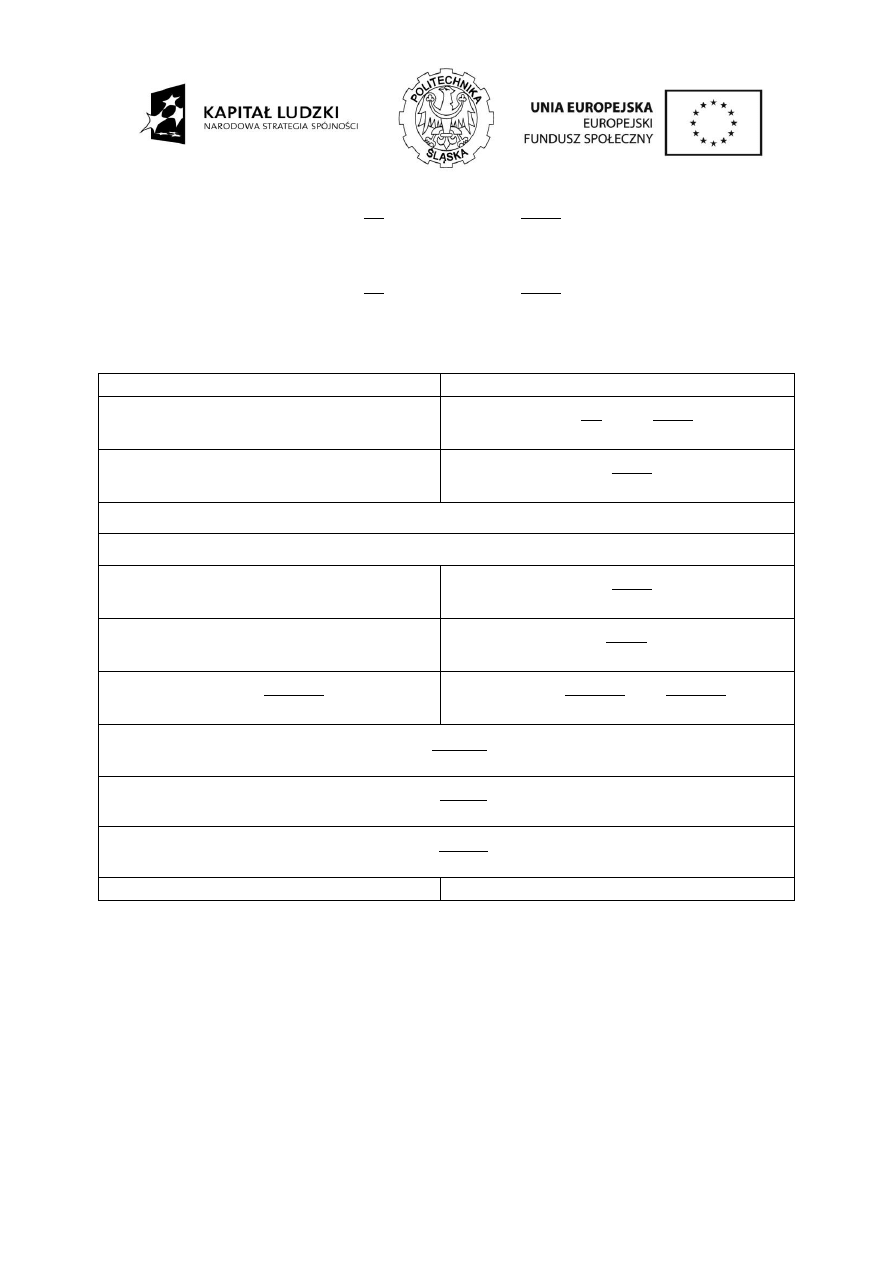
Warunek wytrzymałościowy dotyczący odporności na złamanie stopy zęba jest następujący:

FP

F







FP

F

F

n

t

F

Y

Y

Y

K

bm

F

















F

F

v

I

F

K

K

K

K

K



FX

S

F

F

FP

K

Y

S

min

lim







gdzie:

F



-

naprężenie w podstawie zęba od zginania [MPa],

t

F

-

nominalna siła obwodowa na walcu podziałowym [N],

b

-

szerokość koła [mm],

F

Y

-

liczba uwzględniająca kształt zęba,



Y

-

liczba uwzględniająca wpływ wskaźnika zazębienia,



Y

-

liczba uwzględniająca wpływ kąta pochylenia linii zęba,

FP



-

naprężenie dopuszczalne [MPa]

I

K

-

liczba określająca dodatkowe dynamiczne siły zewnętrzne,

v

K

-

liczba określająca dodatkowe dynamiczne siły wewnętrzne,



F

K

- liczba

uwzględniająca rozkład obciążenia na pary zębów będące w zazębieniu,



F

K

-

liczba uwzględniająca rozkład obciążenia wzdłuż szerokości koła,

lim

F



-

wytrzymałość trwała przy zginaniu [MPa],

S

Y

- liczb

a działania karbu,

FX

K

-

liczba uwzględniająca wielkość koła,

min

F

S

-

minimalna liczba bezpieczeństwa.

Na tej podstawie można wyznaczyć liczbę bezpieczeństwa na złamanie:

min

lim

F

F

F

v

I

F

t

FX

s

n

F

F

S

K

K

K

K

Y

Y

Y

F

K

Y

bm

S















Siłę

t

F

obliczymy z zależności:

d

M

F

s

t

2



gdzie:

s

M

-

moment skręcający,

d

-

średnica podziałowa.

Moment skręcający można wyznaczyć z zależności:

]

[

9550

Nm

n

P

M

s



gdzie:

P

- moc

przenoszona przez koło [kW],

n

-

prędkość obrotowa [obr./min].

Pozostałe parametry:







1



Y















































































2

2

1

,

0

4

1

5

,

0

2

1

2

1

1

1



























dla

F

b

f

q

q

dla

q

dla

q

dla

q

K

t

w

pb

L

L

L

L

L

F



cos

pt

pb

f

f



120

1









Y

Jeżeli promień zaokrąglenia głowy narzędzia, którym zostało wykonane uzębienie jest
większy niż 0,25m

n

, to:

1



S

Y

kolejnym warunkiem który należy sprawdzić jest warunek wytrzymałościowy dotyczący
odporności na naciski powierzchniowe boku zęba. Wyznaczamy go w punkcie biegunowym
C, gdzie

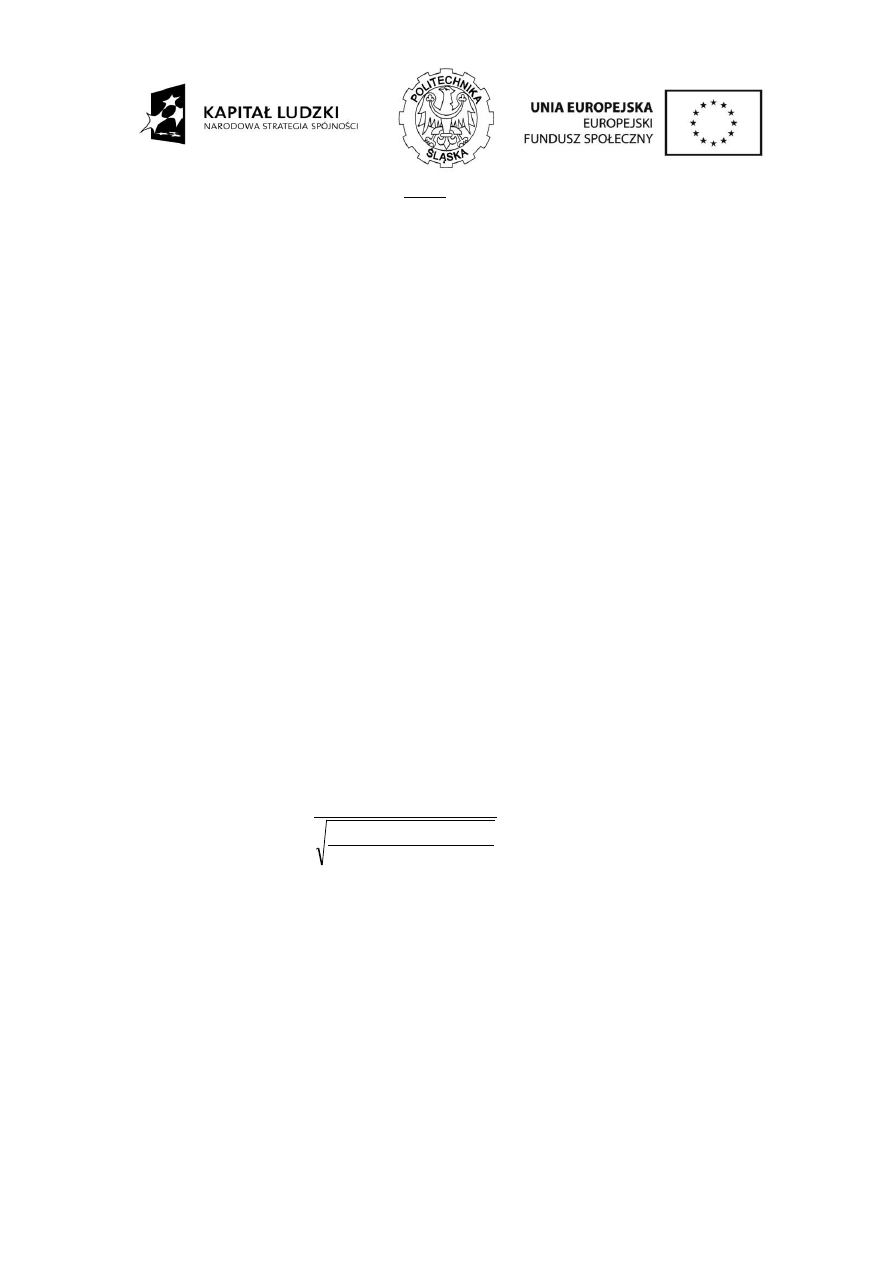
obciążenie jest największe. Naprężenia stykowe są równe:

HP

M

H

H

H

v

I

t

H

Z

Z

Z

u

u

bd

K

K

K

K

F

















1

v

R

HX

L

H

H

HP

Z

Z

K

K

S

min

lim







gdzie:

t

F

-

nominalna siła obwodowa na walcu podziałowym [N],

b

-

szerokość koła [mm],

d

-

średnica podziałowa [mm],

u

-

przełożenie geometryczne,

I

K

-

liczba określająca dodatkowe dynamiczne siły zewnętrzne,

v

K

-

liczba określająca dodatkowe dynamiczne siły wewnętrzne,



H

K

-

liczba uwzględniająca rozkład obciążenia na pary zębów będące w zazębieniu,



H

K

-

liczba uwzględniająca rozkład obciążenia wzdłuż szerokości koła,

H

Z

-

liczba uwzględniająca kąty

tw

t

b







,

,

,

M

Z

-

liczba uwzględniająca własności sprężyste tworzyw,



Z

-

liczba uwzględniająca czołowy wskaźnik zazębienia,

lim

H



-

wytrzymałość stykowa trwała [MPa],

min

H

S

- minimalna

liczba bezpieczeństwa,

L

K

-

liczba uwzględniająca wpływ smaru,

HX

K

-

liczba uwzględniająca wpływ wielkości koła, najczęściej

1



HX

K

,

R

Z

- liczba

uwzględniająca wpływ chropowatości,

v

Z

-

liczba uwzględniająca wpływ prędkości obwodowej.

Liczbę bezpieczeństwa na wykruszenie można obliczyć z zależności:

min

lim

)

1

(

H

M

H

H

H

v

I

t

L

R

v

HX

H

H

S

Z

Z

Z

bdu

u

K

K

K

K

F

K

Z

Z

K

S















4.2

Projektowanie przekładni pasowych

Rys. 4.3.

Rys. 4.4.

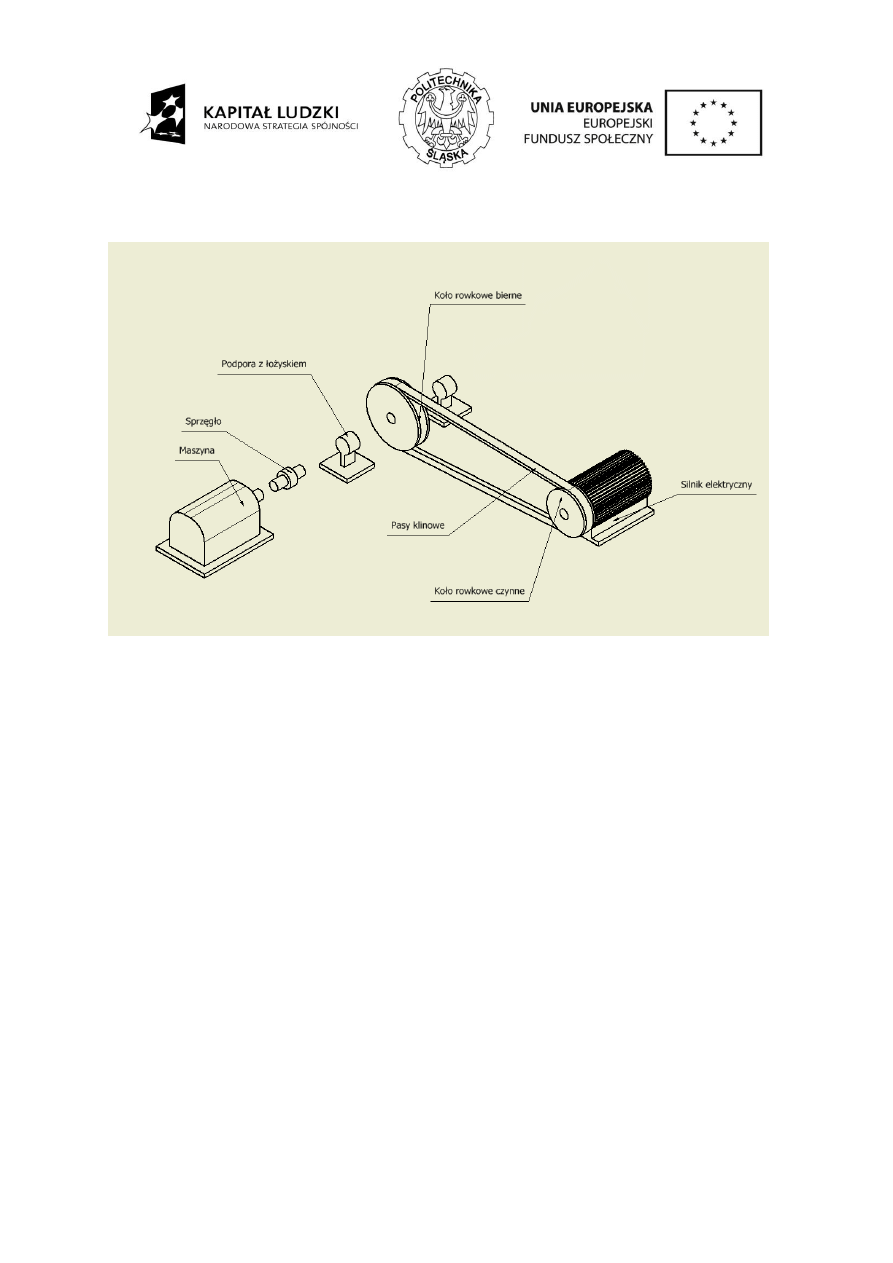
Należy opracować konstrukcję układu napędowego przedstawionego na Rys. 4.3.

Dane do zadania:
N

2

= 5 kW



2

= 240 ± 10 rad/s

L

H

= 15 godz

L

0

≤ 700

d = 18j6
l = 40
h = 150
b = 4h9
c = 19,5

Warunki pracy = lekkie. Liczba sztuk do wykonania = 2 szt.

Zdecydowano się na rozwiązanie układu napędowego złożonego z silnika elektrycznego i
przekładni paskowej z pasami klinowymi jak na Rys. 4.3.

Etap 1: Dobór silnika
Dobrano silnik indukcyjny trójfazowy klatkowy Sf-160M-1A. Parametry silnika:



moc 11 kW,



prędkość obrotowa 2920 obr/min => prędkość kątowa



1

= 305,8 rad/s

Etap 2: Obliczenie przełożenia przekładni

2

1







i

27

,

1

240

8

,

305





i

Etap 3: O

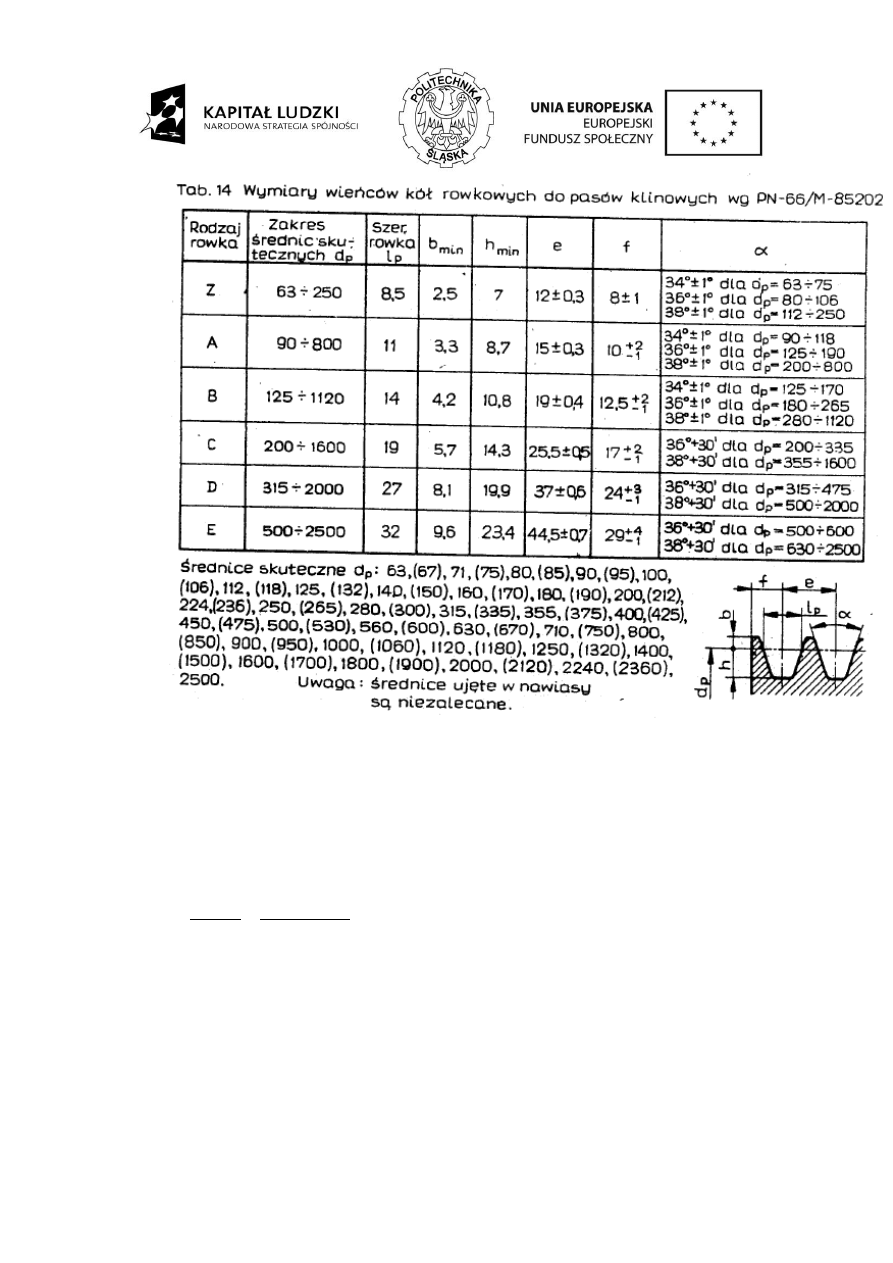
kreślenie wielkości kół paskowych oraz typów pasków klinowych



Wstępna wartość średnicy skutecznej mniejszego koła paskowego (najmniejsza ze
znormalizowanych)

– patrz tablica nr Tab 14

d

p1

= 63 mm



Dla tej średnicy średnica równoważna wynosi

1

1

k

d

D

p

e





gdzie k

1

to współczynnik, który jest zależny od przełożenia przekładni Dla i = 1,27

współczynnik ten jest równy k

1

= 1,10 (z tablicy Tab 19)

3

,

69

10

,

1

63







e

D

mm



Obliczenie prędkości pasa

6

,

9

2

063

,

0

8

,

305

2

1

1











p

d

v



m/s



Sprawdzenie mocy przenoszonej przez 1 pas

Z tablicy Tab 15 dla D

e

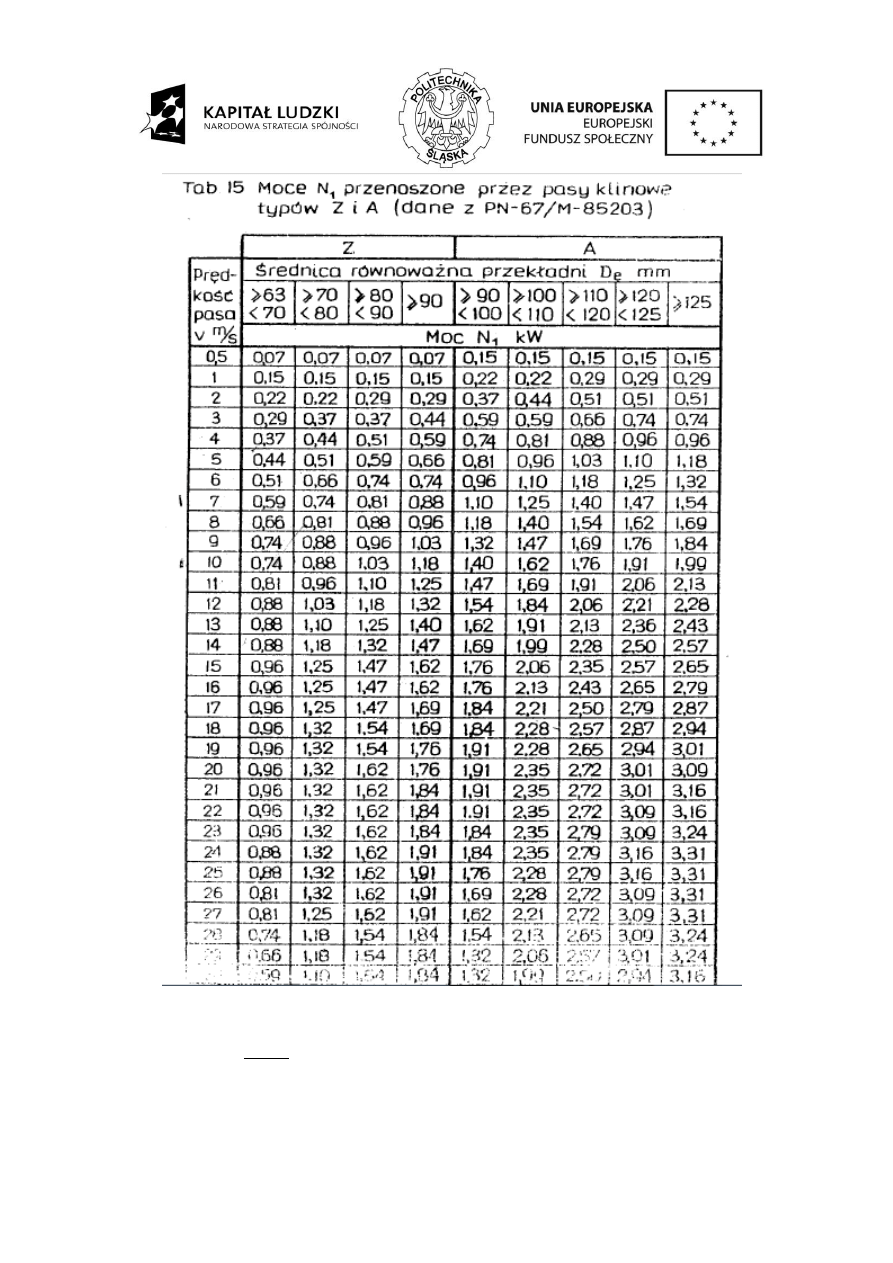
= 69,3 mm i v = 9,6 m/s jeden pas typu Z przenosi moc N

1

=

0,74 kW



Moc przenoszona przez zespół pasów

T

L

k

k

k

N

z

N











1

gdzie
z

– liczba pasów

k

L

, k



, k

T

-

współczynniki

Zakładamy, że

1





T

L

k

k

k



stąd

14



z

WNIOSEK:

Wyliczona liczba pasów jest zbyt duża. Należy dążyć do jej zmniejszenia.

W związku z tym w kolejnym kroku iteracji należy zwiększyć średnicę skuteczną
małego koła rowkowego



d

p1

= 140 mm



Dla tej średnicy średnica równoważna wynosi

1

1

k

d

D

p

e





gdzie k

1

to współczynnik, który jest zależny od przełożenia przekładni

Dla i = 1,27 współczynnik ten jest równy k

1

= 1,10 (z tablicy Tab 19)

154

10

,

1

140







e

D

mm



Obliczenie prędkości pasa

4

,

21

2

140

,

0

8

,

305

2

1

1











p

d

v



m/s



Sprawdzenie mocy przenoszonej przez 1 pas

Z tablicy Tab 14 dla D

e

= 154 mm i v = 21,4 m/s:

o jeden pas typu Z przenosi moc N

1

= 1,84 kW

o jeden pas typu A przenosi moc N

1

= 3,16 kW

o jeden pas typu B przenosi moc N

1

= 3,75 kW



Sprawdzenie liczby pasów

o

dla pasów typu Z liczba pasów z ≥ 6

o

dla pasów typu A liczba pasów z ≥ 4

o

dla pasów typu B liczba pasów z ≥ 3

Przyjęto pasy typu A w liczbie z=4



Obliczenie średnicy dużego koła paskowego

1

2

p

p

d

i

d





8

,

177

140

27

,

1

2







p

d

mm

W oparciu o tablicę Tab. 14 przyjęto średnicę znormalizowaną

180

2



p

d

mm

Etap 4: Wyznac

zenie przełożenia rzeczywistego



























1

1

1

2

p

p

pc

pb

rz

d

d

d

d

i

gdzie



to miara poślizgu pasa (przyjęto 0,02)





31

,

1

02

,

0

1

140

180









rz

i

Etap 5: Wyznaczenie rzeczywistej

prędkości kątowej wału maszyny



4

,

233

31

,

1

8

,

305

1

2







rz

rz

i





rad/s

Etap 6: Wyznaczenie odległości międzyosiowej





2

1

2

1

2

50

2

p

p

p

p

d

d

a

d

d

















180

140

2

50

2

180

140













a

640

210





a

Wstępnie przyjęto a = 250 mm

Etap 7: Wyznaczenie długości pasa

Współczynniki pomocnicze j i k

29

,

1

140

180

1

2







p

p

d

d

j

79

,

1

140

250

1







p

d

a

k

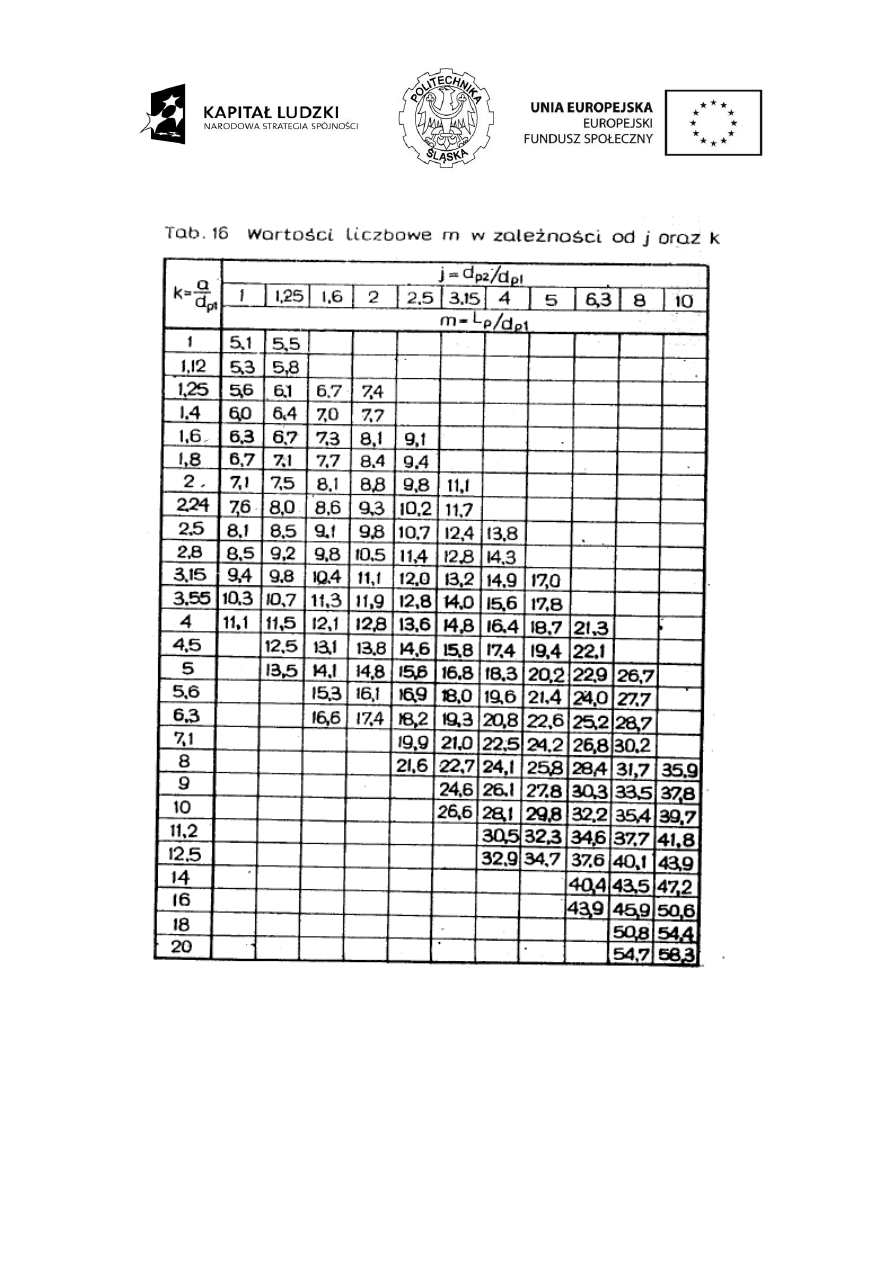
Na podstawie otrzymanych wartości z tablicy Tab 16 odczytano wartość m = 7,2.

W związku z tym można obliczyć długość pasa wg zależności:

1

P

P

d

m

L





1008

140

2

,

7







P

L

mm

Z tablicy Tab. 17 d

obrano najbliższą znormalizowaną wartość równą L

p

= 1000 mm

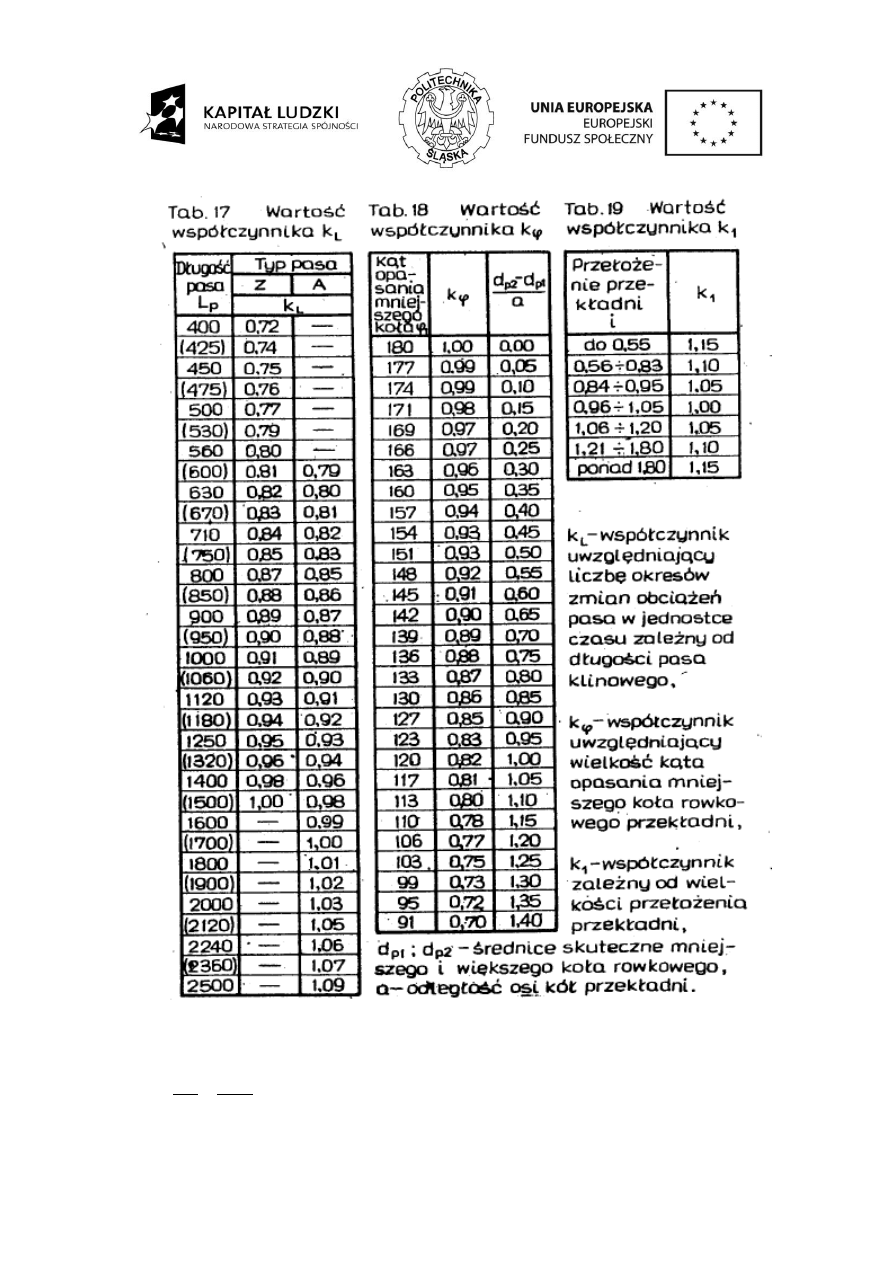
Etap 8: Przeliczenie odległości międzyosiowej

14

,

7

140

1000

1







p

p

d

L

m

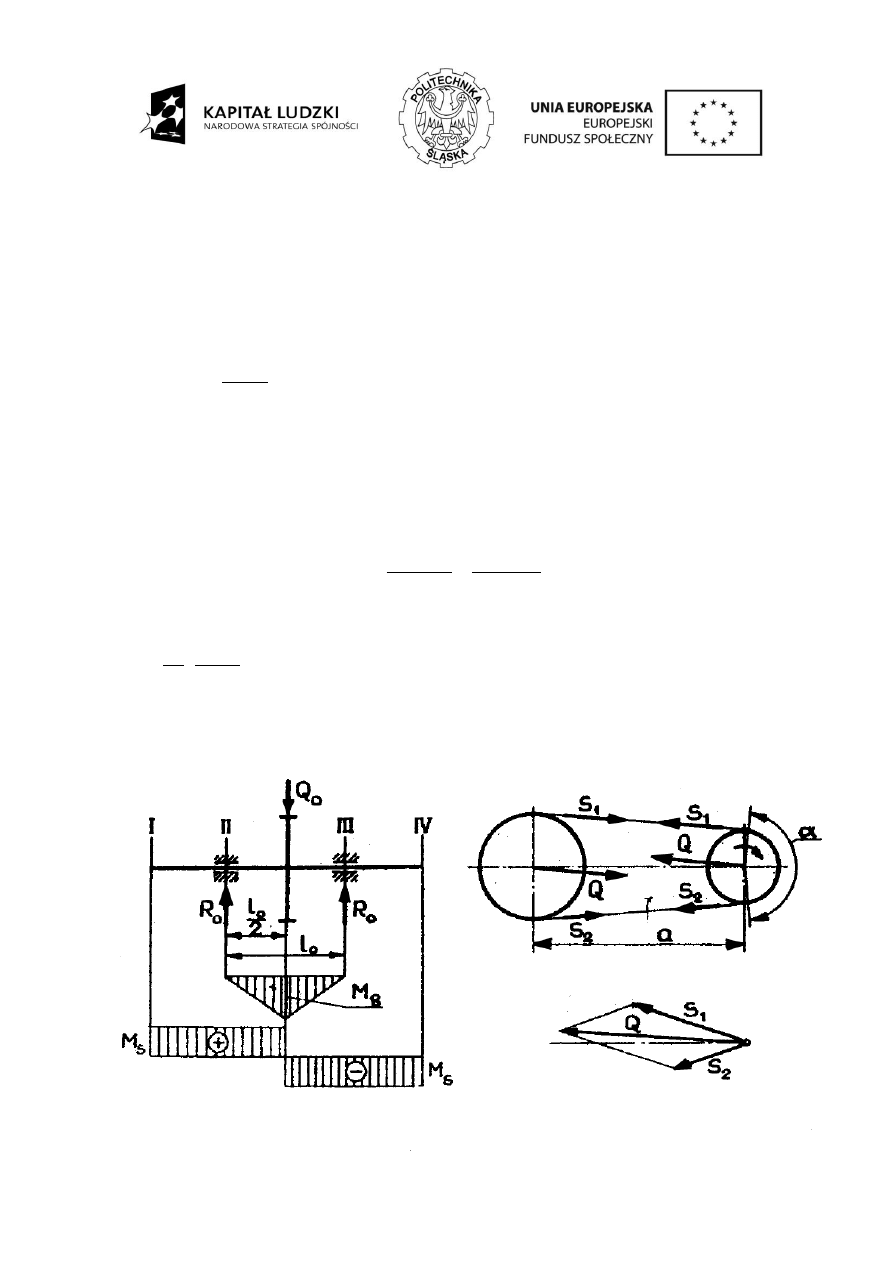
Z tablicy Tab. 14 dla wartości j=1,29 i m=7,14 odczytano wartość k=1,8

Odległość międzyosiowa wynosi:

252

140

8

,

1

1











p

d

k

a

mm

Etap 9: Wyznaczenie liczby pasów

T

L

k

k

k

N

z

N











1



Z tablicy Tab 14 dla D

e

= 154 mm i v = 21,4 m/s:

o jeden pas typu A przenosi moc N

1

= 3,16 kW



Z tablicy Tab. 20 k

T

= 1,1



Z tablicy Tab. 17 k

L

= 0,89



Z tablicy Tab. 16 k



= 0,98 dla

16

,

0

252

140

180

1

2









a

d

d

p

p

Wymagana liczba pasów wynosi:

99

,

3

1











k

k

k

N

N

z

L

T

przyjęto z = 4

Etap 10: Wyznaczenie cech konstrukcyjnych wału



Moment obrotowy na wale silnika

7

,

32

8

,

305

10000

1

1









N

M

Nm

Siła obwodowa

467

140

,

0

7

,

32

2

2

1

1











p

d

M

P

N

Napięcie wstępne pasa

z

F

S







0

0



gdzie:

0



-

naprężenie wstępne pasa

dla ciężkich warunków pracy

0



=0,9 N/mm

2

dla średnich warunków pracy

0



=1,2 N/mm

2

dla lekkich warunków pracy

0



=1,5 N/mm

2

F

– pole przekroju poprzecznego pasa

dla pasów typu Z F = 47 mm

2

dla pasów typu Z A = 81 mm

2

z

– liczba pasów

486

4

81

5

,

1

0

0















z

F

S



N



Wyznaczenie sił w pasach

















0

2

1

2

1

2 S

S

S

P

S

S

720

2

467

486

2

0

1











P

S

S

N

253

467

720

1

2











P

S

S

N



Wyznaczenie kąta opasania

07936

,

0

252

2

140

180

2

2

cos

2

1















a

d

d

p

p



'

27

85

2







'

54

170







Wypadkowa siła

972

cos

2

2

1

2

2

2

1

















S

S

S

S

Q

N



Do obliczeń wytrzymałościowych przyjmuje się siłę

1458

972

5

,

1

5

,

1











Q

Q

N

4.3

Przykład rozwiązania zadania

4.3.1 WYZNACZANIE

CECH

KONSTRUKCYJNYCH

ZAZĘBIENIA

ŚRUBOWEGO

Przykład opracowany na podstawie materiałów wewnętrznych Katedry Podstaw Konstrukcji
Maszyn przez przygotowanych przez Prof. dr hab. inż. Wojciecha Cholewę.

OPIS POTRZEBY
Dysponując silnikiem o mocy Ns = 11 kW i prędkości obrotowej ns = 975 obr/min należy
napędzać wał maszyny z prędkością obrotową nt = 4 obr/s. Dopuszczalna odchyłka
nominalnej prędkości wału maszyny wynosi



n =



0,15 obr/s. Zmienność oporów ruchu wału

ur

ządzenia technologicznego opisana jest liczbą KI = 1,2.

ZAŁOŻENIA



Zastosować przekładnię walcową o uzębieniu śrubowym ewolwentowym.



Do wykonania uzębienia należy zastosować tworzywo stal ulepszona cieplnie,
umożliwiające wykonanie uzębień o twardości boku zęba 250 HB, dla którego na
podstawie badań uzębień próbek na stanowisku doświadczalnym wyznaczono
naprężenia krytyczne





eH

eF

MN m

MN m

lim

lim

oraz





530

220

2

2

.



Wymagane mi

nimalne liczby bezpieczeństwa



F

= 2,



H

= 1,5.

Rozwiązanie:

Obliczenia wstępne przeprowadza się przy przyjęciu, że przekładnia posiada uzębienie

proste. Dopuszczalne obciążenie zazębienia prostego jest około 20% mniejsze od
dopuszczalnego obciążenia podobnego zazębienia śrubowego.

Zakłada się, że przekładnia może przenieść obciążenie wynikające z mocy nominalnej
silnika:

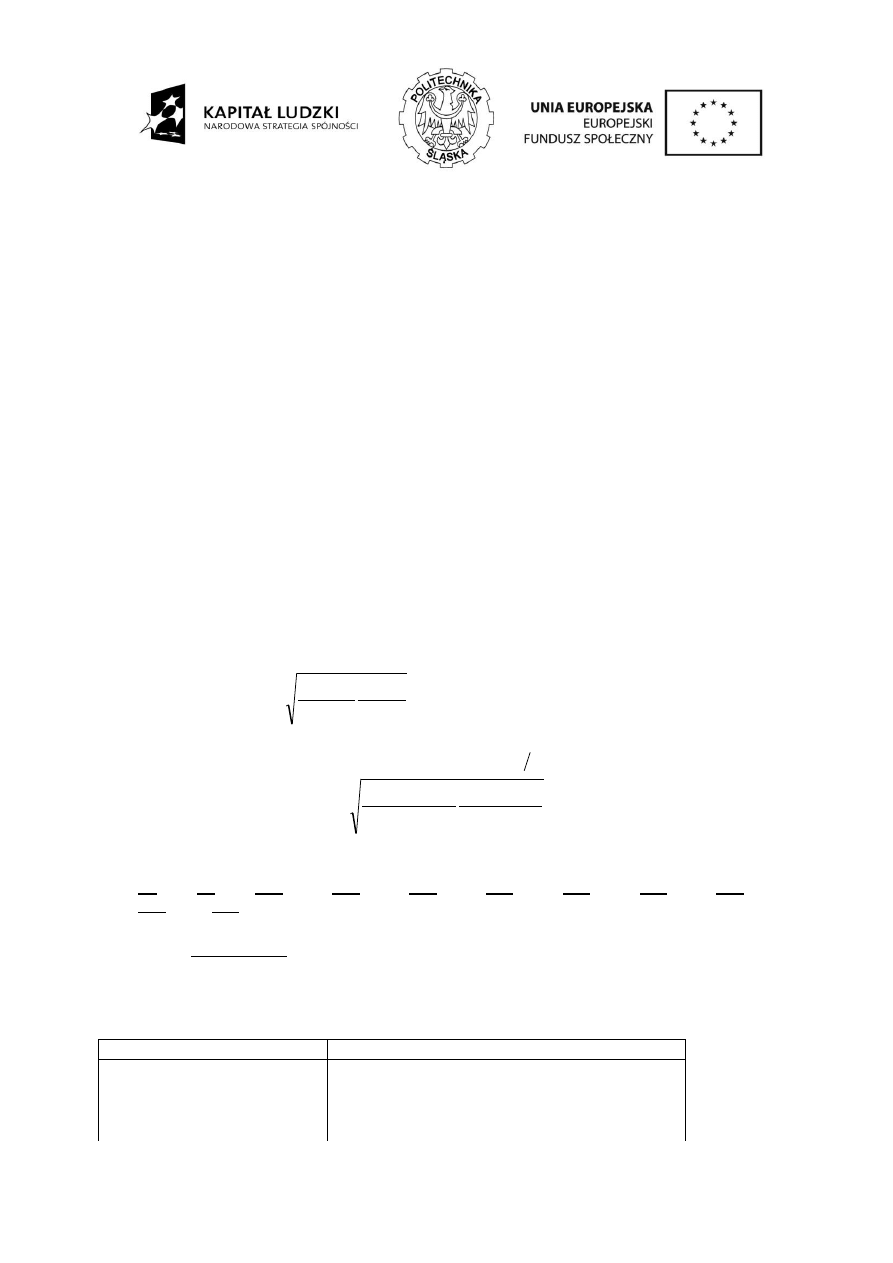
N

N

kW

kW

OBL WST

S









0 80

0 80 11

8 8

.

.

.

Prędkość kątowa zębnika i koła:

s

rad

n

s

obr

n

s

rad

min

obr

n

n

s

/

1

.

25

4

2

2

/

4

/

1

.

102

30

/

975

/

975

2

2

2

1

1









































Przełożenie przekładni:

i







 

1

2

102 1 25 1

4 068

/

. /

.

.

Moment działający na wał zębnika:

Nm

N

M

WST

OBL

WST

OBL

2

.

86

1

.

102

/

8800

/

1

1









Naciski dopuszczalne

k

MN m

H

e H

H











lim

/

/ .

/

530 1 3

408

2

Oszacowanie odległości międzyosiowej

 

3

4

2

1

1

1

4400

i

i

k

M

a

H

Wst

Obl

w







(kryterium pittingu)

Założenie: względna szerokość wieńca zębnika

1

1

1





d

b

w











m

a

w

193

.

0

068

.

4

1

068

.

4

10

408

1

2

.

86

4400

3

4

2

6











Typoszereg odległości międzyosiowych wg PN - 68/M - 88508:

68, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 225, 250, 280, 315, 355, 400, 450,
500, 560, 630 [mm].

Przyjęto:

a

m

w



0 200

.

Szacowanie liczby zębów

Zaleca się [3] następujące

z

i max

ze względu na wytrzymałość stopy zęba

Bok zęba

i = 1

2

3

4

5

6

250 HB



=0

94

73

64

59

57

56

250 HB



>0

110

88

78

73

69

68

300 HB



=0

75

58

51

48

46

45

300 HB



>0

94

73

64

59

57

56

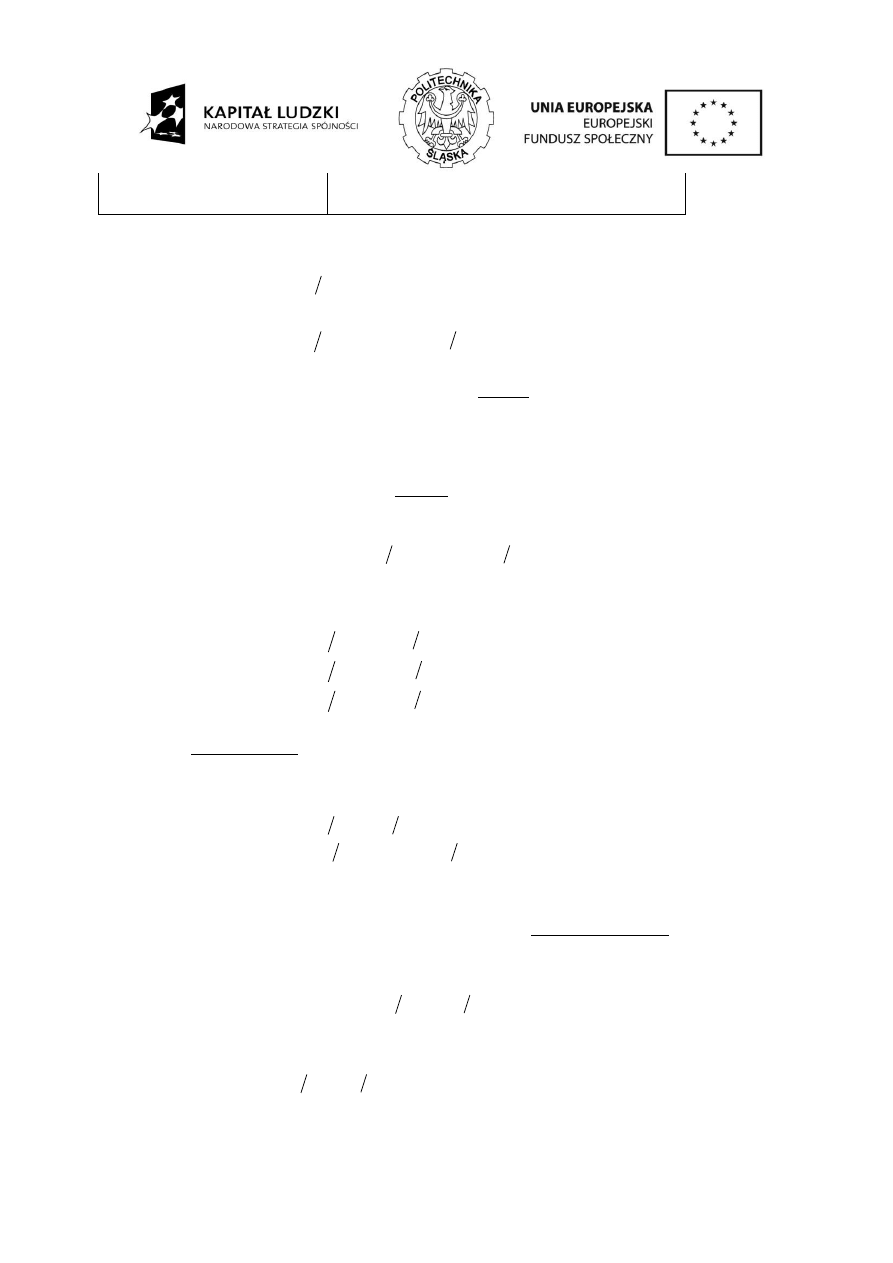
58 HB



=0

37

30

26

24

23

22

58 HB



>0

48

38

32

30

29

28

Moduł





1

2

2

1

,

2

z

i

z

z

z

a

m

w

t













73

0

,

250

,

4

max

1











HB

i

z

 





08

.

1

1

068

.

4

73

200

2

1

2

max

1













i

z

a

m

w

t

W świetle kryteriów technologicznych przyjęto:

m

n



3

.

Kąt pochylenia kierunku linii zęba

Z warunku stałej długości linii zęba będącego w przyporze wynika:













b

m

w

n

sin

, , , ...

1 2 3

z założenia

 





mm

i

a

b

w

w

93

.

78

068

.

4

1

200

2

1

1

2

1

1

1

























przyjęto

b

mm

w



80



 







 







 





















 

  













 

  













 

  









1

1

3 80

0 1178097

6 76572

2

2

3 80

0 2356195

13 62814

3

3

3 80

0 3534292

20 69722

m b

m b

m b

n

w

n

w

n

w

.

.

.

.

.

.

Przyjęto:







13 62814

.

Moduł czołowy

mm

m

m

n

t

08691

.

3

62814

.

13

cos

3

cos











 





01

.

104

57

.

25

068

.

4

57

.

25

068

.

4

1

08691

.

3

200

2

1

2

1

2

1























z

i

z

i

m

a

z

t

w

Przyjęto następujące względnie pierwsze liczby zębów:

z

z

1

2

25

104





,

Przełożenie rzeczywiste przekładni:

i

z

z







2

1

104 25

4 16

.

Prędkość obrotowa wału wyjściowego przekładni:

n

n i

obr

obr s

2

1

975 4 16 234 375

3 906







.

.

/ min

.

/

Jest spełniony warunek

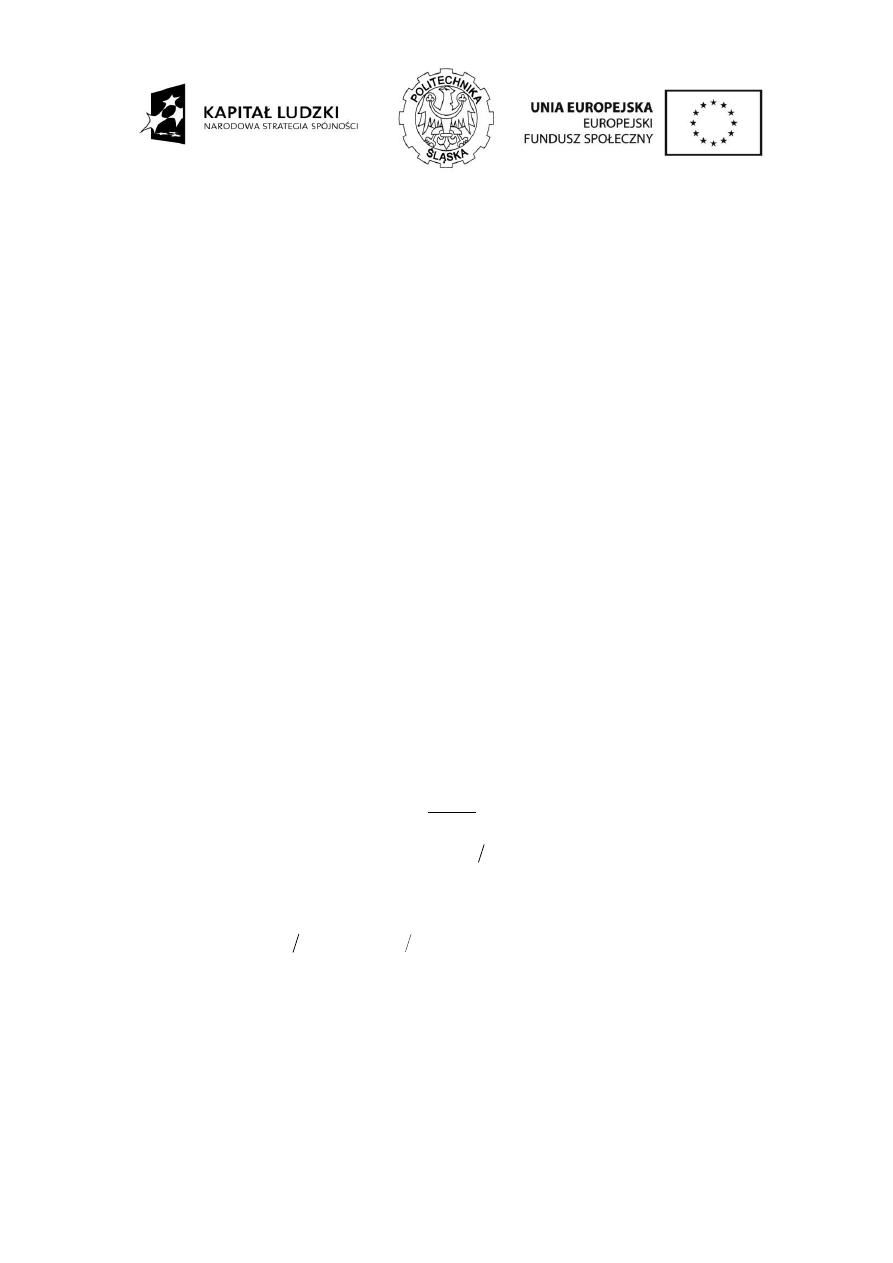
n

n

n

t

2

  

poniewa

ż

3 906

4 00 0 15

.

.

.

/





obr s

Odległość osi zerowa









mm

z

z

m

a

t

1057

.

199

104

25

08619

.

3

5

.

0

5

.

0

2

1













Kąt zarysu czołowy















53465

,

20

3745145

,

0

62814

,

13

cos

/

20

cos

/

t

n

t

tg

tg

tg









Kąt pochylenia linii zęba na walcu zasadniczym



















79186

,

12

975180

,

0

53165

,

20

cos

/

20

cos

62814

,

13

cos

cos

/

cos

cos

cos

b

t

b











Kąt przyporu czołowy (w płaszczyźnie czołowej)















20518

,

21

9322911

,

0

200

/

53165

,

20

cos

1057

,

199

/

cos

cos

tw

w

t

tw

a

a







Przesunięcie zarysu











2942947

.

0

53165

.

20

2

104

25

0161695

.

0

0178783

.

0

2

0178783

.

0

3701002

.

0

20518

.

21

3701002

.

0

20518

.

21

0161695

.

0

3582449

.

0

53165

.

20

3582449

.

0

53165

.

20

2

1

2

1



























































tg

tg

z

z

inv

inv

x

x

x

tg

tg

inv

rad

tg

tg

inv

rad

t

t

tw

t

t

t

tw

tw

tw

tw

t

t

t

t























Przyjęto rozdział przesunięcia zarysu:

x

x

x

x

x

x

t

t

t

n

t

n

1

2

1

1

2

0 2943

0

0 2943

13 62814

0 3028

0











 



.

;

cos

.

cos

.

.

;



Pozorna odległość osi









0141

.

200

0

.

3

0

3028

.

0

1057

.

199

2

1

















n

n

n

p

m

x

x

a

a

Sprawdzenie zmniejszenia luzu wierzchołkowego



y

a

a

mm

p

w











200 0141 200 0

0 0141

.

.

.

Ponieważ



y

m

mm

n





 

0 1

0 1 3

0 3

.

.

.

nie istnieje konieczność skracania wysokości głowy zęba.



Średnice toczne

 





mm

d

i

d

mm

i

a

d

w

w

w

w

4806

.

322

5194

.

77

16

.

4

5194

.

77

16

.

4

1

200

2

1

2

1

2

1























Średnice podziałowe

d

m z

mm

d

m z

mm

t

t

1

1

2

2

3 08691 25

77 1728

3 08691 104

321 0386



 















.

.

.

.

Średnice zasadnicze

d

d

mm

d

d

mm

b

t

b

t

1

1

2

2

77 1728

20 53165

72 2706

321 0386

20 53165

300 6458









 









 

cos

.

cos

.

.

cos

.

cos

.

.





Wysokości głów i stóp podziałowych

















mm

m

x

h

h

mm

m

x

h

h

n

a

n

a

0000

.

3

0

.

3

0

.

0

1

9084

.

3

0

.

3

3028

.

0

1

2

*

2

1

*

1





































mm

m

x

c

h

h

mm

m

x

c

h

h

n

f

n

f

7500

.

3

0

.

3

0

.

0

25

.

0

1

8416

.

2

0

.

3

3028

.

0

25

.

0

1

2

*

*

2

1

*

*

1





























Średnice wierzchołków i podstaw

d

d

h

mm

d

d

h

mm

a

a

a

a

1

1

1

2

2

2

2

77 1728 2 3 9084

84 9896

2

321 0386 2 3 0000

327 0386







 









 



.

.

.

.

.

.

d

d

h

mm

d

d

h

mm

f

f

f

f

1

1

1

2

2

2

2

77 1728 2 2 8416

71 4896

2

321 0386 2 3 7500

313 5386







 









 



.

.

.

.

.

.

Luzy wierzchołkowe (sprawdzenie poprawności obliczeń)

















mm

d

d

a

c

mm

d

d

a

c

f

a

w

f

a

w

7359

.

0

4896

.

71

0386

.

327

5

.

0

0

.

200

5

.

0

7359

.

0

5386

.

313

9896

.

84

5

.

0

0

.

200

5

.

0

1

2

2

2

1

1

































Luz wymagany









mm

m

c

n

75

.

0

45

.

0

0

.

3

25

.

0

15

.

0

25

.

0

15

.

0













Długość odcinka przyporu (Odcinka wzębiania gf, wyzębiania ga):









]

[

03

,

6

20518

,

21

sin

4086

,

322

6458

,

300

0386

,

327

5

,

0

sin

5

,

0

2

2

2

2

2

2

2

mm

d

d

d

g

tw

w

b

a

f































]

[

34

,

8

sin

5

,

0

1

2

1

2

1

mm

d

d

d

g

tw

w

b

a

a















a

f

g

g

g







Podziałka przyporu:

p

m

et

t

t

  







cos

,

9 0818

Czołowa liczba przyporu











g

p

et

1 58

,

Skokowa liczba przyporu:



 









b

tg

m

w

t

2 00

,

Weryfikacja geometrycznych cech konstrukcyjnych zazębienia

Moment

skręcający przekazywany z silnika na zębnik (wielkość nominalna):

M

N

Nm

s

1

1

107 7







,

[

]

Siła obwodowa:

F

M d

N

b





2

2791

1

1

[

]

Jednostkowe obciążenie obwodowe boku zęba:

3

,

1

]

)

2

(

1

[

4

,

0

]

[

10

6

i

dokladnosc

Klasa

]

[

4

6

,

1

]

[

400

200

1

0

>

350

<

HB

]

[

96

,

3

1

,

102

0771728

,

0

2

=

v

6

2

,

1

2

1

1













































































t

w

pe

l

n

pe

V

I

F

b

f

q

m

mm

m

mm

d

f

s

m

d

i

dokladnosc

klasa

K

K







Uwaga: Dla wyznaczenie gL podstawić [fpe]=



m, [bwe]=mm, [Ft]=kG. Obliczoną wartość ql

ogranicza się do zakresu [0,1] - przyjęto gL=1gL

Z

b





 





cos

,

0 786









62

,

1

1

1

5

,

0

2

1

2

















Z

q

K

L

H

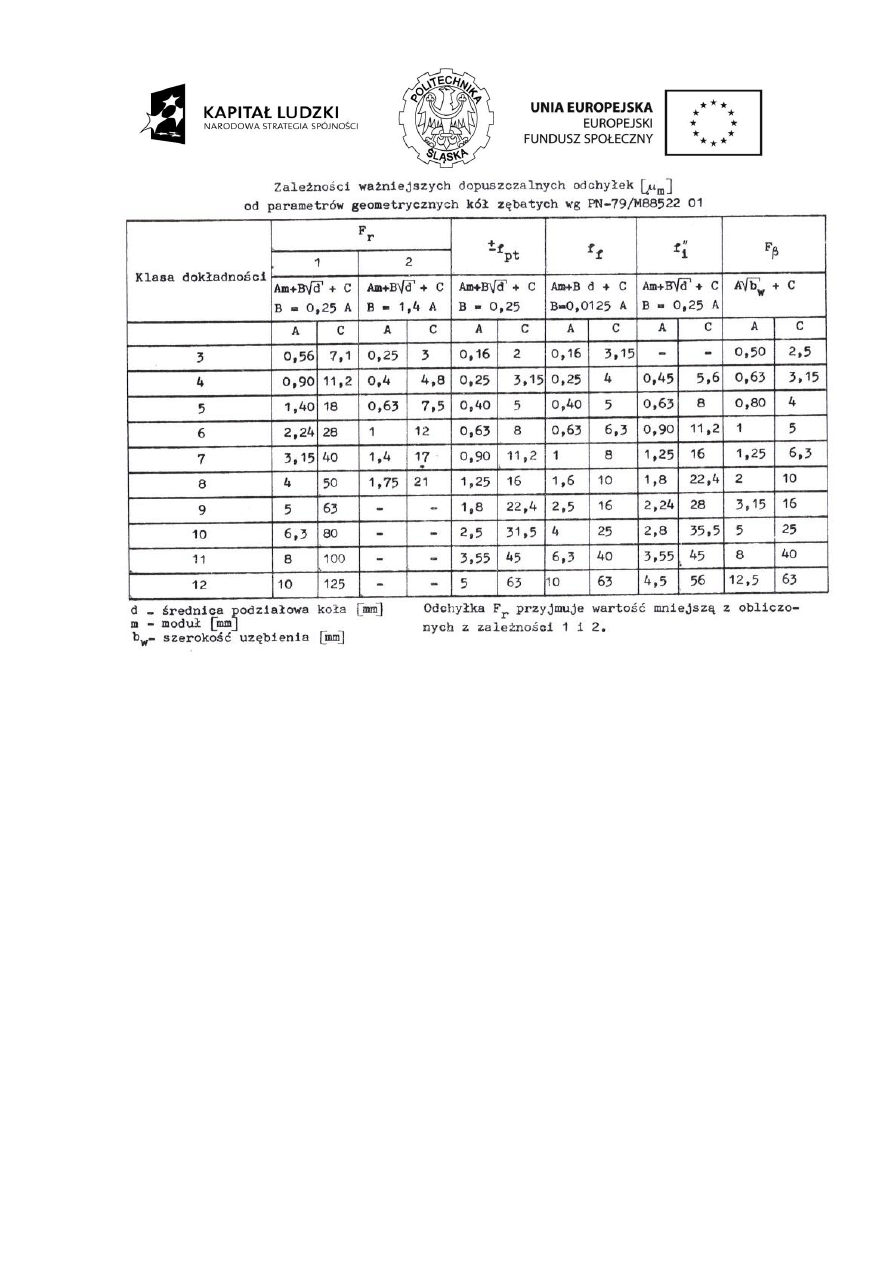
wg za

łączonego wykresu:

045

,

1

04

,

1

iowa

jednostopn

a

przekladni

350

1

1





























d

b

HB

K

w

H









]

/

[

071

,

0

m

MN

K

K

K

K

b

F

w

H

H

V

I

w

t

Ht









Naprężenia kryterialne boku zęba:
(ponieważ zastępcza liczba zębów zębnika zn1>20, to naprężenia kryterialne wyznacza się
wyłącznie dla punktu biegunowego C:
Liczba wpływu zarysu boku zęba:

Z

tg

H

b

t

tw







cos

cos

,







2

1 69

Liczba wp

ływu tworzywa:

0 35

265

0 786

,

[

]

,

E

Z

MPa

Z

M

 













H

Ht

H

M

w

d

i

i

Z Z Z

MPa









1

1

403 [

]

Liczba bezpieczeństwa dla boku zęba:









H

eH

H

H Min









lim

,

,

1 32

1 3

Jednostkowe obciążenie obwodowe stopy zęba:





58

,

1

1

;

58

,

1

;

1

1

2

,

1































L

L

L

F

V

I

q

q

q

K

K

K

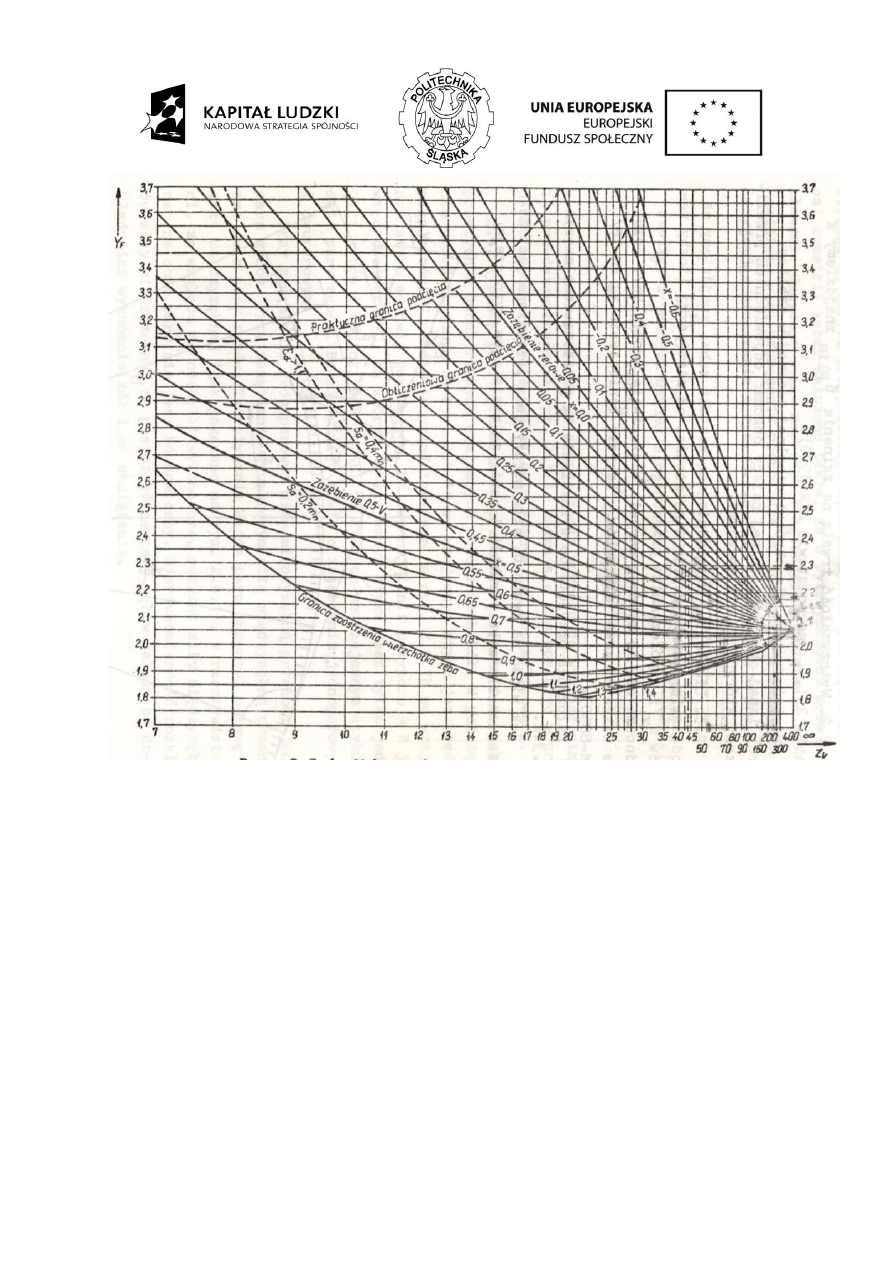
wg załączonego wykresu:

KF



(HB<350, przekładnia jednostopniowa,



=104 [mm])=1,09

b

b

mm

mm

b

b

mm

w

w

1

2

5

85

80











[

]

[

]

[

]









]

/

[

68

]

/

[

64

2

2

1

1

mm

N

K

K

K

K

b

F

w

mm

N

K

K

K

K

b

F

w

F

F

V

I

t

Ft

F

F

V

I

t

Ft

















Zastępcze liczby zębów , liczba analogii stereomechanicznej:

z

z

z

z

n

b

n

b

1

1

2

2

2

2

27 05

112 53













cos

cos

,

cos

cos

,









liczby kszałtu wg wykresu [1] rys.10 lub [2] rys.3.16









2

,

2

0

;

53

,

112

33

,

2

3028

,

0

;

05

,

27

1

2

2

1

1

1













n

n

F

n

n

F

x

z

Y

x

z

Y

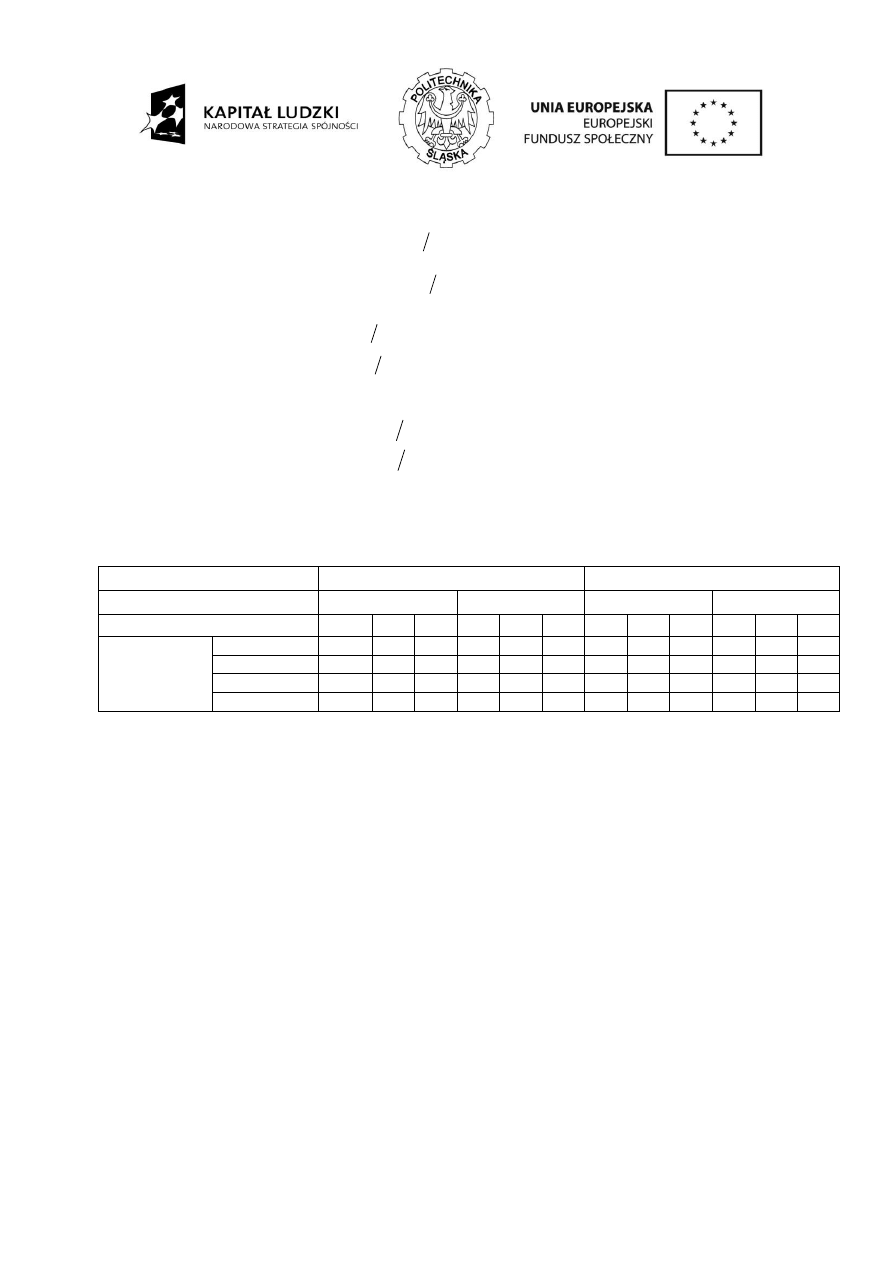
Naprężenia kryterialne stopy zęba:

liczba wpływu czołowego wskaźnika zazębienia:

Y











1

0 633

,

liczba

wpływu kąta pochylenia zęba:

Y

o





 



1

120

0 886

,









]

/

[

28

]

/

[

28

2

2

2

2

2

1

1

1

m

MN

Y

Y

Y

m

w

m

MN

Y

Y

Y

m

w

F

n

Ft

F

F

n

Ft

F

































Liczba bezpieczeństwa dla stopy zęba:

















F

F

1

1

2

2

7 9

2 0

7 9

2 0

















eF

F

F MIN

eF

F

F MIN

lim

lim

,

,

,

,

Wykresy i tabele

Tabela: Liczba wpływu nadwyżki dynamicznej K

v

:

Kąt kierunku linii zęba



= 0



> 0

Twardość boku zęba



350 HB

> 350 HB



350 HB

> 350 HB

Klasa dokładności

6

7

8

6

7

8

6

7

8

6

7

8

Prędkość
obwodowa v

< 3 m/s

1,0

1,15 1,25

1,0

1,15

1,2

1,0

1,0

1,1

1,0

1,0

1,1

3 ÷ 8 m/s

1,2

1,35 1,45

1,15 1,25 1,35

1,0

1,0

1,3

1,0

1,0

1,2

8 ÷ 12,5 m/s

1,3

1,45

-

1,25 1,35

-

1,1

1,2

1,4

1,0

1,1

1,3

12,5 ÷ 30 m/s

1,45

-

-

1,35

-

-

1,2

1,3

-

1,1

1,1

-

Rys. 4.5. Tablica odchyłek [15]

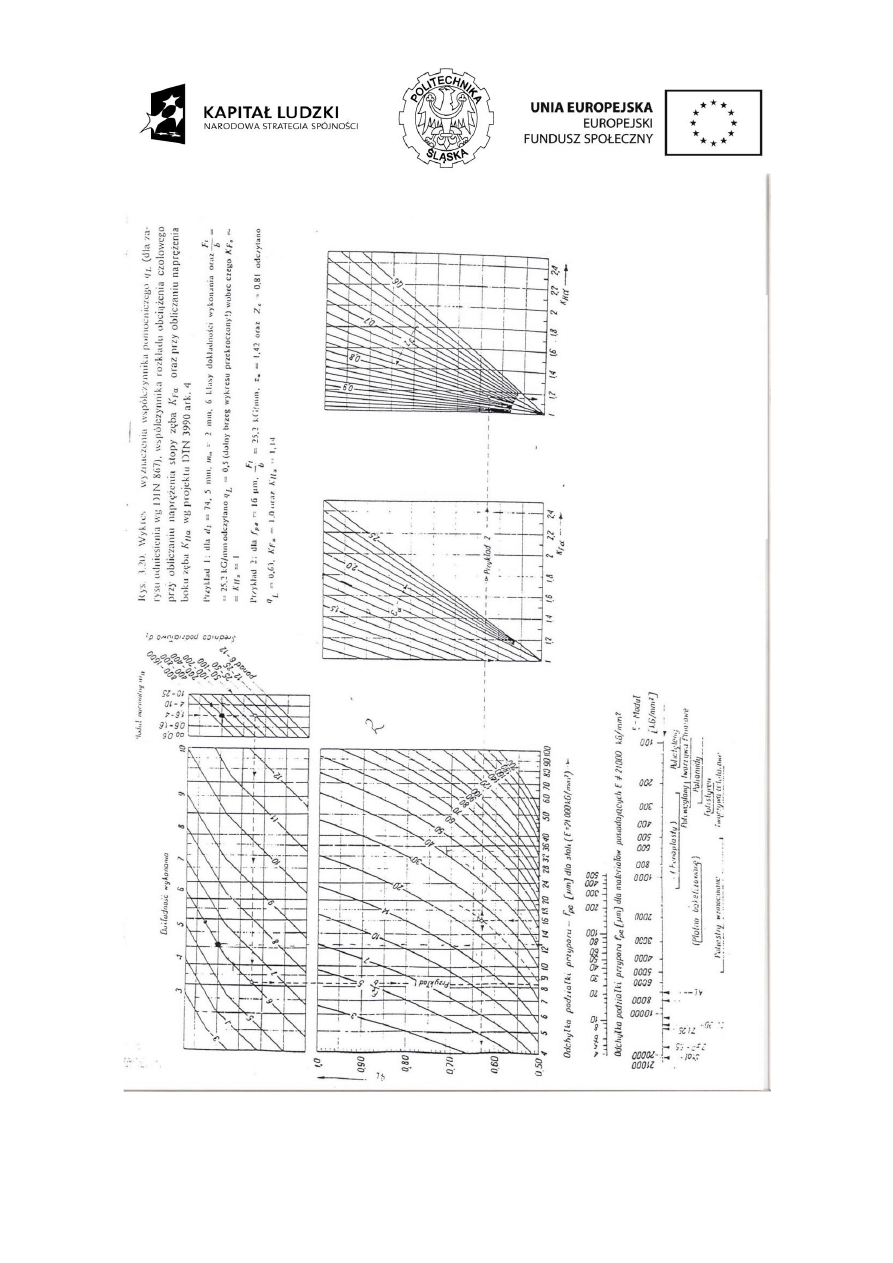
Rys. 4.6. Wyznaczenie współczynnika qL

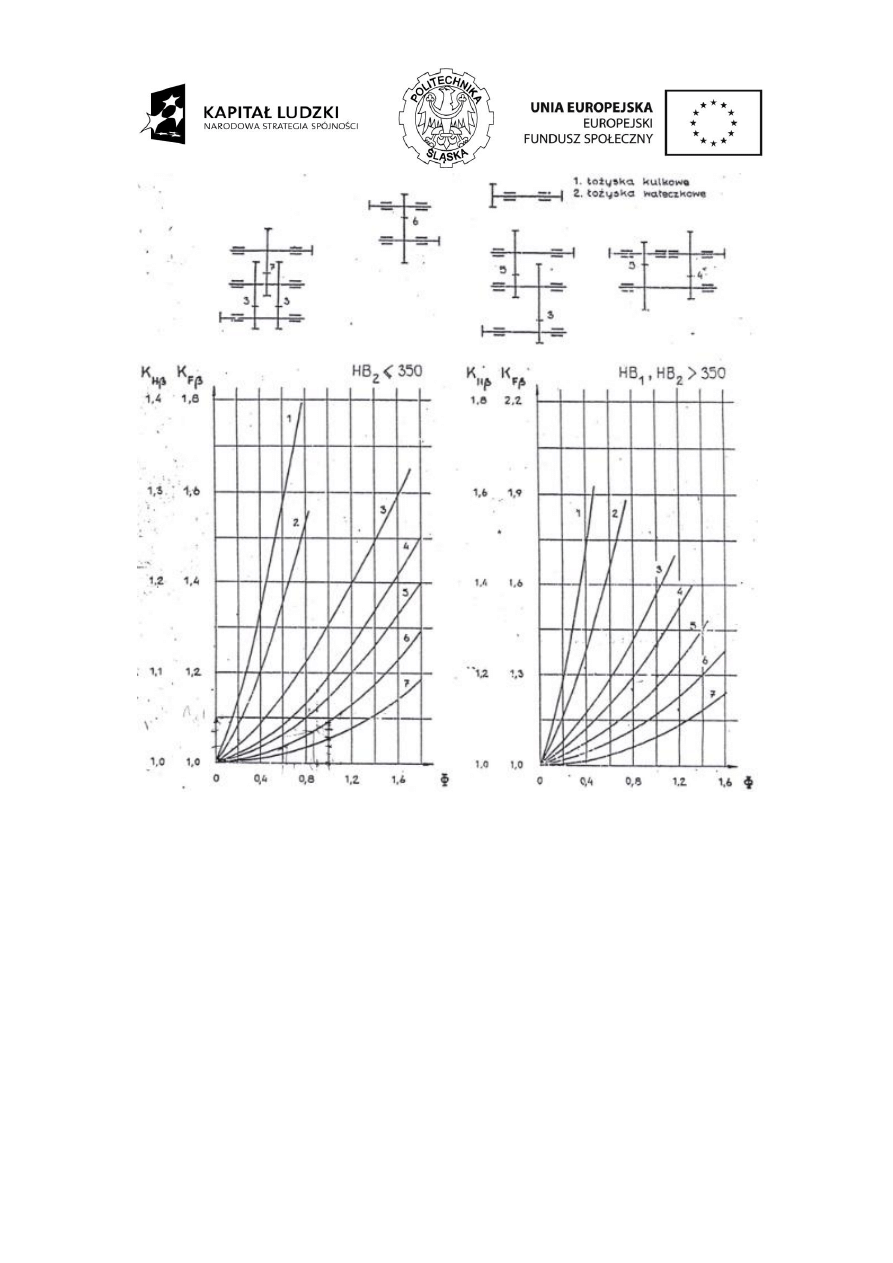
Rys. 4.7. Liczba wpływu rozkładu obciążenia wzdłuż boku zęba

Rys. 4.8. Wykres do wyznaczania współczynnika Y

F

[15]

4.4

Zadania do samodzielnego rozwiązania

4.4.1 Zadanie 1

Rys. 3

W oparciu o schemat z Rys. 3 opracować konstrukcję układu napędowego, w którym
napędzana jest tylko jedna maszyna.

Dane do zadania:
N

2

= 8 kW



2

= 240 ± 10 rad/s

L

H

= 21 godz

d = 18j6
l = 40
h = 150
b = 4h9
c = 19,5

Warunki pracy = ciężkie. Liczba sztuk do wykonania = 1 szt.

4.4.2 Zadanie 2

Obliczyć główne wymiary kół zębatych dla następujących danych:
a) z = 19, m = 3,5 [mm],





25



,

b) z = 19, m = 3,5 [mm],





0



.

4.4.3 Zadanie 3

Dobrać cechy konstrukcyjne przekładni zębatej o zębach śrubowych, zgodnie z
przedstawionymi poniżej założeniami.

Dysponując silnikiem o mocy Ns = 7,5 kW i prędkości obrotowej ns = 980 obr/min należy
napędzać wał maszyny z prędkością obrotową nt = 5 obr/s. Dopuszczalna odchyłka
nominalnej prędkości wału maszyny wynosi



n =



0,15 obr/s. Zmienność oporów ruchu wału

urządzenia technologicznego opisana jest liczbą KI = 1,2.
Wymagania:



Zastosować przekładnię walcową o uzębieniu śrubowym ewolwentowym.



Do wykonania uzębienia należy zastosować tworzywo stal ulepszona cieplnie,
umożliwiające wykonanie uzębień o twardości boku zęba 250 HB, dla którego na
podstawie badań uzębień próbek na stanowisku doświadczalnym wyznaczono
naprężenia krytyczne





eH

eF

MN m

MN m

lim

lim

oraz





530

220

2

2

.



Wymagane minimalne liczby bezpieczeństwa



F

= 2,



H

= 1,5.

5

Projektowanie połączeń czopowych

Projektowanie połączeń czopowych będzie dotyczyło doboru podstawowych parametrów i
weryfikacji kilku najczęściej stosowanych połączeń czopowych. Zostanie omówiona
weryfikacja:



połączeń wpustowych,



połączeń wielowypustowych,



połączeń wciskowych.

5.1

Połączenia wpustowe.

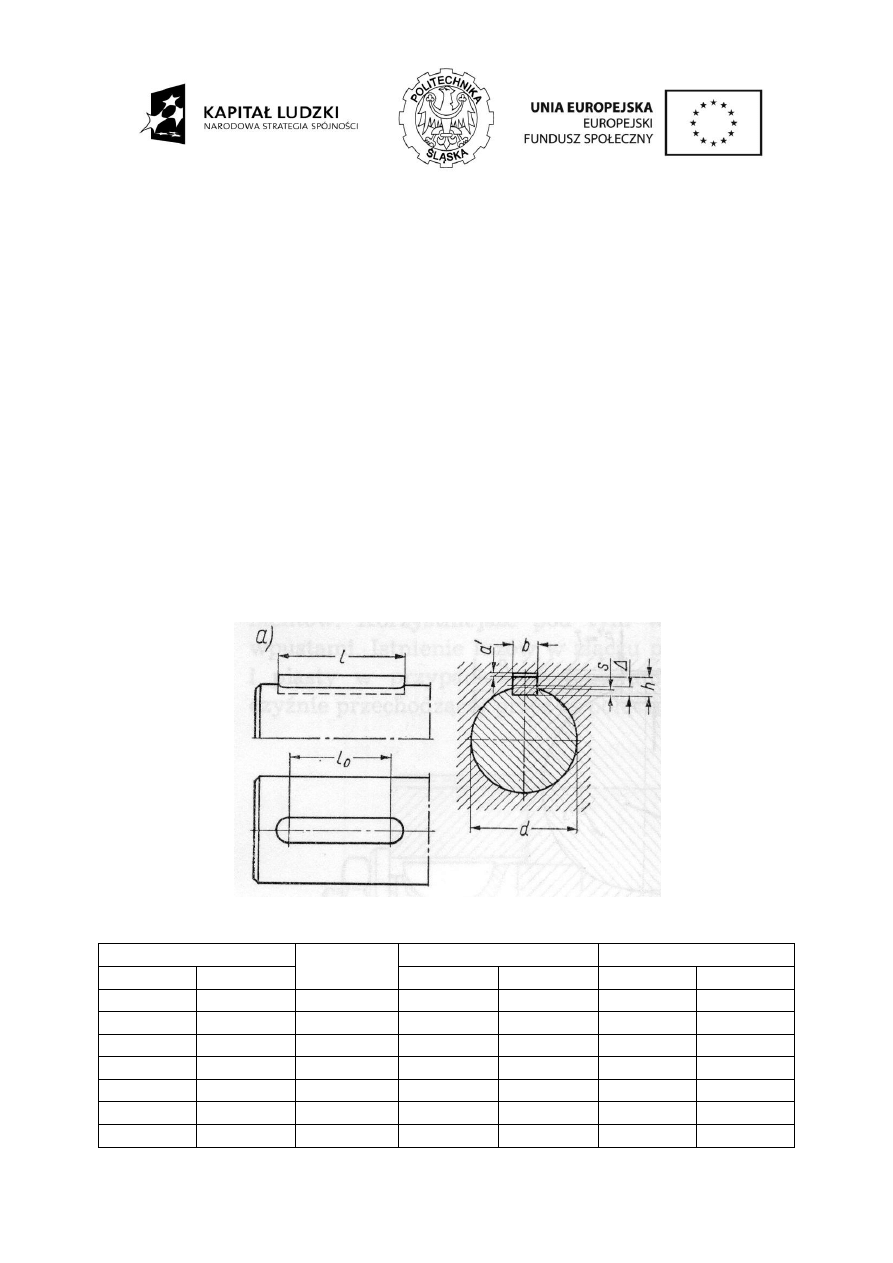
Wpusty są elementami znormalizowanymi (PN-70/M-85005, PN-88/M-85008). Dobór wpustu
do danego połączenia, odbywa się na podstawie średnicy nominalnej czopa/piasty, która
występuje w danym połączeniu. Na podstawie średnicy nominalnej dobiera się wymiary
zarówno samego wpustu jak również wymiary rowka na wpust, który należy wykonać w wale
oraz rowka który należy wykonać w piaście. Wymiary te odczytuje się z normy. Przykładowe
wartości wymiarów poprzecznych wpustów oraz rowków na wpusty zamieszczono w Tablicy
1.

Rys. 1. Dobór połączenia wpustowego

Tablica 1

Zakres średnic

Wymiary

wpustu bxh

Głębokości rowków

Długość wpustu l

od

do

Czop t

1

Piasta t

2

od

do

6

8

2 x 2

1,2

1,0

6

20

8

10

3 x 3

1,8

1,4

6

36

10

12

4 x 4

2,5

1,8

8

45

12

17

5 x 5

3,0

2,3

10

56

17

22

6 x 6

3,5

2,8

14

70

22

30

8 x 7

4,0

3,3

18

90

30

38

10 x 8

5,0

3,3

22

110

38

44

12 x 8

5,5

3,3

28

140

44

50

14 x 9

6,0

3,8

36

160

50

58

16 x 10

7,0

4,3

45

180

58

65

18 x 11

7,5

4,4

50

200

65

75

20 x 12

9,0

4,9

56

220

75

85

22 x 14

9,0

5,4

63

250

85

95

25 x 14

10,0

5,4

70

280

95

110

28 x 16

11,0

6,4

80

320

110

130

32 x 18

12,0

7,4

90

360

Weryfikacja połączenia wpustowego sprowadza się do sprawdzenia nacisków
dopuszczalnych występujących w takim połączeniu oraz sprawdzeniu, czy wpust nie
zostanie ścięty.
W przeprowadzaniu obliczeń uwzględnia się długość czynną wpustu l

0

, która nie uwzględnia

zaokrągleń we wpustach pryzmatycznych (Rys. 2).

Rys. 2. Czynna długość wpustu

Sprawdzenie nacisków powierzchniowych:

0

0

p

kl

P

p





gdzie:

p

- naciski powierzchniowe, na powierzchni bocznej wpustu,

P

-

siła działająca w połączeniu,

k

-

głębokość rowka wpustowego,

0

l

-

długość czynna wpustu,

0

p

-

naciski dopuszczalne tworzywa najsłabszego elementu (wpustu, wałka lub piasty).

Dla stali St5, na

ciski dopuszczalne wynoszą 15-20 MPa.

Oprócz sprawdzenia nacisków dopuszczalnych, połączenie wpustowe weryfikuje się na
ścinanie:

t

k

b

l

P





0



gdzie:



-

naprężenia styczne (wytrzymałość na ścinanie),

P

-

siła działająca w połączeniu,

b

-

szerokość wpustu,

0

l

-

długość czynna wpustu,

t

k

-

naprężenia dopuszczalne na ścinanie.

5.2 P

ołączenia wciskowe

Obliczenia konstrukcyjne połączeń wciskowych, służą do ustalania najkorzystniejszych
kształtów, wymiarów i pasowania elementów łączonych. Obciążenia połączenia wciskowego
przez siłę styczną P (kierunek może być skośny obwodowy lub wzdłużny) nie może
przekroczyć najmniejszej siły tarcia występującej między powierzchniami styku:







p

l

d

F

p

T

T

P







gdzie:

p

- nacisk powierzchniowy,

F

- pole powierzchni,



-

współczynnik tarcia,

d

-

średnica czopa,

l

-

długość czynna połączenia.

W przypadku połączenia momentem skręcającym, warunek przyjmie postać:





p

l

d

M

s

2

5

,

0



Z podanych warunków ustala się najmniejszy wymagany nacisk jednostkowy na powierzchni
styku w warunkach eksploatacyjnych:





l

d

P

p

wym









l

d

M

p

s

wym

2

2



W dalszej kolejności oblicza się wymagany montażowy wcisk skuteczny oraz wcisk
nominalny. Mając do dyspozycji wcisk nominalny dobieramy złożenie pasowania, a
następnie sprawdzamy, czy nie została przekroczona granica plastyczności w czopie wału
lub piaście koła.
Kolejność działań jest więc następująca:
1)

obliczamy żądany montażowy wcisk skuteczny,

2) obliczamy wcisk nominalny,
3) dobieramy pasowanie,
4) sprawdzamy czy nie przekroczono granicy plasty

czności w czopie,

5)

sprawdzamy wytrzymałość piasty,

6)

obliczamy wartość siły potrzebnej do wtłoczenia czopa do otworu piasty lub osadzenia
piasty na czopie wału.

Przykład
Dobra złożenie pasowania dla połączenia wtłaczanego przedstawionego na rysunku, jeżeli
średnica nominalna walcowej powierzchni styku wynosi d, jej długość l, średnica otworu

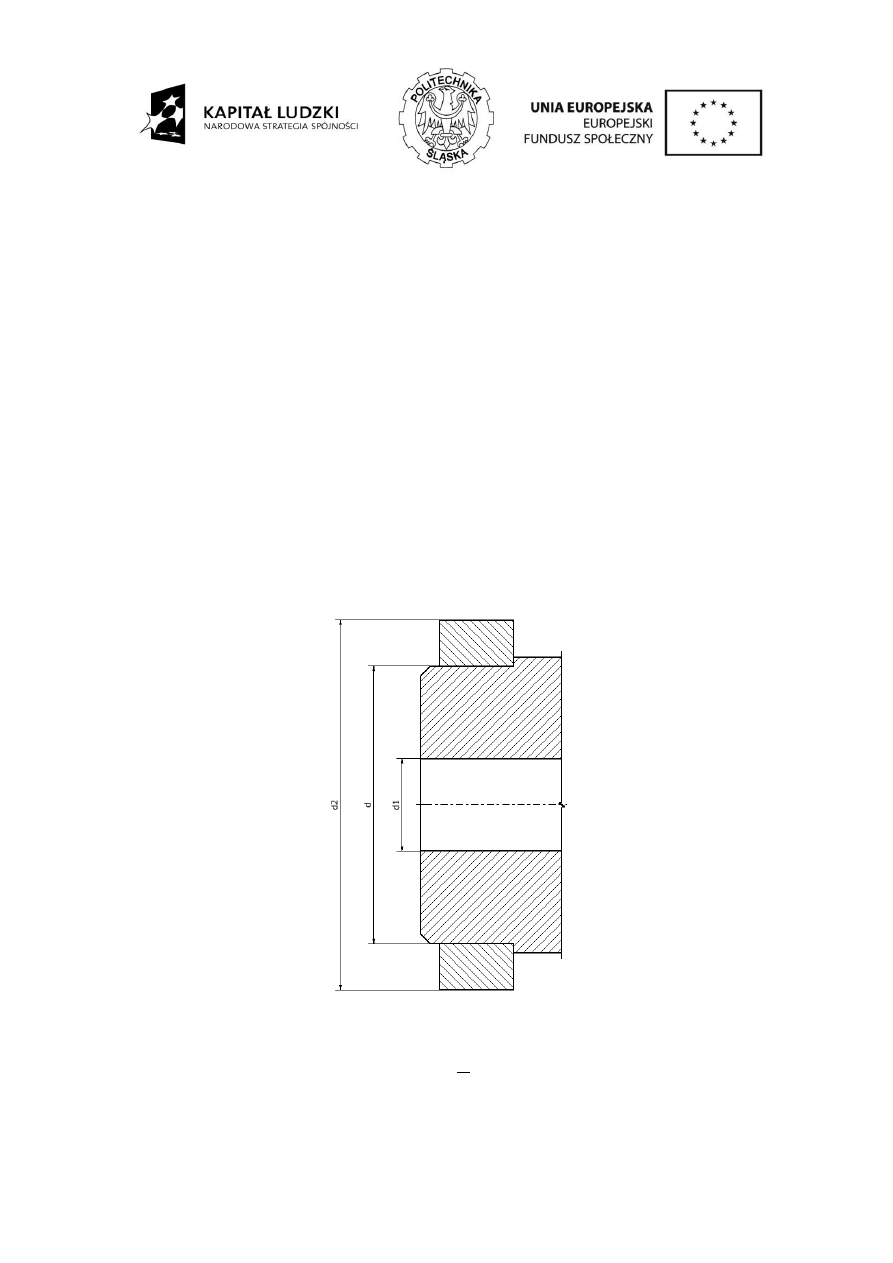
wydrążonego w czopie d

1

, średnica zewnętrzna piasty d

2

. Połączenie obciążone jest

momentem skręcającym, którego wartość maksymalna wynosi M

smax

.

Dane:
d = 150 [mm]
l = 40 [mm]
d

1

= 50 [mm]

d

2

= 200 [mm]

M

smax

= 250 [Nm]

Tworzywo piasty: Zl200
Tworzywo wału: St4
współczynnik tarcia: stal/żeliwo



= 0,08,



w

= 0,1

Dane dla tworzyw:
Czop:
E

1

= 2,1 10

5

[MPa]



= 0,3

R

e

= 240 [MPa]

R

m

= 410 [MPa]

Piasta:
E

1

= 0,9 10

5

[MPa]



= 0,25

R

e

= 200 [MPa]

R

c

= 750 [MPa]

1. Określenie wymaganych nacisków powierzchniowych.





p

l

d

T

d

T

M

s





2





l

d

M

p

s

2

2



]

[

21

,

2

]

[

10

21

,

2

08

,

0

04

,

0

15

,

0

250

2

6

2

MPa

Pa

p



















2. Obliczanie wcisków.
a) montażowego

Wartość względną montażowego wcisku skutecznego (wyrażoną w promilach) można
wyznaczyć z zależności:

]

[

1000

2

1

oo

o

d

w















gdzie:
w -

montażowy wcisk skuteczny,

1



,

2



-

odkształcenie względne powierzchni styku czopa i piasty,

Wielkości

1



i

2



można wyznaczyć z zależności:























1

2

1

2

1

1

1

1

1

1000





x

x

E

p























2

2

1

2

1

2

2

1

1

1000





x

x

E

p

gdzie:
x

1

i x

2

-

współczynniki wydrążenia czopa i piasty

E

1

, E

2

-

moduły Young'a dla czopa i piasty

1



,

1



- liczby Poissona czopa i piasty

75

,

0

200

150

333

,

0

150

50

2

2

1

1













d

d

x

d

d

x

]

[

094

,

0

25

,

0

75

,

0

1

75

,

0

1

10

9

,

0

21

,

2

1000

]

[

010

,

0

3

,

0

333

,

0

1

333

,

0

1

10

1

,

2

21

,

2

1000

2

2

5

2

2

2

5

1

oo

o

oo

o

























































Wartość względna montażowego wcisku skutecznego wynosi:

oo

o

104

,

0

094

,

0

010

,

0

2

1

















Żądany montażowy wcisk skuteczny jest równy:

]

[

16

6

,

15

150

104

,

0

m

d

w

















Wiadomo, że podczas montażu połączenia wtłaczanego wygładzają się nierówności
powierzchni. Badania wykazały, że wysokość nierówności zmniejsza się przeciętnie o 60%.
Dlatego wcisk nominalny powinien być większy i przed zmontowaniem elementów powinien
wynosić:

)

(

2

,

1

'

2

1

Rz

Rz

w

w







Dla gładkiego toczenia lub szlifowania wartości

2

1

, Rz

Rz

wynoszą:

]

[

6

2

1

m

Rz

Rz







]

[

4

,

30

)

6

6

(

2

,

1

16

'

m

w











3. Dobór pasowania
Na podstawie obliczonego wcisku nominalnego dobrano pasowanie lekko wtłaczane ø150
H6/r5.
Dla tego pasowania:

w

min

= 38 [



m]

w

max

= 81 [



m]

4. Sprawdzenie czy nie przekroczono granicy plastyczności

W przypadku czopa drążonego współczynnik obciążalności jest równy:





2

1

1

58

,

0

Re

x

p

e





W przypadku czopa pełnego:

Re



e

p

Dla czopa:









]

[

9

,

123

333

,

0

1

58

,

0

240

1

58

,

0

2

2

1

MPa

x

R

p

e

e















Naciski maksymalne są równe:

p

p





max

max



d

w

max

max





]

[

9

,

123

]

[

475

,

11

104

,

0

150

21

,

2

81

max

max

MPa

p

MPa

d

p

w

p

e

















5. Sprawdzenie wytrzymałości piasty
Obliczamy współczynnik wytrzymałości oprawy:

c

m

r

dop

R

R

x

x

k

p









2

2

2

2

1

1

1

26

,

0

750

200

75

,

0

1

75

,

0

1

1

2

2











r

dop

k

p

r

dop

k

p

26

,

0



s

m

r

x

R

k



Przyjęto x

s

= 3.

]

[

3

,

17

3

200

26

,

0

MPa

p

dop





Dopuszczalne odkształcenie względne powierzchni piasty wynosi:

dop

dop

dop

dop

p

p

p

p















oo

o

dop

81

,

0

3

,

17

21

,

2

104

,

0







Stąd wcisk dopuszczalny jest równy:

]

[

122

81

,

0

150

m

d

w

dop

dop















max

w

w

dop



6. Obliczamy siłę P

w

potrzebną do wtłoczenia czopa wału do piasty:

T

P

w



]

[

6

,

32

1

,

0

3

,

17

40

150

kN

p

l

d

P

w

dop

w





























5.3

Zadania do samodzielnego rozwiązania

5.3.1 Zadanie 1

Na pełny wał, o średnicy d

wz

osadzono skurczowo pierścień oporowy o średnicy zewnętrznej

d

pz

i średnicy wewnętrznej d

pw

. Długość pierścienia wynosi l. Obliczyć siłę wzdłużną, jaką

można obciążyć pierścień oporowy. Wyznaczyć wymaganą temperaturę, do jakiej należy
ogrzać pierścień przy osadzaniu.
Dane:



















053

,

0

066

,

0

5

60s

d

wz















0

019

,

0

5

60s

d

pw

200



pz

d

Współczynnik tarcia:



= 0,14

Współczynnik rozszerzalności cieplnej:



t

= 11 10

-6

Moduł Young'a: E = 2,1 10

5

[MPa]

Liczba Poisson'a:



= 0,30

Wałek

Pierścień

Tworzywo: 20
Re: 250 [MPa]

Tworzywo: St5
Re: 280 [MPa]

5.3.2 Zadanie 2

Piastę o długości l i średnicy zewnętrznej d

Z

, osadzono na drążonym wale, o średnicy wewn. d

w

, który

obciążony jest momentem skręcającym M

S

. Średnica nominalna połączenia wynosi d.

Określić maksymalny moment, jakim może być obciążone połączenie.
Dane:
l

=

40

[mm]

d

=

150 H6/r5 [mm]

d

W

=

50

[mm]

d

Z

=

200

[mm]



= 0,14

ES =

+25

[



m]

EI =

0

[



m]

Tworzywo wałka: St6
R

e

=

310

[MPa]

E

1

=

2,1 · 10

5

[MPa]



1

=

0,3

es =

+83

[



m]

ei

=

+65

[



m]

Tworzywo piasty: St4
R

e

=

260

[MPa]

E

1

=

2,1 · 10

5

[MPa]



1

=

0,3

5.3.3 Zadanie 3

Dobrać odpowiednie złożenie pasowania dla połączenia wieńca koła zębatego o uzębieniu
prostym nasadzonego skurczowo na odlewanym kole bosym. Przenoszony przez to
połączenie moment skręcający wynosi Ms. Wymiary połączenia przedstawiono na rysunku.
Określić również temperaturę, do jakiej należy ogrzać wieniec przed montażem.

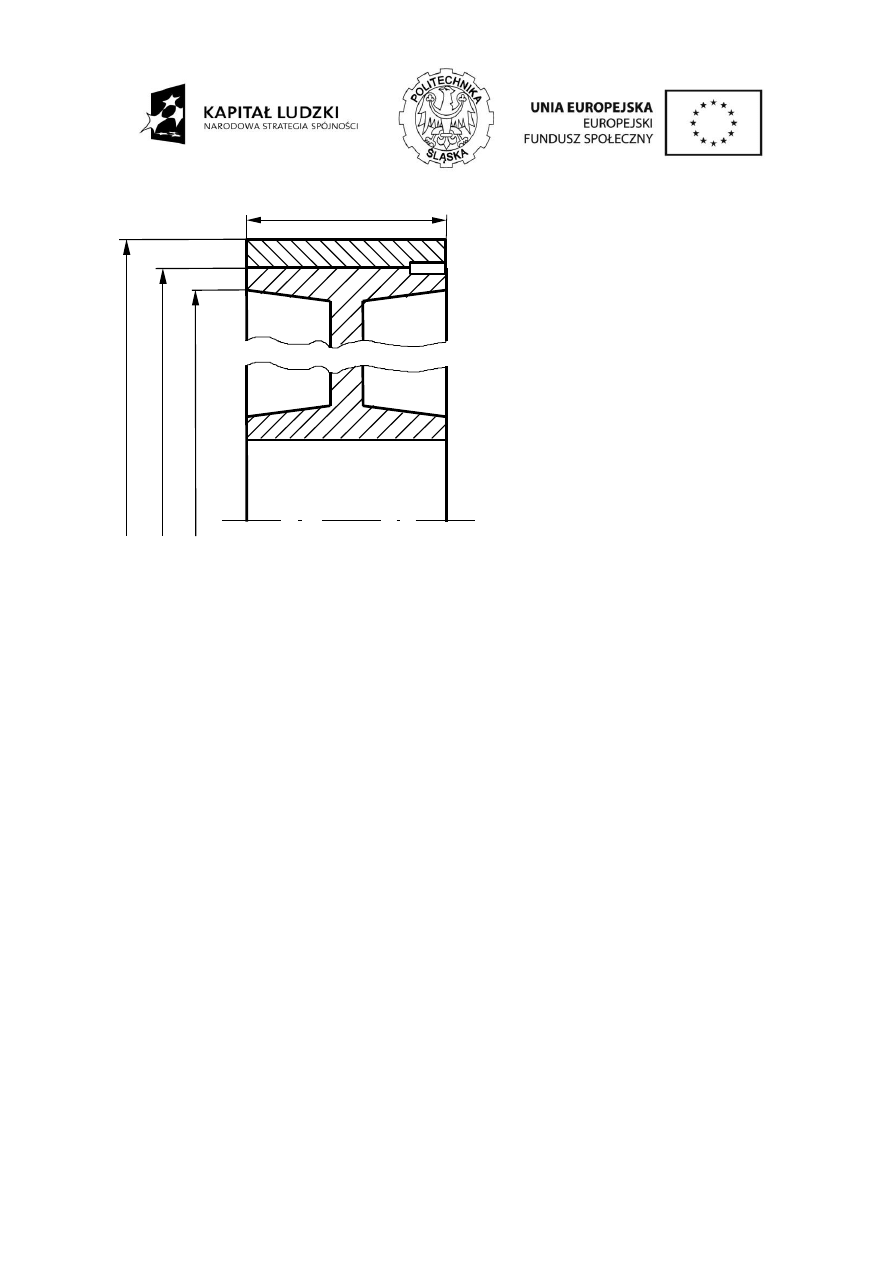
Dane:
Ms =

150

[Nm]

L

=

60

[mm]

d

=

300

[mm]

d

1

=

250

[mm]

d

2

=

350

[mm]



=

0,08



w

=

0,1

Tworzywo koła: ZL200
R

e

=

260

[MPa]

R

m

=

260

[MPa]

E

1

=

0,9 10

5

[MPa]



1

=

0,25

Tworzywo wieńca: 45H
R

e

=

830

[MPa]

E

2

=

2,1 · 10

5

[MPa]



2

=

0,3

d

1

d

d

2

L

6

Dobór łożysk

6.1

Prawo trwałości łożysk

Weryfikacja łożyska tocznego sprowadza się do wyznaczenia jego trwałości w określonych
warunkach pracy. Dlatego też konieczne jest poznanie zależności, nazywanej prawem
trwałości łożysk (1). Obliczona w ten sposób trwałość łożyska jest wyznaczana w milionach
obrotów.

q

P

C

L















10

(1)

gdzie:

10

L



minimalna trwałość łożyska w [mln obr.] przy niezawodności 90%

C



nominalna nośność dynamiczna łożyska,

P



równoważne obciążenie dynamiczne

q



wykładnik zależny od rodzaju łożyska:

3



q



dla łożysk kulkowych,

3

10



q



dla łożysk wałeczkowych.

Jeżeli trwałość łożysk ma być określona w godzinach pracy łożyska, to należy uwzględnić
prędkość obrotową i wówczas prawo trwałości łożysk przyjmuje postać:

n

L

L

h

60

10

10

6

10



(2)

gdzie:

h

L

10



minimalna trwałość łożyska w [h] przy niezawodności 90%

n



pr

ędkość obrotowa w [obr/min.]

Niektórzy producenci łożysk tocznych podają bardziej szczegółowe zależności pozwalające
na obliczenie trwałości łożyska. W zależnościach tych uwzględniana jest temperatura pracy,
wpływ obciążeń udarowych czy kierunek działania obciążenia. Dlatego też przy doborze
łożysk należy zapoznać się z zaleceniami producentów łożysk, zawartych w katalogach lub
na stronach internetowych (np. www.fag.de lub www.skf.com).
Równoważne obciążenie dynamiczne wyznaczamy z zależności:

a

r

YF

XF

P





(3)

gdzie:

r

F



obciążenie promieniowe łożyska,

a

F



obciążenie poosiowe łożyska,

X



współczynnik przeliczeniowy obciążenia promieniowego,

Y



współczynnik przeliczeniowy obciążenia osiowego.

Określenie wartości równoważnego obciążenia dynamicznego zależy również od typu
łożyska. Jest to związane z faktem, że wartości obciążenia promieniowego i poosiowego
łożyska nie zawsze da się wyznaczyć w sposób bezpośredni. Np. w przypadku łożysk
kulkowych

i stożkowych, obciążenie promieniowe łożyska „generuje” dodatkowe obciążenie

poosiowe, co jest związane z konstrukcją tych łożysk. Dlatego też przy wyznaczaniu
równoważnego obciążenia dynamicznego należy to uwzględnić.

6.2

Łożyska kulkowe skośne i łożyska stożkowe

Łożyska kulkowe skośne oraz łożyska stożkowe mogą być montowane pojedynczo lub w
parach. W zależności od sposobu zamontowania tego typu łożysk, dobranych parami,
można wyróżnić trzy układy łożyskowań:

1)

układ łożyskowania łożysk kulkowych skośnych i stożkowych typu „O”,

2)

układ łożyskowania łożysk kulkowych skośnych i stożkowych typu „X”,

3)

układ łożyskowania łożysk kulkowych skośnych i stożkowych typu tandem.

Rys. 1

Układy łożyskowań łożysk kulkowych skośnych i łożysk stożkowych

W przypadku łożysk stożkowych i kulkowych skośnych równoważne obciążenie dynamiczne
wyznacza się z innych zależności. Zależności te zależą od kierunku działania zewnętrznej
siły poosiowej oraz zastosowanego układu łożyskowania takich łożysk. Poniżej
przedstawiono zależności umożliwiające określenie wartości obciążenia promieniowego oraz
poosiowego dla tego typu łożysk.

Rys. 1. Przykłady łożyskowania wału w łożyskach kulkowych skośnych

Rys. 1. Przykłady łożyskowania wału w łożyskach kulkowych skośnych

1. Łożyska kulkowe skośne
Przedstawione poniżej zależność dotyczą wyznaczania wartości obciążenia poosiowego
łożysk kulkowych skośnych montowanych w układzie „O” lub „X” i obciążonych jak
przedstawiono na rysunku poniżej:

B

A

A

B

K

a

K

a

F

rB

F

rB

F

rA

F

rB

F

rA

Rys. Rozkład obciążeń łożysk kulkowych skośnych

Przypadek 1:

0





a

rB

B

rA

A

K

F

e

F

e

a

aA

aB

rA

A

aA

K

F

F

F

e

F







Przypadek 2:

rA

A

rB

B

a

rB

B

rA

A

F

e

F

e

K

F

e

F

e







a

aA

aB

rA

A

aA

K

F

F

F

e

F







Przypadek 3:

rA

A

rB

B

a

rB

B

rA

A

F

e

F

e

K

F

e

F

e







rB

B

aB

a

aB

aA

F

e

F

K

F

F







2. Łożyska stożkowe
Przedstawione poniżej zależność dotyczą wyznaczania wartości obciążenia poosiowego
łożysk stożkowych montowanych w układzie „O” lub „X” i obciążonych jak przedstawiono na
rysunku poniżej:

B

A

A

B

K

a

K

a

F

rB

F

rA

F

rB

F

rA

Rys. 2. Rozkład obciążeń łożysk stożkowych

Przypadek 1:

0





a

B

rB

A

rA

K

Y

F

Y

F

a

aA

aB

A

rA

aA

K

F

F

Y

F

F







5

,

0

Przypadek 2:



















A

rA

B

rB

a

B

rB

A

rA

Y

F

Y

F

K

Y

F

Y

F

5

,

0

a

aA

aB

A

rA

aA

K

F

F

Y

F

F







5

,

0

Przypadek 3:



















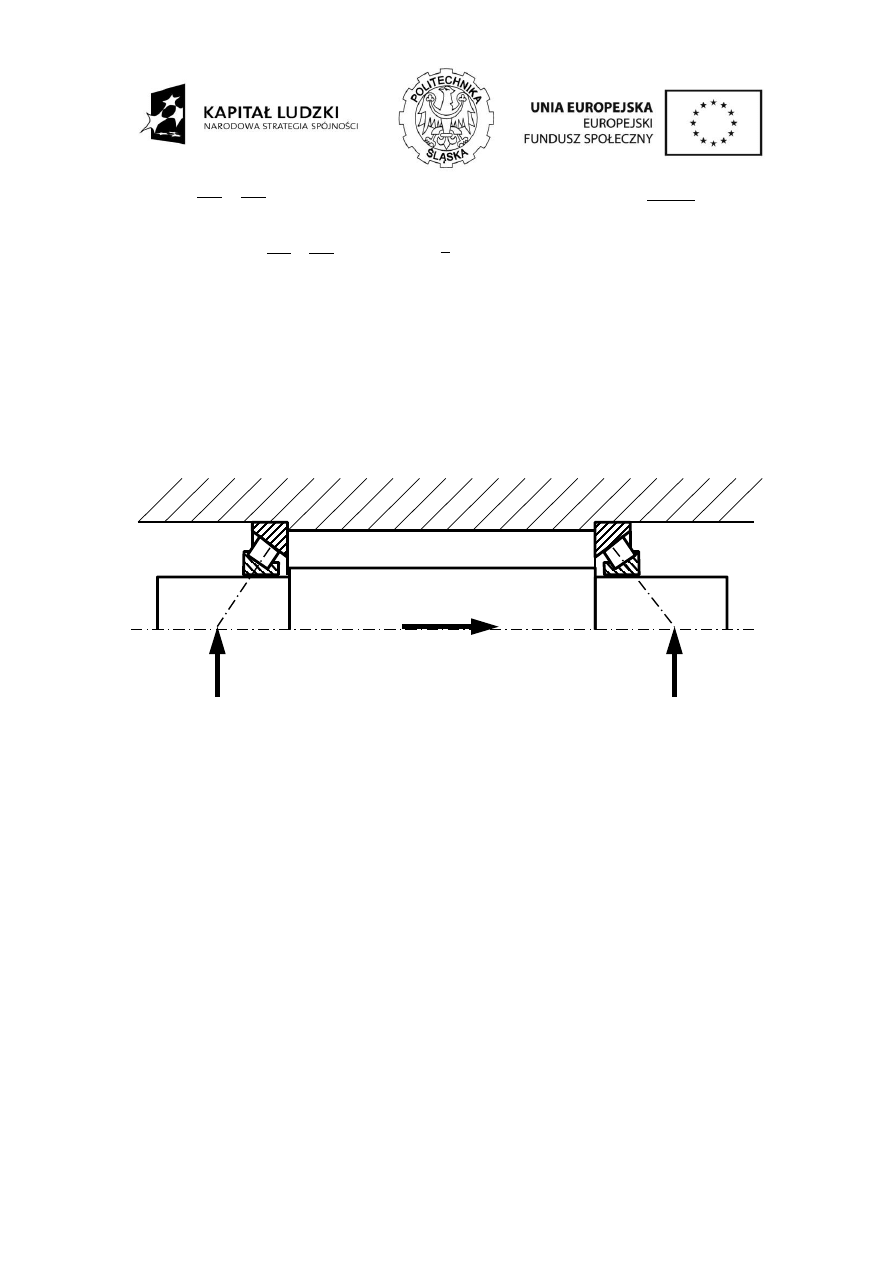
A

rA

B

rB

a

B

rB

A

rA

Y

F

Y

F

K

Y

F

Y

F

5

,

0

B

rB

aB

a

aB

aA

Y

F

F

K

F

F

5

,

0







6.3

Przykład rozwiązania zadania

Wał wejściowy przekładni zębatej osadzony został na dwóch łożyskach stożkowych,
rozmieszczonych w układzie „O”, jak przedstawiono na rysunku. W wyniku przeprowadzonej
analizy obciążeń, wyznaczono wartości reakcji w węzłach łożyskowych wału. Wał obraca się
z pr

ędkością obrotową n. Obliczyć trwałość dobranych łożysk.

R

B

R

W

R

A

Dane:

]

/

[

3000

]

[

2000

]

[

2500

]

[

3000

min

obr

n

N

R

N

R

N

R

W

B

A









Dla przedstawionego wałka dobrane zostały dwa łożyska stożkowe 33207, o następujących
parametrach:

]

[

35

9

,

0

7

,

1

35

,

0

]

[

106000

]

[

84200

0

0

mm

d

Y

Y

e

N

C

N

C













Wyznaczenie

obciążenia zastępczego

W celu wyznaczenia obciążenia zastępczego należy określić wartości sił promieniowych i
poosiowych występujących w węzłach łożyskowych. Ponieważ są to łożyska stożkowe,
konieczne jest uwzględnienie oddziaływania sił promieniowych na kierunku poosiowym. W
tym celu posłużymy się zależnościami przedstawionymi w punkcie 2.
Przyjmijmy, oznaczenia zgodnie z zastosowanymi na Rys. 3:

]

[

2000

]

[

2500

]

[

3000

N

R

K

N

R

F

N

R

F

W

A

B

rB

A

rA













Obliczenia podpory A.
W celu obliczenia obciążenia zastępczego należy wyznaczyć wartość siły F

a

powstałą w

łożysku.
W tym celu przeprowadzamy następujące sprawdzenia:

6

,

1470

7

,

1

2500

7

,

1764

7

,

1

3000









B

rB

A

rA

Y

F

Y

F

czyli

B

rB

A

rA

Y

F

Y

F



Na podstawie tego warunku obliczamy wartość siły F

a

:

]

[

35

,

2885

2000

35

,

882

]

[

35

,

882

7

,

1

3000

5

,

0

5

,

0

N

K

F

F

N

Y

F

F

a

aA

aB

A

rA

aA



















Zgodnie z wzorem (3) na wartość równoważnego obciążenia dynamicznego mają wpływ
współczynniki X oraz Y. Wartości tych współczynników zależą od proporcji wartości siły
poosiowej do promieniowej oraz liczby e podanej dla danego łożyska.
Wyznaczamy wartość ilorazu siły poosiowej do promieniowej:

Dla podpory A:

Dla podpory B:

e

F

F

e

F

F

rA

aA

rA

aA









35

,

0

29

,

0

3000

35

,

882

e

F

F

e

F

F

rB

aB

rB

aB









35

,

0

15

,

1

2500

35

,

2882

Jeżeli wartość ilorazu siły poosiowej do promieniowej jest mniejsza lub równa wartości e,
wówczas:

0

1





Y

X

w przeciwnym przypadku wartości X i Y należy odczytać z katalogu łożysk dla danego
łożyska.
Dla podpory A, zastępcze obciążenie dynamiczne wynosi:

]

[

3000 N

F

P

rA





A trwałość łożyska wyniesie:

]

.

[

7

,

67189

3000

84200

3

10

10

obr

mln

P

C

L

q































Trwałość godzinowa będzie wynosić:

]

[

373276

3000

60

7

,

67189

10

60

10

6

10

6

10

h

n

L

L

h











6.4

Zadania do samodzielnego rozwiązania

6.4.1 Zadanie 1

Dla zadania rozwiązanego w przykładzie obliczyć trwałość łożyska w podporze B.

6.4.2 Zadanie 2

Zaprojektować wał i układ łożyskowania wału wentylatora osiowego. Na wale wentylatora
umieszczono wirnik

o masie m i niewyrównoważeniu e, obracający się z prędkością

obrotową n. Wirnik ustawiony jest w pozycji poziomej. Dla przygotowanego rozwiązania
dobrać łożyska i zaproponować sposób ich zamontowania.
Dane:
m = 50 [kg]
n = 1000 [obr./min]
e = 10 [mm]

Wirnik o masie m i promieniu
niewyważenia e

6.4.3 Zadanie 3

Zaprojektować wał i układ łożyskowania wału wentylatora osiowego. Na wale wentylatora
umieszczono

wirnik o masie m i niewyrównoważeniu e, obracający się z prędkością

obrotową n. Wirnik ustawiony jest w pozycji pionowej. Dla przygotowanego rozwiązania
dobrać łożyska i zaproponować sposób ich zamontowania. Przedstawić dwa rozwiązania:
jedno z łożyskami kulkowymi zwykłymi, drugie z łożyskami kulkowymi skośnymi.
Dane:
m = 30 [kg]
n = 500 [obr./min]
e = 5 [mm]

7

Wytrzymałość zmęczeniowa

Typowym stanem naprężenia występującym w budowie maszyn są naprężenia zmienne.
Naprężenia takie przybliża się często za pomocą przebiegów opisanych sinusoidą (rys. 7.1).
Przebieg taki opisany je

st za pomocą następujących wielkości:



naprężeń średnich

m



,



naprężeń amplitudalnych

a



,



liczby stałości naprężeń

a

m









.

Wirnik o masie m i promieniu
niewyważenia e

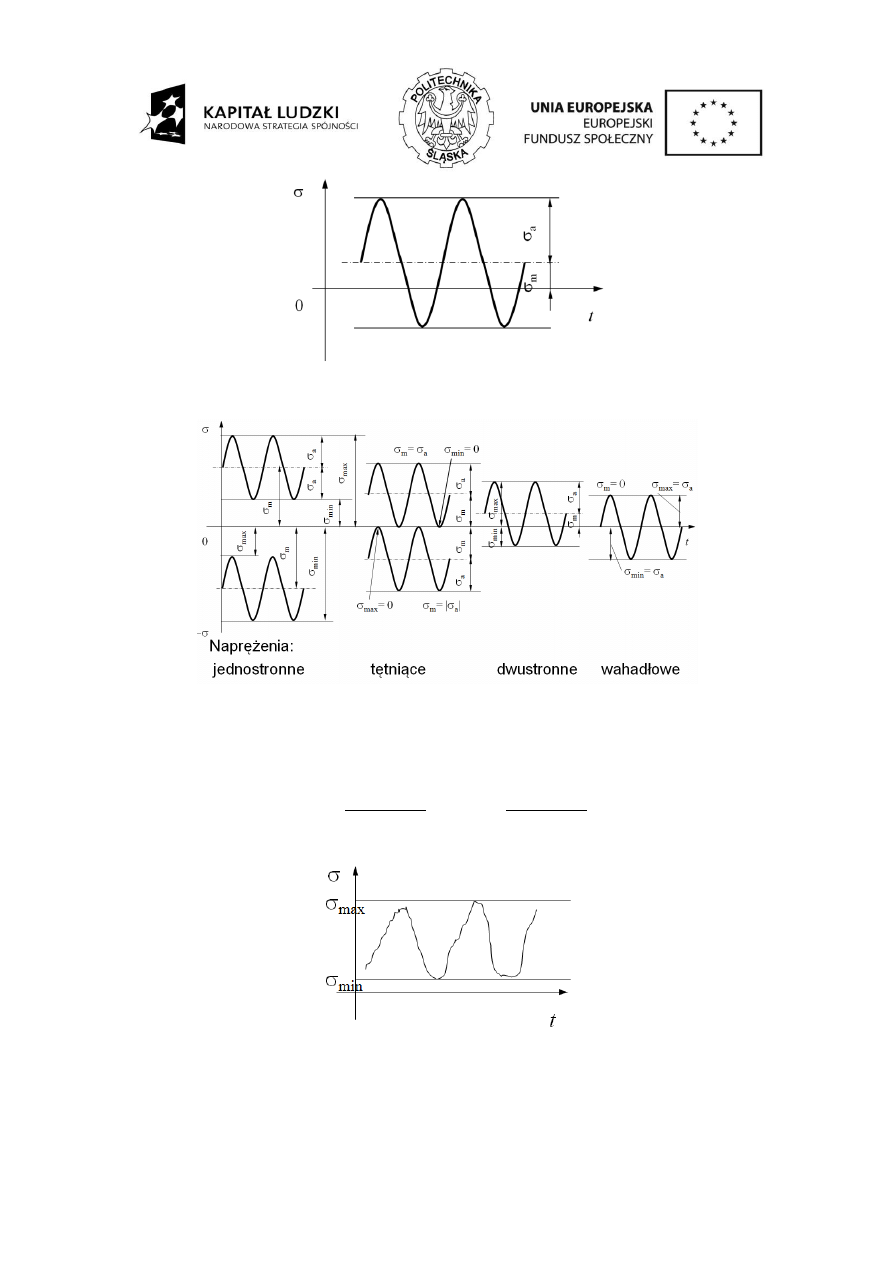
Rys. 7.1. Opis zmienności naprężeń

Rozróżnia się kilka podstawowych typów przebiegów zmian naprężeń. Przedstawiono je na
rysunku 7.2.

Rys. 7.2. Typy zmian naprężeń

W rzeczywistości przebieg zmian nie jest czystą sinusoidą, ale ma postać do niej podobną
(rys. 7.3). Dlatego też opisuje się go za pomocą wartości maksymalnych i minimalnych, a na
ich podstawie wyznacza się wartości

a



i

m



, na podstawie zeleżności:

2

,

2

min

max

min

max





















a

m

Rys. 7.3. Przykładowy przebieg zmian naprężeń

W przypadku występowania w elementach naprężeń zmiennych, elementy takie poddaje się
weryfikacji. W takim przypadku określa się przekrój niebezpieczny i na podstawie jednej w
dostępnych hipotez wyznacza się liczbę bezpieczeństwa w tym przekroju.

Na podstawie hipotezy opartej na wykresie Soderberga, liczby bezpieczeństwa dla
elementów w których występują naprężenia normalne wyznacza się z następującej
z

ależności:

a

zg

go

eg

g

m

eg

g

Z

R

R

















gdzie:

𝛿

𝑔

-

liczba bezpieczeństwa dla zginania,

𝑅

𝑒𝑔

-

granica plastyczności dla zginania,

𝑍

𝑔𝑜

-

wytrzymałość zmęczeniowa dla zginania przy obciążeniach obustronnych,

𝜀

𝑔

-

współczynnik wielkości przedmiotu dla



= 1

𝜀

𝑧𝑔

-

współczynnik wielkości przedmiotu,

𝜍

𝑚

-

naprężenia średnie,

𝜍

𝑎

-

naprężenia amplitudalne,

𝛽 - liczba działania karbu.

W przypadku występowania naprężeń stycznych, liczbę bezpieczeństwa wyznacza się z
zależności:

a

zs

es

s

m

es

s

Z

R

R













0





gdzie:

𝛿

𝑠

-

liczba bezpieczeństwa dla skręcania,

𝑅

𝑒𝑠

-

granica plastyczności dla skręcania,

𝑍

𝑠𝑜

-

wytrzymałość zmęczeniowa dla skręcania przy obciążeniach obustronnych,

𝜀

𝑠

-

współczynnik wielkości przedmiotu dla



= 1

𝜀

𝑠𝑔

-

współczynnik wielkości przedmiotu,

𝜍

𝑚

-

naprężenia średnie,

𝜍

𝑎

-

naprężenia amplitudalne,

𝛽 - liczba działania karbu.

Wartości współczynników podanych w tych zależnościach oblicza się z wzorów, bądź
odczytuje z wykresów załączonych do tego opracowania.

1







p

k







)

1

(

1







k

k

k







Wartości

k

k

p







,

,

odczytujemy z wykresów.

W przypadku gdy w elemencie występują zarówno naprężenia normalne jak i naprężenia
styczne, wyznacza się zastępczą liczbę bezpieczeństwa:

2

2

s

g

s

g

















Poniżej przedstawiono przykład opisujący wyznaczenie liczby bezpieczeństwa w wybranym
przekroju wału przekładni zębatej.
Poniżej dołączono również wykresy wykorzystywane do wyznaczenia liczb bezpieczeństwa.

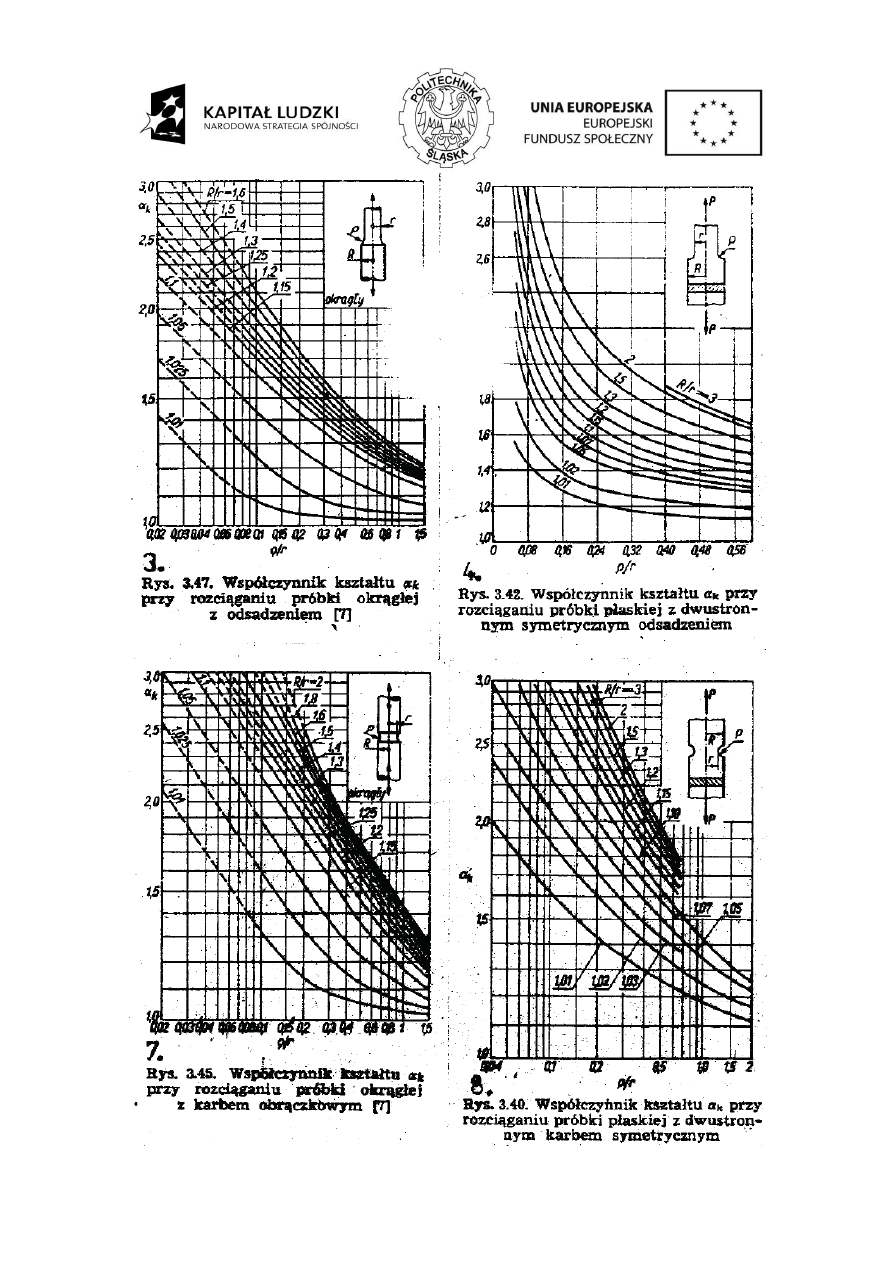
7.1

Przykład rozwiązania zadania

Dany

jest wał przekładni zębatej

Stan obciążenia wałów
Stan obciążenia wałów przekładni jest złożonym stanem obciążenia, charakteryzującym się
występowaniem zmiennego momentu skręcającego i momentu zginającego. Zmienność

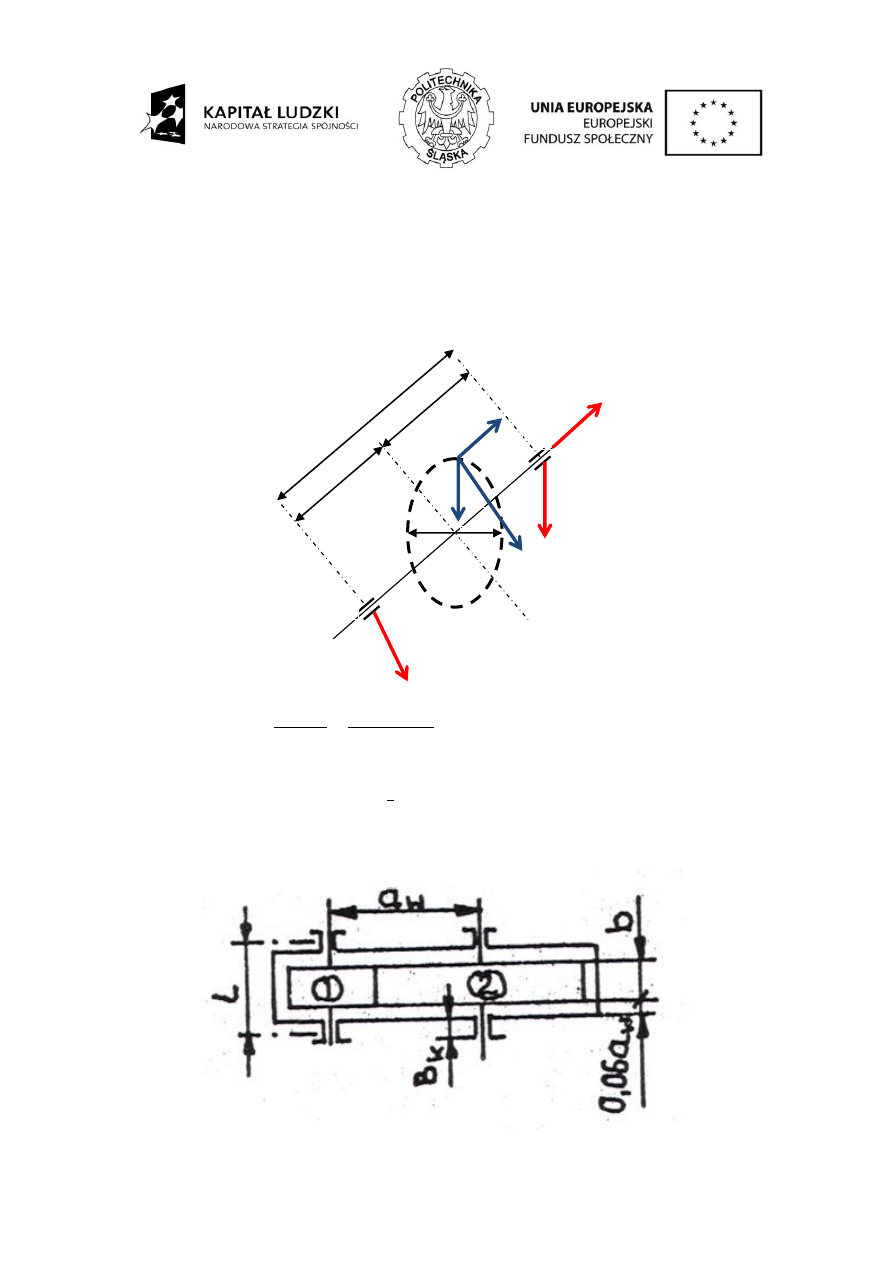
momentu skręcającego wynika przede wszystkim ze zmienności oporów ruchu maszyny
napędzanej i ocenić ją można w sposób następujący:

𝑀

𝑠𝑚𝑎𝑥

= 𝑇

01

∗ 𝐾

3

= 441,0 ∗ 1,25 = 551,3 𝑁𝑚

𝑀

𝑠𝑚 1

= 𝑇

01

= 441,0 𝑁𝑚

𝑀

𝑠𝑎1

= 𝑀

𝑠𝑚𝑎𝑥

− 𝑀

𝑠𝑚 1

= 551,2 − 441,0 = 110,3 𝑁𝑚

𝑀

𝑠𝑚𝑖𝑛 1

= 𝑀

𝑠𝑚 1

− 𝑀

𝑠𝑎1

= 441,0 − 110,3 = 330,7 𝑁𝑚

Moment zginający przyjmujemy jako stały i wyznaczamy następująco:

𝐹

𝑡𝑚𝑎𝑥

=

𝑀

𝑠𝑚𝑎𝑥 1

0,5𝑑

𝑤1

=

551,3

0,5 ∗ 0,0922

= 11963,3 𝑁

𝐹

𝑡0

= 𝐹

𝑡𝑚𝑎𝑥

∗ tan 𝛽 = 11963,3 ∗ tan 9,0687° = 1909,5 𝑁

𝐹

𝑡𝑟

= 𝐹

𝑡𝑚𝑎𝑥

∗ tan 𝛼

𝑡

= 11963,3 ∗ tan 20,2327° = 4409,4 𝑁

Ponieważ

𝑅

𝐼𝐼1

> 𝑅

𝐼1

->

𝑀

𝑔𝑚𝑎𝑥 1

= 𝑅

𝐼𝐼1

∗

𝐿
2

oraz

𝑀

𝑔𝑚 1

= 0 i 𝑀

𝑔𝑎1

= 𝑀

𝑔𝑚𝑎𝑥 1

Rozstaw łożysk

Przyjęto:

𝐵

𝑘

= 15 ÷ 40 𝑚𝑚 → 𝐵

𝑘

= 30 𝑚

II

I

R

II1

F

t0

F

t0

F

t

F

tr

R

I1

d

w

L

I

=L/

2

L

II

=L/2

L

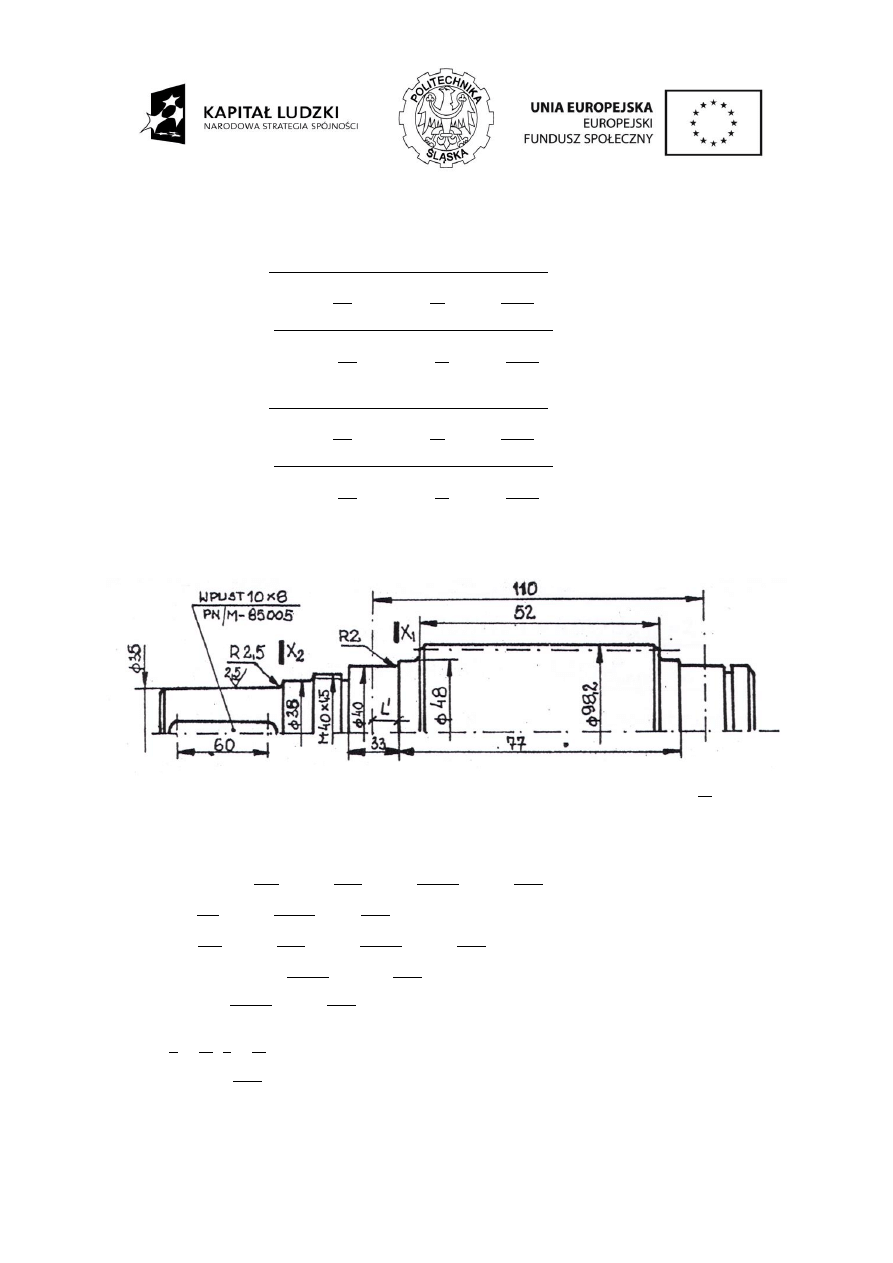
𝐿 = 𝑏 + 2 ∗ 0,06 ∗ 𝑎

𝑤

+ 𝐵

𝑘

= 52 + 2 ∗ 0,06 ∗ 202,25 + 30 = 106,27 𝑚𝑚 → 𝐿 = 110 𝑚𝑚

Reakcje w łożyskach:
Dla walcowego koła o uzębieniu śrubowym, osadzonego między łożyskami, reakcje
wyznacza się w sposób następujący:
-

dla koła 1:

𝑅

𝐼1

= 𝐹

𝑡𝑚𝑎𝑥

∗

𝐿

𝐼𝐼

𝐿

2

+ 𝐹

𝑡𝑟

∗

𝐿

𝐼

𝐿

− 𝐹

𝑡0

∗

𝑑

𝑤1

2 ∗ 𝐿

2

= 6144,3 𝑁

𝑅

𝐼𝐼1

= 𝐹

𝑡𝑚𝑎𝑥

∗

𝐿

𝐼𝐼

𝐿

2

+ 𝐹

𝑡𝑟

∗

𝐿

𝐼

𝐿

+ 𝐹

𝑡0

∗

𝑑

𝑤1

2 ∗ 𝐿

2

= 6694,0 𝑁

-

dla koła 2:

𝑅

𝐼2

= 𝐹

𝑡𝑚𝑎𝑥

∗

𝐿

𝐼𝐼

𝐿

2

+ 𝐹

𝑡𝑟

∗

𝐿

𝐼

𝐿

− 𝐹

𝑡0

∗

𝑑

𝑤2

2 ∗ 𝐿

2

= 6003,1 𝑁

𝑅

𝐼𝐼2

= 𝐹

𝑡𝑚𝑎𝑥

∗

𝐿

𝐼𝐼

𝐿

2

+ 𝐹

𝑡𝑟

∗

𝐿

𝐼

𝐿

+ 𝐹

𝑡0

∗

𝑑

𝑤2

2 ∗ 𝐿

2

= 7742,7 𝑁

Stan obciążenia w przekrojach krytycznych zębnika:

- dla X

1

:

𝑀

𝑠𝑚

= 441 𝑁𝑚; 𝑀

𝑠𝑎

= 110,3 𝑁𝑚; 𝑀

𝑔𝑚

= 0; 𝑀

𝑔𝑎

= 𝑅

𝐼𝐼1

∗ 𝐿

′

= 6694 ∗

33

2

∗ 10

−3

=

110,5 𝑁𝑚
- dla X

2

:

𝑀

𝑠𝑚

= 441 𝑁𝑚; 𝑀

𝑠𝑎

= 110,3 𝑁𝑚; 𝑀

𝑔𝑚

= 𝑀

𝑔𝑎

= 0

Stan naprężeń:
- dla X

1

:

𝜏

𝑚

=

𝑀

𝑠𝑚

𝑊

0

= 16 ∗

𝑀

𝑠𝑚

𝜋∗𝑑

3

= 16 ∗

441000

𝜋∗40

3

= 35,1

𝑁

𝑚𝑚

2

𝜏

𝑎

=

𝑀

𝑠𝑎

𝑊

0

= 16 ∗

110300

𝜋∗40

3

= 8,8

𝑁

𝑚𝑚

2

𝜍

𝑎

=

𝑀

𝑔𝑎

𝑊

𝑥

= 32 ∗

𝑀

𝑔𝑎

𝜋∗𝑑

3

= 32 ∗

110500

𝜋∗40

3

= 17,6

𝑁

𝑚𝑚

2

- dla X

2

:

𝜏

𝑚

= 16 ∗

441000

𝜋∗35

3

= 52,38

𝑁

𝑚𝑚

2

𝜏

𝑎

= 16 ∗

110300

𝜋∗35

3

= 13,1

𝑁

𝑚𝑚

2

Liczba działania karbu:
- dla X

1

:

𝐷
𝑑

=

48
40

;

𝜌

𝑟

=

2

20

= 0,1 → 𝛼

𝑘𝑠

= 1,78; 𝛼

𝑘𝑔

= 1,85 (wykresy na Rys. 1 do 8)

𝑅

𝑚

= 883

𝑁

𝑚𝑚

2

; 𝜌 = 2 𝑚𝑚 → 𝑛

𝑘

= 0,895

𝛽

𝑘𝑠

= 0,895 ∗ 1,78 − 1 + 1 = 1,70

𝛽

𝑘𝑔

= 0,895 ∗ 1,85 − 1 + 1 = 1,76

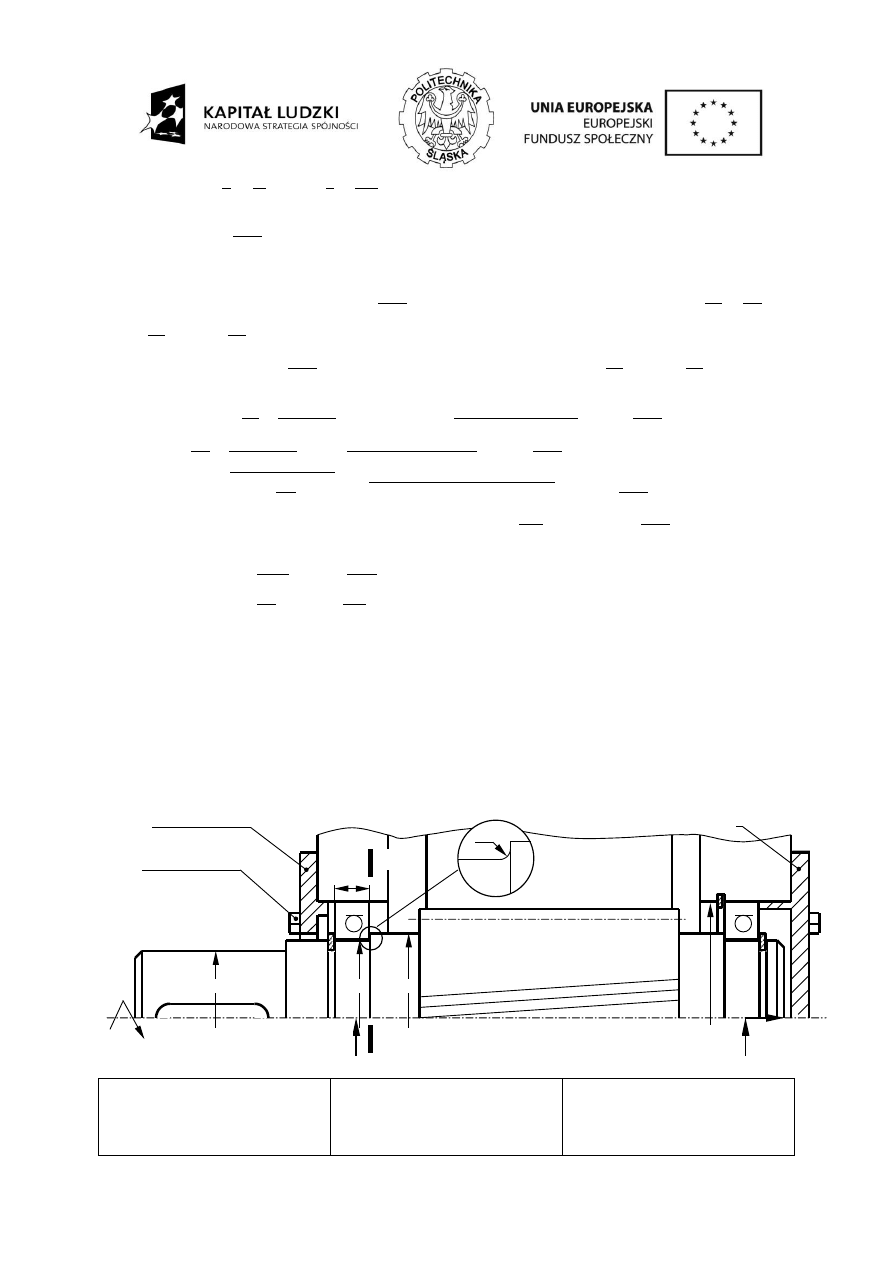
- dla X

2

:

:

𝐷
𝑑

=

38
35

= 1,09;

𝜌

𝑟

=

2,5

17,5

= 0,14 → 𝛼

𝑘𝑠

= 1,4; 𝛼

𝑘𝑔

= 1,78 (wykresy na Rys. 1 do

8)

𝑅

𝑚

= 883

𝑁

𝑚𝑚

2

; 𝜌 = 2,5 𝑚𝑚 → 𝑛

𝑘

= 0,91

𝛽

𝑘𝑠

= 0,91 ∗ 1,4 − 1 + 1 = 1,36

Liczba wpływu wielkości przedmiotu:
- dla X

1

:

𝑍

𝑔0

= 0,42 ∗ 𝑅

𝑚

= 371

𝑁

𝑚𝑚

2

; 𝛼

𝑘𝑠

= 1,78; 𝛼

𝑘𝑔

= 1,85; 𝑑 = 40 𝑚𝑚 →

1

𝜀

𝑒𝑠

=

1

𝜀

𝑒𝑔

=

1,08;

1

𝜀

𝑧𝑠

= 1,33;

1

𝜀

𝑧𝑔

= 1,36

- dla X

2

:

𝑍

𝑔0

= 371

𝑁

𝑚𝑚

2

; 𝛼

𝑘𝑠

= 1,4; 𝛼

𝑘𝑔

= 1,78; 𝑑 = 35 𝑚𝑚 →

1

𝜀

𝑒𝑠

= 1,04;

1

𝜀

𝑧𝑠

= 1,22

Naprężenia maksymalne:
- dla X

1

:

𝜏 =

𝜏

𝑚

𝜀

𝑒𝑠

+

𝑅

𝑒𝑠

∗𝛽

𝑘

∗𝜏

𝑎

𝑧

𝑧

∗𝜀

𝑧𝑠

= 35,1 ∗ 1,08 +

0,62∗785∗1,7∗8,8∗1,33

0,25∗883

= 81,8

𝑁

𝑚𝑚

2

𝜍 =

𝜍

𝑚

𝜀

𝑒𝑔

+

𝑅

𝑒𝑔

∗𝛽

𝑘𝑔

∗𝜍

𝑎

𝑧

𝑔0

∗𝜀

𝑧𝑔

= 0 +

1,1∗785∗1,76∗17,6∗1,36

0,42∗883

= 98,1

𝑁

𝑚𝑚

2

𝜍

𝑧𝑟𝑒𝑑

= 𝜍

2

+

𝑅

𝑒𝑔

𝑅

𝑒𝑠

∗ 𝜏

2

= 98,1

2

+ 1,1 ∗ 81,8/0,62

2

= 175,1

𝑁

𝑚𝑚

2

- dla X

2

:

𝜏 = 52,4 ∗ 1,04 + 0,62 ∗ 785 ∗ 1,36 ∗ 13,1 ∗

1,22
0,25

∗ 883 = 89,7

𝑁

𝑚𝑚

2

Liczby bezpieczeństwa w przekrojach krytycznych:

- dla X

1

:

𝛿

𝑥1

=

𝑅

𝑒𝑔

𝜍

𝑧𝑟𝑒𝑑

= 1,1 ∗

785

175,1

= 4,93 > 𝛿

𝑤𝑦𝑚 .

=2

- dla X

2

:

𝛿

𝑥2

=

𝑅

𝑒𝑠

𝜏

= 0,62 ∗

785

89,7

= 5,43 > 𝛿

𝑤𝑦𝑚 .

=2

7.2

Zadania do samodzielnego rozwiązania

7.2.1 Zadanie 1

Dany jest wał wejściowy dwustopniowej przekładni zębatej, przedstawiony na rysunku. Wał
obraca się z prędkością obrotową n=2850 [obr./min]. Wał został podparty w dwóch łożyskach
kulkowych zwykłych. Wyznaczyć wartość liczby bezpieczeństwa



w przekroju A-A

wału,

d

1

d

2

d

3

4

śruby M8

Pokrywa 1

A

A

r

a

Ray

Rby

Rbx

Pokrywa 2

D

Ms

B

Dane:
d

1

=

45

[mm]

d

2

=

50

[mm]

d

3

=

55

[mm]

D

= 110

[mm]

Ray

= 2,35

[kN]

Rby

=

3,5

[kN]

Rbx

=

0,8

[kN]

T

O1

= Ms = 460

[Nm]

Rm

= 730

[MPa]

Reg

= 500

[MPa]

Res

= 260

[MPa]

Zgo

= 280

[MPa]

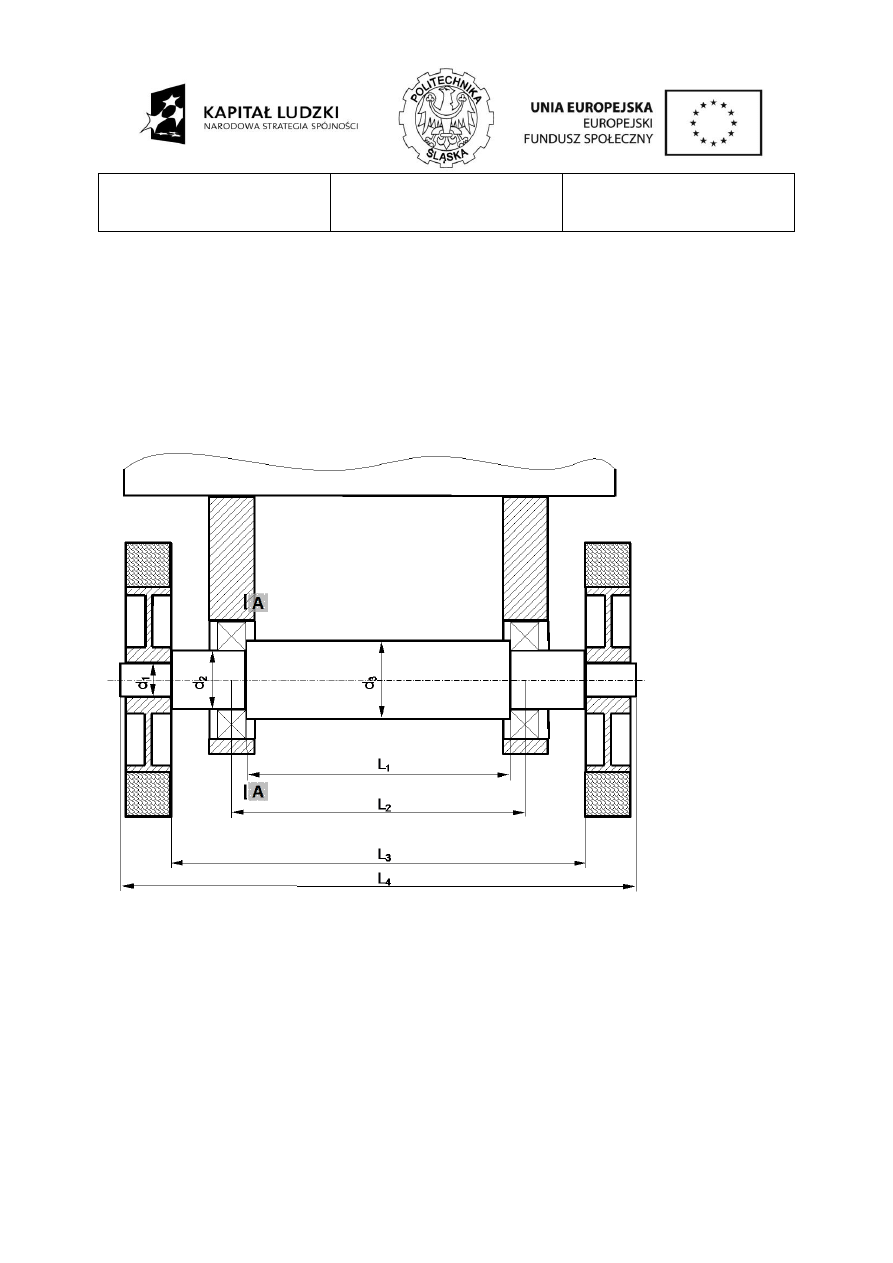
B

=

28

[mm]

r

a

=

2

[mm]

Ki

=

1,3

Zso

= 170

[MPa]

7.2.2 Zadanie 2

Na przyczepę jednoosiową, której masa wynosi m

1

= 120 [kg], załadowano ładunek o masie m = 350

[kg]. Przyczepa została doczepiona do samochodu, który porusza się z średnią prędkością v = 70
[km/h]. Postać i wymiary osi zamontowanej w przyczepie, a także sposób jej zamocowania
przedstawiono na rysunku poniżej. Oś przyczepy została wykonana ze stali 35 ulepszanej cieplnie.
Z

weryfikować przekrój A-A osi (przy założeniu nieskończonej wytrzymałości), jeżeli żądana liczba

bezpieczeństwa wynosi 3, a promień przejścia w tym przekroju wynosi r. Działanie sił poosiowych w
oponie należy pominąć.

Dane:
L

1

= 1100 [mm]

L

2

= 1200 [mm]

L

3

= 1600 [mm]

L

4

= 1900 [mm]

d

1

= 40 [mm]

d

2

= 50 [mm]

d

3

= 60 [mm]

r = 2,5 [mm]

Tworzywo

osi:

35

R

m

= 600 [MPa]

R

er

= 360 [MPa]

R

eg

= 430 [MPa]

R

es

= 230 [MPa]

Z

go

= 250 [MPa]

Z

so

= 150 [MPa]

7.2.3 Zadanie 3

W trójkołowym rowerze napęd na tylne koła przenoszony jest za pomocą przekładni
łańcuchowej. Wał napędzany przekładni (wał na którym osadzono tylne koła roweru)
przenosi moment skręcający Ms (współczynnik wpływu obciążenia zewnętrznego wynosi K

I

).

Siła wynikająca z oddziaływań łańcucha działająca w płaszczyźnie prostopadłej do
płaszczyzny rysunku wynosi F. Maksymalne obciążenie roweru (masa człowieka i
przewożonego bagażu) wynosi m. Koło zębate łańcuchowe bierne osadzone jest na wale jak
pokazano na rysunku

. Zweryfikować przekrój A-A wału, jeżeli liczba bezpieczeństwa

wynosi 3.

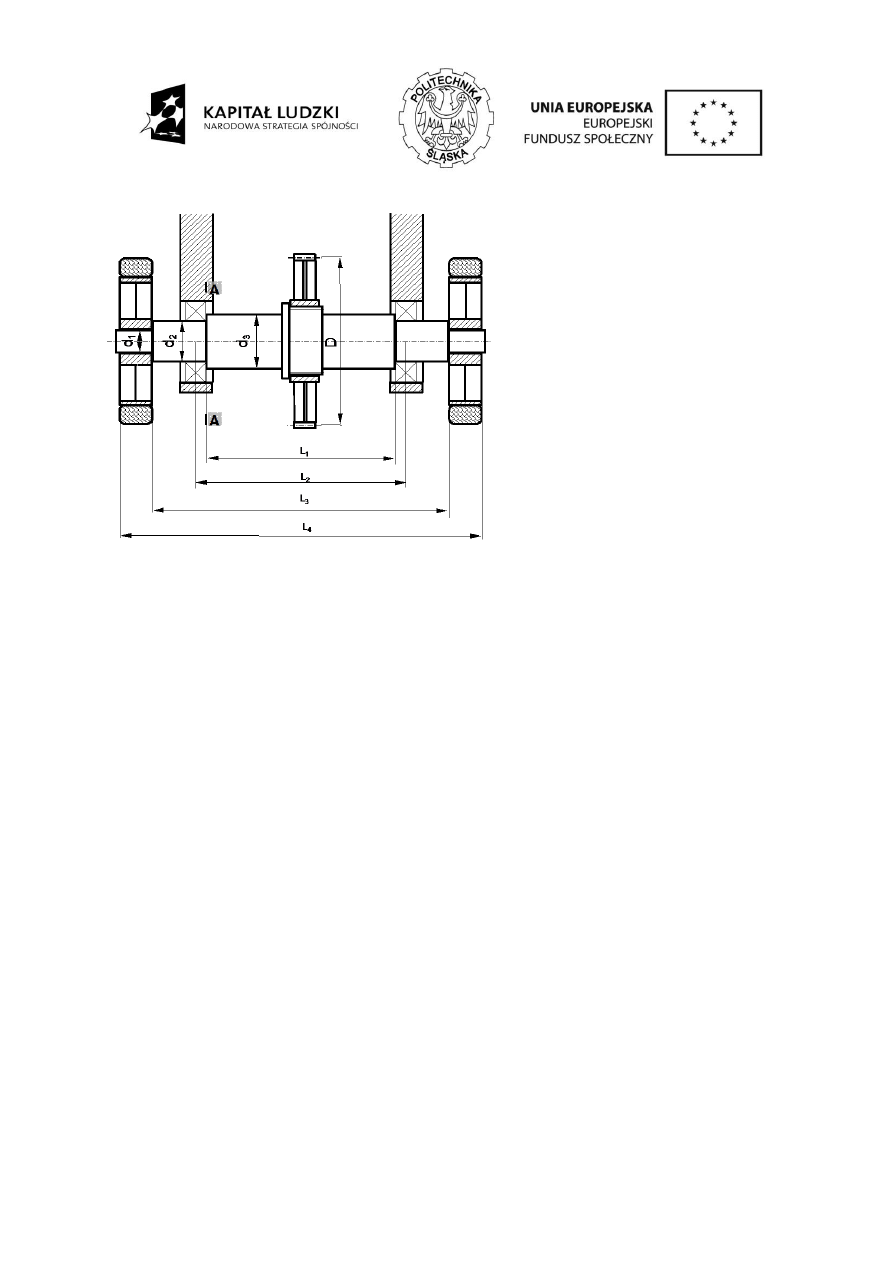
Dane:

m = 160 [kg]
Ms = 60 [Nm]
F = 1200 [N]
K

I

= 1,7

L

1

= 980 [mm]

L

2

= 1000 [mm]

L

3

= 1140 [mm]

L

4

= 1200 [mm]

d

1

= 25 [mm]

d

2

= 30 [mm]

d

3

= 40 [mm]

D = 70 [mm]

r = 1,5 [mm]

Tworzywo osi:

45

R

m

= 700 [MPa]

R

er

= 420 [MPa]

R

eg

= 462 [MPa]

R

es

= 256 [MPa]

Z

go

= 285 [MPa]

Z

so

= 170 [MPa]

Literatura

[1]

Dąbrowski Z (1999): Wały maszynowe. Warszawa, PWN.

[2] Dietrich M. (red.) (1999,2003): Podstawy konstrukcji maszyn t. I-III. Warszawa, WNT.
[3]

Dudziak M. (1997): Przekładnie cięgnowe. Warszawa, PWN.

[4]

Dziama A., Michniewicz M., Niedźwiedzki A. (1995): Przekładnie zębate. Warszawa, PWN.

[5] Garncarz G., Markusik S.(2004): Pomoce projektowe w budowie maszyn. , Gliwice, Wydawnictwo

Politechniki Śląskiej

[6] Godzimirski J

. (2002): Wytrzymałość doraźna konstrukcyjnych połączeń klejowych. WNT

[7]

Kocańda S., Szala J. (1991): Podstawy obliczeń zmęczeniowych. Warszawa, PWN.

[8]

Machowski B., Ochoński W.(1991): Uszczelnienia. Warszawa, PWN.

[9] Mazanek E. (red.) (2005)

: Przykłady obliczeń z podstaw konstrukcji maszyn. Tom 1, Połączenia. Sprężyny.

Zawory. Wały maszynowe. Warszawa , WNT

[10] Mazanek E. (red.): (2005)

Przykłady obliczeń z podstaw konstrukcji maszyn. Tom 2, Łożyska. Sprzęgła i

hamulce. Przekładnie mechaniczne. Warszawa, WNT, Warszawa

[11]

Müller L. (1996): Przekładnie zębate - projektowanie. Warszawa, WNT.

[12]

Niezgodziński M.E. Niezgodziński T. (2004): Wzory, wykresy i tablice wytrzymałościowe. WNT

[13]

Osiński Z. (red.) (1999): Sprzęgła i hamulce. Warszawa, PWN.

[14]

Osiński Z. (red.) (2003): Podstawy konstrukcji maszyn. Warszawa, PWN.

[15]

Purzyński R. (1991): Podstawy konstrukcji maszyn. Przekładnia zębata walcowa. Skrypt Politechniki Śląskiej
nr 1521, Gliwice, Wydawnictwo Politechniki Śląskiej

[16]

Skoć A., Spałek J., Markusik S.(2008): Podstawy konstrukcji maszyn. t. 1, Warszawa, WNT

[17]

Skoć A., Spałek J., Markusik S.(2008): Podstawy konstrukcji maszyn. t. 2, Warszawa, WNT

[18]

Szewczyk K. (1991): Połączenia gwintowe. Warszawa, PWN.

[19] Tarnowski W. (1997): Podstawy projektowania technicznego. WNT
[20]

Winkler T.: (2005): Komputerowo wspomagane projektowanie układów antropotechnicznych. WNT