1

3.

LUMINESCENCJA.

WYZNACZENIE

WYDAJNOŚCI

KWANTOWYCH

FLUORESCENCJI

1.

Wprowadzenie

Luminescencją nazywana jest każda emisja promieniowania, która nie jest świeceniem

ciał ogrzanych do wysokich temperatur. Luminescencja zachodzi z elektronowo -

oscylacyjnie wzbudzonej cząsteczki będącej w równowadze termicznej z otoczeniem. Różne

rodzaje luminescencji związane są z różnymi sposobami dostarczania energii wzbudzenia.

Fotoluminescencją nazywamy emisję atomów lub cząsteczek, które po zaabsorbowaniu

promieniowania ultrafioletowego, widzialnego lub podczerwonego o odpowiedniej energii

powracają do stanu podstawowego.

Schemat procesów fotofizycznych, związanych z absorpcją i emisją promieniowania w

cząsteczkach wieloatomowych o podstawowym stanie singletowym (S

0

), przedstawiono na

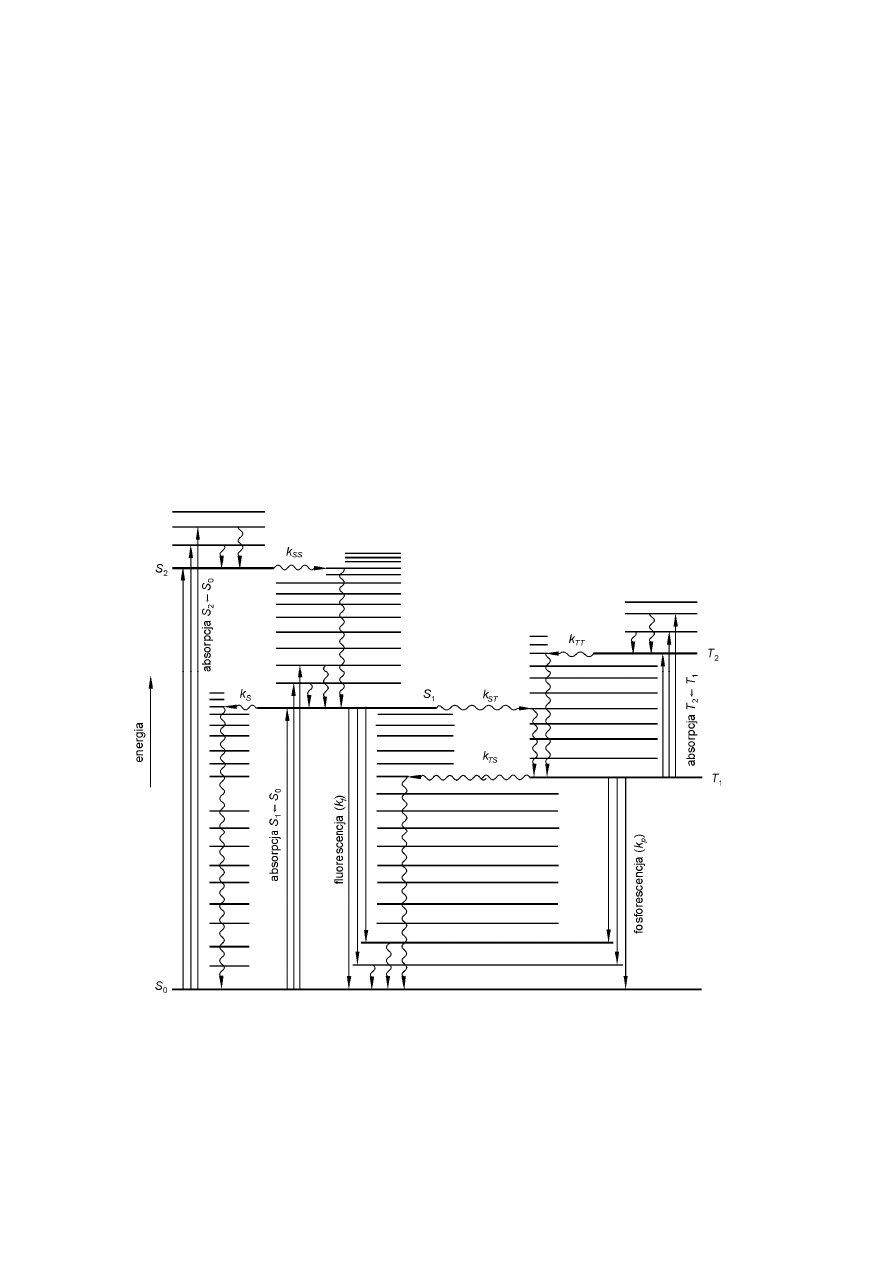
diagramie, nazywanym od nazwiska jego twórcy, diagramie Jabłońskiego (por. rys. 1).

Rys. 1. Diagram Jabłońskiego dla cząsteczki o singletowym podstawowym

stanie elektronowym. Strzałki proste oznaczają przejścia promieniste,

strzałki faliste – przejścia bezpromieniste

2

Na rys. 1 elektronowe przejścia promieniste zaznaczono strzałkami prostymi, elektronowe

przejścia bezpromieniste falistymi strzałkami poziomymi, procesy zaś relaksacji oscylacyjnej,

tj. utraty nadmiaru energii oscylacyjnej w danym stanie elektronowym, falistymi strzałkami

pionowymi. Literą k z odpowiednimi indeksami oznaczono stałe szybkości promienistych i

bezpromienistych przejść elektronowych i mają one wymiar [s

–1

].

Fotoluminescencja, która powstaje w wyniku przejścia z najniższego poziomu

oscylacyjnego wzbudzonego stanu elektronowego S

1

na dowolny oscylacyjno-rotacyjny

poziom stanu podstawowego S

0

. (por. przejście S

1

→

S

0

rys. 1) nazywana jest fluorescencją.

Bezpromieniste przejście elektronu z poziomu S

1

do metastabilnego poziomu trypletowego

T

1

powoduje pojawienie się emisji związanej z przejściem elektronowym T

1

→

S

0

, przesuniętej

ku dłuższym falom w stosunku do fluorescencji S

1

→

S

0

,

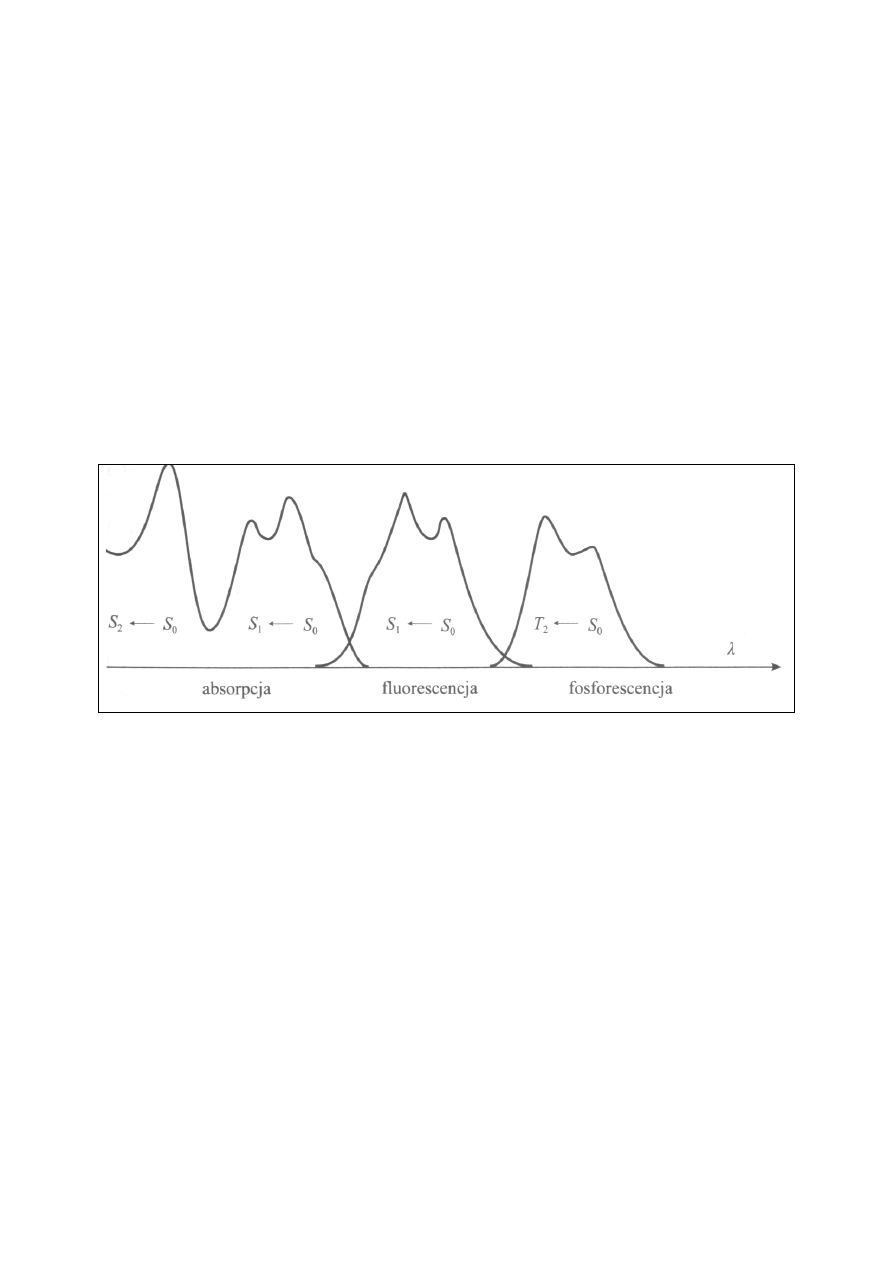
zwanej fosforescencją, (por. rys. 2).

Rys 2. Względne położenia widm: A – absorpcji, B – fluorescencji, C – fosforescencji.

Przejścia bezpromieniste pomiędzy stanami elektronowymi o jednakowej krotności

(S

2

~~

>

S

1

, T

2

~~

>

T

1

) nazywamy konwersją wewnętrznej, natomiast przejścia bezpromieniste,

które zachodzą pomiędzy stanami o różnej krotności (S

1

~~

>

T

1

i T

1

~~

>

S

0

na rys. 1)

nazywamy przejściami międzysystemowymi. Wymienione przejścia bezpromieniste następują

wówczas, gdy wielowymiarowe hiperpowierzchnie energii potencjalnej odpowiednich stanów

elektronowych dostatecznie zbliżają do siebie w otoczeniu pewnego punktu albo nawet

przecinają się ze sobą, a konwersja zarówno S

1

~~

>

S

0

(T

2

~~

>

T

1

),

jak i S

1

~~

>

T

1

(T

1

~~

>

S

0

)

zachodzą bez zmiany konfiguracji i pędów jąder. Przejście cząsteczki ze stanu S

1

na wysoki

poziom oscylacyjny stanu S

0

jest równoznaczne z zamianą jej energii wzbudzenia

elektronowego na energię oscylacji w stanie niewzbudzonym. Energia ta zostaje następnie

odprowadzona przez zderzenia z innymi cząsteczkami w szybkim, trwającym 10

–11

–10

–13

s,

procesie relaksacji oscylacyjnej, a więc ostatecznie zamieniona na energię kinetyczną

3

cząsteczek. Proces ten jest bardzo szybki i podobnie jak relaksacja oscylacyjna następuje po

wzbudzeniu cząsteczki do wyższych stanów wibronowych.

1.1. Prawa absorpcji. Prawo Bouguera-Lambert i Lamberta-Beera

W myśl prawa sformułowanego przez P. Bouguera J. H. Lamberta, zmniejszenie natężenia

monochromatycznej wiązki przechodzącej przez bardzo cienką warstwę jednorodnego

ośrodeka, złożonego z pochłaniających promieniowanie cząsteczek, jest proporcjonalne do

natężenia wiązki wchodzącej do tej warstwy i do grubości warstwy.

Natężeniem wiązki promieniowania (I) nazywamy energię przepływającą w jednostce

czasu przez jednostkowy przekrój wiązki, prostopadły do kierunku jej biegu. Wymiarem

natężenia promieniowania jest [W· m

–2

].

Gdy natężenie wiązki padającej prostopadle na warstwę elementarną o grubości dx

wynosi I, to:

dI

kIdx

− =

(1)

Oznaczając przez I

0

natężenie wiązki wchodzącej do absorbującej warstwy o skończonej

grubości d, natomiast przez I

p

natężenie, jakie ma ta wiązka po przejściu przez warstwę,

obliczamy rozdzielając zmienne w równaniu i całkując jego lewą stronę w granicach od I

= I

0

do I = I

p

, zaś prawą w granicach od x = 0 do x = d:

0

0

ln

ln

p

p

I

I

kd

I

I

−

=

=

,

0

e

kd

p

I

I

−

=

(2)

Współczynnik k w równaniach (2) nazywamy

naturalnym współczynnikiem absorpcji; ma

on wymiar [m

–1

]. Wartość k dla danej substancji jest zależna od długości fali absorbowanego

promieniowania i od parametrów określających gęstość absorbującej substancji (T, p).

Przechodząc z logarytmów naturalnych na dziesiętne, ze wzoru (2) otrzymujemy:

0

log

p

I

ad

I

=

(3)

Współczynnik a = k/2,303 nazywamy

współczynnikiem absorpcji. Zarówno równanie

różniczkowe (1), jak i jego scałkowane postacie (2,3) przedstawiają różne sposoby zapisu

prawa

Bouguera-Lamberta.

Badając absorpcję substancji rozpuszczonych w ciekłych rozpuszczalnikach, które same

pochłaniają promieniowanie w innym obszarze widma, prawdopodobieństwo, że foton

penetrujący warstwę roztworu napotka cząsteczkę, przez którą zostanie zaabsorbowany,

zależy od iloczynu grubości warstwy i stężenia roztworu. Oznaczając przez c stężenie

roztworu, wyrażone w mol

⋅

dm

–3

, zastępujemy k we wzorze (1) iloczynem 2,303

ε

c, w którym

4

współczynnik

ε

ma wymiar [cm

–1

·(mol·dm

–3

)

–1

] i nazywany jest

molowym współczynnikiem

absorpcji.

Otrzymujemy wówczas równanie wyrażające w postaci różniczkowej

prawo

Lamberta–Beera, a po scałkowaniu równanie to przybiera postać:

0

log

p

I

cd

A

I

ε

=

≡

,

0

0

10

10

cd

A

p

I

I

I

ε

−

−

=

=

(4)

Wyrażenie log (I

0

/I

p

) nazywamy

absorbancją i oznaczamy symbolem A.

Maksymalna wartość molowego współczynnika absorpcji,

ε

maks

, jest miarą

intensywności przejścia. Ponieważ pasmo absorpcji rozciąga się na pewien zakres liczb

falowych,

1

ν

λ

=

%

[cm

−

1

], podanie wartości

molowego współczynnika absorpcji tylko dla jednej

liczby falowej może nie być prawdziwym wskaźnikiem intensywności pasma.

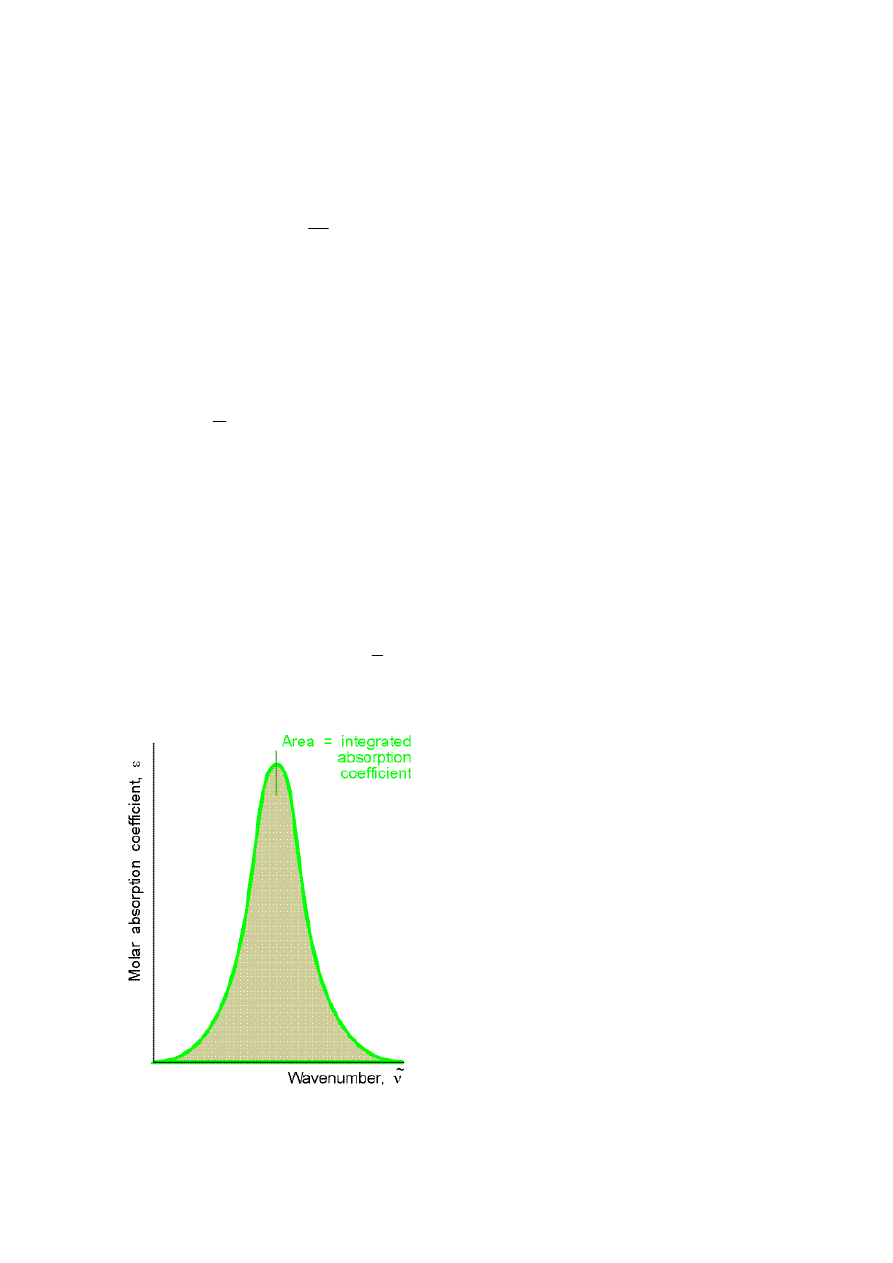
Integralny współczynnik absorpcji jest sumą (całką) współczynników absorpcji w

całym paśmie i odpowiada polu pod krzywą, obrazującą zależność molowego współczynnika

absorpcji od liczby falowej (por. rys. 3).

2

1

int

( ) d

ν

ν

ε

ε ν ν

=

∫

%

%

%

%

(5)

Rys. 3. Zależność molowego współczynnika absorpcji od liczby falowej promieniowania

zaabsorbowanego przez substancję.

5

Inną

wielkością

charakteryzującą

absorpcję

promieniowania

w

ośrodku

pochłaniającym jest stosunek

I

p

/

I

0

zwany

przepuszczalnością (transmitancją), podawany

także w procentach:

0

I

I

T

p

=

lub

100

%

0

I

I

T

p

=

(6)

Pomiędzy absorbancją a przepuszczalnością zachodzi prosty związek:

T

A

log

−

=

lub

%)

log(

2

T

A

−

=

(7)

1.2.

Moment przejścia. Moc oscylatora

Dane przejście jest obserwowane w widmie absorpcji, jeżeli spełnione są następujące

warunki na absorpcję promieniowania elektromagnetycznego o natężeniu E=E

0

cos(

ω

t):

1. Warunek konieczny –

warunek rezonansu:

Energia promieniowania padającego h

ν

musi być równa różnicy energii pomiędzy badanymi

stanami:

n

m

h

E

E

ν

= −

(8)

2. Warunek wystarczający -

warunek niezerowego momentu przejścia

O szybkości i intensywności absorpcji decyduje

moment przejścia (moment dipolowy

przejścia pomiędzy stanami m i n).

Tylko jego niezerowa wartość umożliwia cząsteczce

„opuszczenie” stanu.

*

0

mn

m

n

d

ψ ψ τ

=

≠

∫

M

µ

(9)

E

0

-amplituda pola elektrycznego promieniowania,

ω

ω

ω

ω

- częstość kołowa promieniowania (w s

-1

)

µµµµ

- operator momentu dipolowego cząsteczki:

∑

∑

−

=

atomy

A

elektrony

i

i

A

A

e

e

r

R

Z

µµµµ

Z

A

- ładunek jądra, wektory

R

A

i

r

i

- położenie jąder i elektronów.

ψ

m

i

ψ

n

–pełne funkcje falowe obu stanów cząsteczki, między którymi zachodzi przejście.

Szybkość przejścia w

mn

(szybkość zmiany prawdopodobieństwa przejścia)

2

2

0

2

6

mn

mn

mn

dt

dP

w

M

E

h

π

=

=

(10)

6

Kwadrat momentu przejścia jest miarą intensywności absorpcji, opisywaną przez

wielkość nazywaną

mocą lub siłą oscylatora przejścia:

(11)

B

mn

-

współczynnik absorpcji wymuszonej Einsteina

B

mn

=

2

2

0

6

1

mn

M

h

ε

(12)

(m

e

i e - masa i ładunek elektronu).

Siła (moc) oscylatora –jest bezwymiarową wielkością i podaje efektywną liczbę elektronów

biorących udział w określonym przejściu. W warunkach doświadczalnych, przy zadanej

częstości promieniowania padającego, w miejsce „ostrego” przejścia między stanami m i n

otrzymujemy rozmyte pasmo odpowiadające

integralnemu współczynnikowi absorpcji.

Wówczas doświadczalnie wyznaczoną moc oscylatora określa wyrażenie:

(13)

1.3. Czas życia cząsteczek w stanie wzbudzonym

Przejścia elektronów w cząsteczce z niższych poziomów na wyższe zachodzi dzięki

absorpcji

promieniowania,

odwrotnym

przejściom

towarzyszy

emisja.

Jednakże

prawdopodobieństwa tych przejść są różne i różne w związku z tym natężenia linii widmowych.

Emisja samorzutna (spontaniczna) polega na wyemitowaniu fotonu

h

νννν

przez cząsteczkę

niezależnie od działania nań czynników zewnętrznych.

Pomiędzy wymuszoną absorpcją i spontaniczną emisją istnieje ścisły związek:

(14)

A

nm

-współczynnik emisji spontanicznej Einsteina,

B

mn

-

współczynnik absorpcji wymuszone Einsteina.

Jeśli wzbudzone cząsteczki B* ulegają dezaktywacji tylko przez emisję fluorescencji, to

natężenie fluorescencji, wynoszące z chwilą przerwania wzbudzania I

0

, maleje z upływem

czasu wykładniczo, zgodnie z równaniem:

0

/

0

0

e

e

f

k t

t

t

I

I

I

τ

−

−

=

=

(15)

Symbolem

k

f

oznaczona została stałą szybkości promienistego zaniku fluorescencji (por.

rys. 1) i stała ta jest tożsama ze

współczynnikiem emisji spontanicznej Einsteina A

nm

. Chwi-

lowe natężenie emisji jest proporcjonalne do chwilowej szybkości zaniku wzbudzonych

cząsteczek B*, wyrażonej pochodną (-d[B*]/dt). W równaniu (15)

τ

0

= 1/k

f

oznacza

2

0

2

2

2

2

4

3

e

e

mn

mn

mn

mn

mn

m

m

f

M

B

e

e

ε

ω

ω

=

=

h

h

h

( )

9

12

4, 33 10

f

d

ε ν ν

−

=

⋅

∫

%

%

3

8

nm

mn

h

A

B

c

π ν

=

7

naturalny średni czas życia cząsteczek B

*

w stanie wzbudzonym i jest zależny jedynie od

prawdopodobieństwa samorzutnego przejścia promienistego B*

→

B. Korzystając z

zależności pomiędzy współczynnikiem emisji spontanicznej

Einsteina

A

nm

i współczynnikiem

absorpcji wymuszone

j Einsteina B

mn

(14) i związku pomiędzy

B

mn

z integralnym

współczynnikiem absorpcji można wnosić, że wartość

τ

0

musi być odwrotnie proporcjonalna

do

int

ε

.Uproszczony wzór okreslający tę zależność, po podstawieniu liczbowych wartości

stałych fizycznych, przybiera postać:

2

1

8

0

2

3, 44·10

( )

m

d

ν

ν

τ

ν ε ν ν

=

∫

%

%

%

%

%

(16)

m

ν

~ - liczba falowa odpowiadająca maksimum pasma absorpcji przejścia S

1

←

S

0

, a

∫

2

1

~

~

~

)

~

(

ν

ν

ν

ν

ε

d

jest wyznaczonym eksperymentalnie molowym współczynnikiem absorpcji scałkowany po

całym paśmie absorpcji.

Ze schematu przedstawionego na rys. 1 wynika, że wzbudzony stan elektronowy

odpowiedzialny za fluorescencję ulega dezaktywacji również na inne sposoby, co prowadzi

do zależności:

τ

t

o

e

I

I

−

=

(17)

gdzie:

τ

−

średni mierzony doświadczalnie najkrótszy czas zaniku, po którym wartość

o

I

I

maleje do

wartości

e

1

i wynosi:

(

)

ISC

IC

f

k

k

k

+

+

=

1

τ

(18)

k

IC

−

stała szybkości konwersji wewnętrznej (S

1

S

o

)

i może zmieniać się w szerokich

granicach, często oceniana jest na 10

5

-10

7

s

-1

;

k

ISC

−

stała szybkości konwersji międzysystemowej i jej wartość jest zwykle zawarta w

granicach 10

5

-10

10

s

-1

;

k

f

−

stała szybkości emisji fluorescencji i wynosi 10

8

-10

9

s

-1

,

jeśli przejście S

1

→

S

o

(por. rys.

1) jest dozwolone wszystkimi regułami wyboru.

8

1.4. Wydajność kwantowa fluorescencji

Wydajność kwantową fluorescencji

ϕ

f

definiuje się jako stosunek liczby

wyemitowanych fotonów do liczby fotonów promieniowania wzbudzającego, pochłoniętych

przez substancję w tym samym czasie i tej samej objętości. Wartość wydajności kwantowej

(

ϕ

f

) jest niemal zawsze mniejsza od jedności i na ogół zmienia się proporcjonalnie do

τ

(wyjątek stanowią rozrzedzone gazy),

f

f

o

f

IC

ISC

k

k

k

k

τ

φ

τ

=

=

+

+

(19)

o

τ

−

naturalny średni czas życia cząsteczek w stanie wzbudzonym i można go w przybliżeniu

wyznaczyć korzystając z relacji (16).

2. Pomiary spektrofotometryczne i spektrofluorymetryczne

2.1. Pomiar widma absorpcji

Pomiar widm absorpcji roztworów w obszarze widzialnym i nadfiolecie, czyli

zależności

A(

λ

) [lub

T(

λ

)] względnie

A(

ν

% ) [lub T(

ν

% )], przeprowadzamy przy użyciu

klasycznych spektrofotometrów UV-VIS.

Każdy spektrofotometr składa się z czterech zasadniczych elementów:

1.

źródła promieniowania polichromatycznego,

2.

monochromatora, rozszczepiającego wiązkę promieniowania polichromatycznego na

szereg wiązek monochromatycznych,

3.

detektora czułego na dany zakres promieniowania i zamieniającego sygnał świetlny

na elektryczny,

4.

elementu pomiarowego odczytującego i przetwarzającego sygnał wysyłany z detektora

na właściwą wielkość pomiarową (

A lub T) oraz zapisującego go w funkcji długości

fali lub liczby falowej. Zwykle zadaniem tego przyrządu jest też sterowanie

eksperymentem, np. powodowanie zmiany długości fali, przy której mierzona jest

absorpcja po każdym kolejnym odczycie.

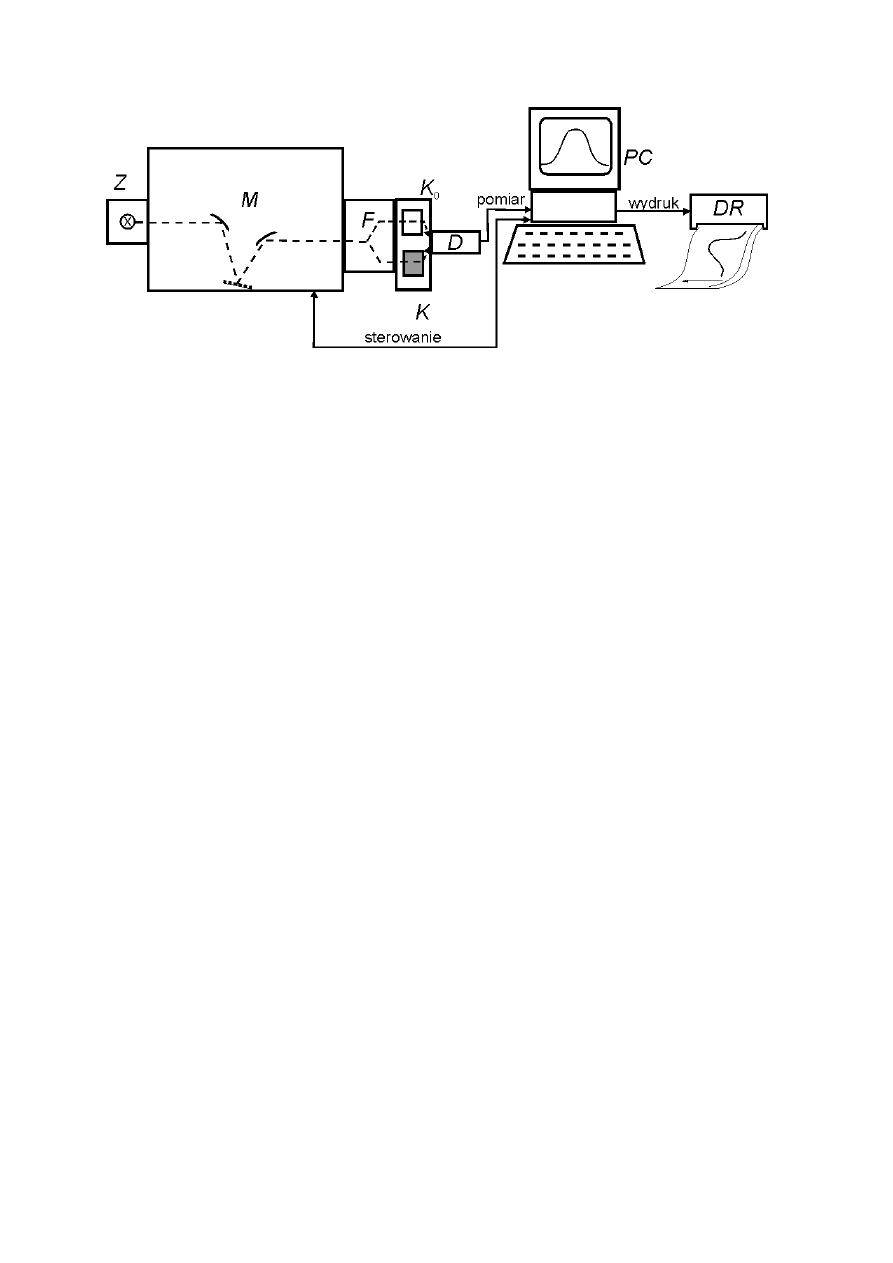
Schemat blokowy typowego spektrofotometru przedstawiono na rys. 3.

9

Rys. 3. Schemat blokowy spektrofotometru absorpcyjnego.

Z – źródło promieniowania

polichromatycznego,

M – monochromator, F – fotometr, K

0

,

K, – kuwety z odnośnikiem i

badaną próbką,

D – detektor promieniowania, PC – komputer lub inne urządzenie sterujące i

zapisujące wyniki.

DR – urządzenie peryferyjne, np. drukarka

Ponieważ celem pomiaru jest wyznaczenie absorbancji

A lub przepuszczalności T,

należy zmierzyć zarówno

I

0

jak i

I [patrz wzory (4) i (6)]. Realizuje się to przepuszczając

ś

wiatło opuszczające monochromator na przemian przez kuwetę

K z badaną substancją i

przez identyczną kuwetę porównawczą (odnośnik)

K

0

. W przypadku pomiarów absorpcji

roztworów w obszarze widzialnym lub nadfiolecie, kuweta

K

0

jest wypełniona

rozpuszczalnikim, w którym rozpuszczono substancję badaną w kuwecie

K. Kuwety są to

naczynia o płasko–równoległych wypolerowanych ścianach, wykonanych z kwarcu (lub ze

szkła, jeśli pomiar wykonuje się tylko w zakresie widzialnym).

2.2. Pomiar widma fluorescencji

Pomiar widma fluorescencji i widma wzbudzenia fluorescencji roztworów w obszarze

widzialnym i nadfiolecie, czyli zależności

intensywność fluorescencji = f(

λ

) przeprowadzamy

przy użyciu klasycznych spektrofluorymetrów.

Spektrofluorymetr wyposażony jest w dwa monochromatory zazwyczaj siatkowe, w

lampę ksenonową oraz fotopowielacz pracujący w reżimie zliczania pojedynczych fotonów.

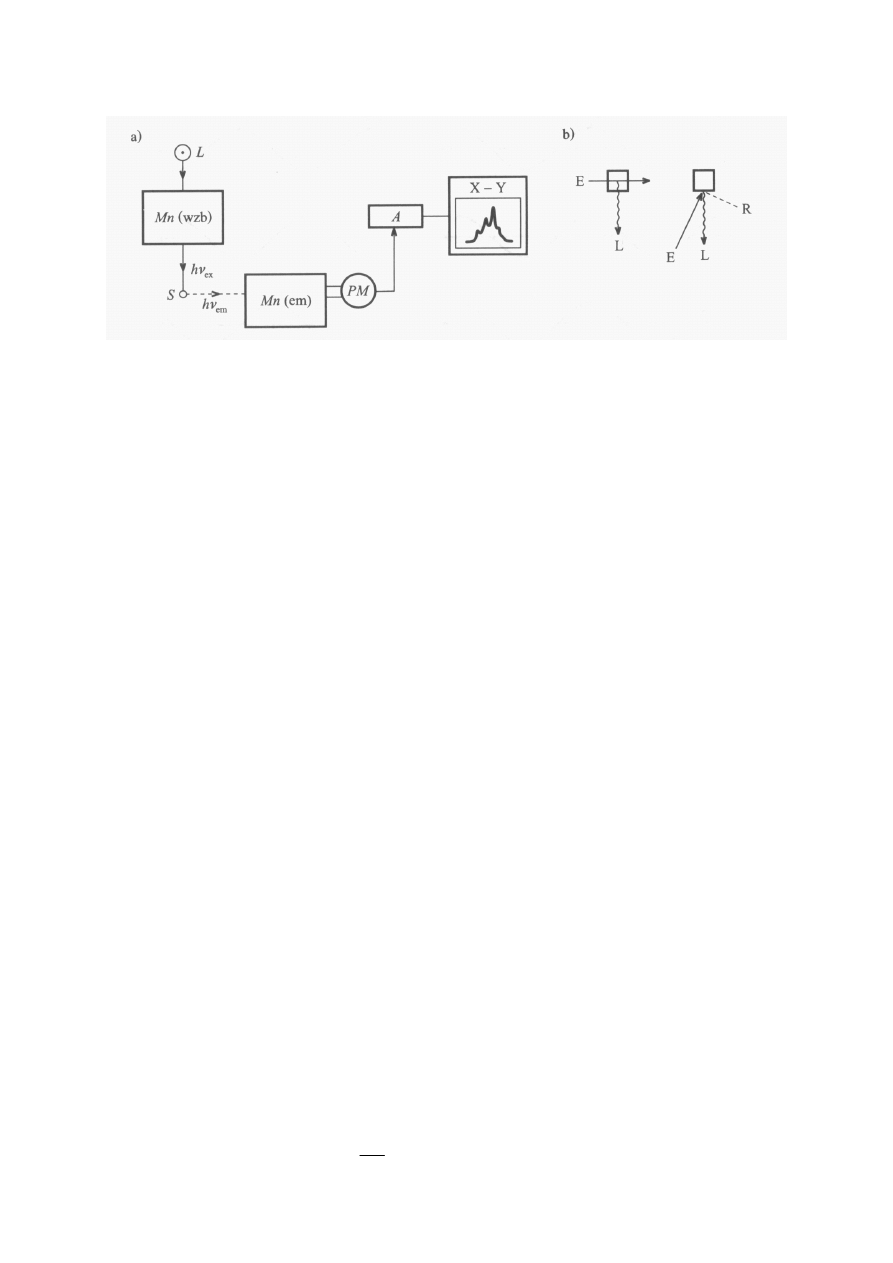
Schemat blokowy takiego spektrofluorymetru przedstawiono na rysunku 4.

10

Rys. 4. (a) Schemat blokowy spektrofluorymetru.

L – źródło światła, Mn(wzb) –

monochromator wybierający światło wzbudzające,

S – próbka, Mn(em) –

monochromator do analizy widma emisji,

PM – fotopowielacz, A – wzmacniacz, X-

Y –rejestrator.

(b)

Obserwacja pod kątem prostym (po lewej) i obserwacja czołowa (po prawej).

E – wiązka wzbudzająca, L – luminescencja, R – rozproszenie.

2. Pomiary wydajności kwantowych

Pomiary bezwzględnej wydajności kwantowej luminescencji są pomiarami trudnymi,

dlatego też wykonywane są najczęściej względem wzorców luminescencyjnych. W

pomiarach aktynometrycznych dla określenia bezwzględnej wydajności luminescencji

mierzymy natężenie promieniowania wzbudzającego i natężenie emisji próbki aktynometrem

chemicznym, a stosunek natężeń emisji do wzbudzenia stanowi bezwzględną wydajność

kwantową. Całkowite natężenie wiązki wyemitowanej przez próbkę jest mierzone roztworem

aktynometru chemicznego. Metoda ta została szczegółowo opisana w [1,2].

2.1. Wyznaczenie wydajności kwantowej z pomiaru czasu zaniku fluorescencji

Bezwzględną wydajność kwantową można wyznaczyć korzystając z relacji (19), jako

stosunek zmierzonego czasu życia fluorescencji

τ

do wyznaczonego z integralnego

współczynnika absorpcji, naturalnego średniego czasu życia cząsteczek w stanie

wzbudzonym

τ

o

.

f

o

τ

φ

τ

=

(20)

11

Wartości wydajności kwantowych uzyskane tą metodą obarczone są znacznym

błędem. Błąd wynika z niedokładności oznaczania wartości

τ

o

,

tj. pola powierzchni pod

krzywą pasma absorpcji odpowiadającej pierwszemu przejściu elektronowemu S

0

→

S

1

.

Zazwyczaj każde pasmo w widmie absorpcji jest obwiednią kilku nakładających się na siebie

pasm, dlatego też dokładniejsze informacje o składowych poszczególnych pasm można

uzyskać przez ich rozkład.

Również wyznaczony doświadczalnie czas życia fluorescencji próbki obarczony jest

ok. dziesięcioprocentowym błędem.

2.1.1. Pomiary czasów zaniku fluorescencji

Wyznaczenie czasu życia fluorescencji polega na zarejestrowaniu czasu zaniku emisji

badanego luminoforu po jego krótkotrwałym wzbudzeniu.

Do

pomiarów

czasów

ż

ycia

fluorescencji stosujemy między innymi lampy błyskowe, dające dostatecznie krótkie

(nanosekundowe) i stromo opadające impulsy świetlne.

Emisję próbkujemy po każdym błysku wzbudzającym za pomocą szybkiego

fotopowielacza. Po uwzględnieniu czasowego zaniku impulsu wzbudzającego, można

otrzymać czasowy zanik emisji substancji badanej. Rozwinięciem tej metody jest metoda

zliczania pojedynczych fotonów. W metodzie tej część światła wzbudzającego (lasera

impulsowego lub impulsowej lampy np. deuterowej) kierowana jest do fotodiody (lub

fotopowielacza)

PD, która ustala zero w skali czasu. Impuls ten wyzwala liniowo narastające

napięcie uzyskane z przetwornika czasu na napięcie (lub na amplitudę). W chwili zauważenia

przez fotopowielacz

PM pierwszego wyemitowanego fotonu, wzrost napięcia jest zatrzymany,

a impuls z przetwornika zostaje zarejestrowany w odpowiednim kanale analizatora

wielokanałowego. W analizatorze wielokanałowym każdy kanał jest określony czasem, jaki

upłynął od chwili rozbłysku impulsu wzbudzającego, a dla każdego impulsu wzbudzającego

zliczany jest tylko pierwszy foton. Eksperyment jest powtarzany wielokrotnie i w ten sposób

zostaje zarejestrowana cała krzywa zaniku emisji. Uproszczony schemat układu do zliczania

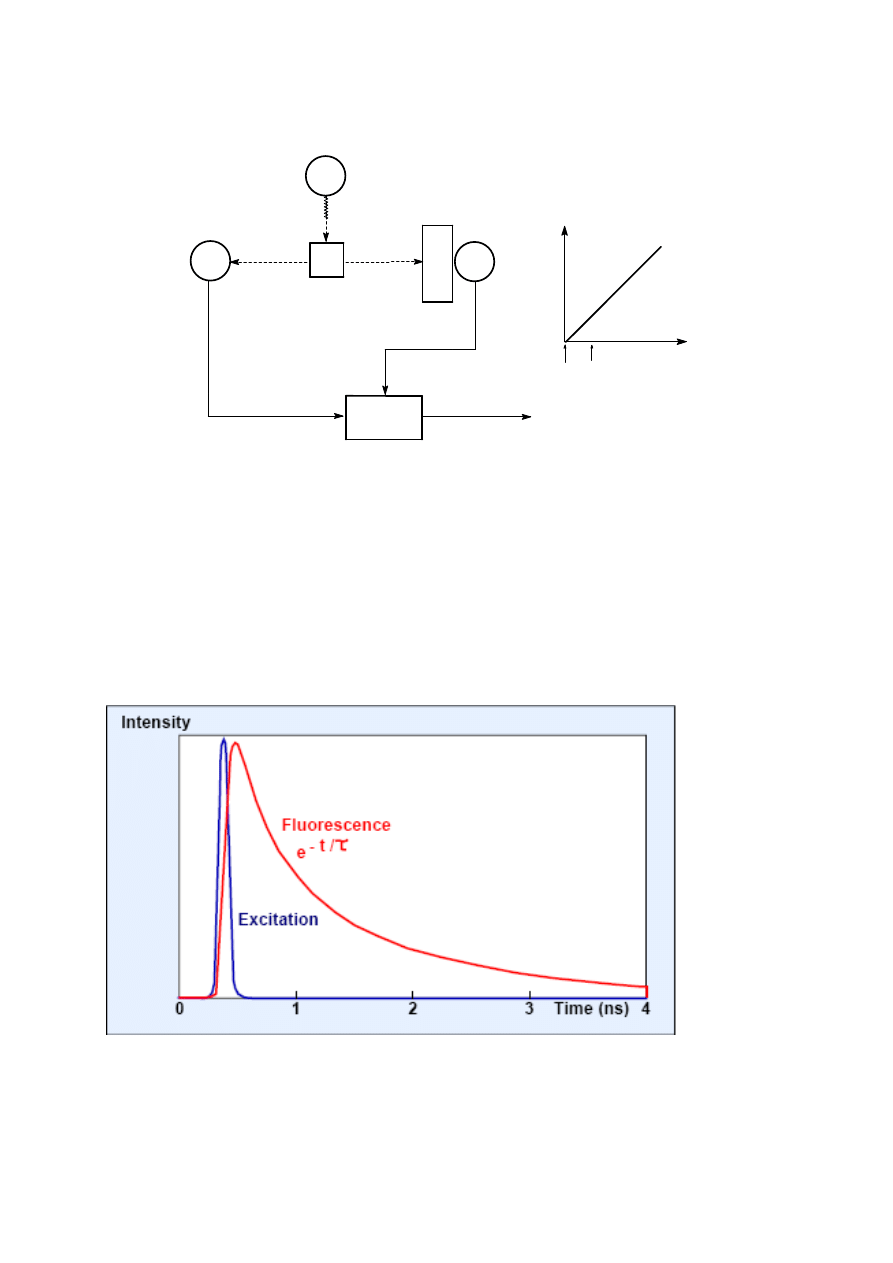
pojedynczych fotonów przedstawiony jest na rys. 5.

12

Rys.5. (a) Schemat układu do zliczania pojedynczych fotonów: L - impulsowe źródło światła,
PD - fotodioda, S- próbka, F- filtr interferencyjny lub monochromator, PM- fotopowielacz, R-
generator liniowo narastającego napięcia (1-start, 0-stop), AW- analizator wielokanałowy.
(b) liniowa zmiana napięcia w czasie.

Analizator AW zlicza impuls wyjściowy w kanałach odpowiadających poszczególnym

wartościom napięcia impulsów wyjściowych. Wynikiem pomiaru jest krzywa rozkładu liczby

fotonów, proporcjonalna do czasu zaniku natężenia fluorescencji (por. rys. 6).

Rys.6. Czas trwania emisji fluorescencji (

czerwony

) po wzbudzeniu krótkim impulsem lasera

(

niebieski

).

L

S

F

PM

R

AW

PD

V

czas

1

0

V

1

0

(a)

(b)

13

2.2 Wyznaczenie względnej wydajności kwantowej metodą porównawczą

W metodzie porównawczej względną wydajność kwantową oblicza się z zależności:

2

2

2

2

2 2 2

2

2

2

2

2

2

1

1

1 1 1

1

1

1

1

o

o

F

c l I

n

A

n

F

c l I

n

A

n

ϕ ε

ϕ

ϕ ε

ϕ

=

⋅

⋅

=

⋅

⋅

(21)

gdzie:

F

2

i

F

1

oznaczają powierzchnię pod krzywymi rozkładu natężeń fluorescencji w

widmach emisji próbki i wzorca,

ϕ

1

i

ϕ

2

są odpowiednio bezwzględne wydajności kwantowe

wzorca o znanej wydajności kwantowej i próbki,

ε

2

i

ε

1

- molowe współczynniki absorpcji

próbki i wzorca przy długości fali światła wzbudzającego (takiej samej dla wzorca i próbki),

c

2

i

c

1

- stężenie badanej próbki i wzorca,

l

2

i

l

1

- długości drogi optycznej w warstwach

roztworów próbki i wzorca,

I

0

- intensywność początkowa,

n

2

i

n

1

- współczynniki załamania

ś

wiatła rozpuszczalnika próbki i wzorca,

A

2

i

A

1

-

absorbancja próbki i wzorca przy długości

fali światła wzbudzającego fluorescencję (istotne jest, aby absorbancja próbki i wzorca nie

przekraczała wartości 0,1 tj. w zakresie, w którym występuje liniowa zależność natężenia

fluorescencji od stężenia).

Zastosowany wzorzec powinien posiadać pasmo absorpcji oraz fluorescencji w tym

samym zakresie spektralnym jak i badana próbka. Ponadto, aby pomiar wydajności

kwantowej fluorescencji był najdokładniejszy, wzbudzenie próbki i wzorca powinno odbywać

się w identycznych warunkach. Współczynniki załamania światła w równaniu (21) pozwalają

uwzględnić różnicę w stosowanych rozpuszczalnikach.

Aby wydajność kwantowa była poprawnie wyznaczona, wymagany jest prawidłowy

dobór wzorca. Najczęściej stosowane wzorce fluorescencyjne oraz ich wydajność kwantowa

fluorescencji zostały przedstawione w tabeli 1.

Tabela1. Wzorce fluorescencyjne oraz ich wydajność kwantowa fluorescencji

Związek

Rozpuszczalnik

λ

ex

[nm]

φ

f

Sulfonowana chinina

0.1 M H

2

S0

4

350

366

0.577

0.53

±

0.023

Fenol

Woda

275

0.14

±

0.01

Rodamina 6G

Etanol

488

0.94

Rodamina 101

Etanol

450-465

1.0

Chlorofil a

Metanol

644

0.21

±

0.02

Chlorofil a

Eter etylowy

_

0.20

±

0.02

Chlorofil b

Metanol

_

0.048

±

0.007

Chlorofil b

Eter etylowy

_

0.074

±

0.007

Ftalocyjanina Zn

Toluen

610

0.30

±

0,02

14

3. Wykonanie ćwiczenia i opracowanie wyników

Celem ćwiczenia jest wyznaczenie wydajności kwantowej fluorescencji wodnego

roztworu ftalocyjaniny, wykorzystując zmierzony czasu życia fluorescencji (

τ

) oraz obliczony

naturalny czasu życia fluorescencji (

τ

0

).

3.1 Opracowanie widm absorpcji roztworu badanego związku

Wykonanie ćwiczenia polega na pomiarze widm absorpcji badanych związków przy

użyciu spektrofotometru UV – VIS, którego schemat blokowy przedstawiono na rysunku 7.

Spektrofotometr wyposażony jest w dwa źródła światła: lampę deuterową (w zakresie

promieniowania UV) i lampę halogenową (w zakresie widzialnym). W układzie

monochromatora znajdują się szczeliny do regulacji szerokości wiązki światła, siatka

dyfrakcyjna i modulator.

Rys.7.

Schemat

blokowy

spektrofotometru

(UV-2101PC)

UV-VIS

(Scanning

Spectrophotometr Shimadzu).

Widmo absorpcji zapisane jest w postaci pliku danych z rozszerzeniem

.ASC, w

którym w pierwszej kolumnie jest długość fali [nm], w drugiej - absorbancja przy danej

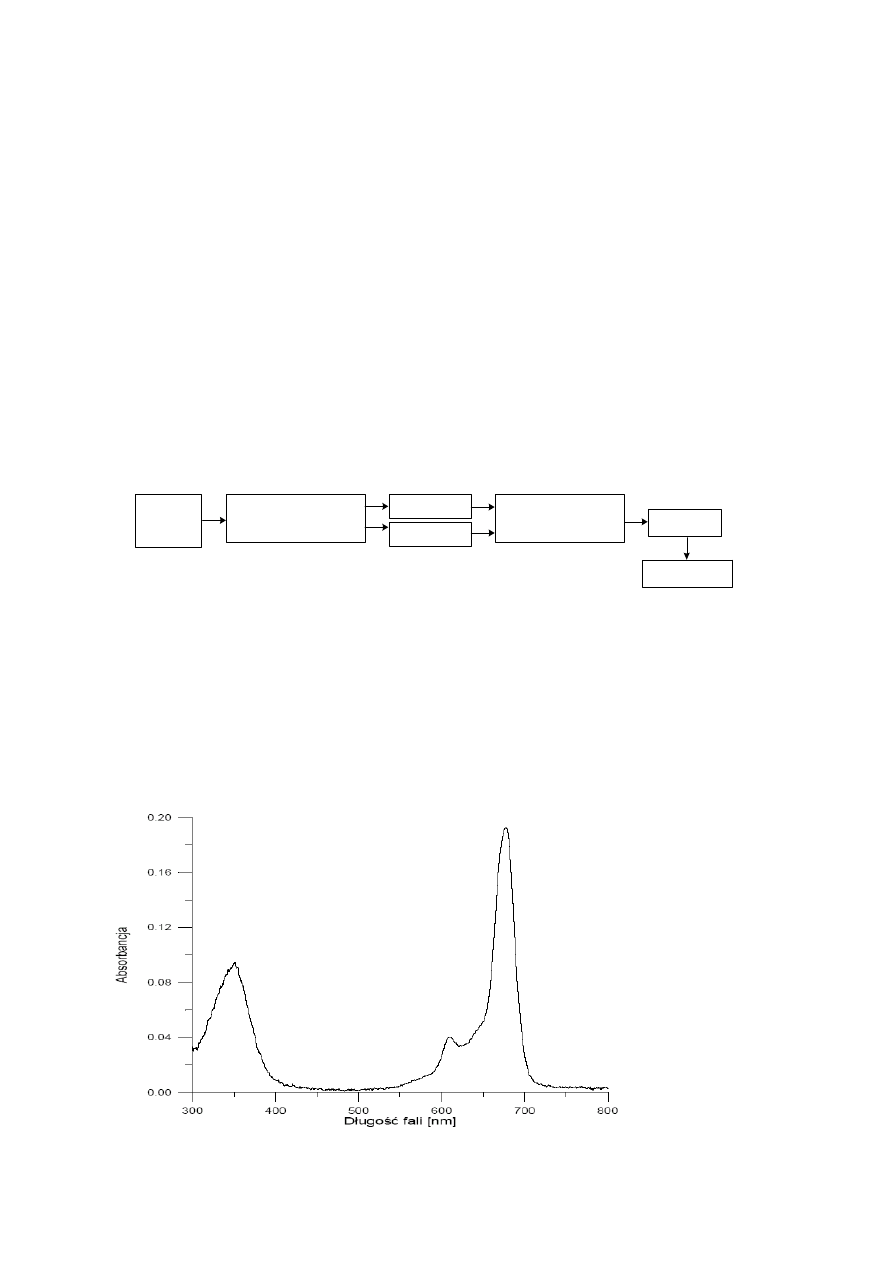
długości fal. Przykładowe widmo przedstawiono na rys. 8.

Rys. 8. Widmo absorpcji wodnego roztworu ftalocyjaniny (c= 1,25

⋅

10

−

6

mol

⋅

dm

−

3

)

Ź

RÓDŁO

Ś

WATŁA

MONOCHROMATOR

PRÓBKA

ODNO

Ś

NIK

FOTOPOWIELACZ

KOMPUTER

MIERNIK

15

Z widma zarejestrowanego w całym mierzonym zakresie spektralnym należy wybrać pasmo

odpowiadające pierwszemu przejściu absorpcyjnemu S

1

←

S

0

. W przypadku roztworów

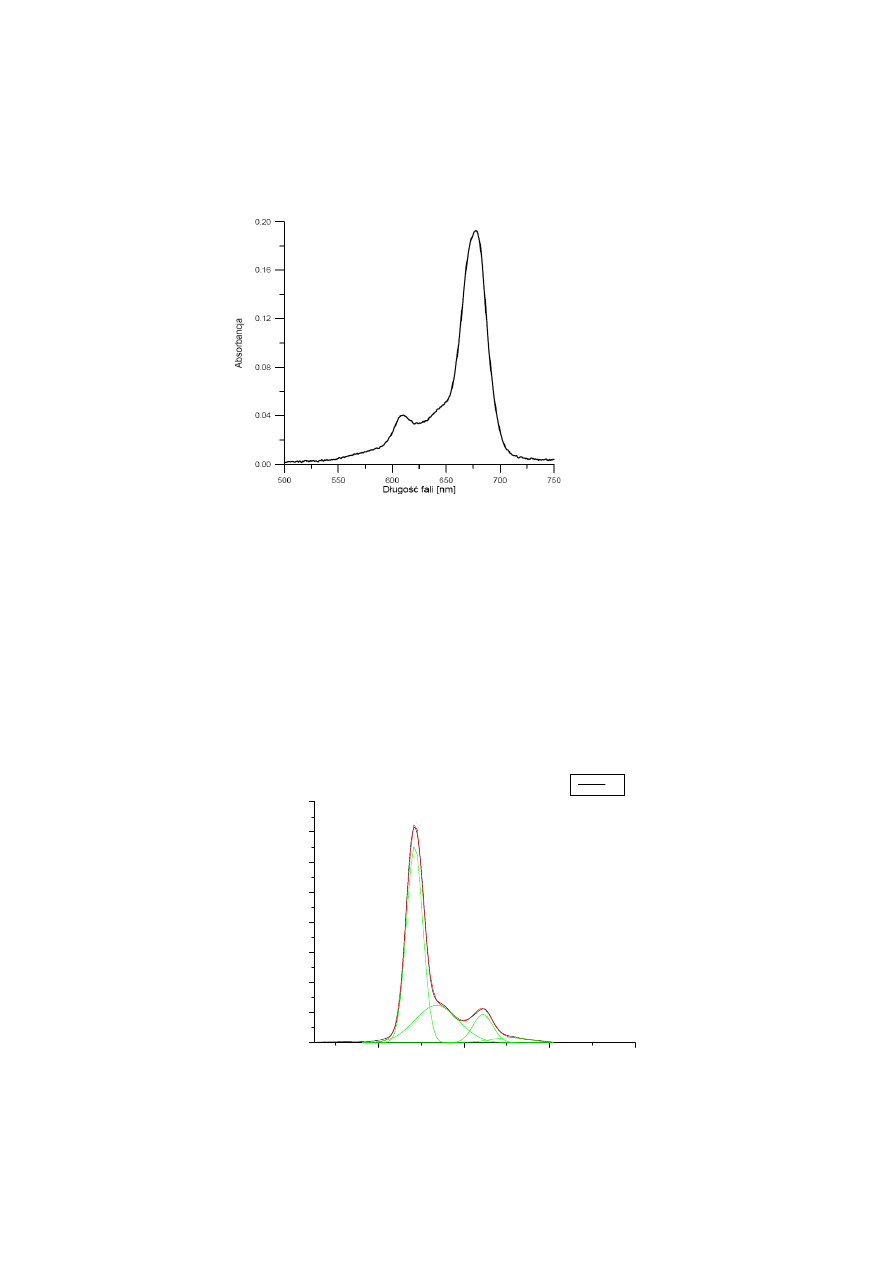
ftalocyjaniny należy wybrać fragment 500-750 nm (por. rys. 9).

Rys. 9. Fragment widma absorpcji wodnego roztworu ftalocyjaniny (c= 1,25

⋅

10

−

6

mol

⋅

dm

−

3

)

Znając stężenie roztworu i stosując

prawa Lamberta – Beera zmieniamy skalę absorbancji na

skalę molowego współczynnika absorpcji. W tym celu należy podzielić absorbancję przez

stężenie substancji w roztworze i grubość warstwy (1 cm).

Również skalę długość fali należy zamienić na skalę liczb falowych wyrażoną w cm

−

1

. Na

rys.10 przedstawiono fragment widma absorpcji po dokowaniu tych zamian.

14000

16000

18000

20000

0,0

2,0x10

5

4,0x10

5

6,0x10

5

8,0x10

5

1,0x10

6

1,2x10

6

1,4x10

6

1,6x10

6

M

o

lo

w

y

w

s

p

ó

łc

z

y

n

n

ik

a

b

s

o

rp

c

ji

Liczba falowa

D

Rys. 10. Fragment widma absorpcji wodnego roztworu ftalocyjaniny (c= 1,25

⋅

10

−

6

mol

⋅

dm

−

3

)

16

Kolejnym krokiem jest rozkładanie widma w tym zakresie na kilka pasma (np. programem

ORIGIN), których obwiednią jest funkcja Gaussa (Gaussiany). Liczba pasm powinna być

dobrana tak, aby powierzchnia pod każdym pasmem była dodatnia, dopasowanie sumaryczne

do kształtu pasma zmierzonego było najbliższe jedności i aby najintensywniejsze, pierwsze

pasmo, było odtworzone najwierniej jedną funkcją Gaussa (por. rys.10).

Z tak rozłożonego widma należy odczytać integralny współczynnik absorpcji pierwszego,

najintensywniejszego pasma oraz liczbę falową określającą maksimum tego pasma, a

następnie korzystając z zależności (13) i (16) obliczyć siłę oscylatora przejścia (

f) i naturalny

czas życia fluorescencji (

τ

0

).

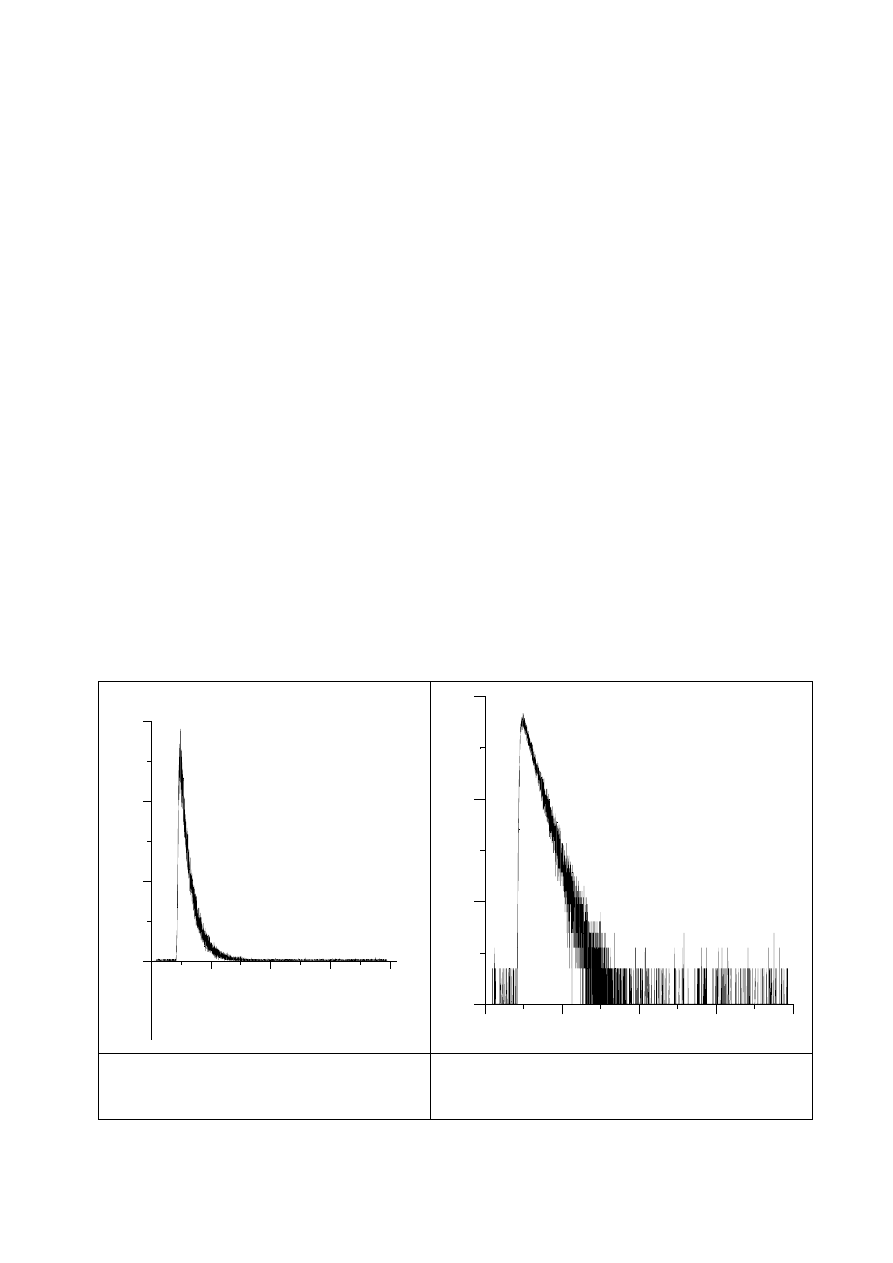
3.2.Opracowanie wyników pomiaru czasu zaniku fluorescencji

Dane z pomiaru czasu zaniku fluorescencji otrzymujemy w postaci pliku z

rozszerzeniem

.TXT, gdzie w pierwszej kolumnie jest numer kanału, w drugiej – liczba

pojedynczych zliczonych fotonów w odpowiednim kanale. Krzywa rozkładu liczby fotonów

w kolejnych kanałach w funkcji numeru kanału odpowiada czasowemu zanikowi

fluorescencji (por. rys 11a). Jest to zależność ekspotencjalna, natomiast w skali

logarytmicznej – otrzymujemy liniową zależność ln (liczby impulsów) =

f (nr kanału).

Zależność ta przedstawiona jest na rys.11b.

0

2000

4000

6000

8000

Numer kanału

0

100

200

300

L

ic

z

b

a

i

m

p

u

ls

ó

w

0

2000

4000

6000

8000

numer kanału

0

2

4

6

ln

(

lic

z

b

y

i

m

p

u

ls

ó

w

)

Rys. 11a. Liczba impulsów (fotonów) emisji

zliczona w każdym kanale analizatora

Rys. 11b. Logarytm naturalny z liczby impulsów

emisji w funkcji numeru kanału .

17

Przed każdym pomiarem dobierana jest skala podstawy czasu, tj. czas, w którym rejestrujemy

liczbę impulsów pojawiających się od chwili t = 0 do t = podstawie czasu. Skala podstawy

czasu wybierana jest w zależności od spodziewanego czasu zaniku fluorescencji.

W Tabeli 1 zestawiono wartości podstawy czas i czas przypadający na każdy kanał.

Tabela 1. Wartości podstawy czasu i ilość nanosekund przypadająca na jeden kanał.

podstawa czasu [ns]

ns/ kanał [ns]

100

0,01455

200

0,02919

500

0,06322

Iloczyn liczby kanałów użytych w pomiarze i czasu, jaki jest potrzebny na zarejestrowanie

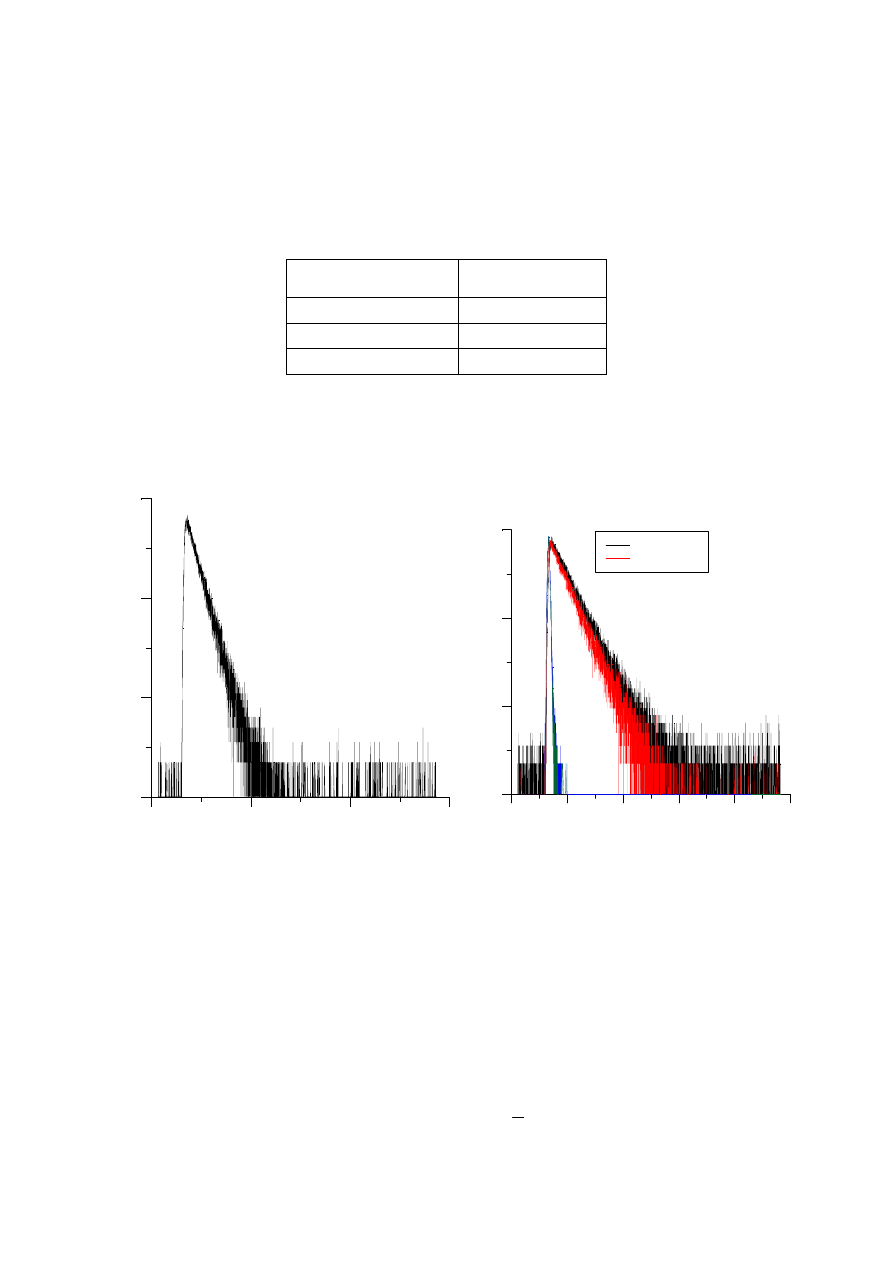
impulsów w każdym kanale, zamienia skalę liczby kanałów na czas [w ns] (por. rys 12a).

(a) (b)

0

40

80

120

czas [ns]

0

2

4

6

ln

(

lic

z

b

y

i

m

p

u

ls

ó

w

)

ln (liczba zliczeń)

Rys. 12. (a) Wykres zależności ln (liczba zliczeń)=

f (czas). (b) Wykres zależności ln (ilości

zliczeń)=

f (czasu) dla próbki sulfonowanej ftalocyjaniny glinu w wodzie o stężeniu

c=6

⋅

10

-5

M. Pomiar zarejestrowany w kuwecie kwadratowej (

τ

=7,7ns) i w kuwecie trójkątnej

(

τ

=6,66ns). Linie zaznaczone kolorem zielonym i niebieskim odnoszą się do wzorca

fluorescencyjnego.

Zależność ln

I od czasu jest zależnością liniową, jeśli zanik emisji jest monoeksponencjalny,

a współczynnik kierunkowy prostej: ln(

I)=f (t);

ln

ln

o

t

I

I

τ

= −

+

jest równy

−

1/

τ

.

0

20

40

60

80

100

0.00

2.00

4.00

6.00

kuweta kwadratowa

kuweta trojkatna

18

Z zależności tej obliczmy czas zaniku fluorescencji.

3.3 Sprawozdanie z ćwiczenia.

Student otrzymuje dwa komplety danych. Jeden plik z rozszerzeniem .ASC zawiera

dane pomiaru widma absorpcji, który należy opracować tak, jak to zostało przedstawione w

punkcie 3.1. W sprawozdaniu należy umieścić wszystkie widma oraz obliczoną siłę

oscylatora pierwszego przejścia absorpcyjnego i obliczony naturalny czas życia fluorescencji.

Drugi plik, z rozszerzeniem .TXT zawiera dane mierzonego czasu zaniku fluorescencji, który

należy opracować tak, jak to zostało przedstawione w punkcie 3.2. W sprawozdaniu należy

przedstawić wszystkie krzywe zaniku oraz obliczony czas zaniku fluorescencji.

Iloraz

τ

/

τ

0

jest wielkością wydajności kwantowej fluorescencji, którą również należy

obliczyć.

Literatura:

[1] K. Pigoń, Z. Ruziewicz, „Chemia fizyczna”, PWN, Warszawa, (1986), (rozdz. 11.2.3, 11.3.4,

11.3.5).

[2] A. Kawski, „Fotoluminescencja roztworów”, PWN, Warszawa, (1992), (rozdz.1, 6).

Opracowała dr hab. Krystyna Palewska