Zarządzanie i Inżynieria Produkcji

Lista zadań nr 5

1.

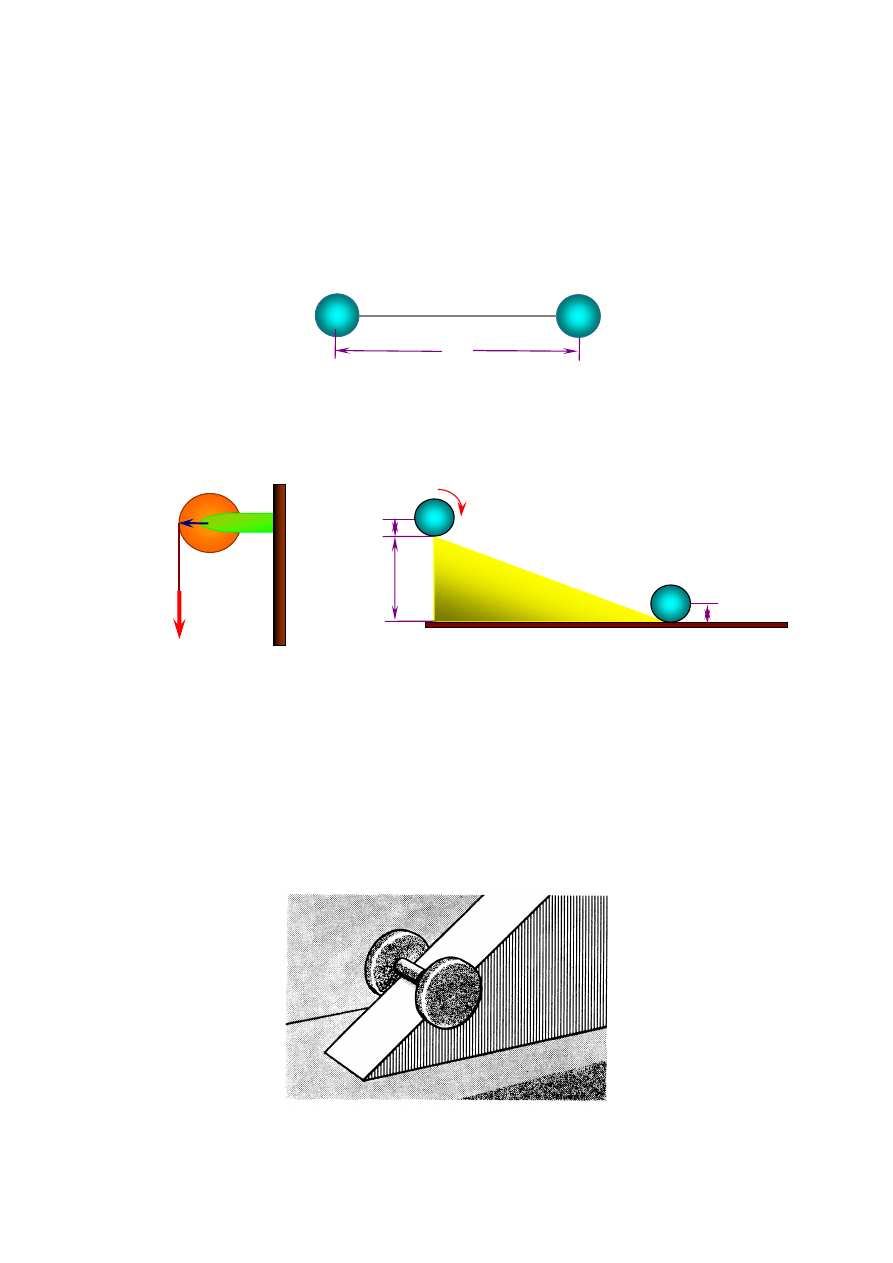
Na rysunku (rys.1) przedstawiono układ dwóch kul o masie m = 3 kg każda połączonych lekkim
sztywnym prętem. Odległość pomiędzy środkami kul jest równa d = 0.8 m. Traktując kule jako ciała
punktowe i pomijając masę pręta oblicz moment bezwładności J: a) względem osi normalnej
przechodzącej przez środek pręta, b) osi normalnej przechodzącej przez jedną z kul.

Rys.1. Ilustracja do zadania nr 1.

2.

Jednorodny krążek o promieniu R i masie M zawieszono na łożysku, które obraca się bez tarcia. Na
obwodzie krążka nawinięty jest lekki sznur, do którego przyłożono stałą siłę F skierowaną w dół.
Znaleźć przyspieszenie kątowe

α

krążka

Rys.2. Ilustracja do zadania nr 2. Rys.3. Ilustracja do zadania nr 3.

3.

Jednorodny walec o masie M i promieniu R, toczy się w dół równi pochyłej bez poślizgu. Wysokość

równi jest równa h. Wyznaczyć prędkość środka masy walca przy podstawie równi. Moment
bezwładności walca względem głównej jego osi jest równy J = MR

2

/2 Powtórzyć rozumowanie dla

staczającej się kuli. Dla kuli moment bezwładności względem osi środkowej J = 2MR

2

/5.

4.

Dwa ciężkie krążki połączone są krótkim prętem, którego promień jest o wiele mniejszy od promieni

krążków. Układ ten umieszczono na równi pochyłej tak, że krążki wiszą po obu jej stronach, a pręt
stacza się po równi bez poślizgu (rys..4). Gdy krążki dotkną stołu na której stoi równia, zaczną się po
nim toczyć. Wyjaśnij dlaczego prędkość liniowa toczących się po stole krążków będzie większa od
prędkości liniowej krążków staczających się po równi..

Rys.4. Ilustracja do zadania nr 4

.

m

m

d

M

R

F

R

R

h

5.

Rower jedzie ze stałą prędkością gdy siła działająca pomiędzy nawierzchnią i kołem F

2

= 4 N. Z jaką

siłą F

1

łańcuch musi ciągnąć zębatkę jeżeli stosunek R

2

/R

1

= 10?

Rys. 5. Ilustracja do zadania nr 5.

6.

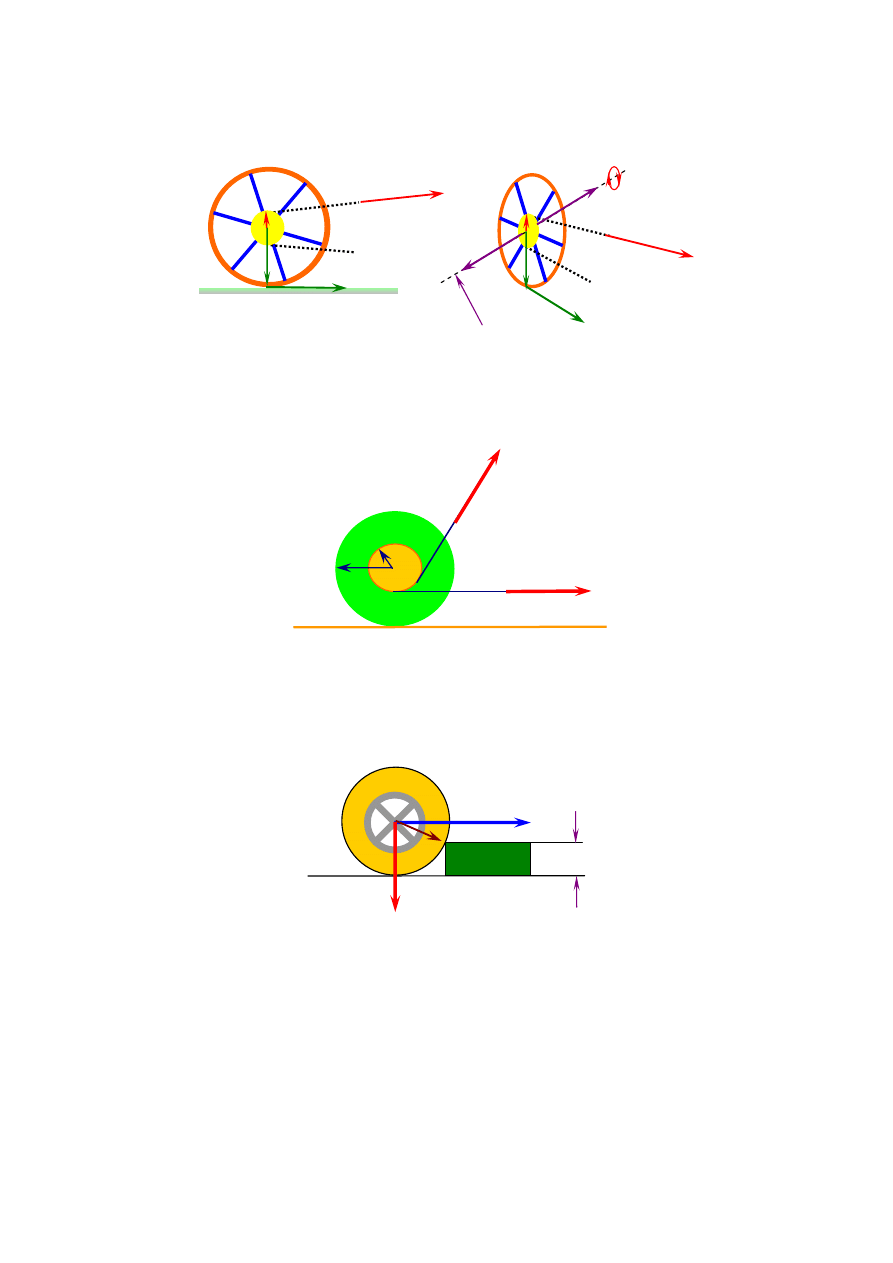
Na poziomym stole znajduje się szpula mogąca się po nim toczyć. W którą stronę będzie się ona toczyć

jeżeli pociągniemy za nawiniętą na szpulę nić: a) siłą F

1

, b) siła F

2

.. Odpowiedź uzasadnij.

Rys. 6. Ilustracja do zadania nr 6.

7.

Z jaką minimalną siłą F , przyłożoną do osi koła i skierowaną poziomo (rys.7) należy działać aby koło o
masie m i promieniu R wjechało na krawężnik o wysokości h?

Rys. 7. Ilustracja do zadania nr 7.

h

R

?

=

F

r

g

m

Q

r

r

=

1

F

r

2

F

r

1

R

2

R

2

1

R

R 〉

oś obrotu

1

R

2

R

1

F

2

F

2

F

1

F

2

R

1

R

1

τ

r

2

τ

r