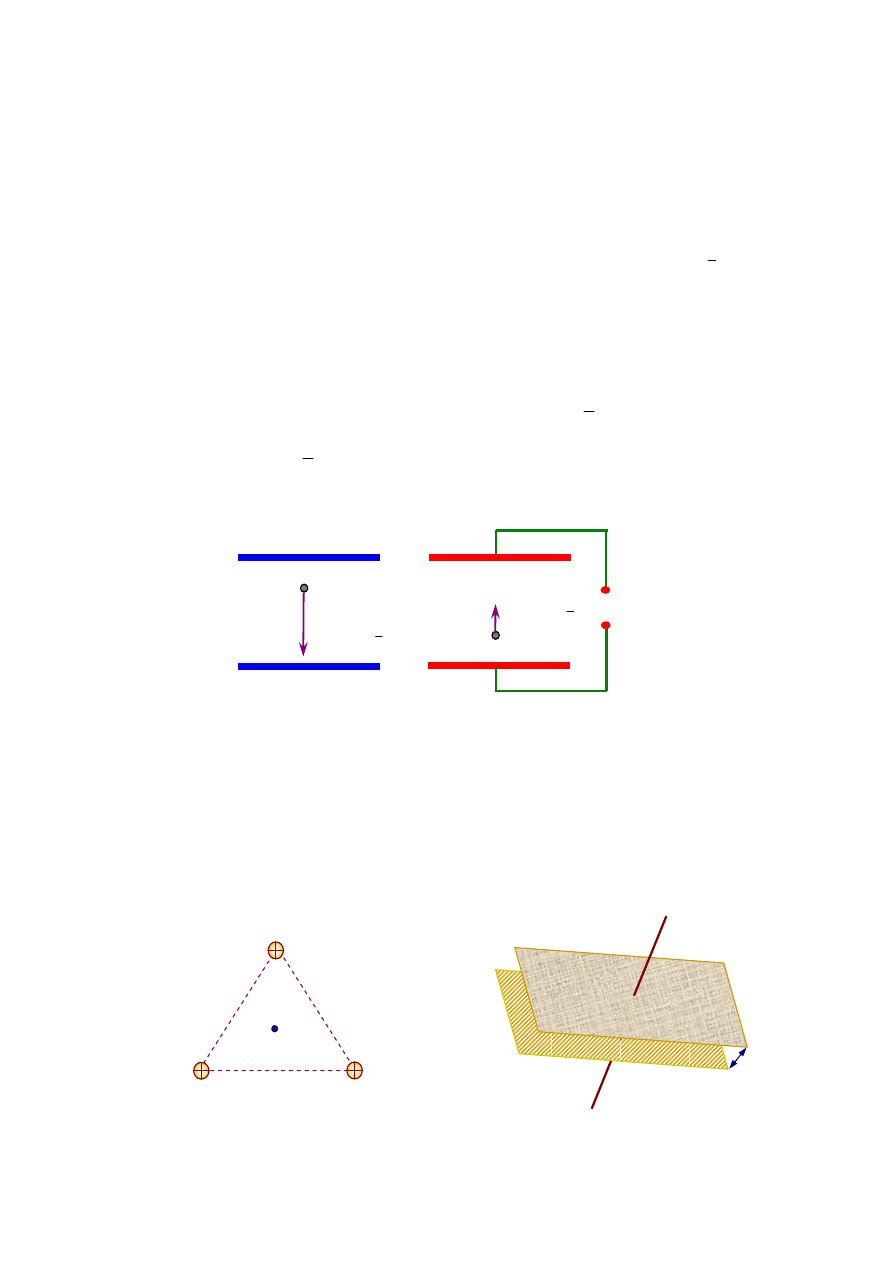
Zarządzanie i Inżynieria Produkcji

Fizyka

Lista zadań nr 8

1)

W płaskim, poziomo usytuowanym kondensatorze, w którym odległość pomiędzy okładzinami
wynosi d, znajduje się naładowana kropelka oliwy o masie m. Przy braku pola elektrycznego,
kropelka wskutek oporu powietrza, opada ze stałą prędkością

1

v

. Natomiast po przyłożeniu

do okładzin kondensatora napięcia U, kropelka opada ze stałą prędkością

1

2

1

2

v

v

=

. Oblicz

ładunek elektryczny zgromadzony na kropelce. Uwaga!!! Pominąć siłę wyporu działającą na
kropelkę.

2)

W umieszczonym w płaszczyźnie poziomej kondensatorze płaskim o odległości między
okładkami równej d = 0.01 m, znajduje się naładowana ładunkiem elektrycznym kropelka

oleju parafinowego o masie

kg

m

16

10

4

.

6

−

⋅

=

. Gdy nie ma napięcia elektrycznego pomiędzy

okładkami, kropelka opada ze stałą prędkością

s

m

v

5

1

10

8

.

7

−

⋅

=

. Po przyłożeniu do okładek

napięcia elektrycznego U = 90 V kropelka porusza się ruchem jednostajnym ku górze z

prędkością

s

m

5

10

6

.

1

−

⋅

. Oblicz ładunek elektryczny Q zgromadzony na kropelce.

Uwaga!!! Pominąć siłę wyporu działającą na kropelkę.

Rys.1.Ilustracja do zadania 2.

3)

Między okładkami kondensatora płaskiego naładowanego do różnicy potencjałów U = 40 V i
umieszczonego w płaszczyźnie poziomej utrzymuje się nieruchomo kropla cieczy obdarzona

ładunkiem

C

Q

19

10

8

.

4

−

⋅

=

. Wzajemna odległość okładek kondensatora d = 4 mm. Oblicz

jaka jest masa m kropli?

Uwaga!!! Pominąć siłę wyporu działającą na kroplę.

4)

W wierzchołkach trójkąta równobocznego o boku a = 5 cm umieszczono jednakowe ładunki
elektryczne Q = 2 C. Wyznacz:: potencjał elektryczny V w środku geometrycznym P trójkąta.

Rys.. 2 Ilustracja do zadania 4. Rys..3 Ilustracja do zadania 5.

V

U

90

=

s

m

v

5

1

10

8

.

7

−

⋅

=

s

m

v

5

2

10

6

.

1

−

⋅

=

kg

m

16

10

4

.

6

−

⋅

=

kg

m

16

10

4

.

6

−

⋅

=

S

d

P

Q

Q

Q

a

a

a

5)

Oblicz jaka jest powierzchnia S jednej płyty kondensatora płaskiego, znajdującego się w
próżni, o pojemności elektrycznej C = 1F, jeżeli odległość pomiędzy płytami jest równa
d = 1mm. Ile będzie wynosić pojemność tego kondensatora jeżeli pomiędzy jego płytami
umieści się (na całej powierzchni) dielektryk o stałej dielektrycznej

5

.

6

=

=

r

ε

κ

6)

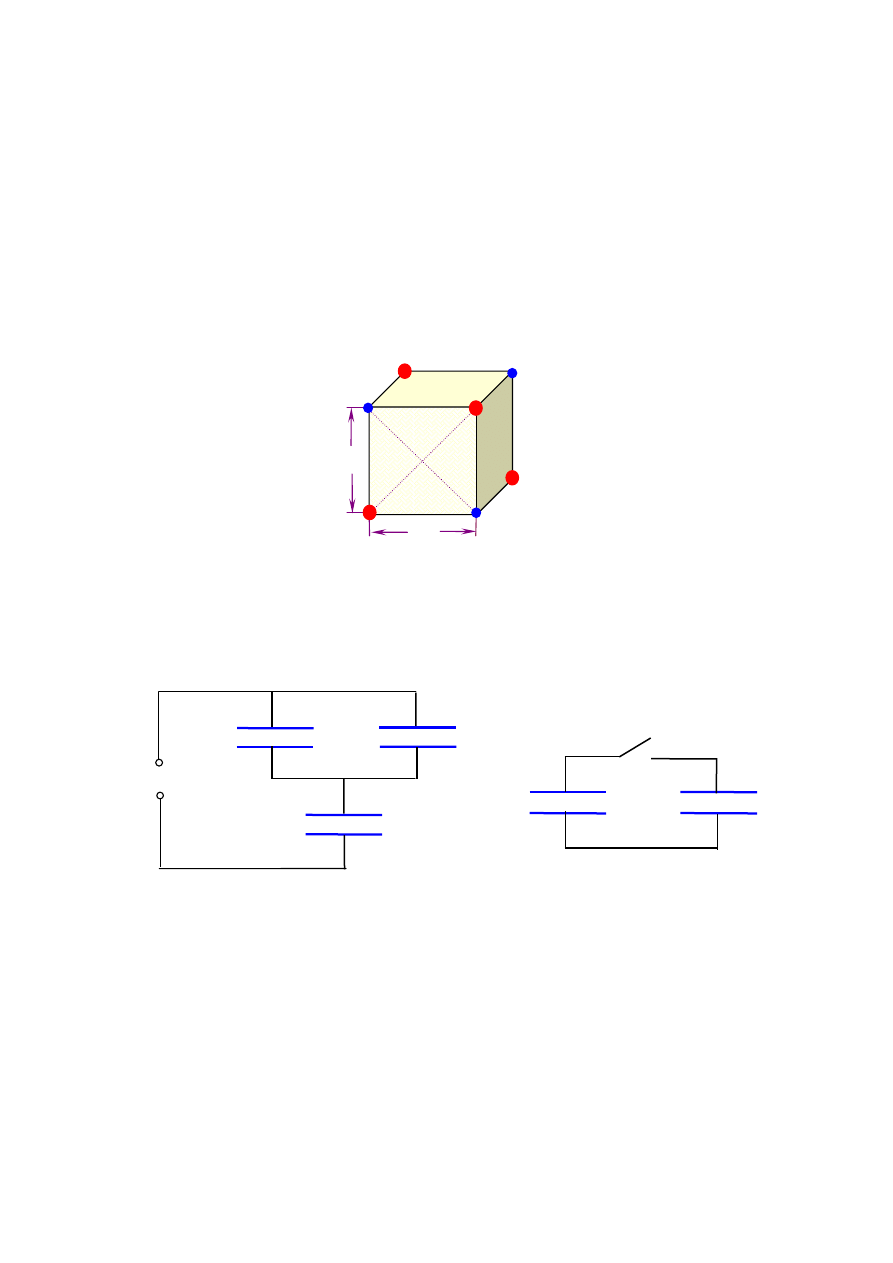
Elementarna komórka kryształu NaCl ma strukturę kubiczną o stałej sieciowej

m

a

o

10

10

63

.

5

−

⋅

=

(rys.4) W wierzchołkach sześcianu znajdują się na przemian jony sodu

+

Na

i chloru

−

Cl

. Oblicz jaki jest potencjał elektryczny w punkcie P będącym środkiem

geometrycznym jednej ze ścian sześciennej komórki elementarnej. W obliczeniach wziąć pod
uwagę kationy i aniony tylko jednaj komórki.

Rys.4 Ilustracja do zadania 6.

7)

Oblicz pojemność zastępczą C

z

dla kondensatorów C

1

= 12

µ

F, C

2

= 5.3

µ

F i C

3

= 4.5

µ

F

przedstawionych na rysunku (4.). Różnica potencjałów przyłożona do zacisków wejściowych
układu jest równa U = 12.5 V .Oblicz jaki ładunek elektryczny zgromadzi się na
kondensatorze o pojemności C

1

.

Rys. 5 Ilustracja do zadania 7. Rys. .6 Ilustracja do zadania

8)

Kondensator o pojemności elektrycznej C

1

= 3.55

µ

F zostaje naładowany do różnicy

potencjałów U

o

. = 6.3 V. Następnie bateria ładująca zostaje odłączona a kondensator ten

zostaje połączony z nienaładowanym kondensatorem o pojemności C

2

= 8.89

µ

F

(rys.6.)..Gdy

klucz

zostaje

zamknięty,

ładunek

elektryczny

przepływa

pomiędzy

kondensatorami aż uzyskają taką samą różnicę potencjałów. Jaka różnica potencjałów U
ustali się w tym układzie po zamknięciu klucza K?

−

Cl

−

Cl

+

Na

P

o

a

o

a

1

C

2

C

3

C

V

U

5

.

12

=

1

C

2

C

o

U

o

Q

K