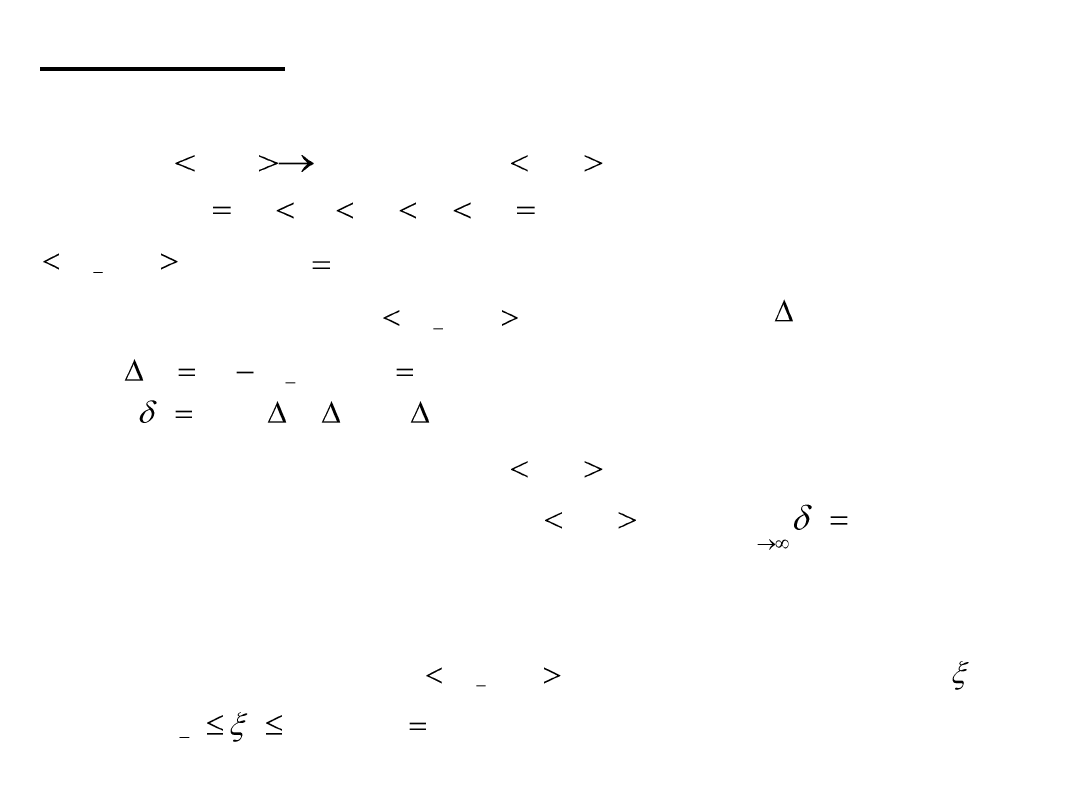
Całka oznaczona
Definicja całki oznaczonej
Niech Przedział podzielmy za pomocą
punktów na przedziałów częściowych
gdzie Oznaczmy ten podział przez
Długośd podprzedziału oznaczmy przez
czyli
Liczbę nazywamy średnicą podziału
Ciąg podziałów przedziału nazywamy ciągiem
normalnym podziałów przedziału jeżeli
W dalszym ciągu będziemy zakładad, że ciąg podziałów jest
ciągiem normalnym podziałów.
W każdym podprzedziale obierzmy dowolny punkt
taki, że
R.
b
a
f
,
:
b
a,
b
x
x
x
x
a
n
...
2
1
0
n
.
n
P
,
,
1
k
k
x
x
.
,...,
3
,
2
,
1
n
k
k
k
x
x
,
1
,
k
x
.
,...,
3
,
2
,
1
dla
1
n
k
x
x
x
k
k
k
}
,...,
,
max{
2
1
n
n
x
x
x
.
n
P
)
(
n
P
b
a,
,
,b
a
.
0
lim
n
n
)
(
n
P
k
k
x
x
,
1
k
.
,...,
3
,
2
,
1
dla
1
n
k
x
x
k
k
k
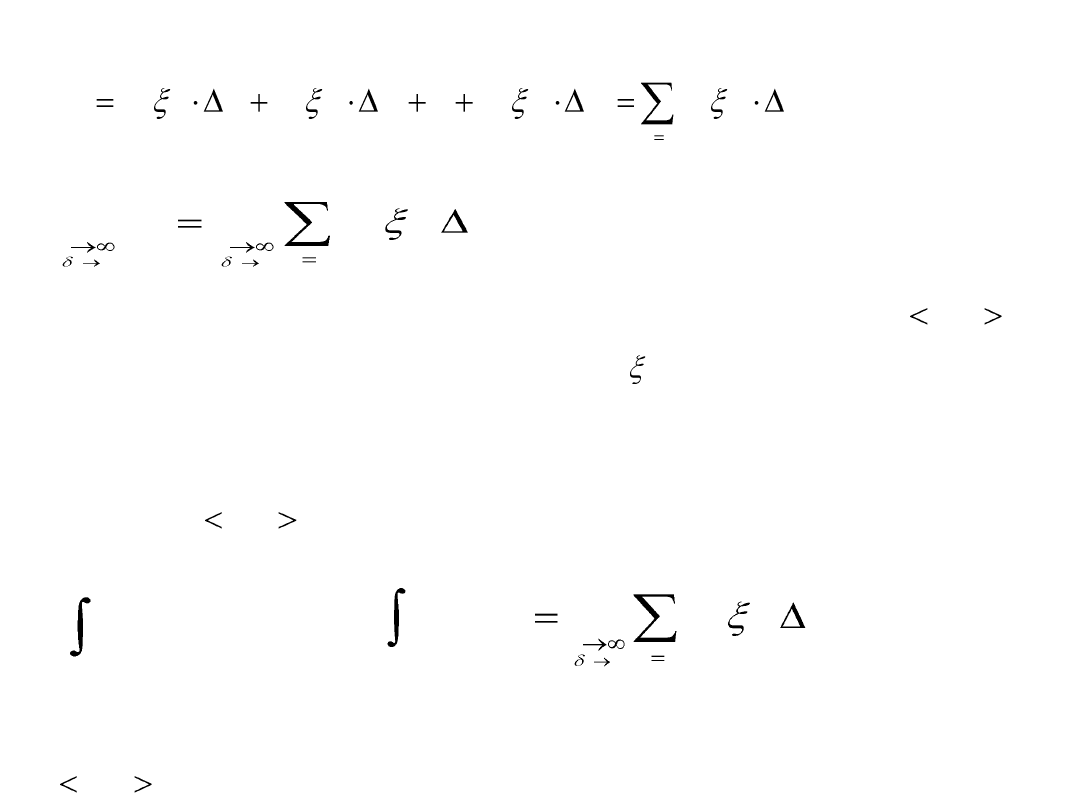
Utwórzmy sumę
i rozważmy granicę
Jeżeli dla każdego normalnego ciągu podziałów przedziału
i każdego wyboru punktów pośrednich w przedziałach
częściowych tych podziałów istnieje ta sama skooczona granica
ciągu to tę granicę nazywamy całką oznaczoną funkcji na
przedziale i oznaczamy symbolem
Zatem
– dolna granica całkowania, – górna granica całkowania,
- przedział całkowania.
n
k
k
k
n
n
n
x
f
x
f
x
f
x
f
S
1
2
2
1
1
)
(
)
(
...
)
(
)
(
.
)
(
lim
lim
1
)
0
(
)
0
(
k
n
k
k
n
n
n
x
f
S
n
n
b
a
dx
x
f
.
)
(
.
)
(
lim
)
(
1
)
0
(
k
n
k
k
n
b
a
x
f
dx
x
f
n
b
a,
k
),
(
n
S
b
a,
f
b
a,
b
a
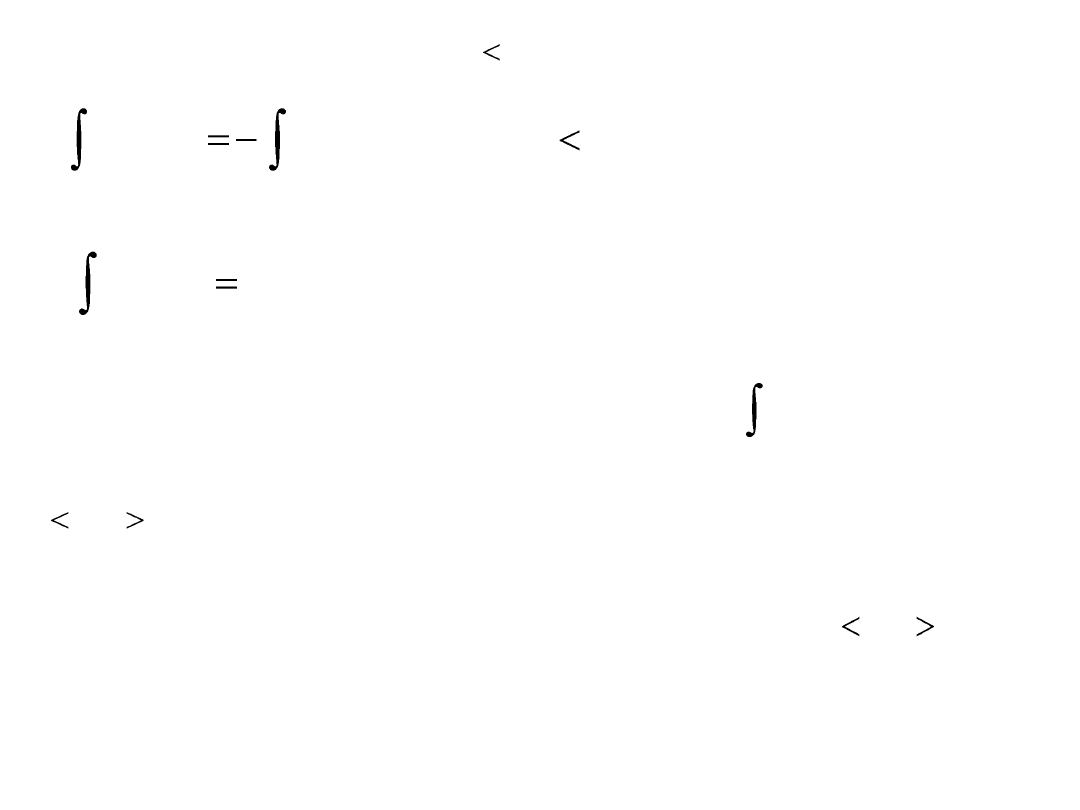
Do tej pory zakładaliśmy, że Dodatkowo przyjmujemy, że
oraz
Definicja
Funkcję dla której istnieje całka oznaczona
nazywamy funkcją całkowalną (w sensie Riemanna) na przedziale
Twierdzenie (warunek konieczny całkowalności)
Jeżeli funkcja jest funkcją całkowalną na przedziale to
jest funkcją ograniczoną na tym przedziale.
a
b
dx
x
f
dx
x
f
a
b
def
b
a
gdy
,
)
(
)
(
.
0
)
(
def
a
a
dx
x
f
b
a
dx
x
f
)
(
.
b
a
,
f
.
,b
a
f
,
,b
a
f
Twierdzenie ( trzy warunki wystarczające całkowalności)
Jeżeli spełniony jest dowolny z warunków
1. jest funkcją ciągłą na
2. jest funkcją ograniczoną na i ma na tym przedziale
skooczoną liczbę punktów nieciągłości,
3. jest funkcją monotoniczną na
to jest funkcją całkowalną na
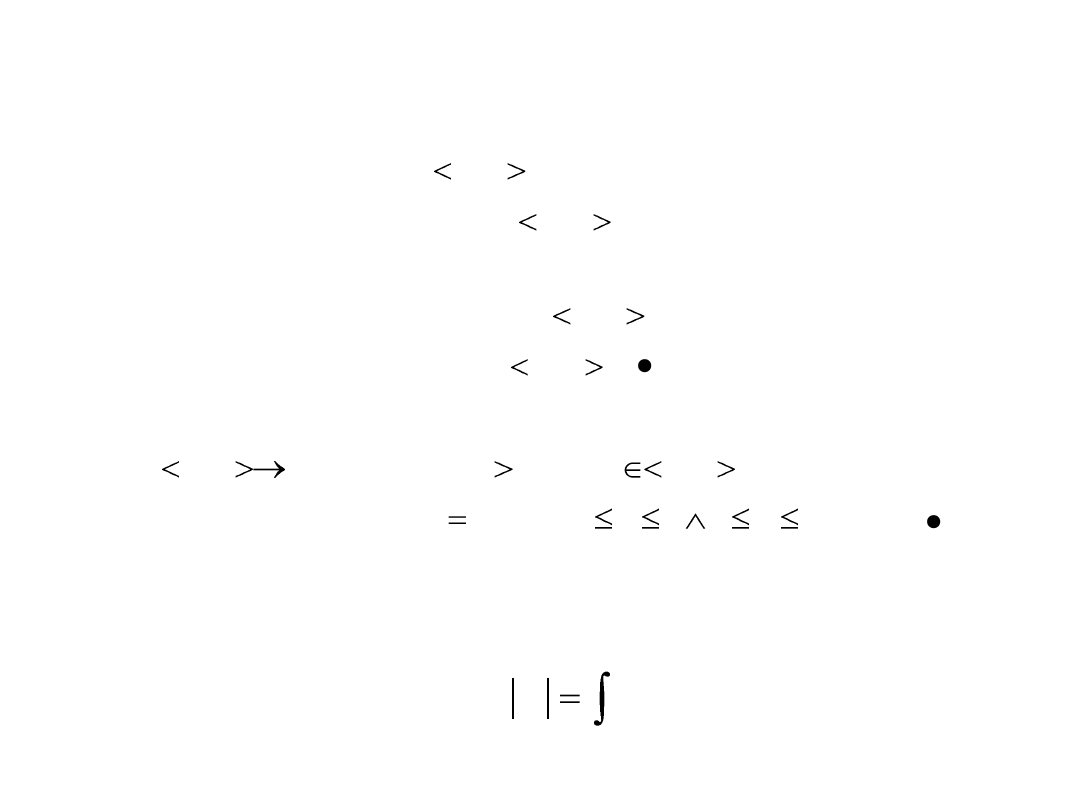
Interpretacja geometryczna całki oznaczonej
Niech
Wprowadźmy oznaczenie
Obszar nosi nazwę trapezu krzywoliniowego .
Z definicji całki oznaczonej wynika, że pole powierzchni trapezu
krzywoliniowego jest równe
b
a
dx
x
f
D
.
)
(
.
,b
a
.
,
dla
0
)
(
niech
i
,
:
b
a
x
x
f
b
a
f
R
b
a,
,
,b
a
,
,b
a
f
f
f
f
)}.
(
0
:
)
,
{(
x
f
y
b
x
a
y
x
D
D
D
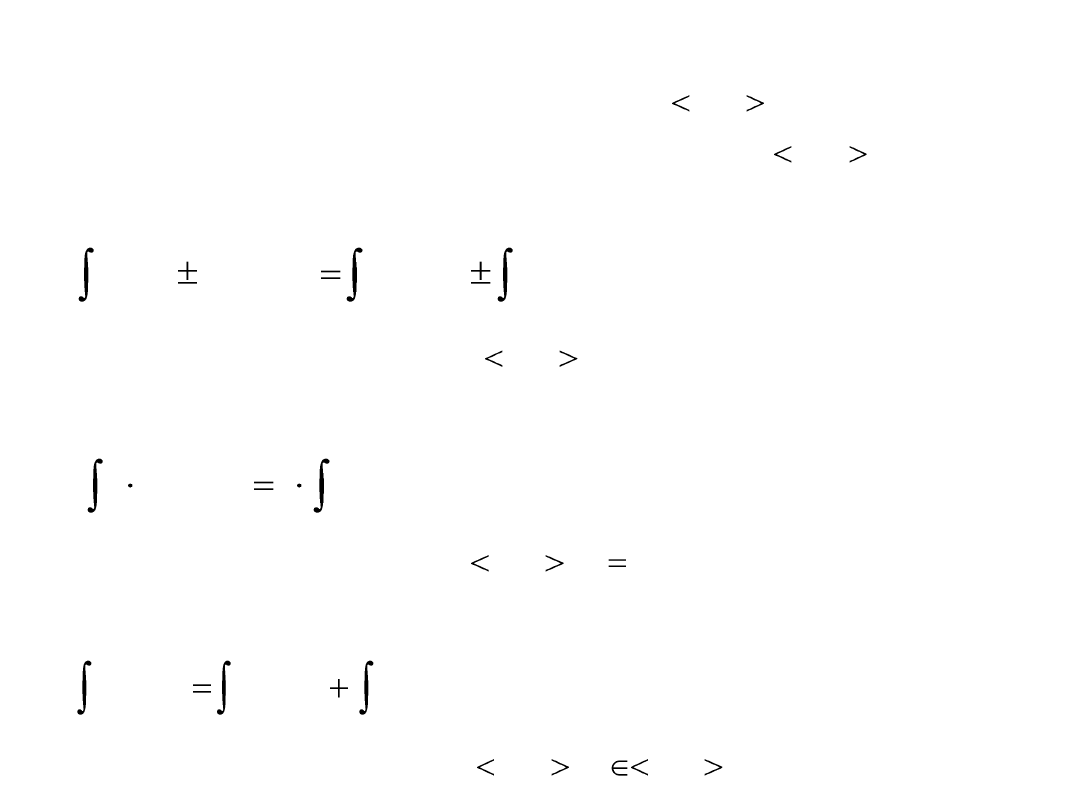
Własności całek oznaczonych
Własnośd 1. Jeżeli jest całkowalna na to jest również
całkowalna na każdym podprzedziale przedziału
Własnośd 2.
gdzie są całkowalne na
Własnośd 3.
gdzie jest całkowalna na
Własnośd 4.
gdzie jest całkowalna na
,
)
(
)
(
)]
(
)
(
[
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f
,
)
(
)
(
b
a
b
a
dx
x
f
k
dx
x
f
k
,
)
(
)
(
)
(
b
c
c
a
b
a
dx
x
f
dx
x
f
dx
x
f
f
.
,b
a
,
,b
a
g
f ,
.
,b
a
f
.
,
,
const
k
b
a
f
.
,
,
,
b
a
c
b
a
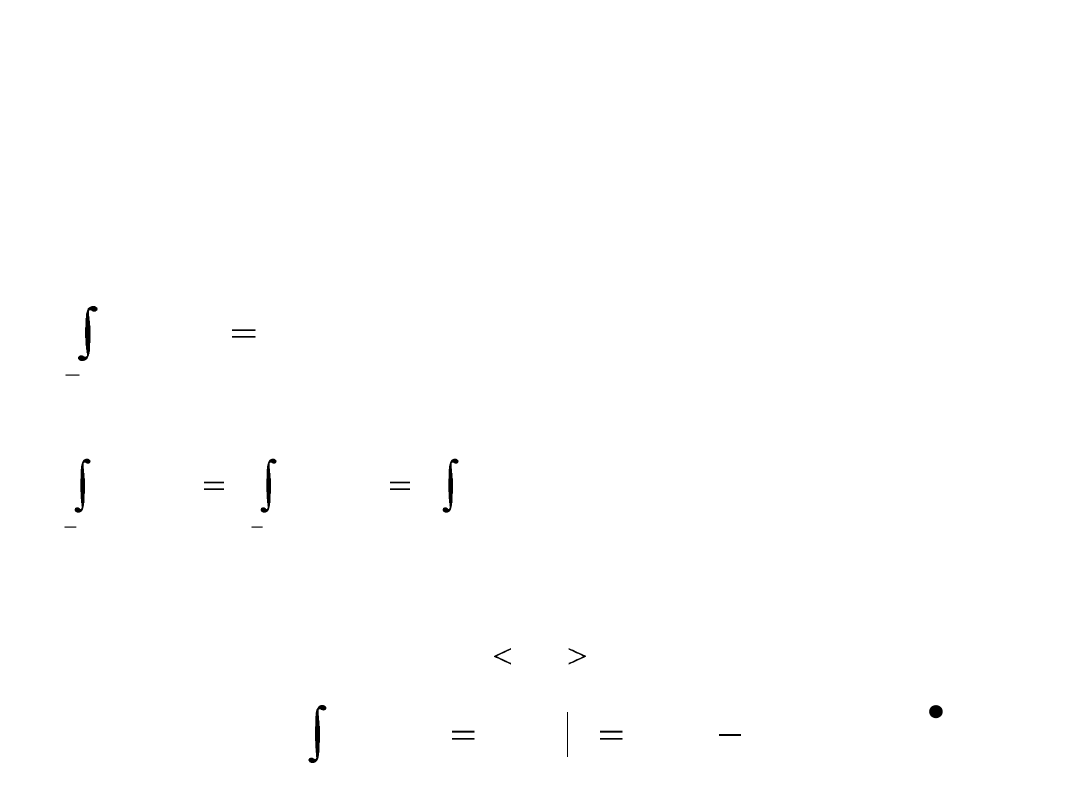
Własnośd 5. Zmiana wartości funkcji w skooczonej liczbie punktów
przedziału ( nie wyklucza się przy tym kraoców przedziału) nie
wpływa ani na całkowalnośd tej funkcji w rozważanym przedziale,
ani na wartośd całki, jeżeli funkcja ta jest całkowalna.
Własnośd 6. Jeżeli jest funkcją nieparzystą i całkowalną, to
Własnośd 7. Jeżeli jest funkcją parzystą i całkowalną, to
Twierdzenie (Newtona-Leibniza, o związku całki oznaczonej z całką
nieoznaczoną)
Jeżeli jest funkcją ciągłą na jest jej dowolną funkcją
pierwotną, to
a
a
dx
x
f
.
0
)
(
a
a
a
a
dx
x
f
dx
x
f
dx
x
f
0
0
.
)
(
2
)
(
2
)
(
).
(
)
(
)
(
)
(
a
F
b
F
x
F
dx
x
f
b
a
b
a
f
f
f
F
b
a
i
,
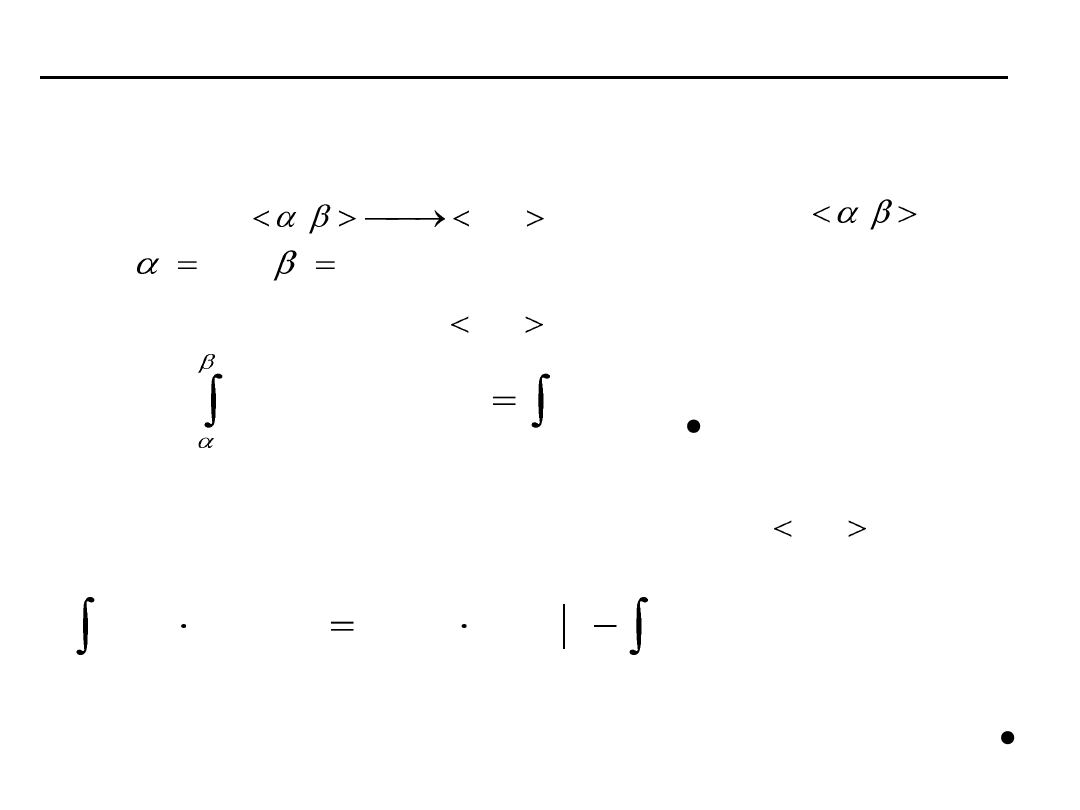
Całkowanie przez podstawienie i przez części dla całki oznaczonej
Twierdzenie (o całkowaniu przez podstawienie )
Jeżeli
1. funkcja jest klasy na
2.
3. funkcja jest ciągła na
to
Twierdzenie (o całkowaniu przez części)
Jeżeli funkcje oraz są klasy na przedziale to
b
a
dt
t
f
dx
x
g
x
g
f
)
(
)
(
'
))
(
(
b
a
b
a
b
a
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
.
)
(
)
(
'
)]
(
)
(
[
)
(
'
)
(
b
a
g
na
,
,
:
,
,
1
C
,
)
g(
,
)
(
b
a
g
f
,
,b
a
f
1
C
,
,b
a
g
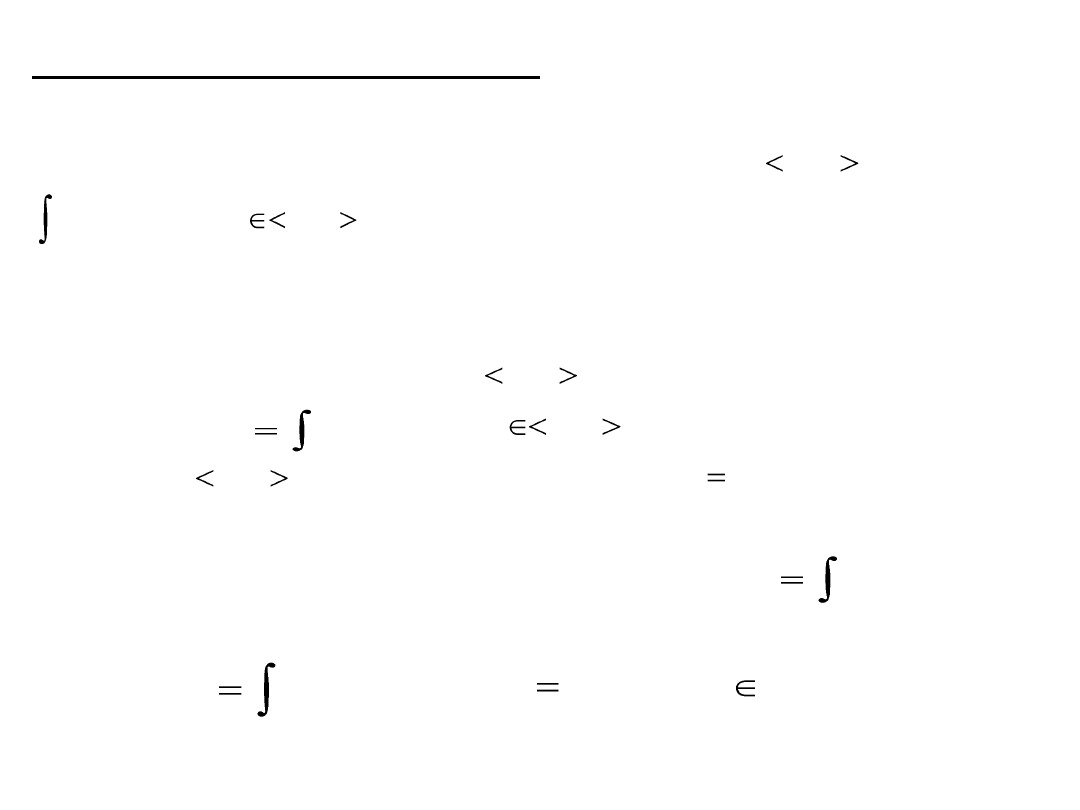
Funkcja górnej granicy całkowania
Definicja (funkcji górnej granicy całkowania)
Niech funkcja będzie całkowalna na przedziale Funkcję
nazywamy funkcją górnej granicy całkowania.
Twierdzenie (o pochodnej funkcji górnej granicy całkowania)
Jeżeli jest funkcją ciągłą na to funkcja określona
wzorem dla ma w każdym punkcie
przedziału pochodną i przy tym
Uwaga. Istotą powyższego twierdzenia jest możliwośd obliczenia
pochodnej funkcji bez wyznaczania całki
Przykład.
Jeżeli , to
b
a
x
dt
t
f
x
a
,
gdzie
,
)
(
x
a
dt
t
f
x
F
)
(
)
(
.
)
(
)
(
x
a
dt
t
f
x
F
x
a
t
dt
e
x
F
2
)
(
R.
x
e
x
F
x
dla
)
(
'
2
f
F
f
.
,b
a
,
,b
a
,
,b
a
x
b
a,
).
(
)
(
'
x
f
x
F
F
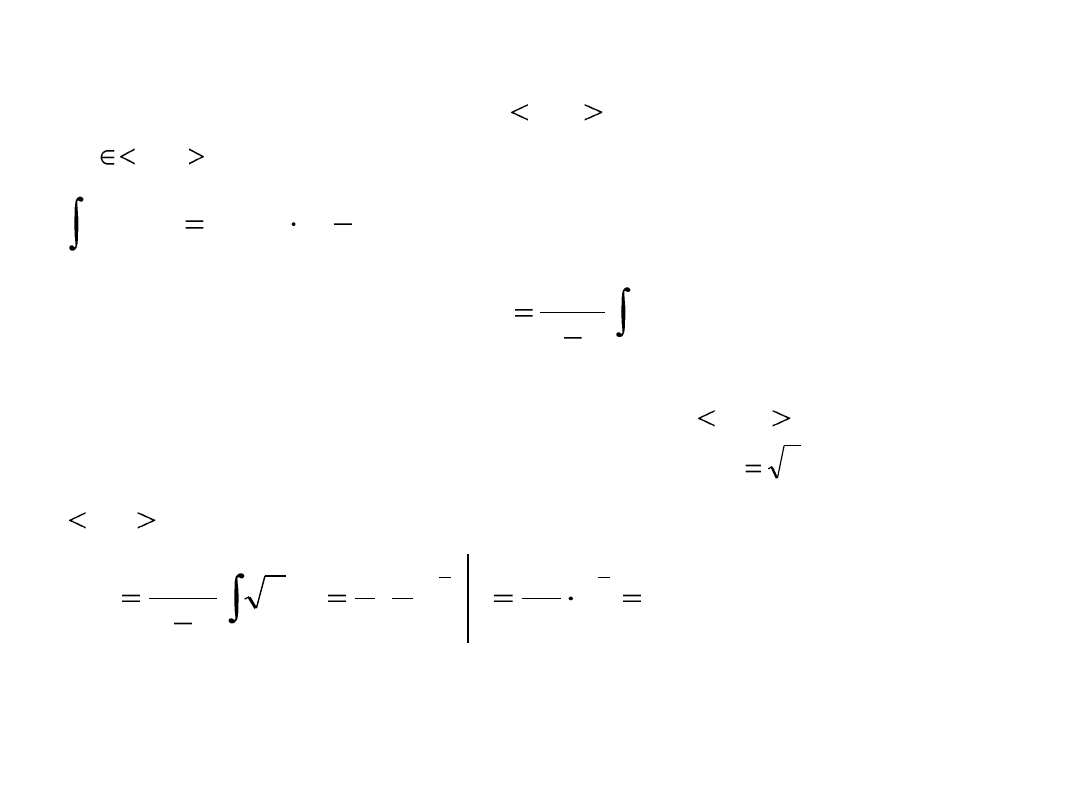
Twierdzenie (o wartości średniej rachunku całkowego)
Jeżeli jest funkcją ciągłą na to istnieje taki punkt
że
Liczbę daną równością nazywamy
wartością średnią funkcji na przedziale
Przykład Obliczyd wartośd średnią funkcji na przedziale
b
a
a
b
x
f
dx
x
f
).
(
)
(
)
(
0
b
a
śr
dx
x
f
a
b
y
)
(
1
x
x
f
)
(
2
9
27
2
]
3
2
[
9
1
0
9
1
2
3
9
0
2
3
9
0
x
dx
x
y
śr
f
,
,b
a
,
,
0
b
a
x
śr
y
f
.
,b
a
.
9
,
0
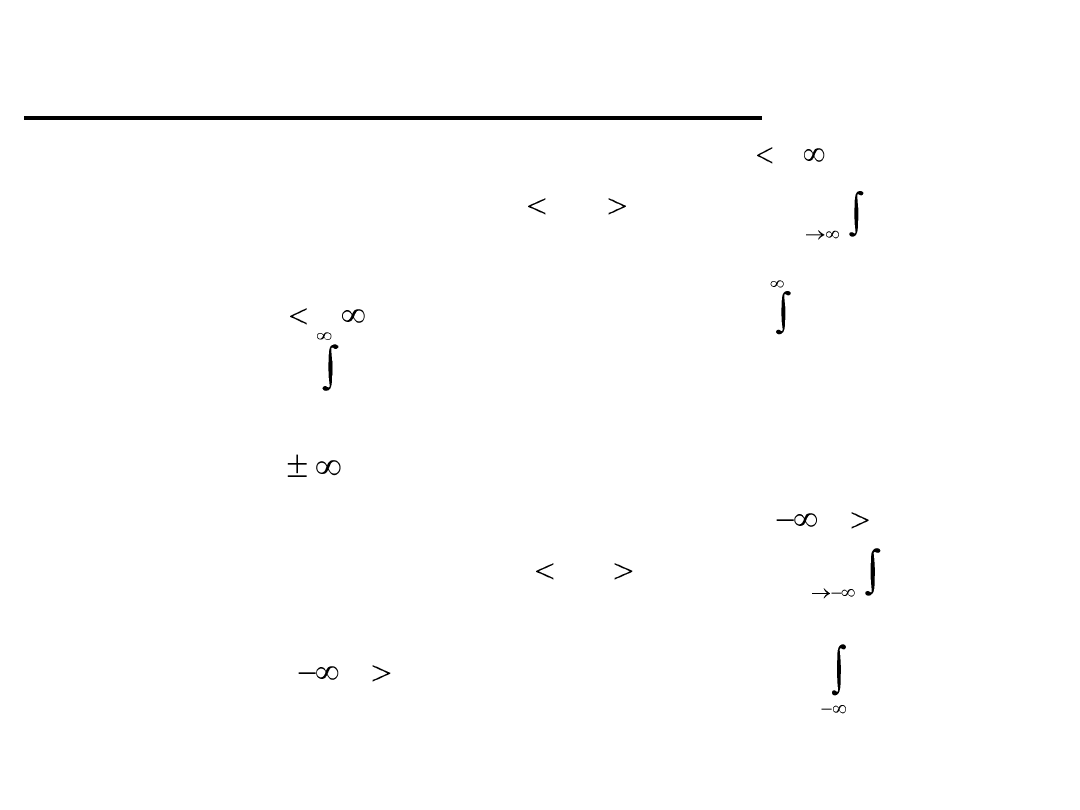
CAŁKI NIEWŁAŚCIWE
Całka niewłaściwa na przedziale nieograniczonym
I. Niech będzie funkcją określoną na przedziale i całkowalną
na każdym skooczonym przedziale Granicę
nazywamy całką niewłaściwą funkcji na przedziale
nieograniczonym i oznaczamy symbolem
Całka niewłaściwa jest zbieżna, gdy rozważana granica jest
właściwa, natomiast całka ta jest rozbieżna, gdy rozważana granica
jest niewłaściwa ( ) albo nie istnieje.
II. Niech będzie funkcją określoną na przedziale całkowalną
na każdym skooczonym przedziale Granicę
nazywamy całką niewłaściwą funkcji na przedziale
nieograniczonym i oznaczamy symbolem
Zbieżnośd oraz rozbieżnośd rozważanej całki niewłaściwej określamy
analogicznie, jak poprzednio.
A
a
A
dx
x
f
)
(
lim
a
dx
x
f
)
(
b
B
B
dx
x
f
)
(
lim
.
, A
a
f
f
.
,b
B
f
b
,
(
)
,
a
)
,
a
.
)
(
a
dx
x
f
f
b
,
(
b
dx
x
f
)
(
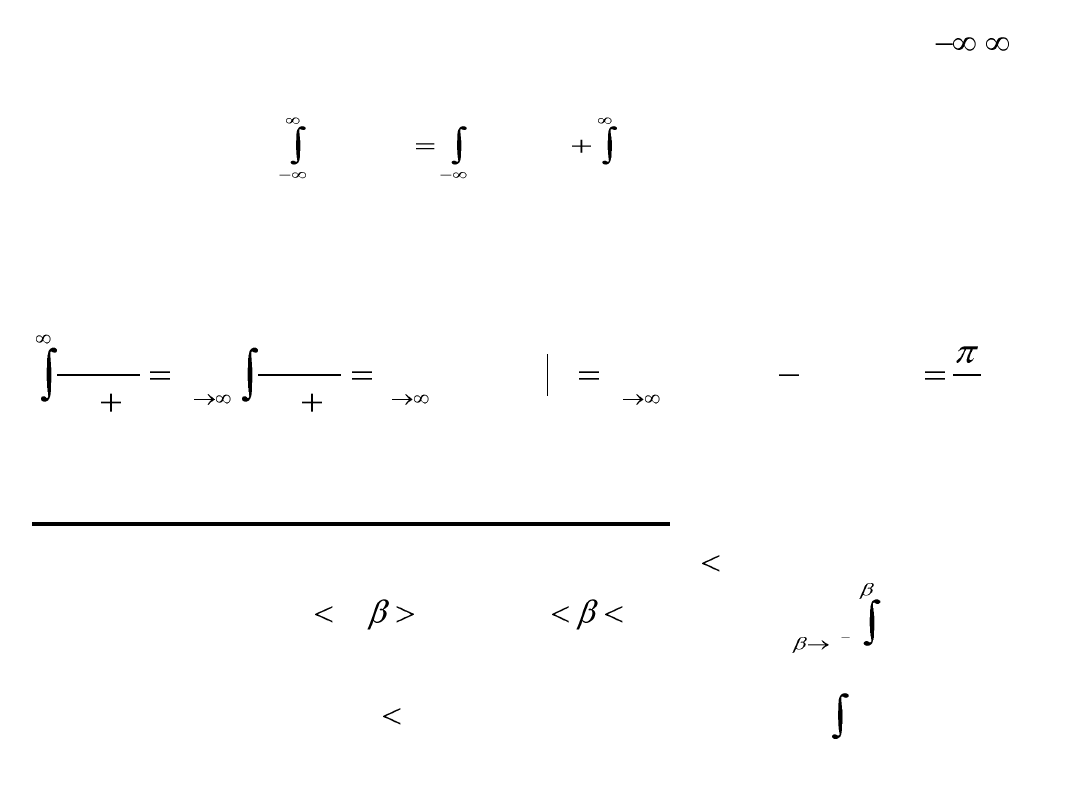
III. Całka niewłaściwa funkcji określonej na przedziale
i całkowalnej na każdym skooczonym przedziale jest zdefiniowana
następująco:
Całkę tę uważamy za zbieżną jedynie wtedy, gdy obie całki
niewłaściwe występujące po prawej stronie równości są zbieżne.
Przykład
więc jest to całka niewłaściwa zbieżna.
Całki niewłaściwe z funkcji nieograniczonej
I. Niech będzie funkcją nieograniczoną na i całkowalną na
każdym przedziale gdzie Granicę
nazywamy całką niewłaściwą nieograniczonej
funkcji na przedziale i oznaczamy symbolem
Zbieżnośd i rozbieżnośd tej całki określamy tak, jak poprzednio.
.
)
(
)
(
)
(
c
c
def
dx
x
f
dx
x
f
dx
x
f
,
2
)
0
(
lim
]
[
lim
1
lim
1
0
0
2
0
2
arctg
arctgA
arctgx
x
dx
x
dx
A
A
A
A
A
a
b
dx
x
f
,
)
(
lim
f
f
)
,b
a
,
,
a
.
b
a
)
,
(
f
)
,b
a
b
a
dx
x
f
.
)
(
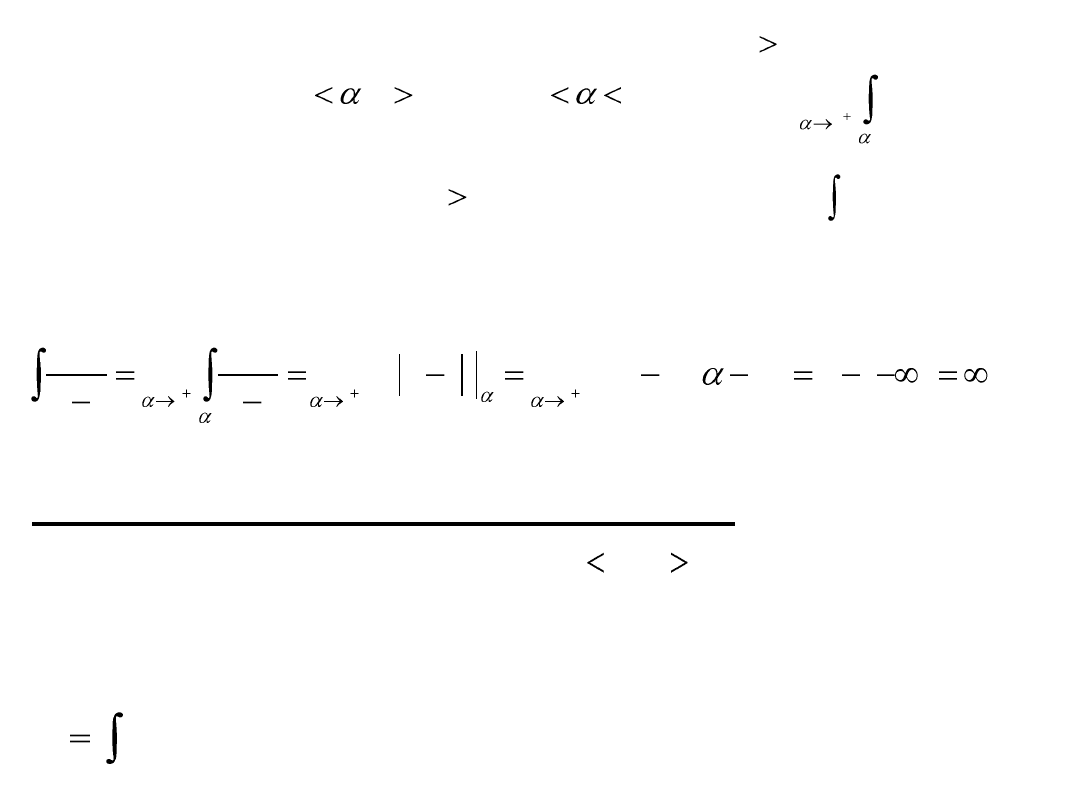
II. Niech będzie funkcją nieograniczoną na i całkowalną na
każdym przedziale gdzie Granicę
nazywamy całką niewłaściwą nieograniczonej
funkcji na przedziale i oznaczamy symbolem
Zbieżnośd i rozbieżnośd tej całki określamy tak, jak poprzednio.
Przykład
a więc jest to całka rozbieżna.
Przykład interpretacji fizycznej całki oznaczonej
Droga przebyta w przedziale czasu ruchem
prostoliniowym z prędkością ( co do modułu) równą jest
całką oznaczoną z tej prędkości na rozważanym przedziale , czyli
b
a
dx
x
f
,
)
(
lim
,
)
(
0
))
1
ln(
1
(ln
lim
]
1
[ln
lim
1
lim
1
1
2
1
2
1
2
1
x
x
dx
x
dx
.
)
(
0
T
t
dt
t
v
s
b
a,
(
f
,
,b
.
b
a
T
t ,
0
)
(t
v
s
f
b
a,
(
b
a
dx
x
f
.
)
(
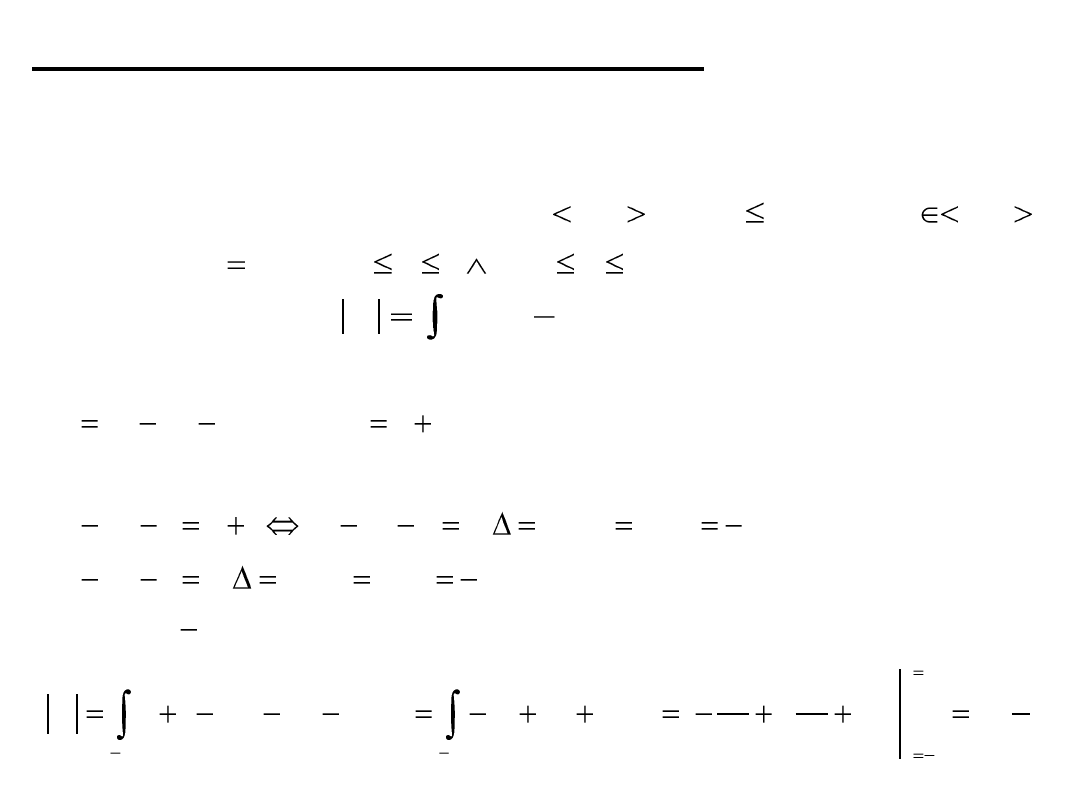
Zastosowania geometryczne całki oznaczonej
Pole figury płaskiej
Twierdzenie
Jeżeli funkcje oraz są ciągłe na
natomiast to pole figury
wyraża się wzorem
Przykład. Obliczyd pole figury ograniczonej liniami
Rozwiązanie
.
1
oraz
3
2
2
x
y
x
x
y
.
6
5
20
]
4
2
3
3
[
)
4
3
(
)]
3
2
(
1
[
)
0
,
1
(
),
5
,
4
(
1
,
3
,
16
,
0
3
2
1
,
4
,
25
,
0
4
3
1
3
2
4
1
2
3
2
4
1
2
4
1
2
1
2
1
2
2
1
2
2
x
x
x
x
x
dx
x
x
dx
x
x
x
D
P
P
x
x
x
x
x
x
x
x
x
x
x
.
)]
(
)
(
[
b
a
dx
x
g
x
f
D
b
a
x
x
f
x
g
b
a
,
dla
)
(
)
(
i
,
f
g
,
)}
(
)
(
:
)
,
{(
x
f
y
x
g
b
x
a
y
x
D
D
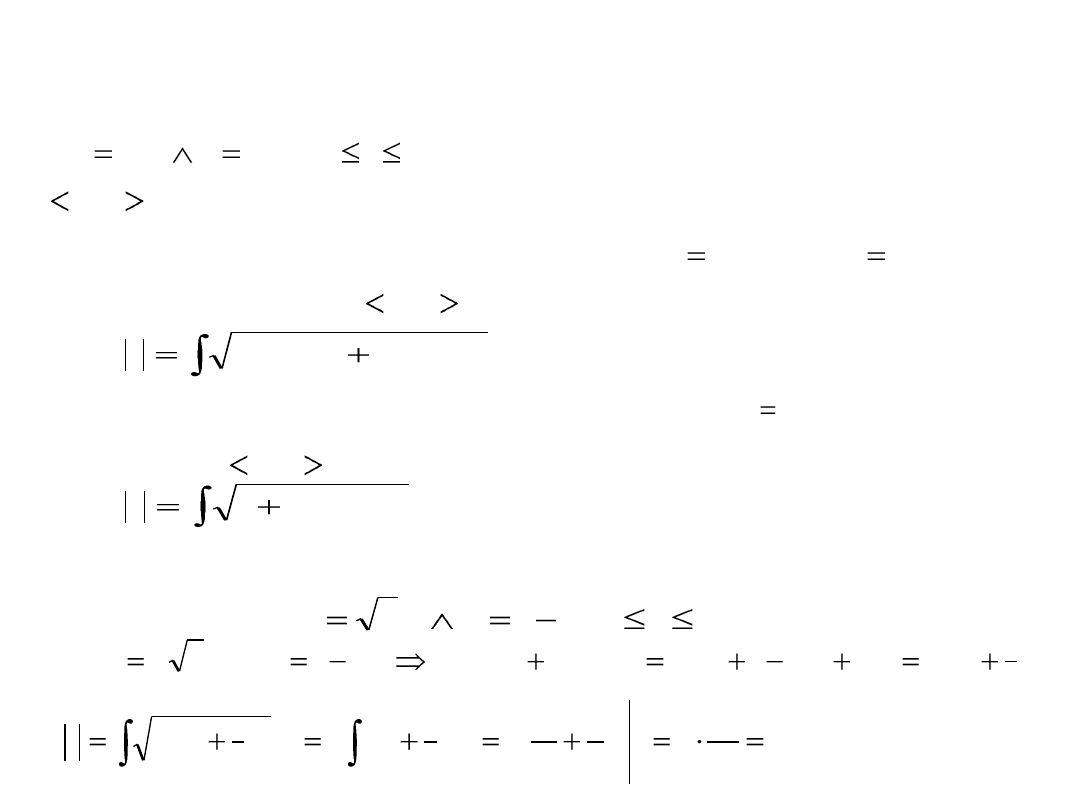
Długośd łuku linii
Twierdzenie. Jeżeli łuk jest dany równaniami parametrycznymi
i przy tym różnym punktom z przedziału
odpowiadają różne punkty tego łuku oraz łuk nie ma
punktów wielokrotnych natomiast funkcje są
klasy na przedziale to długośd łuku wyraża się wzorem
Twierdzenie Jeżeli łuk jest wykresem funkcji klasy
na przedziale to jego długośd wyraża się wzorem
Przykład Obliczyd długośd krzywej danej równaniami
parametrycznymi Rozwiązanie:
1
C
.
)]
(
'
[
)]
(
'
[
2
2
dt
t
y
t
x
l
b
a
1
C
.
)]
(
'
[
1
2
dt
t
f
l
b
a
.
2
0
,
3
3
2
t
t
t
y
t
x
.
10
3
10
3
]
3
1
3
[
3
)
(
3
)
(
9
)
(
9
9
6
1
12
)]
(
'
[
)]
(
'
[
3
1
)
(
'
,
3
2
)
(
'
2
0
3
2
0
3
1
2
2
0
2
3
1
2
2
3
1
2
4
2
2
2
2
2
t
t
dt
t
dt
t
l
t
t
t
t
t
y
t
x
t
t
y
t
t
x
,
),
(
)
(
:
b
t
a
t
y
y
t
x
x
l
)
(
oraz
)
(
t
y
y
t
x
x
b
a,
l
,
,b
a
l
l
,
,b
a
)
(x
f
y
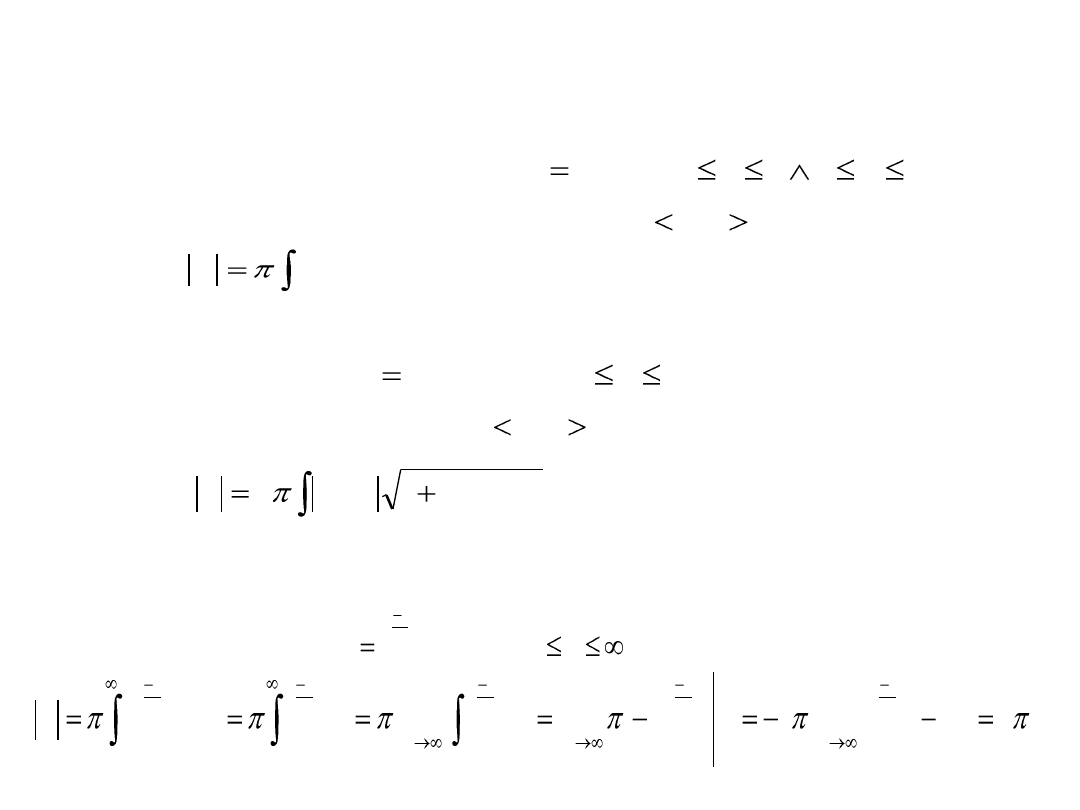
Objętośd i pole powierzchni brył obrotowych
Twierdzenie. Objętośd bryły powstałej w wyniku obrotu wokół
osi trapezu krzywoliniowego
gdzie jest funkcją ciągłą na przedziale wyraża się
wzorem
Twierdzenie. Pole powierzchni powstałej w wyniku obrotu
wokół osi krzywej natomiast jest
funkcją klasy na przedziale wyraża się wzorem
Przykład. Obliczyd objętośd bryły powstałej przez obrót wokół osi
linii o równaniu
b
a
dx
x
f
V
.
)
(
2
1
C
.
)]
(
'
[
1
)
(
2
2
dx
x
f
x
f
S
b
a
.
0
gdzie
,
4
1
x
e
y
x
.
2
]
[
lim
2
]
2
[
lim
lim
)
(
0
2
1
0
2
1
0
0
2
1
2
1
2
0
4
1
e
e
e
dx
e
dx
e
dx
e
V
M
M
M
x
M
M
x
M
x
x
b
a,
f
V
Ox
Ox
Ox
S
f
b
a,
)},
(
0
:
)
,
{(
x
f
y
b
x
a
y
x
D
,
gdzie
),
(
b
x
a
x
f
y
Wyszukiwarka
Podobne podstrony:
ZiIP Wykład 7 Całka nieoznaczona
ZiIP Wyklad 10 Macierze
10 11 wyklad calka oznaczonaid Nieznany (2)
9 wyklad calka nieoznaczona
Ekonomika- wykład 6, studia AGH, ZiIP, Inżynier, Ekonomika, Wykłady
Filozofia wykład 2, Studia, ZiIP, SEMESTR V, Fizozofia
zasady zaliczeń PP IG, Politechnika Białostocka, ZiIP (PB), Semestr 1, Podstawy programowania, Progr
Filozofia wykład 1, Studia, ZiIP, SEMESTR V, Fizozofia
Makroekonomia - Wykład 5, Studia, ZiIP, SEMESTR II, Makroekonomia
zaliczenie wykladu gr B ściąga, Zarządzanie i Inżynieria Produkcji Politechnika Lubleska, metrologia
wyklad2 -przekroje ZiIP IM [tryb zgodnosci]
Makroekonomia - Wykład 6, Studia, ZiIP, SEMESTR II, Makroekonomia
Metro-wyklad (cz.2 gr. B), ZiIP, ZiIP, R2, SI, Metrologia
więcej podobnych podstron