Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
92
42
Całka nieoznaczona
Całkowanie jest czynno ci odwrotn do ró niczkowania. Daje odpowied na pytanie, czego to jest pochod-
na?” Całkowanie przypomina wyszukiwanie „pochodzenia” funkcji, podczas gdy ró niczkowanie polega na znajdowaniu
„potomstwa” funkcji.
Funkcj
)
(x
F
tak , e
)
(
)
(
x
f
x
F
=
′
dla x, w których funkcja
)
(x
f
jest okre lona, nazywamy
funkcj pierwotn
funk-
cji
)
(x
f
. Zauwa my, e je li
)
(x
F
jest funkcj pierwotn funkcji
)
(x
f
, to funkcja
C
x
F
+
)
(
, gdzie C jest stał , jest te
funkcj pierwotn funkcji
)
(x
f
. Zbiór wszystkich funkcji pierwotnych funkcji
)
(x
f
oznaczamy symbolem
dx
x
f )
(
(całka f od x, dx) i nazywamy
całk nieoznaczon
funkcji
)
(x
f
.
C
x
F
dx
x
f
+
=
)
(
)
(
⇔
)
(
)
(
x
f
x
F
=
′
Wyznaczanie całki nieoznaczonej nazywamy
całkowaniem
funkcji.
Przykłady.
C
x
dx
x
+
=
2
2
;
C
x
dx
x
+
−
= cos
sin
;
C
x
dx
x
+
=
)
5
sin(
)
5
cos(
5
1
.
43
Podstawowe wzory całek
1.
C
x
dx
x
k
k
k
+
=
+
+
1
1
1
,
1
−
≠
k
;
2.
C
x
dx
x
+
= ln
1
;
3.
C
a
dx
a
x
a
x
+
=
ln
1
;
4.
C
e
dx
e
x
x
+
=
β
β
β
1
;
5.
C
x
dx
x
+
α
=
α
α
)
sin(
)
cos(
1
;
6.
C
x
dx
x
+
α
−
=
α
α
)
cos(
)
sin(
1
;
7.
C
x
dx
x
+
= tg
2
cos
1
;
8.
C
x
dx
x
+
−
= ctg
2
sin
1
;
9.
C
x
a
dx
a
x
+
=
−
|
|
2
2
arcsin
;
10.
C
a
x
dx
a
x
a
+
=
+
arctg
1
2
2
44
Podstawowe reguły całkowania
1.
C
x
F
dx
x
F
+
=
′
)
(
)
(
− w wyniku ró niczkowania, a nast pnie całkowania otrzymujemy t sam funkcj z dokład-
no ci do stałej C.
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
93
2.
)
(
)
(
)
)
(
(
x
f
x
F
dx
x
f
=
′
=
′
− w wyniku całkowania, a nast pnie ró niczkowania otrzymujemy t sam funkcj .
3.
⋅
α
=
⋅
α
dx
x
f
dx
x
f
)
(
)
(
− stał α mo na wył czy przed znak całki,
4.
±
=
±
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)]
(
)
(
[
− całka sumy (ró nicy) jest równa sumie (ró nicy) całek.
5. Je eli funkcj podcałkow daje si zapisa w postaci iloczynu funkcji zło onej
)]
(
[ x
g
f
i pochodnej funkcji we-
wn trznej
)
(x
g
, to prawdziwy jest wzór
=
′
⋅
dt
t
f
dx
x
g
x
g
f
)
(
)
(
)]
(
[
, gdzie
)
(x
g
t
=
,
który opisuje
całkowanie przez podstawienie
.
6. Je eli funkcj podcałkow daje si zapisa w postaci iloczynu jednej funkcji
)
(x
f
i pochodnej innej funkcji
)
(x
g
, to
prawdziwy jest wzór
⋅
′
−
⋅
=
′
⋅
dx
x
g
x
f
x
g
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
)
(
)
(
,
który opisuje metod
całkowania przez cz ci
.
Przykład 1
C
x
dx
x
+
=
6
6
1
5
Zastosowali my wzór
C
x
dx
x
k
k
k
+
=
+
+
1
1
1
.
Przykład 2
C
x
x
C
x
dx
x
dx
x
+
=
+
=
=
4
5
4
5
4
4
4
5
4
1
Zastosowali my wzór
C
x
dx
x
k
k
k
+
=
+
+
1
1
1
.
Przykład 3
C
dx
x
x
+
=
3
ln
3
3
Zastosowali my wzór
C
a
dx
a
x
a
x
+
=
ln
1
.
Przykład 4
(
)
C
x
C
x
xdx
dx
dx
x
x
x
x
x
+
−
=
+
−
+
=
+
=
+
cos
3
2
ln
2
cos
3
2
ln
2
sin
3
2
)
sin
3
2
(
Przykład 5
C
x
x
dx
+
=
−
5
arcsin
5
2
Zastosowali my wzór
C
x
a
dx
a
x
+
=
−
|
|
2
2
arcsin
.
Przykład 6
Zilustrujemy metod całkowania przez cz ci.
=
dx
x
x cos
x
v
u
x
v
x
u
sin
1
cos
=
=
′
=
′
=
+
+
=
−
=
C
x
x
x
xdx
x
x
cos
sin
sin
sin
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
94
Przykład 7
=
−
dx
xe
x
x
x
e
v
u
e
v
x
u
−
−
−
=
=
′
=
′
=
1
C
x
e
C
e
xe
dx
e
xe
x
x
x
x
x
+
+
−
=
+
−
−
=
+
−
=
−
−
−
−
−
)
1
(
Przykład 8
Zilustrujemy metod całkowania przez podstawienie.
=
−
dx
x
20
)
1
2
(
dt
dx
t
x
dx
dt
2
1
2
1
2
=
=
=
−
C
t
dt
t
+
⋅
=
=
21
21
1
2
1
20
2
1
C
x
+
+
=
21
42
1
)
1
2
(
Przykład 9
=
+
5
2
)
7
(x
dx
x
dt
dx
x
x
t
x
dx
dt
2
1
2
2
7
=
=
=
+
C
t
dt
t
t
dt
+
−
=
=
=
−
−
4
4
1
2
1
5
2
1
5
2
1
)
(
C
x
+
+
−
=
4
2
)
7
(
8
1
Przykład 10
=
dt
t
t
2
sin
dx
dt
x
t
x
t
dt
dx
2
1
2
2
=
=
=
C
x
C
t
dx
x
+
−
=
+
−
=
=
2
2
1
2
1
2
1
cos
cos
sin
Przykład 11
=
x
dx
3
cos
2
2
dt
dx
t
x
dx
dt
3
1
3
3
=
=
=
C
x
C
t
t
dt
+
=
+
=
=
3
cos
6
1
6
1
2
6
1
tg
tg
Przykład 12
=
+ k
x
dx
2
dt
dx
x
t
x
k
x
t
k
t
t
k
t
2
2
2
2
2
2
+
−
=
=
−
=
+
C
k
x
x
C
t
t
dt
+
+
+
=
+
−
=
−
=
2
ln
|
|
ln
Przykład 13
C
x
x
dx
+
+
=
+
7
ln
2
7
2
Zastosowali my wzór
C
x
f
dx
x
f
x
f
+
=
′
)
(
ln
)
(
)
(
.
Przykład 14
+
−
dx
x
x
1
1
2
2
Jest to całka z funkcji wymiernej (iloraz wielomianów). Poniewa stopie licznika pokrywa si ze stopniem mianownika,
wi c funkcj pod znakiem całki przedstawiamy w postaci sumy wielomianu i funkcji wymiernej wła ciwej:
1
2
1
1
2
1
1
1
2
2
2
2
2
+
−
=
+
−
+
=
+
−
x
x
x
x
x
Zatem
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
95
C
x
x
dx
x
dx
dx
x
dx
x
x
+
−
=
+
−
=
+
−
=
+
−
arctg
2
1
1
2
)
1
2
1
(
1
1
2
2
2
2
.
Przy obliczaniu drugiej całki korzystali my ze wzoru
C
a
x
dx
a
x
a
+
=
+
arctg
1
2
2
.
45
Równania ró niczkowe
Definicja.
Równanie o niewiadomej
)
(x
y
y
=
postaci
)]
(
),
(
,
[
x
y
x
y
x
F
′
, gdzie F jest funkcj trzech zmiennych okre lon i ci gł na
pewnym obszarze, nazywamy
równaniem ró niczkowym
zwyczajnym pierwszego rz du.
Równaniem ró niczkowym
zwyczajnym pierwszego rz du w postaci jawnej (rozwikłanej) nazywa si równanie
)]
(
,
[
)
(
x
y
x
f
x
y
=
′
.
Rozwi zaniem
ogólnym
tego równania nazywa si zbiór funkcji
)
(x
y
, z których ka da spełnia to równanie. Jest ono
postaci
)
,
( C
x
y
y
=
, gdzie
R
∈
C
.
Ka d funkcj postaci
)
,
(
0
C
x
y
, gdzie
0
C jest ustalon stał spełniaj c to równanie, nazywa si
rozwi zaniem szcze-
gólnym
. Rozwi zanie ogólne jest zbiorem wszystkich rozwi za szczególnych.
Przykład 15
Rozwi za równanie ró niczkowe
x
x
x
y
−
+
=
′
2
1
.
Rozwi zanie
Równanie to jest równaniem do bezpo redniego całkowania.
−
+
=
dx
x
x
x
y
2
1
Jest to całka z funkcji wymiernej wła ciwej (st. L < st. M). Poniewa mianownik jest rozkładalny na iloczyn czynników,
wi c dokonujemy rozkładu funkcji podcałkowej na sum ułamków prostych:
)
1
(
)
(
)
1
(
)
1
(
1
)
1
(
1
1
2
−
−
+
=
−
+
−
=
−
+
=
−
+
=
−
+
x
x
A
x
B
A
x
x
Bx
x
A
x
B
x
A
x
x
x
x
x
x
Współczynniki A, B wyznaczamy z to samo ci
A
x
B
A
x
−
+
=
+
)
(
1
(przyrównuj c współczynniki przy jednakowych pot gach):
=
−
=
+
.
1
,
1
A
B
A
Dlatego
1
2
1
1
2
−
+
−
=
−
+
x
x
x
x
x
i ostatecznie
C
x
x
dx
x
dx
x
dx
x
x
x
y
+
−
+
−
=
−
+
−
=
−
+
=
|
1
|
ln
2
|
|
ln
1
1
2
1
1
2
(- Rozwi zanie ogólne)
Przykład 16
Rozwi za równanie ró niczkowe
1
1
2
2
−
+
=
′
x
x
y
.
Rozwi zanie:
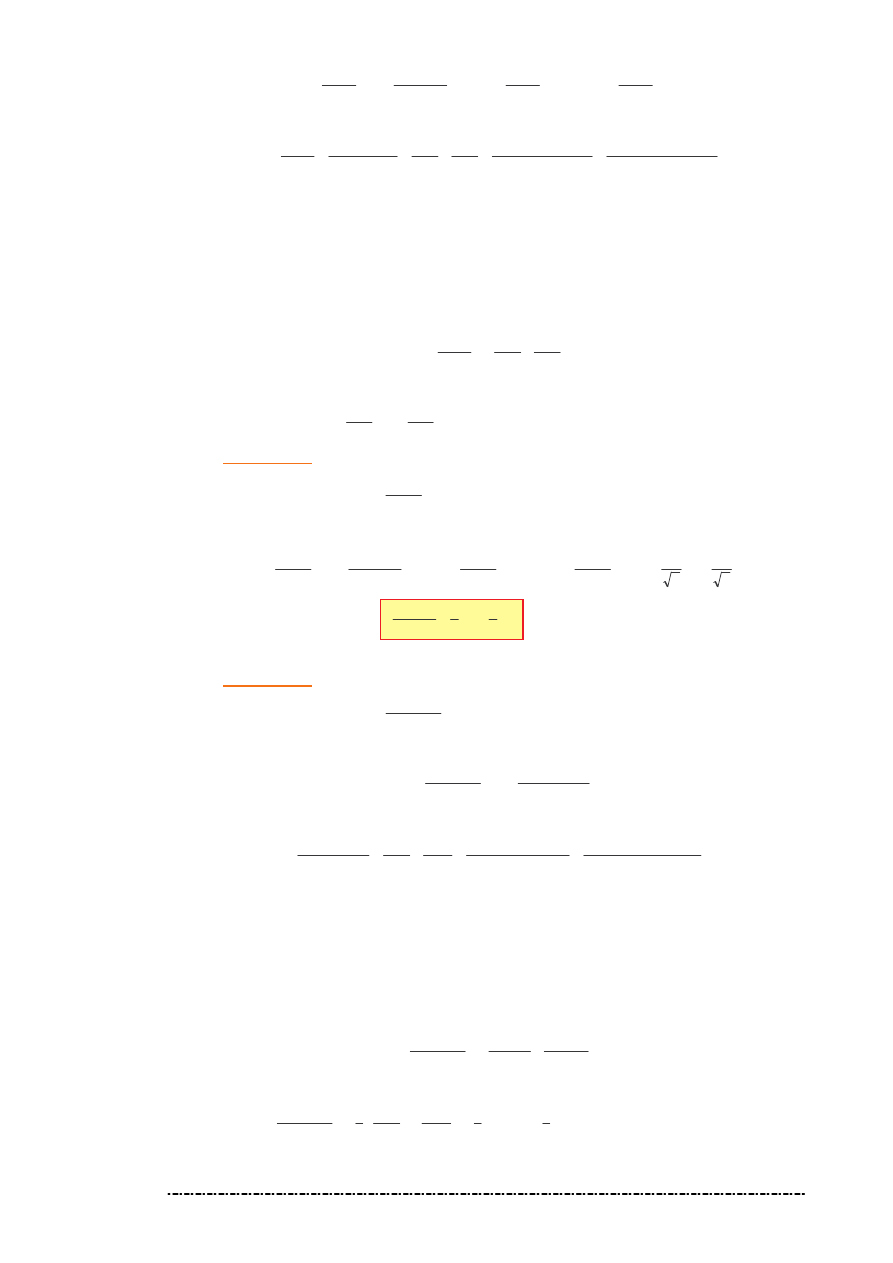
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
96
(???)
1
2
)
1
2
1
(
1
2
1
1
1
2
2
2
2
2
2
=
−
+
=
−
+
=
−
+
−
=
−
+
=
dx
x
dx
dx
x
dx
x
x
dx
x
x
y
Do drugiej całki stosujemy rozkład funkcji wymiernej wła ciwej na sum ułamków prostych.
)
1
)(
1
(
)
(
)
(
)
1
)(
1
(
)
1
(
)
1
(
1
1
)
1
)(
1
(
2
1
2
2
−
+
+
−
+
+
=
−
+
+
+
−
=
−
+
+
=
−
+
=
−
x
x
B
A
x
B
A
x
x
x
B
x
A
x
B
x
A
x
x
x
Współczynniki A, B wyznaczamy z to samo ci
)
(
)
(
2
B
A
x
B
A
+
−
+
+
=
(przyrównuj c współczynniki przy jednakowych pot gach):
=
+
−
=
+
.
2
,
0
B
A
B
A
Dlatego
1
1
1
1
1
2
2
−
+
+
−
=
−
x
x
x
i ostatecznie
C
x
x
x
dx
x
dx
x
dx
+
−
+
+
−
=
−
+
+
−
=
|
1
|
ln
|
1
|
ln
1
1
1
1
(???)
(- Rozwi zanie ogólne)
Przykład 17
Rozwi za równanie ró niczkowe
2
1
2
2
+
+
=
′
x
x
y
.
Rozwi zanie:
=
+
−
=
+
−
=
+
−
+
=
+
+
=
dx
x
dx
dx
x
dx
x
x
dx
x
x
y
2
1
)
2
1
1
(
2
1
2
2
1
2
2
2
2
2
2
C
x
x
+
−
2
2
1
arctg
Do drugiej całki zastosowali my wzór
C
a
x
dx
a
x
a
+
=
+
arctg
1
2
2
.
Przykład 18
Rozwi za równanie ró niczkowe
2
1
2
−
−
=
′
x
x
y
.
Rozwi zanie:
dx
x
x
dx
x
x
y
−
+
=
−
−
=
)
2
)(
1
(
1
2
1
2
Do drugiej całki stosujemy rozkład funkcji wymiernej wła ciwej na sum ułamków prostych.
)
2
)(
1
(
)
2
(
)
(
)
2
)(
1
(
)
1
(
)
2
(
2
1
)
2
)(
1
(
1
−
+
+
−
+
+
=
−
+
+
+
−
=
−
+
+
=
−
+
x
x
B
A
x
B
A
x
x
x
B
x
A
x
B
x
A
x
x
Współczynniki A, B wyznaczamy z to samo ci
)
2
(
)
(
1
B
A
x
B
A
+
−
+
+
=
(przyrównuj c współczynniki przy jednakowych pot gach):
=
+
−
=
+
.
1
2
,
0
B
A
B
A
Dlatego
)
2
(
3
1
)
1
(
3
1
2
1
2
−
+
+
−
=
−
−
x
x
x
x
i ostatecznie
C
x
x
x
dx
x
dx
x
x
dx
y
+
−
+
+
−
=
−
+
+
−
=
−
−
=
|
2
|
ln
|
1
|
ln
2
1
2
3
1
3
1
3
1
2
(- Rozwi zanie ogólne)
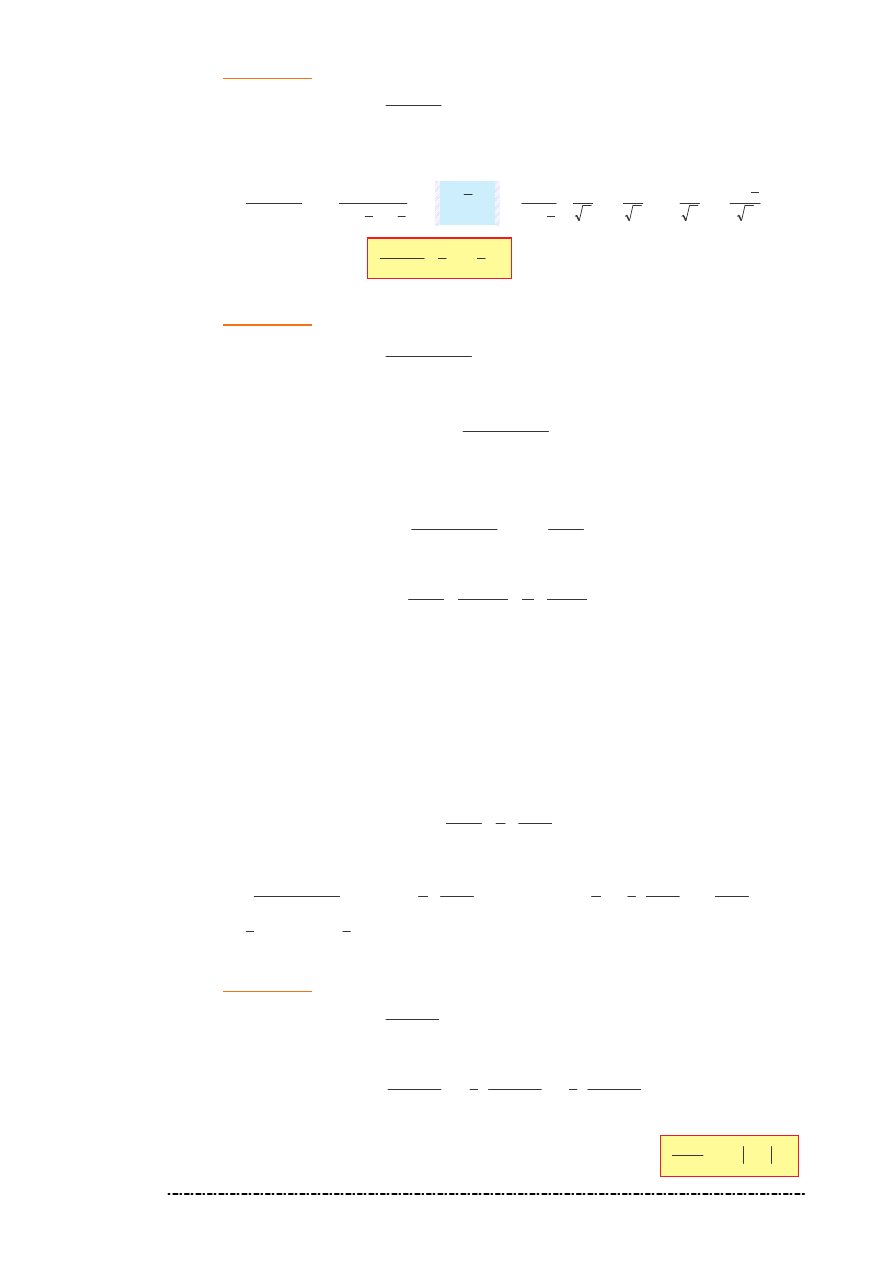
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
97
Przykład 19
Rozwi za równanie ró niczkowe
2
1
2
+
−
=
′
x
x
y
.
Rozwi zanie:
=
+
−
=
+
−
=
dx
x
dx
x
x
y
4
7
2
2
1
2
)
(
1
2
1
dt
dx
t
x
=
=
−
2
1
C
x
C
t
t
dt
+
−
=
+
=
+
=
7
7
2
7
7
2
2
1
4
7
2
arctg
arctg
Do obliczenia całki stosujemy wzór
C
a
x
dx
a
x
a
+
=
+
arctg
1
2
2
.
Przykład 20
Rozwi za równanie ró niczkowe
x
x
x
x
x
y
+
+
+
−
=
′
3
2
3
4
1
.
Rozwi zanie:
dx
x
x
x
x
x
y
+
+
+
−
=
3
2
3
4
1
Poniewa wielomian wyst puj cy w mianowniku ma stopie mniejszy ni wielomian wyst puj cy w liczniku, wi c w
wyniku dzielenia otrzymamy
x
x
x
x
x
x
x
x
x
+
+
+
−
=
+
+
+
−
3
3
2
3
4
1
1
1
.
Z kolei
1
)
1
(
1
1
2
2
3
+
+
+
=
+
+
=
+
+
x
C
Bx
x
A
x
x
x
x
x
x
.
Współczynniki A, B i C wyznaczamy z to samo ci
x
C
Bx
x
A
x
)
(
)
1
(
1
2
+
+
+
=
+
(przyrównuj c współczynniki przy jednakowych pot gach):
=
=
=
+
1
,
1
,
0
A
C
B
A
Dlatego
1
1
1
1
2
3
+
−
−
=
+
+
x
x
x
x
x
x
i ostatecznie
C
x
x
x
x
x
dx
x
dx
x
x
dx
x
dx
dx
x
dx
x
x
x
x
dx
x
x
x
x
x
y
+
+
+
−
+
−
=
=
+
+
+
−
+
−
=
+
−
−
+
−
=
+
+
+
−
=
arctg
)
1
ln(
|
|
ln
1
1
1
2
1
1
1
1
1
1
2
2
1
2
2
1
2
2
2
1
2
3
2
3
4
Przykład 21
Rozwi za równanie ró niczkowe
1
1
3
2
+
+
−
=
′
x
x
x
y
.
Rozwi zanie:
)
2
(
2
2
5
)
1
(
2
2
3
2
1
1
1
2
1
1
3
+
+
−
+
+
+
=
+
+
−
=
x
x
dx
dx
x
x
x
dx
x
x
x
y
W całce (1) w liczniku jest pochodna mianownika; do jej obliczenia korzystamy ze wzoru
C
x
f
dx
x
f
x
f
+
=
′
)
(
ln
)
(
)
(
.

Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
98
Zatem
1
2
2
1
ln
1
1
2
)
1
(
C
x
x
dx
x
x
x
+
+
+
=
+
+
+
=
Do całki (2) stosujemy posta kanoniczn trójmianu kwadratowego.
=
+
+
=
+
+
=
4
3
2
2
1
2
)
(
1
)
2
(
x
dx
x
x
dx
dt
dx
t
x
=
=
+
2
1
=
+
=
4
3
2
t
dt
=
+
2
3
2
3
2
C
t
arctg
2
3
1
2
3
2
C
x
+
+
arctg
Piszemy odpowied :
=
+
+
⋅
−
+
+
=
+
+
−
C
x
x
x
dx
x
x
x
3
1
2
1
ln
1
1
3
3
2
2
5
2
2
3
2
arctg
C
x
x
x
+
+
−
+
+
3
1
2
1
ln
3
5
2
2
3
arctg
46
Równania ró niczkowe o zmiennych rozdzielonych
Równanie ró niczkowe, które mo na zapisa w postaci
)
(
)
(
y
h
x
g
y
⋅
=
′
nazywamy równaniem o zmiennych rozdzielo-
nych. Je eli funkcje
)
(x
g
i
)
(y
h
s ci głe, przy czym
0
)
(
≠
y
h
dla ka dego y , to całka równania ró niczkowego o
zmiennych rozdzielonych dana jest wzorem:
+
=
C
dx
x
g
y
h
dy
)
(
)
(
, gdzie C jest dowolna stał rzeczywist .
Przykład 22
Rozwi za równanie ró niczkowe
0
)
(
)
(
2
2
2
2
=
−
+
+
dy
y
x
x
dx
y
xy
.
Rozwi zanie:
Jest to równanie, w którym zmienne daj si rozdzieli . Aby rozdzieli zmienne, wystarczy wykona operacje:
dy
x
y
dx
y
x
2
2
)
1
(
)
1
(
−
=
+
,
dy
y
y
dx
x
x
2
2
1
1
−
=
+
.
Po rozdzieleniu zmiennych całkujemy obie strony równania.
−
=
+
dy
y
y
dx
x
x
2
2
1
1
,
C
y
y
x
x
+
+
=
−
1
ln
1
ln
.
Przykład 23
Rozwi za równanie ró niczkowe
dy
xy
dx
y
=
+
)
1
(
2
.
Rozwi zanie:
2
1 y
dy
y
x
dx
+
=
,
Po rozdzieleniu zmiennych całkujemy obie strony równania.
+
=
+
=
2
2
1
2
1
1
y
dy
y
y
dy
y
x
dx
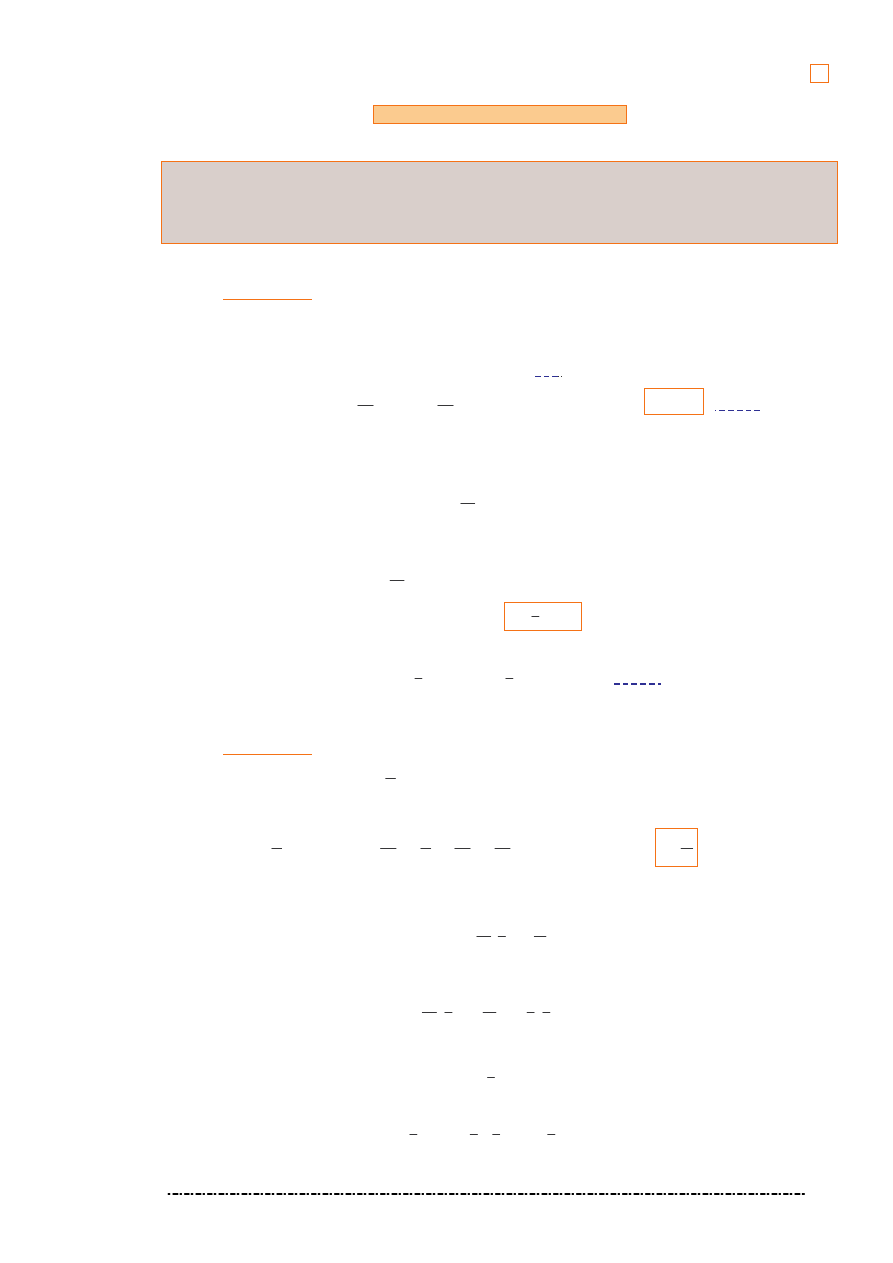
( )
2
2
1
1
ln
ln
y
C
x
+
=
+
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
99
47
Równanie ró niczkowe liniowe
Równanie ró niczkowe, które mo na zapisa w postaci
)
(
)
(
x
q
y
x
p
y
=
+
′
,
gdzie
)
(x
p
i
)
(x
q
s funkcjami ci głymi,
nazywamy
równaniem liniowym
pierwszego rz du. Je eli
0
)
(
≡/
x
q
, to równanie nazywamy
liniowym niejednorod-
nym
. W przeciwnym przypadku nazywamy je
równaniem liniowym jednorodnym
.
Przykład 24
Rozwi za równanie ró niczkowe
2
2
2
2
x
e
x
xy
y
−
=
+
′
.
Rozwi zanie.
Etap 1°°°°
Tworzymy i rozwi zujemy równanie liniowe jednorodne (
RLJ
)
0
2
=
+
′
xy
y
→
xy
dx
dy
y
2
−
=
=
′
→
dx
x
y
dy
⋅
−
= 2
→
C
x
y
ln
ln
2
+
−
=
→
2
x
Ce
y
−
=
-
RORLJ
Etap 2°°°°
Uzmienniamy stał metod Lagrange’a. Ró niczkujemy RORLJ (rozwi zanie ogólne równania liniowego jedno-
rodnego) przy zała eniu
)
(x
C
C
=
.
2
2
2
x
x
dx
dC
Cxe
e
y
−
−
−
=
′
.
Wracamy do wyj ciowego równania
2
2
2
2
2
2
2
2
x
y
x
y
x
x
dx
dC
e
x
Ce
x
Cxe
e
−
−
′
−
−
=
+
−
dx
x
dC
2
2
=
→
K
x
C
+
=
3
3
2
Kładziemy wyliczone C do RORLJ
2
2
2
2
3
3
2
3
3
2
)
(
x
x
x
x
Ke
e
x
e
K
x
Ce
y
−
−
−
−
+
=
+
=
=
-
RORLN
Przykład 25
Rozwi za równanie ró niczkowe
2
x
x
y
y
=
+
′
.
Rozwi zanie:
=
+
′
x
y
y
-
RLJ
→
x
y
dx
dy
y
−
=
=
′
→
x
dx
y
dy
−
=
→
C
x
y
ln
ln
ln
+
−
=
→
x
C
y
=
-
RORLJ
Uzmienniamy stał .
Ró niczkujemy RORLJ
2
1
1
x
x
dx
dC
C
y
⋅
−
⋅
=
′
Wracamy do wyj ciowego równania
2
1
1
1
1
2
x
C
C
x
y
x
y
x
x
dx
dC
=
⋅
⋅
+
⋅
−
⋅
′
dx
x
dC
3
=
K
x
C
+
=
4
4
1
Kładziemy wyliczone C do RORLJ
x
x
K
x
K
x
y
1
3
4
1
1
4
4
1
)
(
⋅
+
=
⋅
+
=
-
RORLN
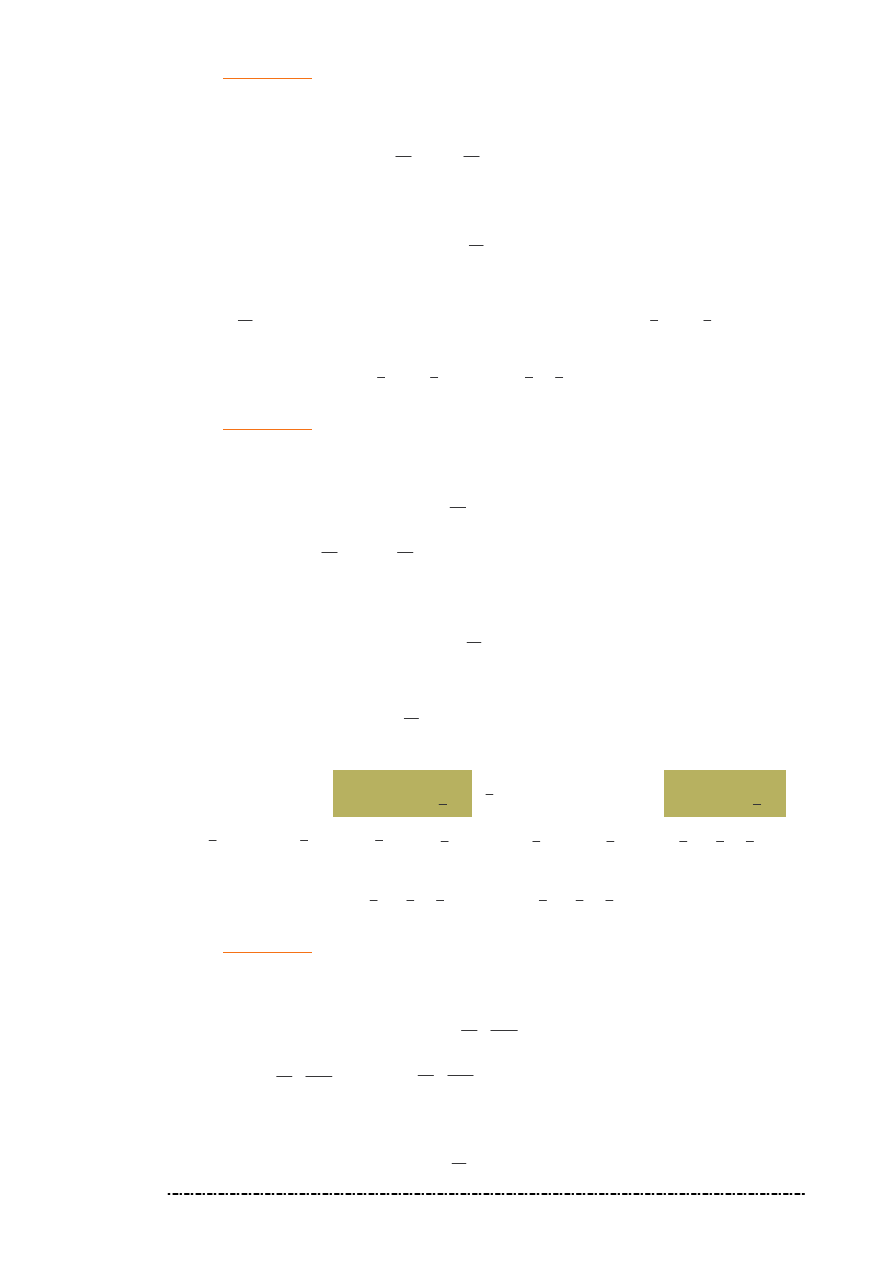
Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
100
Przykład 26
Rozwi za równanie ró niczkowe
x
e
y
y
x
−
=
−
′ 2
.
Rozwi zanie:
0
2
=
−
′
y
y
-
RLJ
→
y
dx
dy
y
2
=
=
′
→
dx
y
dy
2
=
→
C
x
y
ln
2
ln
+
=
→
x
Ce
y
2
=
-
RORLJ
Uzmienniamy stał .
Ró niczkujemy RORLJ
x
x
dx
dC
Cxe
e
y
2
2
2
+
=
′
Wracamy do wyj ciowego równania
x
e
x
Ce
Cxe
e
x
y
x
y
x
x
dx
dC
−
=
−
+
′
2
2
2
2
2
→
dx
xe
e
dC
x
x
)
(
2
−
−
−
=
→
K
e
xe
e
C
x
x
x
+
+
+
−
=
−
−
−
2
4
1
2
2
1
Kładziemy wyliczone C do RORLJ
x
x
x
x
x
x
Ke
e
x
e
K
e
xe
e
y
2
4
1
2
1
2
2
4
1
2
2
1
)
(
+
−
+
=
+
+
+
−
=
−
−
−
-
RORLN
Przykład 27
Rozwi za równanie ró niczkowe
dx
y
x
x
dy
)
2
2
(
2
−
+
=
.
Rozwi zanie:
y
x
x
dx
dy
2
2
2
−
+
=
y
dx
dy
y
2
−
=
=
′
→
dx
y
dy
2
−
=
→
C
x
y
ln
2
ln
+
−
=
→
x
Ce
y
2
−
=
-
RORLJ
Uzmienniamy stał .
Ró niczkujemy RORLJ
x
x
dx
dC
Ce
e
y
2
2
2
−
−
−
=
′
Wracamy do wyj ciowego równania
x
x
Ce
Ce
e
y
x
y
x
x
dx
dC
2
2
2
2
2
2
2
+
=
+
−
′
−
dx
e
x
x
dC
x
2
2
)
2
(
+
=
+
=
dx
e
x
x
C
x
2
2
)
2
(
=
x
x
e
g
x
f
e
g
x
x
f
2
2
1
2
2
2
2
2
=
+
=
′
=
′
+
=
=
+
−
+
=
dx
e
x
e
x
x
x
x
2
2
2
2
1
)
1
(
)
2
(
x
x
e
g
f
e
g
x
f
2
2
1
2
1
1
=
=
′
=
′
+
=
=
=
+
+
−
+
=
dx
e
e
x
e
x
x
x
x
x
2
2
1
2
2
1
2
2
2
1
)
1
(
)
2
(
=
+
+
+
−
+
K
e
e
x
e
x
x
x
x
x
2
4
1
2
2
1
2
2
2
1
)
1
(
)
2
(
K
e
x
x
x
+
−
−
2
4
1
2
1
2
2
1
)
(
Kładziemy wyliczone C do RORLJ
[
]
x
x
x
Ke
x
x
e
K
e
x
x
y
2
4
1
2
1
2
2
1
2
2
4
1
2
1
2
2
1
)
(
−
−
+
−
−
=
⋅
+
−
−
=
Przykład 28
Rozwi za równanie ró niczkowe
0
]
)
1
(
2
[
)
1
(
4
=
+
+
−
+
dx
x
y
dy
x
.
Rozwi zanie:
3
)
1
(
1
2
+
=
+
−
x
y
x
dx
dy
0
1
2
=
+
−
y
x
dx
dy
RLJ
→
1
2
+
=
x
dx
y
dy
→
C
x
y
ln
)
1
ln(
2
ln
+
+
=
→
2
)
1
(
+
=
x
C
y
-
RORLJ
Uzmienniamy stał .
Ró niczkujemy RORLJ
)
1
(
2
)
1
(
2
+
+
+
=
′
x
C
x
y
dx
dC

Stanisław Kowalski: Wykłady z matematyki –
Całka nieoznaczona
– wykład 9
101
Wracamy do wyj ciowego równania
3
2
2
)
1
(
)
1
(
1
2
)
1
(
2
)
1
(
+
=
+
+
−
+
+
+
′
x
x
C
x
x
C
x
y
y
dx
dC
dx
x
dC
)
1
(
+
=
K
x
x
C
+
+
=
2
2
1
Kładziemy wyliczone C do RORLJ
2
2
2
2
1
2
2
2
1
)
1
(
)
1
)(
(
)
1
)(
(
+
+
+
+
=
+
+
+
=
x
K
x
x
x
x
K
x
x
y
Wyszukiwarka
Podobne podstrony:
ZiIP Wykład 7 Całka nieoznaczona
1 Calka nieoznaczona wyklad druk
ZiIP Wyklad 8 Całka
CAŁKA NIEOZNACZONA WZORY
CAŁKA NIEOZNACZONA
Całka nieoznaczona?f i tw
Całka nieoznaczona
Całka nieoznaczona cz 2 Zadania
Analiza matematyczna. Wykłady CAŁKI NIEOZNACZONE
Arkusz zadan Calka nieoznaczona id 68887 (2)
C08 Całka nieoznaczona
całka nieoznaczona1
Analiza matematyczna Wykłady, CAŁKI NIEOZNACZONE
6 Całka nieoznaczona
calka nieoznaczona
Zadania całka nieoznaczona Politechnika Poznańska PP, Automatyka i Robotyka, Analiza matematyczna
matma, CAŁKA OZNACZONA = liczba, CAŁKA NIEOZNACZONA = funkcja
więcej podobnych podstron