1

Charakterystyki statyczne i dynamiczne podstawowych

członów układów automatyki

Do przedstawienia charakterystyk dynamicznych członu używa się:

• odpowiedzi członu na skok jednostkowy sygnału wejściowego,

• odpowiedzi członu na impuls jednostkowy,

• odpowiedzi członu na sygnał wejściowy narastający liniowo.

Oprócz charakterystyk statycznych i dynamicznych do opisu własności
członu podaje się niekiedy charakterystyki częstotliwościowe.
Określają one zależność sygnału wyjściowego od wejściowego w postaci
przebiegu sinusoidalnego.

2

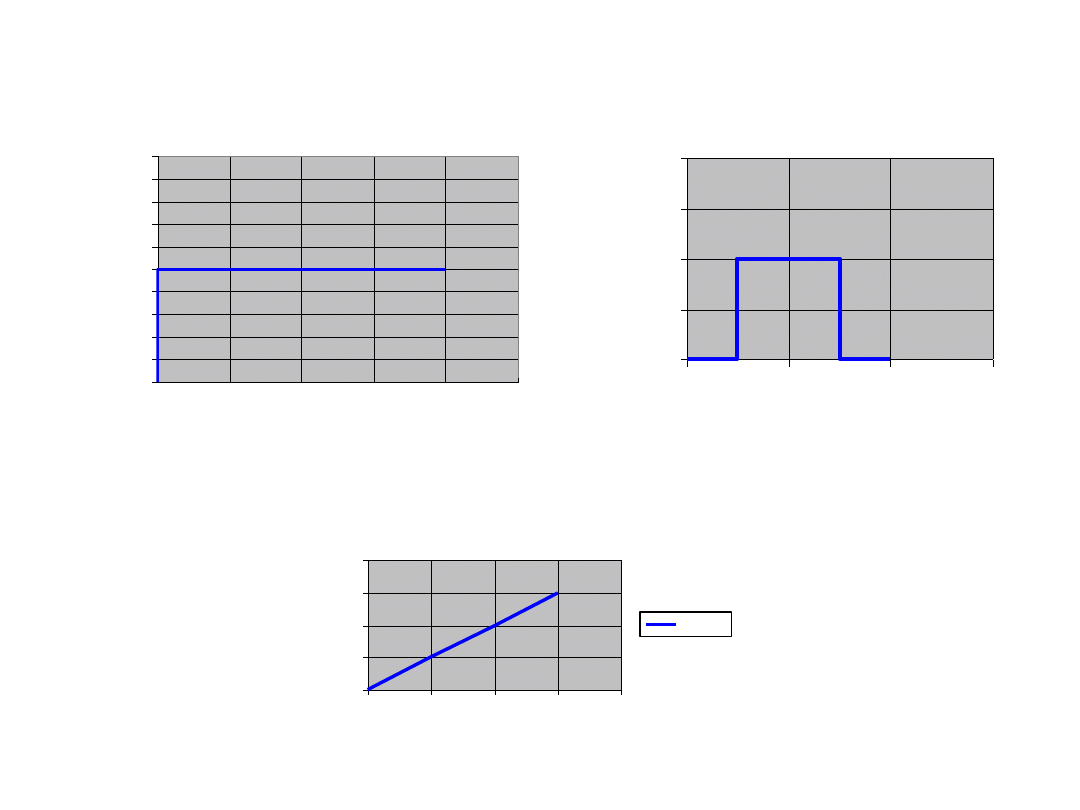
Skok jednostkowy

0

0,2

0,4

0,6

0,8

1

1,2

1,4

1,6

1,8

2

0

1

2

3

4

5

czas t

x

Impuls jednostkowy

0

0,5

1

1,5

2

0

2

4

6

czas t

x

Narastający liniowo

0

1

2

3

4

0

1

2

3

4

czas t

x

Wsch.

3

Rodzaje członów

:

• proporcjonalny

• inercyjny

• całkujący

• różniczkujący

• oscylacyjny

• opóźniający

1. Bezinercyjny człon proporcjonalny

Definicja: Człon bezinercyjny to człon, którego właściwości
dynamiczne mogą być pominięte.

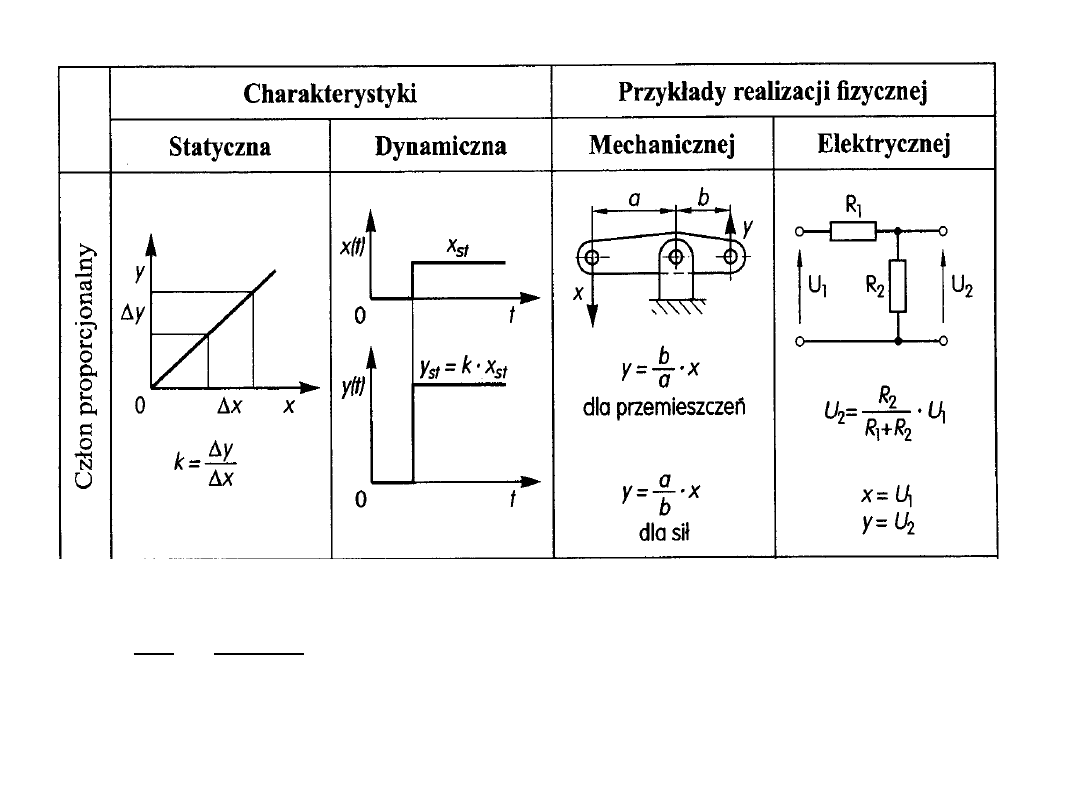
Człon proporcjonalny charakteryzuje się istnieniem współczynnika
wzmocnienia członu.

4

1

2

1

2

x

x

y

y

x

y

k













y=k·x

k – współczynnik wzmocnienia członu

5

Realizacja mechaniczna: dźwignia dwustronna, dźwignia jednostronna, prasa
hydrauliczna.

Dla prasy hydraulicznej: F

2

=i · F

1

A

2

, A

1

–

pola powierzchni

tłoków

1

2

A

A

i 

Realizacja elektryczna: dzielnik napięcia

U

1

=I·R

1

+ I·R

2

U

1

=I·(R

1

+ R

2

)

U

2

=I·R

2

x – napięcie U

1

, y

– napięcie U

2

U

2

=k·U

1

y =k·x

2

1

1

R

R

U

I





2

2

1

1

2

R

R

R

U

U







1

2

1

2

2

U

R

R

R

U







2

1

2

R

R

R

k





6

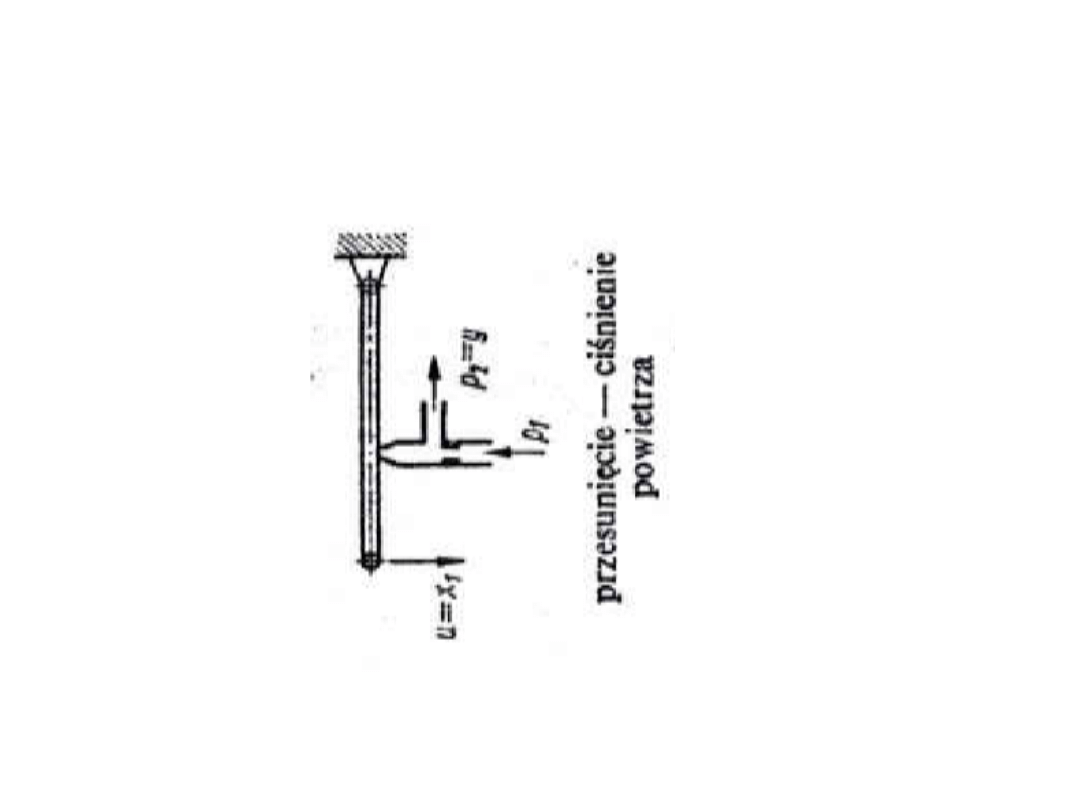
Realizacja pneumatyczna

7

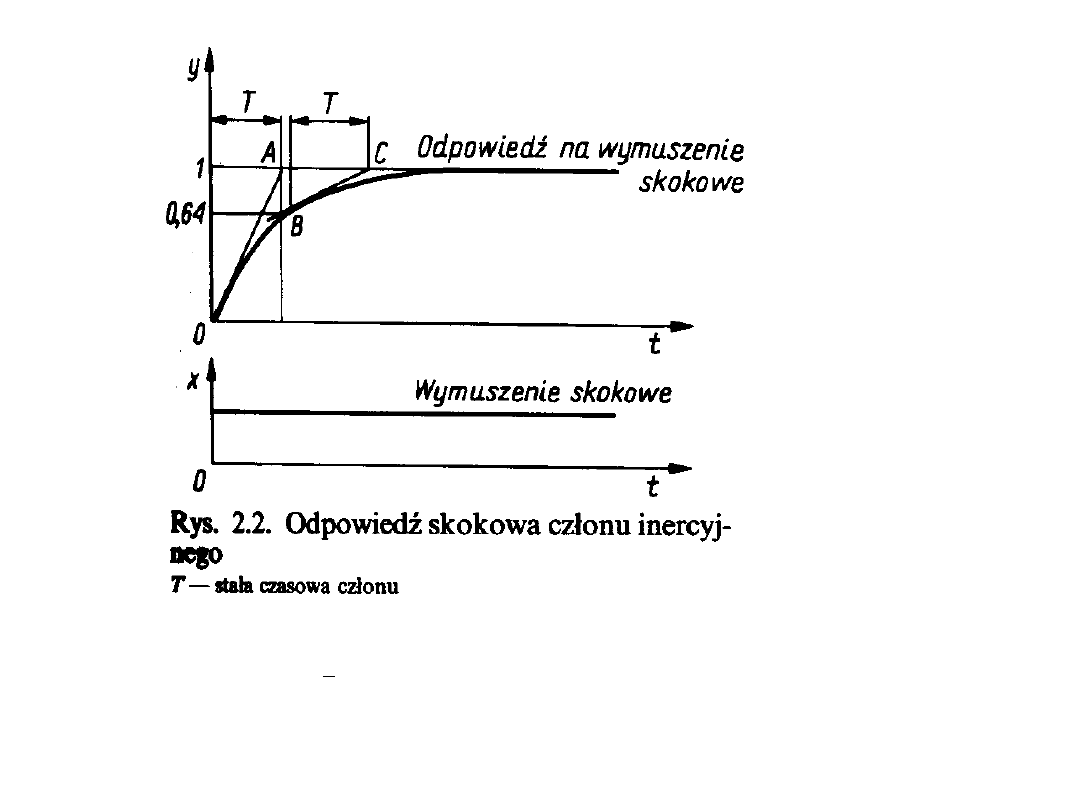
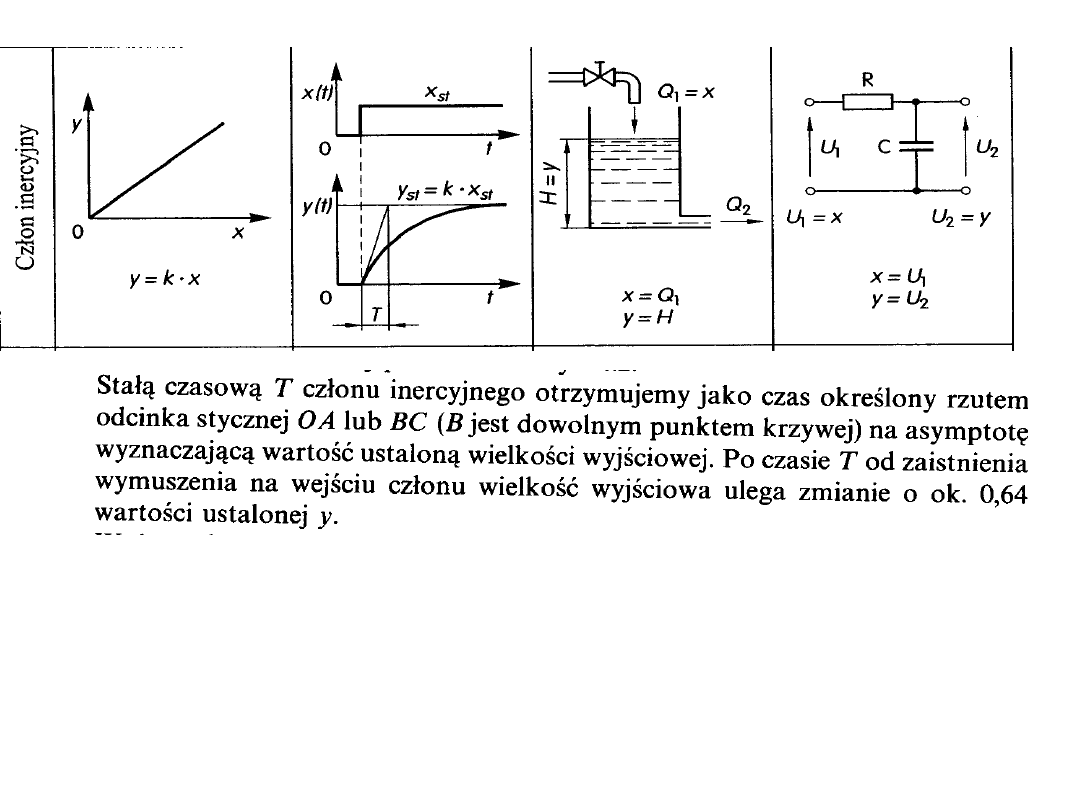
2. Człon inercyjny.

Wielkość wyjściowa członu inercyjnego wykazuje pewną bezwładność w
stosunku do sygnału wejściowego.

Charakterystyka statyczna członu jest identyczna do charakterystyki statycznej
członu proporcjonalnego. Z charakterystyki dynamicznej tego członu wynika,
że wartość wyjściowa osiągana jest dopiero po pewnym czasie.

Przykładem realizacji mechanicznej jest
napełnianie zbiornika wody z odpływem.
Po pewnym czasie poziom wody osiągnie
wartość przy której prędkość dopływu i
odpływu zrównają się i poziom cieczy
osiągnie wartość stałą równą h.

8

e ≈ 2,72 podstawa logarytmów naturalnych

Graficzne wyznaczanie stałej czasowej.

)

1

(

T

t

e

k

y









9

Definicja: Stała czasowa to czas, po którym wielkość wyjściowa uzyskuje
wartość około 0,64 wartości w stanie ustalonym.

10

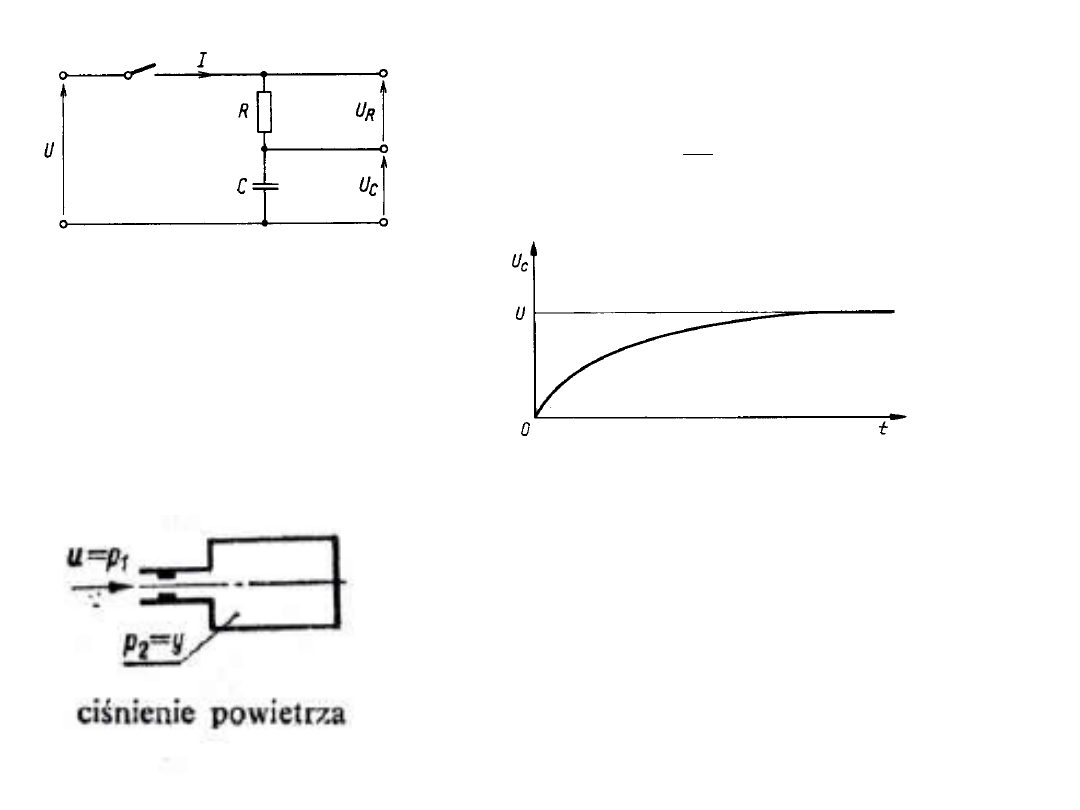
Realizacja elektryczna

U= U

R

+U

C

)

1

(

RC

t

C

e

U

U









R·C – stała
czasowa

Realizacja pneumatyczna

11

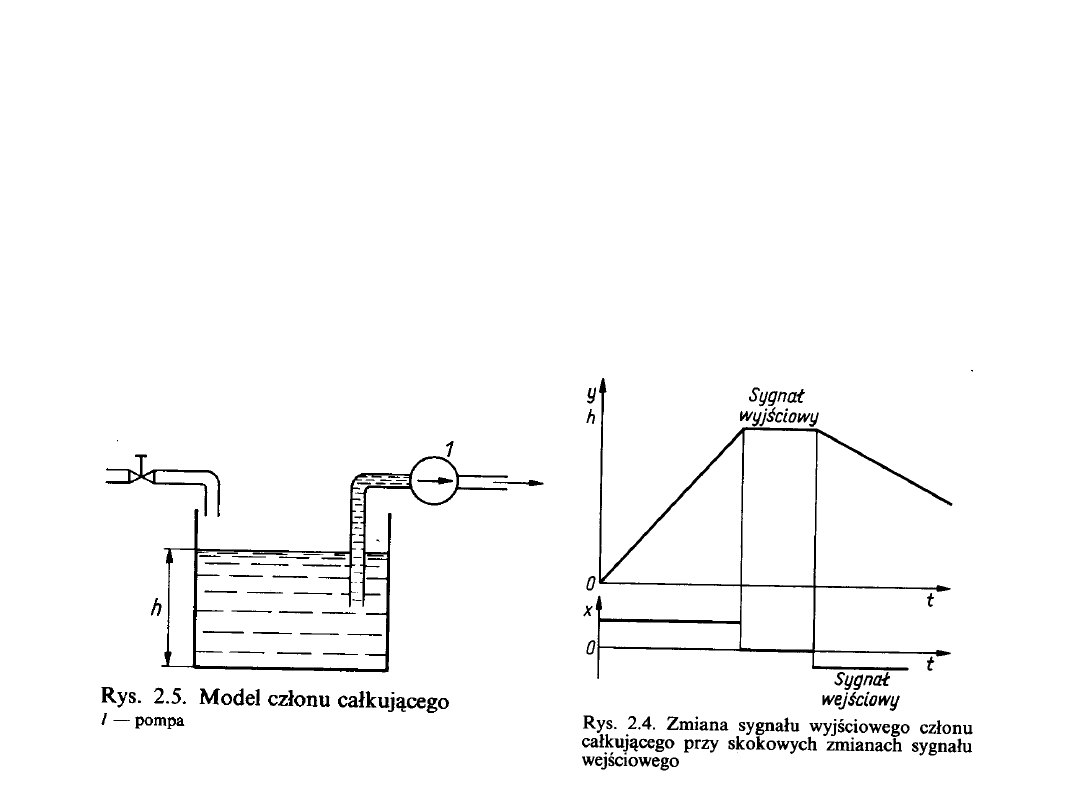
3. Człon całkujący.

Człon całkujący, inaczej człon astatyczny nie posiada charakterystyki statycznej.

Stan ustalony istnieje w nim tylko przy zerowej wartości sygnału wejściowego.

Człon całkujący charakteryzuje się liniową odpowiedzią skokową. Dobre przyb-

liżenie członu całkującego daje człon inercyjny z dużą stałą czasową. Przy bardzo

dużych stałych czasowych człon inercyjny można traktować jak człon całkujący.

12

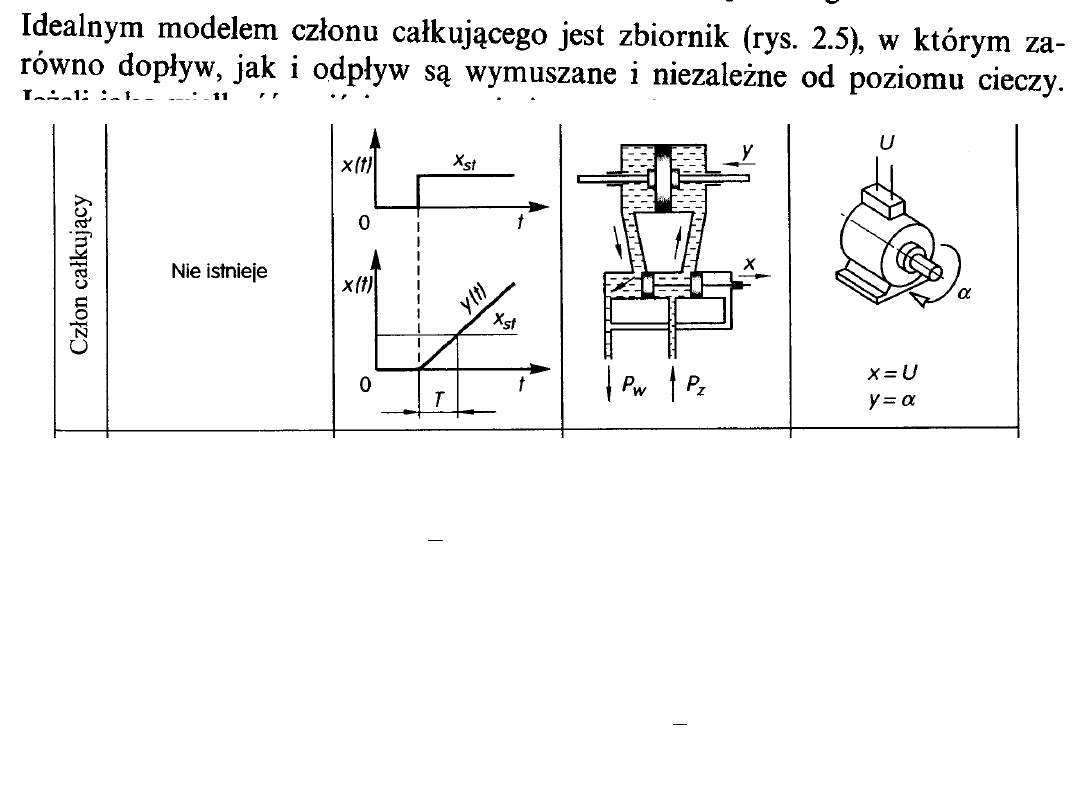
y =k·t + c

- odpowiedź członu całkującego na skok jednostkowy jest

linią prostą o nachyleniu zaczynającą się od wartości wielkości
wyjściowej, jaka istniała w chwili wprowadzenia sygnały wejściowego.

A – wartość funkcji skokowej, c – wartość początkowa sygnału wejśc.

T

A

k 

Odpowiedź rzeczywistego członu całkującego na skok jednostkowy
wyraża się równaniem:

)

1

(

T

t

e

T

k

t

k

y













13

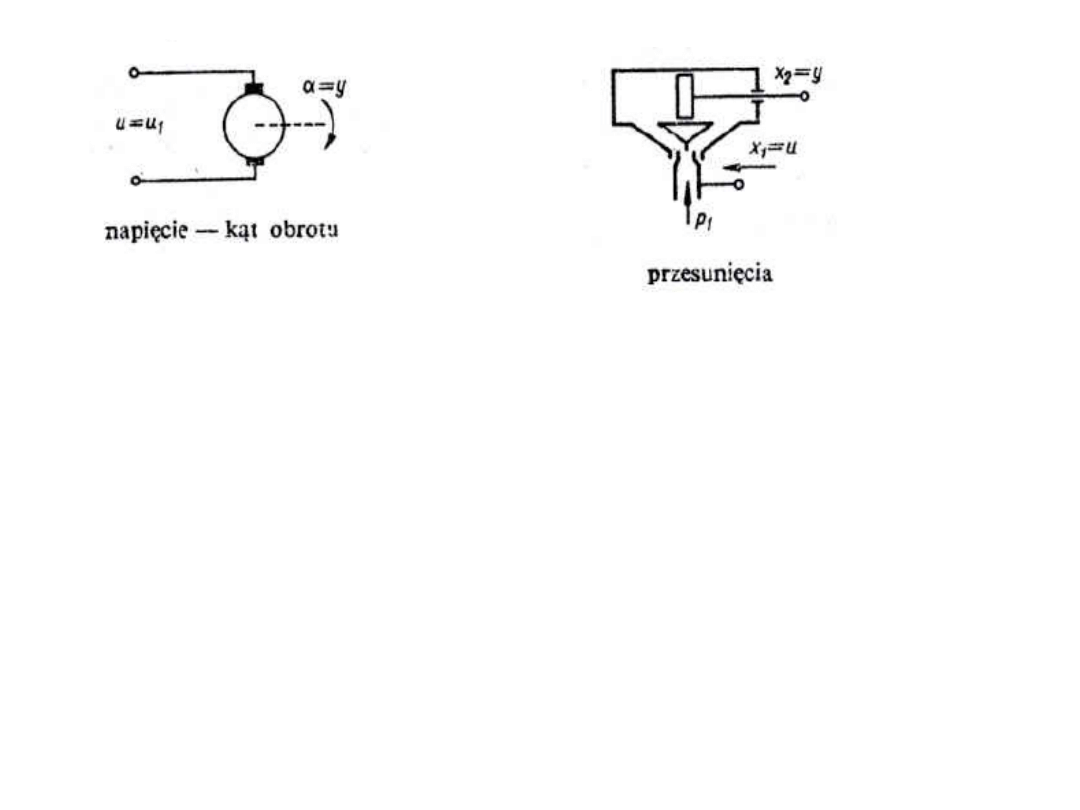
Realizacja elektryczna Realizacja pneumatyczna

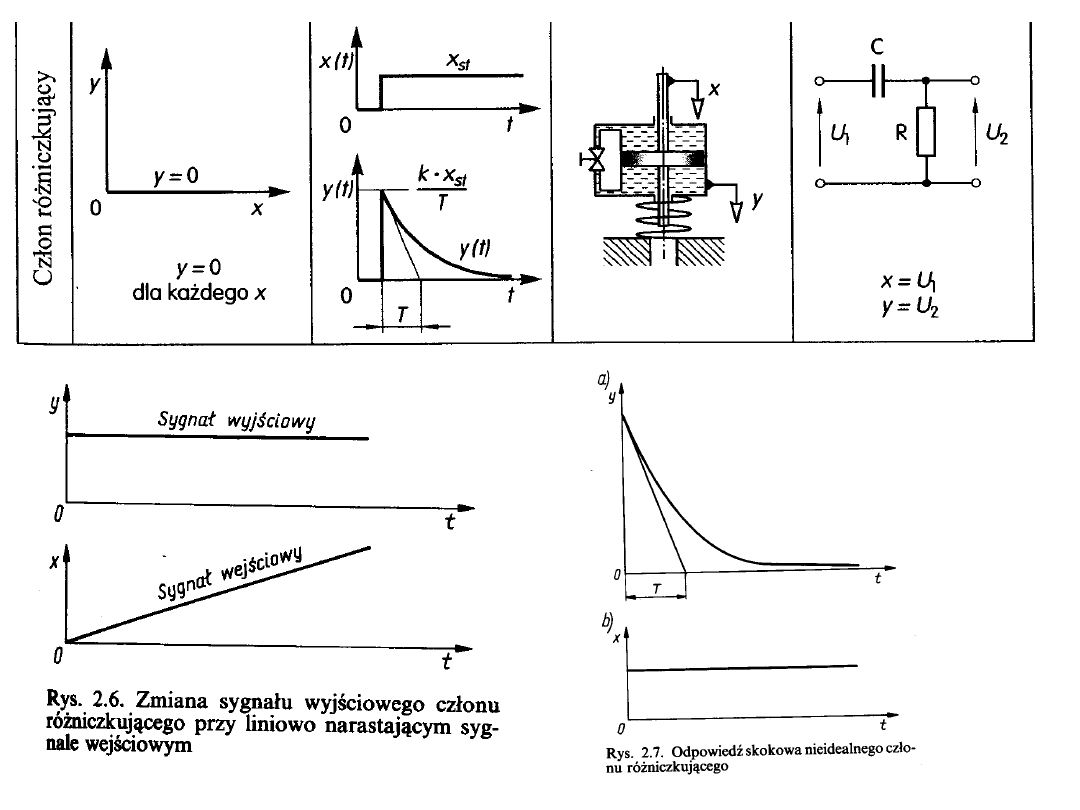
4. Człon różniczkujący.

Wartość sygnału wyjściowego członu różniczkującego jest proporcjonalna do
szybkości zmian sygnału wejściowego; nie zależy natomiast od wartości
sygnału wejściowego. Odpowiedź skokowa idealnego członu różniczkują-
cego ma postać impulsu o zerowym czasie trwania i o nieograniczonej
amplitudzie (szpilka). Do badania rzeczywistych członów różniczkujących
stosuje się na wejściu zamiast skoku jednostkowego sygnał narastający
liniowo. Odpowiedzią członu na takie wymuszenie będzie linia prosta
równoległa do osi czasu.

14

15

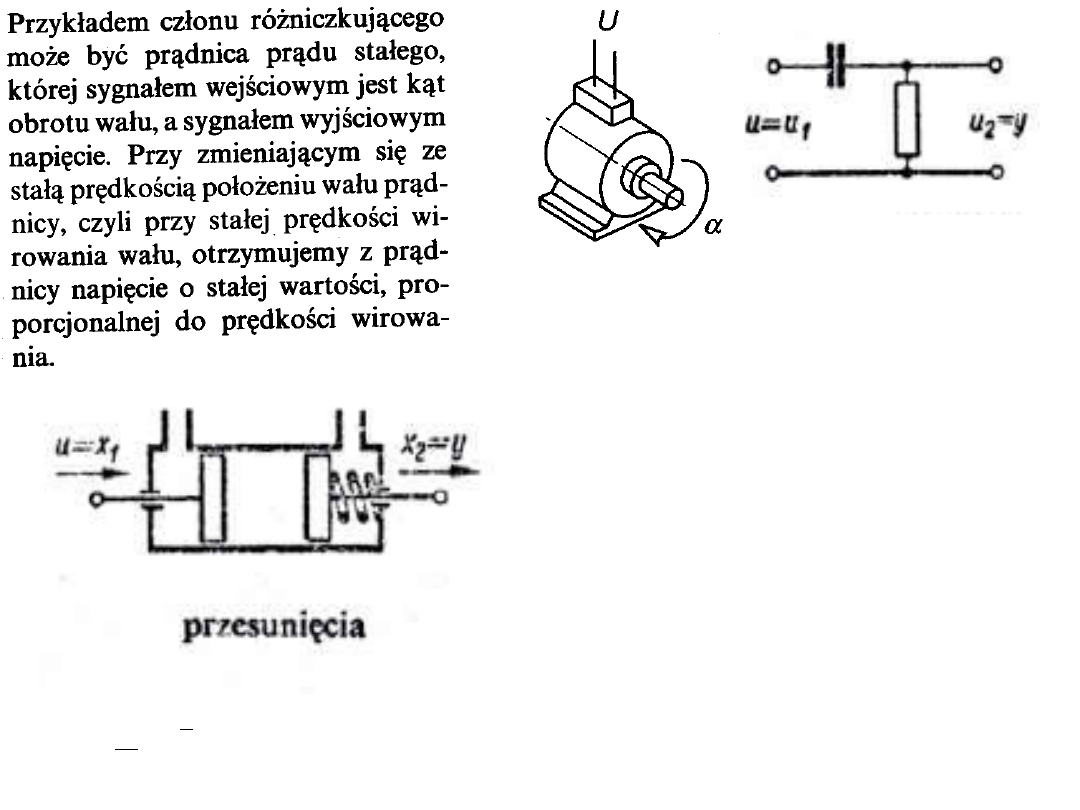
x=α y=U x=U

1

y=U

2

Kąt obrotu- napięcie

Realizacja
pneumatyczna

T

t

e

T

k

y







odpowiedź rzeczywistego członu różniczkującego na
skok jednostkowy

16

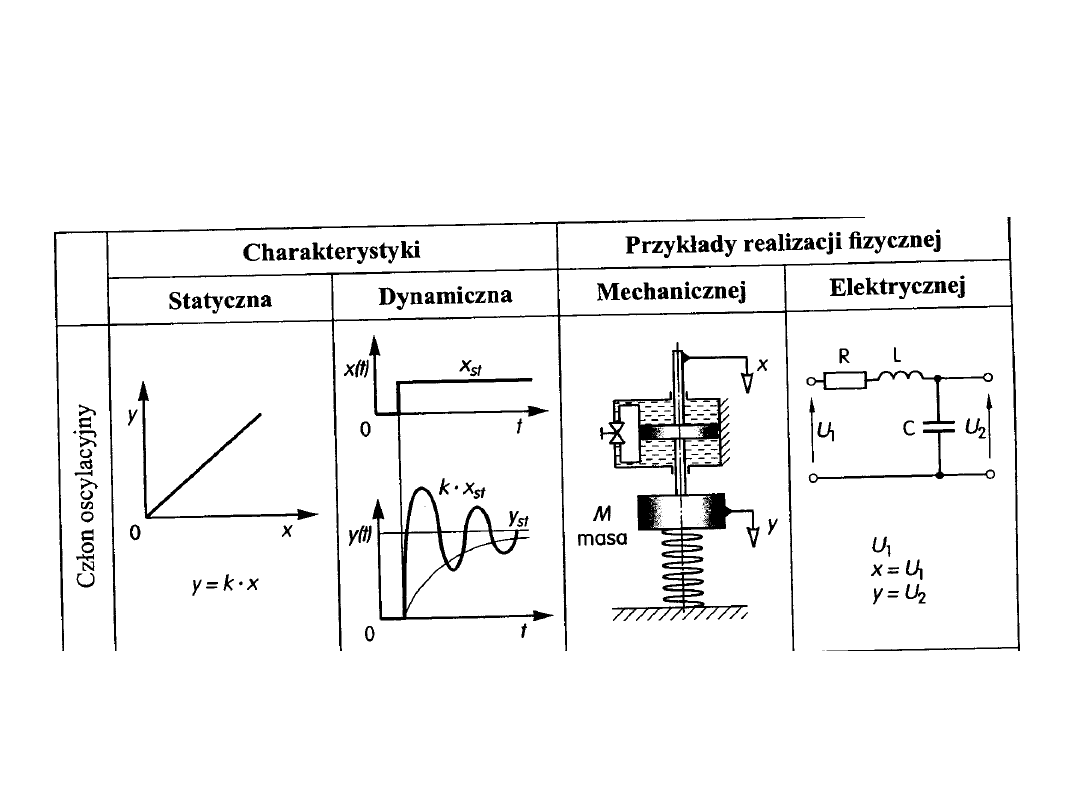
5. Człon oscylacyjny.

Człon oscylacyjny charakteryzuje się powstawaniem drgań gasnących po
podaniu na wejście skoku jednostkowego.

17

Odpowiedź członu na skok jednostkowy przedstawia się dość
skomplikowanym wzorem:



































)

sin(

1

1

2











t

t

e

k

y

w

n

k – współczynnik wzmocnienia

ω

n

– pulsacja drgań własnych tłumionych ω=2·π·f f – częstotliwość drgań

ς – współczynnik tłumienia względnego

ω

w

= ω

n

·

pulsacja drgań własnych tłumionych

φ=arctg

2

1









2

1

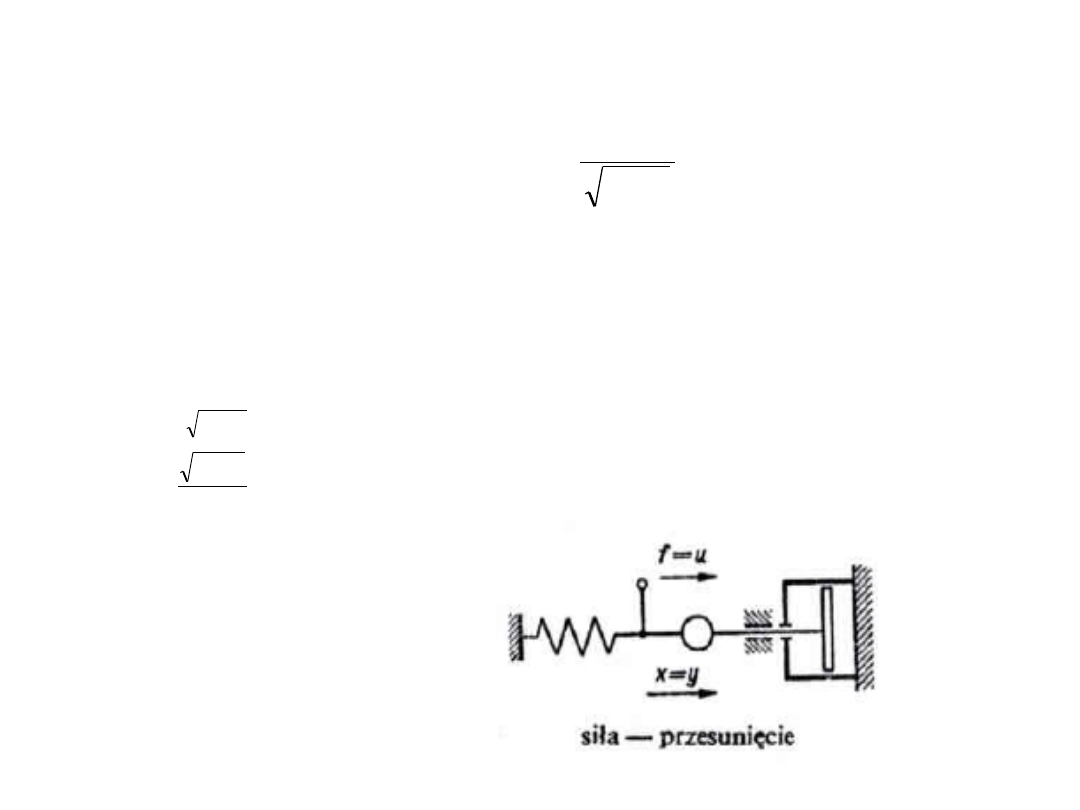
Realizacja mechaniczna

18

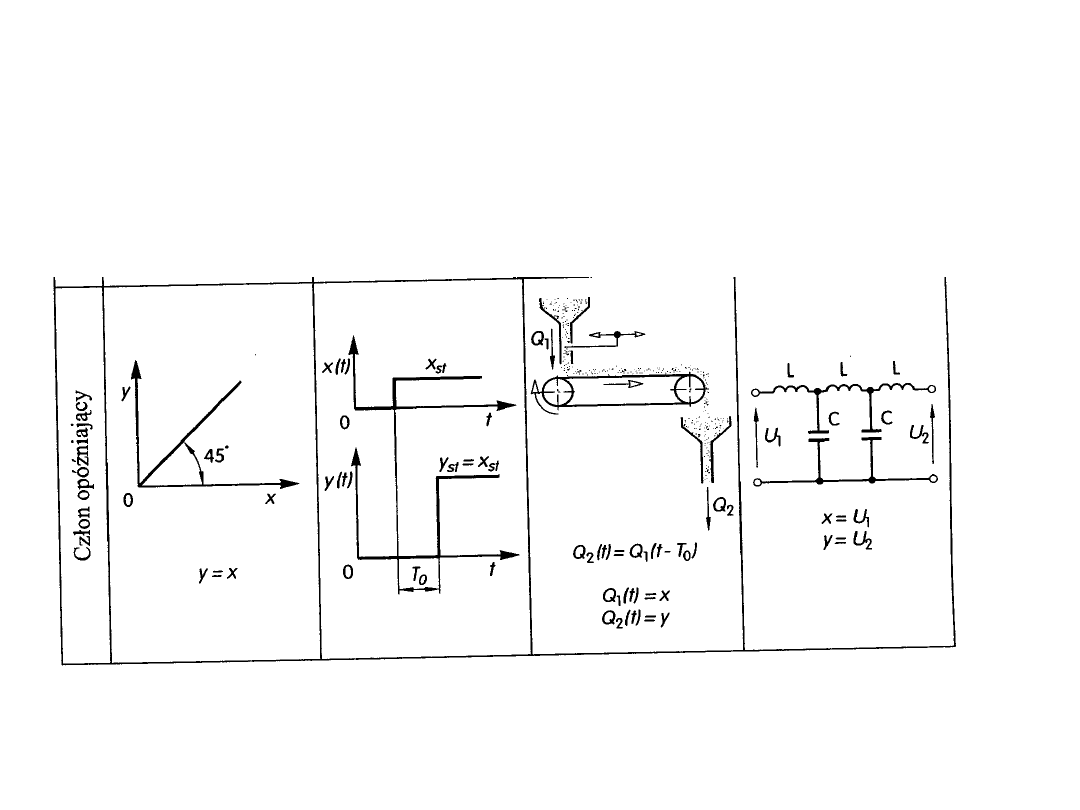
6. Człon opóźniający.

Człon ten charakteryzuje się współczynnikiem wzmocnienia równym
jedności oraz opóźnieniem w powstawaniu sygnału wyjściowego. Sygnał
wyjściowy ma taki sam przebieg jak sygnał wejściowy ale jest opóźniony o
czas T

0

.

Q

2

(t)=Q

1

·(t-T

0

) dla taśmociągu, realizacja mechaniczna

y =x·(t-T

0

)

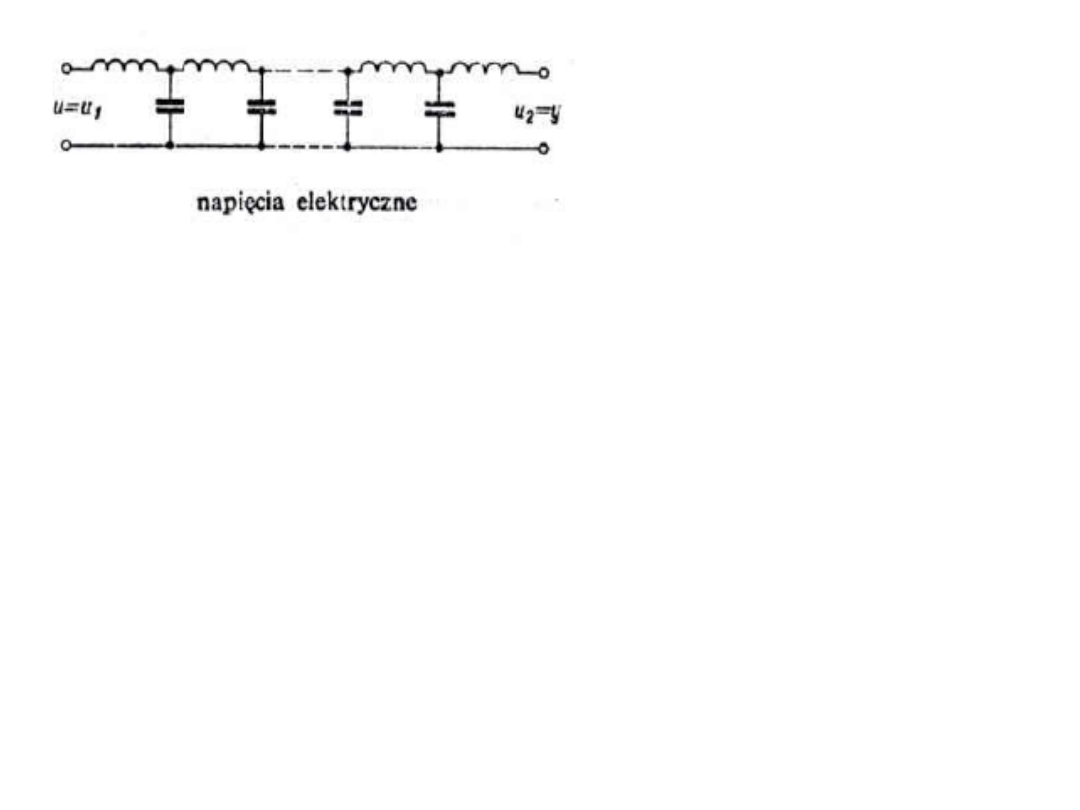
19

T

0

=n·√L·C n – liczba ogniw, L – indukcyjność w H, C – pojemność w F

K O N I E C