Obciążenie stałe obliczeniowe od chodnika:

•

gch 14.27

kN

m

2

⋅

=

Obciążenie stałe charakterystyczne pionowe poręczy na pasmo 1m:

•

Gbal.k

Gbal 1

⋅ m

0.5 kN

⋅

=

:=

Obciążenie stałe obliczeniowe pionowe poręczy na pasmo 1m:

•

Gbal.d

Gbal 1.35

⋅

1

⋅ m

0.675 kN

⋅

=

:=

Obciążenie stałe charakterystyczne pionowe od bariery ochronej na pasmo 1m:

•

Gb.k

Gb 1

⋅ m

0.3 kN

⋅

=

:=

Obciążenie stałe obliczeniowe pionowe od bariery ochronej na pasmo 1m:

•

Gb.d

Gb 1.35

⋅

1

⋅ m

0.405 kN

⋅

=

:=

Obciążenie stałe charakterystyczne pionowe od gzymsu na pasmo 1m:

•

Ggz.k

Ggz 1

⋅ m

4.253 kN

⋅

=

:=

Obciążenie stałe obliczeniowe pionowe od gzymsu na pasmo 1m:

•

Ggz.d

Ggz 1.35

⋅

1

⋅ m

5.741 kN

⋅

=

:=

Obciążenie stałe charakterystyczne od krawężnika na pasmo 1m:

•

Gk.k

Gk 1

⋅ m

1 kN

⋅

=

:=

Obciążenie stałe obliczeniowe od krawężnika na pasmo 1m:

•

Gk.d

Gk 1.35

⋅

1

⋅ m

1.35 kN

⋅

=

:=

ZMIENNE

Obciążenie tłumem na pasmo 1m

•

Qt.k

5

kN

m

2

:=

Qt.d

Qt.k 1.35

⋅

1

⋅ m

6.75 m

kN

m

2

⋅

=

:=

Wartość oblic zeniowa na 1m długoś ć

Qt

Qt.d 1

⋅ m

6.75 m

kN

m

⋅

=

:=

Obciążenie wspornika:

1) Sytuacja trwała:

ciężar własny:

gch.d

gch 1.35

⋅

19.265

kN

m

2

⋅

=

:=

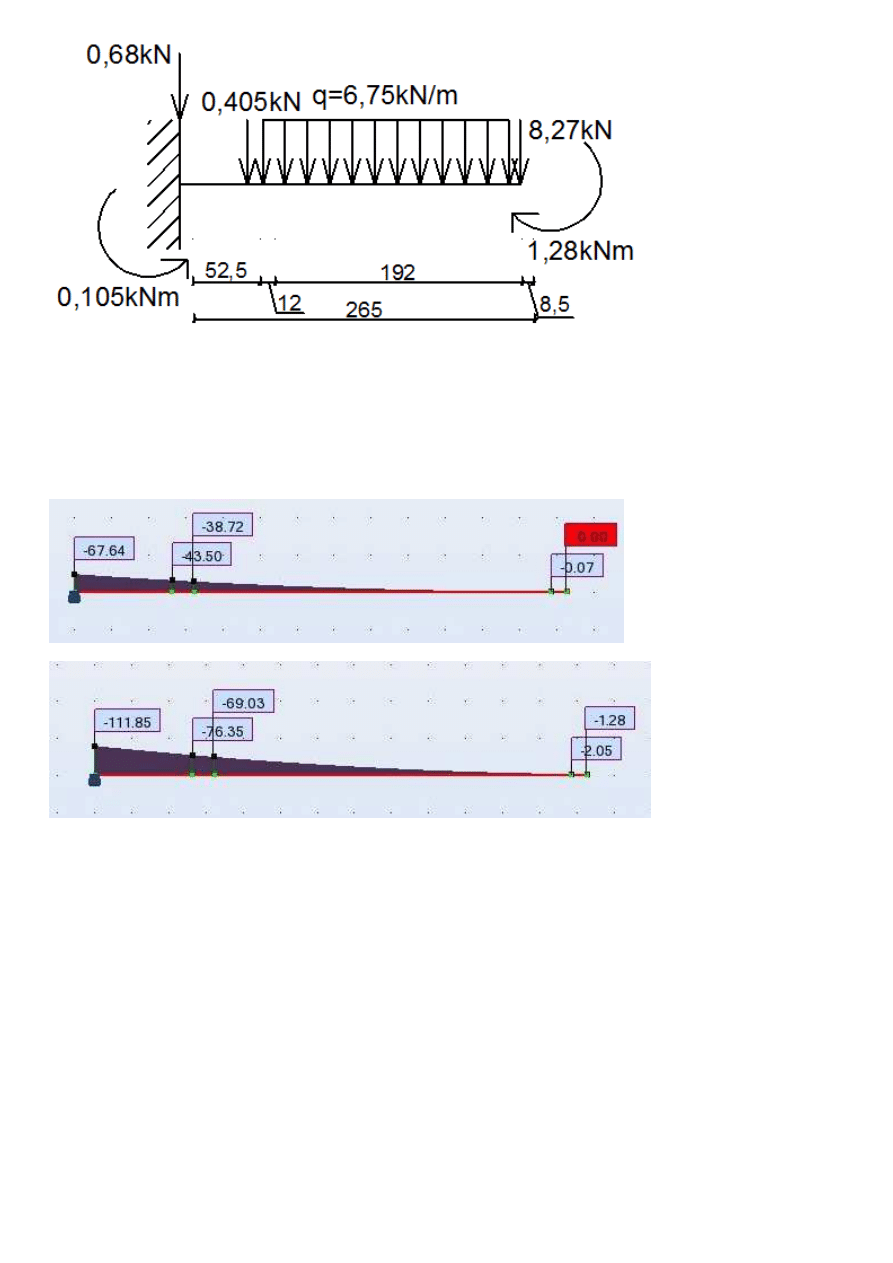
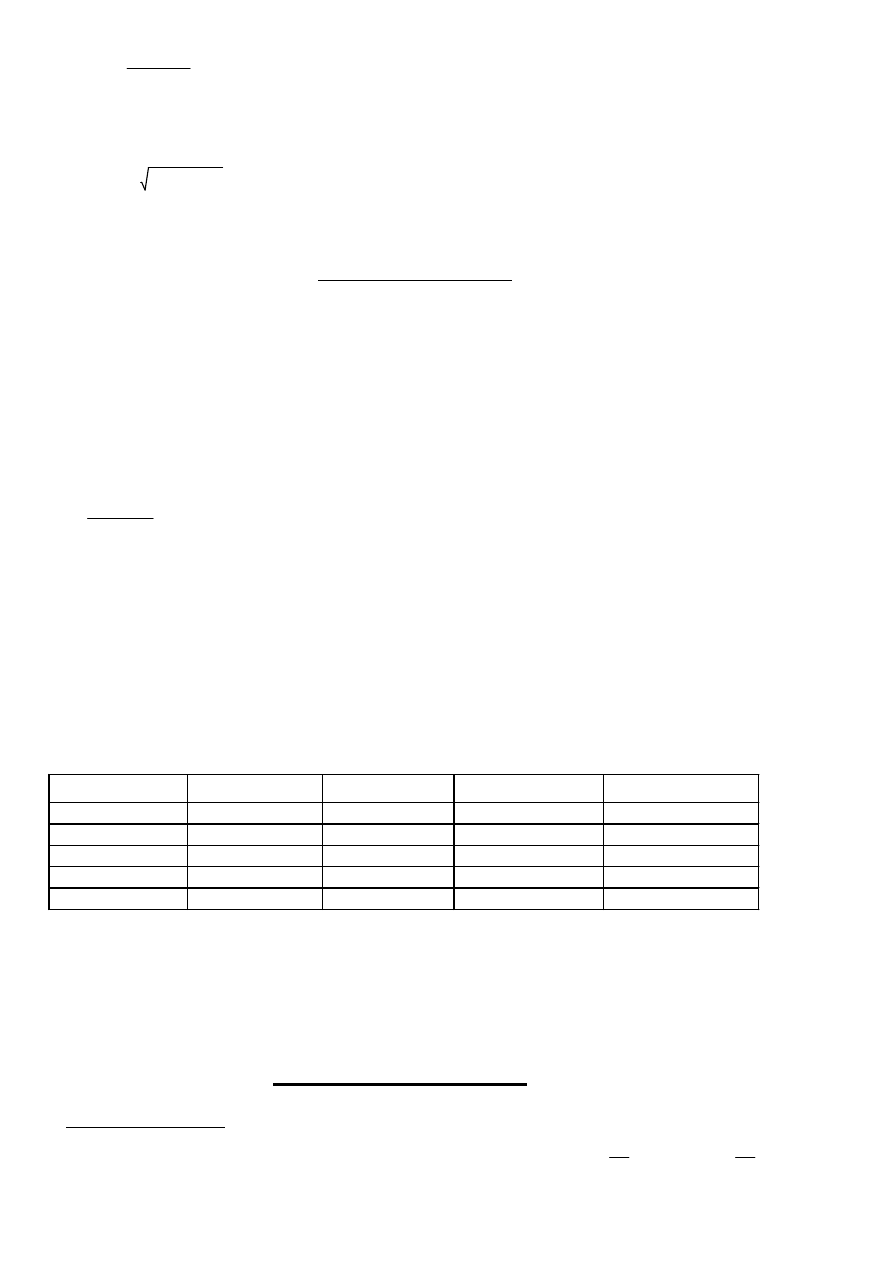
Na schemacie obciążeń rozrysowane są obciążenia na wartościach charakterystycznych.

Obciążenia skupione znajdujące się na kapie chodnikowej poza rozpiętością płyty
zamieniono na siłę skupioną+moment

Wykres momentów:

moment od obciążeń stałych:

MG

67.64kN m

⋅

:=

MEd.w.st

111.85kN m

⋅

:=

2) Sytuacja wyjątkowa:

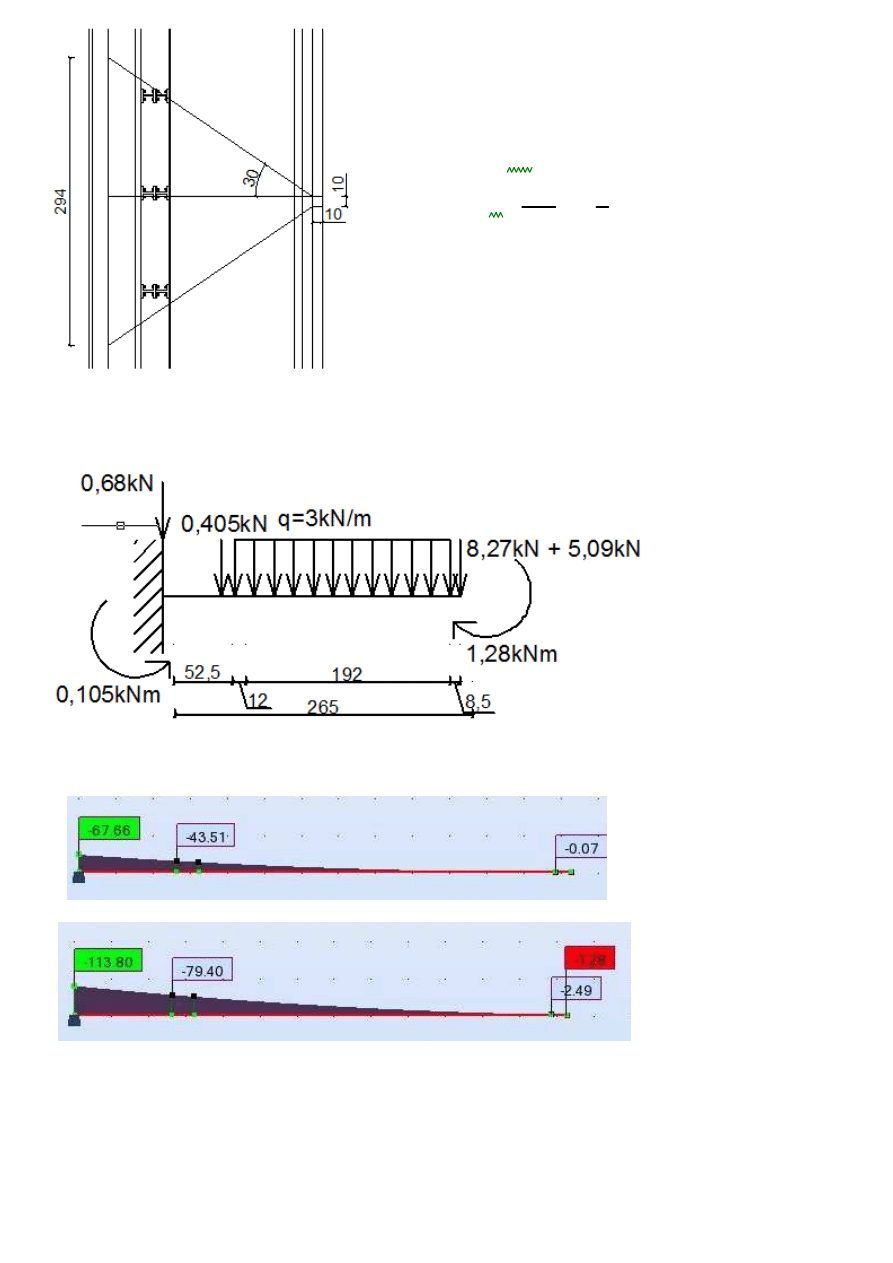
bm

2.94m

:=

F

15kN

bm

5.1

1

m

kN

⋅

=

:=

Wykres momentów:

moment od obciążeń stałych:

MG1

67.66kN m

⋅

:=

MEd.w.sw

113.80kN m

⋅

:=

Miarodajny obliczeniowy moment zginający wspornika w SGN przyjęto jako max z sytuacji
trwałej i wyjątkowej:

MEd.w

max MEd.w.st MEd.w.sw

,

(

)

113.8 kN m

⋅

⋅

=

:=

- max moment na wsporniku występuje dla
sytuacji wyjątkowej

[kNm]

SYTUACJA TRWAŁA

111,85

SYTUACJA WYJĄTKOWA

113,8

MIARODAJNY

113,80

ZESTAWIENIE MOMENTÓW - WSPORNIK

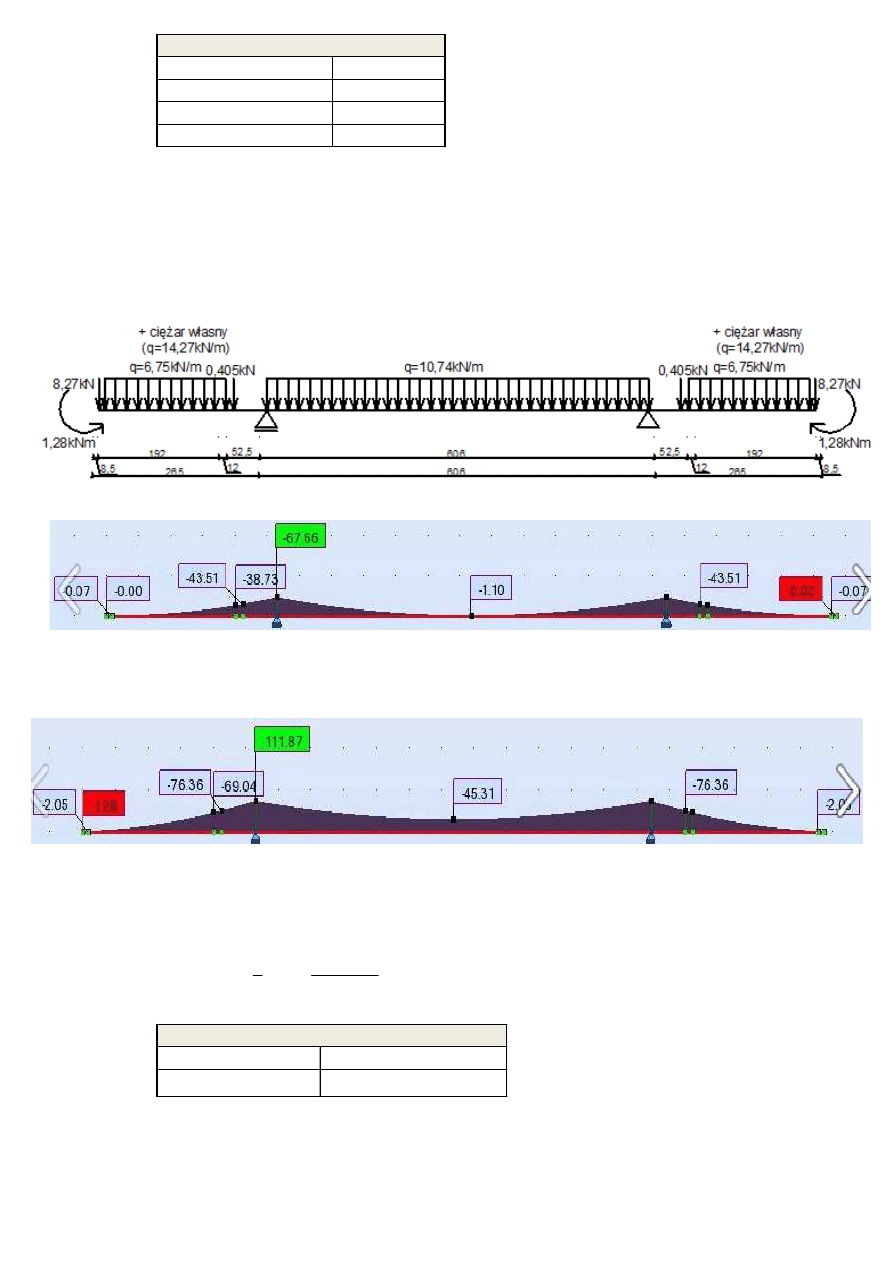
6.Kombinacja na max moment przesłowy ( rozciąganie górą )

Przęsło - obciążenie stałe
Wsporniki - obciążenie stałe + obciążenie tłumem

Schemat obciążenia:

moment od obciążeń stałych:

Msc

67.56kN m

⋅

:=

MsA

1.10kN m

⋅

:=

MsB

67.56kN m

⋅

:=

Mc

111.87kN m

⋅

:=

MA

45.31kN m

⋅

:=

MB

111.87kN m

⋅

:=

MEd.rg

1

3

Mc

MA MB

+

2

+













63.487 kN m

⋅

⋅

=

:=

[kNm]

M

Ed

63.487

MOMENT DO WYMIAROWANIA PRZĘSŁA GÓRĄ

7. WYMIAROWANIE PŁYTY POMOSTOWEJ

7.1 Charakterystyka betonu

klasa betonu

•

C 50/60

wytrzymałość charakterystyczna naściskanie:

•

fck

50MPa

:=

wytrzymałość średnia na ściskanie:

•

fcm

58MPa

:=

wytrzymałość średnia na rozciąganie:

•

fctm

4.1MPa

:=

wytrzymałość charakterystyczna na rozciądanie

•

fctk.0.05

2.9MPa

:=

moduł sprężystości

•

Ecm

32GPa

:=

maksymalne dopuszczalne odkształcenie

•

εcu2

0.35%

:=

współczynnik uwzględniający efekty długotrwałe

•

acc

1

:=

współczynnik częściowy

•

γc

1.4

:=

fcd

acc

fck

γc

⋅

35.714 MPa

⋅

=

:=

wytrzymałośc obliczeniowa na ściskanie

•

-

7.2 Charakterystyka stali

charakterystyczna granica plastyczności

•

fyk

500MPa

:=

współczynnik częściowy

•

γs

1.15

:=

obliczeniowa granica plastyczności

•

fyd

fyk

γs

434.78 MPa

⋅

=

:=

modół sprężystości

•

Es

200GPa

:=

charakterystyczne odkształcenie przy max sile

•

εuk 5%

>

7.3 Klasa konstrukcji

Przyjęto klase konstrukcji S3 ( Na podstawie tab.4,3N zmniejszono klase

konstrukcji o 1 z S4)

7.4 Otulina prętów zbrojenia:

średnica prętów zbrojenia

•

ϕ

16mm

:=

otulina nominalne:

•

cnom

cmin ∆dev

+

:=

cmin

otulina minimalne:

•

cmin

max cminb cmindur ∆cdury

+

∆cdurst

−

cduradd

−

,

10mm

,

(

)

:=

cminb

cminb

ϕ

16 mm

⋅

=

:=

(przy ułożeniu prętów zwykłych równe jest średnicy
pręta -tab. 4.2)

cmindur

20mm

:=

(dla S3 i XC3; tab 4.4N)

∆cdury

0mm

:=

(zalecane)

∆cdurst

0mm

:=

(zalecane)

∆cduradd

0mm

:=

(zalecane)

cmin

max 16mm 20mm

0mm

+

0mm

−

0mm

−

,

10mm

,

(

)

20 mm

⋅

=

:=

Otulenie nominalne wynosi :

•

-dodatek ze względu na odchyłkę

∆cdev

10mm

:=

(zalecane)

cnom

cmin ∆cdev

+

30 mm

⋅

=

:=

7.5 Minimalne i maksymalne pola przekroju zbrojenia:

minimalne:

•

fctm

2.9MPa

:=

bt

1m

:=

hpł

30cm

:=

d1

hpł cnom

−

0.5

ϕ

−

0.262 m

=

:=

fyk 500 MPa

⋅

=

1)

Asmin1

0.26

fctm

fyk

⋅

bt

⋅

d1

⋅

:=

Asmin1 3.951 cm

2

⋅

=

2)

Asmin2

0.0013bt d1

⋅

:=

Asmin2 3.406 cm

2

⋅

=

k

1

:=

σs

280MPa

:=

(tab. 7.2 dla ϕ=8mm, w

k

=0.3mm)

Act

0.5 bt

⋅

hpł

⋅

0.15 m

2

=

:=

kc

0.4

:=

fct.eff

fctm 2.9 MPa

⋅

=

:=

3)

Asmin3

kc k

⋅ f

ct.eff

⋅

Act

⋅

σs

:=

Asmin3 6.214 cm

2

⋅

=

Asmin

max Asmin1 Asmin2

,

Asmin3

,

(

)

6.214 cm

2

⋅

=

:=

d

1

- wysokość użyteczna

b

t

- średnia szerokość strefy rozciąganej

f

ctm

- średnia wytrzymałość betonu na rozciąganie

A

ct

-pole przekroju strefy rozciąganej betonu

σ.s - wartość bewzględną max dozwolonego napręzeina w zbrojeniu

k - współczynnik zależny od wpływu nierównomiernych, samorównoważących się napręzeń
kc- współczynnik zależny od rozkłądu napręzeń w przekroju w chwili bezpośrednio
poprzedzającej zarysowanie oraz od zmiany ramienia sił wewnętrznych.

zbrojenie maksymalne:

•

Ac

bt hpł

⋅

0.3 m

2

=

:=

Asmax

0.04 Ac

⋅

120 cm

2

⋅

=

:=

7.6 Graniczna wartośc wysokośći strefy ściskanej:

εyd

fyd

−

Es

0.22

−

%

⋅

=

:=

odkształcenie stali odpowiadające granicy plastyczności

εcu

0.35%

:=

graniczne odkształcenia betonu ściskanego
(zmiażdzenie betonu)

ξlim

εcu

εcu

εyd

+

(

)

0.617

=

:=

graniczne względna wysokość strefy ściskanej

ξeff.lim

0.8

ξlim

⋅

0.493

=

:=

graniczna wartość efektywnej wysokośći strefy ściskanej

xlim

ξlim d1

⋅

0.162 m

=

:=

graniczna wysokość strefy ściskanej

xeff.lim

0.8 xlim

⋅

0.129 m

=

:=

graniczna efektywna wysokość strefy ściskanej

MEd.rg

7.7 Wymiarowanie zbrojenia na zginanie :

MEd.pł 131 kN m

⋅

⋅

=

max moment przęsłowy

MEd.pod 133.3 kN m

⋅

⋅

=

max moment podporowy

MEd.w 113.8 kN m

⋅

⋅

=

max moment na wsporniku

MEd

MEd.pł

MEd.pod

MEd.w

MEd.rg





























131

133.3

113.8

63.487

















kN m

⋅

⋅

=

:=

fcd 35.714 MPa

⋅

=

bt 1 m

=

hpł 0.3 m

=

d1 0.262m

=

fyd 434.783 MPa

⋅

=

Sc.eff

MEd

fcd bt

⋅

d1

2

⋅

0.053

0.054

0.046

0.026

















=

:=

ξeff

1

1

2 Sc.eff

⋅

−

−

0.055

0.056

0.048

0.026

















=

:=

ξeff ξeff.lim

<

1

1

1

1

















=

przekrój pojedyńczo zbrojony

xeff

ξeff d1

⋅

14.395

14.656

12.458

6.875

















mm

⋅

=

:=

As1

fcd bt

⋅

xeff

⋅

fyd

11.825

12.039

10.233

5.647

















cm

2

⋅

=

:=

i

Asmin 6.214 cm

2

⋅

=

=>

As1

11.825cm

2

12.039cm

2

10.233cm

2

6.214cm

2

























:=

4.6 Rozstaw max prętów:

max rozstaw prętów

•

Zbrojenie główne:

smax.gł.ppk

min 3 hpł

⋅

400mm

,

(

)

40 cm

⋅

=

:=

smax.gł.pk

min 2 hpł

⋅

250mm

,

(

)

25 cm

⋅

=

:=

-obszary występowania obc. skupionych
lub max momentów

PRZYJĘTE ZBROJENIE

Zbrojenie

A.

s1.req

[cm

2

/mb]

A.

s1.prov

[cm

2

/mb] Średnica/Rozstaw Momenty max [kNm]

płyta przęsło

11,825

12,83

14/12cm

131

płyta podpora

12,039

12,83

14/12cm

133,3

wspornik

10,233

12,83

14/12cm

113,8

płyta góra

6,214

6,54

10/12cm

63,487

Pręty rozdzielcze 12,83*0,2=2,566

2,64

10/30cm

OBLICZENIA BELKI

1. OBCIĄŻENIA STAŁE

Obciążenie stałe charakterystyczne od płyty pomostu:

Gk1

10.74

kN

m

2

2.88

⋅

m

30.931

kN

m

⋅

=

:=

Obciążenie stałe obliczeniowe od płyty pomostu:

Gd1

14.499

kN

m

2

2.88m

41.757

kN

m

⋅

=

:=

Obciążenie stałe charakterystyczne od wspornika chodnikowego:

Gk2

14.27

kN

m

2

2.5

⋅

m

35.675

kN

m

⋅

=

:=

Obciążenie stałe obliczeniowe od wspornika chodnikowego:

Gd2

19.265

kN

m

2

2.5

⋅

m

48.163

kN

m

⋅

=

:=

Obciążenie stałe pionowe od balustrady:

Gbal1

0.50

kN

m

:=

Obciążenie stałe pionowe od bariery ochronej:

Gbar

0.30

kN

m

:=

Obciążenie stałe pionowe od gzymsu:

Ggzyms

0.35m 0.7

⋅

m 27

⋅

kN

m

3

6.615

kN

m

⋅

=

:=

Obciążenie stałe od krawężnika:

Gkr

1

kN

m

⋅

:=

Obciążenie stałe od ciężaru własnego dźwigara:

Gk3

1.24m

1m

+

(

) 1

⋅ m

2









27

⋅

kN

m

3

⋅

30.24

kN

m

⋅

=

:=

Suma obciążen stałych :

Gk

Gk1 Gbal1

+

Gbar

+

Ggzyms

+

Gkr

+

Gk3

+

69.586

kN

m

⋅

=

:=

Gd

Gk 1.35

⋅

93.941

kN

m

⋅

=

:=

2. OBCIĄŻENIA ZMIENNE

l1

1.795m

:=

l2

3m

:=

l3

4.545m

:=

n1

0.994

:=

n2

0.698

:=

n3

0.535

:=

n4

0.229

:=

n5

1.453

:=

n6

1.191

:=

n7

1.071

:=

n8

0.612

:=

Obciążenie tłumem na chodniku o wartości kombinacyjnej :

t1

3

kN

m

2

n5 n6

+

(

)

l1

⋅

2

⋅

7.119

kN

m

⋅

=

:=

Obciążenie ciągłe pasów:

q1

9

kN

m

2

n7 n8

+

(

)

l2

⋅

2

⋅

2.5

kN

m

2

n8

( )

l3

⋅

2

⋅

+

26.197

kN

m

⋅

=

:=

Obciążenie od koła pojazdu:

P

150kN n1

⋅

150kN n2

⋅

+

100kN n3

⋅

+

100kN n4

⋅

+

330.2 kN

⋅

=

:=

Wyznaczenie długości efektywnej belki

•

Długość efektywna belki:

leff

ln a1

+

a2

+

:=

a2

ln.

11.2m

:=

Rozpiętość w świetle:

Oparcie :

a1.

0.5m

:=

a2.

a1.

:=

- konstrukcja symetryczna

leff

ln. a1.

+

a2.

+

12.2 m

⋅

=

:=

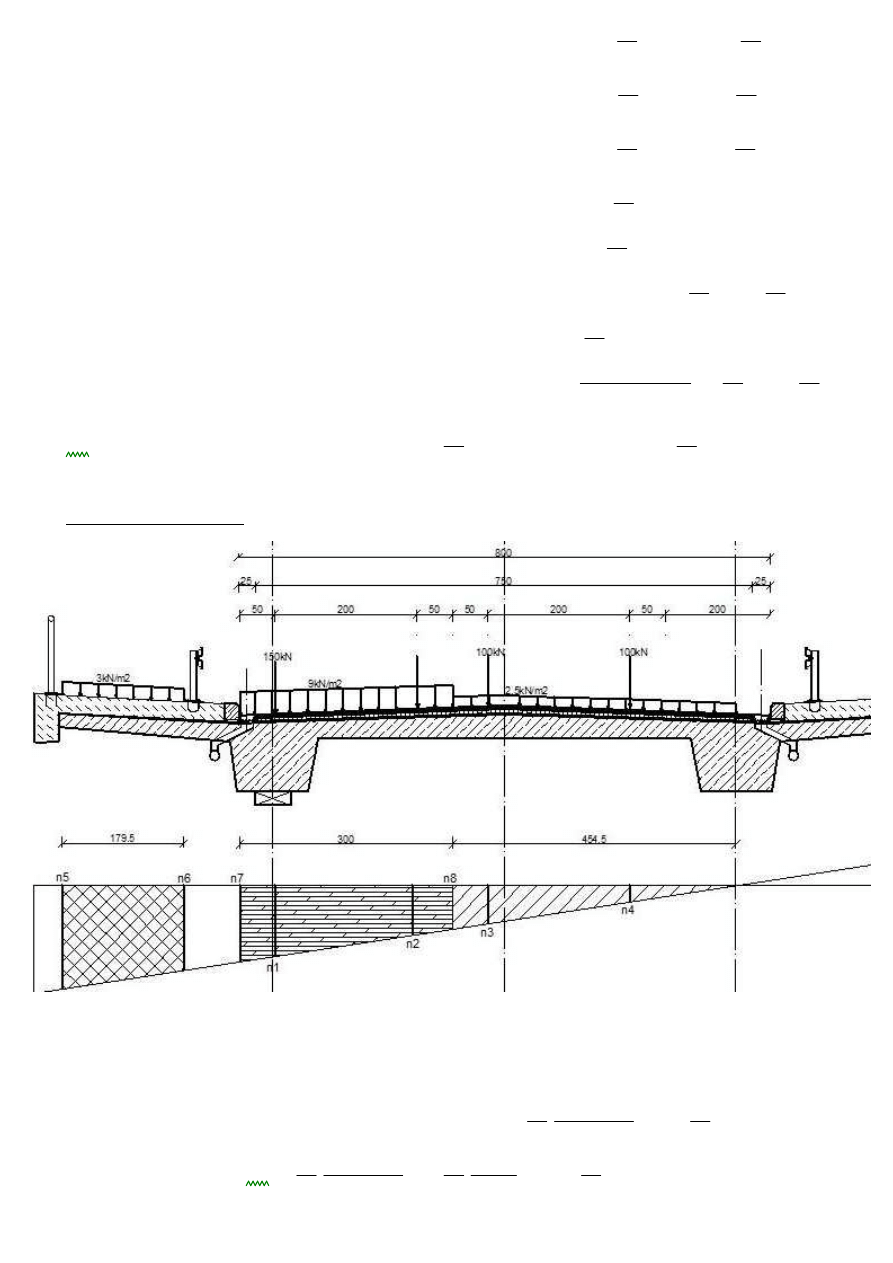
3. KOMBINACJA NA MAX MOMENT PRZĘSŁOWY

Obciążenie dżwigara:

Jako obciążenia równomiernie rozłożone przykładamy ciężar własny konstrukcji, obciążenie tłumem
na chodniku oraz obciążenia ciągłe pasów umownych, o wartościach podanych w punktach 1 i 2.
Ponadto przykładamy obciążenie skupione o wartości 2*P - od osi samochodu, w środku rozpiętości
dźwigara (dla belek o rozpiętości większej od 10m).

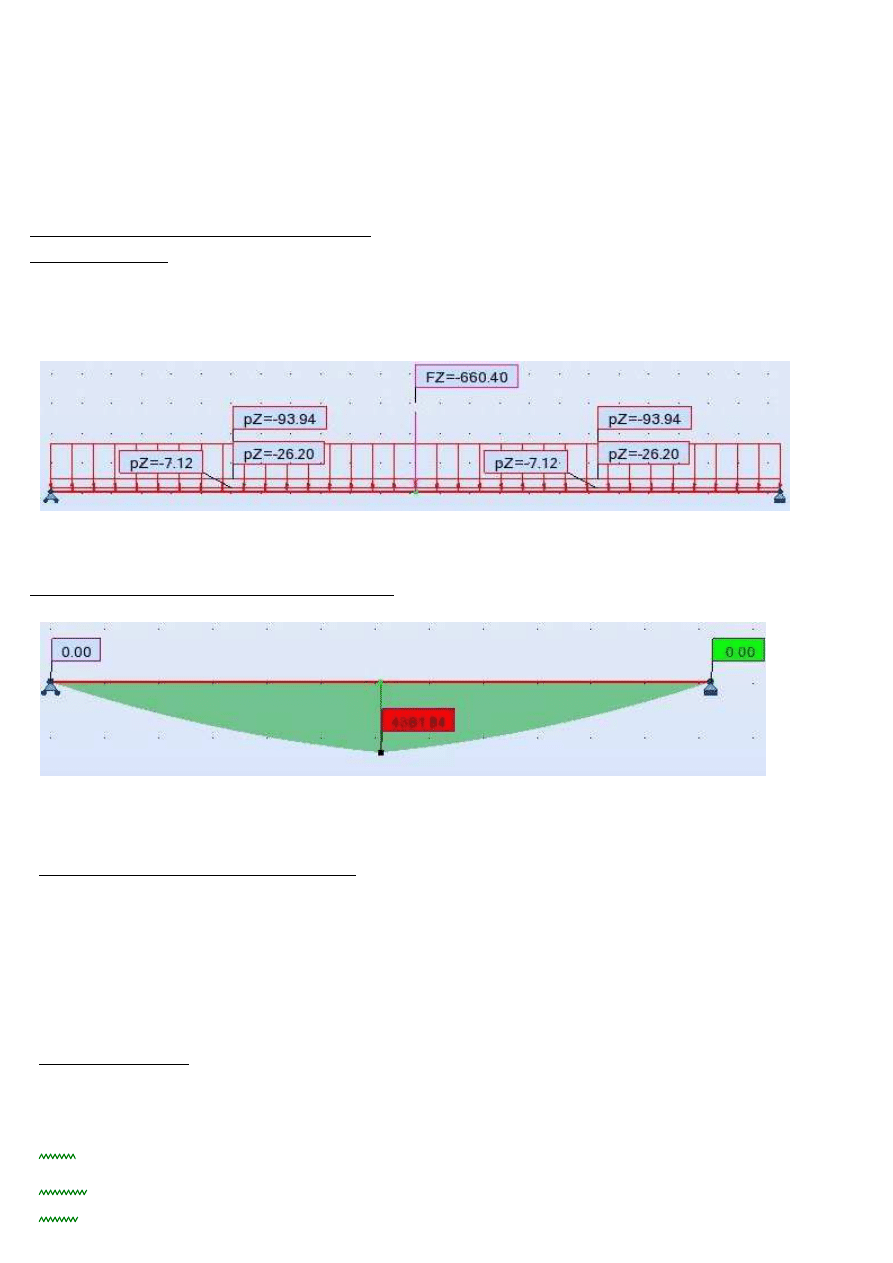
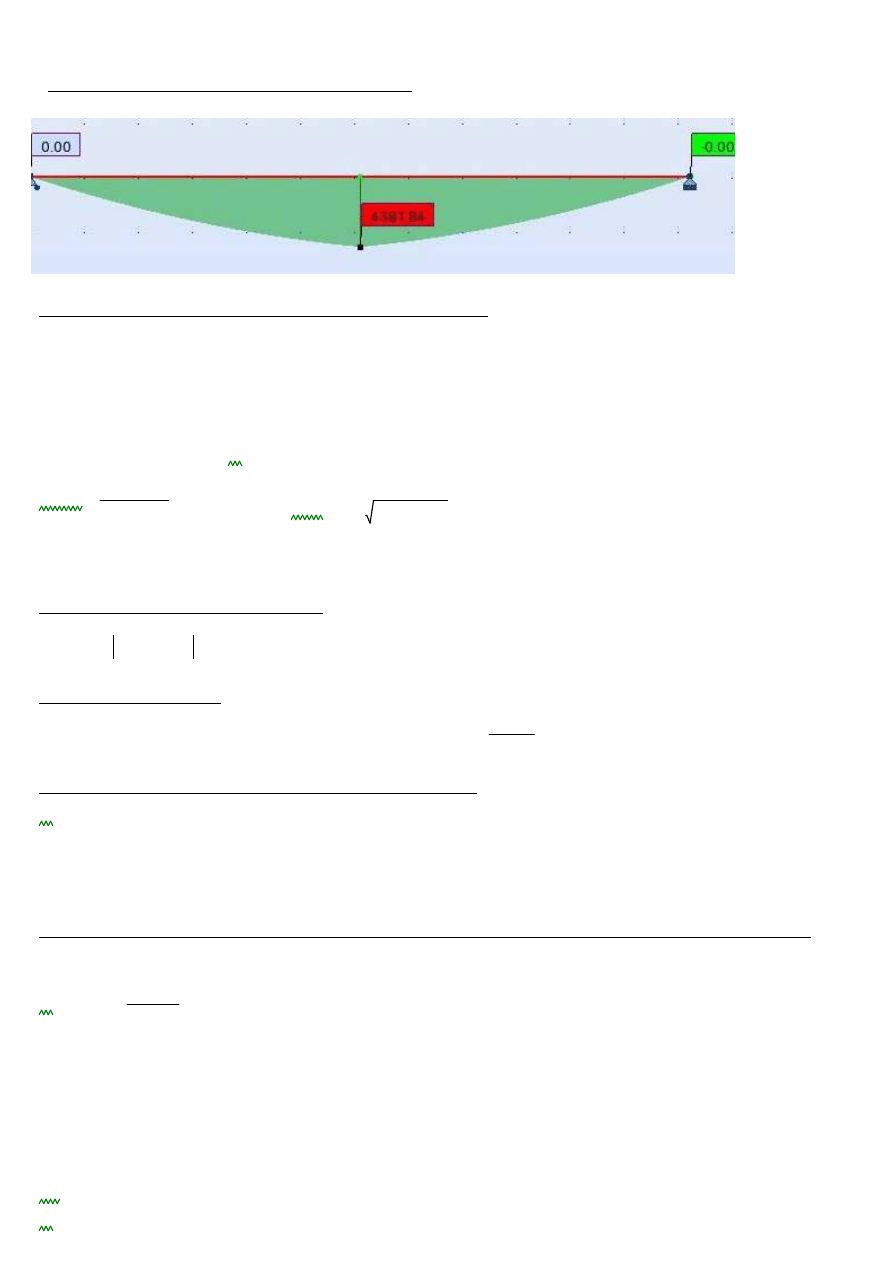
Wykres obliczeniowych momentów zginających dźwigar:

MEd.d

4381.84kN m

⋅

:=

4. WYMIAROWANIE PODCIĄGU NA ZGINANIE

Beton C50/60, stal RB550W - charakterystyki materiałowe jak dla płyty.

ϕp

32mm

:=

-średnica zbrojenia głównego podciągu

ϕpł

14mm

:=

-średnica zbrojenia głównego płyty

ϕs

10mm

:=

-średnica strzemion podciągu

4.1. Otulina zbrojenia

cmin.b

ϕp 32 mm

⋅

=

:=

cmin.dur

25mm

:=

EC2 tab. 4.3N, 4.4N

cmin

max cmin.b cmin.dur

,

10mm

,

(

)

32 mm

⋅

=

:=

∆cdev

10mm

:=

cnom

cmin ∆cdev

+

42 mm

⋅

=

:=

4.2. Wysokośc użyteczna dźwigara

wysokość dźwigara:

hp

1m

:=

szerokość dolnej podstawy przekroju teowego:

bw

1m

:=

wysokość płyty:

hpł 30 cm

⋅

=

dd

hp cnom

−

ϕs

−

0.5

ϕp

−

93.2 cm

⋅

=

:=

4.3.Zbrojenie w przęsłach

4.3.1. Zbrojenie minimalne przęsłowe.

bt

bw 100 cm

⋅

=

:=

d

dd 93.2 cm

⋅

=

:=

(dla przęsła)

Zalecana wartość minimalnego przekroju zbrojenia (EC2 p. 9.2.1.1 (1), wzór 9.1N)

As.min.1

0.26

fctm

fyk

⋅

bt

⋅

d

⋅

14.055 cm

2

⋅

=

:=

As.min.2

0.0013 bt

⋅

d

⋅

12.116 cm

2

⋅

=

:=

Minimalne zbrojenie ze względu na rysy (EC2 p. 7.3.2 (2))

kc

0.9

:=

k

0.65

:=

(dla środników większych od 0,80m)

fct.eff

fctm 2.9 MPa

⋅

=

:=

σs

220MPa

:=

(tab. 7.2N dla w

k

=0,3mm)

Act

0.5 hp

⋅

bt

⋅

5

10

3

×

cm

2

⋅

=

:=

pole przekroju betonu rozciąganego

As.min.3

kc k

⋅ f

ct.eff

⋅

Act

⋅

σs

38.557 cm

2

⋅

=

:=

-

As.min

max As.min.1 As.min.2

,

As.min.3

,

(

)

38.557 cm

2

⋅

=

:=

Zbrojenie maksymalne (EC2 p. 9.2.1.1 (3))

Acc

0.5 hp

⋅

bt

⋅

5000 cm

2

⋅

=

:=

pole przekroju betonu ściskanego

As.max

0.04 Acc

⋅

200 cm

2

⋅

=

:=

(wartość zalecana przez EC2-1-1)

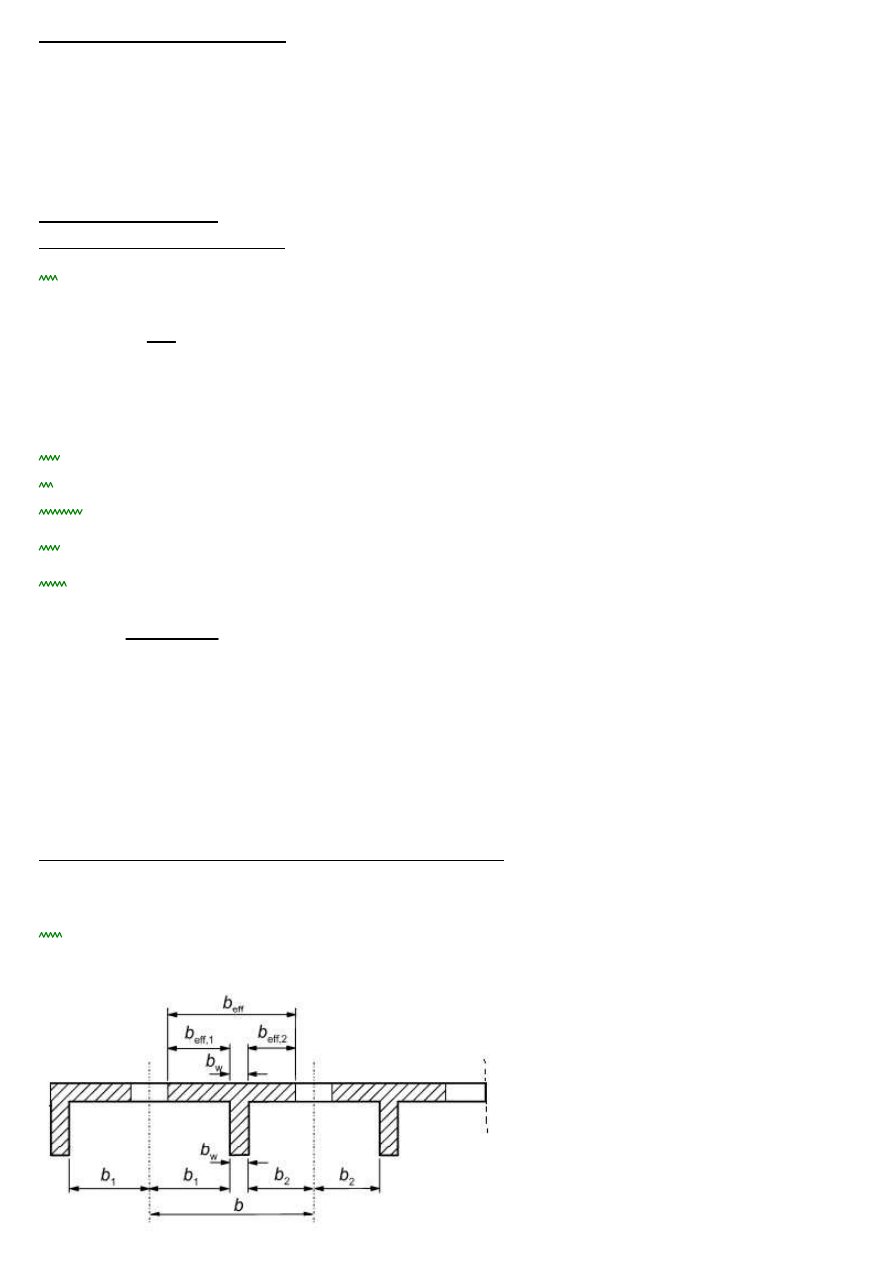
4.3.2. Szerokość efektywna belki teowej w przęśle wg. 5.3.2.1. EC2-1-1

bw 1 m

=

b1

288cm

:=

b2

142.5cm

:=

wg Rys.5.2 EC2

l0

leff 12.2 m

=

:=

(

)

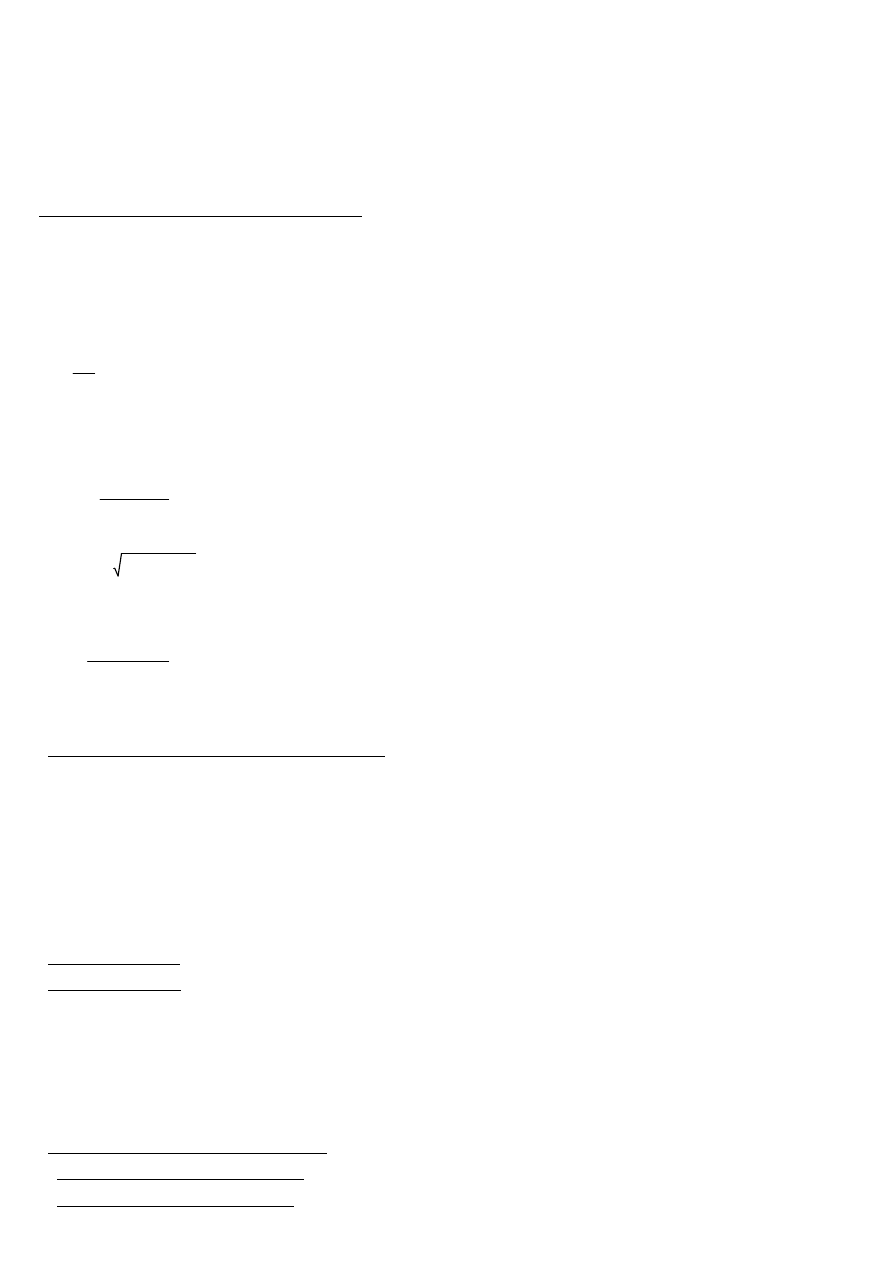
beff.1

min 0.2 b1

⋅

0.1 l0

⋅

+

0.2 l0

⋅

,

b1

,

(

)

1.796 m

=

:=

beff.2

min 0.2 b2

⋅

0.1 l0

⋅

+

0.2 l0

⋅

,

b2

,

(

)

1.425 m

=

:=

beff

beff.1 beff.2

+

bw

+

4.221 m

=

:=

<

b

6.36m

:=

4.3.3.Moment płytowy (wymiarowanie na zginanie)

MEd

MEd.d 4381.84 kN m

⋅

⋅

=

:=

d

0.932 m

=

(d=d

d

)

fcd 35.714 MPa

⋅

=

wytrzymałość obliczeniowa na ściskanie

beff 4.221 m

=

hpł 0.3 m

=

β

hpł

d

0.322

=

:=

η

1

:=

Mrdp.eff

β 1

0.5

β

−

(

)

⋅

d

2

⋅ b

eff η

⋅ f

cd

⋅

35365.95 kN m

⋅

⋅

=

:=

Mrdp.eff

35365.95 kN m

⋅

⋅

=

.

.

>

MEd 4381.84 kN m

⋅

⋅

=

Przekrój pozornie teowy

Sc.eff

MEd

fcd beff

⋅

d

2

⋅

0.033

=

:=

ξeff

1

1

2 Sc.eff

⋅

−

−

0.034

=

:=

.

.

<

ξeff.lim 0.493

=

przekrój pojedyńczo zbrojony

χeff

ξeff d

⋅

3.173 cm

⋅

=

:=

χeff hpł

<

1

=

As1

fcd beff

⋅

χeff

⋅

fyd

100.007 cm

2

⋅

=

:=

Przyjęto 13ϕ32, A

s1.prov

= 104.52 cm

2

4.3.4.Minimalny rozstaw prętów w świetle wg 8.2.(2)

zalecane :

k1.

1

:=

k2.

5mm

:=

dg

31.5mm

:=

- maksymalny wymiar ziaren kruszywa

smin

max

ϕs k1.

⋅

dg k2.

+

,

20mm

,

(

)

36.5 mm

⋅

=

:=

<

sprov

50mm

:=

ok

Przyjęto zbrojenie dźwigara dołem w przęśle 13 prętów ϕ32

4.4. Zbrojenie górą

Podpora A (skrajna)

Zbrojenie minimalne jak dla przęseł:

As.min 38.557 cm

2

⋅

=

Nad podporą przyjmujemy zbrojenie minimalne, ponieważ nie ma tam momentów ani sił
poprzecznych i przedłużamy je na całą długość belki górą:

As.prov.g

40.1cm

2

:=

5 fi 32

4.5. Zakotwienie prętów i zakład prętów.

4.5.1. Zakotwienie zbrojenia w przęśle

Graniczne naprężenie przyczepności

αct

1.0

:=

fctd

αct

fctk.0.05

γc

⋅

2.071 MPa

⋅

=

:=

η1

1

:=

dla warunków "dobrych" (współczynnik zależny od jakości warunków przyczepności i
pozycji pręta w czasie betonowania)

η2

1

:=

dla średnicy <= 32mm( współczynnik zależny od średnicy pręta)

wartość obliczeniowa granicznego naprężenia przyczepności dla prętów żebrowanych:

fbd

2.25

η1

⋅

η2

⋅

fctd

⋅

4.661 MPa

⋅

=

:=

Podstawowa długość zakotwienia

ϕp 32 mm

⋅

=

As1.req

202.862cm

2

:=

As1prov

203.58cm

2

:=

σsd

As1.req

As1prov

fyd

⋅

476.574 MPa

⋅

=

:=

lb.rqd

ϕp

4

σsd

fbd

⋅

81.803 cm

⋅

=

:=

Przyjęto:

lb.rqd

85cm

:=

Obliczeniowa długość zakotwienia

α1

1

:=

rozstaw prętów

s

82mm

:=

otulenie zbrojenia

cnom 42 mm

⋅

=

cd

min 0.5 s

⋅ c

nom

,

(

)

41 mm

⋅

=

:=

α2

1

0.15

cd ϕp

−

ϕp

⋅

−

0.958

=

:=

oraz

0.7

α2

≤

1

≤

przyjęto

α2

0.963

:=

α3

1

:=

α4

0.7

:=

α5

1

:=

lbd

α1 α2

⋅

α3

⋅

α4

⋅

α5

⋅

lb.rqd

⋅

57.298 cm

⋅

=

:=

lbd

60cm

:=

Przyjęto długość zakotwienia prętów na podporze równą 60cm.

4.5.2. Obliczeniowa długość zakładu

zgodnie z p 8.7.4.1 (3) dla średnicy równej 20 mm
lub większej zbrojenie poprzeczne na dł zakładu
musi mieć powierzchnię równą co najmniej
powierzchni pręta łączonego

λ

ϕp

2

4

π

⋅

ϕp

2

4

π

⋅

σsd

fyd

⋅

















−

ϕp

2

4

π

⋅

3.527

10

3

−

×

=

:=

K

0.05

:=

zbrojenie poprzeczne (strzemiona) bardziej od zewnętrznej powierzchni niż pręty główne

α3

min 1 max 1

K

λ

⋅

−

0.7

,

(

)

,

(

)

1

=

:=

pręty proste, rozciągane

α2 α3

⋅

0.7

≥

1

=

α6

1.5

:=

wg tablicy 8.3 (>50% prętów łączonych na zakład w całym
przekroju zbrojenia)

l0.min

max 0.3

α6

⋅

lb.rqd

⋅

15

ϕp

⋅

,

200mm

,

(

)

48 cm

⋅

=

:=

l0

max

α1 α2

⋅

α3

⋅

α6

⋅

lb.rqd

⋅

l0.min

,

(

)

122.761 cm

⋅

=

:=

-przyjmuję połączenie na zakład 125cm

4.6. KOMBINACJA NA MAX SIŁĘ ŚCINAJĄCĄ

Obciążenie dżwigara:

Jako obciążenia równomiernie rozłożone przykładamy ciężar własny konstrukcji, obciążenie tłumem na chodniku oraz
obciążenia ciągłe pasów umownych, o wartościach podanych w punktach 1 i 2. Ponadto przykładamy obciążenie
skupione o wartości 2*P - od osi samochodu, w odległości d (wys. użyteczna przekroju) od podpory (dla belek o
rozpiętości większej od 10m)

d

93.2 cm

⋅

=

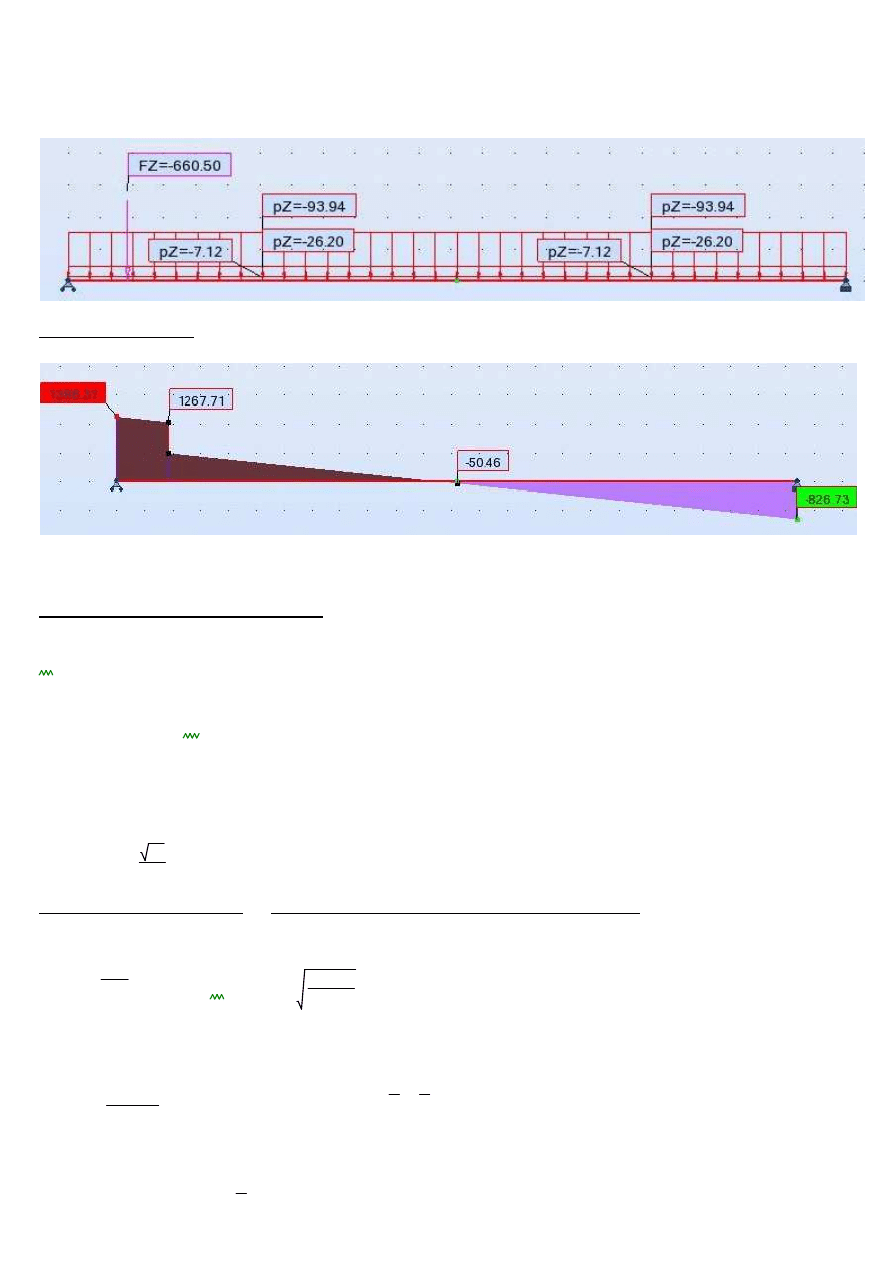
Wykres sił ścinających:

-

4.7. Wymiarowanie dźwigara na ścinanie

4.7.1. Zbrojenie w przęśle

d

dd 0.932 m

=

:=

wysokość użyteczna

z

0.9d

83.88 cm

⋅

=

:=

fywd

fyd 478.261 MPa

⋅

=

:=

Maksymalny rozstaw zbrojenia na ścinanie (EC2, p. 9.2.2 (6))

Θ

45deg

:=

α

90deg

:=

sl.max

0.75 d

⋅

1

cot

α

( )

+

(

)

⋅

69.9 cm

⋅

=

:=

Minimalny stopień zbrojenia na ścinanie (EC2 p. 9.2.2 (5))

fck 50 MPa

⋅

=

fyk 500 MPa

⋅

=

ρw.min

0.08

30

500

⋅

0.088 %

⋅

=

:=

4.7.1.1.wyznaczenie wartości V

Rd.c

potrzebnej do określenia odcinków I i II rodzaju w przęśle

bw 100 cm

⋅

=

najmniejsza szerokość strefy rozciąganej

CRd.c

0.18

γc

0.129

=

:=

k

min 1

200mm

d

+

2

,













1.463

=

:=

As1prov 203.58 cm

2

⋅

=

pole przekroju zbrojenia rozciąganego , które sięga na odl mnie mniejsza niz l.bd+d poza

rozważany przekrój

ρl

min

As1prov

bw d

⋅

0.02

,













0.02

=

:=

νmin

0.035 k

3

2

⋅

30

1

2

⋅

MPa

⋅

0.339 MPa

⋅

=

:=

σcp

0

:=

(siła podłużna zerowa)

k1

0.15

:=

VRd.c1

CRd.c k

⋅

100

ρl

⋅

30

⋅

(

)

1

3

⋅

MPa

⋅

k1 σcp

⋅

+









bw

⋅

d

⋅

686.425 kN

⋅

=

:=

VRd.c2

νmin k1 σcp

⋅

+

(

)

bw

⋅

d

⋅

316.241 kN

⋅

=

:=

VRd.c

max VRd.c1 VRd.c2

,

(

)

686.425 kN

⋅

=

:=

4.7.1.2. odcinek A -1

VEd

1386.31kN

:=

>

VRd.c 686.425 kN

⋅

=

=> odcinek II rodzaju

Przyjęto strzemiona sześciocięte

ϕs 10 mm

⋅

=

Asw

6

π ϕs

2

⋅

4

⋅

4.712 cm

2

⋅

=

:=

Rozstaw zbrojenia

s1

Asw z

⋅ f

ywd

⋅

cot

Θ

( )

⋅

VEd

13.637 cm

⋅

=

:=

s1

13cm

:=

<

sl.max 69.9 cm

⋅

=

OK

Przyjęto strzemiona sześciocięte ϕ10 co 13cm

Sprawdzenie krzyżulców betonowych ściskanych

αcw

1

:=

ν1

0.6 1

fck

250MPa

−













⋅

0.48

=

:=

-

VRd.max

αcw bw

⋅

z

⋅ ν

1

⋅

fcd

⋅

cot

Θ

( )

tan

Θ

( )

+

7189.714 kN

⋅

=

:=

>

VEd 1386.31 kN

⋅

=

krzyżulce nie ulegną zmiażdżeniu

Stopień zbrojenia na ścinanie (EC2 p. 9.2.2 (5))

ρw

Asw

s1 bw

⋅

sin

α

( )

⋅

0.362 %

⋅

=

:=

>

ρw.min 0.088 %

⋅

=

4.7.1.3. Wymiarowanie zbrojenia na odcinku 1-C

1267.71kN

660.4kN

−

607.31 kN

⋅

=

VEd

607.31kN

:=

<

VRd.c 686.425 kN

⋅

=

- odcinek I rodzaju

Przyjęto strzemiona czterocięte

ϕs 10 mm

⋅

=

Asw

6

π ϕs

2

⋅

4

⋅

4.712 cm

2

⋅

=

:=

Rozstaw zbrojenia

ρw.min 0.088 %

⋅

=

smax

Asw

ρw.min bw

⋅

53.773 cm

⋅

=

:=

sl.max 69.9 cm

⋅

=

max rozstaw zbrojenia w przęśle AB

Przyjęto strzemiona czterocięte ϕ10 co 30cm

Sprawdzenie krzyżulców ściskanych betonowych

ν

0.6 1

fck

250MPa

−













⋅

0.48

=

:=

0.5 bw

⋅

d

⋅ ν

⋅ f

cd

⋅

7988.571 kN

⋅

=

>

VEd 607.31 kN

⋅

=

=> krzyżulce nie ulegną zmiażdżeniu

-

4.7.2. Zbrojenie na ścinanie w poszczególnych częsciach podciągu

odcinek A-1 : strzemiona sześciocięte ϕ10 co 13cm
odcinek 1-C : strzemiona czteroocięte ϕ10 co 30cm

4.7.3. Ścinanie między półką a środnikiem

Wykres obliczeniowych momentów zginających dźwigar:

4.7.3.1. Wymiarowanie stref o półkach ściskanych (odcinki A-C, C-B)

W pdoporze A i B nie występuje zbrojenie podłużne w półkach - styki nie wymagają dozbrojenia.

∆xAC

6.1m

:=

xeff.A

0

:=

Fd.A

0

:=

10.2.1. Obliczenie wysokości strefy ściskanej i siły w punkcie C

MEd.C

4381.84kN m

⋅

:=

d

dd 0.932 m

=

:=

beff 4.221 m

=

Sc.eff

MEd.C

fcd beff

⋅

d

2

⋅

0.033

=

:=

ξeff

1

1

2 Sc.eff

⋅

−

−

0.034

=

:=

< ξeff.lim 0.493

=

xeff.C

ξeff d

⋅

31.728 mm

⋅

=

:=

Fd.C

0.5 beff bw

−

(

)

⋅

xeff.C

⋅

fcd

⋅

1824.912 kN

⋅

=

:=

4.7.3.2. Różnica sił przypadających na styk

∆FdAC

Fd.C Fd.A

−

1824.912 kN

⋅

=

:=

4.7.3.3. Naprężenia w styku

Odcinek A-C:

∆x

∆xAC

:=

∆Fd

∆FdAC

:=

vEd.AC

∆Fd

hpł ∆x

⋅

819.672 kPa

⋅

=

:=

4.7.3.4. Sprawdzenie czy jest konieczne dodatkowe zbrojenie styku

k

0.4

:=

vEd.AC 819.672 kPa

⋅

=

<

k fctd

⋅

828.571 kPa

⋅

=

Naprężenia na odcinku A-C spełniają warunek normowy. Odcinek ten nie wymagaja dozbrojenia.

4.7.3.5. Sprawdzenie krzyżulców betonowych ściskanych w półce z uwagi na zmiażdżenie dla największego naprężenia

Θf

45deg

:=

ν

0.6 1

fck

250MPa

−













⋅

0.48

=

:=

vEd.max

vEd.AC 819.672 kPa

⋅

=

:=

<

ν fcd

⋅

sin

Θf

( )

⋅

cos

Θf

( )

⋅

8571.429 kPa

⋅

=

krzyżulce betonowe nie ulegną zmiażdżeniu

4.7.4. Zbrojenie przeciwskurczowe

Minimalne zbrojenie ze względu na rysy (EC2 p. 7.3.2 (2))

kc

0.9

:=

k

0.65

:=

(dla środników większych od 0,80m)

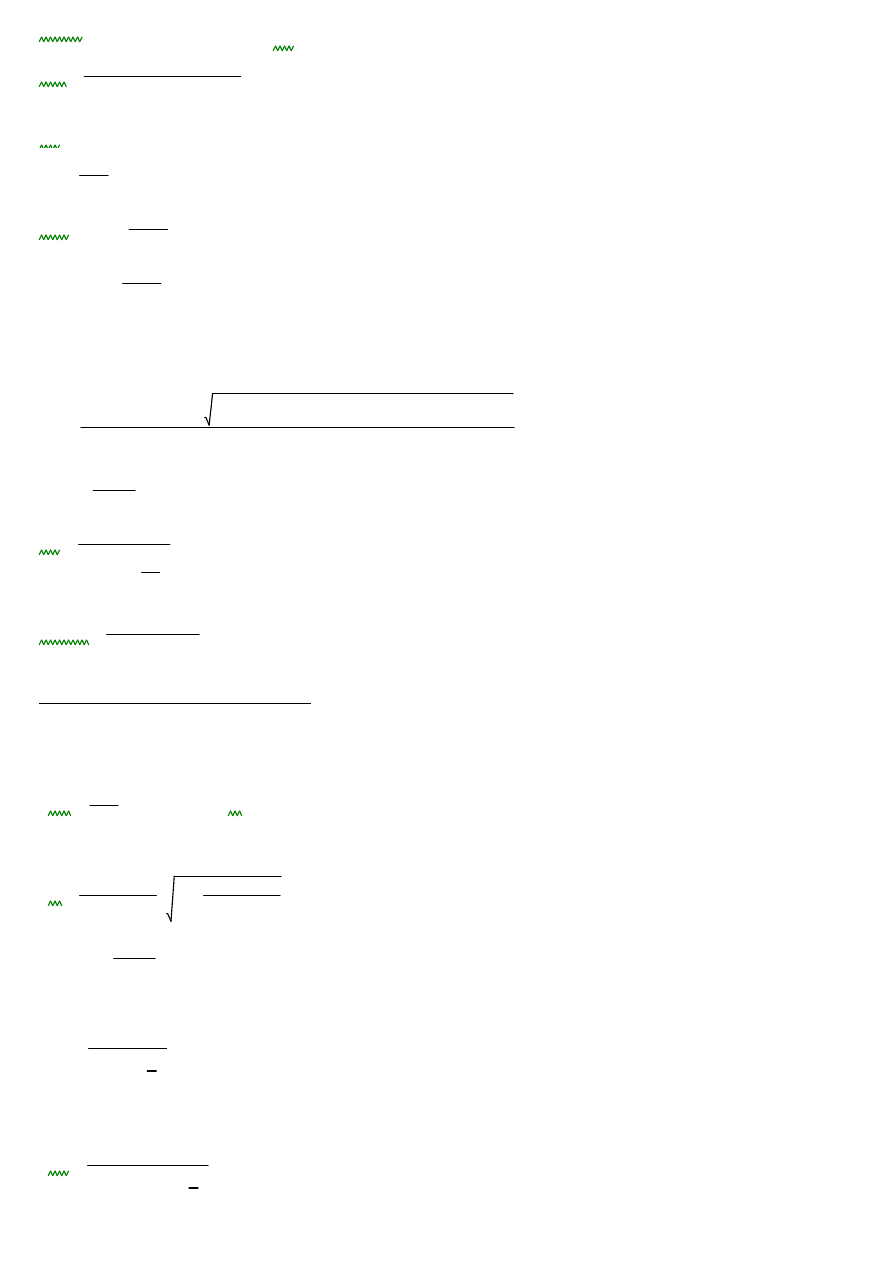
fct.eff

fctm 2.9 MPa

⋅

=

:=

σs

280MPa

:=

(tab. 7.2N dla w

k

=0,3mm)

Act

164cm

190cm

+

(

) 115

⋅

cm

2

2.036 m

2

⋅

=

:=

k

0.65

=

kc

0.4

:=

αe

Es

Ecm

6.25

=

:=

As1

26

π

⋅

32mm

2









2

⋅

209.104 cm

2

⋅

=

:=

As2

6

π

⋅

32mm

2









2

⋅

48.255 cm

2

⋅

=

:=

beff 4.221 m

=

a2

cnom ϕs

+

0.5

ϕp

+

0.068 m

=

:=

xII

αe

−

As1 As2

+

(

)

⋅

αe

2

As1 As2

+

(

)

2

⋅

2 beff

⋅

αe

⋅

As1 d

⋅

As2 a2

⋅

+

(

)

⋅

+

+

beff

0.207 m

=

:=

MEk

MEd.d

1.35

3245.807 kN m

⋅

⋅

=

:=

σs

MEk

As1 d

xII

3

−













⋅

179.874 MPa

⋅

=

:=

As.min

kc k

⋅ f

ct.eff

⋅

Act

⋅

σs

85.324 cm

2

⋅

=

:=

As.prov

87.92cm

2

:=

28 ϕ20

-

6. WYMIAROWANIE PODCIĄGU W SGU

6.1. Sprawdzenie naprężeń dla kobinacji charakterystycznej w SGU

W przypadku przekroju pozornie teowego naprężenia sprawdzamy jak dla prostokąta przyjmując b=b.eff

α1

Es

Ecm

6.25

=

:=

b

beff

:=

dd 0.932m

=

MEd.d 4.382 10

3

×

kN m

⋅

⋅

=

As1.prov

152.72cm

2

:=

Położenie osi obojętnej :

x

α1 As1.prov

⋅

b

1

2 b

⋅ d

⋅

α1 As1.prov

⋅

+

1

−













18.394 cm

⋅

=

:=

MEd.k

MEd.d

1.35

3.246

10

3

×

kN m

⋅

⋅

=

:=

Naprężenia w betonie :

σc

2MEd.k

b x

⋅

d

x

3

−









⋅

9.603 MPa

⋅

=

:=

<

0.6 fck

⋅

30 MPa

⋅

=

OK

d

0.932 m

=

Naprężenia w stali :

σs

MEd.k

As1.prov dd

x

3

−









⋅

244.098 MPa

⋅

=

:=

<

0.8 fyk

⋅

400 MPa

⋅

=

OK

6.1. Sprawdzenie zarysowania dla kombinacji prawie stałej

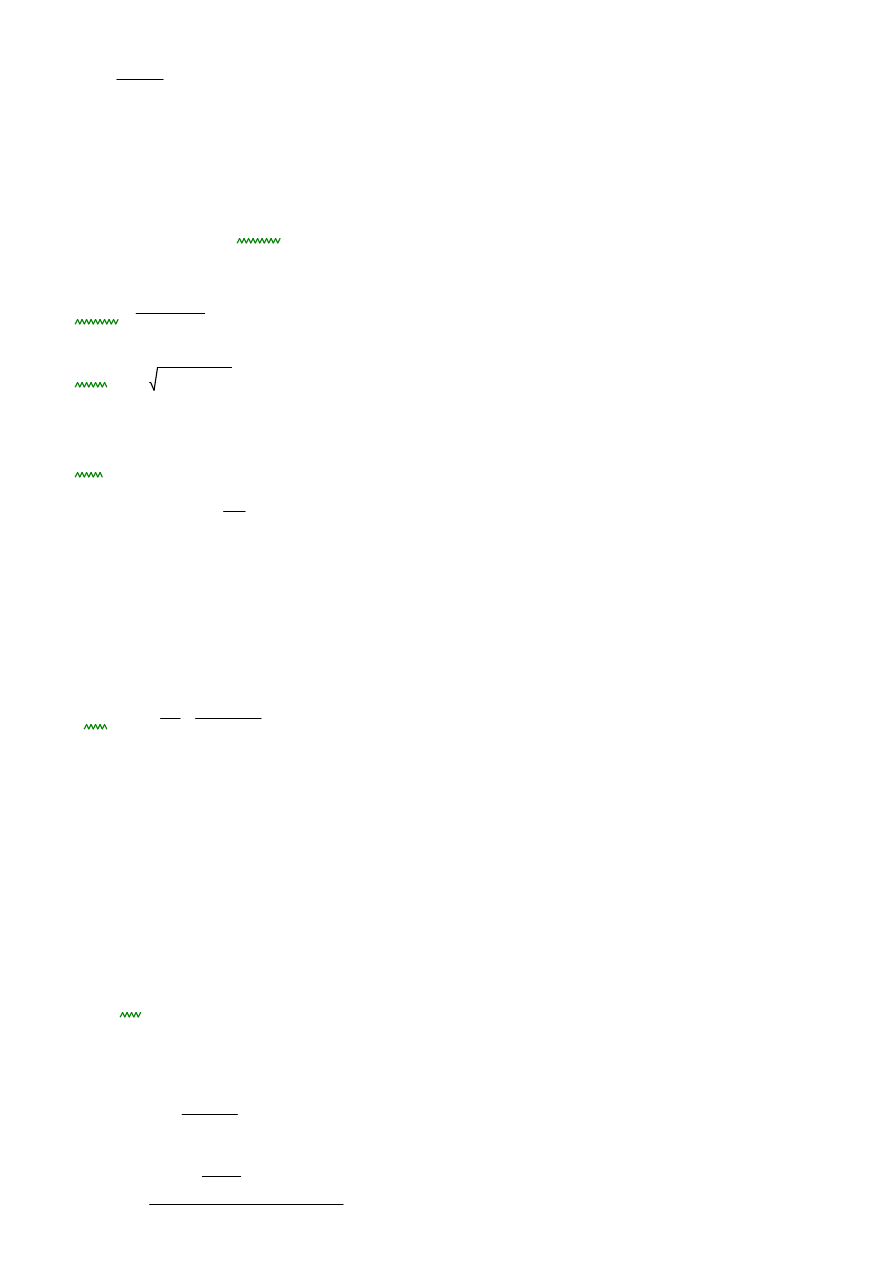
6.1.1 Moment rysujący:

wc

bw hp

2

⋅

6

0.167 m

3

⋅

=

:=

Mcr

fctm wc

⋅

483.333 kN m

⋅

⋅

=

:=

MEd.k 3.246 10

3

×

kN m

⋅

⋅

=

.

.

>

Mcr 483.333 kN m

⋅

⋅

=

przekrój zarysowany

6.1.2 Minimalne zbrojenie ze względu na zarysowanie

k

0.65

=

kc 0.4

=

fct.eff

fctm

:=

Act 2.036m

2

=

A.ct - pole przekroju strefy rozciąganej betonu wyznaczane obliczeniowo dla momentu rysującego

Sc.eff

Mcr

fcd beff

⋅

d

2

⋅

3.691

10

3

−

×

=

:=

ξeff

1

1

2 Sc.eff

⋅

−

−

3.698

10

3

−

×

=

:=

.

.

<

ξeff.lim 0.493

=

χeff.1

ξeff d

⋅

0.345 cm

⋅

=

:=

χeff.1 hpł

<

1

=

Act

hpł χeff

−

(

)

beff

⋅

hp hpł

−

(

)

bt

⋅

+

1.832 m

2

=

:=

As.min.z

k kc

⋅

fct.eff

⋅

Act

σs

⋅

56.601 cm

2

⋅

=

:=

.

.

<

As1.prov 152.72 cm

2

⋅

=

OK

-

6.1.3 Metoda uproszczona

fctm 2.9 MPa

⋅

=

ϕ

ϕs

≤

ϕsg

8mm

:=

wg. tab 7.2 dla σ.s=360 MPa

hcr

hp 0.5

⋅

0.5 m

=

:=

ϕs

ϕsg

2.9

2.9









⋅

hcr

8 hp d

−

(

)

⋅

⋅

7.353

10

3

−

×

m

=

:=

.

.

<

ϕp 0.032 m

=

Warunek spełniony

6.1.4 Obliczenie szerokości rys

maksymalna średnica rys przyjęta z tablicy 7.1

•

wmax

0.3mm

:=

szerokość rysy

•

wk

sr.max εsm εcm

−

(

)

:=

sr.max

s.r.max - maksymalny rozstaw rys w obliczanym elemencie

ε.sm- średnie odkształcenie zbrojenia rozciąganego pod wpływem odpowiedniej kombinacji obciązeń

ε.cm - średnie odkształcenie betonu na odcinku między rysami

εsm εcm

−

r

:=

εsm εcm

−

k1

0.4

:=

przy obciążeniach długotrwałych

χeff 3.173 cm

⋅

=

Ac.eff

hpł χeff

−

(

)

beff

⋅

hp hpł

−

(

)

bw

⋅

+

1.832 m

2

=

:=

ρp.eff

As1.prov

Ac.eff

:=

r

σs k1

fct.eff
ρp.eff

⋅

1

α1 ρp.eff

⋅

+

(

)

⋅

−

Es

4.883

10

4

−

×

=

:=

maksymalny rozstaw rys

•

sprov 50 mm

⋅

=

.

.

<

smax

5 cnom 0.5 ϕp

⋅

+

(

)

⋅

290 mm

⋅

=

:=

OK możemy korzystać z wzoru:

k1

0.8

:=

współczynnik dla prętów żebrowanych zależny od warunków przyczepnośći

k2

0.5

:=

współczynnik zależny od rozkładu odkształceń na wysokości przekroju przy zginaniu

k3

3.4

:=

k4

0.425

:=

slmax

0.75 d

⋅

69.9 cm

⋅

=

:=

maksymalny rozstaw podłuzny strzemion

sr.max

k3 cnom

⋅

k1 k2

⋅

k4

⋅

ϕp

ρp.eff

⋅

+

79.551 cm

⋅

=

:=

spod sbmax

<

warunek spełniony

szerokość rys :

maksymalny poprzeczny rozstaw
ramion strzemion

stmax

min 0.75d 600mm

,

(

)

60 cm

⋅

=

:=

wk

sr.max r⋅ 0.388 mm

⋅

=

:=