P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

1

1.

Przekształcenie zadania programowania liniowego w model zapisany

w arkuszu Excela

Przykładowe zadanie programowania liniowego

Rozwiązać następujące zadanie programowania liniowego wykorzystując Excela oraz dodatek Solver.

1

x

,

2

x

,

3

x

- zmienne decyzyjne

max

6

,

4

9

7

3

2

1

→

+

+

x

x

x

funkcja celu

przy ograniczeniach

9900

4

7

8

3

2

1

≤

+

+

x

x

x

2800

9

,

0

2

5

,

2

3

2

1

≤

+

+

x

x

x

ograniczenia funkcyjne

11700

1

,

4

10

1

3

2

1

=

+

+

x

x

x

12100

9

4

3

,

4

3

2

1

≥

+

+

x

x

x

0

,

0

,

0

3

2

1

≥

≥

≥

x

x

x

- warunki nieujemności zmiennych

Podstawową zasadą, na jakiej jest oparte przenoszenie do Excela modeli programowania liniowego i nielinio-
wego jest konieczność podjęcia przez użytkownika decyzji, które komórki w arkuszu będą rolę zmiennych. Wg
tej zależności („komórka-zmienna”) tworzone są formuły oraz wpisy w polach dodatku Solver.

Przykładowy schemat rozmieszczenia danych w Excelu dla zadania programowania liniowego

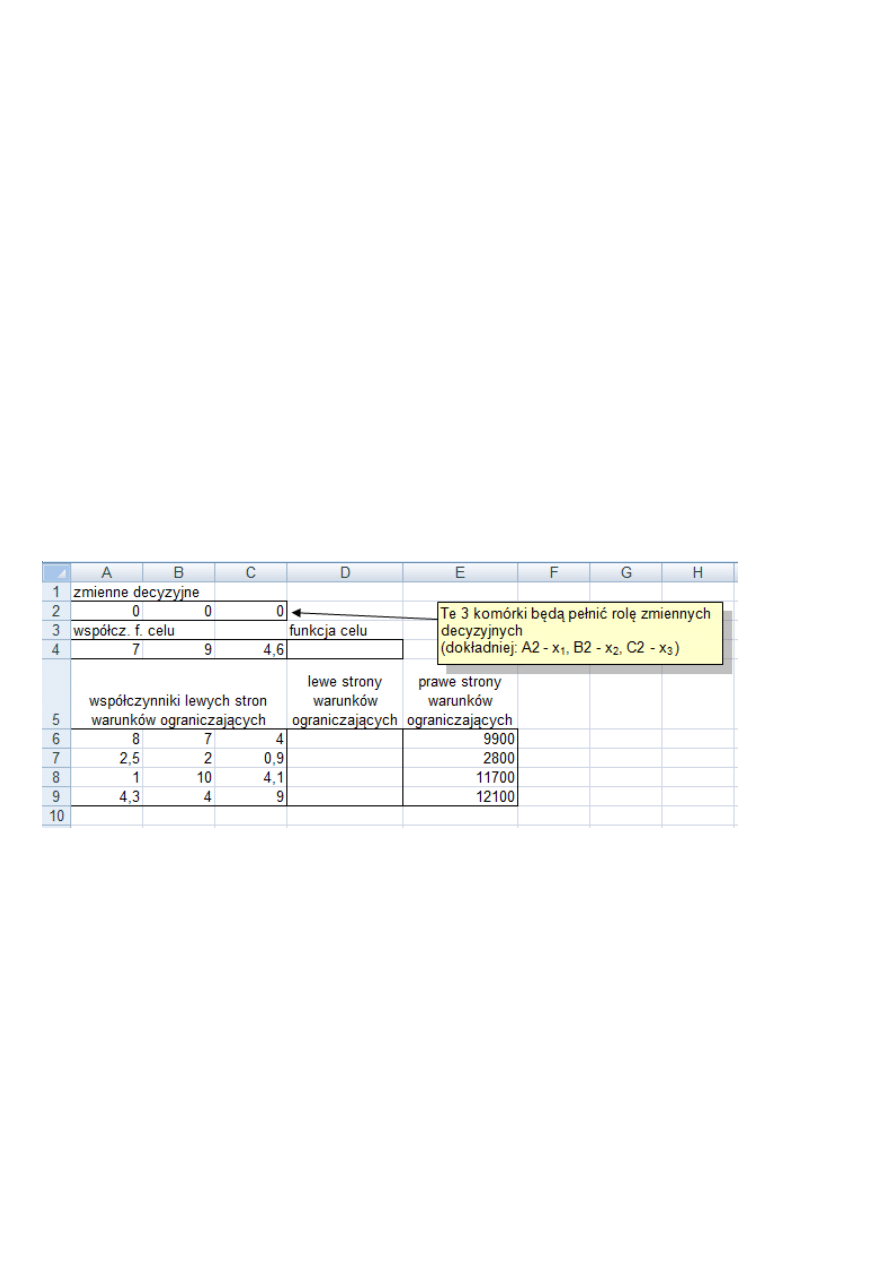
Przyjmujemy, że zmiennym decyzyjnym odpowiadają w arkuszu następujące komórki:

A2 -

1

x

, B2 -

2

x

, C2 -

3

x

.

Komórki pełniące rolę zmiennych zostały wypełnione zerami. Nie jest to jednak konieczne – komórki te mogą
pozostać puste, ponieważ zostaną potraktowane przez Excela tak, jakby zawierały zera.
W arkuszu umieszczone są także parametry tzn. liczby będące współczynnikami funkcji (A4:C4) celu oraz wa-
runków ograniczających (A6:C9, E6:E9). Rozmieszczenie to może być w zasadzie dowolne, ale jego odpo-
wiedni dobór ma bardzo duże znaczenie dla wygody wprowadzania formuł.

Ponieważ współczynniki funkcji celu znajdują się w komórkach A4, B4 i C4, a zatem odpowiednikiem funkcji
celu

3

2

1

6

,

4

9

7

x

x

x

+

+

będzie formuła

=A4*A2+B4*B2+C4*C2

Zastosujemy jednak prostszą we wprowadzaniu (zwłaszcza, jeżeli użyty zostanie kreator funkcji0 równoważną
formułę

=SUMA.ILOCZYNÓW(A4:C4;A2:C2).

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

2

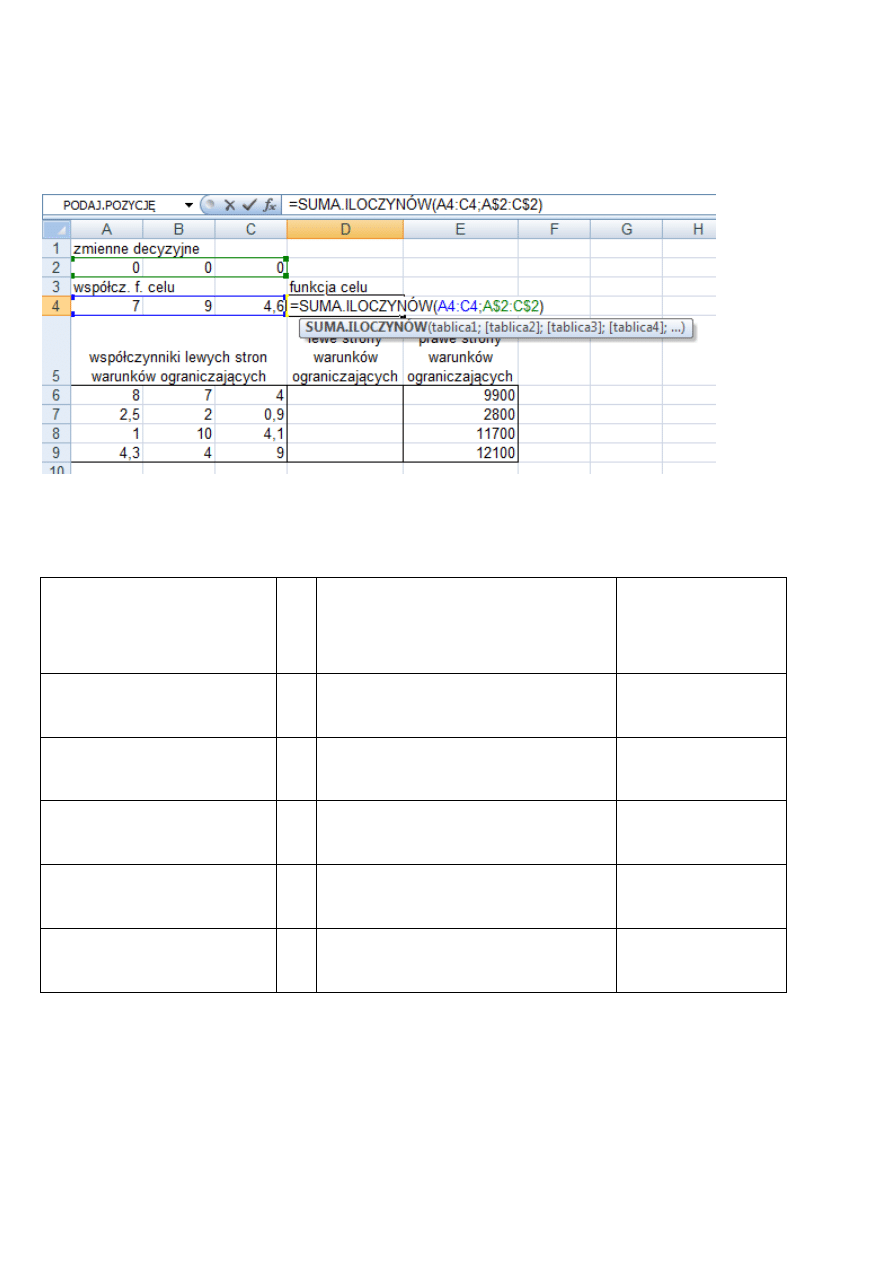
Jak widać, funkcja celu jest podobna do lewych stron warunków ograniczających (wszystkie są sumami ilo-
czynów liczb i zmiennych). Dzięki temu formuła reprezentująca w arkuszu funkcję celu zostanie wykorzystana
do stworzenia, przy pomocy kopiowania, formuł reprezentujących lewe strony warunków ograniczających W
tym celu formuła ta musi być wpisana w postaci

=SUMA.ILOCZYNÓW(A4:C4;A$2:C$2)

Dzięki zastosowaniu adresacji względnej („zablokowania” przy pomocy znaków $ odwołań do zakresu A2:C2)
po skopiowaniu D4 do D6:D9 otrzymamy formuły oznaczające lewe strony warunków ograniczających.
W tabeli poniżej jest podane są zależności pomiędzy formułami matematycznymi a „Excelowymi”.

Informacja na temat formuł: wprowadzanej i kopiowanych

Zapis matematyczny

Formuły „dosłowne” tzn. takie, które

należałoby wpisać przy literalnym

„przełożeniu” zapisu matematycznego

na składnię Excela

K

om

ór

ka

Formuły z SUMA.ILOCZYNÓW odpowiada-

jące formułom „dosłownym”

Uwagi

3

2

1

6

,

4

9

7

x

x

x

+

+

=A4*A2+B4*B2+C4*C2

D4

=SUMA.ILOCZYNÓW(A4:C4;A$2:C$2)

Wprowadzona przez użyt-

kownika

3

2

1

4

7

8

x

x

x

+

+

=A6*A2+B6*B2+C6*C2

D6

=SUMA.ILOCZYNÓW(A6:C6;A$2:C$2)

Otrzymana przez

kopiowanie z D4

3

2

1

9

,

0

2

5

,

2

x

x

x

+

+

=A7*A2+B7*B2+C7*C2

D7

=SUMA.ILOCZYNÓW(A7:C7;A$2:C$2)

Otrzymana przez

kopiowanie z D4

3

2

1

1

,

4

10

1

x

x

x

+

+

=A8*A2+B8*B2+C8*C2

D8

=SUMA.ILOCZYNÓW(A8:C8;A$2:C$2)

Otrzymana przez

kopiowanie z D4

3

2

1

9

4

3

,

4

x

x

x

+

+

=A9*A2+B9*B2+C9*C2

D9

=SUMA.ILOCZYNÓW(A9:C9;A$2:C$2)

Otrzymana przez

kopiowanie z D4

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

3

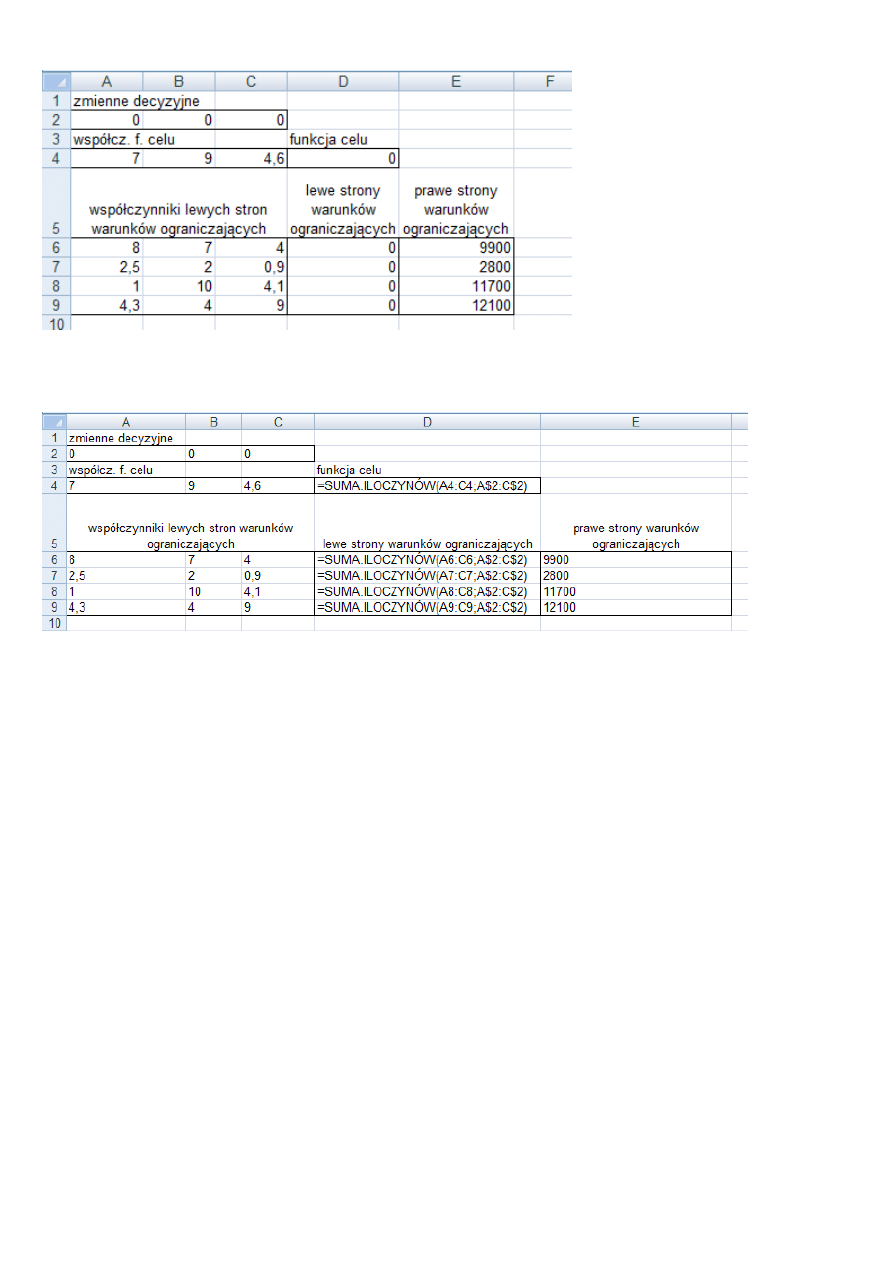
Widok arkusza po skopiowaniu D4 na D6:D11. Zarówno komórka z funkcją celu (D4) jak i komórki z lewymi
stronami warunków ograniczających (D6, D7, D8, D9, czyli zakres D6:D9) wyświetlają wartości zerowe, po-
nieważ komórki pełniące rolę zmiennych („iksów”) zawierają wyłącznie zera.

Widok formuł w arkuszu otrzymanych po skopiowaniu.

Pełna lista zależności pomiędzy zapisem matematycznym a modelem Excelowym zapisana przy pomocy adre-
sów komórek wygląda następująco:

A2 B2 C2

1

x

,

2

x

,

3

x

- zmienne decyzyjne

D4

max

6

,

4

9

7

3

2

1

→

+

+

x

x

x

funkcja celu

przy ograniczeniach

D6

9900

4

7

8

3

2

1

≤

+

+

x

x

x

E6

D7

2800

9

,

0

2

5

,

2

3

2

1

≤

+

+

x

x

x

E7

ograniczenia funkcyjne

D8

11700

1

,

4

10

1

3

2

1

≤

+

+

x

x

x

E8

D9

12100

9

4

3

,

4

3

2

1

≤

+

+

x

x

x

E9

A2 B2 C2

0

,

0

,

0

3

2

1

≥

≥

≥

x

x

x

warunki nieujemności zmiennych

Wszystkie niezbędne liczby oraz formuły zostały wprowadzone do arkusza. Należy teraz uruchomić dodatek
optymalizacyjny Solver (Menu Narzędzia – Solver, w Excelu 2007/2010 Dane-Solver).

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

4

Opis wprowadzania danych do Solvera - Excel w wersjach do 2007 włącznie

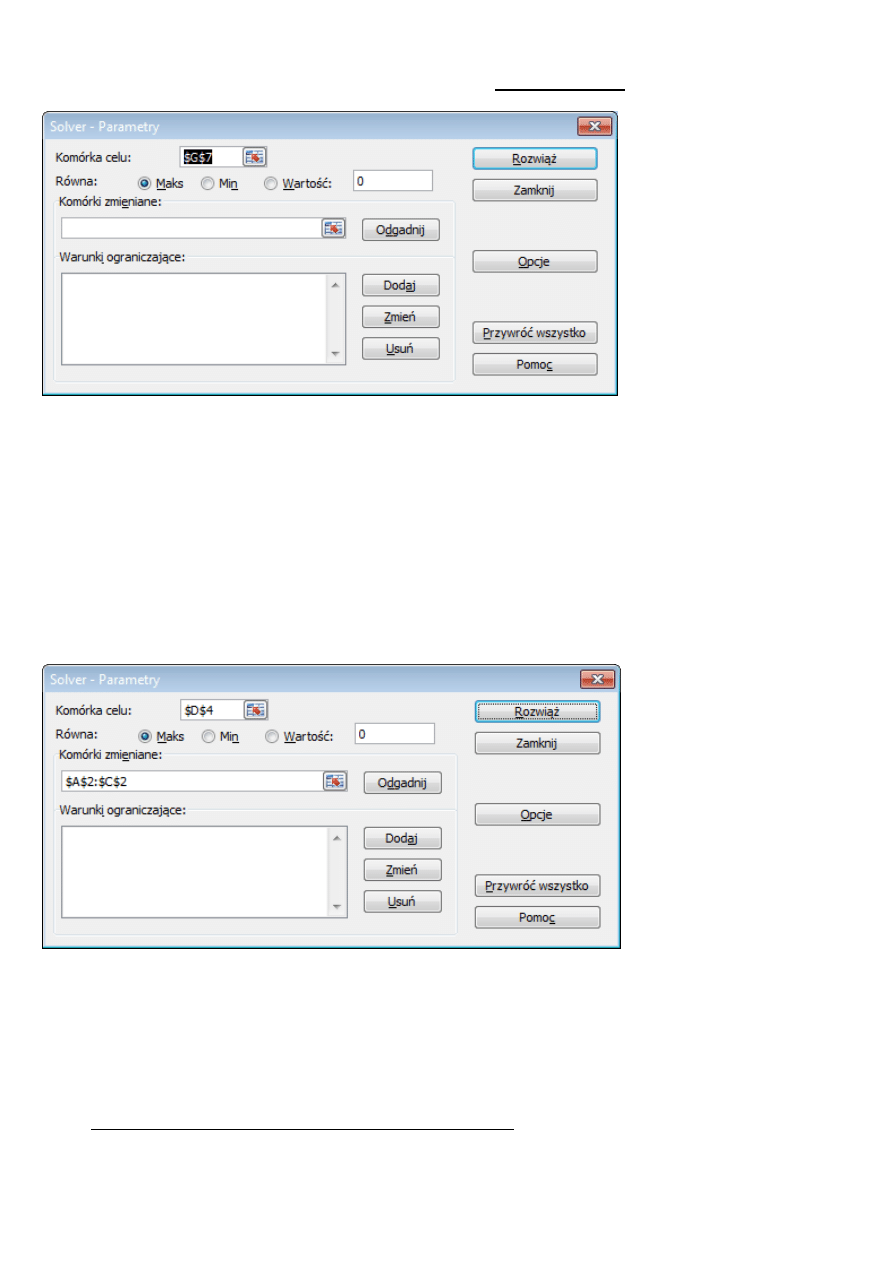
Główne okno Solvera (Solver-Parametry) po uruchomieniu Solvera

Pole Komórka celu w nowootwartym oknie Solvera Solver- Parametry jest zawsze ustawiona na komórkę bie-
żą

cą (na zrzucie ekranu G7). Z powyższego powodu najwygodniej jest ustawić wcześniej jako komórkę bieżącą

komórkę pełniącą rolę funkcji celu (tzn. zawierającą odpowiednią formułę). W przypadku niniejszego zadania
będzie to komórka D4.

Następnie należy wybrać typ optymalizacji tzn. maksymalizację funkcji celu w opcji Równa. Ponieważ Maks
jest ustawieniem domyślnym tej opcji, można ja pominąć.

W pole Komórki zmieniane należy wpisać zakres A2:C2.

Wygląd okna Solver-Parametry po wprowadzeniu w/w danych jest przedstawiony na rys. 7.

Główne okno Solvera (Solver-Parametry) z ustawionymi polami Komórka celu, Równa i Komórki zmieniane.

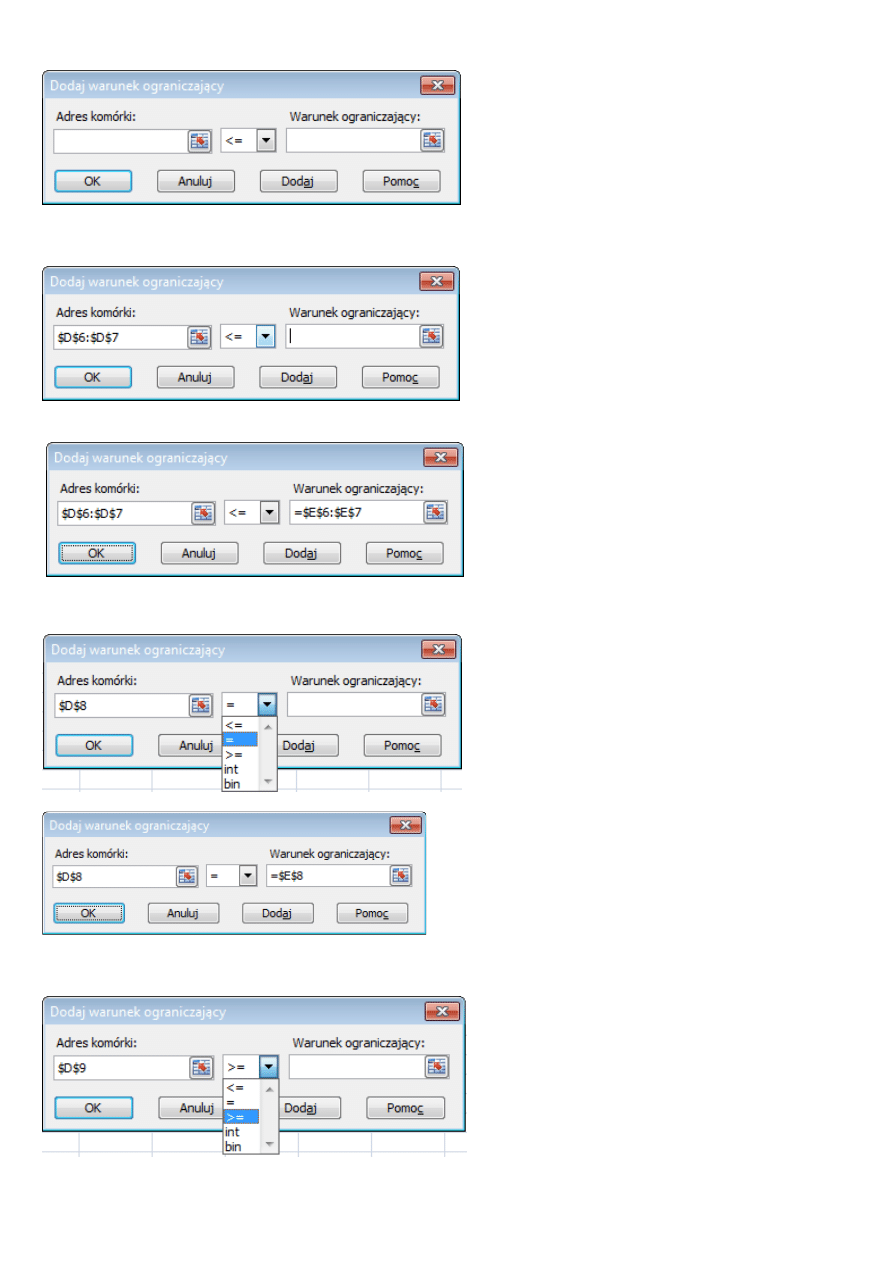
Warunki ograniczające wpisuje się w oddzielnym oknie Dodaj warunek ograniczający otwieranym po kliknię-
ciu Dodaj w oknie Solver-Parametry.

Uwaga! Pole Warunki ograniczające jest tylko listą – nie można w nie nic wpisywać!

Uwaga

! Gdy jest otwarte okno Dodaj warunek ograniczający (lub analogiczne Zmień warunek ograniczający),

wtedy główne okno Solvera (Solver-Parametry) jest niewidoczne.
Uwaga! Można wpisywać adresy bez dolarów (znaki $ i tak zostaną przez Excela dostawione, podobnie
jak znaki = w polu Warunek ograniczający

).

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

5

Nowootwarte okno Dodaj warunek ograniczający.

Wpisywanie dwóch warunków D6<=E6, D7<=E7 „wspólnie”.

Nierówność <= jest ustawieniem domyślnym więc nie trzeba nic zmieniać w środkowym polu i można przejść
do wpisywania prawej strony (pole Warunek ograniczający).

Ten zapis odpowiada grupie warunków D6<=E6, D7<=E7,

Po kliknięciu Dodaj otwiera się ponownie okno dodawania warunków. Należy wpisać warunek D8=E8.

Uwaga – trzeba pamiętać o wyborze równości = (domyślne ustawienie to <=).

Warunek D8=E8.

Po kliknięciu Dodaj otwiera się ponownie okno dodawania warunków. Należy wpisać warunek D9>=E9.

Uwaga – trzeba pamiętać o wyborze nierówności >= (domyślne ustawienie to <=).

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

6

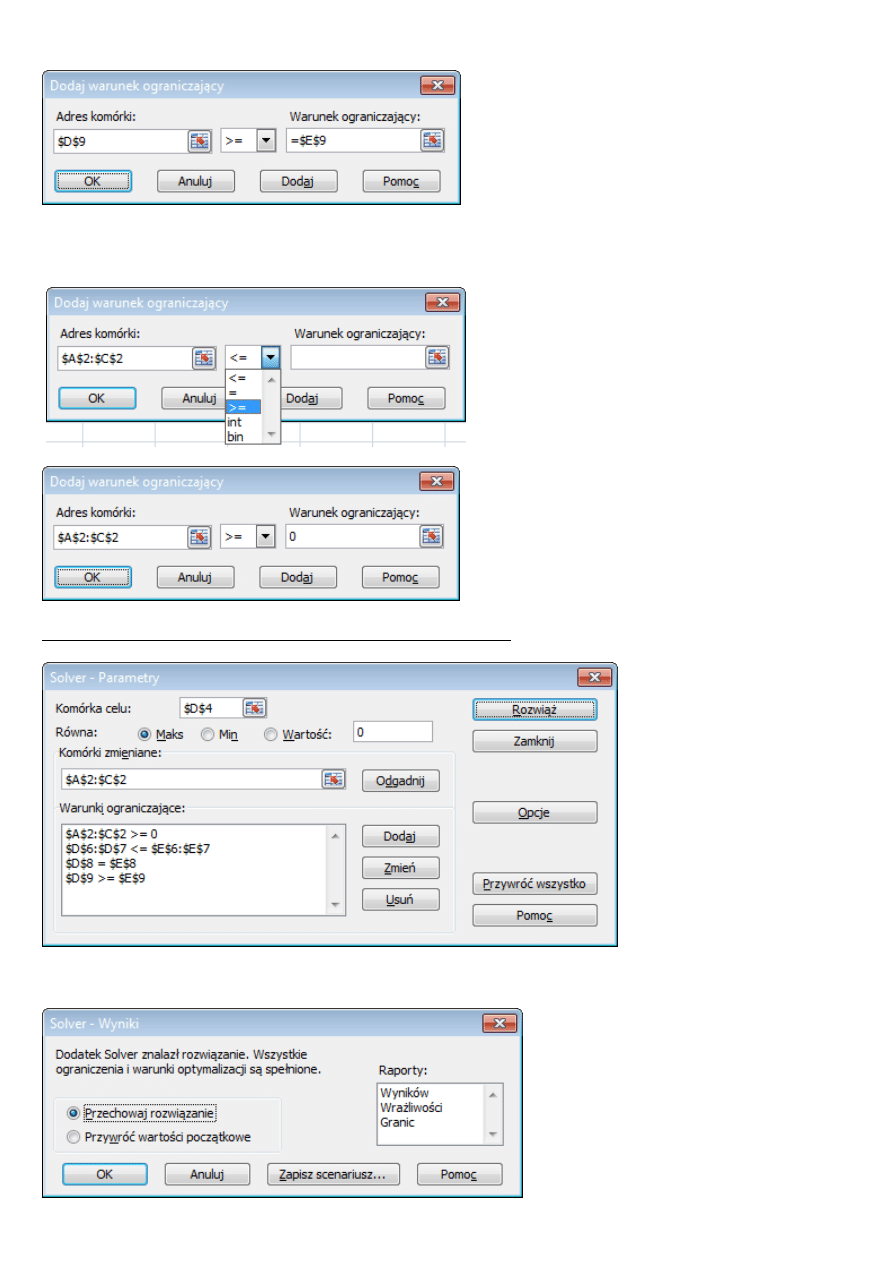
Warunek D9=E9.

Po kliknięciu Dodaj otwiera się ponownie okno dodawania warunków. Należy wpisać warunki nieujemności
zmiennych A2:C2>=0 „wspólnie”.

Uwaga – trzeba pamiętać o wyborze nierówności >= (domyślne ustawienie to <=)

Ten zapis odpowiada grupie warunków A2>=0, B2>=0, C2>=0.
Warunki te są wpisywane jako ostatnie i zatwierdzone przez OK

.

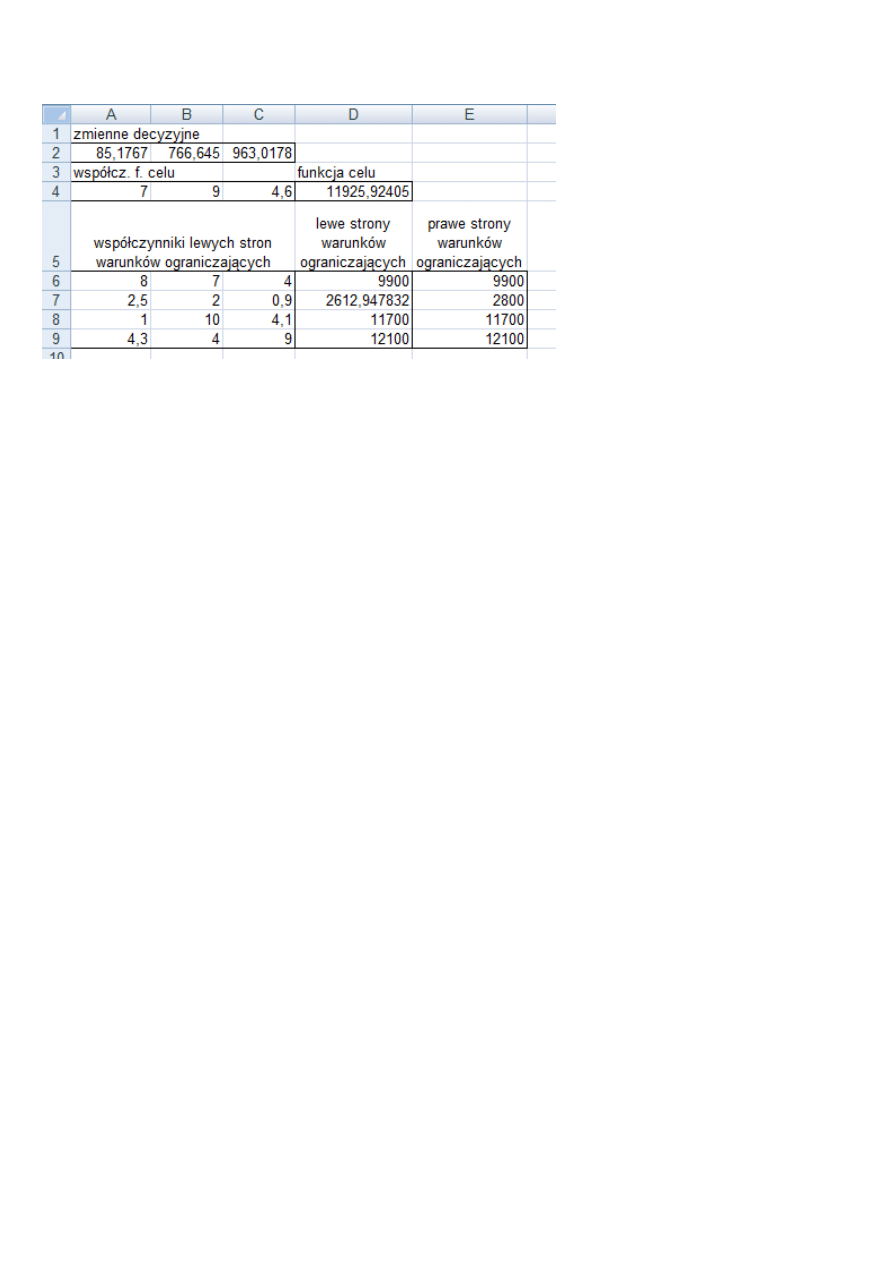
Kompletne ustawienia. Warunki ograniczające sortują się alfabetycznie, niezależnie od kolejności wpisywana,

Należy teraz kliknąć w Rozwiąż, a gdy pojawi się okno jak poniżej, kliknąć OK.

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

7

Widok po wykonaniu obliczeń Solverem

.

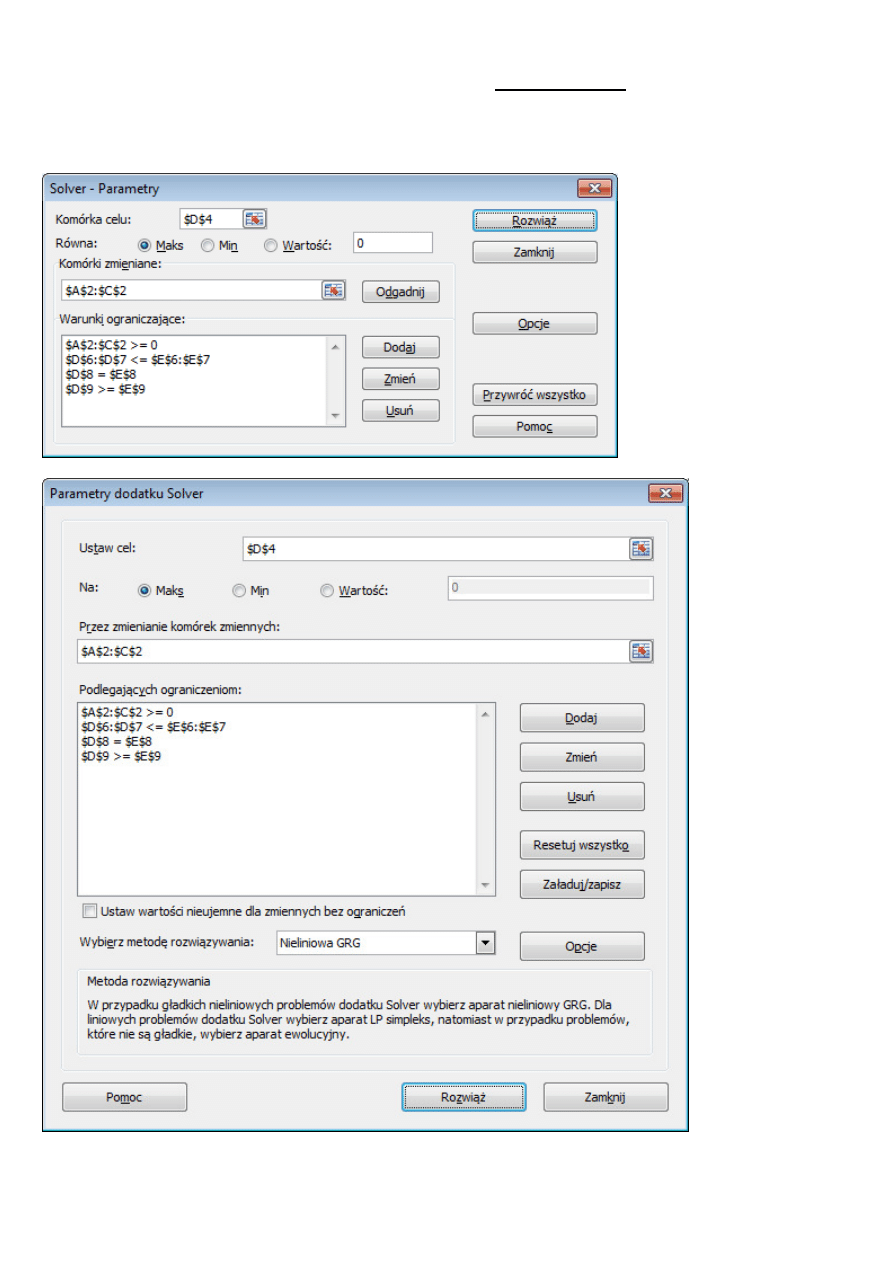
Rozwiązanie
Optymalna (maksymalna) wartość funkcji celu to 11925,92405. Optymalne wartości zmiennych (tzn. wartości,
dla których osiągnięte zostało maksimum) to

=

*

1

x

85,1767,

=

*
2

x

766,645 oraz

=

*

3

x

963,0178

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

8

Opis wprowadzania danych do Solvera - Excel w wersjach 2010, 2013, 2016

W Excelu 2010 w porównaniu z poprzednimi wersjami został w Solverze zmieniony interfejs użytkownika.

Poniżej dla porównania umieszczono zrzuty ekranów Solvera z Excela 2007 i 2010.

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

9

Wykaz najważniejszych różnic między oknami Solvera

Opis

Excel 2007 i wcześniejsze

Excel 2010,2013,2016

Uwagi

Nazwa okna głównego

Solver-Parametry

Parametry dodatku Solver

Adres komórki zawierającej formu-
łę z funkcją celu lub ewentualnie
jedną z komórek zmienianych

Komórka celu

Ustaw cel

Domyślne ustawienie tego pola to
komórka bieżąca

Rodzaj optymalizacji: maksy-
malizacja, minimalizacja, ustalona
wartość liczbowa funkcji celu

Równa

Na

Domyślne ustawienie to Maks

Deklaracja zakresu/zakresów ko-
mórek pełniących rolę zmiennych

Komórki zmieniane

Przez zmienianie komórek
zmiennych

Brak ustawienia domyślnego

„Odgadnięcie” zakresu/zakresów
komórek pełniących rolę zmien-
nych na podstawie formuły z funk-
cją celu

Odgadnij

brak

Najczęściej „odgadnięcie” jest błędne

Lista warunków ograniczających

Warunki ograniczające

Podlegające ograniczeniom

Jest to lista służącą tylko do wyświe-
tlania, a nie do wpisywania/edycji

Otwiera okno dodawania nowego
warunku ograniczającego

Dodaj

Dodaj

W Excelu 2010 zmieniono okno do-
dawania warunków ograniczających

Otwiera okno edycji istniejącego
warunku ograniczającego (wymaga
wybrania go na liście)

Zmień

Zmień

W Excelu 2010 zmieniono okno edy-
cji warunków ograniczających

Usuwa z listy istniejący warunek
ograniczający (wymaga wybrania
go na liście)

Usuń

Usuń

Otwiera okno opcji, umożliwiające
zmianę domyślnych ustawień
wpływających na proces obliczeń

Opcje

Opcje

W Excelu 2010 zmieniono okno opcji

Skasowanie wszystkich danych
wprowadzonych przez użytko-
wnika oraz przywrócenie opcji do-
myślnych

Przywróć wszystko

Resetuj wszystko

Zapis modelu z Solvera w postaci
grupy formuł w arkuszu

Dostępne jako Zapisz model/
Załaduj model

w oknie op-

cji)

Załaduj/zapisz

Ustawienie nieujemności wszyst-
kich zmiennych bez dodawania sto-
sownego warunku ograniczającego
do listy

Dostępne jako Przyjmij nieu-
jemne

w oknie opcji; domy-

ś

lnie niezaznaczone - brak

nieujemności wszystkich
zmiennych)

Ustaw wartości nieujemne
dla zmiennych bez ograni-
czeń

(domyślnie zaznaczone

- ustawiona nieujemność
wszystkich zmiennych)

Typ algorytmu używanego do obli-
czeń

Brak jawnego ustawienia
(przełączenie na algorytm
simpleks poprzez zaznacze-
nie opcji Przyjmij model li-
niowy

w oknie opcji)

Wybierz metodę rozwiązy-
wania

(ustawienie domyślne

jest opisane jako Nieliniowa
GRG

)

Ustawienie domyślne to algorytm
„uniwersalny” GRG, a alternatywą
jest algorytm simpleks dla programo-
wania liniowego. W Excelu 2010 do-
dano do wyboru tzw. algorytm ewo-
lucyjny

Porównanie wyglądu okien dodawania/edycji warunków ograniczających

Excel 2007 i wcześniejsze

Excel 2010 i 2013

Okno dodawania nowych warunków ograniczających

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

10

Okno edycji istniejących warunków ograniczających

P. Kowalik, Laboratorium badań operacyjnych: wstęp do rozwiązywania zadań programowania liniowego w Excelu

11

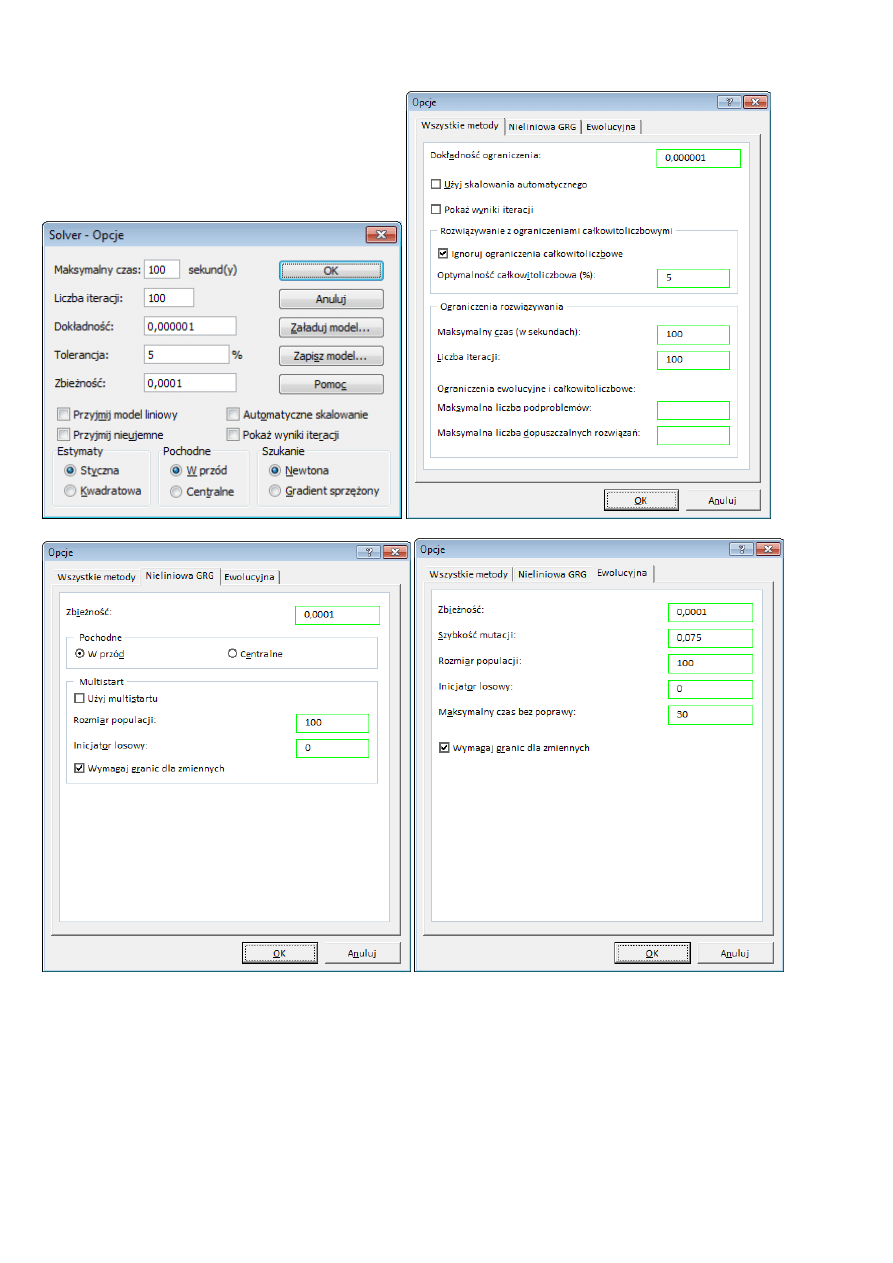
Porównanie okna opcji Solvera dla Excela 2007 i wcześnieszych (pojedyncze okno – zrzut w lewym górnym
rogu strony) oraz dla Excela 2010 i późniejszych (pozostałe zrzuty – okno z trzema zakładkami).