Rezonans w obwodach elektrycznych 

POJĘCIA PODSTAWOWE DOTYCZĄCE 

ZJAWISKA REZONANSU 

Zjawisko  rezonansu  może  wystąpić  w  obwodzie 

elektrycznym  wówczas,  gdy  reaktancja  wypadkowa,  lub 

susceptancja wypadkowa jest równa zero. Obwód w którym 

zjawisko  rezonansu  występuje  nosi  nazwę  obwodu 

rezonansowego. Podczas jego występowania napięcie i prąd 

na zaciskach obwodu rezonansowego są w fazie, natomiast 

moc bierna ulega kompensacji (moc bierna pojemnościowa 

jest  równa  mocy  biernej  indukcyjnej)  i  układ  jej  nie 

pobiera.  

Częstotliwość  przy  której  wypadkowa  reaktancja  lub 

susceptancja  wynosi  zero  jest  nazywana  częstotliwością 

rezonansową  f

r

.  Możliwe  jest  uzyskanie  w  obwodzie 

rezonansu,  jeżeli  doprowadzane  do  zacisków  obwodu 

napięcie  sinusoidalne  posiada  częstotliwość  równą 

rezonansowej. 

W  układach  elektrycznych  RLC  może  występować 

rezonans napięć lub prądów, przy czym który wystąpi jest 

zależne od sposobu połączenia elementów. 

 

Rezonans w obwodach elektrycznych 

REZONANS NAPIĘĆ 

Rezonans napięć to zjawisko rezonansu występujące w 

szeregowym układzie RLC, z tej przyczyny jest nazywane 
także  rezonansem  szeregowym.  Charakteryzuje  się  ono 
tym,  że  reaktancja  indukcyjna  jest  równa  reaktancji 
pojemnościowej. 

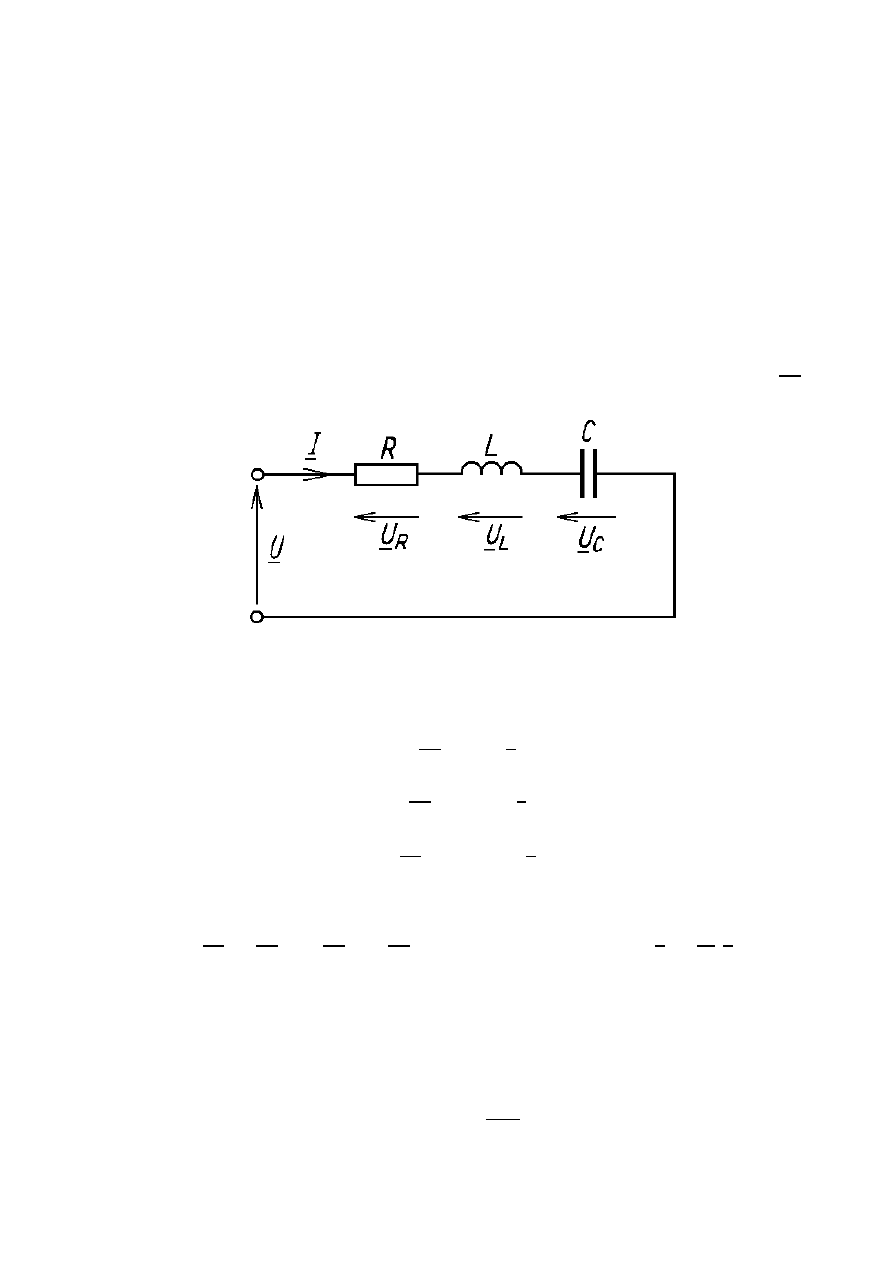
Do  dwójnika  szeregowego  RLC  przyłączone  jest 

napięcie  sinusoidalne  o  wartości  skutecznej  zespolonej  U. 
Układ dla rezonansu napięć ma postać: 

 

Na  poszczególnych  elementach  układu  ustalą  się 

następujące napięcia: 

U

R

 = RI 

U

L

 = jX

L

I 

U

C

 = 



jX

C

I 

Całkowite napięcie na zaciskach dwójnika: 

U = U

R

 + U

L

 + U

C

 = [R + j(X

L

 



 X

C

)]I = Z



I 

Warunkiem  wystąpienia  rezonansu  jest  zerowa 

wypadkowa reaktancja układu, co nastąpi gdy: 

X

L

 = X

C 



L = 

C

1



 

Rezonans w obwodach elektrycznych 

Warunek  ten  spełniony  jest  dla  częstotliwości 

rezonansowej danej wzorem: 

f

r

 = 

LC



2

1

 

 

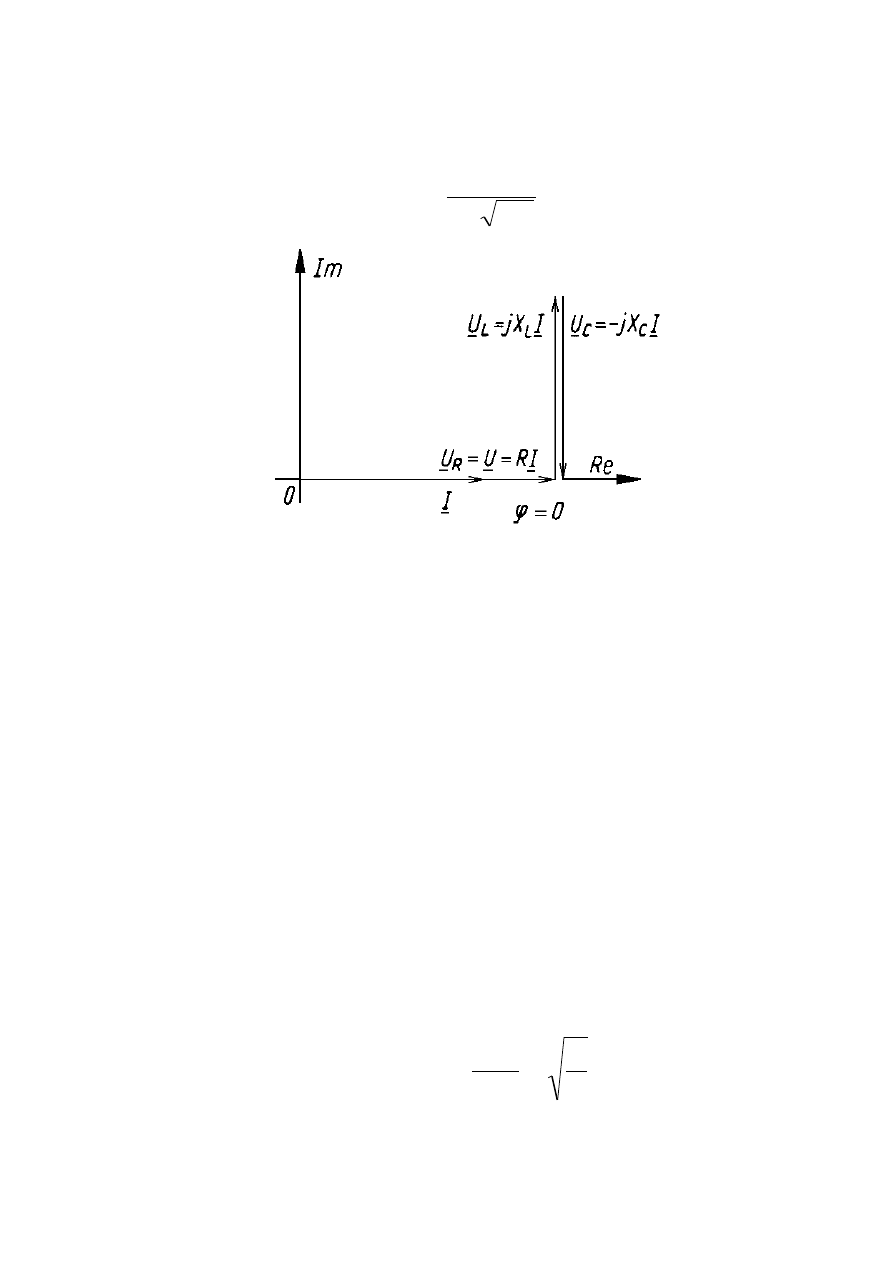
Wykres wektorowy odpowiadający stanowi rezonansu 

Gdy  obwód  znajduje  się  w  rezonansie  słuszne  są 

poniższe zależności: 

Z = R;     U = U

R  

U

L

 + U

C

 = 0;   U

L

 = U

C

 

Obwód 

rezonansowy 

można 

scharakteryzować 

kilkoma parametrami: 



 

impedancją falową; 



 

dobrocią obwodu rezonansowego; 



 

rozstrojeniem względnym i bezwzględnym. 

Impedancja  falowa 



  to  reaktancja  indukcyjna  lub 

pojemnościowa obwodu przy częstotliwości rezonansowej. 
Można ją wyznaczyć ze wzoru: 



 = 



r

L = 

C

L

C

r





1

 

Rezonans w obwodach elektrycznych 

Dobroć  szeregowego  obwodu  rezonansowego  RLC 

pracującego  w  warunkach  rezonansu  napięć  dana  jest 
wzorem: 

Q = 

CR

R

L

RI

LI

U

U

U

U

r

r

r

R

C

R

L







1









 

Uwzględniając 

wzór 

na 

impedancję 

falową 

otrzymujemy: 

Q = 

R



 

Rozstrojenie  bezwzględne 



  obliczane  jest  jako 

stosunek reaktancji obwodu do jego rezystancji: 



 = 

R

C

L

R

X





1





 



 = tg 



 

Rozstrojenie  bezwzględne  zmienia  się  wraz  ze  zmianą 

pulsacji 



 i jej zbliżaniem się do 



r

. Rozstrojenie względne 



 to stosunek reaktancji obwodu do impedancji falowej: 



 = 



X

 

Korzystając  z  definicji  impedancji  falowej,  powyższą 

zależność można przedstawić w funkcji impedancji falowej 
i częstotliwości rezonansowej: 

L = 

r





 

C = 





r

1

 

Rezonans w obwodach elektrycznych 

Z kolei reaktancja obwodu szeregowego RLC: 

X = 

C

L





1



 

Po  podstawieniu  do  niej  wzorów  określających 

pojemność i indukcyjność: 

X = 

























r

r

 

Rozstrojenie względne 



: 

f

f

f

f

X

r

r

r

r























 

Przyjmując,  stosunek  częstotliwości  źródła  do 

częstotliwości rezonansowej jako k można zapisać: 

k

k

1







 

Pomiędzy  rozstrojeniem  bezwzględnym  a  względnym 

istnieje  zależność,  którą  można  przedstawić  w  oparciu  o 
wyprowadzone wzory w następującej postaci: 



 = Q



 

W warunkach rezonansu zmienia się szereg parametrów 

układu,  czego  ilustracją  są  krzywe  rezonansowe, 
przedstawiające  zmieniające  się  parametry  w  funkcji 
częstotliwości: 

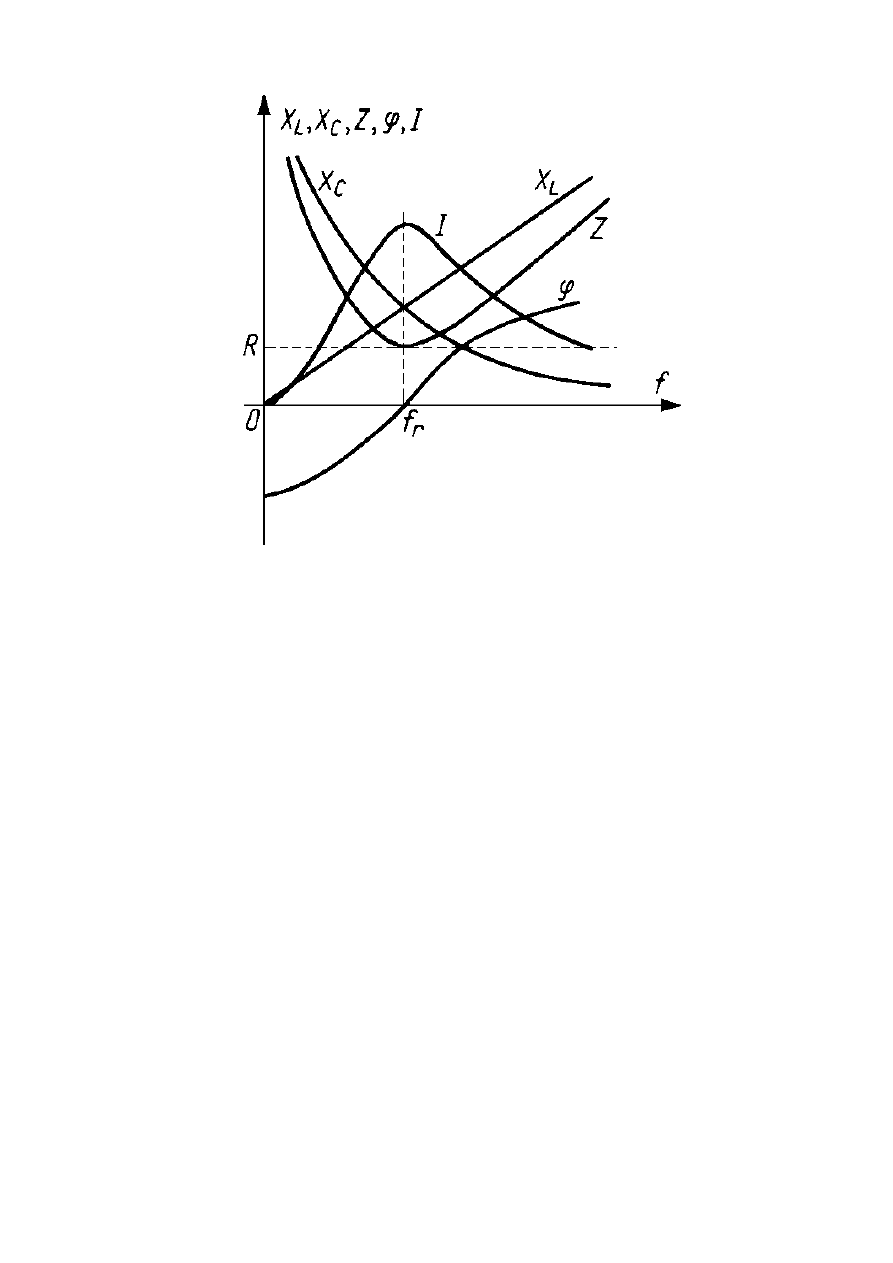
Rezonans w obwodach elektrycznych 

 

Rezonans w obwodach elektrycznych 

REZONANS PRĄDÓW 

W  układzie  równoległym  RLC  występuje  drugi  rodzaj 

rezonansu  – rezonans prądów nazywany  także rezonansem 
równoległym.  

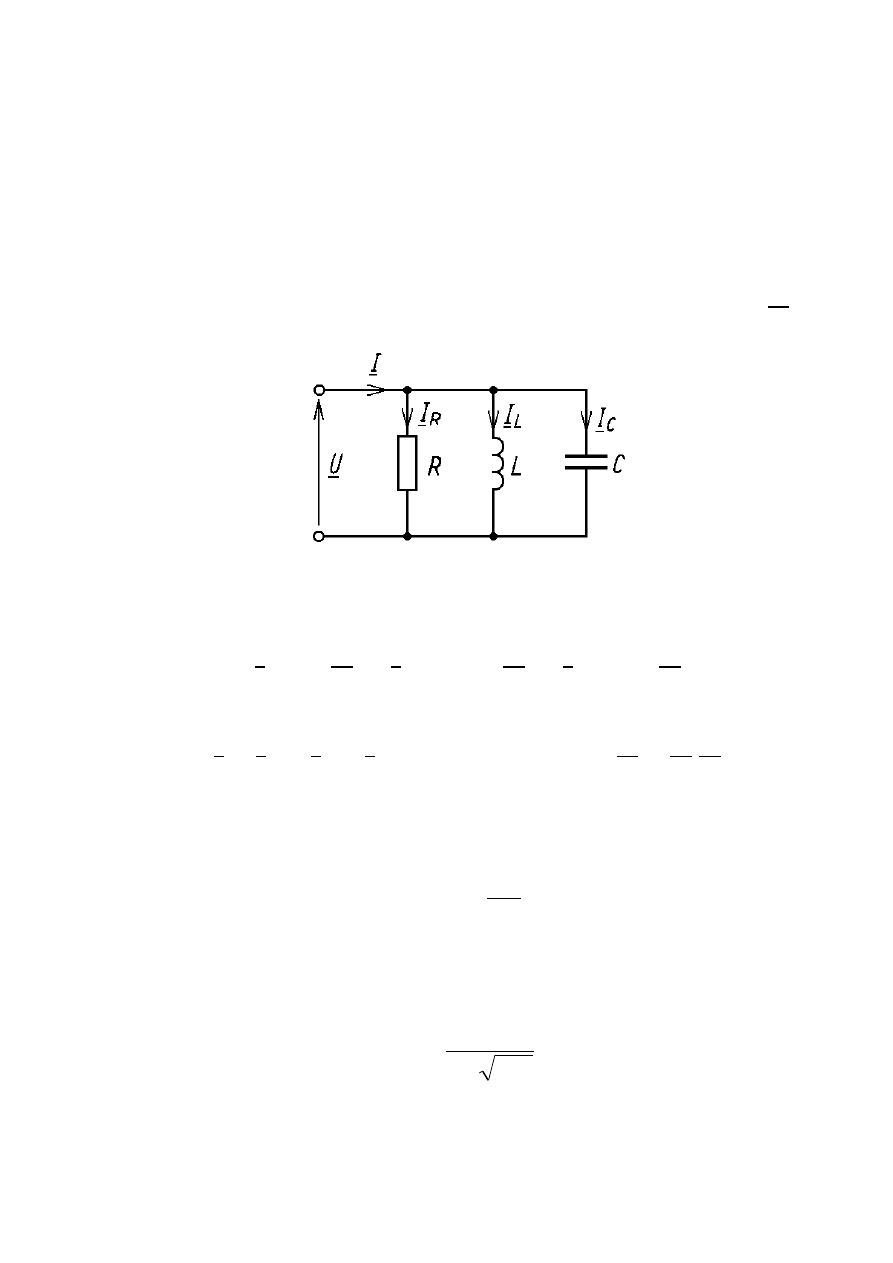
Do  zacisków  układu  równoległego  RLC  przyłożono 

napięcie sinusoidalne o wartości skutecznej zespolonej U i 
pulsacji 



=2



f. Schemat układu przedstawiono poniżej: 

 

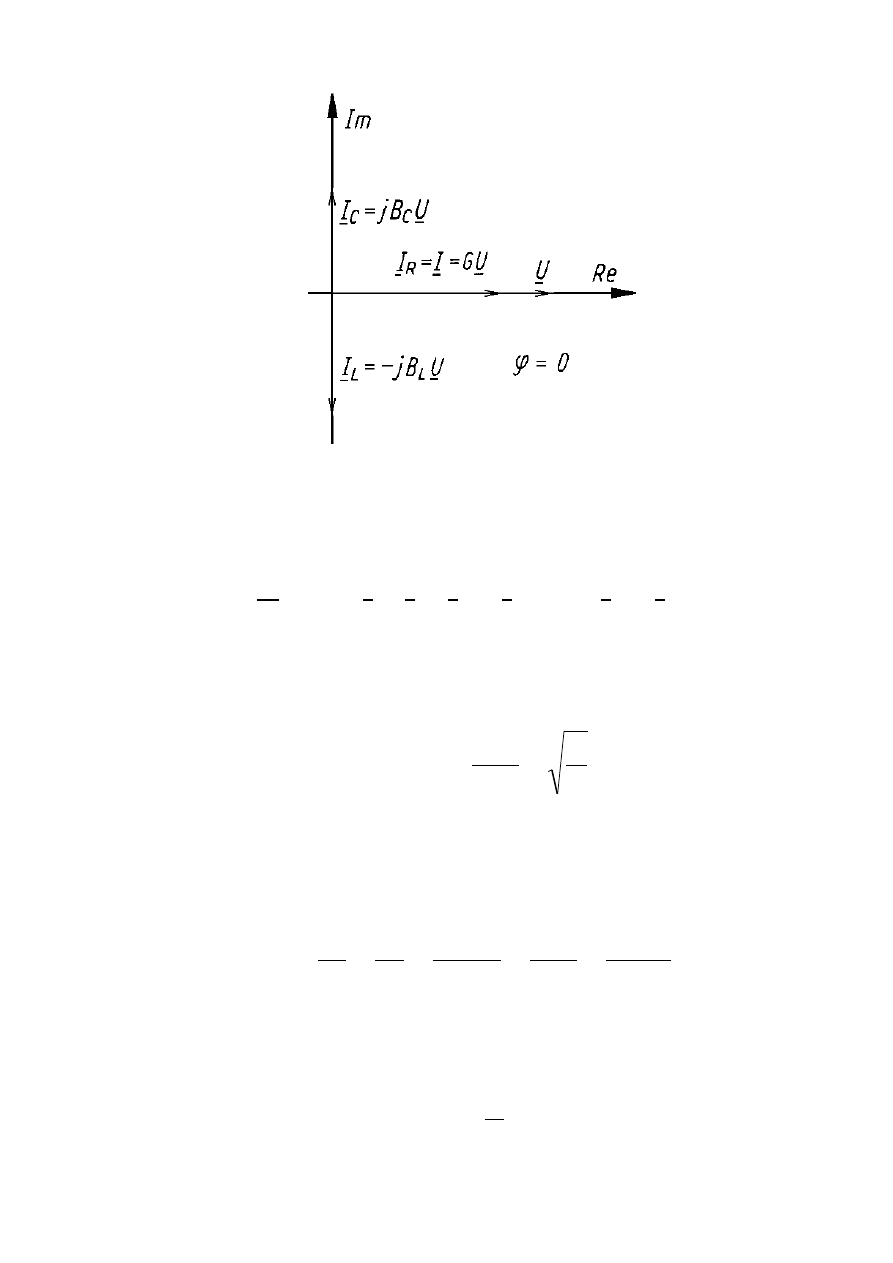
W  poszczególnych  gałęziach  układu  płyną  pod  jego 

wpływem prądy: 

I

R

 = GU;    I

L

 = - jB

L

U;    I

C

 = jB

C

U 

Prąd całkowity dopływający do dwójnika: 

I = I

R

 + I

L

 + I

C

 = [G + j(B

C

 – B

L

)]U = Y



U 

Zjawisko rezonansu wystąpi, gdy B=0, czyli: 

B

C

 = B

L 



C = 

L



1

 

Warunek  ten  zostaje  spełniony,  gdy  częstotliwość 

osiągnie wartość: 

f

r 

= 

LC



2

1

 

Rezonans w obwodach elektrycznych 

 

Wykres wektorowy dla rezonansu prądów 

 
Słuszne są przy tym następujące zależności: 

Y = G;   I = I

R    

I

L

 + I

C

 = 0    I

L

 = I

C

  

W  przypadku  równoległego  układu  rezonansowego 

definiuje  się  impedancję  falową 



  zgodnie  ze  wzorem, 

który podany jest dla układu szeregowego: 



 = 



r

L = 

C

L

C

r





1

 

Dla  równoległego  obwodu  rezonansowego  podawana 

jest też dobroć układu rezonansowego, z tym, że obliczana 
jest ona z innej zależności: 

Q = 

LG

G

C

GU

CU

I

I

I

I

r

r

r

R

C

R

L







1









 

Uwzględniając  w  niej,  że  G=1/R  uzyskuje  się 

ostatecznie: 

Q = 



R

 

Rezonans w obwodach elektrycznych 

Pracę  układu  w  warunkach  zbliżonych  do  rezonansu 

charakteryzują  podobnie  jak  w  przypadku  układu 
szeregowego 

pojęcia 

rozstrojenia. 

Rozstrojenie 

bezwzględne oblicza się według wzoru: 



 = 

G

B

B

G

B

B

G

B

C

L

L

C













 

Natomiast rozstrojenie względne: 



 = 

k

k

f

f

f

f

B

r

r

1

1











 

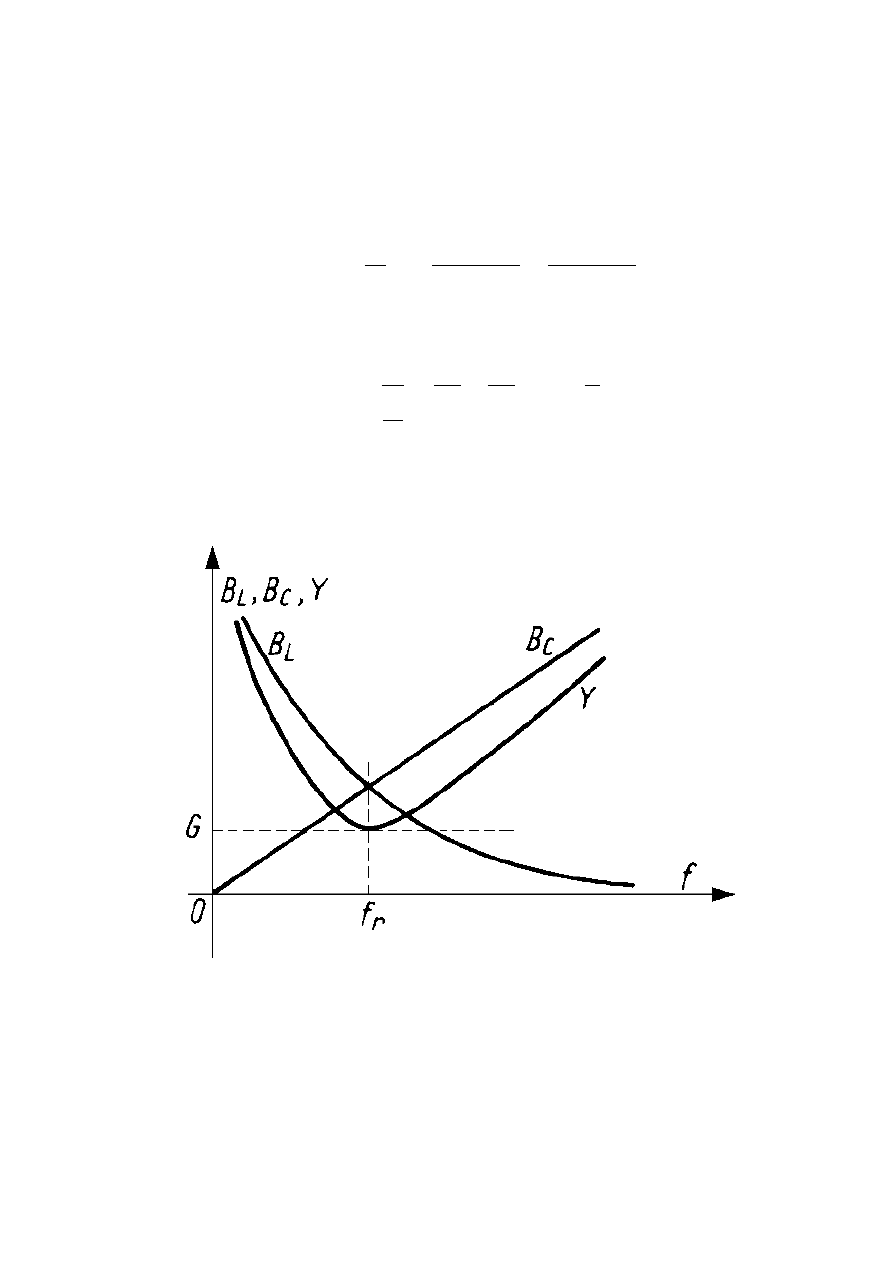
Zmianę  parametrów  układu  przedstawiają  krzywe 

rezonansowe, które przedstawiono na poniższym rysunku: