1

ZADANIA

Z HYDROMECHANIKI

Opracowali:

mł. bryg. dr inż. Jerzy GAŁAJ

st. kpt. dr inż. Tomasz DRZYMAŁA

2

Ćwiczenie z hydromechaniki dla studiów zaocznych

1.

Własności cieczy, warunki równowagi, ciśnienie, prawo Pascala i Eulera

Zadania z rozwiązaniami:


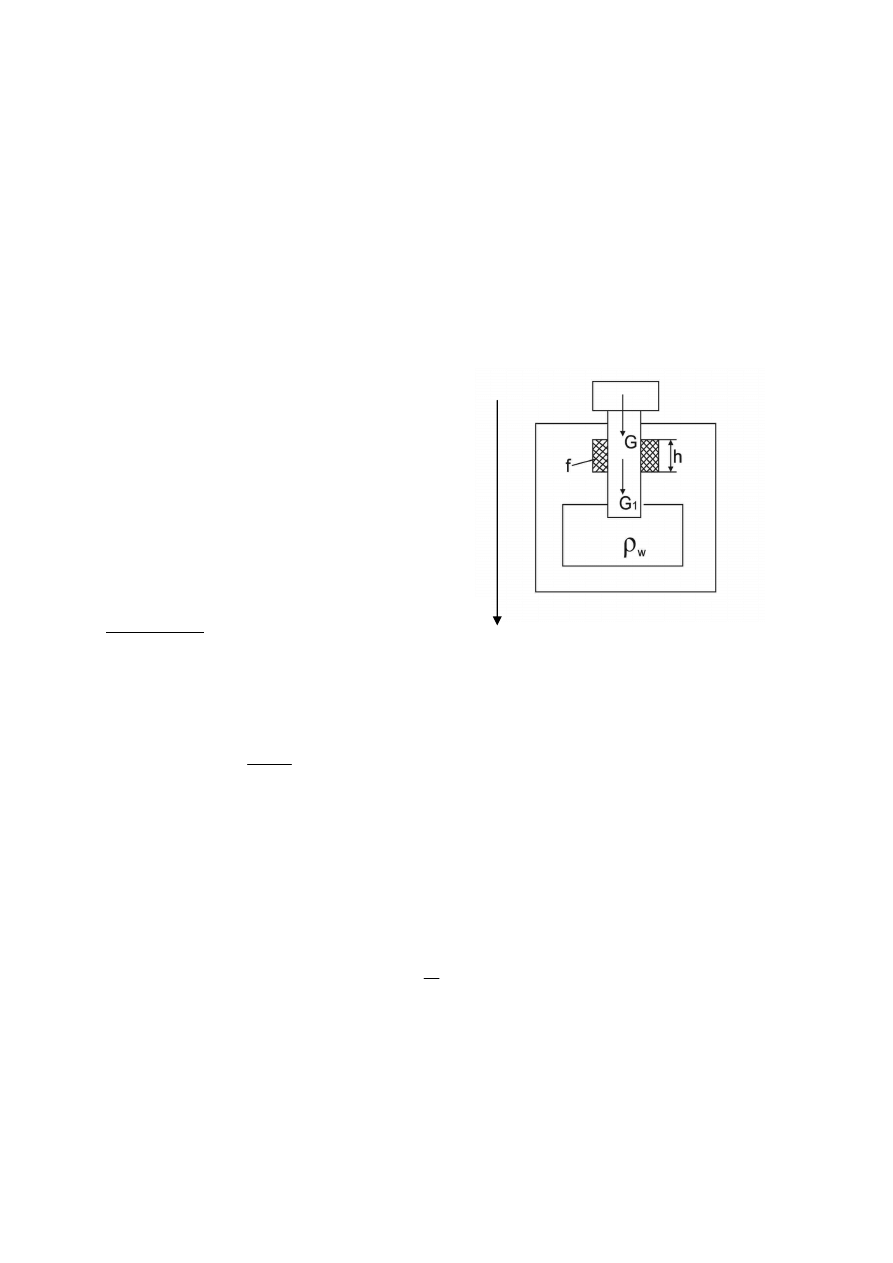
1. Jakim ciężarem G należy obciążyć tłok akumulatora wodnego o średnicy D=0,5 m
i ciężarze G

1

=10

4

kG, aby w przestrzeni cylindrycznej akumulatora wytworzyć ciśnienie

p = 24 at ? Wysokość kołnierza uszczelniającego wynosi h=0,1 m, a współczynnik tarcia
f=0,15.


Dane: Szukane

D = 0,5 m G = ? [N]
G

1

= 10

4

kG = 9,81·10

4

N

p = 24 at = 24·10

5

N/m

2

h = 0,1 m
f = 0,15
g = 9,81 m/s

2

Rozwiązanie:

Równanie równowagi sił na oś z:

Σ Z = G + G

1

- P - T = 0

gdzie: P = p·F = p·

4

D

2

⋅

π

- siła pochodząca od ciśnienia działającego na dolną część tłoka

T = f·N = f·p·π·D·h - siła tarcia działająca między tłokiem a uszczelniaczem (siła
nacisku N prostopadła do tłoka i przeciwnie skierowana do ruchu
zgodnie z prawem Pascala pochodzi od tej samej wartości
ciśnienia p, które panuje w komorze akumulatora)

Po podstawieniu i uporządkowaniu otrzymano wzór na siłę G w postaci:

1

G

4

D

h

f

p

D

G

−













+

⋅

⋅

⋅

⋅

π

=

Po podstawieniu wartości liczbowych do powyższego wzoru otrzymano G = 427 kN.

z

3

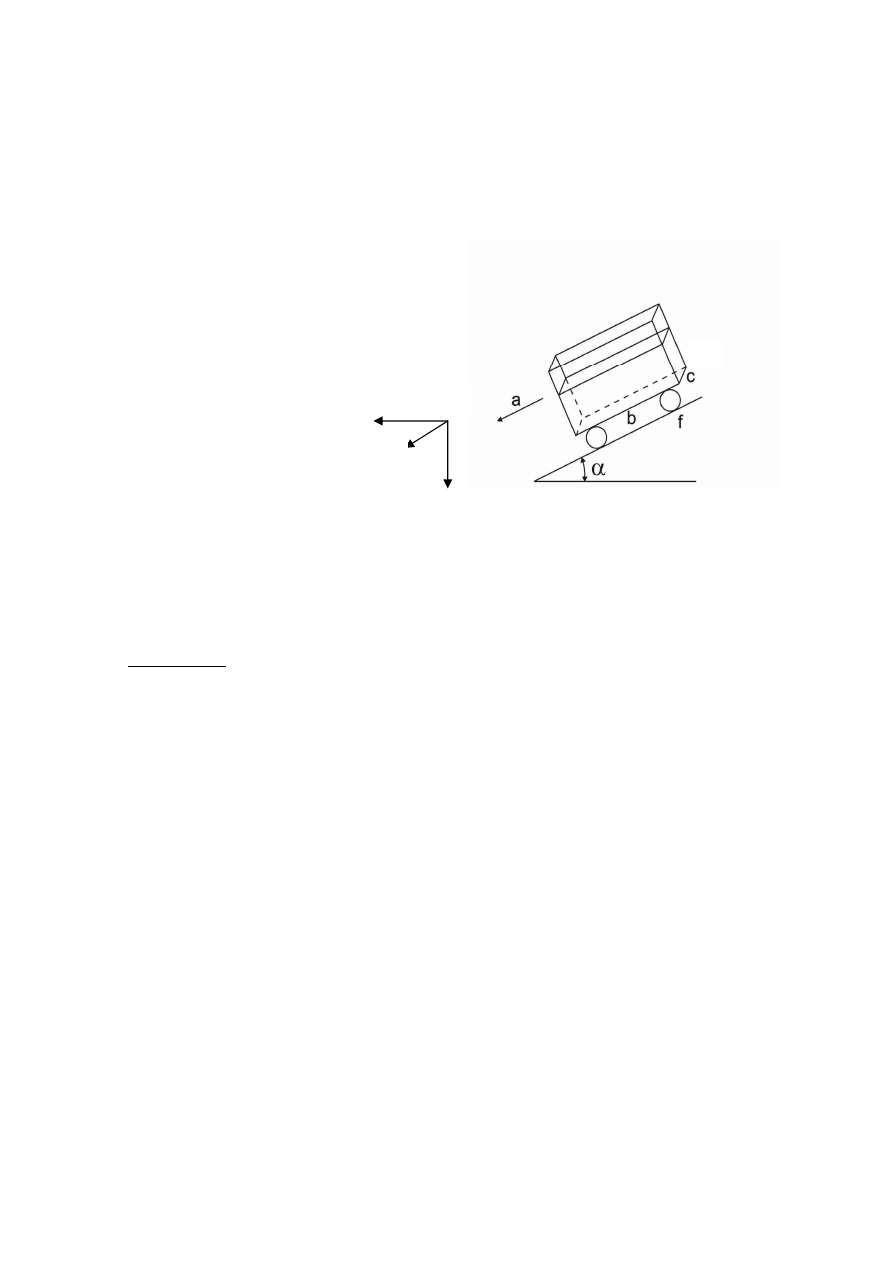
2. Dane jest naczynie prostopadłościenne o wymiarach b=2m (szerokość) i c=1m (głębokość)
wypełnione wodą o objętości V=3m

3

i masie m=3600 kg, które zjeżdża bez tarcia ruchem

jednostajnie przyspieszonym z przyspieszeniem a=3 m/s

2

po równi pochyłej o kącie

nachylenia

α

=0,523 rad. Obliczyć maksymalne ciśnienie wywierane przez ciecz na tylną

ścianę naczynia.

Dane: Szukane:

b = 2 m p

max

= ? [N/m

2

]

c = 1 m
V = 3 m

3

m = 3600 kg x
a = 3 m/s

2

α

= 0,523 rad

g = 9,81 m/s

2

ρ = 1000 kg/m

3

p

a

= 1013 hPa = 1,013·10

5

Pa

Układ współrzędnych Oxyz został tak przyjęty, że punkt O leży na powierzchni swobodnej

cieczy w połowie szerokości naczynia. Powoduje to, że niezależnie od zmiany kąta
nachylenia powierzchni swobodnej, punkt ten podczas ruchu leży zawsze na powierzchni
swobodnej cieczy.

Rozwiązanie:

Ogólne równanie różniczkowe wynikające z warunku równowagi cieczy ma postać:

(

)

Zdz

Ydy

Xdx

ρ

dp

+

+

⋅

=

gdzie:

α

⋅

=

cos

-a

X

- jednostkowa siła masowa działająca wzdłuż osi x

0

Y

=

- jednostkowa siła masowa działająca wzdłuż osi y

α

⋅

=

sin

a

-

g

Z

- jednostkowa siła masowa działająca wzdłuż osi z

Po podstawieniu składowych sił do równania otrzymano:

(

)

(

)

[

]

dz

sin

a

-

g

dx

cos

a

-

ρ

dp

α

⋅

+

α

⋅

⋅

=

Po obustronnym scałkowaniu otrzymano:

(

)

C

z

sin

a

-

g

ρ

x

cos

a

ρ

z)

y,

p(x,

+

α

⋅

⋅

+

⋅

α

⋅

⋅

−

=

Ponieważ początek układu jest położony zawsze na powierzchni swobodnej, to warunek

brzegowy dla powyższej funkcji ciśnienia można zapisać w następujący sposób:

p(0,0,0) = p

a

z

y

O

A

4

Po podstawieniu x=0 i z=0 do równania ciśnienia otrzymano wartość stałej całkowania

C = p

a

Po podstawieniu jej do wzoru na p(x,y,z) otrzymano ogólną funkcję przedstawiającą

przestrzenny rozkład ciśnienia w poruszającym się naczyniu z wodą o następującej postaci:

(

)

a

p

z

sin

a

-

g

ρ

x

cos

a

ρ

z)

y,

p(x,

+

α

⋅

⋅

+

⋅

α

⋅

⋅

−

=

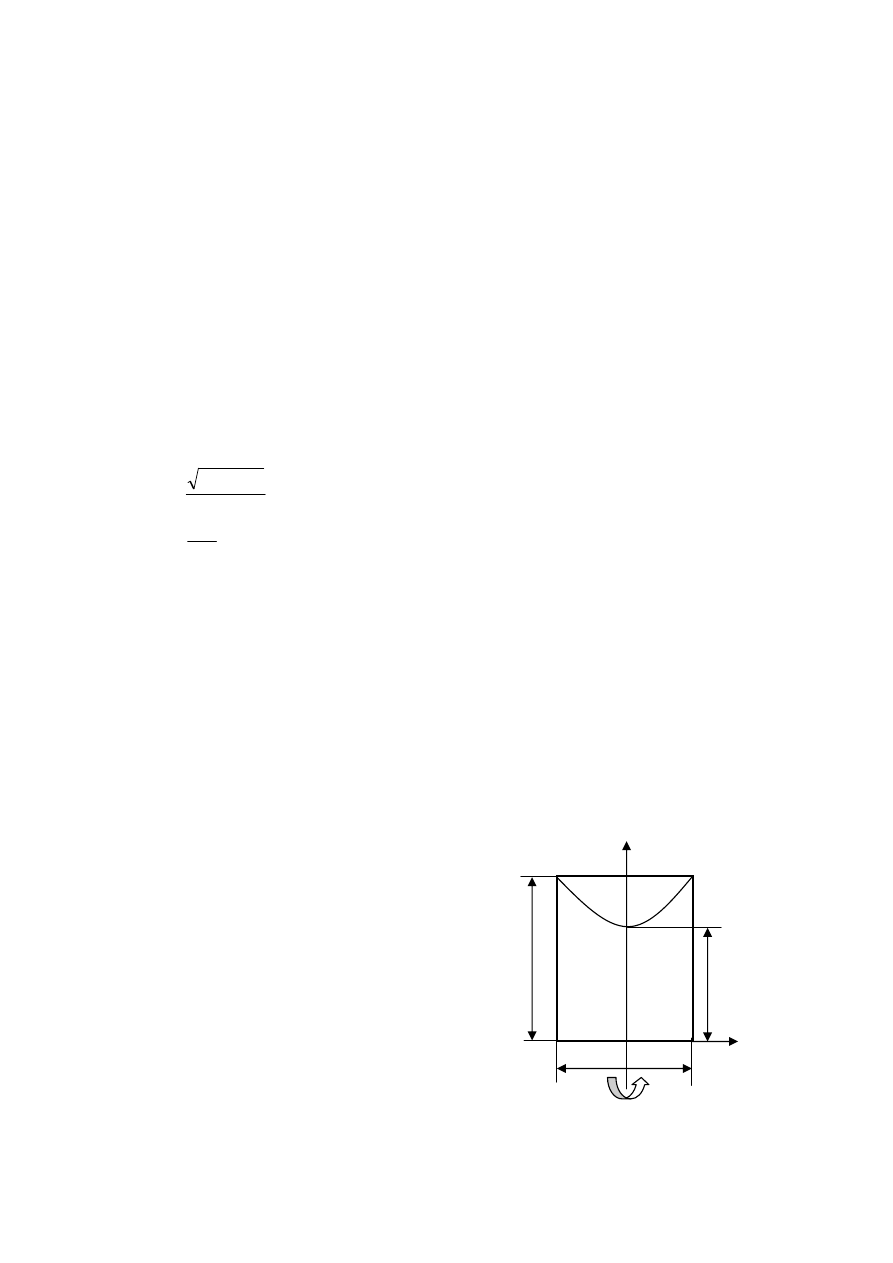
Aby wyznaczyć maksymalną wartość ciśnienia, które działa na tylną ściankę naczynia,

wystarczy do powyższego równania podstawić współrzędne punktu A, w którym panuje takie
ciśnienie. Na podstawie rysunku można stwierdzić, że są one równe:

x

A

= - d·cosα y

A

= y z

A

= d·sinα

gdzie:

2

b

4h

d

2

2

+

=

- odległość punktu A od punktu O (początku układu współrzędnych)

c

b

V

h

⋅

=

- wysokość wody w naczyniu

Po podstawieniu współrzędnych punktu A do równania otrzymano wzór na wartość

maksymalnego ciśnienia w następującej postaci:

(

)

a

2

A

max

p

sin

d

sin

a

-

g

ρ

cos

d

a

ρ

p

p

+

α

⋅

⋅

α

⋅

⋅

+

α

⋅

⋅

⋅

=

=

Po podstawieniu wartości liczbowych otrzymano, że p

max

= 1,173·10

5

Pa.

3. Otwarty zbiornik cylindryczny o średnicy

D i wysokości H wypełniony jest całkowicie

cieczą o ciężarze właściwym

γγγγ

. Zbiornik zaczął wirować ze stałą prędkością kątową

ω

ω

ω

ω

.

Ile wynosiła ta prędkość, jeżeli przez obrzeże wylała się połowa cieczy.

Dane: Szukane:

D ω = ? [rad/s]
γ
H
g

z

H
zzzz z

o

x

D

ω

γ

5

y

x

Rozwiązanie zadania:

Poszukujemy równania powierzchni swobodnej spełniającej warunek, że z naczynia wylała

się połowa cieczy.

W tym celu korzystamy z poniższego równania powierzchni stałego ciśnienia

(ekwipotencjalnej), ponieważ na w każdym punkcie powierzchni swobodnej ciśnienie jest
takie same i jest równe ciśnieniu atmosferycznemu:

0

dz

Z

dy

Y

dx

X

=

+

+

gdzie:

x

X

2

⋅

ω

=

- jednostkowa siła masowa działająca wzdłuż osi x (siła odśrodkowa)

y

Y

2

⋅

ω

=

- jednostkowa siła masowa działająca wzdłuż osi y (siła odśrodkowa)

g

−

=

Z

- jednostkowa siła masowa działająca wzdłuż osi z (siła ciężkości)

Po podstawieniu składowych sił do równania równowagi otrzymano:

0

dz

g

dy

y

dx

x

2

2

=

−

ω

+

ω

Po scałkowaniu i uwzględnieniu zależności

2

2

2

y

x

r

+

=

otrzymano równanie paraboloidy

obrotowej o postaci:

C

z

g

r

2

1

2

2

=

⋅

−

⋅

ω

Stałą całkowania C można wyznaczyć podstawiając do równania współrzędne wierzchołka

paraboloidy (0,z

o

):

C

z

g

0

o

=

⋅

−

czyli ostatecznie:

o

z

g

C

⋅

−

=

r

F

od

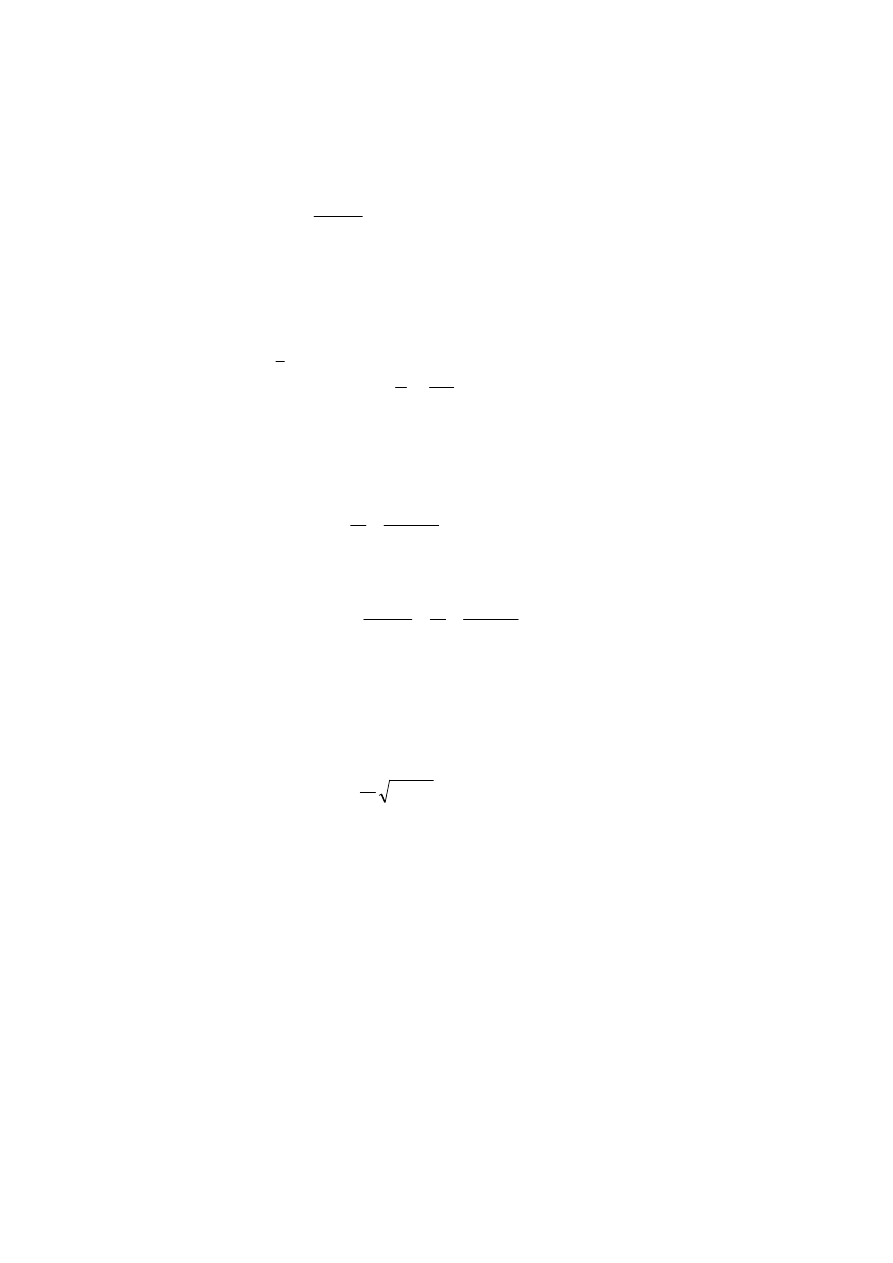
6

Po podstawieniu powyższego wyrażenia do równania paraboloidy i odpowiednim

przekształceniu otrzymano zależność na współrzędną z w funkcji promienia o postaci:

( )

o

2

2

z

2g

r

ω

r

z

+

⋅

=

Do rozwiązania zadania niezbędna jest znajomość współrzędnej z

o

. Aby ją wyznaczyć,

należy skorzystać z warunku, że objętość wirującej cieczy jest równa połowie objętości
cieczy, która znajdowała się w naczyniu zanim zaczęło wirować. Powyższy warunek można
zapisać w następujące formie matematycznej:

( )

H

4

D

2

1

dr

r

z

r

2

2

2

D

0

⋅

⋅

π

=

⋅

⋅

π

∫

Po podstawieniu wyrażenia na funkcję z(r), scałkowaniu i wykonaniu szeregu

przekształceń otrzymano następujące wyrażenie na współrzędną z wierzchołka paraboloidy:

16g

D

ω

2

H

z

4

2

o

⋅

−

=

Po podstawieniu powyższego wyrażenia do równania na z(r) otrzymano:

( )

16g

D

ω

2

H

2g

r

ω

r

z

2

2

2

2

⋅

−

+

⋅

=

Aby wyznaczyć prędkość kątową, należy do powyższego równania podstawić współrzędne

punktu, który należy do tej paraboloidy. Z rysunku wynika, że jest nim na pewno
punkt o współrzędnych (D/2,H). Po wykonaniu powyższej czynności i niezbędnych
przekształceniach otrzymano następujące wyrażenie na ω:

H

2g

D

2

⋅

=

ω

[rad/s]

7

Zadania do samodzielnego rozwiązania:

1.

W prasie hydraulicznej wałek śruby o średnicy d=3,5 cm i skoku h=1 cm, przez
pokręcanie koła o promieniu a=15 cm może być wciśnięty do wnętrza cylindra
o wewnętrznej średnicy D=25 cm i wysokości H=20 cm całkowicie napełnionego wodą.
Określić wzrost ciśnienia w cylindrze oraz siłę z jaką należy obracać koło, gdy śruba
wykona 10 obrotów. Tarcie należy pominąć.

2.

Hydrauliczne urządzenie do zwiększania ciśnienia pozwala uzyskiwać nadciśnienie
p

2

=10

7

N/m

2

. Pod jakim nadciśnieniem p

1

należy podawać ciecz pod duży tłok o średnicy

D=250 mm, jeżeli średnica tłoka nurnikowego d=50 mm. Opory tarcia pominąć.

3.

Zbiornik wypełniony do wysokości

h płynem nieściśliwym o gęstości

ρ

, znajduje się

w ruchu postępowym jednostajnie przyspieszonym. Napisać równanie rodziny
powierzchni stałego ciśnienia oraz wyrażenie na ciśnienie w dowolnym punkcie
przestrzeni wypełnionej płynem wiedząc, że przyspieszenie wynosi

a i jest nachylone

pod kątem

ββββ

do poziomu.

4.

Naczynie prostopadłościenne wypełnione do wysokości

h cieczą o ciężarze właściwym

γγγγ

porusza się po płaszczyźnie poziomej ze stałym przyspieszeniem skierowanym

zgodnie z kierunkiem ruchu. Przy jakiej wartości przyspieszenia

a woda zacznie

wylewać się z naczynia, jeżeli jego wysokość wynosi

H.

5.

W prostopadłościennym zbiorniku dziobowym statku o szerokości

L znajduje się paliwo

o ciężarze właściwym

γγγγ

. Wyznaczyć maksymalne opóźnienie statku podczas hamowania,

przy którym paliwo nie przeleje się przez luk znajdujący się na pokładzie. Powierzchnia
swobodna w ruchu jednostajnym znajduje się w odległości

h od pokładu. Dla obliczonego

opóźnienia wyznaczyć wielkość ciśnienia w punktach B i C (rys.).

6.

Naczynie walcowe o wysokości

H i promieniu R napełnione cieczą do wysokości h

obraca się jednostajnie wokół swej osi geometrycznej zorientowanej pionowo.
Wyznaczyć prędkość kątową

ω

ω

ω

ω

, przy której ciecz zacznie się wylewać z naczynia.

Ciężar właściwy cieczy

γγγγ

.

7.

Zamknięte naczynie walcowe o średnicy

D i wysokości H jest wypełnione do wysokości

h = H/2 cieczą o ciężarze

γγγγ

. Określić z jaką prędkością

ω

o

musi wirować naczynie wraz

z cieczą wokół centralnej pionowej osi, aby wierzchołek paraboloidy dotknął dna
naczynia.

8.

Mikromanometr z rurką pochyłą napełniony spirytusem (

ρ

sp

=790 kg/m

3

) podłączony jest

do komina pieca. Nachylenie rurki do poziomu

α

=

π

/6 rad. Podciśnienie w kominie

powoduje podniesienie się cieczy w rurce na długości l=155 mm. Określić całkowite
ciśnienie w kominie p

x

, jeżeli wysokość ciśnienia barometrycznego wynosi 755 mmHg.

8

2.

Napór hydrostatyczny na ściany płaskie i zakrzywione

Zadania z rozwiązaniami:

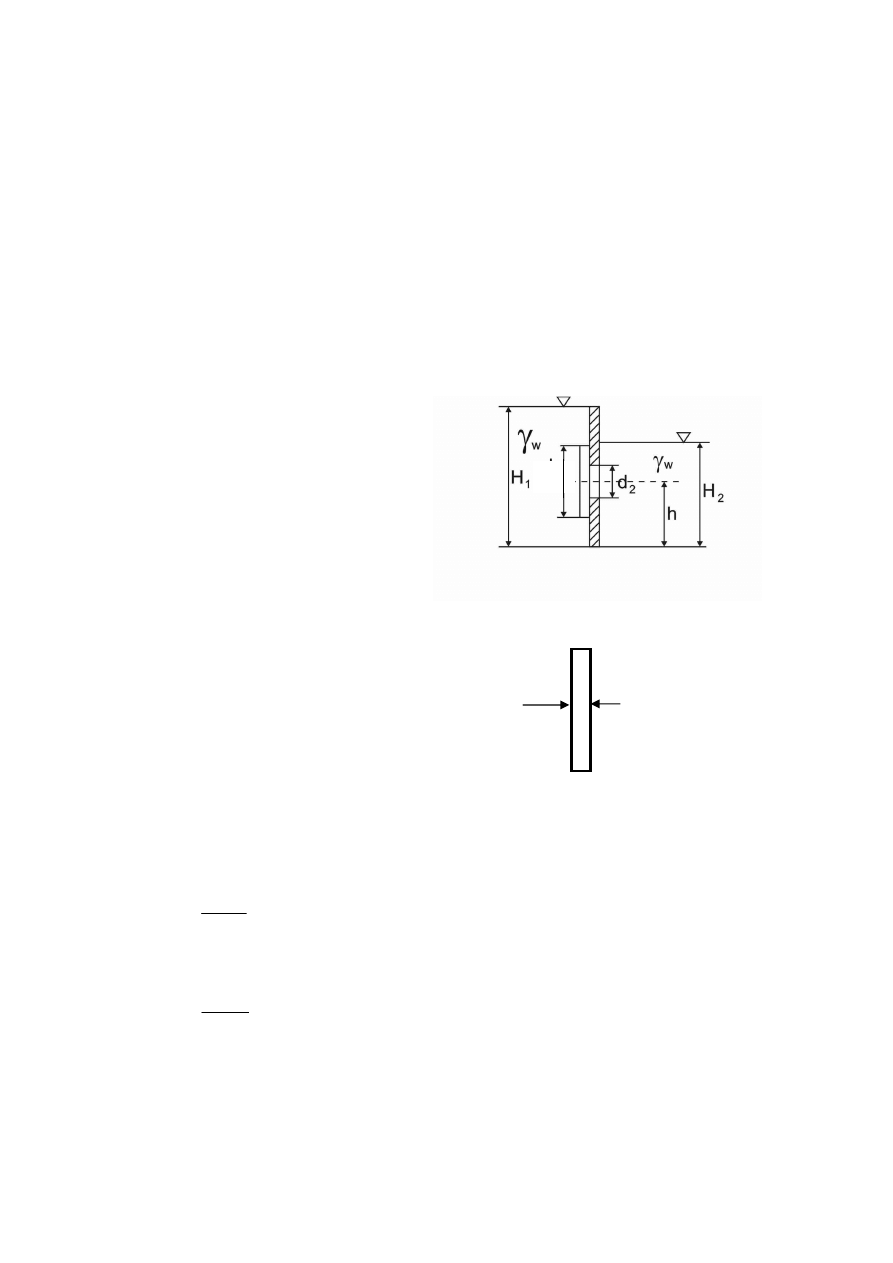
1.

Obliczyć wypadkowy napór wody na plaster zamykający otwór w grodzi rozdzielającej
dwie sąsiednie komory statku. Dane:
-

poziom wody z lewej strony grodzi H

1

,

-

poziom wody z prawej strony grodzi H

2

,

-

położenie pionowe środka otworu h,

-

średnica otworu d

2

,

-

średnica plastra d

1

,

-

ciężar właściwy wody

γ

w

.

Dane: Szukane:

H

1

P = ? [N]

H

2

h
d

2

d

1

Rozwiązanie zadania:

Wypadkowy napór wody na plaster zamykający

otwór w grodzi jest równy różnicy sił parcia
działających na niego z lewej (P'

x

) i prawej

strony (P"

x

), czyli:

"

x

'

x

P

-

P

P

=

gdzie:

'

'

s

w

'

x

F

z

P

⋅

⋅

γ

=

F"

z

P

"

s

w

"

x

⋅

⋅

γ

=

h

-

H

z

1

'

s

=

- współrzędna z środka ciężkości pola powierzchni plastra względem

powierzchni swobodnej wody napierającej z lewej strony

4

d

F

2

1

'

⋅

π

=

- pole powierzchni plastra, na które napiera woda z lewej strony

h

-

H

"

z

2

s

=

- współrzędna z środka ciężkości pola powierzchni plastra względem

powierzchni swobodnej wody napierającej z prawej strony

4

d

"

F

2

2

⋅

π

=

- pole powierzchni plastra, na które napiera woda z prawej strony

Po podstawieniu powyższych zależności do równania na siłę parcia P i odpowiednich
przekształceniach otrzymano ostatecznie:

P

x

'

P

x

"

d

1

9

(

)

(

)

[

]

2

2

2

2

1

1

w

d

h

-

H

-

d

h

-

H

4

P

⋅

⋅

⋅

γ

⋅

π

=

2.

Obliczyć wielkość i określić położenie linii działania naporu hydrostatycznego na
zakrzywioną część powierzchni poszycia burty statku o promieniu

R zawartą między

dwiema sąsiednimi wręgami oddalonymi od siebie o

a. Statek pływa przy zanurzeniu T,

a wewnątrz na rozpatrywanym odcinku znajduje się zbiornik paliwa wypełniony do
wysokości

h olejem o ciężarze właściwym

γγγγ

ol

.

Dane: Szukane:

R P = ? [N]
a α = ? [rad]
T
h
γ

ol

γ

w

Rozwiązanie zadania:

Aby wyznaczyć wypadkową siłę naporu działającą na zakrzywioną część burty statku, należy
najpierw obliczyć składowe sił pochodzących od oleju (działające na wewnętrzną część burty)
poziomą P

x

'

i pionową P

z

'

oraz składowe sił pochodzących od wody (działające na zewnętrzną

część burty) poziomą P

x

"

i pionową P

z

"

.

Składowe poziome wyznacza się ze wzorów na napór hydrostatyczny działający na ścianę
płaską będącą rzutem powierzchni zakrzywionej na płaszczyznę pionową, czyli:

'

z

'

s

ol

x

F

z

'

P

⋅

⋅

γ

=

"

z

"

s

w

"

x

F

z

P

⋅

⋅

γ

=

gdzie:

2

R

-

h

z

'

s

=

- współrzędna z środka ciężkości figury (prostokąt o bokach R i a),

będącej rzutem powierzchni zakrzywionej liczona od powierzchni
swobodnej oleju

2

R

-

T

z

"

s

=

- współrzędna z środka ciężkości figury (prostokąt o bokach R i a),

będącej rzutem powierzchni zakrzywionej liczona od powierzchni
swobodnej wody

R

a

F

F

"

z

'

z

⋅

=

=

- pole figury będącej rzutem powierzchni zakrzywionej na

płaszczyznę pionową (prostokąt o bokach R i a)

Składową poziomą wypadkowej siły naporu wyznaczymy z następującej zależności (oś Ox
skierowana w prawo):

10

"

x

'

x

x

P

-

P

P

=

Po wstawieniu zależności na współrzędne z

s

'

i z

s

"

i powierzchnie F

z

'

i F

z

"

oraz wykonaniu

prostych przekształceń matematycznych otrzymano:

























⋅

γ













⋅

γ

⋅

⋅

=

2

R

-

T

-

2

R

-

h

R

a

P

w

ol

x

Składowe pionowe można wyznaczyć z następujących zależności:

ABE

ol

'

z

V

P

⋅

γ

=

FGE

w

"

z

V

P

⋅

γ

=

gdzie: V

ABE

- objętość bryły ograniczonej powierzchnią swobodną oleju, powierzchnią burty,

oraz dwoma powierzchniami pionowymi przechodzącymi przez krańce
powierzchni zakrzywionej
V

FGE

- objętość bryły ograniczonej przedłużeniem powierzchni swobodnej wody,

powierzchnią burty, oraz dwoma powierzchniami pionowymi przechodzącymi
przez krańce powierzchni zakrzywionej

Powyższe objętości można wyznaczyć przez zsumowanie objętości odpowiednich
graniastosłupów V

ABCD

i V

FGCD

oraz ćwiartki walca V

DCE

. I tak:

(

)

4

R

R

-

h

R

a

V

V

V

2

DCE

ABCD

ABE

⋅

π

+

⋅

⋅

=

+

=

(

)

4

R

R

-

T

R

a

V

V

V

2

DCE

FGCD

FGE

⋅

π

+

⋅

⋅

=

+

=

Składową pionową wypadkowej siły naporu wyznaczymy z następującej zależności (oś Oz
skierowana w dół):

"

z

'

z

z

P

-

P

P

=

Po wstawieniu zależności na objętości V

ABE

i V

FGE

oraz wykonaniu prostych przekształceń

matematycznych otrzymano:

(

)

(

)

[

]

(

)

w

ol

2

w

ol

z

-

4

R

R

-

T

-

R

-

h

R

a

P

γ

γ

⋅

π

+

⋅

γ

⋅

γ

⋅

⋅

=

Wypadkową siłę naporu działającego na zakrzywioną część burty obliczymy z następującego
wzoru:

2

z

2

x

P

P

P

+

=

[N]

natomiast kąt określający kierunek działania tej siły ze wzoru:

11

x

z

P

P

arctg

=

α

[rad]

Po podstawieniu zależności na składową poziomą P

x

i pionową P

z

do powyższych wzorów i

sprowadzeniu do najprostszej postaci uzyskano ostatecznie:

Zadania do samodzielnego rozwiązania:

1.

Obliczyć parcie hydrostatyczne działające na obie części muru pionową i ukośną

o wysokości H=6 m oraz parcie całkowite wody działającej na mur, jeżeli szerokość
muru b=1 m, a pochylenie

α

=0,785 rad, zaś

ρ

w

=1000 kg/m

3

. (A.2.4)

2.

Walec kołowy o osi poziomej zamyka otwór prostokątny w pionowej ścianie zbiornika
z cieczą (rys.). Dane są promień

r i długość L walca oraz głębokość zanurzenia jego osi

H. Ciężar właściwy cieczy

γγγγ

. Wyznaczyć wektor siły naporu na walec. (A.2.18)

3.

W prostokątny otwór wykonany w pionowej ścianie zbiornika wypełnionego cieczą
wstawiono walec kołowy o średnicy

D i długości L (rys). Walec ten może się obracać

wokół centralnej osi poziomej leżącej w płaszczyźnie ściany na głębokości

H. Wykazać,

że wypadkowy napór hydrostatyczny na walec nie daje momentu względem osi obrotu
walca. Przyjąć ciężar właściwy cieczy

γγγγ

. (A.2.25)

4.

Drewniana belka w kształcie walca kołowego o średnicy

D i długości L pływa w cieczy

o ciężarze właściwym

γγγγ

w położeniu pokazanym na rysunku. Obliczyć poziomą siłę,

z jaką belka jest dociskana do gładkiej pionowej ściany oraz ciężar właściwy drewna.
(A.2.26)

5.

Naczynie półkuliste o średnicy

D napełniono cieczą o gęstości

ρρρρ

i przykryto płytą szklaną.

Następnie naczynie odwrócono i położono na płaskiej poziomej (rys.). Wyznaczyć ciężar
naczynia G, jaki może zapobiec podniesieniu go przez parcie zawartej w niej cieczy.
(A.2.28)

12

2.

Przepływ cieczy doskonałej

Zadania z rozwiązaniami:

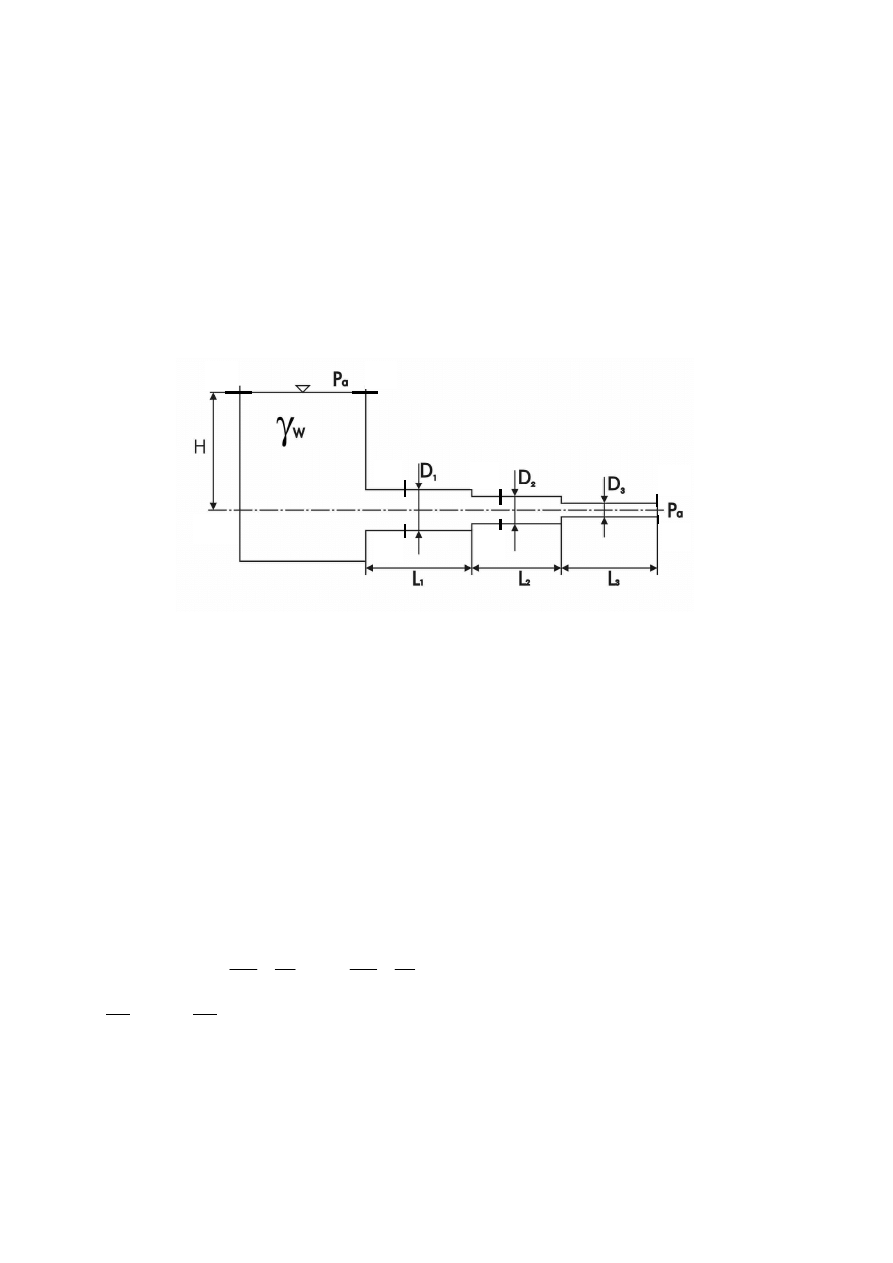
1.

Ciecz doskonała wypływa ze zbiornika przewodem o zmiennych średnicach D

1

=100 mm,

D

2

=60 mm i D

3

=40 mm. Długości poszczególnych odcinków są następujące:

L

1

=20 m, L

2

=30 m, L

3

=10 m. Wzniesienie zwierciadła cieczy w zbiorniku ponad oś

przewodu H=2 m. Ciśnienie atmosferyczne p

a

=1,013 10

5

N/m

2

. Określić:

a)

prędkości cieczy we wszystkich odcinkach przewodu,

b)

rozkład ciśnienia w przewodzie,

c)

wykres piezometryczny.

Dane: Szukane:

D

1

= 100 mm = 0,1 m a) v

1

= ?, v

2

= ?, v

3

= ?

D

2

= 60 mm = 0,06 m b) p

1

= ?, p

2

= ?, p

3

= ?

D

3

= 40 mm = 0,04 m c) H

p

= f(L)

L

1

= 20 m

L

2

= 30 mL

3

= 10 mH = 2 m

p

a

=1,013 10

5

N/m

2

g = 9,81 m/s

2

Rozwiązanie zadania:

adn. a) Równanie Bernoulliego dla przekrojów 0-0 i 3-3:

0-0 3-3

v

0

≈

0 v

3

= ?

p

0

= p

a

p

3

= p

a

z

0

= H z

3

= 0

Po podstawieniu parametrów do równania i wykonaniu prostych przekształceń
matematycznych otrzymano następujące wyrażenie na prędkość w przekroju wylotowym:

3

3

2

3

0

0

2

0

z

p

2g

v

z

p

2g

v

+

+

=

+

+

γ

γ

0

0

1

1

2

2

3

3

PO

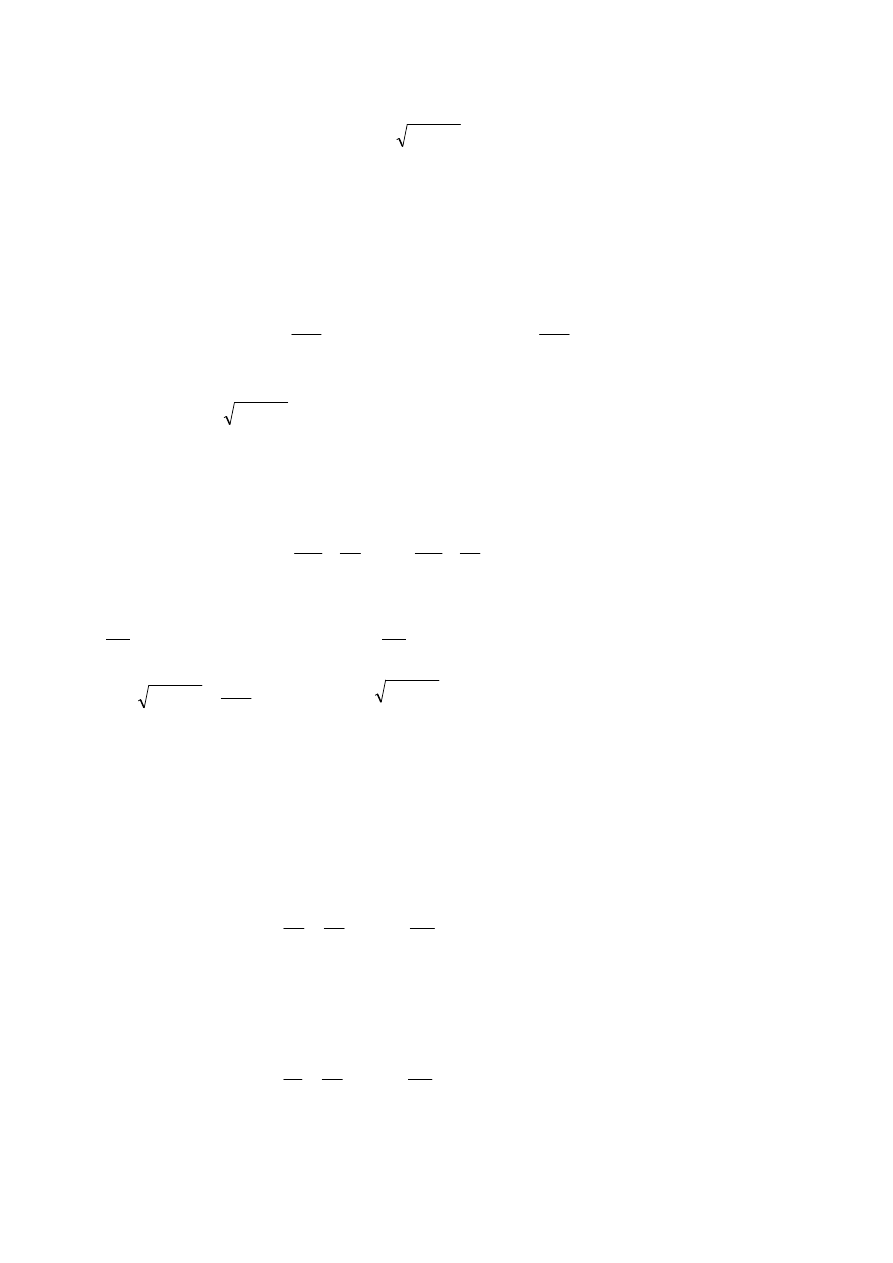
13

Prędkości w przekrojach 2-gim (w przewodzie o średnicy D

2

) i pierwszym (w przewodzie o

średnicy D

1

) wyznaczono z zasady ciągłości przepływu (F

⋅

v = const).

Po prostych przekształceniach wyrażenia na te prędkości można przedstawić w następującej
postaci:

gdzie:

adn. b) Aby wyznaczyć ciśnienie w przekroju 2-2, należy rozwiązać równanie Bernoulliego
dla przekrojów 2-2 i 3-3:

2-2 3-3

p

2

= ? p

3

= p

a

z

2

= 0 z

3

= 0

Po podstawieniu powyższych parametrów do równania i wykonaniu przekształceń
matematycznych otrzymano wzór na wysokość ciśnienia w przekroju 2-2:

Podobnie porównując przekroje 1-1 i 3-3 można wyznaczyć zależność na wysokość ciśnienia
w przekroju 1-1:

H

g

2

v

3

⋅

⋅

=

2

2

3

3

2

D

D

v

v















⋅

=

2

1

3

3

1

D

D

v

v















⋅

=

3

3

2

3

2

2

2

2

z

p

2g

v

z

p

2g

v

+

+

=

+

+

γ

γ

H

g

2

v

3

⋅

⋅

=

2

2

3

2

D

D

H

g

2

v















⋅

⋅

⋅

=

H

g

2

v

3

⋅

⋅

=



























+

=

4

2

3

a

2

D

D

-

1

H

p

p

γ

γ



























+

=

4

1

3

a

1

D

D

-

1

H

p

p

γ

γ

14

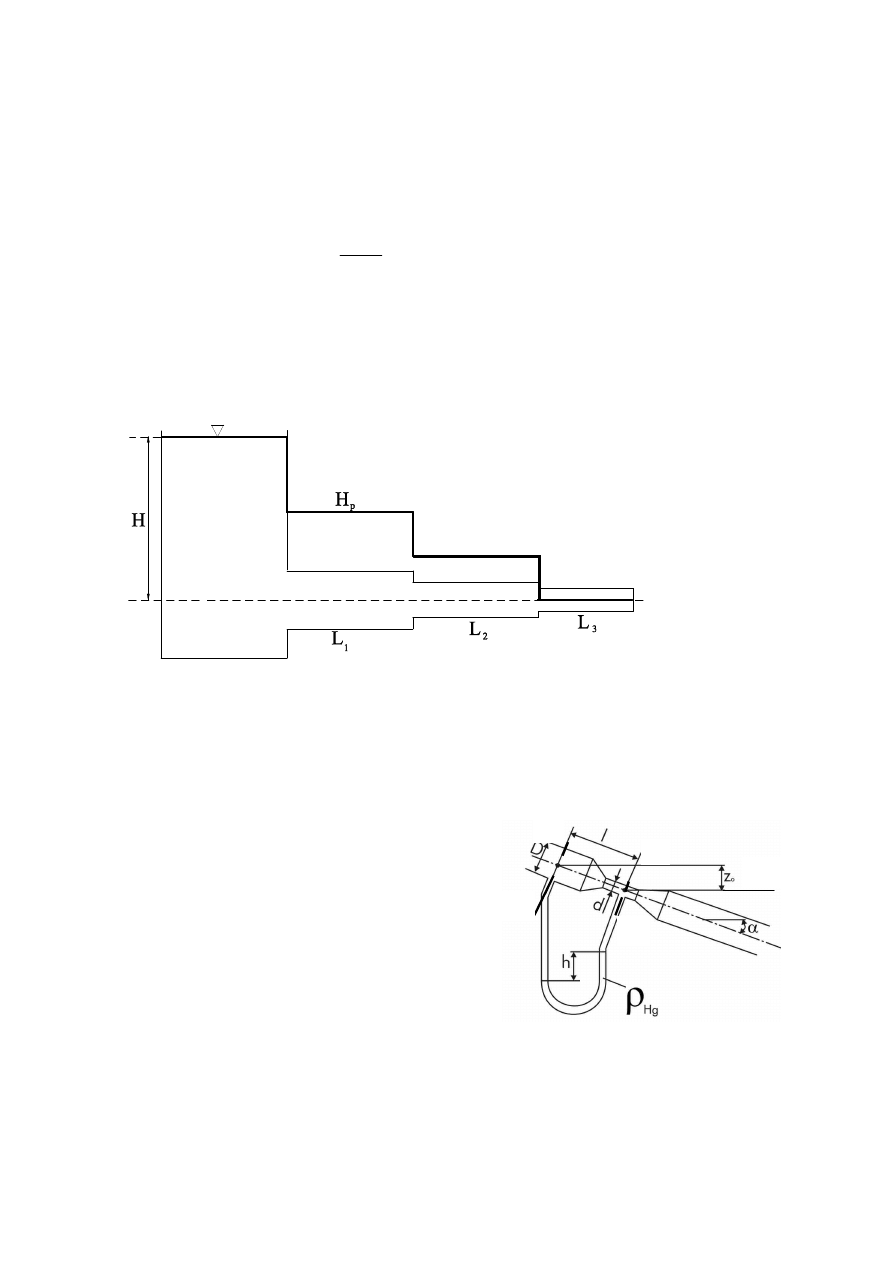
adn. c) Wykres piezometryczny

Na podstawie wyliczonych wartości ciśnień statycznych w przekrojach 1-1, 2-2 i 3-3
można narysować wykres piezometryczny przedstawiający przebieg wysokości ciśnienia
względnego:

γ

=

a

p

p

-

p

H

gdzie: p - całkowite ciśnienie statyczne w poszczególnych przekrojach.

Na poniższym rysunku przedstawiono orientacyjny wykres piezometryczny. Do bardziej
precyzyjnego narysowania jego w skali, należy obliczyć wartości ciśnień w przekrojach 1-1 i
2-2. Ciśnienie piezometryczne w przekroju 3-3 jest równe zeru, bo p

3

= p

a

.

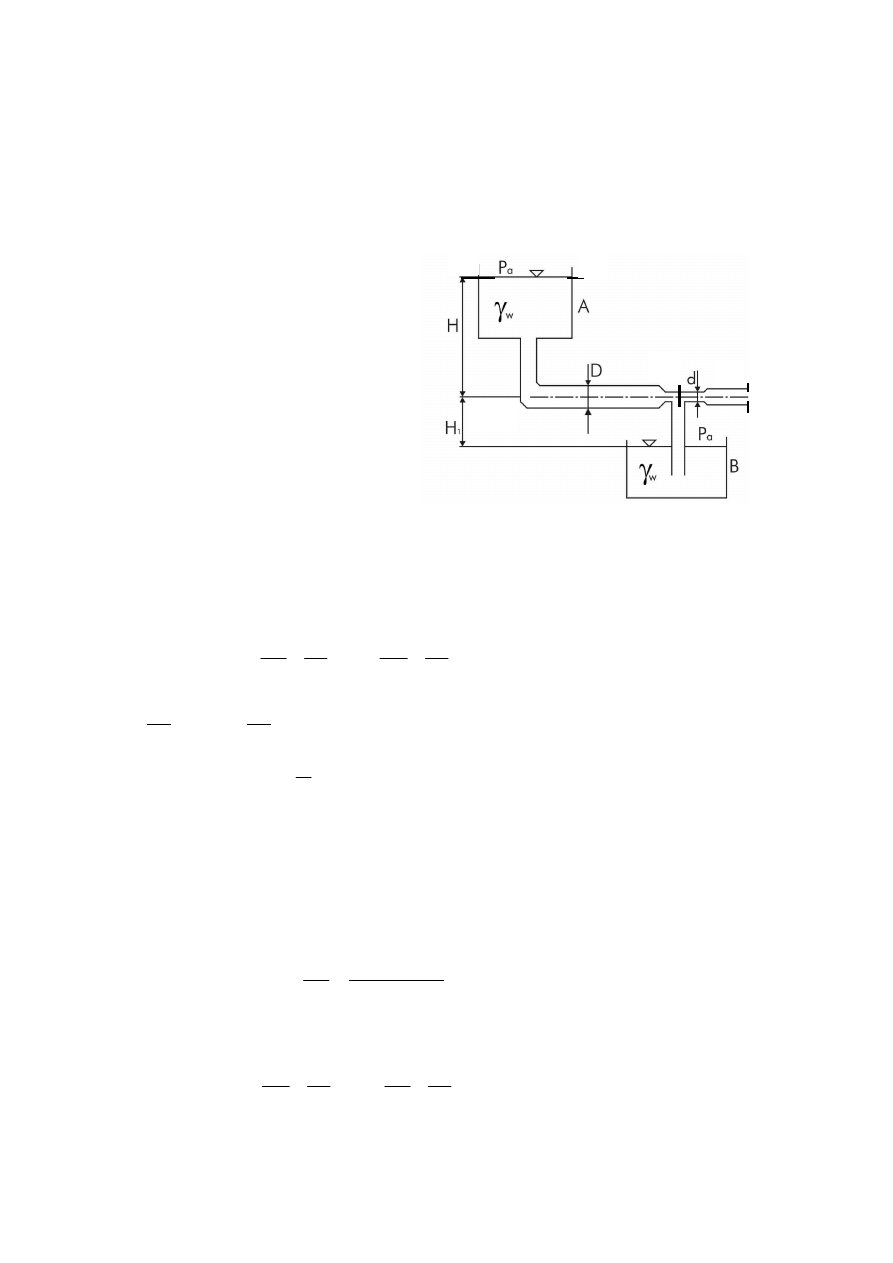
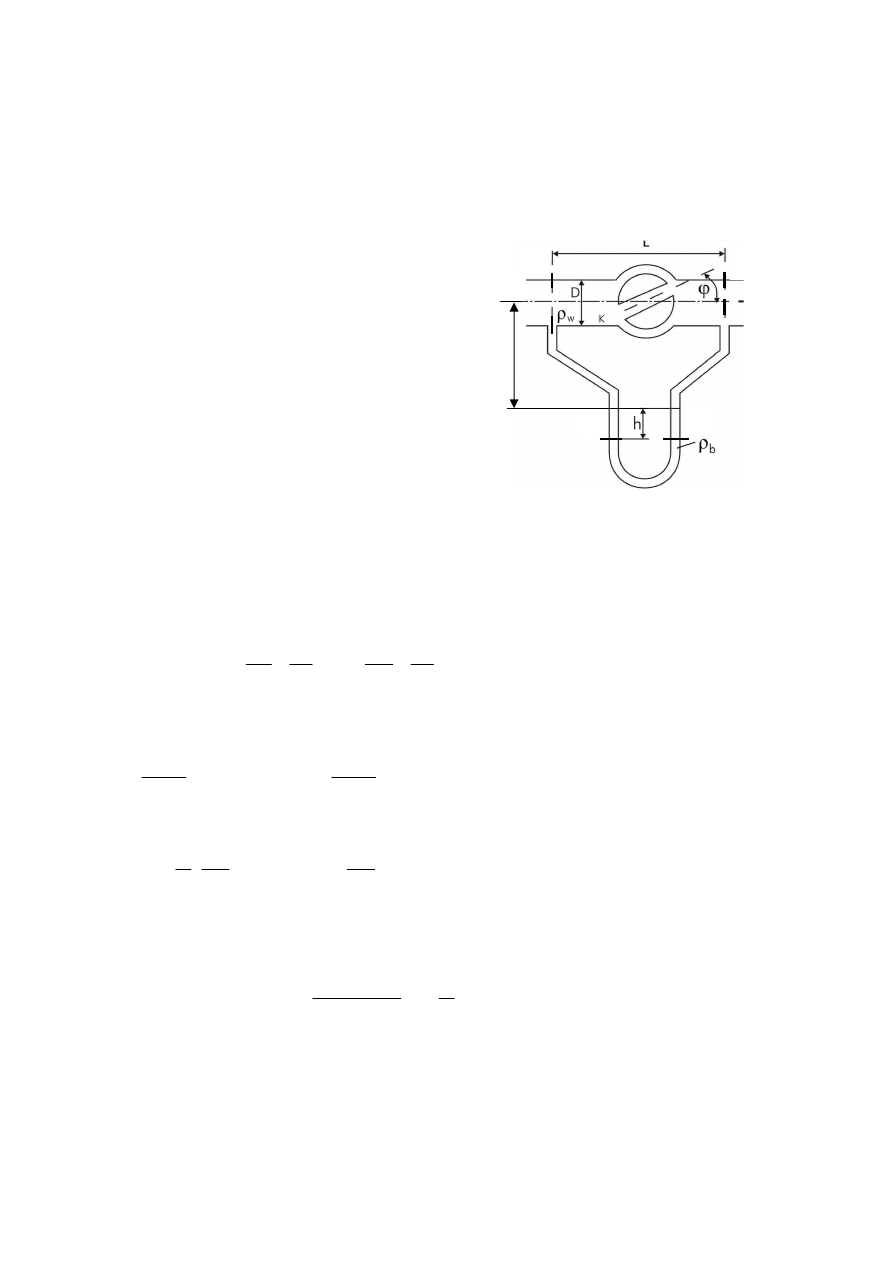
2.

Określić teoretyczny wydatek cieczy doskonałej przepływającej przez zwężkę Venturiego
usytuowaną pod kątem

α

=

π

/6 rad do poziomu (rys.). Różnica poziomów rtęci w

manometrze różnicowym wynosi h=600 mm Hg (

ρ

Hg

=13600 kg/m

3

). Dane geometryczne:

D=200 mm, d=75 mm, L=100 mm (

ρ

c

=1000 kg/m

3

).

Dane: Szukane:

α

=

π

/6 rad Q = ? [m

3

/s]

h = 600 mm Hg = 0,6 m

ρ

Hg

=13600 kg/m

3

ρ

c

=1000 kg/m

3

D=200 mm = 0,2 m
d=75 mm = 0,075 m
l=100 mm = 0,1 m

PO

1

1

2

2

15

Rozwiązanie zadania:

W zadaniu mamy do czynienia z układem przeznaczonym do pomiaru prędkości oraz
wydatku cieczy płynącej przez zwężkę Venturiego, na której końcach umieszczono ramiona
różnicowego manometru różnicowego. Wydatek można wyznaczyć posługując się równaniem
Bernoulliego dla przekrojów 1-1 i 2-2.



Ma ono następującą postać ogólną:

1-1 2-2

2

1

D

π

Q

4

v

⋅

⋅

=

2

2

d

π

Q

4

v

⋅

⋅

=

p

1

= ? p

2

= ?

z

1

= z

0

= l·sinα z

2

= 0

Po podstawieniu powyższych wartości do równania i wykonaniu niezbędnych uproszczeń
otrzymano:

(

)

(

)

4

4

c

2

1

2

2

d

-

D

ρ

2

p

-

p

2

D

d

Q

⋅

⋅

⋅

⋅

π

=

Do wyznaczenia wydatku niezbędna jest znajomość różnicy ciśnień p

1

-p

2

.

W tym celu przyrównujemy ciśnienia w lewym i prawym ramieniu U-rurki na poziomie β-β.
(aby to zrobić, należy wprowadzić pomocniczą zmienną H - patrz rysunek). W efekcie
uzyskujemy następujące równanie:

(

)

(

)

h

g

ρ

sin

l

-

H

g

ρ

p

h

H

ρ

p

Hg

c

2

c

1

⋅

⋅

+

α

⋅

⋅

⋅

+

=

+

⋅

⋅

+

g

Po prostych przekształceniach uzyskano wyrażenie na różnicę ciśnień w postaci:

(

)

[

]

α

⋅

⋅

⋅

⋅

=

sin

l

ρ

-

ρ

-

ρ

h

g

p

-

p

c

c

Hg

2

1

Po podstawieniu do wzoru na wydatek Q otrzymano ostatecznie:

(

)

[

]

(

)

4

4

c

c

c

Hg

2

2

d

-

D

ρ

2

sin α

l

ρ

-

ρ

-

ρ

h

g

2

D

d

π

Q

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

[m

3

/s]

2

c

2

2

2

1

c

1

2

1

z

p

2g

v

z

p

2g

v

+

γ

+

=

+

γ

+

16

3.

Wodna pompa strumieniowa służy do wypompowywania wody ze zbiornika B.
Jaka musi być wysokość wody w zbiorniku A, aby przy pozostałych wymiarach podanych
na rysunku nastąpiło zassanie wody ze zbiornika B ? Przyjąć, że przepływ jest ustalony
i że ciśnienia na powierzchniach swobodnych w zbiornikach A i B oraz w przekroju
wylotowym są równe ciśnieniu atmosferycznemu p

a

.

Dane: Szukane:

H

1

H = ?

γ

W

D
d
p

a

Rozwiązanie zadania:

Równanie Bernoulliego dla przekrojów 1-1 i 2-2 ma ogólną postać:

1-1 2-2

v

1

= ?

2

1

2

D

d

v

v













⋅

=

p

1

= ? p

2

= p

a

z

1

= 0 z

2

= 0

Po podstawieniu parametrów do równania Bernoulliego i odpowiednich przekształceniach
otrzymano wyrażenie na energię kinetyczną strumienia w przekroju 1-1 o postaci:

Równanie Bernoulliego dla przekrojów 0-0 i 1-1 ma ogólną postać:

2

w

2

2

2

1

w

1

2

1

z

p

2g

v

z

p

2g

v

+

γ

+

=

+

γ

+

(

)

(

)

4

4

w

4

1

a

2

1

d

-

D

D

p

-

p

2g

v

⋅

⋅

=

γ

1

w

1

2

1

0

w

0

2

0

z

p

2g

v

z

p

2g

v

+

γ

+

=

+

γ

+

PO

0

0

1

2

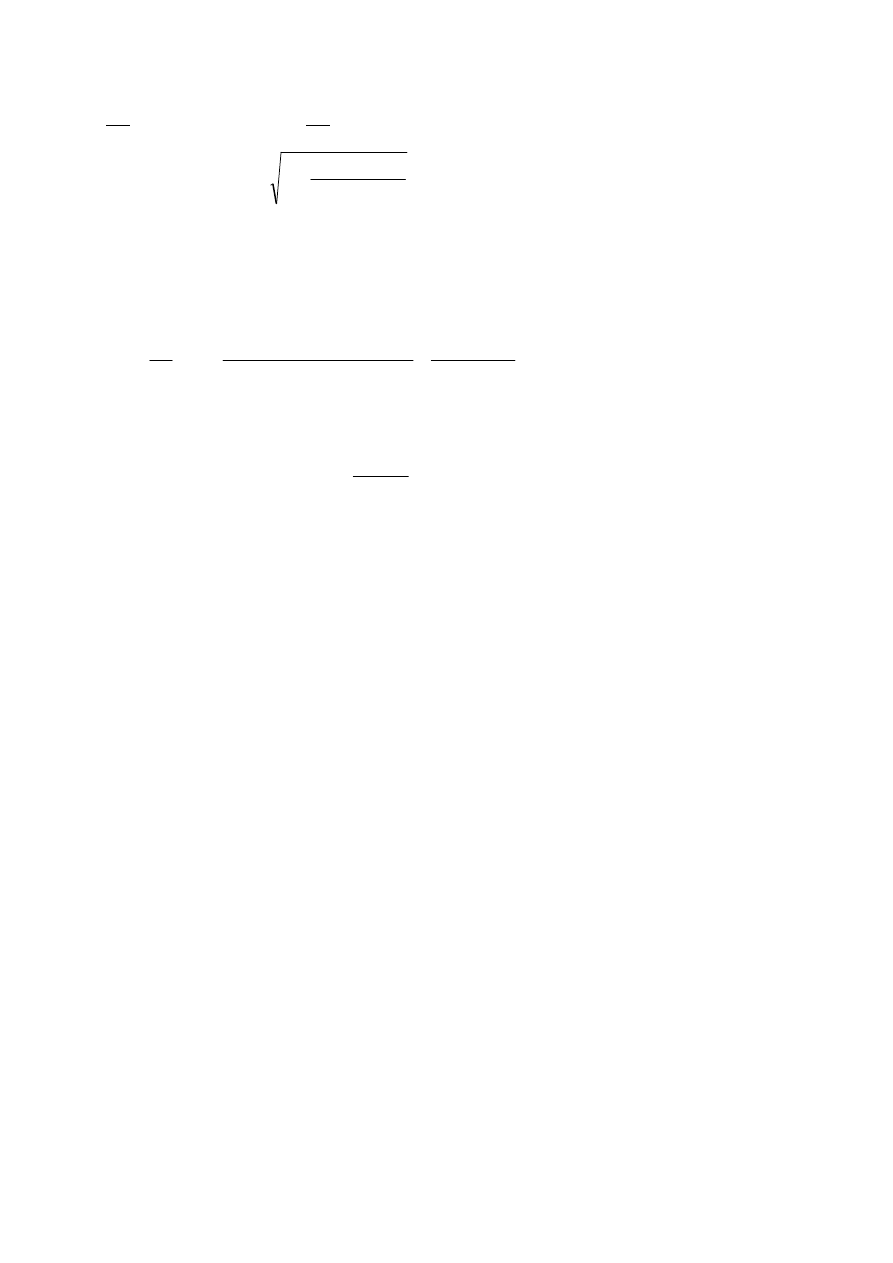
17

0-0 1-1

v

0

≈

0 v

1

(

)

(

)

4

4

w

4

1

a

d

-

D

D

p

-

p

g

2

⋅

⋅

⋅

=

γ

p

0

= p

a

p

1

= p

a

-

γ

w

⋅

H

1

z

0

= H z

1

= 0

Po podstawieniu do równania Bernoulliego otrzymano:

(

)

(

)

w

γ

⋅

γ

+

⋅

γ

⋅

⋅

⋅

γ

+

⋅

=

+

γ

1

w

a

4

4

w

4

1

w

a

a

w

a

H

-

p

d

-

D

2g

D

H

p

-

p

2g

H

p

Po dokonaniu odpowiednich redukcji i przekształceń otrzymano ostatecznie:

4

4

4

1

d

-

D

d

H

H

⋅

=

[m]

Zadania do samodzielnego rozwiązania:

1.

Ciecz doskonała wypływa ze zbiornika przewodem o zmiennej średnicy D

1

=150 mm,

i D

2

=200 mm. Długości poszczególnych odcinków są następujące:

l

1

=20 m i l

2

=30 m. Wzniesienie H=1 m. Ciśnienie atmosferyczne p

a

=1,013 10

5

N/m

2

.

Obliczyć:
a)

prędkości cieczy w obu odcinkach przewodu,

b)

rozkład ciśnienia w przewodzie,

c)

wykonać wykres piezometrycznej linii ciśnień. (B.1.2)

2.

Obliczyć objętościowe natężenie przepływu cieczy doskonałej przewodem poziomym
o średnicy D=40 mm. Rolę przepływomierza spełnia zwężka Venturiego o średnicy
przewężenia d=10 mm, a do pomiaru różnicy ciśnień służą dwa piezometry, w których
różnica poziomów cieczy doskonałej wynosi

∆

p/

γ

=0,5 m. (B.1.5)

3.

Rurka Pitote’a wstawiona jest w przepływ wody . Wyznaczyć zależność między
prędkością przepływu v a wysokością h spiętrzenia wody w rurce (p

a

= 1 at). (B.1.14)

4.

Dla zmierzenia objętościowego natężenia przepływu benzyny płynącej przewodem o
średnicy D=50 mm wmontowano dyszę normalną o średnicy d=30 mm (rys.). Określić:
a)

objętościowe natężenie przepływu benzyny, jeżeli różnica poziomów rtęci wynosi

h=175 mm Hg (

ρ

Hg

=13600 kg/m

3

),

b) stratę ciśnienia na przepływomierzu,

b)

przy jakim ciśnieniu przed dyszą powstanie kawitacja, jeżeli wysokość ciśnienia

pary nasyconej benzyny wynosi p/

γ

Hg

=150 mm Hg (

ρ

b

=800 kg/m

3

). (B.1.17)

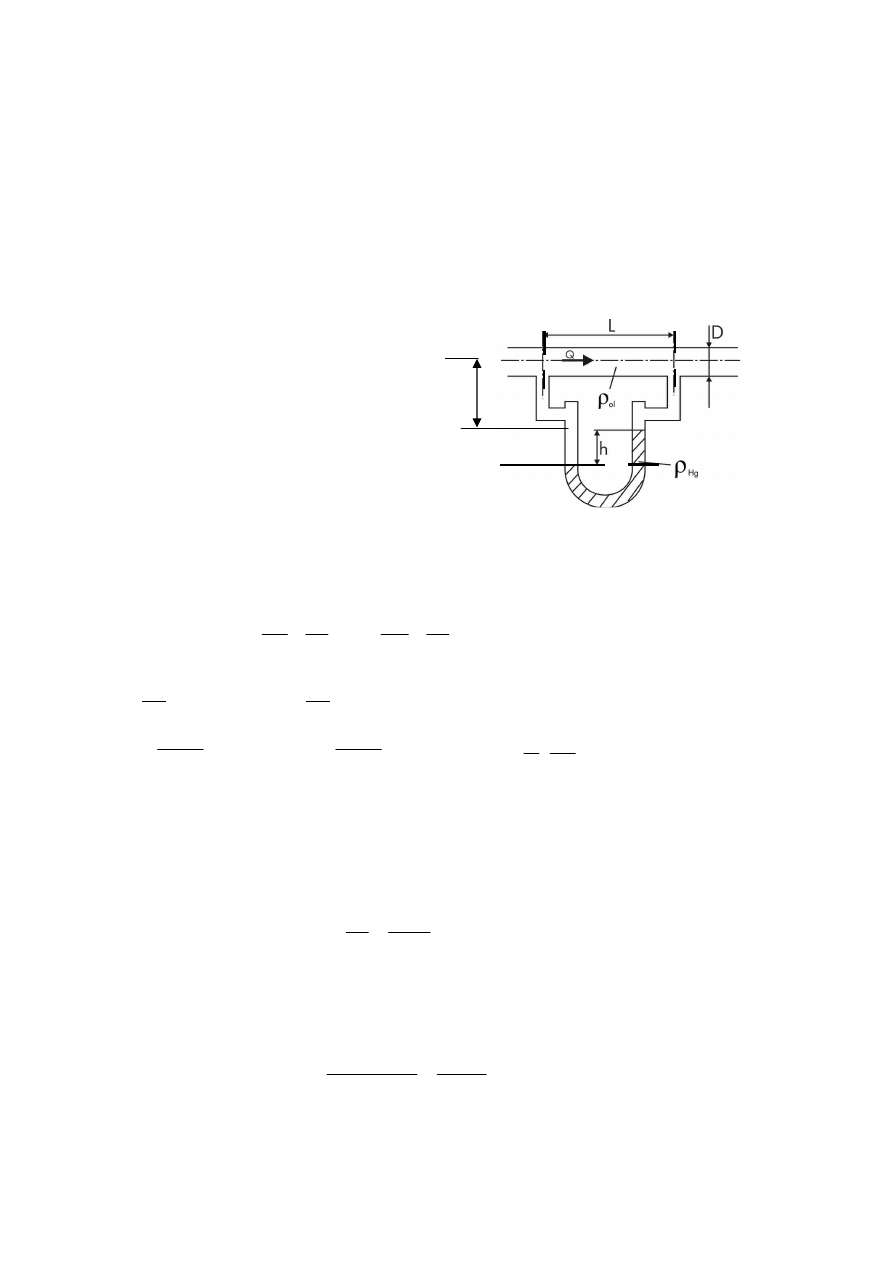
18

3.

Przepływ cieczy rzeczywistej

Zadania z rozwiązaniami:

1.

Dla określenia lepkości oleju (

ρ

ol

=900 kg/m

3

) mierzy się stratę ciśnienia w kalibrowanym

odcinku pomiarowym o średnicy D=6 mm i długości L=2 m. Jaka jest wartość
kinematycznego współczynnika lepkości, jeżeli przy natężeniu przepływu
Q=7,3 10

-6

kg/m

3

. Spadek ciśnienia mierzony rtęciowym manometrem różnicowym

(

ρ

Hg

=13600 kg/m

3

) wynosi h=120 mm Hg.

Dane: Szukane:

ρ

ol

= 900 kg/m

3

ν

= ? [m

2

/s]

D=6mm = 0,006 m
L=2 m
Q=7,3

⋅

10

-6

m

3

/s

ρ

Hg

=13600 kg/m

3

h=120 mm = 0,12 m Hg

g=9,81 m/s

2

Rozwiązanie zadania:

Równanie Bernoulliego ze stratami dla przekrojów 1-1 i 2-2 ma postać:

1-1 2-2

p

1

= ? p

2

= ?

z

1

= 0 z

2

= 0

Ze względu na mały wydatek i niewielką średnicę możemy przyjąć, że przepływ jest
laminarny. W takim przypadku obowiązuje analityczna zależność na

λ

o następującej

postaci:

Po podstawieniu powyższych zależności do równania Bernoulliego i wykonaniu
odpowiednich uproszczeń i przekształceń matematycznych otrzymano:

PO

1

2

α

α

H

m

l

2

ol

2

2

2

1

ol

1

2

1

h

h

z

p

2g

v

z

p

2g

v

∆

+

∆

+

+

+

=

+

+

γ

γ

2

1

D

4Q

v

⋅

=

π

2

1

2

D

4Q

v

v

⋅

=

=

π

g

2

v

D

L

h

2

1

l

⋅

⋅

=

∆

λ

0

h

m

=

∆

D

v

64

Re

64

1

⋅

⋅

=

=

ν

λ

ol

2

1

4

p

-

p

D

g

Q

L

128

γ

π

ν

=

⋅

⋅

⋅

⋅

⋅

19

Różnicę ciśnień p

1

-p

2

można wyznaczyć z równowagi ciśnień na poziomie

α

-

α

w lewym i

prawym ramieniu U-rurki. Wynika z tego następujące równanie:

Po prostych przekształceniach otrzymano:

Po uwzględnieniu powyższej zależności w równaniu Bernoulliego i jego rozwiązaniu ze
względu na

ν

otrzymano ostatecznie:

Po podstawieniu wartości liczbowych otrzymano, że

ν

= 36,17

⋅

10

-6

m

2

/s

2.

Dany jest duży zbiornik, z którego wyprowadzono poziomy przewód o średnicy
d=200 mm, długości L=1000 m i chropowatości k=0,2 mm. Znając wzniesienie
zwierciadła wody w piezometrze H=5 m umieszczonym w odległości 0,2L od końca
przewodu nad jego osią, obliczyć wydatek Q oraz wzniesienie wody x w zbiorniku
nad osią przewodu (

ν

=1,3 10

-6

m

2

/s).

Dane: Szukane:

d=200 mm=0,2 m x = ? [m]

L=1000 m Q = ? [m

3

/s]

k=0,2 mm
H=5 m
ν=1,3 10

-6

m

2

/s

g=9,81 m/s

2

L

1

=0,2L

γ

w

= 10

4

N/m

3

PO

0

0

1

2

(

)

h

H

p

h

H

p

Hg

ol

2

ol

1

⋅

+

⋅

+

=

+

⋅

+

γ

γ

γ

(

)

ol

Hg

2

1

ρ

-

ρ

h

p

p

⋅

⋅

=

−

g

(

)

ol

ol

Hg

4

ρ

Q

L

128

ρ

-

ρ

D

h

g

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

π

ν

20

Rozwiązanie zadania:

Rozważmy równanie Bernoulliego dla przekrojów 0-0 i 2-2. Jego ogólna postać została
podana poniżej:

gdzie:

v

0

≈

0 v

2

= ?

p

0

= p

a

p

2

= p

a

z

0

= x z

2

= 0

2g

v

d

L

h

2

2

l

⋅

⋅

λ

=

∆

0

h

m

=

∆

Po podstawieniu do równania Bernoulliego i dokonaniu odpowiednich uproszczeń otrzymano:

Z kolei rozważmy równanie Bernoulliego dla przekrojów 1-1 i 2-2. Ogólna postać takiego
równania wygląda następująco:

gdzie:

v

1

= v

2

H

p

p

w

a

1

⋅

γ

+

=

2g

v

d

0,2L

h

2

2

l

⋅

⋅

λ

=

∆

0

h

m

=

∆

z

1

= 0

Po podstawieniu do równania Bernoulliego, dokonaniu uproszczeń i rozwiązaniu do
względem prędkości v

2

otrzymano:

L

d

H

g

10

v

2

⋅

λ

⋅

⋅

⋅

=

Ponieważ współczynnik strat liniowych λ jest zależny od prędkości v

2

, do rozwiązania

powyższego równania należy użyć metody kolejnych przybliżeń.

1˚ Pierwsze przybliżenie

Zakładamy początkową wartość λ

(0)

odczytaną z wykresu Nikuradsego dla danej

chropowatości względnej:

m

l

2

w

2

2

2

0

w

0

2

0

h

h

z

p

2g

v

z

p

2g

v

∆

+

∆

+

+

γ

+

=

+

γ

+













⋅

λ

+

⋅

=

d

L

1

2g

v

x

2

2

m

l

2

w

2

2

2

1

w

1

2

1

h

h

z

p

2g

v

z

p

2g

v

∆

+

∆

+

+

γ

+

=

+

γ

+

21

3

-

10

1,0

200

0,2

d

k

⋅

=

=

=

ε

w obszarze kwadratowej zależności strat (w tym obszarze współczynnik λ nie zależy od
liczby Reynoldsa Re, a tym samym od prędkości v

2

). Wartość tego współczynnika wynosi:

λ

(0)

= 0,0192. Po podstawieniu tej wartości do wzoru na prędkość v

2

otrzymano pierwsze

przybliżenie tej prędkości:

m/s

1,01

1000

0,0192

0,2

9,81

10

L

d

H

g

10

v

)

0

(

(0)

2

=

⋅

⋅

⋅

=

⋅

λ

⋅

⋅

⋅

=

Z kolei dla tej prędkości obliczamy wartość pierwszego przybliżenia liczby Reynoldsa:

5

6

-

(0)

2

(0)

10

55

,

1

10

1,3

0,2

1,01

ν

d

v

Re

⋅

=

⋅

⋅

=

⋅

=

Dla wyliczonej wartości Re i ε z wykresu Nikuradsego odczytujemy kolejne (drugie)
przybliżenie wartości współczynnika λ przechodząc jednocześnie do kolejnego etapu:

2˚ Z wykresu Nikuradsego dla Re

(0)

= 1,55·10

5

i ε = 1,0·10

-3

odczytano, że:

λ

(1)

= 0,0208. Porównując tę wartość z poprzednią otrzymamy:

0016

,

0

0192

,

0

-

0208

,

0

-

(0)

(1)

=

=

λ

λ

=

λ

∆

Uzyskana wartość różnicy jest większa od wymaganego minimum równego
∆λ

min

=0,0005. W związku z powyższym powtarzamy ten sam cykl obliczeń, biorąc pod

uwagę ostatnie przybliżenie współczynnika strat liniowych.

m/s

0,97

1000

0,0208

0,2

9,81

10

L

d

H

g

10

v

)

1

(

(1)

2

=

⋅

⋅

⋅

=

⋅

λ

⋅

⋅

⋅

=

5

6

-

(1)

2

(1)

10

49

,

1

10

1,3

0,2

0,97

ν

d

v

Re

⋅

=

⋅

⋅

=

⋅

=

Z wykresu Nikuradsego odczytano kolejne przybliżenie współczynnika λ:
λ

(2)

= 0,0209. Różnica pomiędzy tą wartości a poprzednią wynosi 0,0001, a więc jest mniejsza

od założonej równej 0,0005. Pozwala to na zakończenie obliczeń i przyjęcie ostatnio
wyliczonej wartości prędkości v

2

= 0,97 m/s do dalszych rozważań.

Na podstawie znanej wartości prędkości można w prosty sposób wyliczyć wydatek
korzystając ze wzoru:

/s

m

0,03

4

2

,

0

97

,

0

4

d

v

Q

3

2

2

(1)

2

=

⋅

π

⋅

=

⋅

π

⋅

=

Wysokość wzniesienia wody w zbiorniku x obliczymy z otrzymanego wcześniej wzoru
podstawiając do niego wyznaczone metodą kolejnych przybliżeń wartości prędkości i
współczynnika strat liniowych.

( )

m

5,035

0,2

1000

0,0208

1

9,81

2

0,97

d

L

1

2g

v

x

2

(1)

2

(1)

2

=













⋅

+

⋅

=













⋅

λ

+

⋅

=

22

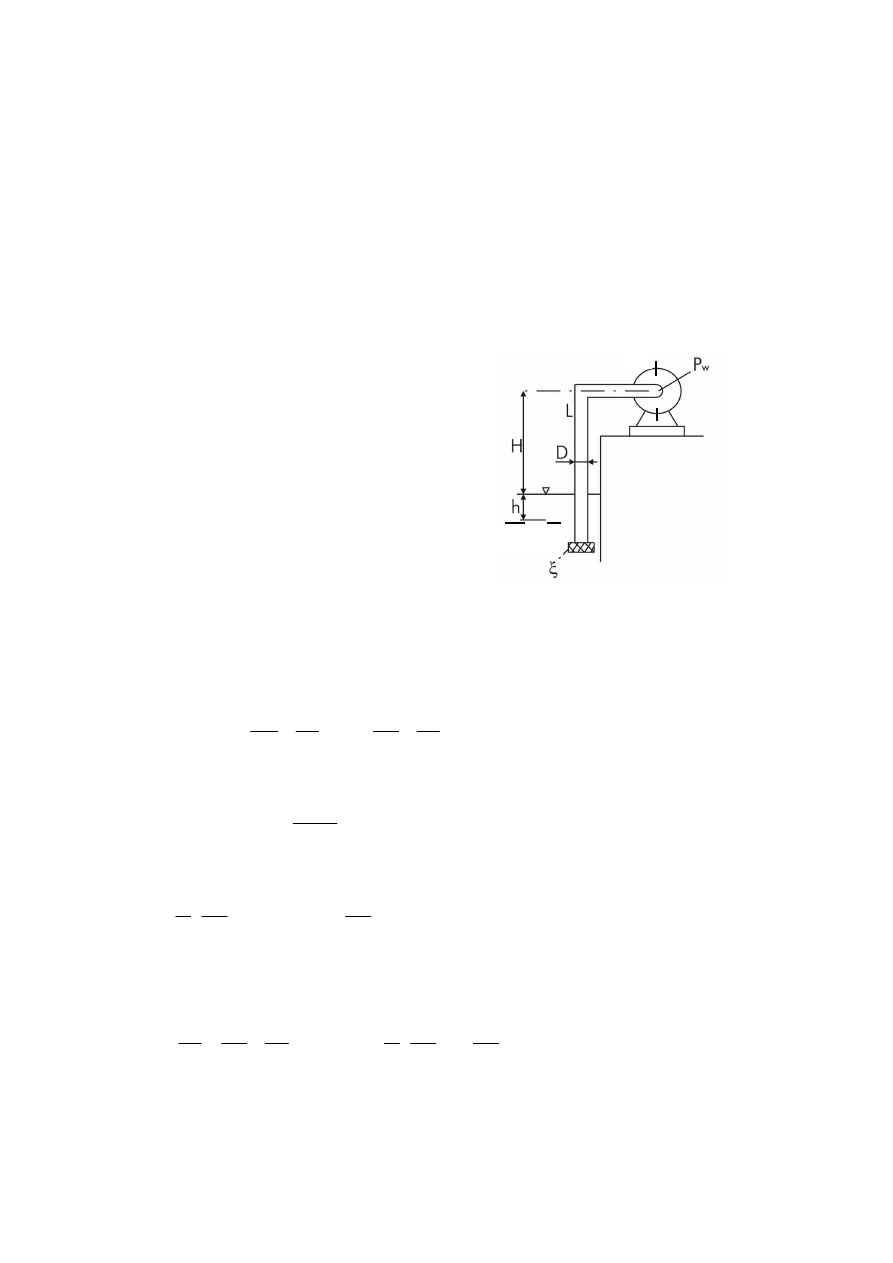
3.

Obliczyć współczynnik strat lokalnych na kurku przymkniętym o kąt

π

/12 rad.

Przewodem o średnicy D=200 mm i k=0,2 mm płynie woda w ilości Q=0,06 m

3

/s.

Różnica wysokości na manometrze różnicowym wypełnionym bromoformem
(

ρ

b

=2800 kg/m

3

) wynosi h=130 mm, przy czym odległość między punktami

podłączenia manometru do przewodu wynosi L=5 m (

ν

=1,3 10

-6

m

2

/s)

Dane: Szukane:

D=200 mm = 0,2 m ζ = ?

k=0,2 mm
Q=0,06 m

3

/s

ρ

b

=2800 kg/m

3

h=130 mm = 0,13 m

L=5 m

ν

=1,3 10

-6

m

2

/s

g=9,81 m/s

2

ρ

w

=1000 kg/m

3

Rozwiązanie zadania:

Rozważmy równanie Bernoulliego dla przekrojów 1-1 i 2-2, którego ogólna postać jest
następująca:

gdzie:

v

1

=

2

D

4Q

⋅

π

v

2

= v

1

=

2

D

4Q

⋅

π

p

1

= ?

p

2

= ?

z

1

= 0 z

2

= 0

2g

v

D

L

h

2

2

l

⋅

⋅

λ

=

∆

2g

v

h

2

2

m

⋅

ζ

=

∆

Po wstawieniu do równania Bernoulliego, dokonaniu niezbędnych uproszczeń i rozwiązaniu
względem zmiennej ζ otrzymano:

Aby obliczyć wartość współczynnika strat lokalnych, należy najpierw wyznaczyć różnicę
ciśnień p

1

-p

2

i odczytać z wykresu Nikuradsego wartość współczynnika strat liniowych λ na

podstawie wcześniej obliczonych wartości liczby Reynoldsa Re i chropowatości względnej ε.

PO

1

2

m

l

2

w

2

2

2

1

w

1

2

1

h

h

z

p

2g

v

z

p

2g

v

∆

+

∆

+

+

γ

+

=

+

γ

+

(

)

D

L

v

p

-

p

2g

w

2

2

2

1

⋅

λ

+

γ

⋅

⋅

=

ζ

α

α

H

23

Z porównania wartości ciśnień w lewym i prawym ramieniu U-rurki pomiarowej na poziomie
α-α wynika, że (wysokość H - zmienna pomocnicza):

(

)

h

g

ρ

H

g

ρ

p

h

H

g

ρ

p

b

w

2

w

1

⋅

⋅

+

⋅

⋅

+

=

+

⋅

⋅

+

Stąd po prostych przekształceniach:

(

)

w

b

2

1

ρ

-

ρ

h

g

p

p

⋅

⋅

=

−

Z kolei obliczamy liczbę Reynoldsa ze wzoru:

5

6

-

2

10

2,94

0,2

10

1,3

0,06

4

D

ν

π

Q

4

ν

D

v

Re

⋅

=

⋅

⋅

⋅

π

⋅

=

⋅

⋅

⋅

=

⋅

=

oraz współczynnik chropowatości względnej:

3

-

10

1,0

200

0,2

D

k

⋅

=

=

=

ε

Na podstawie wyżej wyliczonych wartości odczytujemy z wykresu Nikuradsego wartość
współczynnika strat liniowych:

0202

,

0

=

λ

Po podstawieniu wzorów na różnicę ciśnień oraz prędkość do wzoru na ζ otrzymano:

Po podstawieniu wartości liczbowych otrzymano wartość współczynnika strat liniowych
równą ζ = 1,76

(

)

D

L

ρ

Q

16

ρ

-

ρ

h

D

g

2

w

2

w

b

4

2

⋅

λ

+

⋅

⋅

⋅

⋅

⋅

⋅

π

⋅

=

ζ

24

4.

Oś pompy jest wzniesiona o H=4 m ponad normalne zwierciadło wody w zbiorniku
wyrównawczym. Wydajność pompy jest równa Q=2,78 10

-3

m

3

/s. O ile może się obniżyć

zwierciadło wody w zbiorniku, aby pompa mogła jeszcze pracować, jeżeli ciśnienie pary
nasyconej p

w

=0,0123 10

5

N/m

2

. Przewód zakończono smokiem o współczynniku strat

lokalnych

ξ

=10. Pozostałe opory należy pominąć. Pozostałe dane:

-

średnica przewodu ssącego D=50 mm,

-

długość przewodu ssącego L=10 m,

-

chropowatość przewodu k=0,2 mm,

-

lepkość

ν

=1,03 10

-6

m

2

/s,

Dane: Szukane:

H = 4 m h = ? [m]

Q=2,78 10

-3

m

3

/s

p

w

=0,0123 10

5

N/m

2

ξ

=10

D=50 mm = 0,05 m

L=10 m

k=0,2 mm

ν

=1,03 10

-6

m

2

/s

g=9,81 m/s

2

γ

w

= 10

4

N/m

3

p

a

= 1,013·10

5

N/m

2

Rozwiązanie zadania:

Równanie Bernoulliego ze stratami dla przekrojów 0-0 i 1-1 ma następującą postać:

gdzie:

v

0

= 0 v

1

=

2

D

4Q

⋅

π

p

0

= p

a

p

1

= p

w

z

0

= 0 z

1

= H+h

2g

v

D

L

h

2

1

l

⋅

⋅

λ

=

∆

2g

v

h

2

1

m

⋅

ζ

=

∆

Po podstawieniu powyższych zależności do równania Bernoulliego otrzymano:

PO

0

1

m

l

1

w

1

2

1

0

w

0

2

0

h

h

z

p

2g

v

z

p

2g

v

∆

+

∆

+

+

γ

+

=

+

γ

+

2g

v

2g

v

D

L

h

H

p

2g

v

p

2

1

2

1

w

w

2

1

w

a

⋅

ζ

+

⋅

⋅

λ

+

+

+

γ

+

=

γ

25

Po uporządkowaniu, podstawieniu wzoru na prędkość i rozwiązaniu względem niewiadomej h
otrzymano:

Aby wyznaczyć wartość h, należy jeszcze odczytać z wykresu Nikuradsego wartość
współczynnika λ na podstawie wcześniej wyliczonych wartości Re i ε.
Liczbę Reynoldsa obliczamy ze wzoru:

4

6

-

-3

1

10

6,87

0,05

10

1,03

10

2,78

4

D

ν

π

Q

4

ν

D

v

Re

⋅

=

⋅

⋅

⋅

π

⋅

⋅

=

⋅

⋅

⋅

=

⋅

=

oraz współczynnik chropowatości względnej:

3

-

10

4,0

50

0,2

D

k

⋅

=

=

=

ε

Na podstawie wyżej wyliczonych wartości odczytujemy z wykresu Nikuradsego wartość
współczynnika strat liniowych:

0295

,

0

=

λ

Po podstawieniu wartości liczbowych do wzoru na h otrzymano, że h = 0,9 m

Zadania do samodzielnego rozwiązania:

1.

Obliczyć nadciśnienie powietrza, jakie musi panować w zbiorniku hydroforowym,
który ma dostarczać wodę o temp. T=283

°

K w ilości Q=5 10

-3

m

3

/s na wysokość H=25 m.

Woda będzie prowadzona przewodem żeliwnym o średnicy D=50 mm, długości L=30 m
oraz chropowatości bezwzględnej k=0,2 mm. Położenie zwierciadła przyjąć za stałe
i pominąć prędkość wody dopływającej do zbiornika (

ν

=1,308 10

-6

m

2

/s). Na przewodzie

występują następujące elementy powodujące straty lokalne przepływu: jedno zwężenie
przy wlocie do przewodu (

ξ

1

=0,5), trzy łuki kołowe o kącie zagięcia

ψ

=

π

/2 i R/r=0,5

(

ξ

2

=0,5) i kurek o kącie przymknięcia

ϕ

=

π

/9 rad (

ξ

3

=2,3). (B.2.2)

2.

Obliczyć współczynnik strat lokalnych na nagłym przewężeniu przekroju przewodu
charakteryzującego się średnicami: większą D

1

=150 mm i mniejszą D

2

=125 mm.

Przewodem płynie woda o temp. 283

°

K (

ν

=1,308 10

-6

m

2

/s) w ilości Q=0,03 m

3

/s.

Różnica ciśnień zanotowana na manometrze różnicowym wypełnionym rtęcią
(

ρ

Hg

=13600 kg/m

3

) wynosi h=143 mm Hg. Odległości odbiorów ciśnienia od miejsca

zmiany średnicy wynoszą L

1

=15 m i L

2

=20 m. Bezwzględna chropowatość przewodu

wynosi k=0,3 mm. (B.2.3)

3.

Obliczyć wysokość ssania pompy H

s

o wydajności Q=3,6 10

-3

m

3

/s, jeżeli średnica rury

ssącej D=50 mm, jej długość L=15 m, a k=0,2 mm. Przewód zakończony jest smokiem z
klapą zwrotną (

ξ

1

=10), a na swej długości posiada dwa kolana o kącie zagięcia

ϕ

=

π

/2 i R/r=1 (

ξ

2

=2). Ciśnienie wrzenia wody p

w

=0,0123 10

5

N/m

2

,

a lepkość

ν

=1,3 10

-6

m

2

/s. (B.2.6)

H

D

L

D

g

Q

8

p

-

p

h

4

2

w

w

a

−













ζ

+

⋅

λ

⋅

⋅

⋅

π

⋅

−

γ

=

26

4.

Woda wypływa ze zbiornika układem przewodów o chropowatości względnej

ε

=0,0175. Natężenie przepływu wody o lepkości

ν

=10

-6

m

2

/s wynosi Q=0,1 m

3

/s,

a średnice przewodów wynoszą odpowiednio d

1

=0,4 m, d

2

=0,2 m, d

3

=0,3 m, zaś

ich długości wynoszą odpowiednio: l

1

=50 m, l

2

=100 m, l

3

=40 m, l

4

=35 m i h=20 m.

Jaka musi być wysokość napełnienia H, aby miał miejsce opisany przepływ. (B.2.14)

5.

Woda o temp. T=283

°

K (

ν

=1,308 10

-6

m

2

/s) przepływa ze zbiornika zamkniętego do

otwartego przewodem o średnicy D=50 mm i długości L=100 m. Zwierciadła wody
wzniesione są ponad oś przewodu:
a)

w zbiorniku zamkniętym o H

1

=1,5 m z nadciśnieniem p

n1

=0,5 bar,

b)

w zbiorniku otwartym o H

2

=2,5 m

Obliczyć wydatek Q w przewodzie. Chropowatość bezwzględna k=0,2 mm. (B.2.21)

27

4. Obliczenia taktycznych układów rozwinięć linii wężowych


Zadania z rozwiązaniami:

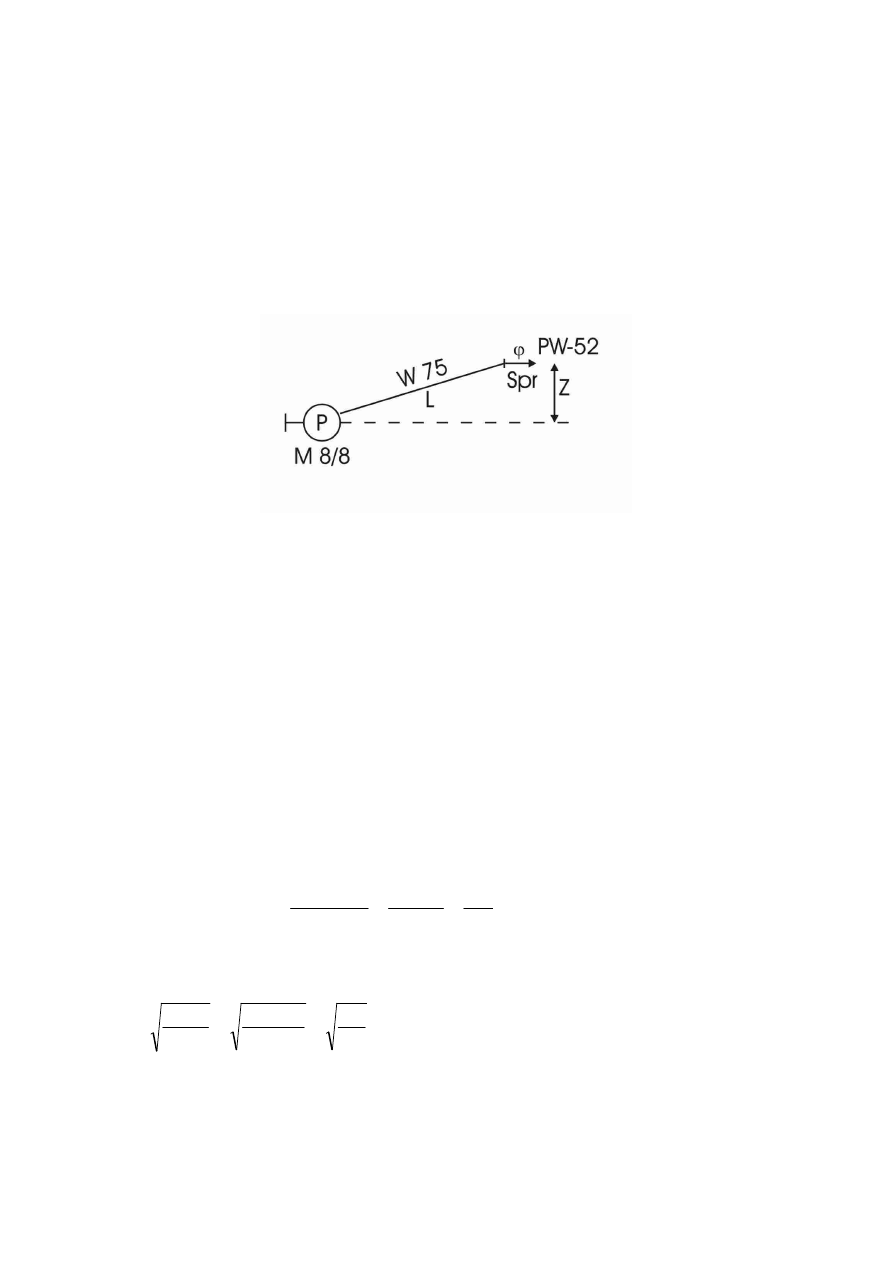
1. Dla układy pompa M8/8, linia tłoczna W75, prądownica PW-52 określić parametry pracy

prądownicy (rys.). Dane pompy: H

max

=120 m, Q

max

=20 l/s, długość linii tłocznej l=100m,

różnica poziomów z=20 m, dane prądownicy: S

pr

=2,89 ms

2

/l

2

, φ=0,016, m=0,8.

Dane: Szukane:

H

max

= 120 m Q

pr

= ? [l/s]

Q

max

= 20 l/s

H

pr

= ? [m]

l = 120 m

H

wzl

=? [m]

z = 20 m

H

zw

=? [m]

S

pr

= 2,89 ms

2

/l

2

l

max

=? [m]

φ=0,016

m=0,8
S

75

=1,01· 10

-3

s

2

/l

2

Rozwiązanie

:

S

z

= S

75

· l + S

pr

= 1,01· 10

-3

· 100 + 2,89 = 2,99≈3 ms

2

/l

2

m

120

Hmax

a

=

=

,

(

)

0,3

400

120

20

1

120

)

Q

(n

Hmax

b

2

2

max

=

=

⋅

=

⋅

=

ms

2

/l

2

z

Q

S

Q

b

a

2

p

z

2

p

+

⋅

=

⋅

−

z

a

b)

(S

Q

z

2

p

−

=

+

⋅

5,5

3,3

100

0,3

3

20

120

b

S

z

a

Q

z

p

=

=

+

−

=

+

−

=

Q

p

= 5,5 l/s

p

pr

Q

Q

=

28

Q

pr

= 5,5 l/s

87,6

(5,5)

2,89

Q

S

H

2

2

pr

pr

pr

=

⋅

=

⋅

=

H

pr

= 87,6m

36,5

87,6

0,016

1

87,6

H

1

H

H

pr

pr

wzl

=

⋅

+

=

⋅

+

=

ϕ

H

wzl

= 36,5 m

29,2

36,5

0,8

0,8H

H

wzl

zw

=

⋅

=

=

H

zw

= 29,2 m

29,3

3

4

H

3

4

l

wzl

max

=

=

l

max

≈39 m

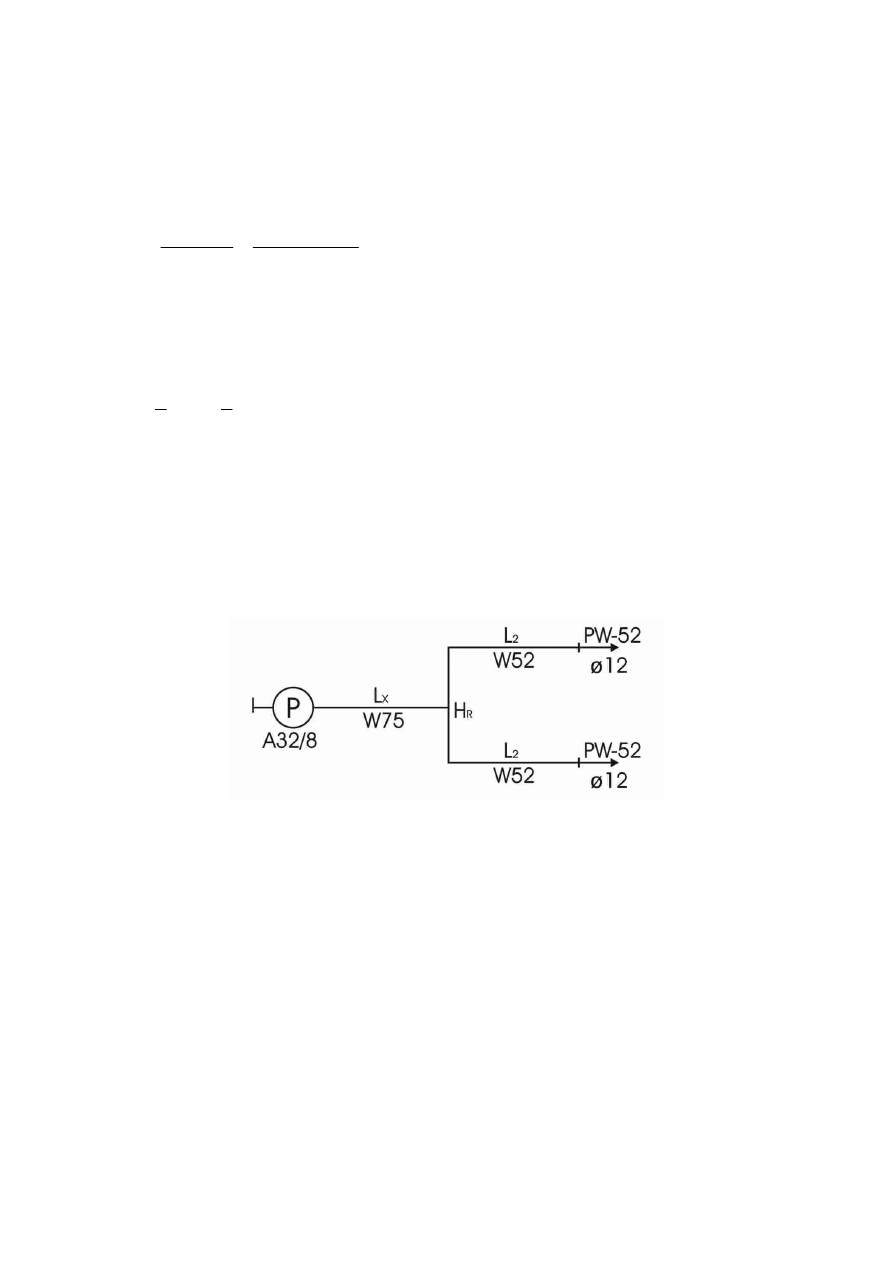
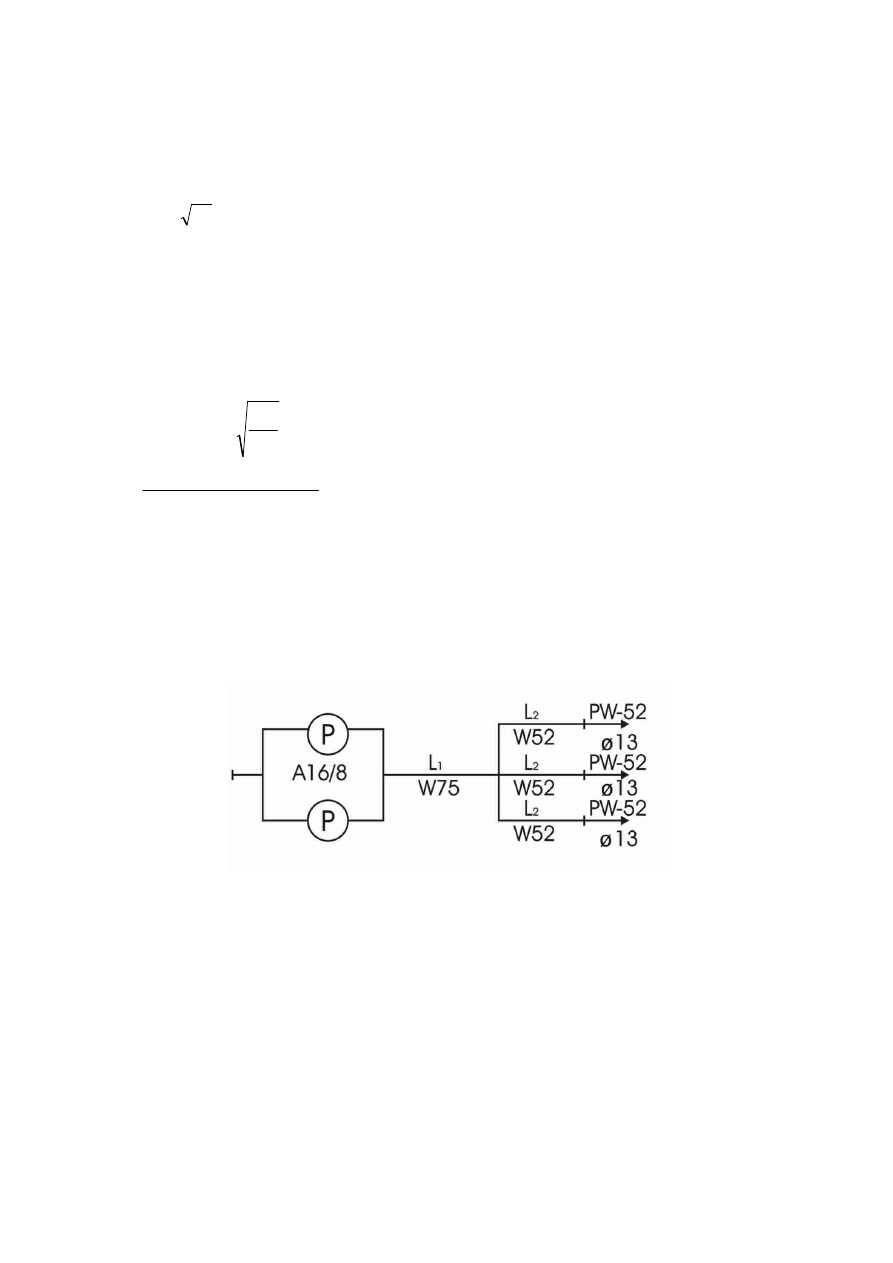
2. Dobrać długość l

x

linii głównej W75 w układzie symetrycznym pokazanym na rysunku

składającym się z autopompy A32/8, linii głównej i dwóch linii gaśniczych W52 o długości
l

2

=40m zakończonych prądownicami PW-52 o średnicy pyszczka d=12mm. Przeprowadzić

dyskusję możliwych rozwiązań.

Dane: Szukane:

H

max

= 138 m l

max

=? [m]

Q

max

= 60 l/s

l

2

= 40 m

S

pr

= 5,41 ms

2

/l

2

d=12mm
S

75

=1,01· 10

-3

s

2

/l

2

29

Rozwiązanie

:

x

52

r

p

3

2

pr

2

52

pr

r

l

S

H

H

d

10

H

l

S

H

H

⋅

+

=

⋅

=

⋅

+

=

∗

∗

Równanie pompy na następującą postać:

2

p

p

Q

b

a

H

⋅

−

=

(1)

Podstawiając równanie (1) do wzoru

x

l

S

H

H

52

r

p

⋅

+

=

otrzymamy:

x

l

S

l

S

H

bQ

a

75

2

52

pr

2

p

⋅

+

⋅

+

=

−

∗

Wiemy, że

pr

pr

pr

S

H

Q

∗

=

oraz

∗

⋅

=

pr

p

Q

2

Q

otrzymamy:

75

2

52

pr

2
p

x

S

l

S

H

Q

b

a

l

⋅

−

−

⋅

−

=

∗

[m]

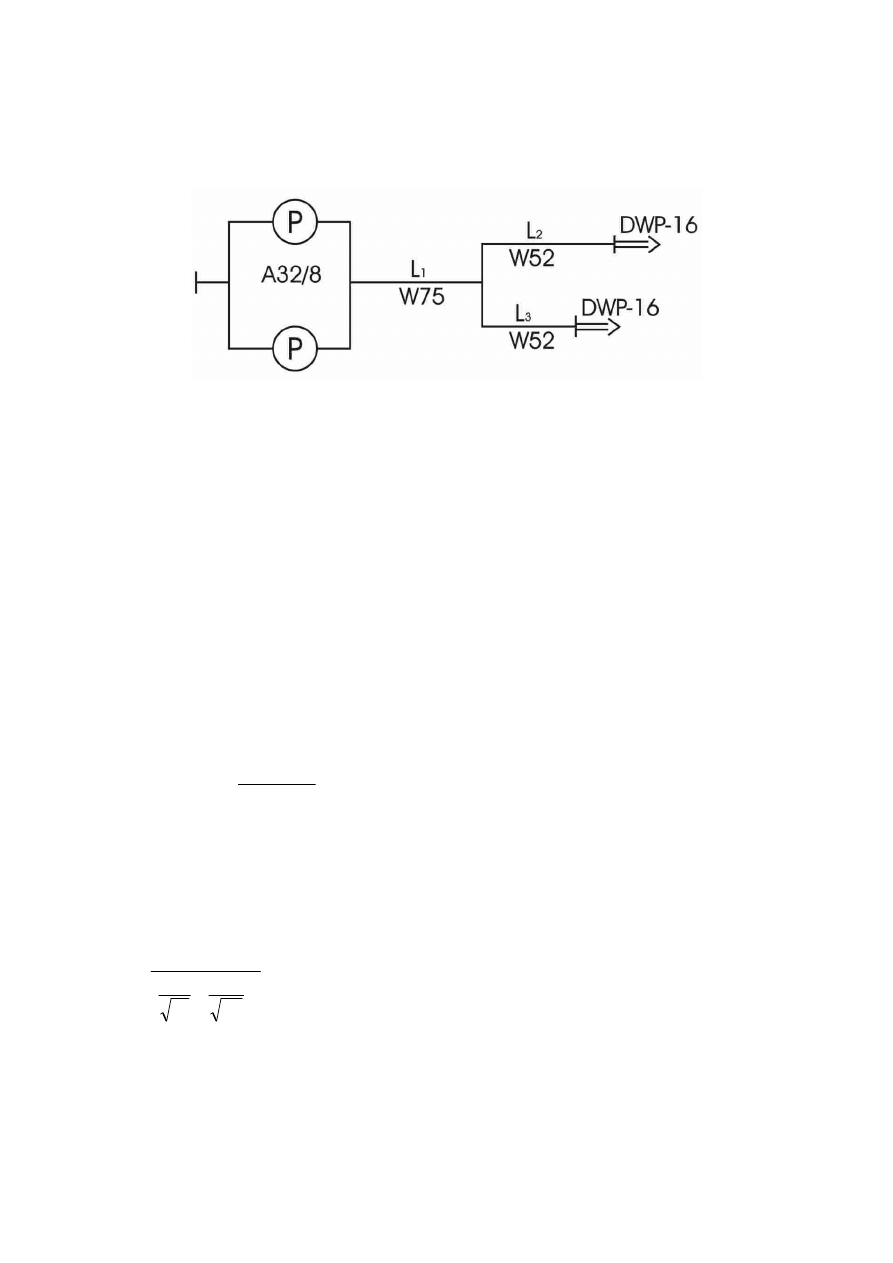
3. Dobrać długość linii upustowej W52, w układzie symetrycznym składającym się z dwóch

pomp A16/8 połączonych równolegle, linii głównej W75 o długości l

1

=80m oraz trzech linii

gaśniczych W52 o długości l

2

=40m zakończonych pradownicami PW-52 o średnicy pyszczka

d=13mm.

Dane: Szukane:

H

max

= 128 m l

u

=? [m]

Q

max

= 40 l/s

l

1

= 80 m

l

2

= 40 m

d=13mm
S

pr

= 2,89 ms

2

/l

2

30

Rozwiązanie

:

W pierwszej kolejności należy obliczyć H

*

pr

oraz Q

*

pr

podstawiając do poniższych wzorów

(1) oraz (2):

3

2

pr

d

10

H

⋅

=

∗

(1)

pr

pr

pr

S

H

Q

∗

=

(2)

Równania H

*

R

oraz H

*

p

otrzymują następującą postać (3) oraz (4):

2

*

pr

2

52

pr

*

R

)

(Q

l

S

H

H

⋅

⋅

+

=

∗

(3)

2

*

pr

1

75

*

R

*

p

)

Q

(3

l

S

H

H

⋅

⋅

⋅

+

=

(4)

Wartości H

*

p

oraz Q

*

p

należy obliczyć z poniższych zależności (5):

2

*

p

r

r

*

p

)

(Q

b

a

H

⋅

−

=

(5)

gdzie:

Hmax

a

r

=

,

2
max

r

Q

4

Hmax

b

⋅

=

Równanie Q

*

p

przybierze postać (6):

r

*

p

r

*

p

b

H

a

Q

−

=

(6)

Ogólne równanie wydatku Q

u

w linii upustowej przybierze następującą postać (7):

*

pr

*

p

u

Q

3

Q

Q

⋅

−

=

(7)

Dyskusja rozwiązania zdania:

1) Jeżeli

0

Q

u

≥

to:

2

u

52

*

p

u

2

u

u

52

*

p

)

(Q

S

H

l

)

(Q

l

S

H

⋅

=

⇒

⋅

⋅

=

2) Jeżeli

0

Q

u

≤

to regulacja upustem jest niemożliwa. Nie można otrzymać parametrów

optymalnych.

31

4. Wyznaczyć ciśnienia na działkach w układzie niesymetrycznym składającym się z dwóch

pomp A32/8 połączonych równolegle, linii głównej W75 o długości l

1

=200 m i dwóch linii

gaśniczych W52 o długości l

2

=60 m i l

3

=20 m zakończonych działkami DWP-16.

Dane: Szukane:

H

max

= 138 m H

dz

= ? [m]

Q

max

= 60 l/s

l

1

= 200 m

l

2

= 60 m

S

dz

= 0,113 ms

2

/l

2

φ=0,016

z=0

Rozwiązanie

:

2

p

r

r

*

p

)

(Q

b

a

H

⋅

−

=

gdzie:

max

r

H

a

=

,

2

max

r

)

(Q

4

Hmax

b

⋅

=

dz

2

52

I

S

l

S

S

+

⋅

=

dz

3

52

II

S

l

S

S

+

⋅

=

2

II

I

III

)

S

1

S

1

(

1

S

+

=

Oporność zastępcza dla całego układu wyraża się poniższym wzorem:

III

1

75

z

S

l

S

S

+

⋅

=

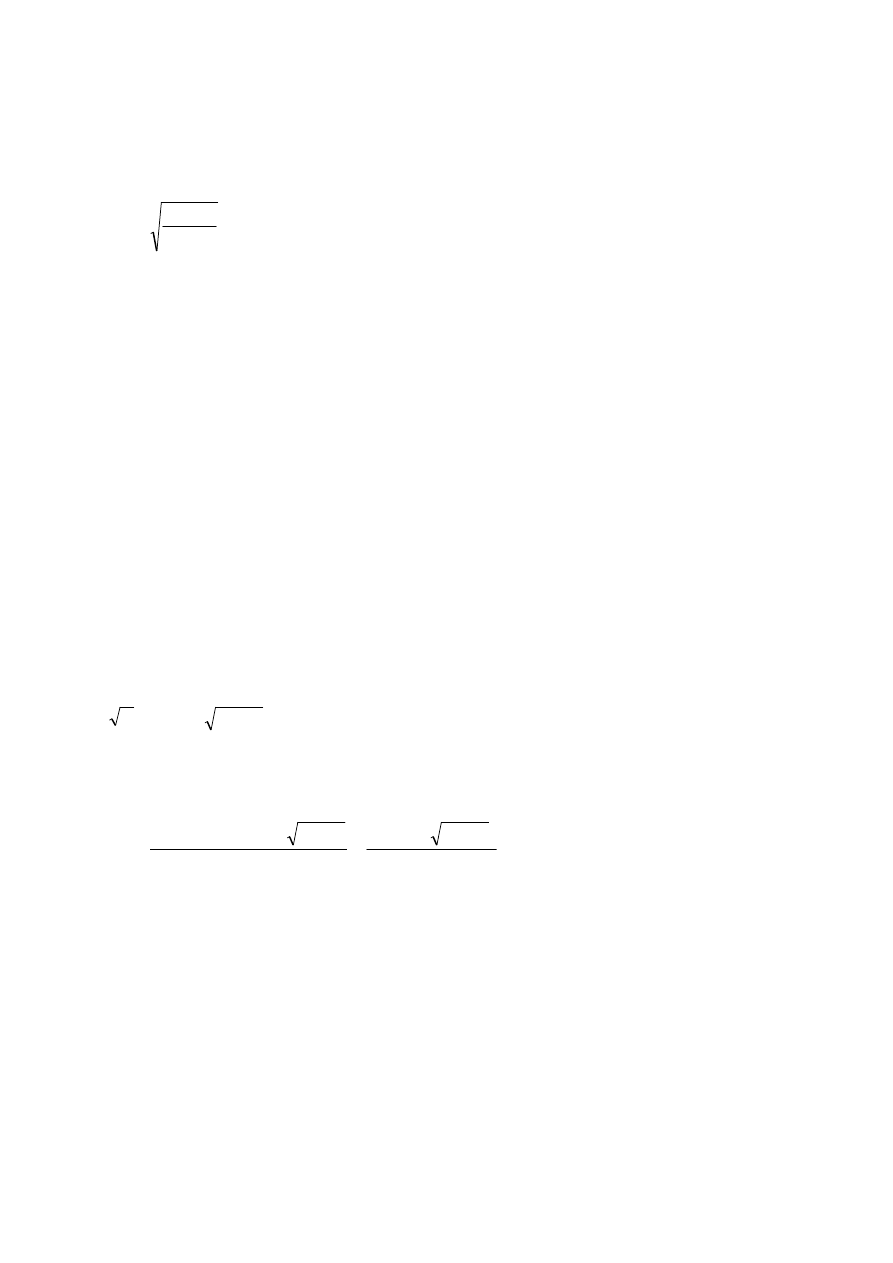
32

Wobec powyższego:

z

Q

S

)

(Q

b

a

2
p

z

2

p

r

r

+

⋅

=

⋅

−

r

z

r

p

b

S

z

a

Q

+

−

=

Z układu równań wynikają następujące zależności:

{

{

2
2

II

2

2

p

2
2

II

2

1

I

2

p

1

2

1

p

Q

S

)

Q

(Q

Q

S

Q

S

Q

Q

Q

Q

Q

Q

⋅

=

−

→

⋅

=

⋅

−

=

→

+

=

(1)

2
2

II

2
2

2

p

2
p

I

Q

S

)

Q

Q

Q

2

(Q

S

⋅

=

+

⋅

⋅

−

(2)

0

Q

S

Q

S

Q

Q

S

2

Q

S

2
2

II

2
2

I

2

p

I

2
p

I

=

⋅

−

⋅

+

⋅

⋅

⋅

−

⋅

(3)

0

Q

S

Q

Q

S

2

)Q

S

(S

2
p

I

2

p

I

2
p

II

I

=

⋅

+

⋅

⋅

⋅

−

−

(4)

Z równania (4) poniżej obliczono ∆:

2
p

I

II

I

2
p

2
I

Q

S

)

S

4(S

Q

S

4

∆

⋅

⋅

+

−

⋅

⋅

=

2
p

II

I

Q

S

4S

∆

⋅

⋅

=

II

I

p

S

S

Q

2

∆

⋅

⋅

⋅

=

(5)

Zatem poszczególne wydatki na działkach Q

1

’

oraz Q

2

’

wyrażą się następującymi

zależnościami:

II

I

II

I

I

p

II

I

II

I

p

p

I

'
2

S

S

)

S

S

(S

Q

)

S

(S

2

S

S

Q

2

Q

S

2

Q

−

⋅

+

=

−

⋅

⋅

⋅

⋅

+

⋅

⋅

=

(6)

'
2

p

'

1

Q

Q

Q

−

=

(7)

Dysponując zależnościami (6) oraz (7) otrzymujemy następujące rozwiązanie zadania (8), (9):

2

'

1

dz

dz1

)

(Q

S

H

⋅

=

(8)

2

'
2

dz

dz2

)

(Q

S

H

⋅

=

(9)

33

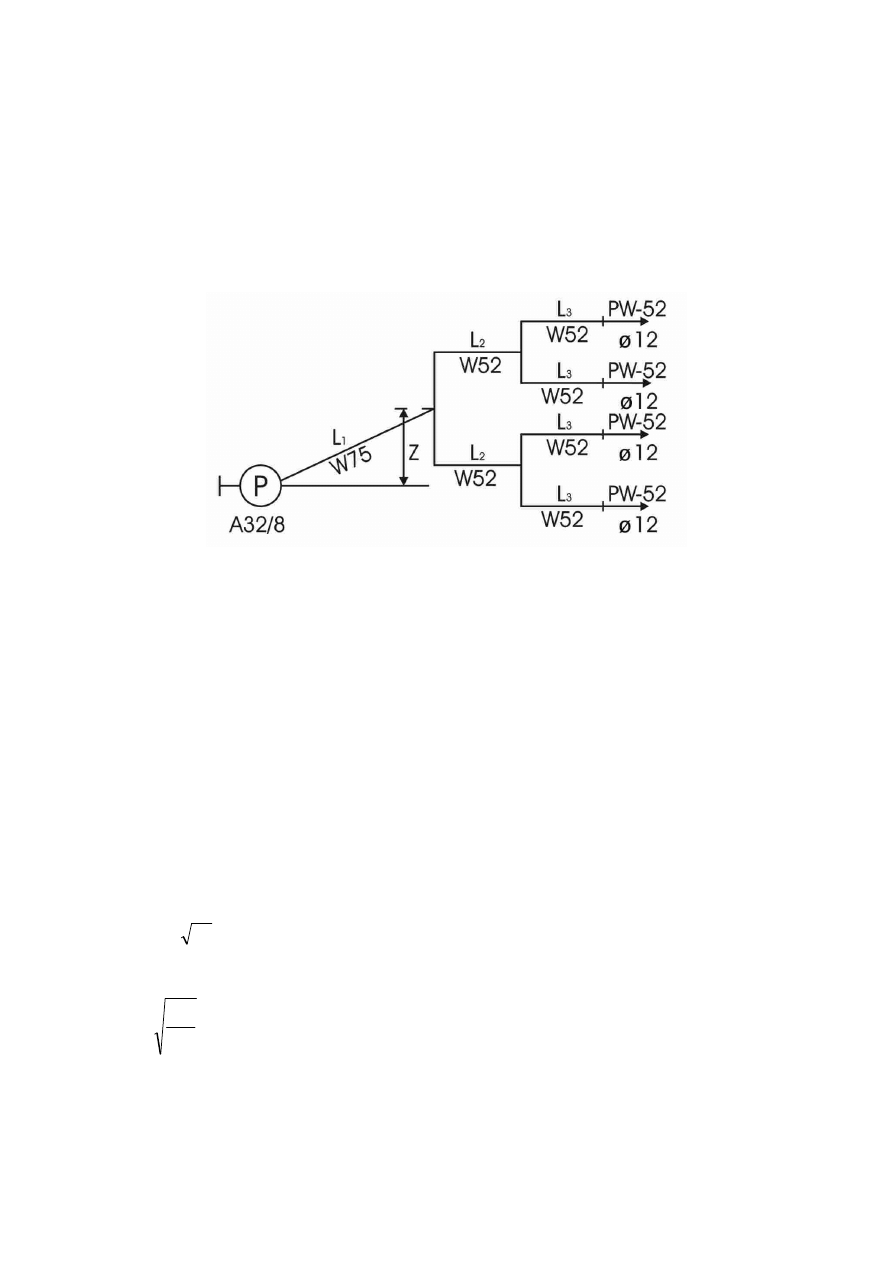
5. Wyznaczyć obroty pompy A 32/8 o parametrach nominalnych: n

n

=2700 obr/min i H

n

=80

m, przy których zostaną osiągnięte optymalne parametry pracy prądownicy w układzie
symetrycznym (rys.) składającym się z linii głównej W75 o długości l

1

=100 m i dwóch

poziomów linii gaśniczych W52: pierwszego zawierającego dwie linie o długościach l

2

=80 m

i drugiego zawierającego również dwie linie o długościach l

3

=60 m zakończone

prądownicami PW-52 o średnicy pyszczka d=12 mm. Różnica poziomów pomiędzy pompą
a drugim poziomem linii gaśniczych wynosi z=15 m.

Dane: Szukane:

H

n

= 80 m n

x

= ? [obr/min]

n

n

= 2700 obr/min

l

1

= 100 m

l

2

= 80 m

l

3

= 60 m

S

pr

= 3,98 ms

2

/l

2

d= 12 mm

z =15 m

Rozwiązanie

:

3

2

pr

d

10

H

⋅

=

∗

d – podstawiamy w [mm], H

pr

*

– otrzymujemy w [msw],

(1)

pr

pr

pr

S

H

Q

∗

=

(2)

2

*

pr

3

52

pr

1

*

R

)

(Q

l

S

H

H

⋅

⋅

+

=

∗

(3)

34

2

*

pr

2

52

R1

2

*

R

)

Q

(2

l

S

H

H

⋅

⋅

⋅

+

=

∗

(4)

2

*

pr

1

75

R2

*

p

)

Q

(4

l

S

H

H

⋅

⋅

⋅

+

=

∗

(5)

Z prawa powinowactwa otrzymujemy następujące zależności (6):

2

2

1

2

1

)

n

n

(

H

H

=

(6)

Podstawiając do równania (6) wielkości znane i poszukiwaną otrzymujemy równanie (7):

n

*

p

n

x

2

x

x

n

*

p

H

H

n

n

)

n

n

(

H

H

=

→

=

(7)

35

6. Na jaką odległość można przetłoczyć wodę w ilości Q=20 l/s w układzie składającym się

z dwóch pomp A 16/8 (pierwsza i trzecia) i trzech pomp A 32/8 (druga, czwarta i piąta), linii
głównych W75 i układu gaśniczego zawierającego jedną linię W75 zakończoną działkiem
DPW-24 (S

24

=0,05 ms

2

/l

2

, d=24 mm). Napływy na pompy wynoszą: na drugą n

1

=5 m, na

trzecią n

2

=10 m, na czwartą i na piątą n

3

=15m.

Dane: Szukane:

Pompa A16/8

H

’

max

= 120 m l

max

=? [m]

Q

’

max

= 40 l/s

Pompa A32/8

H

”

max

= 120 m

Q

”

max

= 40 l/s

Q = 20 l/s

H

n1

= 5 m

H

n2

= 10 m

H

n3

= 15 m

H

n4

= 15 m

S

75

=1,01· 10

-3

s

2

/l

2

z

1

= z

2

= z

3

= z

4

= z

5

= 0

Rozwiązanie

:

5

4

3

2

1

max

l

l

l

l

l

l

+

+

+

+

=

(1)

Poszczególne długości (l

1

, l

2,

l

3,

l

4,

l

5

) obliczymy z następujących zależności:

I:

1

2

1

75

2

I

I

z

Q

l

S

(Q)

b

a

+

⋅

⋅

=

⋅

−

gdzie:

'
max

I

H

a

=

,

2

'
max

'
max

I

)

(Q

H

b

=

Przekształcając powyższe ( I ) otrzymujemy zależność na l

1

(2):

2

75

1

2

I

I

1

Q

S

z

Q

b

a

l

⋅

−

⋅

−

=

(2)

Wynik (2) zaokrąglamy do wielokrotności 20 – stu w dół z uwagi na długość węży pożarniczych.

36

II:

2

2

2

75

2

II

II

z

Q

l

S

(Q)

b

a

+

⋅

⋅

=

⋅

−

gdzie:

n1

''

max

II

H

H

a

+

=

,

2

''

max

n1

''

max

II

)

(Q

H

H

b

+

=

Przekształcając powyższe ( II ) otrzymujemy zależność na l

2

(3):

2

75

2

2

II

II

2

Q

S

z

Q

b

a

l

⋅

−

⋅

−

=

(3)

Wynik (3) zaokrąglamy do wielokrotności 20 – stu w dół z uwagi na długość węży pożarniczych.

III:

3

2

3

75

2

III

III

z

Q

l

S

(Q)

b

a

+

⋅

⋅

=

⋅

−

gdzie:

n2

'
max

III

H

H

a

+

=

,

2

'
max

n2

'
max

III

)

(Q

H

H

b

+

=

Przekształcając powyższe ( III ) otrzymujemy zależność na l

3

(4):

2

75

3

2

III

III

3

Q

S

z

Q

b

a

l

⋅

−

⋅

−

=

(4)

Wynik (4) zaokrąglamy do wielokrotności 20 – stu w dół z uwagi na długość węży pożarniczych.

IV:

4

2

4

75

2

IV

IV

z

Q

l

S

(Q)

b

a

+

⋅

⋅

=

⋅

−

gdzie:

n3

''

max

IV

H

H

a

+

=

,

2

''

max

n3

''

max

IV

)

(Q

H

H

b

+

=

Przekształcając powyższe ( IV ) otrzymujemy zależność na l

4

(5):

2

75

4

2

IV

IV

3

Q

S

z

Q

b

a

l

⋅

−

⋅

−

=

(5)

Wynik (4) zaokrąglamy do wielokrotności 20 – stu w dół z uwagi na długość węży pożarniczych.

V:

5

2

z

2

V

V

z

Q

S

(Q)

b

a

+

⋅

=

⋅

−

gdzie:

n4

''

max

V

H

H

a

+

=

,

2

''

max

n4

''

max

V

)

(Q

H

H

b

+

=

dz

5

75

z

S

l

S

S

+

⋅

=

Przekształcając powyższe (V) otrzymujemy zależność na l

5

(6):

37

2

75

2

dz

3

2

V

V

3

Q

S

Q

S

z

Q

b

a

l

⋅

⋅

−

−

⋅

−

=

(6)

Wynik (6) zaokrąglamy do wielokrotności 20 – stu w dół z uwagi na długość węży pożarniczych.


Podstawiając zależności (2), (3), (4), (5), (6), do równania (1) otrzymamy rozwiązanie
zadania:

5

4

3

2

1

max

l

l

l

l

l

l

+

+

+

+

=

We wszystkich zadaniach z tego działu należy przyjąć następujące dane:

oporność węża W75: S

75

= 1,01 10

-3

s

2

/l

2

oporność węża W52: S

52

= 5,4 10

-3

s

2

/ l

2

oporność węża W110: S

110

= 1,29 10

-4

s

2

/ l

2

oporność prądownicy PW-52 o średnicy pyszczka d=12 mm: S

pr

= 3,98 ms

2

/ l

2

oporność prądownicy PW-52 o średnicy pyszczka d=13 mm: S

pr

= 2,89 ms

2

/ l

2

oporność prądownicy PW-75 o średnicy pyszczka d=16 mm: S

pr

= 1,24 ms

2

/ l

2

oporność działka DWP-24 o średnicy pyszczka d=24 mm: S

dz

= 0,05 ms

2

/ l

2

oporność działka DWP-16 o średnicy pyszczka d=16 mm: S

dz

= 0,113 ms

2

/ l

2

różnica poziomów z = 0 m, jeżeli nie podano inaczej
Do celów obliczeniowych przyjąć ciężar właściwy wody γ = 10

4

N/m

3

.

Zadania do samodzielnego rozwiązania:


1.

Wyznaczyć parametry pracy prądownic w układzie niesymetrycznym pokazanym na
rysunku, składającym się z motopompy M 8/8, linii głównej W75 o długości l

1

=100 m,

dwóch linii gaśniczych 52, jednej o długości l

2

=20 m zakończonej prądownicą PW-52

o średnicy pyszczka 13 mm i drugiej o długości l

3

=40 m zakończonej prądownicą

PW-52 o średnicy pyszczka 12 mm. Różnica poziomów z=20 m. Dane pompy takie

jak w zad.1, dane prądownicy o średnicy 12 mm: S

pr1

=3,98 ms

2

/l

2

,

ϕ

=0,018, m=0,81,

dane prądownicy o średnicy 13 mm: S

pr2

=2,89 ms

2

/l

2

,

ϕ

=0,016, m=0,8.

2.

Dla układu niesymetrycznego przedstawionego na rysunku obliczyć parametry
pracy prądownic. Dane autopompy A 32/8: H

max

=138 m, Q

max

=60 l/s, linia główna

W75 o długości l

1

=100 m, linie gaśnicze W75 o długościach l

2

=40 m i l

3

=20 m,

prądownice PW-52 o średnicy pyszczka d=13 mm.

3.

Wyznaczyć parametry pracy prądownic w układzie symetrycznym składającym się z
trzech poziomów linii gaśniczych przedstawionym na rysunku. Elementy układu
gaśniczego: dwie pompy A 32/8 połączone równolegle lub szeregowo (dwa warianty),
linia główna W75 o długości l

1

=140 m, dwie linie gaśnicze pierwszego poziomu W52

o długości l

2

=80 m, dwie linie gaśnicze drugiego poziomu W52 o długości l

3

=60 m,

trzy linie gaśnicze ostatniego poziomu W52 o długości l

4

=40 m zakończone

prądownicami PW-52 o średnicy pyszczka d=13 mm.

38

4.

Dobrać prędkość obrotową silnika autopompy A 32/8, aby otrzymać optymalne
ciśnienie na prądownicy PW-52 (d=12 mm) w układzie symetrycznym składającym
się z linii głównej W75 o długości l

1

=100 m i dwóch linii gaśniczych W52 o długości

l

2

=40 m każda. Obroty i ciśnienie nominalne autopompy A 32/8 wynoszą odpowiednio:

n

n

=2700 obr/min. H

n

=80 m.

5.

Dobrać długość linii upustowej W52 w układzie symetrycznym składającym się z dwóch
pomp A 16/8 połączonych równolegle, linii głównej W75 o długości l

1

=80 m oraz dwóch

poziomów linii gaśniczych W52: pierwszego zawierającego dwie linie o długości l

2

=60 m

i drugiego zawierającego dwie linie o długości l

3

=20 m zakończonych prądownicami

PW-52 o średnicy pyszczka d=12 mm.

6.

Dla układu niesymetrycznego przedstawionego na rysunku obliczyć ciśnienia
na obu działkach DWP-16 (S

dz

=0,113 ms

2

/l

2

). Składa się on z dwóch pomp A32/8

połączonych równolegle, linii głównej W75 o długości l

1

=200 m i dwóch linii gaśniczych

W52 o długościach l

2

=60 m i l

3

=20 m.

7.

Wyznaczyć ciśnienia na prądownicach w układzie niesymetrycznym składającym się
z autopompy A 16/8 i dwóch linii głównych W75, jednej o długości l

1

=100 m i drugiej

o długości l

2

=60 m połączonych z prądownicami PW-75.

8.

Wyznaczyć ciśnienia na prądownicach w układzie składającym się z dwóch pomp
A 32/8 połączonych równolegle, jednej linii głównej W75 o długości l

1

=120 m i układu

gaśniczego pokazanego na rysunku (l

2

=60 m, l

3

=40 m, l

4

=60 m, l

5

=40 m, prądownice

PW-52 o średnicy d=12 mm).

9.

Wyznaczyć parametry pracy prądownic w układzie niesymetrycznym składającym się
z pompy A 32/8, linii głównej W75 o długości l

1

=160 m i trzech linii gaśniczych o

długościach l

2

=80m, l

3

=20 m i l

4

=40 m zakończonych prądownicami PW-52 o średnicy

pyszczka d=12 mm. Różnica poziomów pomiędzy pompą a liniami gaśniczymi wynosi
z=5 m.

10.

Wyznaczyć ciśnienia na działkach w układzie niesymetrycznym składającym się
z dwóch pomp A 32/8 połączonych równolegle, linii głównej W75 o długości l

1

=200 m

i dwóch linii gaśniczych W52 o długościach l

2

=60m i l

3

=20 m zakończonych działkami

DWP-16.

11.

Wyznaczyć maksymalną odległość, na jaką można przetłoczyć wodę w ilości Q=10 l/s

przy pomocy układu pokazanego na rysunku, składającego się z trzech pomp M 8/8,

węży W110. Napływy na drugą i trzecią pompę wynoszą odpowiednio n

1

=10 m

i n

2

=15 m.

ERROR: syntaxerror
OFFENDING COMMAND: --nostringval--

STACK:

/Title
()
/Subject
(D:20120228223041)
/ModDate
()
/Keywords
(PDFCreator Version 0.8.0)
/Creator
(D:20120228223041)
/CreationDate
(Tomasz)
/Author
-mark-