1

Roboty Przemysłowe

3. Parametry i charakterystyki robotów

Charakterystyka przestrzeni roboczej – zasady wyznaczania
orientacji chwytaka w przestrzeni roboczej przy wykorzystaniu

przekształcenia jednorodnego – kąty Eulera RPY

1. Podstawy teoretyczne

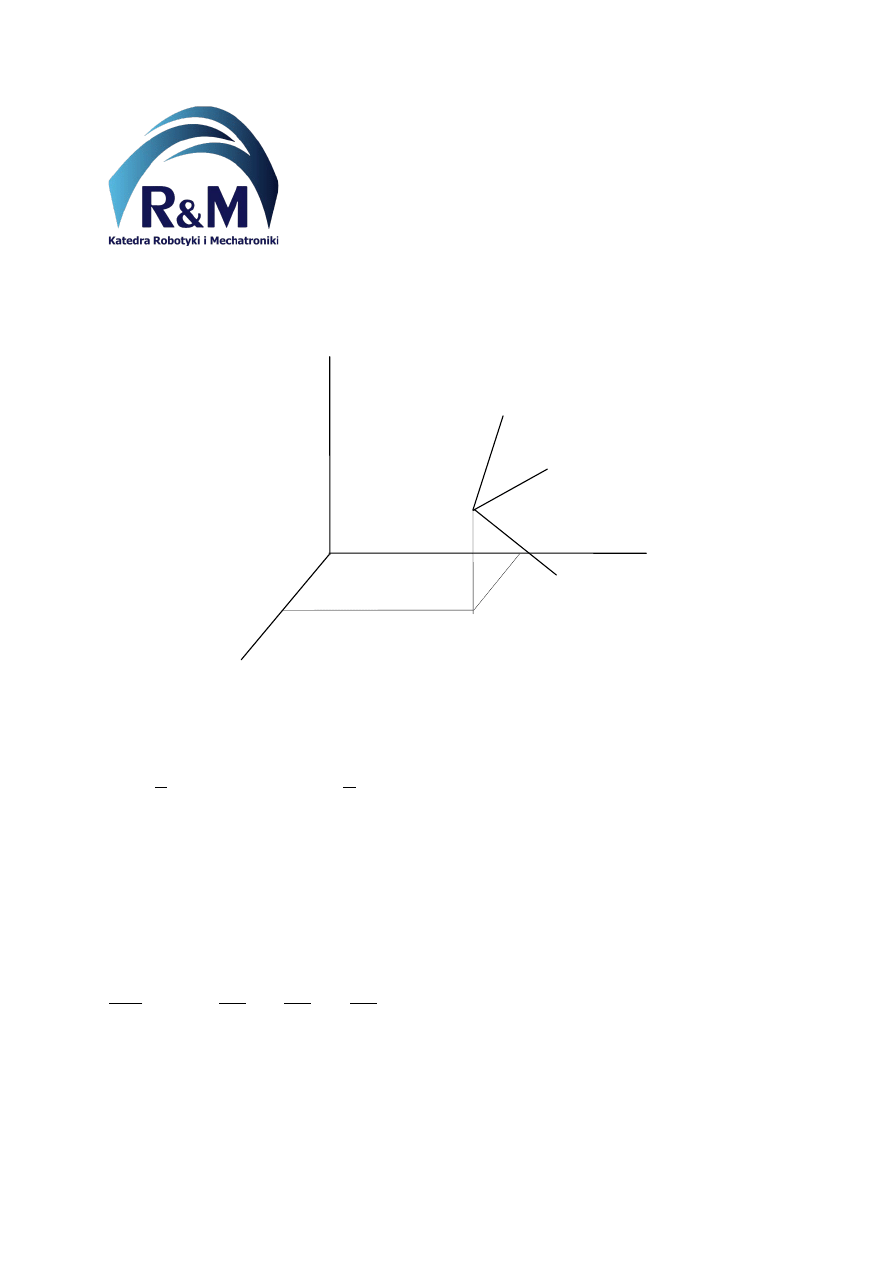
Rys. 1. Wzajemne położenie i orientacja układów współrzędnych odniesienia Oxyz
i lokalnego Puvw

𝐴 = �

𝑢

𝑥

𝑣

𝑥

𝑤

𝑥

𝑥

𝑝

𝑢

𝑦

𝑣

𝑦

𝑤

𝑦

𝑦

𝑝

𝑢

𝑧

𝑣

𝑧

𝑤

𝑧

𝑧

𝑝

0

0

0

1

� 𝑅 = �

𝑢

𝑥

𝑣

𝑥

𝑤

𝑥

𝑢

𝑦

𝑣

𝑦

𝑤

𝑦

𝑢

𝑧

𝑣

𝑧

𝑤

𝑧

� = �

𝚤̂

𝑥

∘ 𝚤̂

𝑢

𝚤̂

𝑥

∘ 𝚥̂

𝑣

𝚤̂

𝑥

∘ 𝑘�

𝑤

𝚥̂

𝑦

∘ 𝚤̂

𝑢

𝚥̂

𝑦

∘ 𝚥̂

𝑣

𝚥̂

𝑦

∘ 𝑘�

𝑤

𝑘�

𝑧

∘ 𝚤̂

𝑢

𝑘�

𝑧

∘ 𝚥̂

𝑣

𝑘�

𝑧

∘ 𝑘�

𝑤

�

Macierz przekształcenia jednorodnego A opisuje położenie i orientacje układu lokalnego

Puvw

w układzie odniesienia Oxyz. Macierz R jest tzw. macierzą rotacji i opisuje orientację

układu lokalnego Puvw w układzie odniesienia Oxyz. Wektory: i, j, k oznaczają wersory

układów współrzędnych Oxyz i Puvw.

Macierz przekształcenia jednorodnego odpowiadająca obrotom o kąty RPY: przechylania

(ang. Roll) -

φ, pochylenia (ang. Pitch) - θ

i skręcenia (ang. Yaw) - ψ jest postaci:

RPY

Rot z

Rot y

Rot x

C C

S C

C S S

S S

C S C

S C

C C

S S S

C S

S S C

S

C S

C C

( , , )

( , )

( , )

( , )

φ θ ψ

φ

θ

ψ

φ θ

φ ψ

φ θ ψ

φ ψ

φ θ ψ

φ θ

φ ψ

φ θ ψ

φ ψ

φ θ ψ

θ

θ ψ

θ ψ

=

=

=

−

+

+

+

−

+

−

























0

0

0

0

0

0

1

x

y

z

u

v

w

O

P

2

Porównanie wyrazów tej macierzy z ogólną postacią macierzy przekształcenia

jednorodnego A:

























=

1

0

0

0

z

z

z

z

y

y

y

y

x

x

x

x

P

A

O

N

P

A

O

N

P

A

O

N

A

pozwala znaleźć wartości kątów Eulera RPY wg wzoru:

poza przypadkiem gdy: N

x

=0 i N

y

=0 (oraz O

z

=0, A

z

=0), wtedy występują 2 możliwości:

o

90

=

θ

o

90

−

=

θ

(

)

(

)

y

x

O

O

=

−

=

−

φ

ψ

φ

ψ

cos

sin

(

)

(

)

y

x

O

O

=

+

=

+

−

φ

ψ

φ

ψ

cos

sin

y

x

O

O

arctg

=

−

φ

ψ

y

x

O

O

arctg

−

=

+

φ

ψ

Wykonanie obrotów układu odniesienia względem jego osi kolejno o kąty: ψ, θ, φ pozwala

wskazać orientacje osi układu reprezentowanego przez przekształcenie RPY(φ, θ, ψ) w

układzie odniesienia.

2.

Uwagi do sporządzenia sprawozdania

W sprawozdaniu z wykonania zadania nr 2 należy zamieścić narysowany układ końcowy

z translacją i rotacją oraz na osobnej kartce narysowane kolejne przekształcenia układu
odniesienia.

z

z

z

z

x

y

A

O

arctg

N

N

arctg

N

N

arctg

=

−

−

=

=

ψ

θ

φ

2

1