Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 1

wersja 4.0.5

Instrukcja do zaj

ęć nr 3. Wprowadzenie do ADINA

Structures cd.

0. Pierwszy krok

Uruchom ADINA-AUI, wybierz ADINA Structures

1. Metody definicji punktów geometrycznych

Najprostszą metodą definicji punktów jest wprowadzenie ich współrzędnych. Ale wynik
takiej operacji zależy od używanego układu współrzędnych.

Przykład 1. Definicja dodatkowego cylindrycznego układu
współrzędnych

Geometry

→Coordinate Systems (albo

), Add, na liście Type

wybierz Cylindrical. Domyślnie mamy układ cylindryczny ze środkiem
w punkcie {0,0,0} (patrz Origin) i osią z układu w kierunku {1, 0, 0}
czyli prostopadle do ekranu (patrz Vector A), w którym kąt Θ odlicza
się od kierunku {0, 1, 0}, czyli osi Y (patrz Vector B). OK

Uwaga! Program domyślnie wykonuje wszystkie operacje w układzie współrzędnych o najwyższym numerze
(czyli od tego momentu – w nowym, cylindrycznym, ponieważ kartezjański ma numer 0) co nie zawsze jest
pożądane. Od tego momentu musimy na to uważać.

Przykład 2. Definicja kilku punktów w różnych układach

Geometry

→ Points (albo

), zwróć uwagę na numer domyślnego układu współrzędnych

(Default Coordinate System).

– Wprowadzenie 5 równoodległych punktów w układzie kartezjańskim. Naciśnij Auto...,
otworzy się okno dialogowe, pozwalające na generację danych metodą podobną do działania
pętli for w językach programowania. Wpisz dane jak na rysunku niżej. OK

– Dwa punkty w układzie cylindrycznym. Wprowadźmy współrzędne dla
punktu pokazanego na rysunku po prawej stronie. W tym celu wracamy do

wprowadzania współrzędnych (

) i w 6 wierszu tabeli Point Coordinates

wpisujemy:

nr punktu 6 w kolumnie Point #
promień 1.5 w kolumnie X1 (dla tego układu X1 oznacza R)
kąt obrotu w stopniach 45 w kolumnie X2 (dla tego układu X2 oznacza Θ)
kliknij na komórkę w kolumnie System i wybierz 1 jako nr układu współrzędnych,

Apply

Następny punkt (nr 7) będzie nieco „zakręcony”, bo ma współrzędne r=1, Θ=720º, z=3.

Wprowadź go i sprawdź jak program interpretuje kąty powyżej 360º.

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 2

wersja 4.0.5

Wyświetl numery wszystkich punktów (

“Point Labels”)

2. Metody definicji linii

ADINA Structures ma 10 rodzajów metod definicji linii. Taka definicja zaczyna się od

Geometry

→ Lines → Define (

), Add, i dalej wybieramy typ linii z listy Type.

Podstawowe typy linii

1. Straight (prosta). Podaje się (albo bezpośrednio, albo przez kliknięcie na odpowiednie
punkty w „trybie wskaźnikowym”) numery punktów.

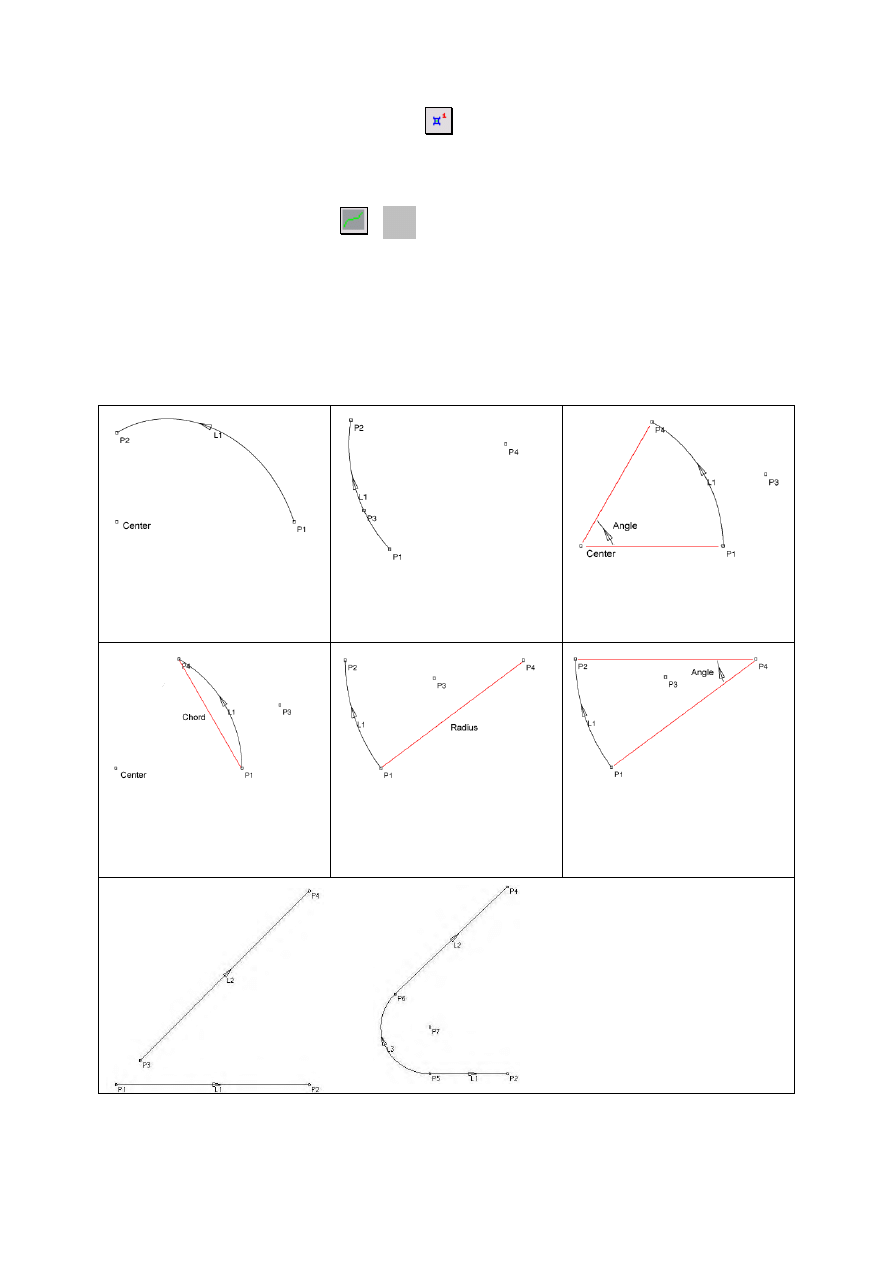
2. Arc (łuk). Łuk można zdefiniować na 7 różnych sposobów określonych na liście
Defined by (zdefiniowany przez) i pokazanych na schematach niżej. We wszystkich
przypadkach punkty P1-P3 podaje użytkownik, punkt P4 jest generowany przez program.

1) 2 punkty i środek. Uwaga!
Krzywa, która powstaje w wyniku
tej operacji jest łukiem tylko jeżeli
odległość od środka do P1 i P2 jest
jednakowa

2) 3 punkty (początkowy P1,
końcowy P2 i P3), nie leżące na
prostej.

3) Punkt początkowy (P1), środek,
kąt (Angle) i punkt dodatkowy
(P3), który pozwala określić
płaszczyznę, w której leży łuk.

4) Początek (P1), środek, długość
cięciwy (Chord) oraz P3, który
wyznacza płaszczyznę łuku i po
której stronie od P1 ten łuk leży.

5) Początek (P1), koniec (P2),
promień

(Radius) i punkt

dodatkowy P3, który wyznacza
płaszczyznę łuku oraz stronę, po
której leży jego środek (P4)

6) Początek (P1), koniec (P2), kąt
(Angle) i punkt dodatkowy P3,
który wyznacza płaszczyznę łuku
oraz stronę, po której leży jego
środek (P4)

7) Dwie linie (L1, L2), które leżą w
jednej płaszczyźnie i nie są równolegle
oraz promień zaokrąglenia. Rysunki
pokazują sytuacje przed i po generacji
łuku. Program usuwa punkty P1 i P3 oraz
dodaje P5, P6 oraz nowy łuk L3.

Ćwiczenie. Zadeklaruj łuk (raczej krzywą) nr 1, który zaczyna się w p.3, kończy się w p.6 i
ma środek w p. 1.

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 3

wersja 4.0.5

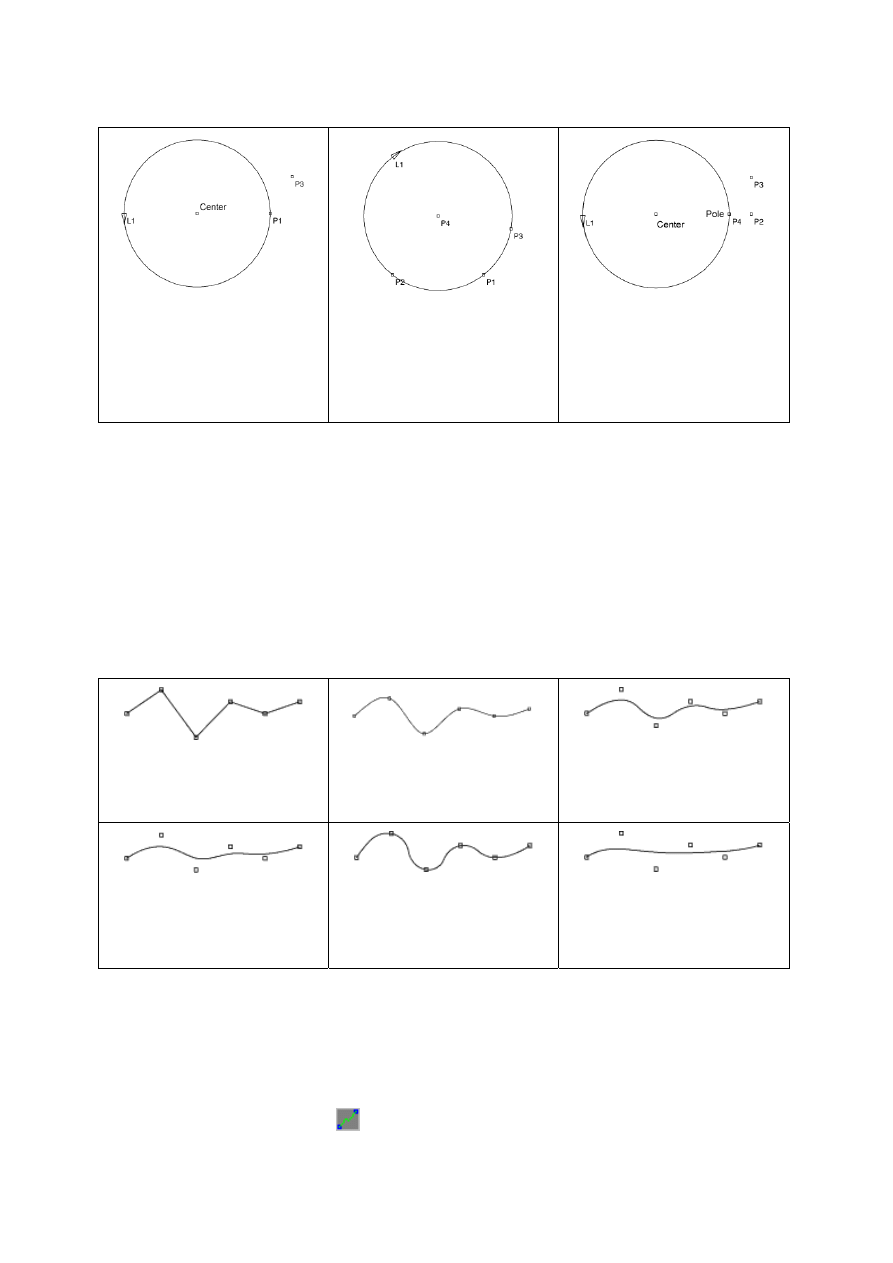
3. Circle (koło). Wyznaczane jest na 3 sposoby

1) Środek, punkt na kole (P1) oraz
punkt dodatkowy (P3), który
wyznacza płaszczyznę koła

2) Trzy punkty (P1, P2, P3) leżące
na kole.

3) Środek, promień i 2 punkty
dodatkowe (P2, P3), które razem
ze

środkiem wyznaczają

płaszczyznę koła. Początek koła
(pole, biegun) wyznacza punkt, w
którym linia przechodząca przez
środek i P2 przecina koło

Ćwiczenie. Zadeklaruj linię 2 jako koło o promieniu 0.3 ze środkiem w p.3, które leży w
płaszczyźnie wyznaczanej dodatkowymi punktami 7 (służy również do wyznaczenia początku
linii) oraz 4.

4. Curvilinear (krzywoliniowa). Ten typ linii można zadeklarować tylko w cylindrycznym
lub biegunowym układach współrzędnych. Deklaracja linii polega na wprowadzeniu
numerów początkowego i końcowego punktów, dokładnie jak przy definicji linii prostej. Tak
samo jak w przypadku prostej punkty pośrednie obliczane przez interpolację liniową lecz w
cylindrycznym lub biegunowym układzie współrzędnych podanym przez użytkownika.
Ćwiczenie. Zadeklaruj linię 3 jako krzywoliniową, która łączy p.3 i p.7 w układzie nr 1.
Dlaczego linia ta ma kształt spirali?

5. Polyline. 6 typów linii zdefiniowanych przez kilka punktów

.

1) Zwykła linia łamana

2) Splajn. Przechodzi przez
wszystkie punkty.

3) Quadratic B-spline (B-splajn
kwadratowy). Przechodzi przez 1 i
ostatni punkt,ale nie koniecznie
przez pozostałe. Wymaga co
najmniej 3 punkty.

4) Cubic B-spline (B-splajn 3
rzędu). Przechodzi przez 1 i ostatni
punkt, ale nie koniecznie przez
pozostałe. Wymaga co najmniej 4
punkty.

5) Bi-Arc (dwa łuki). Każdą parę
punktów

łączy para łuków.

Wymaga co najmniej 3 punkty nie
leżące na prostej

6) Krzywa Beziera. Przechodzi
przez 1 i ostatni punkt, ale nie
koniecznie przez pozostałe.
Wymaga co najmniej 3 punkty.

Cwiczenie. Zadeklaruj linię 4 jako polilinię typu Spline (opcja nr 2), która przechodzi przez
punkty 1, 2, 8, 4, 5. Numery punktów podaje się w „zielonej” kolumnie (Point #).

6. Combined (połączona). Połączenie kilku istniejących linii w jedną całość.

7. Section (część). Linia utworzona jako część już istniejącej linii.

Przykład. Deklaracja linii nr 5, jako środkowej 1/3 linii nr 1.

Wyświetl numery linii (

). Zwróć uwagę, że oprócz numeru program wyświetla na

każdej linii strzałkę. Pokazuje ona kierunek wzrostu lokalnej współrzędnej u, wartość której

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 4

wersja 4.0.5

zmienia się od 0 na początku linii do 1 na jej końcu. Pozwala to na określenie dowolnego
punktu na linii, Przykładowo środku linii odpowiada u=0.5 .

Nasza nowa linia musi zaczynać się od punktu ze współrzędną u=1/3

≈0.333 i kończyć

się w punkcie z u=2/3

≈0.667. Jej definicja składa się z następujących kroków:

1. Zadeklaruj nowa linię: Geometry

→ Lines → Define (

), Add

2. Na liście Type wybierz Section
3. Wpisz 1 w oknie Parent Line (dosłownie linia rodzicielska)
4. Wpisz 0.333 w oknie u(Starting Point) oraz 0.667 w u(End Point), OK

8. Revolved (linia, która powstaje w wyniku obracania punktu wokół osi).

Kolejność postępowania:

1. Po deklaracji nowej linii wybierz Revolved na liście Type
2. Podaj numer punktu, który będzie obracany w okienku Initial Point
3. Wpisz kąt obrotu w okienku Angle of Rotation
4. Typ osi wybiera się z listy Defined by z grupy Axis of Revolution z 4 opcji:

Axis (oś układu współrzędnych, numer którego musi być podany w okienku

Coordinate System),

Line (już istniejąca linia, numer której podaje się w okienku Line),
Two points (niewidoczna linia zdefiniowana przez 2 punkty, numery których

podaje się w okienkach Point 1, Point 2),

Vectors (wektory). Najbardziej uniwersalna metoda, polegająca

na definicji współrzędnych końców 2 wektorów: wektora B, który
wskazuje kierunek osi obrotu oraz wektora A, który wskazuje
punkt od którego ta oś się zaczyna.

Ćwiczenie. Zadeklaruj linię nr 6 typu revolved, w wyniku obracania o 90º punktu 2 wokół osi
Z układu współrzędnych nr 0.

9. Extruded. Linia „wyciśnięta” lub „wytłoczona”. Polega to na
utworzeniu linii od istniejącego punktu ze współrzędnymi na przykład
{x0, y0, z0} do nowego punktu ze współrzędnymi {x0+x, y0+y, z0+z}.
Użytkownik wprowadza nr punktu (w okienku Initial Point), numer
układu współrzednych (lista Coordinate System) oraz współrzędne
przyrostu {x, y, z} w grupie Vector

Ćwiczenie. Zadeklaruj linię nr 7 typu extruded, punkt początkowy 1, układ 0, przyrost {1,1,1}

10. Transformed. Metoda ta służy do „klonowania” jednej lub kilku istniejących linii.

Przykład. Utworzenie trzech kopii linii nr 2 (koła).

Definicja przekształcenia nr 1.

1. Geometry

→ Transformations, Add. Na liście Type masz do wyboru 6 typów

przekształceń: Translation (przesunięcie), Rotation (obrót), Scale (skalowanie),
Reflection (odbicie, np lustrzane), Direct (bezpośrednie) oraz Points (punkty).
Wybieramy Translation.

2. Sprawdź, czy na liście Defined by (zdefiniowany przez) jest wybrane Coordinate Axes

(osi układu współrzędnych). Inne możliwości to Line (linia) i Two points (dwa
punkty).

3. Wprowadź 0 jako numer układu współrzędnych w okienku Coordinate System oraz

0.5 w okienku Z. Oznacza to, że nasze przekształcenie będzie polegać na przesunięciu
wybranego obiektu o 0.5 wzdłuż osi Z. OK

(x0,y0,z0)

(x0+x,

y0+y,

z0+z)

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 5

wersja 4.0.5

Wykorzystanie przekształcenia:

1. Dodaj nową linię typu Transformed
2. Podaj numer linii „macierzystej” 2 w okienku Parent Line
3. Podaj ilość kopii (jako 3) w okienku Number of Copies
4. Wybierz numer przekształcenia na liście Transformation #, OK

3. Metody definicji powierzchni

Definicję powierzchni zaczynamy od Geometry

→ Surfaces → Define (lub

), Add.

Dalej wybieramy rodzaj tworzonej powierzchni na liście Type. Dostępne opcje to:
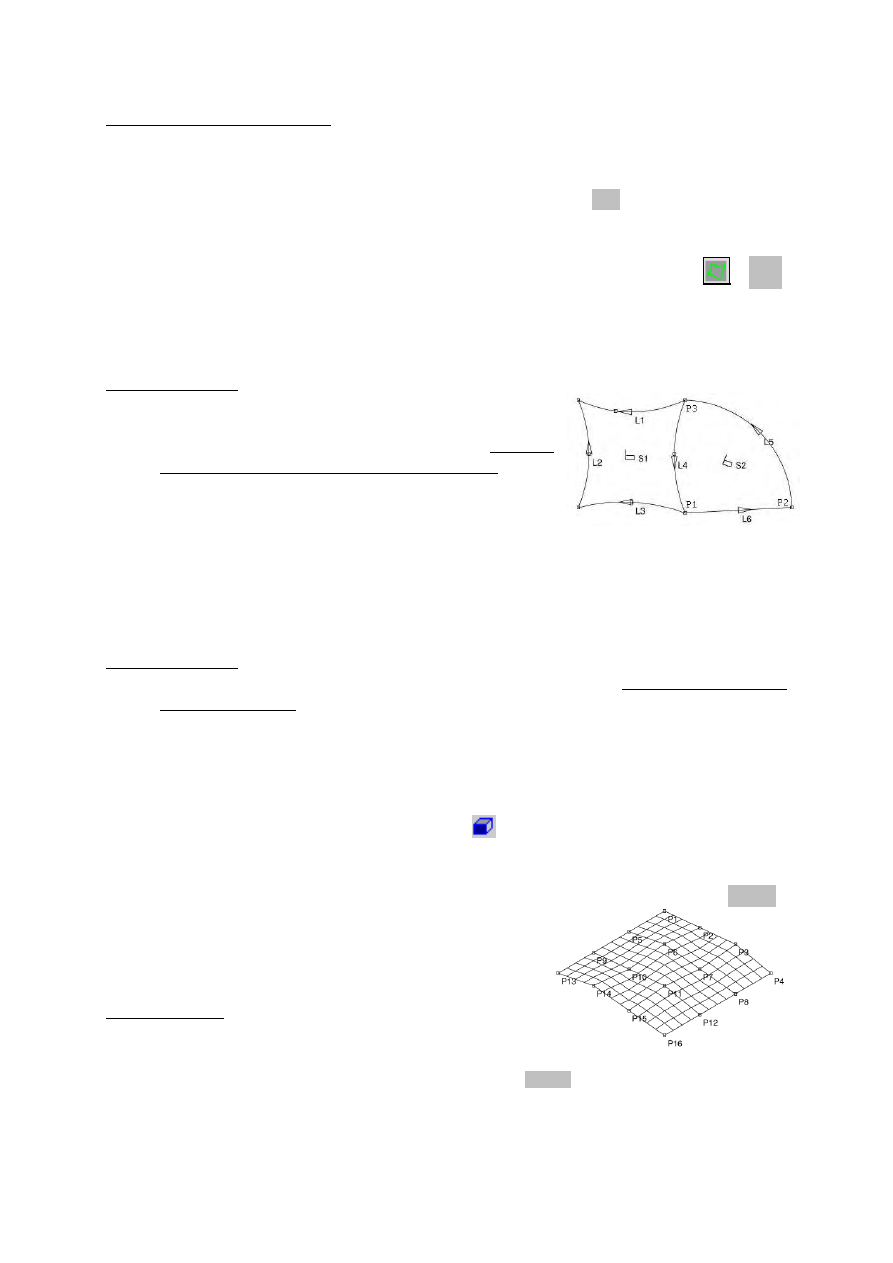
1. Patch (łatka). Jest to powierzchnia, którą tworzą 4 (w przypadku powierzchni
czworokątnej) lub 3 (w przypadku powierzchni trójkątnej) linie. W przypadku trójkąta
podajemy 0 jako nr czwartej linii.
Uwagi praktyczne:

Można podawać numery linii w dowolnej kolejności,

ale zarówno teoria MES jak i dokumentacja programu
stanowczo zalecają podawać je po kolei w kierunku
przeciwnym ruchu wskazówek zegara. Dla
powierzchni 1 na rysunku najlepiej podać numery linii
jako 1,2,3,4 lub 2,3,4,1 a dla trójkątnej powierzchni 2
– jako 6,5,4,0.

Realnie opcja Patch używana jest dość rzadko;

2. Vertex (

wierzchołek)

. Powierzchnia tworzona przez podanie 4 albo 3 numerów punktów,

które znajdują się w jej narożnikach. W drugim przypadku jako czwarty podaje się numer
punktu początkowego, czyli dla powierzchni 2 na rysunku wyżej można było zadeklarować
podając numery punktów 1,2,3,1.
Uwagi praktyczne:

Ponownie zaleca się podawać numery punktów w kierunku przeciwnym do ruchu

wskazówek zegara.

Powierzchnia jest tworzona poprzez połączenie podanych punktów liniami prostymi o

ile te punkty jeszcze nie są połączone. Oznacza to, że jeżeli zamierzamy utworzyć
powierzchnię, w której część linii jest krzywymi, to musimy najpierw utworzyć te
linie, a później użyć metody vertex.

Ćwiczenie. Zadeklaruj powierzchnię, która łączy punkty 3, 6, 12, 7. Żeby uczynić utworzoną

powierzchnie bardziej widoczną kliknij na ikonę

znaną jako „heavy metal”☺ („uczciwa

droga” uzyskania tego samego efektu to Display

→ Geometry/Meshplot → Modify,

Rendering a później zaznaczenie Shade (cień, cieniować) w grupie Shading). Dlaczego
powierzchnia wygląda tak dziwnie? Usuń ją przez Geometry

→ Surfaces → Define, Delete.

3. Grid (siatka). Metoda definicji skomplikowanych powierzchni
typowych dla nadwozi samochodów. Polega na wstępnej definicji siatki
składającej się z wierszy i kolumn (maksymalnie 11x11). Później, przy
definicji powierzchni wypełnia się odpowiednią tabele podając po kolei
nr wierszu, nr kolumny i nr punktu.
Uwagi praktyczne: Jest to dość pracochłonna metoda ponieważ
definicja powierzchni pokazanej na rysunku wymaga wprowadzenia 48
(16x3) liczb. Lepiej przygotować sobie (można za pomocą innego
programu jak Excel lub Mathcad) zwykły plik tekstowy z tymi danymi (tabela składająca się z 16 wierzy po 3
liczby w każdym wierszu) i wczytać go do ADINA przez naciśnięcie Import w okienku Define Surface.

4. Revolved (powierzchnia, która powstaje w wyniku obrócenia linii wokół osi)

Opcja ta jest bardzo podobna do używanej wcześniej przy tworzeniu linii.

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 6

wersja 4.0.5

Przykład. Utworzenie powierzchni sferycznej przez obrót łuku:

, Add, na liście Type wybierz Revolved

Podaj nr linii 6 w okienku Initial line (linia wstępna)
Podaj miarę kąta obrotu (w stopniach) 180 w okienku Angle of Rotation
Podaj parametry osi: typ Axis w okienku Defined by, wybierz nazwę osi X na liście

Axis oraz wpisz 0 jako nr układu współrzędnych w okienku Coord. System. OK lub
Save

5. Extruded. Podobnie jak wcześniej jest to powierzchnia, która powstaje w wyniku
przesunięcia istniejącej linii.
Przykład. Utworzenie powierzchni przez ruch krzywej wzdłuż linii prostej:

, Add, na liście Type wybierz Extruded

Podaj nr linii 4 (jest to polilinia typu Spline) w okienku Initial line
W grupie Extrusion direction (kierunek wyciskania)

zaznacz Line oraz wpisz nr linii wskazującej
kierunek ruchu jako 7. OK

6. Transformed. Analogicznie jak wcześniej jest to „klonowanie”
jednej lub kilku istniejących powierzchni zgodnie ze zdefiniowanym
wcześniej przekształceniem (patrz rysunek).

3. Metody definicji bry

ł

Program pozwala definiować 4 typy brył: sześcian (hexahedron), graniastosłup (prism), ostrosłup (pyramid) i
czworościan (tetrahedron). Zaczynamy definicję bryły od Geometry

→ Volumes → Define (lub na skróty

), Add. Dalej wybieramy jedną z metod na liście Type. Metody tę są bardzo podobne do omówionych

wyżej:
1) Patch – wybieramy typ bryły i wprowadzamy numery powierzchni, które ją tworzą
2) Vertex – to samo, lecz podajemy numery punktów w narożnikach bryły
3) Revolved – bryła tworzona jest przez obrócenie istniejącej powierzchni wokół osi
4) Extruded – bryła tworzona jest przez przemieszczenie istniejącej powierzchni wzdłuż linii prostej
5) Sweep (zataczając łuk) – to samo, lecz linia może być dowolna (w zasadzie jest to nowa udoskonalona wersja
extruded)
6) Transformed – „klonowanie” istniejących brył. Pozwala wyjątkowo łatwo modelować koła zębate, turbiny itp.
Niestety z powodu błędu opcja ta nie jest dostępna z poziomu AUI i jest dostępną tylko z poziomu wiersza
poleceń

.

Usuwanie objektów geometrycznych

Metoda szybka.

1. Klikamy na jedną z ikon

(usunięcie punktów),

(linii),

(powierzchni),

(bryły), wskaźnik myszy automatycznie zmieni kształt na krzyż.

2. Zaznaczamy jeden lub kilka elementów, które chcemy usunąć.
3. Kończymy przez Esc.

Uwaga praktyczna: czasami nie jest łatwo trafić wybrany element (dotyczy to szczególnie
punktów). Zalecam wcześniej wyświetlić numery punktów, linii itp. i „celować” właśnie w te
numery.
Metoda wolniejsza, bardziej elastyczna (nie dotyczy punktów).

1. Klikamy na ikonę służącą do definicji linii, powierzchni lub bryły
2. Wybieramy odpowiedni element na liście istniejących obiektów wybranego typu (w

przypadku linii na liście Line Number, w przypadku powierzchni – Surface Number
itp.)

3. Jeżeli chcemy usunąć tylko ten element klikamy na Delete, jeżeli chcemy dodatkowo

usunąć wszystkie jego części składowe (w przypadku bryły to powierzchnie, linie i

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 7

wersja 4.0.5

punkty) musimy wcześniej zaznaczyć odpowiednią opcję (w przypadku brył „Delete
Surfaces/Lines/Points when Volume is Deleted”)

Kolejność usuwania: najpierw bryły, potem powierzchnie, linie, a na końcu punkty. Nie da się
usunąć linii lub punktu jeżeli są one składnikami istniejącej powierzchni.
Ćwiczenie. Usuń wszystkie utworzone elementy geometryczne po kolei.

4. Podsumowanie i uwagi praktyczne

Wszystkie metody definicji obiektów geometrycznych przedstawione wyżej można podzielić
na 3 grupy:

1. Metody bezpośrednie (prawie wszystkie dla linii, patch i vertex dla powierzchni i brył)

polegające na wstępnym określeniu wszystkich elementów tworzonych obiektów

2. Metody „technologiczne” (revolved, extruded, sweep), które dla definicji N-

wymiarowego obiektu wymagają istnienia tylko jednego jego elementu o wymiarze
N-1 (np. linii do tworzenia powierzchni). W tym przypadku program sam tworzy
brakujące punkty, linie i powierzchnie.

3. Metody „klonowania” (na razie tylko transformed), które też powodują to, że program

sam tworzy nowe punkty, linie itp.

Metody bezpośrednie są bardzo pracochłonne ale pozwalają na pełną kontrolę kształtu

tworzonego modelu. Metody „technologiczne” oraz „klonowanie” są najbardziej efektywne i
powinny być używane jak najczęściej.

5. Metody generacji siatki elementów sko

ńczonych

5.1. Definiowanie nowego modelu p

łaskiego

Wczytaj cześć nowego modelu: File

→ New (albo

), File

→ Open (albo

) odczytaj plik

adina_instr_3.in (jest to zwykły plik tekstowy z poleceniami ADINA Structures. Polecam
zapoznać się z nim (zadanie domowe)). Obraz na ekranie powinien wyglądać podobnie do

tego na rysunku po lewej.

Lokalne układy współrzędnych

Przyjmuje

się, że każdy obiekt geometryczny ma swój

własny układ współrzędnych. W przypadku linii jest to jedna
współrzędna u (zmienia się od 0 do 1, kierunek wzrostu
pokazuje strzałka na linii), w przypadku powierzchni jest to
układ {u,v}, w przypadku powierzchni – układ {u,v,w}. Kierunki
osi układu w przypadku 2D wyznacza „chorągiewka” obok
numeru powierzchni (patrz rysunek po lewej
stronie), której „sztandar” skierowany jest w
kierunku osi u, a „drzewce” – w kierunku osi v. W

przypadku 3D układ osi pokazany jest przez tzw. „triadę” pokazaną po prawej
stronie. Lokalne układy pełnią ważna role przy definicji gęstości siatki.

Wprowadzanie parametrów materiału

Program wymaga, żeby przed generacją siatki elementów skończonych były
zdefiniowane właściwości materiału. Niżej wprowadzimy dane sprężystego materiału
nr 1:

1.

, Isotropic (w części „Elastic”) (albo Model

→ Materials → Elastic →

Isotropic), Add

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 8

wersja 4.0.5

2. Wprowadź w odpowiednich okienkach moduł Younga (np. 2.1e11) oraz współczynnik

Poissona (np. 0.3), OK, , Close

Zapisz utworzony model pod inna nazwą (File

→ Save as)

5.2 Generacja siatki elementów sko

ńczonych

Definicja dowolnej siatki ES (Elementów Skończonych) składa się z trzech kroków:

1. Definicja grup ES
2. Definicja gęstości siatki
3. Definicja typów ES oraz generacja siatki

Definicja grup ES

Każdy realny model składa się z różnych elementów konstrukcyjnych (belki, powłoki, bryły)
oraz różnych materiałów. W programie ADINA wprowadza się pojęcie grupa elementów
skończonych. Grupa taka łączy w sobie ES tego samego typu oraz z tego samego materiału.
Przykład: Tworzenie grupy ES płaskich (płaski stan naprężeń) o grubości 1 (wartość
domyślna):

1. Ikona

„Define Element Groups” (Meshing

→Element Groups), Add

2. Type: „2-D Solid”. Numer materiału (Default Material) i grubość elementów (Default

Element Thickness) pozostawiamy bez zmian.

3. Element Sub-Type: „Plane Stress”, Save

Ćwiczenia:

1. zdefiniuj grupę ES nr 2, która składa się z elementów sprężynowych („Spring”), o

sztywności 1000 (podaje się w okienku po wciśnięciu ... obok wiersza

2. zdefiniuj grupę ES nr 3, która składa się z elementów powłokowych („Shell”) z

materiału nr 1 o ilości warstw („Number of Layers:”) 1.

3. skasuj utworzone grupy 2 oraz 3. Wybrać numer grupy na liście „Group Number”,

nacisnąć Delete i potwierdzić.

5.3 Okre

ślenie gęstości siatki ES. Uwagi ogólne

Gęstość siatki ES jest liczbą elementów na jednostkę wymiaru modelu. Na przykład,

definiując geometrię modelu w milimetrach możemy wymagać generacji siatki ES z gęstością
3 elementów na mm w jednej części modelu, oraz gęstości 0.1 elementu na mm w innej części.
Dla dwu- oraz trójwymiarowych elementów gęstość wyznaczana jest w odniesieniu do
długości krawędzi elementów (tzn. określamy gęstość krawędzi elementów wzdłuż linii
modelu).

W ADINA Structures istnieją trzy metody na określenie gęstości siatki ES:

1. Przez podanie długości krawędzi ES wzdłuż linii modelu („Use Length”), na przykład

wszystkie krawędzie po 23 mm.

2. Przez podanie ilości ES wzdłuż linii modelu („Use Number of Divisions”), na przykład

dzielimy każdą linię na 7 części.

3. Przez podanie długości krawędzi ES obok punktów modelu („Use End-Point Sizes”),

na przykład: obok punktu nr 5 strony wszystkich elementów muszą być po 0,25 mm.

W rożnych częściach modelu mogą byś stosowane rożne metody na określenie

gęstości siatki.

Po rozwinięciu menu definicji gęstości (Meshing

→Mesh Density) mamy do wyboru

8 głównych wariantów wyznaczania gęstości siatki powiązanych z 5 jej nośnikami:
1. Point - gęstość siatki określona będzie w każdym z punktów charakterystycznych modelu.
2. Line - gęstość siatki określona będzie wzdłuż zdefiniowanych wcześniej linii modelu.

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 9

wersja 4.0.5

3. Surface - gęstość siatki określona będzie na zdefiniowanych wcześniej powierzchniach
modelu.
4. Volume - gęstość siatki określona będzie na zdefiniowanych wcześniej bryłach modelu.
5. Edge - gęstość siatki określona będzie na krawędziach ciał zdefiniowanych wcześniej za
pomocą ADINA-M lub programu CAD
6. Face - gęstość siatki określona będzie na powierzchniach ciał zdefiniowanych wcześniej za
pomocą ADINA-M lub programu CAD.
7. Body - gęstość siatki określona będzie na poszczególnych ciałach zdefiniowanych
wcześniej za pomocą ADINA-M lub programu CAD.
8. Complete Model - gęstość siatki określona będzie dla całego modelu

Podstawowym nośnikiem, na którym określana jest gęstość siatki ES jest linia (Line).

Dane, wprowadzone dla innych typów nośników (punktów, powierzchni, brył) są przeliczane
przez ADINA Structures na dane dla odpowiednich linii.

Podział linii modelu na części (tzn. przyszłe krawędzie ES) można zobaczyć

natychmiast po określeniu gęstości siatki (lub naciskając na ikonę

„Redraw”). Jeżeli

wynik jest niezadowalający, można go poprawić przez zmianę parametrów gęstości.

5.4. Generacja siatki. Uwagi ogólne

Po określeniu gęstości siatki można wygenerować ją przez wciśnięcie odpowiedniej

ikony:

„Mesh Lines” (Meshing

→ Create Mesh → Line) – zwykle dla zagadnień

jednowymiarowych (dla krawędzi ciał zdefiniowanych za pomocą modułu ADINA-M lub
programu CAD używamy Meshing

→ Create Mesh → Edge)

„Mesh Surfaces” (Meshing

→ Create Mesh → Surface) – zwykle dla zagadnień

dwuwymiarowych (dla powierzchni ciał zdefiniowanych za pomocą ADINA-M lub programu
CAD używamy Meshing

→ Create Mesh → Face)

„Mesh Volumes” (Meshing

→ Create Mesh → Volume) – dla zagadnień

trójwymiarowych (dla ciał zdefiniowanych za pomocą ADINA-M lub programu CAD
używamy Meshing

→ Create Mesh → Body)

Dla zagadnień dwuwymiarowych (po wyborze ikony „Mesh Surfaces”) trzeba podać

numer grupy ES („Element Group”), ilość węzłów w elemencie („Nodes per Element”) oraz
wpisać do tabeli „Surface #” numery wszystkich powierzchni (po jednym numerze w wierszu
tabeli), na których będą generowane ES.

Niefortunnie wygenerowaną siatkę można skasować częściowo lub w całości przez

wciśnięcie ikony

„Delete Mesh” (Meshing

→ Delete Mesh). Dalej należy wybrać typ

nośnika z menu „Delete Mesh From:” (Line, Surface lub Volume) odpowiedni do typu
zagadnienia oraz wpisać w tabeli numer linii, powierzchni lub bryły, na której siatka ES ma
zostać skasowana.

5.5. Okre

ślenie gęstości oraz generacja siatki ES dla całego modelu:

Meshing

→ Mesh Density → Complete Model

Z listy „Subdivision Mode:” jako metodę podziału można wybrać:

• Use Length - określamy długość strony ES,
• Use Number of Divisions - podział każdej z linii modelu na podaną liczbę równych części
(stron ES),

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 10

wersja 4.0.5

• Use End-Point Sizes - określamy długość krawędzi ES, którzy przylegają do
zdefiniowanych punktów modelu.

Dla niektórych metod podziału niezbędne jest określenie następujących parametrów:

1. Maximum Element Edge Length: maksymalna dopuszczalna długość elementu.
2. Element Edge Length: dokładne określenie długości elementu skończonego.
3. Number of Subdivisions: dokładne określenie liczby elementów skończonych wzdłuż linii
modelu.
4. Progression: metody obliczania współrzędnych dla punktów pośrednich, które będą
generowane na stronach modelu. Do wyboru mamy 2 metody:

• Arithmetic – postęp arytmetyczny pomiędzy wartościami,
• Geometric – postęp geometryczny pomiędzy wartościami.

5. Min. Number of Subdivisions for Curved Lines/Edges: najmniejsza dopuszczalna liczba
elementów dla linii krzywych.
6. Use Central Biasing instead of End Biasing: zamiast zagęszczania siatki w kierunku
jednego z końców linii używa się zagęszczania w kierunku środka lub obydwu końców
jednocześnie.

Przykład: Generacja siatki dla całego modelu przez podanie długości elementu skończonego:
a) określenie gęstości siatki:

Meshing

→ Mesh Density → Complete Model

Subdivision Mode: „Use Length”
Element Edge Length: 0.2, OK

b) generacja siatki z elementów 9-węzłowych:

(albo Meshing

→ Create Mesh → Surface)

Element Group: 1
Nodes per Element: 9
Surface #: 1, 2 (w osobnych wierszach), OK

Wyświetl węzły siatki przed wciśnięcie ikony

("Node Symbols"). Skasuj siatki przez

wciśnięcie ikony

„Delete Mesh” (Meshing

→ Delete Mesh)

Delete Mesh from: „Surface”

Surface #: 1, 2 (w osobnych wierszach), OK

Ćwiczenie:
Wygeneruj siatkę z elementów 4-węzłowych, wykorzystując opcję równomiernego podziału
każdej linii na 5 części. Po skończeniu skasuj ponownie całą siatkę.

5.6. Okre

ślenie gęstości oraz generacja siatki ES dla wybranych

powierzchni:

Przykład: Generacja siatki przez podanie ilości podziałów przeciwległych krawędzi każdej z
powierzchni:
Meshing

→ Mesh Density → Surface

1) Wybierz powierzchnie nr 1 (domyślna) na liście „Surface Number”

Method: „Use Number of Divisions”
Progression: „Arithmetic”
„Number of Subdivisions”:

u: 4

v: 6

„Length Ratio of Element Edges”:

u: 3

v: 2, Save

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 11

wersja 4.0.5

Uwaga! W przypadku nierównomiernej siatki w grupie „Length Ratio of Element Edges”:

podaje się ilorazy długości pierwszej i ostatniej krawędzi ES w kierunkach u i v. Przesuń okienko
dialogowe w dół i przeanalizuj podział krawędzi na powierzchni nr 1 po tym poleceniu

.

2) Wybierz powierzchnie nr 2 na liście „Surface Number”

Method: „Use Number of Divisions”
Progression: „Arithmetic”
„Number of Subdivisions”:

u: 5

v: 6

„Length Ratio of Element Edges”:

u: 0.5 v: 2, OK

3) Wygeneruj siatkę.

Zwróć uwagę, że dla powierzchni nr 1 ADINA Structures zmieniła ilość elementów

wzdłuż linii nr 5, która łączy powierzchnie 1 oraz 2. ZAPAMIĘTAJ: Na linii „styku”
dwóch powierzchni ilość węzłów ES z każdej strony musi być jednakowa! ADINA
Structures zawsze stara się poprawić nasze błędy w określeniu ilości ES wzdłuż wspólnych
linii.

Skasuj wygenerowaną siatkę.

Ćwiczenie:
Dla powierzchni 1 oraz 2 modelu wygenerować siatkę ES w oparciu o następujący podział
krawędzi:

1. Powierzchnia nr 1: w kierunku u - podział na 5 równych części, w kierunku v –

podział na 7 części z 4-krotnym wzrastaniem (postęp geometryczny) długości
krawędzi ES w kierunku pionowej osi (Z) globalnego układu współrzędnych.

2. Powierzchnia nr 2: w kierunku v – podział na 10 równych części, w kierunku u –

podział na 3 części z 4-krotnym wzrastaniem (postęp geometryczny) długości
krawędzi ES w kierunku poziomej osi (Y) globalnego układu współrzędnych.

Po wygenerowaniu siatki ES zwróć uwagę na używaną przez ADINA Structures

metodę zagęszczania siatki oraz wybór odpowiedniego miejsca dla tej operacji. Według
jakiego kryterium Twoim zdaniem zostało wybrane to miejsce?

Skasuj siatkę.

5.7. Okre

ślenie gęstości oraz generacja siatki ES dla wybranych linii:

Przykład:

Meshing

→ Mesh Density → Line

Wybierz linię nr 1 (domyślna) na liście „Line Number”
Method: „Use Length” (tzn. podstawą dla podziału będą długości stron ES wzdłuż

poszczególnych linii)

Element Edge Length: 0.2, Save
W sposób analogiczny wprowadź zalecane długości krawędzi ES dla pozostałych linii:
linia 2 – długość 0.3, linia 3 – 0.3, linia 4 – 0.4, linia 5 – 0.35, linia 6 – 0.4, linia 7 –

0.15, OK

Wygeneruj siatkę i wizualnie oceń jej jakość. Skasuj siatkę.

Ćwiczenie:

Dla linii 1-7 wprowadź dane oraz wygeneruj siatkę ES. Podział każdej linii jest

następujący:
• linia 1 – 4 jednakowe części

Wprowadzenie do ADINA Structures (część 2)

© I.Rokach 1996-2008

Strona 12

wersja 4.0.5

• linia 2 – 5 jednakowych części
• linia 3 – 6 części, wzrost 2-krotny (postęp aryt.) długości krawędzi w kierunku globalnej osi
Y
• linia 4 – 8 części, wzrost 1.5-krotny (postęp geometryczny) długości krawędzi w kierunku
globalnej osi Z
• linia 5 – 7 części, wzrost 2.5-krotny (postęp aryt.) długości krawędzi w kierunku oddalania
się od środka układu współrzędnych
• linia 6 – 7 jednakowych części
• linia 7 – 5 części, wzrost 2-krotny (postęp geometryczny) długości krawędzi w kierunku
globalnej osi Z

Koniec pracy z ADINA Structures: File

→ Exit.